Geographic Targeting of COVID-19 Testing to Maximize Detection in Los Angeles County

Abstract

Background

Many severe acute respiratory syndrome coronavirus 2 infections have not been detected, reported, or isolated. For community testing programs to locate the most cases under limited testing resources, we developed and evaluated quantitative approaches for geographic targeting of increased coronavirus disease 2019 testing efforts.

Methods

For every week from December 5, 2021, to July 23, 2022, testing and vaccination data were obtained in ∼340 cities/communities in Los Angeles County, and models were developed to predict which cities/communities would have the highest test positivity 2 weeks ahead. A series of counterfactual scenarios were constructed to explore the additional number of cases that could be detected under targeted testing.

Results

The simplest model based on most recent test positivity performed nearly as well as the best model based on most recent test positivity and weekly tests per 100 persons in identifying communities that would maximize the average yield of cases per test in the following 2 weeks and almost as well as the perfect knowledge of the actual positivity 2 weeks ahead. In the counterfactual scenario, increasing testing by 1% 2 weeks ahead and allocating all tests to communities with the top 10% of predicted positivity would yield a 2% increase in detected cases.

Conclusions

Simple models based on current test positivity can predict which communities may have the highest positivity 2 weeks ahead and hence could be allocated with more testing resources.

During the coronavirus disease 2019 (COVID-19) pandemic, infected individuals without access to testing and unaware of infection status may have further transmitted the disease. Therefore, testing is a key disease control strategy. However, from February 2020 to September 2021, it was estimated that only 1 out of 4 severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections in the United States was detected and reported [1].

When cases surge, community testing (eg, free tests available for residents provided by the government partnering with local test providers) may be scaled up to detect as many cases as possible and minimize further transmissions. With limited resources, testing resources are often prioritized to those who are most likely positive (eg, showing symptoms or exposed) [2]. Du et al. [3] formalized test allocation as an optimization problem and showed that more cases could be detected if allocation was optimized based on symptom severity and age group. However, our interest is in prioritizing the communities most likely to have the highest test positivity, as this is the quantity that predicts how many cases will be identified per unit testing effort. Within a jurisdiction, a test allocation strategy pertaining to communities should be developed.

Motivated by the need for an efficient test allocation strategy to identify as many cases as possible under resource constraints, we explored how basic testing data and simple statistical models could be used to inform targeted testing. We used data from cities/communities in Los Angeles (LA) County to develop models to predict test positivity in each city/community 2 weeks ahead. We also hypothesized that targeted testing could detect more cases overall by prioritizing the cities/communities with the highest model-predicted test positivity compared with nontargeted testing.

METHODS

Study Population

LA County is the largest county in the United States by population size and has a total of 346 cities/communities as statistical areas for data collection (hereafter referred to as communities) [4]. We obtained daily testing and vaccination data for each community corresponding to individual residential address from the LA County Department of Public Health. Long Beach and Pasadena were not included in the data because they have their own health departments. The 2018 population estimates were used as denominators for calculating the cumulative incidence per 100 residents and the number of tests per 100 residents [5], while the 2019 population estimates were used to calculate vaccination coverage [6].

Testing Data

All cases were determined using the case definition from The Council of State and Territorial Epidemiologists (CSTE) [7, 8]. A confirmed case could be defined by a positive nucleic acid amplification test result, and a probable case could be defined by a positive diagnostic antigen test performed by a provider certified under the Clinical Laboratory Improvement Amendments [9]. Confirmed (polymerase chain reaction) and probable cases (antigen) were summed together as the total number of positive tests in the data set, which was used as the numerator for computing test positivity. LA County cases included reinfections, defined as a repeat positive ≥90 days after a previous confirmed case. Testing data were compiled from multiple data sources including electronic lab reporting and medical provider reporting. However, at-home and over-the-counter tests were not reported to the Department of Public Health.

Inclusion and Exclusion Criteria

Data from June 13, 2021, to July 23, 2022, were included in the analysis, covering both the Delta and Omicron waves (Supplementary Figure 1). Communities were highly heterogeneous in population sizes (interquartile range [IQR], 3592–41 342; range, 0–220 424). We also excluded communities in the lowest 5% of population sizes (<300 individuals) because of the small number of tests conducted and therefore the highly unstable positivity. In addition, weeks with <50 tests were excluded to avoid extreme values in test positivity, but other weeks with ≥50 tests were included in the same community.

Targeted Testing Strategies

Three hypothetical strategies of geographic targeting for intensified COVID-19 testing were evaluated. Communities were selected for intensified testing based on the following strategies: (1) model-predicted test positivity 2 weeks forward, (2) random selection, or (3) perfect knowledge into the future—that is, the observed test positivity 2 weeks forward (not feasible in practice). For each week, the top 10% of communities with the highest predicted or observed positivity were selected (except for random selection) for intensified testing, with the same percent increase in testing for all the selected communities. We constructed counterfactual scenarios to evaluate the strategies by calculating the additional number of cases detected and number needed to test (NNT) per case detected in the targeted communities (see descriptions below). Model-based geographic targeting was expected to yield more additional cases compared with random selection but fewer cases compared with perfect knowledge into the future.

Statistical Models for Model-Based Geographic Targeting

For the model-based geographic targeting for strategy 1, we developed regression models using the most recent week (t) to predict weekly test positivity for each community 2 weeks ahead (t + 2) and select communities with top 10% predicted positivity for intensified testing. Predictors in the models included (1) test positivity of the most recent week (t), (2) the most recent 3-week average test positivity ($t-2,t-1$ and t), (3) testing rate of the most recent week (weekly tests per 100 persons at t), (4) cumulative proportion of residents (aged 12 years and older) who were fully vaccinated as vaccines were widely available for this group from mid-May 2021 [10], and (5) cumulative proportion of residents who tested positive relative to the population (per 100 persons). Variable definitions are in Supplementary Table 1.

The 3 statistical models were as follows: (1) the “simplest” model with 1 predictor—the most recent positivity ($\text{\%}po{s}_{i,t}$), (2) the “reduced” model with 2 predictors ($\text{\%}po{s}_{i,t}$ and $testsper{100}_{i,t}$), and (3) the “full” model with all predictors. Variables in the reduced model were selected because they were more accessible compared with other variables, while the variable ($\text{\%}po{s}_{i,t}$) in the simplest model was selected because this variable was the strongest single predictor among all variables. All models were also evaluated by replacing the most recent positivity ($\text{\%}po{s}_{i,t}$) with the average positivity over the past 3 weeks ($Avg\text{\%}po{s}_{i,t-2tot}$). To account for the temporal autocorrelation of the residuals, different specifications were tested: (1) ordinary least squares (OLS), (2) second-order autoregressive (AR-2) process, and (3) mixed-effects models with community-specific random intercepts.

Model Development and One-Step Forward Forecasting

A total of 58 weeks of data were used in this analysis. From June 13, 2021, to December 25, 2021 (Delta wave: 28 weeks), data were used for developing the initial models, which were tested on the first week of the Omicron period. One-step forward forecasting was performed by refitting the models every week for the Omicron wave (December 26, 2021, to July 23, 2022: 30 weeks) using all previous data (both Delta and Omicron) to predict 2 weeks forward from each week of testing (Supplementary Figure 1). The Delta- and Omicron-predominant periods were defined based on sequencing results from the California Department of Public Health [11]. The steps in model development and evaluation are outlined in Supplementary Figure 2A.

Model Evaluation

To explore how many additional cases could have been detected under targeted testing, a series of counterfactual scenarios was constructed (Supplementary Figure 2B): (1) for each week t, 10% of communities with the highest predicted positivity 2 weeks ahead ($\text{\%}\widehat{po{s}_{i,t+2}}$ for week $t+2$) were selected; (2) the total number of tests in LA County increased by 1%, and all the additional tests were allocated to the selected communities in $t+2$, such that all the selected communities had tests increased by a common multiplier $m\text{\%}$ compared with tests in t; (3) assuming that positivity is unaffected by the relatively small increase in testing, the hypothetical number of cases could be modeled by multiplying the observed test positivity in $t+2$ with the hypothetical number of tests allocated in step 2. The total number of cases in LA County 2 weeks ahead is given by, for targeted communities j and untargeted communities i, ${\mathrm{\Sigma }}_j(100+m)\text{\%}\cdot \text{\%}po{s}_{j,t+2}\cdot test{s}_{j,t}+{\mathrm{\Sigma }}_i\text{\%}po{s}_{i,t+2}\cdot test{s}_{i,t}$. The models were evaluated based on 2 metrics: (1) the total number of additional cases 2 weeks ahead, ${\mathrm{\Sigma }}_{j}m\text{\%}\cdot \text{\%}po{s}_{j,t+2}\cdot test{s}_{j,t}$, and (2) the NNT for each case, $\frac{{\mathrm{\Sigma }}_{j}test{s}_{j,t+2}}{{\mathrm{\Sigma }}_{j}case{s}_{j,t+2}}$, in the selected communities j.

Evaluation of Targeted Testing Strategies

For the other 2 strategies (ie, random selection and perfect knowledge of future positivity), the same evaluation procedures were applied as with the model-based strategy. Specifically, we used the 2 metrics defined above to evaluate the 3 testing strategies for each of the 30 weeks from December 26, 2021, to July 23, 2022. We expected that random allocation of additional tests (ie, 10% of the communities were randomly selected for intensified testing) would be the worst-case scenario that gave a lower bound on the number of additional cases that could be detected, while selecting the communities based on the perfect knowledge of the future test positivity would give an upper bound. The best model was the model that can maximize the number of additional cases (defined in metric 1) given the number of additional tests. Analyses were conducted using R 3.6.2 (R Foundation for Statistical Computing, Vienna, Austria) [12]. Data and R codes are available at https://github.com/c2-d2/LAC_testing.

RESULTS

Descriptive Statistics

A total of 295 communities were included in the training set (the Delta period) and 303 in the validation set (the Omicron period). On average, each community administered 8 tests weekly per 100 persons for the Delta period and 9 tests weekly per 100 persons for the Omicron period. Weekly positivity was 2.8% on average for the Delta period and 7.8% for the Omicron period.

Model Predictions

Current positivity ($\text{\%}po{s}_{i,t}$) and 3-week average positivity ($Avg\text{\%}po{s}_{i,t-2tot}$) were the strongest predictors for positivity 2 weeks ahead (Supplementary Table 2). Supplementary Figure 3 shows estimates from all models that include $\text{\%}po{s}_{i,t}$ (and $Avg\text{\%}po{s}_{i,t-2tot}$ in Supplementary Figure 4). From December 26, 2021, to July 23, 2022 (the Omicron wave), the simplest model with test positivity alone ($\text{\%}po{s}_{i,t}$) correctly predicted ∼48% of communities with top 10% positivity 2 weeks ahead. During the model evaluation period, the best model that maximized the average additional cases was the mixed-effects model with $\text{\%}po{s}_{i,t}$ and $testsper{100}_{i,t}$ as predictors, but this model performed only slightly better than the simplest model by successfully predicting ∼49% of the communities. In general, predictive performances were similar across models (Supplementary Figure 5).

Additional Cases Under Targeted Testing

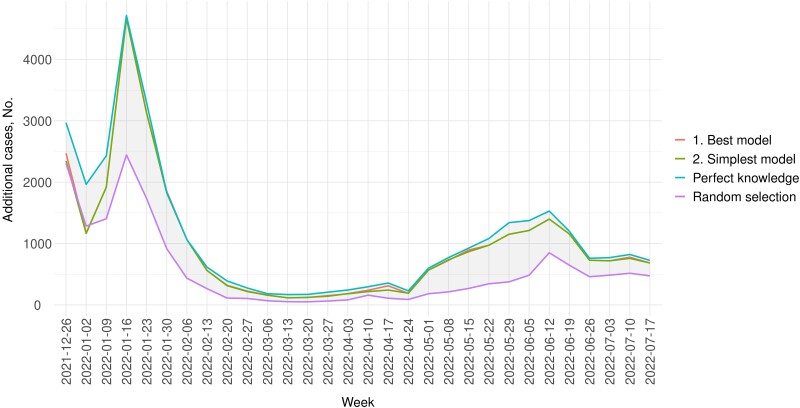
In the counterfactual scenario, testing was increased for the next 2 weeks in communities with the top 10% predicted positivity. Throughout the testing period, 2% more cases could be detected in a week on average if testing were increased by 1%, and all the additional tests were allocated to the selected communities. In general, the number of additional cases was greater in weeks with higher positivity (Figure 1). For example, 4000 more cases could be detected in the week of January 16, 2022, if 1% more tests (n = 17 200) were performed. Of note, in Figure 1, the curves for the simplest and best models are indistinguishable in most weeks, slightly below the best possible model performance (using perfect knowledge of future positivity).

Figure 1.

Number of additional cases in a week under the counterfactual scenario where tests were increased by 1% in LA County compared with 2 weeks back, with all additional tests allocated to communities in the top 10% of predicted positivity. The blue line (the uppermost line) represents the number of additional cases if communities were ranked based on perfect knowledge of future test positivity, $\text{\%}po{s}_{i,t+2}$. While requiring knowledge of the future and thus not practicable, this line serves as the upper bound of the best possible prediction. The purple line represents the yields if communities were randomly selected and serves as the lower bound. The red and green lines represent the number of additional cases that could be detected if communities were selected based on the best and the simplest models, respectively. Test positivity was based on testing data from LA County Department of Public Health.

Compared with selecting communities based on perfect knowledge of future positivity, $\text{\%}po{s}_{i,t+2}$, the simplest model using most recent positivity, $\text{\%}po{s}_{i,t}$, could detect as many as 89% of achievable additional cases (Table 1). Table 1 shows the performance of the simplest and best models. Supplementary Table 3 shows results for all models.

Table 1.

Mean Number of Additional Cases and Number Needed to Test in the Selected Communities Under Different Test Allocation Strategies, December 26, 2021, to July 23, 2022

	No. of Additional Cases		NNT
	Mean No. of Additional Cases	Relative to Perfect Knowledge of Future Positivity	Mean NNT	Relative to Perfect Knowledge of Future Positivity
Simplest model most recent positivity ($\mathit{\text{\%}}\mathit{p}\mathit{o}{\mathit{s}}_{\mathit{i},\mathit{t}}$) only (OLS)	985	0.887	19.3	1.263
Best model most recent positivity ($\mathit{\text{\%}}\mathit{p}\mathit{o}{\mathit{s}}_{\mathit{i},\mathit{t}}$) + most recent tests per 100 ($\mathit{t}\mathit{e}\mathit{s}\mathit{t}\mathit{s}\mathit{p}\mathit{e}\mathit{r}{100}_{\mathit{i},\mathit{t}}$) (mixed-effects model with community-specific intercepts)	994	0.895	19.0	1.241
Perfect knowledge of future positivity ($\mathit{\text{\%}}\mathit{p}\mathit{o}{\mathit{s}}_{\mathit{i},\mathit{t}+2}$)	1110	1.000	15.3	1.000
Random selection	565	0.509	43.8	2.864

Abbreviations: NNT, number needed to test; OLS, ordinary least squares.

Reduction in NNT in the Communities Under Intensified Testing

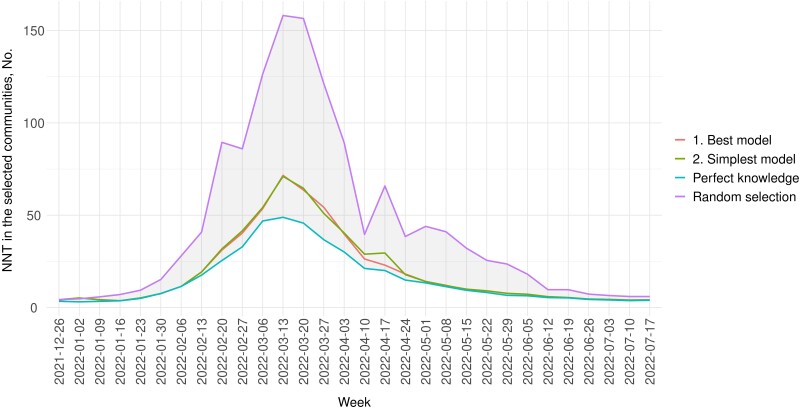
Targeting communities with top 10% predicted positivity could reduce the NNT in those communities. If tests were increased by 1% in LA County and all tests were allocated to selected communities under the simplest or the best model, NNT in the selected communities could be reduced by ∼50% on average compared with randomly selecting the communities for increased testing (Figure 2). Note that this NNT considers the 10% selected communities with increased testing only. Figure 2 and Supplementary Table 3 show the NNT under different test allocation strategies.

Figure 2.

NNT in the selected communities under intensified testing, December 26, 2021–July 23, 2022. The blue line represents NNT in the targeted communities selected based on perfect knowledge of future test positivity, $\text{\%}po{s}_{i,t+2}$, which serves as the lower bound for NNT (ie, the most efficient scenario). The purple line (the uppermost line) represents the expected NNT under random selection of communities for targeted testing (ie, the least efficient) and serves as the upper bound. Abbreviation: NNT, number needed to test.

DISCUSSION

We found that test positivity was temporally correlated—high positivity in the most recent week indicated a high positivity 2 weeks ahead. Through our counterfactual scenarios, we showed that by targeting communities with high positivity in the most recent week, detected cases could increase by 1% to 3% 2 weeks later, on average about 2% given a 1% increase in testing, meaning that these simple approaches can roughly double the yield of additional tests. The simplest model using test positivity alone performed as well as the best model in finding more positive cases and nearly as well as perfect knowledge of future positivity. This simple method could inform a timely prioritization of testing resources to identify cases and mitigate future transmissions. By defining the goal of identifying communities with high future test positivity, we do not make the claim that test positivity is a good indicator of actual disease burden, as this relationship has been shown to be quite dependent on multiple factors; rather, we optimize for test positivity because it is the quantity that predicts the number of cases that can be identified per unit testing effort.

This approach is robust to changes of positivity during different phases of an epidemic. That the communities with the highest positivity in the most recent week were likely to have comparatively high positivity in the next 2 weeks was true in both cases when test positivity for overall LA County was on an uptrend or a downtrend. To illustrate this phenomenon, Supplementary Figure 6 shows the epidemic curves for communities that had the highest cumulative percent testing positive. At the start of the Omicron wave, positivity increased exponentially, but it declined slowly after the peak. Therefore, communities with the highest positivity were likely to continue to top the list in terms of positivity in the next few weeks, even when overall LA County positivity was on a downtrend. If positivity continued to decrease in the next few weeks in a community being targeted, due to either increased testing or reduced incidence, then that area would eventually be dropped from the list as the model would pick up some other community with a higher predicted positivity. The model corrected itself by making new predictions every week and updating the list based on the most recent data.

The simple method is ready to use by any local public health department. This method does not require modeling expertise or complex inaccessible data and provides quick and useful predictions on where the positivity could be highest in the next 2 weeks. However, test allocation strategies informed by complex dynamic transmission models that predict the full epidemic trajectory would require detailed data for model parameterization. Empirical data are often unavailable to account for factors including vaccination coverage, frequency of breakthrough infections, waning immunity, and compliance with mitigation measures. Using this simple method, nearly 90% of additional cases could be detected when compared with perfect knowledge of future positivity. In this case, it is difficult to imagine that the resources devoted to more elaborate approaches would be justified for a further 10% improvement in outcome, which is the upper bound based on perfect knowledge of the future. In addition, this simple approach could substantially improve test efficiency, as the targeted areas based on the simplest model had half the NNT of randomly selected areas. More generally, NNT is a useful measure of test efficiency and could be widely used to inform test allocation strategy.

There is a trade-off between accuracy and the prediction horizon—the longer the prediction horizon, the less accurate the prediction. Out of logistical considerations, the models were used to predict positivity 2 weeks ahead, as it might take ≥2 weeks for the implementation team to increase testing in a community. Model performance decreased slightly when the prediction horizon increased to 3 weeks, but the model would still be useful for informing test allocation (Supplementary Figure 5, Supplementary Table 3).

This study has policy implications beyond the COVID-19 pandemic, and our model could be applied in other infectious disease outbreaks. In general, targeted testing is needed to save resources by prioritizing tests to those with the greatest needs and to maximize the efficiency of testing [13]. For other diseases like HIV where testing services are limited in some countries, targeted testing is also recommended by prioritizing communities with high HIV positivity [14]. We proposed and verified a straightforward approach to target geographical communities using a relatively minimal set of data (eg, the number of tests per 100 persons and positivity by statistical areas) to prioritize testing for transmissible diseases.

If identifying subpopulations with inadequate testing, finer data disaggregated by age, race and ethnicity, or other demographic characteristics would be needed to detect any disparity in access to tests or test positivity [15]. If such data were available, the test allocation strategy could take any disparity into account and address undertesting by looking at test positivity in those subgroups. An ecological analysis on testing trends by ZIP code in New York City showed the total number of tests per capita was higher in ZIP codes with higher percentages of the White population during the early stage of the pandemic (March 2 to April 6, 2020) [16]. Since August 2020, all certified laboratories are required to report demographics for every test [17], but those fields may have a high proportion of data missing unless there is a proper enforcement of the mandate [15].

This study has some limitations. The first limitation is that we did not include at-home or over-the-counter tests as they were not reported to the Department of Public Health. Impacts of the unreported tests depend on positivity and how well the positivity correlates with community testing results. The model evaluation period from December 26, 2021, to July 23, 2022, covered a time period in which at-home tests were more widely available, and the models performed well during that period. If temporal correlation between positivity in the communities is weakened by the wide availability of at-home tests over the course of the pandemic, we would expect the efficiency of the targeting strategy to decrease. Therefore, this approach is expected to be more useful when at-home testing is rare or in settings where the testing rate is more stable over time. Second, we assumed that positivity was unaffected by the number of tests. This assumption was plausible when tests and cases increased by a small amount compared with the large number of untested infections. A 1% increase for testing in LA County was equivalent to a 12%–45% increase of testing in the top 10% communities varying by week. We were not able to test this assumption empirically (ie, to test whether the 1% increase in tests was large enough to bring down the positivity). In Supplementary Figure 7, percent change in positivity is plotted against percent change in tests (compared with the previous weeks) for communities with top 10% cumulative incidence. However, in the majority of weeks from December 26, 2021, to July 23, 2022, test positivity did not decline when the number of tests increased from 0% to 50% compared with the previous week (upper bound corresponding to 1% increase in overall LA County). In practice, if positivity decreased as a result of intensified testing, the chance of the community being targeted in the coming week would also decrease. Ultimately, an increase in tests should be determined by resource availability, and here the 1% increase served as an example only. Third, we did not explore any disparity in testing and positivity across race, ethnicity, or socioeconomic status. Our simple goal was to predict in which communities the additional tests would yield the most positive cases. Further analysis would be needed to identify any systematic disparity in testing and to guide test allocation. Importantly, our model is just one piece of information that can be used to inform decisions and may be considered in conjunction with other factors such as community vulnerability and high-priority population subgroups. Future research could consider how to incorporate these additional factors into quantitative approaches. Fourth, we did not consider the spatial correlation of the positivity between communities. However, given the good performance of the model with test positivity as the sole predictor (the simplest model), spatial correlation may not add much to the predictive performance. Another limitation is that the location indicator of each test corresponded to the residential address of each individual, rather than the testing site. This indicator added complexity to implementing targeted testing, as the communities where people lived might not be the same communities as were tested. Finally, we excluded small communities with a population size below the 5th percentile (ie, <300) and weeks with <50 tests. However, in practice, health authorities should look into reasons for the high positivity in those geographic areas, and more tests may be needed.

CONCLUSIONS

We showed that simple models based on current positivity and proportion of tests relative to population size are useful for identifying communities with high positivity in the next 2 weeks. In particular, more tests can be allocated to communities with the highest current positivity. Using this approach to allocate tests could detect more cases and save resources. Although targeting communities with the highest predicted positivity is shown to be an efficient strategy, health authorities should be cognizant of the community vulnerability and any systematic disparity within the communities when allocating tests.

Supplementary Data

Supplementary materials are available at Open Forum Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.