Cage effects control the mechanism of methane hydroxylation in zeolites

Abstract

Catalytic conversion of methane to methanol remains an economically tantalizing but fundamentally challenging goal. Current technologies based on zeolites deactivate too rapidly for practical application. We found that similar active sites hosted in different zeolite lattices can exhibit markedly different reactivity with methane, depending on the size of the zeolite pore apertures. Whereas zeolite with large pore apertures deactivates completely after a single turnover, 40% of active sites in zeolite with small pore apertures are regenerated, enabling a catalytic cycle. Detailed spectroscopic characterization of reaction intermediates and density functional theory calculations show that hindered diffusion through small pore apertures disfavors premature release of CH₃ radicals from the active site after C-H activation, thereby promoting radical recombination to form methanol rather than deactivated Fe-OCH₃ centers elsewhere in the lattice.

Methane is an abundant source of energy and a potent greenhouse gas. Its direct conversion to methanol under mild conditions remains an economically tantalizing but fundamentally challenging goal of modern chemistry. Iron active sites in zeolites and enzymes have attracted considerable attention because of their capacity to hydroxylate the otherwise largely inert (104 kcal/mol) C-H bond of methane rapidly at room temperature (1–5). In iron-containing zeolites (Fe-zeolites), prior studies have shown that this reaction occurs at a mononuclear square pyramidal high-spin (S = 2) Fe(IV)=O intermediate [α-Fe(IV)=O] that is activated for H-atom abstraction by a constrained coordination geometry enforced by the zeolite lattice (6–9). α-Fe(IV)=O is generated via O-atom transfer from N₂O to an S = 2 square planar Fe(II) precursor, α-Fe(II). At low temperature (<200°C), α-Fe(IV)=O reacts in a noncatalytic fashion with CH₄ (10). Catalytic oxidation of CH₄ is proposed to occur at higher temperatures but with poor selectivity (<10%) for methanol, and on undefined active sites (10, 11). The absence of a closed catalytic cycle for selective methanol synthesis represents a critical barrier to scale-up (4). Mechanistic insight into catalyst deactivation is limited, and despite intensive effort, no strategy or design principle has emerged to mediate this challenge. In nature, many metalloenzymes—including soluble methane monooxygenase (sMMO) (3, 5, 12)—have evolved active-site pockets that exert precise control over hydrocarbon substrate radicals, shutting down deactivating mechanisms that involve radical escape, and instead guiding radical recombination to selectively form R-OH or R-X bonds (3, 12–14). Translating the active-site pocket concept to small molecules (15–18) and microporous materials (19–23) is an appealing strategy to improve catalysis. Zeolite micropore effects have been shown (or proposed) to tune reactivity and/or selectivity across a number of model reactions (9, 20, 24–27). However, micropore effects enabling precise control over the fate of small reactive intermediates, as with the active-site pocket of sMMO, remain elusive. Here, we demonstrate that steric effects from a constricted pore aperture act as a cage, thereby controlling the extremely reactive methyl radical generated by methane C-H activation. A radical recombination pathway for direct methanol synthesis analogous to the sMMO pathway can then ensue.

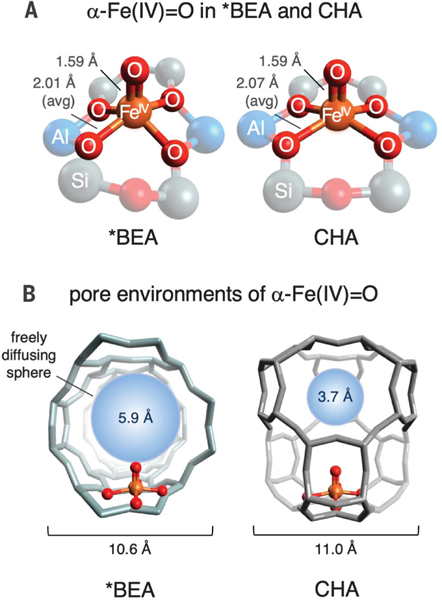
While evaluating Fe active sites in a number of zeolite lattices, we discovered a marked difference in the methane reactivity of α-Fe(IV)=O sites stabilized in zeolite beta (*BEA) (6, 7) and chabazite (CHA) (8). These active sites have highly similar first coordination spheres (Fig. 1A), as reflected in their ⁵⁷Fe Mössbauer spectra, which nearly overlay (Fig. 2A) (7, 8). However, there are differences in the local pore environments of these active sites (Fig. 1B). In *BEA, α-Fe(IV)=O is accessed through large channels defined by 12-membered rings of SiO₄ tetrahedra. In CHA, α-Fe(IV)=O is located in a cage-like pore environment. Although the dimensions of the CHA cage are similar to those of the *BEA pore, substrates must pass through a constricted eight-membered ring aperture to enter the cage (7, 8, 28). The maximum van der Waals diameter of a molecule that can freely diffuse out of this constricted aperture is 3.7 Å, versus 5.9 Å for *BEA (Fig. 1B). Because the van der Waals diameter of CH₄ is larger than 3.7 Å [4.1 to 4.2 Å (29)], diffusion of substrate through the pore aperture should be hindered in CHA but not *BEA.

Fig. 1. Local environments of α-Fe (IV)=O sites in *BEA and CHA.

(A) Comparison of first coordination spheres, with bond lengths from spectroscopically calibrated DFT models (6–8). (B) Comparison of α-Fe(IV)=O pore environments in *BEA and CHA. For each lattice, a freely diffusing sphere of maximal size is included for reference.

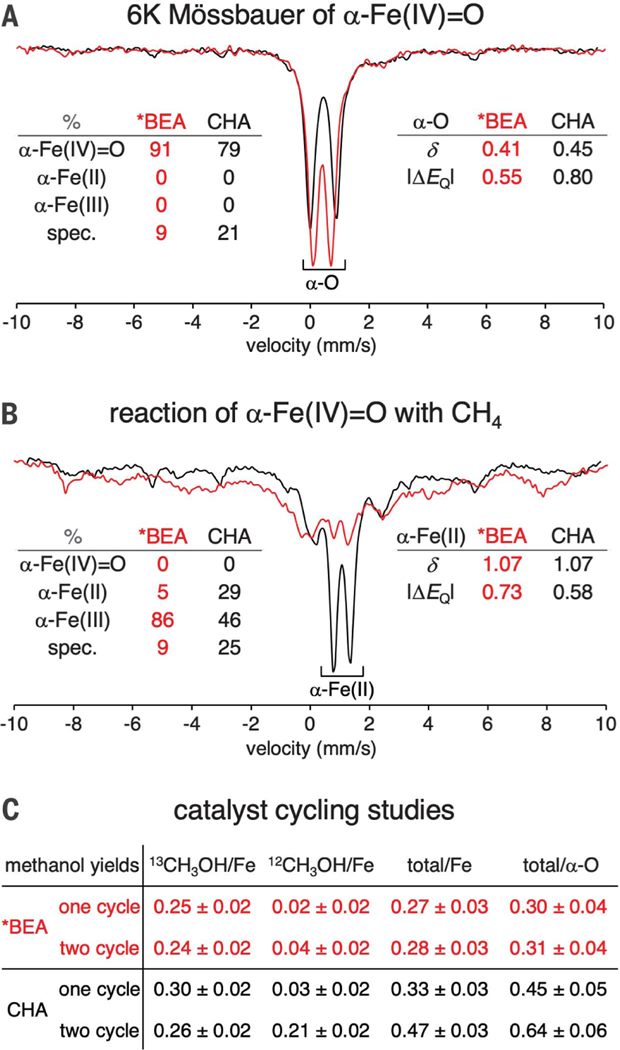
Fig. 2. Effect of lattice topology on active-site regeneration.

(A) Normalized Mössbauer spectra of N₂O-activated Fe-*BEA (red) and Fe-CHA (black) at 6 K. Spectral contributions from each Fe oxidation state are quantified at the left (spec. = spectator components that do not contribute to reactivity). Parameters of the α-Fe(IV)=O components are indicated at the right. (B) Normalized Mössbauer spectra of N₂O-activated Fe-*BEA (red) and Fe-CHA (black) reacted with CH₄ at 300 K and then cooled to 6 K for data collection. Spectral contributions from each oxidation state of the active site are quantified at the left. Parameters of the α-Fe (II) components are indicated at the right. See fig. S1 for details of quantification. The given quantifications have an error of ±5%. δ = isomer shift, ΔE_Q = quadrupole splitting (values given in mm/s). (C) Comparison of methanol yields extracted after one reaction cycle with ¹³CH₄ versus two cycles (¹³CH₄, then ¹²CH₄). Yields based on initial α-Fe(IV)=O content make use of Mössbauer quantifications shown in fig. S2.

We exposed α-Fe(IV)=O active sites in compositionally similar *BEA (Si/Al = 12.3, 0.30 wt% Fe) and CHA (Si/Al = 8.9, 0.24 wt% Fe) to 1 atm of methane at room temperature, and used Mössbauer spectroscopy to track the state of the iron active sites under single-turnover conditions. The low iron loadings used in these samples exclude the presence of multiple Fe active sites in a single CHA cage. As shown by the data in Fig. 2B, there is a remarkable difference in the state of the iron active sites in the post-reaction materials. In *BEA (red trace), a broad distribution of spectral intensity is observed, reflecting the dominant contributions from deactivated, partially oxidized active sites (see below and fig. S1 for assignments). In this lattice, only a small fraction of α-Fe(II) is regenerated (~4%). In contrast, for CHA (Fig. 2B, black trace), a large fraction of α-Fe(II) is regenerated [37 ± 5% yield based on α-Fe(IV)=O], potentially enabling further turnover. To evaluate this possibility, we performed reactivity studies including a second reaction cycle. Samples of Fe-*BEA (Si/Al = 9.4, 0.26 wt% Fe) and Fe-CHA (Si/Al = 8.9, 0.24 wt% Fe) were subjected to either one or two cycles of N₂O activation and room-temperature CH₄ reaction, and the products were desorbed and quantified by on-stream mass spectrometry. (We note that this method results in a modest systematic underestimate of MeOH yields; see supplementary materials.) To parse the desorbed methanol into contributions from different reaction cycles, we used ¹³CH₄ for the first reaction cycle and ¹²CH₄ for the second (see Fig. 2C and supplementary materials). These reactions were also monitored by Mössbauer spectroscopy (fig. S2). The one-cycle yield of CHA (0.33 ± 0.03 MeOH/Fe) is similar to that of *BEA (0.27 ± 0.03 MeOH/Fe). However, after accounting for the different α-Fe(IV)=O concentrations of the samples used for these reactivity studies (74 ± 5% of Fe for CHA, 91 ± 5% for *BEA see fig. S2), the one-cycle yield of CHA was found to be 50 ± 25% greater than that of *BEA. A more pronounced difference was observed in the two-cycle yields. For *BEA, very little ¹²CH₃OH was generated during the second reaction cycle, and the total yield of the two-cycle reaction was the same (within error) as for the one-cycle reaction. This is consistent with the nearly complete deactivation of *BEA observed by Mössbauer spectroscopy after a single turnover (Fig. 2B). For CHA, a large amount of ¹²CH₃OH was generated during the second reaction cycle, and as a result, the total yield of the two-cycle reaction was 40 ± 20% higher than that of the one-cycle reaction. This correlates well to the 37 ± 5% regeneration of α-Fe (II) observed by Mössbauer spectroscopy (Fig. 2B). Finally, accounting for the different α-Fe (IV)=O concentrations of these CHA and *BEA samples, the two-cycle yield of α-Fe(IV)=O in CHA was approximately twice that of *BEA.

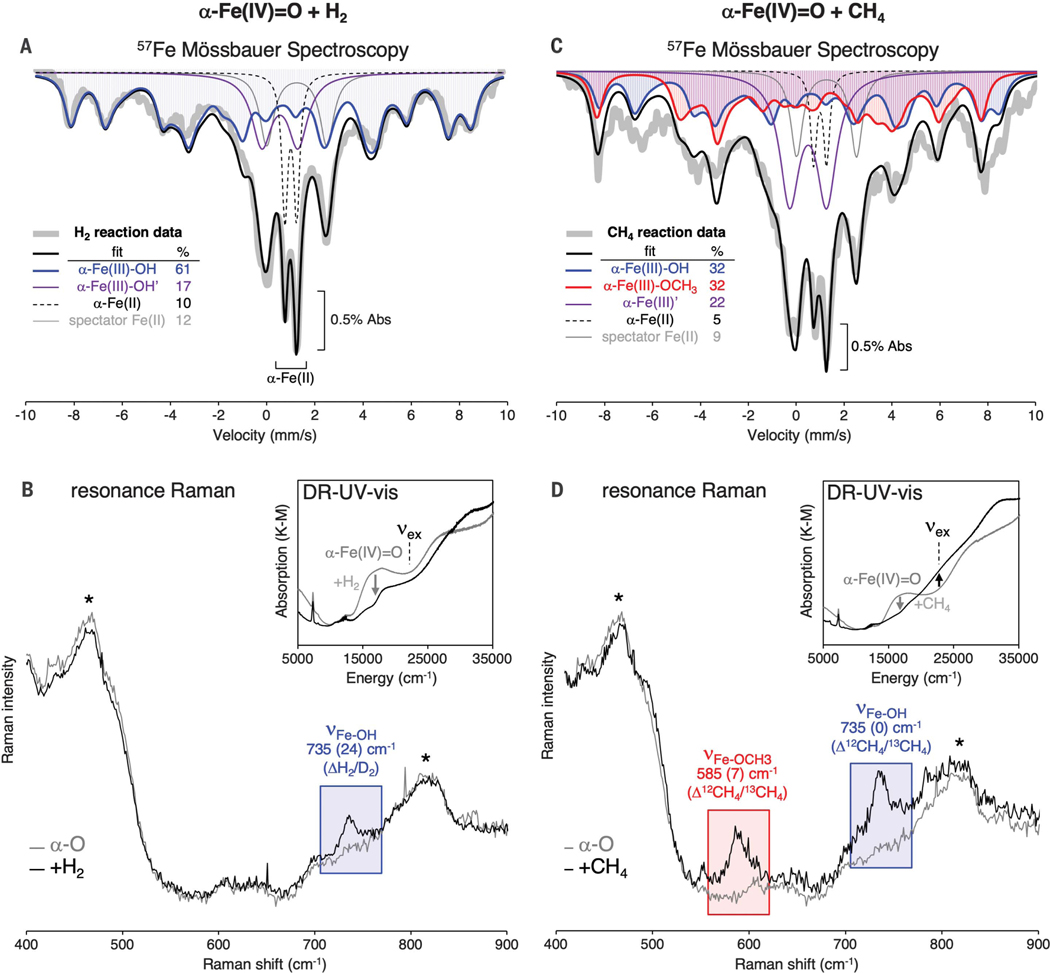
To understand the mechanistic origin of the differences in reactivity between CHA and *BEA, we performed additional spectroscopic experiments to characterize the Fe(III) components present in Fe-*BEA after reaction with CH₄, where only 4% of the α-Fe(II) active site is regenerated. The reaction of H₂ with α-Fe(IV)=O in *BEA was first studied as a reference, as we anticipated this would form a single Fe(III) species: the α-Fe(III)-OH product of H-atom transfer to α-Fe(IV)=O. From Mössbauer spectroscopy, this reaction generates a new majority component that exhibits hyperfine structure in the absence of an external magnetic field (Fig. 3A, blue trace). The signature is consistent with a mononuclear S = 5/2 Fe(III) center with a small zero-field splitting (quadrupole splitting ΔE_Q = −1.6 ± 0.1 mm/s, isomer shift δ = 0.5 ± 0.1 mm/s, axial zero field splitting |D| = 0.3 ± 0.2 cm⁻¹, rhombicity E/D = 0.25 ± 0.05; see supplementary materials). The high population of this component (61% of Fe) indicates that it originated from α-Fe(IV)=O [initially 74% of total Fe; ~80% of α-Fe(IV)=O was converted to this Fe(III) product; see fig. S1]. A quadrupole doublet with an isomer shift and quadrupole splitting identical to α-Fe(III)-OH was also generated (17% of Fe; Fig. 3A, purple trace). On the basis of correlation to post-CH₄ reaction samples (see below), we assign this doublet to a rapidly relaxing α-Fe(III)-OH site [α-Fe(III)-OH′].

Fig. 3. Identification of Fe(III) species after H₂ and CH₄ reactions with Fe-*BEA.

(A) ⁵⁷Fe Mössbauer spectrum of α-Fe(IV)=O in Fe-*BEA at 6 K. The blue trace shows the Mössbauer signal from the α-Fe(III)-OH product of H-atom transfer to α-Fe(IV)=O. (B) Resonance Raman (rR) spectroscopy (v_ex = 21,800 cm⁻¹) of α-Fe(IV)=O before (gray trace) and after (black trace) reaction with H₂ in the Fe-*BEA lattice. Peaks marked with an asterisk are (nonresonant) Raman vibrations of the zeolite lattice. Inset: DR-UV-vis spectrum before (gray trace) and after (black trace) the reaction. (C) ⁵⁷Fe Mössbauer spectrum of α-Fe(IV)=O in Fe-*BEA at 6 K. The blue trace shows the Mössbauer signal from α-Fe(III)-OH; the red trace shows the Mössbauer signal from α-Fe(III)-OCH₃. (D) rR spectroscopy (v_ex = 21,800 cm⁻¹) of α-Fe(IV)=O before (gray trace) and after (black trace) reaction with CH₄ in the Fe-*BEA lattice. Inset: DR-UV-vis spectra before (gray trace) and after (black trace) the reaction.

Resonance Raman (rR) experiments were performed to further characterize the structure of this majority Fe(III) product. As shown in the inset for the H₂ reaction in Fig. 3B, the reaction of α-Fe(IV)=O with H₂ in *BEA results in a change in its diffuse reflectance ultraviolet/visible (DR-UV-vis) spectrum, including the loss of the characteristic 16,900 cm⁻¹ absorption feature of α-Fe(IV)=O (gray trace). Tuning a laser to the 22,000 cm⁻¹ shoulder of the resonance of the sample after H₂ reaction enhances a single Raman vibration at 735 cm⁻¹ (Fig. 3B, blue highlight; see fig. S3A for rR profile). This vibration shifts down by 24 cm⁻¹ using D₂ as the substrate (fig. S3B). The frequency and isotope sensitivity of the 735 cm⁻¹ vibration are consistent with the stretching mode of a terminal Fe(III)-OH bond (30), and we assign this band to the α-Fe(III)-OH product of H-atom abstraction from H₂. The experimentally defined spectroscopic features of α-Fe(III)-OH were reproduced by density functional theory (DFT) calculations (fig. S4A).

Next, we considered the reaction of α-Fe(IV)=O with CH₄ in *BEA. As shown in the inset of Fig. 3D, the 16,900 cm⁻¹ absorption band of α-Fe(IV)=O (gray trace) is eliminated upon reaction with CH₄, and new intensity grows in at ~22,000 cm⁻¹ (black trace). Tuning a laser to this absorption resonance enhances a 735 cm⁻¹ vibration assigned to α-Fe(III)-OH (from correlation to the above results from the H₂ reaction), along with an additional vibration at 585 cm⁻¹ (Fig. 3D, red highlight; see rR profile in fig. S3). Unlike the 735 cm⁻¹ band, this mode shows a ¹²C/¹³C isotope sensitivity (Δ¹²CH₄/¹³CH₄ = 7 cm⁻¹; see fig. S3). It therefore involves motion of a methane-derived ligand. Its frequency and isotope sensitivity are consistent with the stretching mode of an Fe(III)-OCH₃ species. This observation indicates that free methyl radicals generated during C-H activation of CH₄ in *BEA go on to recombine with remote α-Fe(IV)=O sites to form deactivated α-Fe(III)-OCH₃ species. This is consistent with previous identification of -OH and -CH₃ fragments in Fe-zeolites that have reacted with methane (31, 32); however, these fragments were not shown to be related to the iron active sites. The experimentally defined spectroscopic features of α-Fe(III)-OCH₃ are reproduced by DFT calculations shown in fig. S4B.

For the reaction of α-Fe(IV)=O in Fe-*BEA with CH₄ (Fig. 3C), hyperfine features are also observed by Mössbauer spectroscopy, but with a different intensity distribution relative to the sample that reacted with H₂. This observation parallels the rR data, showing that two Fe(III) species are present after the CH₄ reaction: α-Fe(III)-OH and α-Fe(III)-OCH₃. Fitting the broad distribution of Fe(III) hyperfine intensity in the Mössbauer spectrum (Fig. 3C) requires a contribution from α-Fe(III)-OH (blue trace) as well as a second hyperfine-split component that we assign as α-Fe(III)-OCH₃ (red trace). The parameters of α-Fe(III)-OCH₃ are similar to those of α-Fe(III)-OH, but with a smaller E/D (ΔE_Q = −1.6 ± 0.1 mm/s, d = 0.5 ± 0.1 mm/s, |D| = 0.3 ± 0.2 cm⁻¹, E/D = 0.15 ± 0.05; see supplementary materials). The α-Fe(III)-OH and α-Fe(III)-OCH₃ components are present in equal amounts (each 32% of Fe). In addition, a quadrupole doublet representing 22% of Fe and identical to that identified in the H₂ reaction appears (Fig. 3C, purple trace). Given the initial 91% of Fe as α-Fe(IV)=O, this 22% component must derive from α-Fe(IV)=O. This component likely derives from rapidly relaxing α-Fe(III)′ sites, encompassing both α-Fe(III)-OH and α-Fe(III)-OCH₃, leading to both a hyperfine component and a doublet component in their Mössbauer spectra. Together, the α-Fe(III) components sum to 86 ± 9% of Fe in the sample, which is within error of the 91 ± 5% of α-Fe(IV)=O initially present.

Mössbauer and rR data from Fe-*BEA therefore reflect the near-quantitative conversion of α-Fe(IV)=O to a 1:1 mixture of α-Fe(III)-OCH₃ and α-Fe(III)-OH after a single turnover. Parallel spectroscopic data from α-Fe(IV)=O in CHA after reaction with CH₄ show that α-Fe(III)-OCH₃ and α-Fe(III)-OH sites do form in this lattice after reaction with CH₄, but in much lower concentrations relative to *BEA: Only ~60% of the total α-Fe(IV)=O in CHA reacts with CH₄ to form α-Fe(III)-OCH₃/α-Fe(III)-OH (figs. S1 and S5), with the remaining ~40% re-generating α-Fe(II). Because one radical escape event produces two Fe(III) centers [one equivalent each of α-Fe(III)-OH and α-Fe(III)-OCH₃], rebound is favored over cage escape by a ratio of ~4:3 in CHA at room temperature. This model yields two key predictions: (i) The single-cycle yield of CHA should be ~40% greater than that of *BEA, and (ii) the two-cycle yield of CHA should be ~40% greater than the one-cycle yield. Both predictions are borne out in the MeOH yields tabulated in Fig. 2C, further supporting the model of competing cage escape and radical rebound mechanisms.

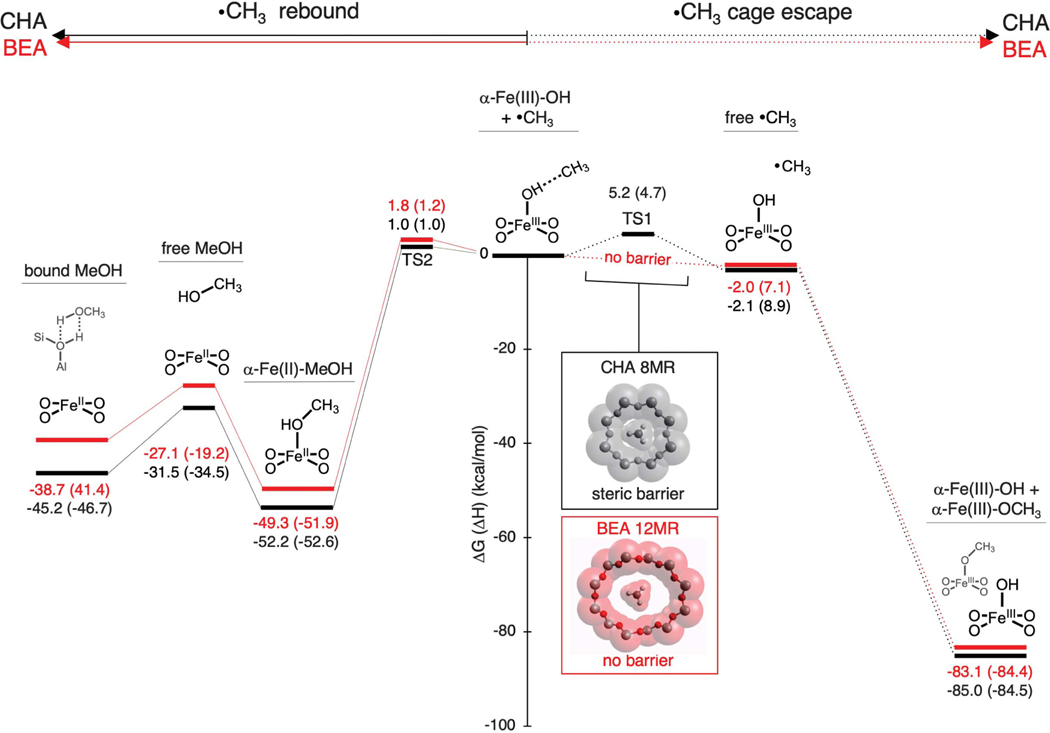
Mössbauer and rR data show that the similar α-Fe(IV)=O sites in CHA and *BEA give different Fe products after their single-turnover reaction with methane. In *BEA, exclusively deactivated Fe(III) species are observed, whereas in CHA, a significant fraction of the active sites is returned to the reduced, catalytically active Fe(II) state. We were interested in correlating this difference in reactivity to the structures of the *BEA and CHA lattices. Because the van der Waals diameter of CH₄ is larger than the 3.7-Å pore aperture of CHA, (29) we performed DFT calculations to evaluate whether the small pore of CHA gates methyl radical escape from the active site (Fig. 4, right path), thus enhancing methanol synthesis through direct radical rebound on the active site (Fig. 4, left path). Cage escape in *BEA and CHA was modeled via passage of CH₃ through a 12MR and an 8MR, respectively (the rings that gate egress from the active site in each zeolite). Proceeding from spectroscopically validated models of α-Fe(III)-OH (fig. S4A) in a van der Waals complex with CH₃ (Fig. 4, center), our calculations indicate a striking difference between the cage escape pathways for *BEA and CHA (Fig. 4, right path). For the large 12MR channel of *BEA, there is no barrier to CH₃ radical escape (Fig. 4, lower inset). The liberated CH₃ radical is then free to react with a remote α-Fe(IV)=O center, forming α-Fe(III)-OCH₃ and leaving behind one equivalent of α-Fe(III)-OH (as observed experimentally in Fig. 3). This reaction is calculated to be highly exergonic (ΔG = −85 kcal/mol), proceeding without an activation barrier. The absence of a rate-limiting barrier for cage escape explains the experimental observation of exclusively ferric products in *BEA. For CHA, on the other hand, there is an activation barrier of 5.2 kcal/mol for CH₃ escape (TS1) through the constricted 8MR pore of the CHA cage (Fig. 4, upper inset). Given the experimentally determined 3:4 branching ratio for cage escape versus radical recombination, this activation barrier is likely overestimated.

Fig. 4. Comparison of reaction coordinates for *BEA (red) and CHA (black) after H-atom abstraction.

The reaction coordinates for radical rebound (left) and cage escape (right) are shown. Free energy changes (ΔG at 300 K, ΔH in parentheses) are given relative to the α-Fe(III)-OH···CH₃ van der Waals complex produced during H-atom abstraction from CH₄ by α-Fe(IV)=O. The insets show how the van der Waals surface of an 8MR of CHA compares to that of a 12MR of *BEA, illustrating how the constricted CHA 8MR creates a steric barrier for radical escape from the CHA active site (TS1).

Although the cage escape pathways for *BEA and CHA differ, their radical rebound mechanisms are similar (Fig. 4, left path): In both cases, radical rebound proceeds with a low barrier (TS2_, ΔG^‡ = 1 to 2 kcal/mol) and is highly exergonic, forming methanol-ligated α-Fe(II) [α-Fe(II)-CH₃OH]. The ~50 kcal/mol of free energy released in this reaction would drive desorption of MeOH into the gas phase, where it is modeled to bind to the Brønsted acid sites present in large excess in this zeolite lattice. This regenerates α-Fe(II), as observed experimentally in CHA but not in *BEA (Fig. 2B).

Thus, in *BEA (and other zeolites with large pore apertures), escape of a CH₃ radical from the α-Fe(III)-OH intermediate is expected to be a diffusive process that leads to catalytically inactivated Fe(III) products [α-Fe(III)-OCH₃/α-Fe(III)-OH]. Steaming is required to recover MeOH via hydrolysis of α-Fe(III)-OCH₃, and high temperatures must then be used to effect autoreduction of the resulting Fe(III) sites back to α-Fe(II) (33). In contrast, the constricted pore apertures of CHA constrain the CH₃ radical, promoting its recombination with α-Fe(III)-OH to form CH₃OH and returning the active site to its reduced α-Fe(II) state to enable further turnover. In analogy to the active-site pocket of a metalloenzyme, the local pore environment of a heterogeneous active site can therefore play a decisive role in selecting between competing reaction pathways with low activation barriers, in this case promoting selective hydroxylation and precluding deactivating side reactions. This strategy is potentially broadly applicable for synthetic control over catalytic mechanisms in microporous materials.

Data and materials availability:

All spectroscopic data presented in the main text are freely available through Zenodo (34).