Modular Incorporation of Deformable Spine and 3D Neck Musculature into a Simplified Human Body Finite Element Model

Abstract

Spinal injuries are a concern for automotive applications, requiring large parametric studies to understand spinal injury mechanisms under complex loading conditions. Finite element computational human body models (e.g., Global Human Body Models Consortium (GHBMC) models) can be used to identify spinal injury mechanisms. However, the existing GHBMC detailed models (with high computational time) or GHBMC simplified models (lacking vertebral fracture prediction capabilities) are not ideal for studying spinal injury mechanisms in large parametric studies. To overcome these limitations, a modular 50^th percentile male simplified occupant model combining advantages of both the simplified and detailed models, M50-OS+DeformSpine, was developed by incorporating the deformable spine and 3D neck musculature from the detailed GHBMC model M50-O (v6.0) into the simplified GHBMC model M50-OS (v2.3). This new modular model was validated against post-mortem human subject test data in four rigid hub impactor tests and two frontal impact sled tests. The M50-OS+DeformSpine model showed good agreement with experimental test data with an average CORrelation and Analysis (CORA) score of 0.82 for the hub impact tests and 0.75 for the sled impact tests. CORA scores were statistically similar overall between the M50-OS+DeformSpine (0.79±0.11), M50-OS (0.79±0.11), and M50-O (0.82±0.11) models (p>0.05). This new model is computationally 6 times faster than the detailed M50-O model, with added spinal injury prediction capabilities over the simplified M50-OS model.

1. Introduction

Spinal injuries are an overlooked area in the injury biomechanics field, and there is a relative lack of understanding of spinal injury mechanisms under different loading conditions. Spinal injuries can be broadly classified into two categories: vertebral fracture and soft tissue injuries (whiplash, herniated disc, spinal cord injury etc.). In automotive crashes, vertebral fractures mostly occur due to direct compression force and flexion or extension moments generated in the spine. In contrast, soft tissue injuries such as whiplash or back pain are mostly associated with sudden movement resulting in strain or sprain in the muscles and ligaments supporting the spine. In some cases, fractured or dislocated vertebrae or other spine injuries can lead to more severe spinal cord or disc injuries (King 2002; Li et al. 2019). While soft tissue injuries such as whiplash are mostly minor, and severe spinal cord and disc injuries are rare, vertebral fractures are a serious issue in automotive crashes. The risk of vertebral fracture has increased in newer vehicles as compared to older vehicles (Kaufman et al. 2013; Doud et al. 2015; Forman et al. 2019), and the spine ranks amongst the top three most frequently injured body region (Jakobsson et al. 2016). Additionally, recent studies suggest that highly reclined seats in autonomous vehicles may increase lumbar spine injury risk in occupants due to increased lumbar forces (Richardson, Donlon, et al. 2020; Richardson, Jayathirtha, et al. 2020).

In automotive environments, occupants can be subjected to omnidirectional loading conditions (frontal, rear, lateral, oblique, roll-over etc.), and spinal injury mechanisms during these conditions largely depend on the complex interaction between the occupant and different seat-restraint systems such as seatbelt angle, seatbelt pretension, seat pan and seat back angles, toe pan angle, knee-bolster etc. (Rawska et al. 2019; Tang et al. 2020; Rawska et al. 2020; Rawska et al. 2021). Large parametric studies are required to completely understand these occupant-seat-restraint system interactions and corresponding spinal injury mechanisms under different loading conditions. Conventional tests using anthropomorphic test devices and post-mortem human subjects (PMHS) are limited for this purpose due to their significant time and cost requirements. These indicate a need for new technologies and tools to study spinal injury mechanisms in a wide variety of applications in a time- and cost-efficient manner.

Finite element (FE) human body models (HBMs) are computational tools for simulating the response of the human body under dynamic loading. Due to their fast turn-around time and cost-effectiveness, FE HBMs are advantageous for studying spinal injury mechanisms in these applications. The Global Human Body Models Consortium (GHBMC) FE HBMs have shown their credibility for predicting injury mechanisms under dynamic loading conditions in sports (Decker et al. 2020; Bruneau and Cronin 2021), automotive (Ramachandra et al. 2021; Costa et al. 2021), space (Jones et al. 2019; Ye et al. 2020), and military (Hostetler et al. 2019; Somasundaram et al. 2019) applications. The GHBMC family consists of models with varying complexity, anthropometry, and postures. Based on the complexity, these models can be broadly classified into two groups – detailed models and simplified models.

GHBMC detailed models are anatomically accurate models of the human body with a finer mesh density, detailed tissue structure, independently modeled internal organs, three-dimensional (3D) musculature, and deformable bones with separately modeled trabecular and cortical structures (Gayzik et al. 2011; Gayzik et al. 2012). Detailed models with the in-depth bio-fidelic spine (Aira et al. 2019) can be used for studying spinal injury mechanisms (Somasundaram et al. 2019; Somasundaram et al. 2023). However, due to their complexity, they require high computational power and time.

Conversely, simplified models have similar habitus, but coarser mesh density, greatly simplified soft-tissue structures, homogenized internal organs, simplified musculature represented as one-dimensional (1D) beam elements, and mostly rigid non-deformable bones (Schwartz et al. 2015). The simplified models are thus computationally faster and good for studying kinematic response under dynamic loading (Perez-Rapela et al. 2019; Devane et al. 2019). However, due to a rigid spine which is unable to deform or predict stress-strain or force responses of the vertebrae, the simplified models cannot be used for comprehensive injury prediction such as thoracolumbar fractures. In summary, detailed models are computationally taxing, whereas simplified models lack in-depth spinal injury prediction capabilities.

Parametric studies such as one to assess the effects of restraint systems and seat configurations on submarining in the automotive environment (Rawska et al. 2020; Rawska et al. 2021) or sensitivity studies to assess astronaut injury risk for spaceflight loading conditions (Lalwala, Devane, et al. 2022) require a computationally efficient model capable of predicting spinal injuries, to minimize the time and cost requirements for such studies. However, neither the detailed model (due to its high computational cost and time requirements) or the simplified model (due to its limited spine injury prediction capabilities) are well-suited for studying spinal injury mechanisms in parametric studies.

To overcome this limitation, the aim of the current study was to develop a new hybrid model combining advantages of both the detailed and simplified models by incorporating the detailed deformable spine and 3D neck musculature from the GHBMC detailed occupant model into the GHBMC simplified occupant model. A goal was for the hybrid model with the deformable spine and 3D neck musculature to have a faster computational run time than the GHBMC detailed model. Previous studies have developed modular GHBMC models by incorporating components of the detailed model such as the brain (Decker, Koya, Davis, et al. 2017), internal organs (Decker et al. 2018), and lower extremity bones (Decker, Koya, and Gayzik 2017) into the simplified model, and have demonstrated these hybrid models have good bio-fidelity for studying regional level injury biomechanics.

Using a similar approach, this study aimed to develop a 50th percentile male modular simplified occupant FE HBM – the M50-OS+DeformSpine – by replacing the rigid spine and simplified neck muscles in the GHBMC simplified 50th percentile occupant model (M50-OS v2.3) with the deformable spine and 3D neck muscles from the GHBMC detailed 50th percentile occupant model (M50-O v6.0). This new modular model was also validated against PMHS test data to assess its bio-fidelity in four rigid hub impacts to the thorax (Kroell 1994; Kemper et al. 2008) and abdomen (Viano 1989; Hardy et al. 2001), and two full-body frontal inertial sled impacts (Forman et al. 2009; Shaw et al. 2009).

2. Methods

2.1. Model Development

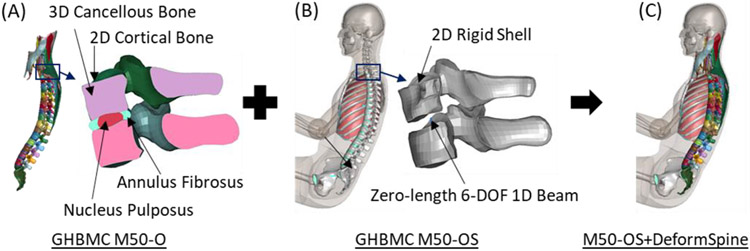
Though development of the detailed and simplified GHBMC models has been reported previously (Gayzik et al. 2011; Gayzik et al. 2012; Schwartz et al. 2015), the approach for the spine and neck muscle modeling in these two models is briefly revisited here. In the detailed models, vertebrae are modeled as a 3D mesh with the inner under-integrated hexahedral solid elements representing cancellous bone and the outer under-integrated quadrilateral shell elements representing cortical bone with LS-DYNA (r10.2.0, ANSYS, Inc., Livermore, CA) plastic kinematic material model *MAT_PLASTIC_KINEMATIC. Vertebral bodies are connected using the detailed intervertebral discs comprising the annulus fibrosus (under-integrated hexahedral solid elements with *MAT_HILL_FOAM) and nucleus pulposus (under-integrated hexahedral solid elements with *MAT_ELASTIC_FLUID) (Figure 1A). Ribs are connected to the thoracic vertebrae using radiate (under-integrated quadrilateral shell elements with *MAT_FABRIC) and costotransverse ligaments (beam elements with *MAT_CABLE_DISCRETE_BEAM). Neck muscles are modeled using 3D solid under-integrated hexahedral elements with passive viscoelastic material with *MAT_SIMPLIFIED_RUBBER/FOAM. The deformable spine in the detailed model has been extensively validated in both functional spinal units and full-body tests to ensure its bio-fidelity (Elemance LLC 2021a).

Figure 1.

The deformable spine and 3D neck muscles (A) from the GHBMC detailed M50-O v6.0 model were incorporated into the GHBMC simplified M50-OS v2.3 model (B) to develop the M50-OS+DeformSpine model (C).

In the simplified models, vertebral bodies are modeled as only outer geometry surfaces using two-dimensional (2D) quadrilateral shell elements with *MAT_RIGID. Cervical vertebrae are connected by simplified osteo-ligaments representation using 3 translational and 3 rotational dampers (Dibb et al. 2013). Thoracic and lumbar vertebrae are connected using zero-length 6-degree-of-freedom (6-DOF) 1D discrete beam elements (*MAT_GENERAL_NONLINEAR _6DOF_DISCRETE_BEAM). Similarly, ribs are attached with the thoracic vertebrae using zero-length 6-DOF 1D discrete beam elements (Figure 1B). Neck muscles are modeled as simple 1D discrete beam elements between the origin and insertion points with constant cross-section area. The neck muscles comprise passive elements with *MAT_ELASTIC_SPRING _DISCRETE_BEAM and active elements with *MAT_MUSCLE with a closed-loop joint angle-based proportional-integral-derivative (PID) controller (Devane et al. 2019). Even with these simplifications, the non-deformable spine in the simplified model is kinematically similar to the deformable spine in the detailed model and has also been validated in full-body tests (Elemance LLC 2021b).

In the current study, the M50-OS+DeformSpine model was developed by replacing the non-deformable spine and 1D neck muscles in the GHBMC simplified 50th percentile occupant model (M50-OS v2.3) with the deformable spine and 3D neck muscles from the GHBMC detailed 50th percentile occupant model (M50-O v6.0; Figure 1). In the M50-OS model, translational and rotational stiffnesses of the neck were achieved by damper connection between the cervical vertebrae in combination with the 1D neck muscles (Dibb et al. 2013). In contrast, in the M50-O model, a biofidelic neck response was achieved by modeling intervertebral discs between the cervical vertebrae and 3D neck muscles supporting the cervical spine. Due to these differences in the modeling approach, only replacing the cervical spine in the M50-OS+DeformSpine model resulted in excessive neck movement under dynamic loading conditions, indicating a need to incorporate 3D neck muscles from the M50-O model into the M50-OS+DeformSpine to achieve a biofidelic neck response.

Conversely, the thoracolumbar spine in the M50-OS model was modeled with 6-DOF 1D beam elements to represent intervertebral discs and surrounding thoracic muscles as 1D beams. Replacing the non-deformable vertebrae and 6-DOF beam elements with deformable vertebrae and intervertebral discs respectively from the M50-O model provided a biofidelic upper body response in the M50-OS+DeformSpine. Hence, to reduce the computational cost and complexity in the M50-OS+DeformSpine model, trunk muscles were retained as simplified 1D beam elements from the M50-OS model. A closed-loop muscle activation strategy from the M50-OS model was retained for all the active muscles in the M50-OS+DeformSpine model, but the single 1D beam elements representing active neck muscles were replaced with a sequence of 1D beam elements following the 3D neck muscle curvature. A comparison of the active muscle modeling approaches for the sternocleidomastoid muscle in the M50-O and M50-OS models is given in Figure A1 (Appendix A). In the M50-O model, the intermediate node for the sequential beam elements were shared between the 3D solid (passive muscle) and 1D beam (active muscle) elements; a similar modeling approach for the active neck muscles was continued in the M50-OS+DeformSpine model.

No scaling for the spine or muscle structures was required as both the M50-O and M50-OS models had the same habitus. Since muscle mass and volume had been merged with the flesh in the M50-OS model, neck flesh in the M50-OS+DeformSpine model was updated to be similar to the M50-O model to account for added 3D neck muscle mass and volume (Figure A2). Origin and insertion points of the 3D neck muscles were attached to the simplified skeleton and deformable spine at appropriate locations. The cervical spine and sacrum were attached to the simplified skull and pelvis respectively, similar to the existing M50-OS model. The ribs in the M50-OS model were retained, but their connection to the thoracic vertebrae was changed to radiate and costotransverse ligaments similar to the M50-O model.

The 1D beam elements representing thoracolumbar muscles in the M50-OS model were then re-attached to the deformable spine in the M50-OS+DeformSpine model. New contact definitions, similar to the M50-O model, were defined between the deformable spine, 3D neck muscles, ribs, and surrounding flesh and organs. New neck (C2, C4, and C7) and lumbar spine (L1) cross-sections for vertebral forces and moments measurements (White et al. 2015), along with C1, C7, T1, T8, T12, and Pelvis history nodes for kinematic measurements were also defined similar to the M50-O model (Elemance LLC 2021a). Comparison of final nodes, elements, mass, and governing timesteps for the M50-O, M50-OS, and M50-OS+DeformSpine models is provided in Table A1 (Appendix A).

2.2. Model Validation

To assess the M50-OS+DeformSpine model bio-fidelity, simulations of four rigid hub-impactor and two sled-impact PMHS tests were carried out. The model was validated for thoracic impacts in Kroell (1994) and Kemper et al. (2008) tests, and abdominal impacts in Viano (1989) and Hardy et al. (2001) tests. In the Kroell (1994) test, the model was subjected to a frontal chest impact with a 23 kg rigid hub at an initial velocity of 6.7 m/s (Figure 2A). The Kemper et al. (2008) test involved a lateral impact with a 23.4 kg plate at 12 m/s to the right arm (Figure 2B). The Viano (1989) test involved an oblique abdominal impact with a 15 cm flat, 23.4 kg pendulum at 6.7 m/s (Figure 2C). The Hardy et al. (2001) test involved a 48 kg bar impact to the abdomen with an initial velocity of 6 m/s (Figure 2D).

Figure 2.

Simulation setup for rigid impact tests for M50-OS+DeformSpine model. (A) Frontal chest hub impact (Kroell, 1994), (B) Lateral sled impact (Kemper et al., 2008), (C) Oblique abdominal hub impact (Viano, 1989), and (D) Frontal abdominal bar impact (Hardy et al., 2001).

For full-body inertial sled-impact tests, the M50-OS+DeformSpine model was validated in front-seat (Shaw et al. 2009) (Figure 3A) and rear-seat (Forman et al. 2009)(Figure 3B) frontal impact tests. For both tests, the model was initially gravity settled into the respective seats for the first 100 ms. Then, the frontal sled impact velocity pulse was applied: 11.8 m/s for the Shaw et al. (2009) test and 13.8 m/s for the Forman et al. (2009) test.

Figure 3.

Simulation setup for full-body sled impacts for M50-OS+DeformSpine model. (A) Front-seat frontal sled impact (Shaw et al., 2009), and (B) Rear-seat frontal sled impact (Forman et al., 2009).

Simulations were performed on the Distributed Environment for Academic Computing (DEAC) high-performance computational cluster at Wake Forest University using 22 CPUs and LS-DYNA R.10.2.0 (ANSYS, Inc., Livermore, CA). All simulations were carried out without muscle activation since the tests were with PMHS. From these simulations, kinematic and dynamic responses were extracted and quantitatively compared against the PMHS test data using the CORA (CORrelation and Analysis, v4.04, Partnership for Dummy Technology and Biomechanics, Germany) scoring method. The CORA rating takes into account corridor and cross-correlation (phase, magnitude, and shape) between the simulation and experimental signals to calculate the level of correlation between them, where a CORA score of 1 indicates a perfect match and a CORA score of 0 indicates a poor match (Gehre and Stahlschmidt 2011). Similar to ISO/TR9790, a continuous rating scale is used to determine a bio-fidelity rating based on the CORA score, which is summarized in Table A2 (Pietsch et al. 2016; Correia et al. 2021).

CORA scores were calculated using the full-time history for force and kinematic response using the parameters in Table A3. Since force-time history data for the Kroell (1994) test is not available, a CORA score was not calculated for this test and the force-deflection response was qualitatively compared against the PMHS data. For each test, an average CORA score for belt forces (shoulder, lap, etc.), and orthogonal kinematic response (typically X, Y, and Z components) at each sensor location (body-region) was calculated using a weighted average method with a signal magnitude-derived weighting factor (Schap et al. 2019). In this method, the weighting factor of each component signal is calculated by normalizing the peak magnitude of the given component signal by the sum of peak magnitudes of all the component signals. This method prevents distortion in the overall quality of the model response when one of the component signals has a significantly higher magnitude response compared to the other components. For this study, weighting factors for each test were calculated from the experiment data (Table A4).

All tests were also simulated with the original GHBMC M50-O and M50-OS models. A paired t-test comparison for CORA scores for all three models for all the tests was carried out to measure similarity or differences between them. In addition, run times (time required to run the simulation) were also compared to estimate the relative computational cost of each model. To account for different test times (duration of the physical test), the run rate was calculated by normalizing simulation run time with test time (Eq 1) and compared between the three models. A lower run rate indicates greater computational efficiency.

$$Runrate=\frac{Simulationruntime(\text{min})}{Testtime(ms)}$$ (1)

3. Results

The M50-OS+DeformSpine model showed a good correlation with the PMHS data across all tests. Model responses are compared with experimental data from the rigid impactor tests in terms of impactor force (Figure 4) and kinematic- and force-time histories (Figure A3 - Figure A8).

Figure 4.

Comparison between the M50-O, M50-OS+DeformSpine, and M50-OS models for the rigid impactor tests. (A) Frontal chest hub impact (Kroell, 1994), (B) Lateral sled impact (Kemper et al., 2008), (C) Oblique abdominal hub impact (Viano, 1989), and (D) Frontal abdominal bar impact (Hardy et al., 2001). Experimental means, corridors, and subject data are taken from corresponding literature.

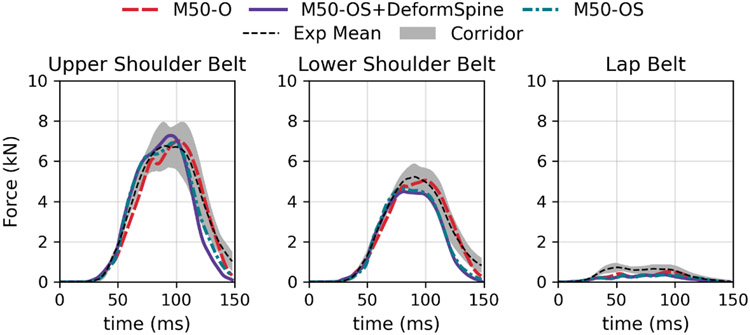
The M50-OS+DeformSpine model also showed good similarity with PMHS data for sled impact tests. A comparison of the belt forces for all the models with PMHS data is provided in Figure 5 and Figure 6, along with comparison of kinematic- and force-time histories in Figure A9 - Figure A16.

Figure 5.

Comparison of shoulder and lap belt forces between the M50-O, M50-OS, and M50-OS+DeformSpine models for front-seat frontal sled impact test (Shaw et al., 2009).

Figure 6.

Comparison of shoulder and lap belt forces between the M50-O, M50-OS, and M50-OS+DeformSpine models for rear-seat frontal sled impact test (Forman et al., 2009).

Quantitative comparison of the model response with PMHS data using CORA scores for the M50-O, M50-OS+DeformSpine, and M50-OS models is provided (Figure 7; Table A5 - Table A7). The M50-OS+DeformSpine model with an overall CORA score of 0.79±0.11 (mean±SD) achieved the same score as the M50-OS (0.79±0.11) and performed a little worse than the M50-O (0.82±0.11) across all tests. No statistically significant difference in the CORA score was observed between the M50-O, M50-OS+DeformSpine, and M50-OS models in paired t-tests (M50-OS+DeformSpine vs M50-O: difference = 0.02, p = 0.51 and M50-OS+DeformSpine vs M50-OS: difference = 0.00, p = 0.94 with α = 0.05, n = 5).

Figure 7.

Comparison of CORrelation and Analysis (CORA) score between the M50-O, M50-OS+DeformSpine, and M50-OS models for all the rigid impactor and sled tests.

Comparison time and run rate for three models for these tests are summarized in Table A8 and Figure 8. The M50-OS+DeformSpine model with an average run rate of 2.43±0.24 min/ms showed a reduction in computation time against the M50-O (15.16±1.48 min/ms) and an increase against the M50-OS (0.79±0.05 min/ms). Overall, the M50-OS+DeformSpine model performed 6.2±0.5 times faster than the M50-O model and showed only 3.1±0.3 fold increase in computation time against the M50-OS model.

Figure 8.

Comparison of computation time reported as run rate (min/ms) between the M50-O, M50-OS+DeformSpine, and M50-OS models for all the rigid impactor and sled tests.

4. Discussion

A modular 50th percentile male occupant model – the GHBMC M50-OS+DeformSpine model – was developed by incorporating the deformable spine and 3D neck muscles from the GHBMC detailed model M50-O into the GHBMC simplified model M50-OS habitus. This modular model can be used to investigate spinal injury mechanisms with improved simulation time- and cost-efficiency. This new modular model showed good agreement with PMHS response in impactor and inertial loading conditions, indicating its bio-fidelity for predicting the force and kinematic response of the human body under dynamic loading conditions.

For the frontal chest impact test (Kroell 1994), a qualitative comparison of force-deflection response showed a good correlation between the PMHS and the M50-OS+DeformSpine model (Figure 4A). For the lateral sled impact test (Kemper et al. 2008), since the corridor data for the kinematic response is not available, only the cross-correlation rating comprising shape, size, and phase was considered for CORA calculation. All the models showed an ‘Excellent’ bio-fidelity rating for this test with CORA scores of 0.89, 0.91, and 0.92 for the M50-O, M50-OS+DeformSpine, and M50-OS models, respectively (Table A5 - Table A7). For both thoracic impact tests, the M50-OS+DeformSpine model showed close similarity with the M50-O for both the force and kinematic responses (Figure 4A-B and Figure A3-Figure A6). This can be expected as the response of the human body under thoracic impacts is driven by the thoracic spine, rib cage and visceral organs. Since both the modular and detailed models share the same deformable spine, their responses for these tests were very similar.

For the oblique abdominal impact (Viano 1989), the M50-OS+DeformSpine model showed a ‘Good’ bio-fidelity rating with a 0.76 CORA score, similar to the M50-OS (CORA: 0.77). The M50-O showed an ‘Excellent’ bio-fidelity rating for this test with a 0.91 CORA score. The difference in the rating is due to the occurrence of the force peak earlier in the modular and simplified models (Figure A7), which can be attributed to the rigid shoulder and upper extremity in these models (Schwartz et al. 2015). For the abdominal bar impact test (Hardy et al. 2001), all models showed a ‘Good’ bio-fidelity rating with CORA scores of 0.81, 0.80, and 0.78 for the M50-O, M50-OS+DeformSpine, and M50-OS models respectively (Table A5 - Table A7). For this test, the force-deflection characteristics matched well with the PMHS data for all three models (Figure 4D). For both abdominal impact tests, the M50-OS+DeformSpine model showed close similarity with the M50-OS (Figure 4C-D and Figure A7 - Figure A8), which can be attributed to the similarity in the abdominal organ and thoracolumbar muscle modeling in both models.

For the front-seat frontal sled impact test (Shaw et al. 2009), all models showed a ‘Fair’ bio-fidelity rating with 0.64, 0.62, and 0.63 CORA scores for the M50-O, M50-OS+DeformSpine, and M50-OS, respectively (Table A5 - Table A7). Though the modular model showed a slightly lower CORA score, it is comparable to the M50-O and M50-OS, indicating negligible differences. The relatively lower CORA scores are associated with the comparatively larger variation in PMHS characteristics (age and stature) in the test. For all the models, shoulder belt forces (Figure 5) along with knee bolster, footrest, and vertical seat forces (Figure A14, Figure A15) showed generally good agreement with the PMHS corridor data. Similarly, for the kinematic response all the body regions showed overall good conformance with the PMHS data for the anterior-posterior (X directional) displacement, though some deviation in lateral (Y directional) and vertical (Z directional) displacements was observed (Figure A9 - Figure A13).

For the rear-seat frontal sled impact test (Forman et al. 2009), both the M50-OS+DeformSpine and M50-OS models showed an ‘Excellent’ bio-fidelity rating with 0.87 and 0.86 CORA scores, respectively, whereas the M50-O showed a ‘Good’ bio-fidelity rating with a 0.82 CORA score (Table A5 - Table A7). For this test, CORA scores for the kinematic responses were calculated using the cross-correlation rating only in absence of the corridor data. Both belt forces and head, shoulder, and pelvis kinematics showed a good correlation with the PMHS data for the modular model (Figure 6 and Figure A16). The lower CORA score for the M50-O model can be attributed to the relatively higher head and shoulder movement.

Overall, the M50-OS+DeformSpine model showed a ‘Good’ bio-fidelity rating with a 0.79±0.11 CORA score, which is only slightly lower than the detailed M50-O model (0.82±0.11) and the same as the simplified M50-OS model (0.79±0.11). The ‘Good’ bio-fidelity rating indicates that the kinematic and dynamic response predicted by the new modular model match well with the human body under these dynamic loading conditions. The paired t-test comparisons between the models also showed that there is no statistically significant difference in model response, indicating the modular model is kinematically and dynamically equivalent to the existing GHBMC models.

In addition, run rate ratio comparison indicates that the M50-OS+DeformSpine model is more than 6 times faster than the M50-O model. This means 6 tests can be run with the modular model in the same time it would take for the detailed model to run a single test. Also, the modular model is only 3 times slower than the simplified model (M50-OS), which can be justified given the ability of the modular model to predict stress and strain in the deformable spine. Using the stress and strain induced in the spine under given dynamic loading conditions, spinal injury mechanisms and injury risk can be investigated using this new modular spine model.

It should be noted that in the current study, the model was only validated for limited rigid impactor and frontal impact loading conditions, and further validation of the model will be required to further assert its biofidelity in more loading conditions. Though the M50-OS+DeformSpine model can simulate active response, the model was only validated against the PMHS data and further validation against volunteer data is required to assess active response of the model. Similarly, though the M50-OS+DeformSpine model is capable of predicting stress-strain based spinal injuries, similar validation was not carried out due to lack of relevant test data. However, the spine model has been used to assess spinal injury in previous studies (Somasundaram et al. 2019; Somasundaram et al. 2023), and since the same modeling methodology has been retained in the M50-OS+DeformSpine model, it can be used for predicting spinal injuries.

One of the limitations of the M50-OS+DeformSpine model is lack of detailed trunk muscles. Though a detailed deformable thoracolumbar spine has been integrated in this model, the trunk muscles were kept as simplified beam elements to reduce computational complexity. While this approach did not affect the spine response of the model, it limits the model’s capability to predict soft-tissue injuries in the thoracolumbar region. However, trunk muscles can also be integrated in the M50-OS+DeformSpine model in the future following a similar approach used in the current study. In the current study, no improvements in the spine modeling approach used in the original GHBMC models were carried out, but future work could address issues identified by Tushak et al. to improve the lumbar spine injury prediction capability (Tushak et al. 2022).

In summary, the GHBMC M50-OS+DeformSpine model, a 50th percentile male modular simplified model with a deformable spine, was developed by incorporating a deformable spine and neck muscles from the detailed GHBMC model M50-O into the simplified GHBMC model M50-OS. The M50-OS+DeformSpine achieved a good bio-fidelity CORA rating against PMHS data from rigid impactor and sled impact tests and is computationally 6 times faster than the detailed GHBMC M50-O model. This new model overcomes the limitations of high computational cost in the detailed model and the lack of spinal injury prediction capabilities in the simplified model. The modular GHBMC M50-OS+DeformSpine model has been used for parametric studies (Lalwala, Devane, et al. 2022) of aerospace impact scenarios, and could be used in other parametric studies to inform the design of safer seat and restraint systems, including for autonomous vehicles or spacecraft that may position occupants in non-traditional postures.