Protein Mobility in the Cytoplasm of Escherichia coli

Abstract

The rate of protein diffusion in bacterial cytoplasm may constrain a variety of cellular functions and limit the rates of many biochemical reactions in vivo. In this paper, we report noninvasive measurements of the apparent diffusion coefficient of green fluorescent protein (GFP) in the cytoplasm of Escherichia coli. These measurements were made in two ways: by photobleaching of GFP fluorescence and by photoactivation of a red-emitting fluorescent state of GFP (M. B. Elowitz, M. G. Surette, P. E. Wolf, J. Stock, and S. Leibler, Curr. Biol. 7:809–812, 1997). The apparent diffusion coefficient, D_a, of GFP in E. coli DH5α was found to be 7.7 ± 2.5 μm²/s. A 72-kDa fusion protein composed of GFP and a cytoplasmically localized maltose binding protein domain moves more slowly, with D_a of 2.5 ± 0.6 μm²/s. In addition, GFP mobility can depend strongly on at least two factors: first, D_a is reduced to 3.6 ± 0.7 μm²/s at high levels of GFP expression; second, the addition to GFP of a small tag consisting of six histidine residues reduces D_a to 4.0 ± 2.0 μm²/s. Thus, a single effective cytoplasmic viscosity cannot explain all values of D_a reported here. These measurements have implications for the understanding of intracellular biochemical networks.

Response times and reaction rates in Escherichia coli often depend on the movement of proteins from one location to another in the cell. These proteins may have regulatory or signaling functions, or they may act as enzymes or substrates for cellular reactions. How do such molecules reach their destinations? In eukaryotic cells, cytoskeletal networks and motor proteins facilitate active transport of molecules (1). In some cases, including Drosophila oocytes, mixing of cytoplasm can also be achieved by the cytoskeleton-dependent process of cytoplasmic streaming (27). However, such structures and processes have not been observed in bacteria. Therefore, in bacteria, diffusion may be the primary means of intracellular movement. The diffusional mobility of cytoplasmic proteins may constrain the rates of some cellular reactions. The in vivo diffusive properties of proteins are therefore of general interest for understanding a variety of processes in the bacterial cell.

The interior of a bacterial cell is an environment crowded with a heterogeneous collection of macromolecules. In E. coli, the concentrations of protein, RNA, and DNA are 200 to 320 mg/ml, 75 to 120 mg/ml, and 11 to 18 mg/ml, respectively (6, 30). These high macromolecular concentrations imply large excluded volume effects, which strongly affect the activities of cytoplasmic molecules (14, 30). The validity of extrapolations from the values of physical or biochemical constants measured at lower macromolecular concentrations in cell-free in vitro systems to their effective values in actual cytoplasm is therefore uncertain (12). In particular, the rate of protein diffusion inside the cell cannot necessarily be inferred from in vitro measurements.

One of the most useful techniques for studying cytoplasmic diffusion in eukaryotic cells and cell membranes has been the method of “fluorescence recovery after photobleaching” (FRAP) (3, 16). By this method, fluorescent tracer molecules are introduced into the cell. Those tracers located in a small region are photobleached by a laser. The size, L, of the bleached area, and the characteristic time, τ, over which unbleached tracer molecules return to it, determine an apparent diffusion coefficient, D_a, which is proportional to L²/τ. In spot photobleaching experiments, L is the diameter of the spot, whereas in the experiments described here, it is the length of the cell. For diffusive particles, D_a is independent of L and equal to the diffusion coefficient, D. In a nonideal medium, on the other hand, particles may behave nondiffusively or exhibit anomalous diffusion, in which case the apparent diffusion coefficient, D_a, will depend on L (21). Because the cytoplasm may be such an environment, mobility measurements are reported here in terms of an apparent diffusion coefficient, D_a, valid specifically at the scale of the cell length.

Until now, it has been difficult to apply FRAP to E. coli cells. These bacteria are smaller than the eukaryotic cells previously studied by FRAP, and it is difficult to introduce fluorescently labeled molecules into them. Here, we have used the Aequorea victoria green fluorescent protein (GFP) as a tracer molecule to measure cytoplasmic protein diffusion. Like fluorochromes used in previous FRAP experiments, GFP can be irreversibly photobleached with sufficiently intense illumination (25). Unlike traditional FRAP fluorophores, however, GFP can be expressed endogenously. Further, it was recently shown that under conditions of low oxygen concentration, a short pulse of blue light converts the normally green-emitting GFP to a red-emitting state (10). Thus, apparent diffusion coefficients can also be measured by photoactivating GFP molecules at one pole and observing their subsequent propagation through the cell. Together, photobleaching and photoactivation techniques permit us to make direct in vivo measurements of protein diffusion in bacterial cytoplasm.

MATERIALS AND METHODS

Bacterial strains and GFP constructs.

The GFPmut2 allele of GFP, obtained by Cormack et al. (7), was selected because it is efficiently excited, photobleached, and photoactivated by the 488-nm argon laser line. GFPmut2 DNA was amplified with primers to generate 5′ BamHI and 3′ HindIII sites (CCGGATCCGGCATGAGTAAAGGAGAAGA and GCCGAAGCTTATTTGTATAGTTCATCCA, respectively). The resulting DNA was cloned into plasmid pQE-12 (Qiagen) and cut with the BamHI and HindIII enzymes, removing the six-His tag sequence. The resulting plasmid, pMGS053, expresses a GFP with a molecular mass of 27.5 kDa. An N-terminal polyhistidine-tagged GFP was generated by amplifying GFPmut2 with primers to generate 5′ BamHI and 3′ BamHI sites (CCGGATCCGGCATGAGTAAAGGAGAAGA and CCGGATCCGGCTTTGTATAGTTCATCCA, respectively) and inserted into the BamHI site of pQE-8 (Qiagen). This BamHI GFP-encoding DNA was also cloned into the BamHI site of plasmid pMAL-C2 (New England Biolabs) to generate a cytoplasmically expressed maltose binding protein (MBP)-GFP fusion of approximately 72 kDa. For most experiments, the plasmids were transformed into E. coli DH5α. In addition, the following E. coli strains transformed with pMGS053 were examined: AB1157 (9), M15(pREP4) (Qiagen), MC1000 (5), MC1061 (5), MG1655 (13), and RP437 (18). For some experiments, the GFPuv gene was expressed from plasmid pGFPuv (Clontech) transformed into strain DH5α. GFPuv is a brighter GFP mutant which has the spectral characteristics of the wild-type protein (8).

Preparation of samples.

Bacterial cultures were grown overnight in Luria broth with ampicillin at 30°C with constant shaking, diluted 1:50 into the same medium, and grown at 30°C. After 2 h, cultures were induced by adding 100 μM (or as indicated) IPTG (isopropyl-β-d-thiogalactopyranoside) and allowed to continue growth for 3 h. Cells from 1 ml of culture were harvested at 3,000 rpm in a microcentrifuge and resuspended in 0.5 ml of minimal medium [7.6 mM (NH₄)₂SO₄, 60 mM K₂HPO₄, 2 mM MgSO₄, 20 μM FeSO₄, 1 mM EDTA (pH 6.8)]. Coverslips were pretreated for 15 min with poly-l-lysine solution (Sigma Chemical Co.) to promote cell adhesion and washed with ∼2 ml of minimal medium. A drop of bacterial suspension (∼100 μl) was incubated on the treated coverslip for <30 min. Coverslips were then rinsed again with minimal medium (∼2 ml) and placed on a microscope slide. Excess fluid was drained from the slide with Kimwipes, and the slides were sealed with candle wax. Poly-l-lysine pretreatment of coverslips resulted in uniform adhesion of cells at high density. Samples prepared without poly-l-lysine, in which cells were stuck nonspecifically to the glass surface, gave similar results (data not shown).

Elongated cells were grown as described above, except that at 1.5 h after addition of IPTG, cephalexin (Sigma) at 1, 2.5, 5, 15, 25, and 100 μg/ml was added to 1-ml aliquots of cells, which were then allowed to grow for another 1 to 2 h. Samples of each culture were examined under the microscope; the culture that contained elongated cells with the lowest concentration of cephalexin (typically, 15 μg/ml) was used for further study.

Optics and microscope setup.

The 488-nm component from a multiline air-cooled He-Ar tabletop laser was separated out with a prism and focused to a small spot (∼0.7 μm in diameter) in the image plane of a custom-modified Zeiss MPS microscope. The beam emerging from the laser was directed through a shutter/timer (UniBlitz) and then coupled to the microscope by means of a dichroic beamsplitter inserted in the optical path above the objective and fluorescence filter cube but below the trinocular eyepiece/camera stand. To permit the laser light to reach the sample, dichroic beamsplitters in the fluorescence filter sets were replaced with 50/50 beamsplitters (Chroma), and fluorescence emission filters were removed from the filter cube and placed above the laser-coupling dichroic with an extra filter slider (Mikro Precision) inserted just below the trinocular but above the laser-coupling dichroic. Fluorescence filters were Chroma HQ-FITC, no. 41001, for green GFP fluorescence and Zeiss rhodamine, no. 487915, for red GFP fluorescence. Prior to microscope entry, the laser beam was directed through a steering telescope consisting of two confocal lenses so that translation of the first lens perpendicular to the beam allowed steering of the laser spot in the sample plane. The total power entering the microscope was 0.25 mW. About 30% was transmitted to the sample, corresponding to a flux of 17 kW/cm² in the sample plane.

A 100× infinity-corrected 0.9-1.3 NA oil objective (Olympus) and a video charge-coupled device (CCD) camera (Paultek) were mounted on the microscope. The video CCD signal was recorded with an SVHS VCR (Sanyo) and later digitized from tape with a Cosmo Compress M-JPEG card (Silicon Graphics) at JPEG quality levels of ≥95 on an Indy Workstation (Silicon Graphics). Custom software was written to decompress and extract regions of interest from the M-JPEG movie file. For some experiments, and for calibrating laser spot size, the video CCD camera was replaced with a cooled CCD camera (Princeton Instruments) running at frame rates of from 5 to 20 frames per second, in which case the digitization step was omitted.

Photobleaching and photoactivation of GFP.

For photobleaching experiments, a cell was positioned in the center of the field of view, laser intensity was cut by a factor of 10³, and the laser spot was moved to one pole of the cell. The shutter was programmed for periodic light pulses of 300 ms, separated by 8-s pauses. The duration of the photobleaching pulse was chosen to be comparable to the diffusion time across the cell, so as to develop a large concentration gradient with minimum photobleaching of GFP. Accordingly, for the (longer) cephelaxin-treated cells, the pulse duration was increased, usually to 500 to 700 ms and always less than 1 s.

For photoactivation, cells were extremely dim or invisible in red fluorescence at the beginning of the experiment (i.e., before photoactivation), so they were selected in bright field (a red long-pass filter above the condenser prevented inadvertent photoactivation). Cells were aligned and irradiated as described above except that much shorter (30-ms) laser pulses (at the same power) were used to photoactivate the red state of GFP. Photoactivation of GFP is optimal in a low-oxygen environment (10). The high density of O₂-consuming cells used here was sufficient to deplete oxygen levels for photoactivation without specific deoxygenating reagents.

For measurements of the GFPuv variant, cells containing plasmid pGFPuv were induced with 1 mM IPTG to compensate for poorer expression and were photoisomerized before use by illumination through a DAPI (4′,6-diamidino-2-phenylindole) filter set for a few seconds at full power with the 100-W Hg arc lamp. This procedure reduces the amplitude of the UV excitation peak while enhancing the amplitude of the blue excitation peak (4).

Note that a potential artifact occurs in cells close to full septation. GFP diffuses much more slowly across the nearly complete septum than it does through the rest of the cell (data not shown), reducing the apparent rate of whole-cell diffusion (mode 1) relative to the corresponding half-cell process (mode 2). Cells undergoing septation were avoided for this reason.

Tethered-cell photodamage assay.

To test phototoxicity by a tethered-cell assay, RP437, a strain commonly used in chemotaxis studies, was transformed with pMGS053 and cells were grown and tethered as described previously (24). Expression of GFPmut2 had no effect on chemotaxis in this strain (data not shown). Cells were videotaped and laser treated as described above. Rotating cells were photobleached with a laser as described above, and their angular velocities were determined, as described previously (2).

Data analysis.

The data set we obtained was a time sequence of fluorescence images of the cell. For analysis, a threshold was chosen and only pixels whose intensities were greater than this value were considered. The cell axis was determined manually. In each frame, the two-dimensional cell image was converted to a one-dimensional intensity profile by grouping pixels in stripes perpendicular to the cell axis. Each stripe was represented by its average projected position on the bacterial axis and by its average intensity value. The ends of the intensity profile were truncated in order to avoid problems due to the curvature of the cell poles and the optical resolution of the microscope. Resulting values of D_a are insensitive to the precise position of this truncation.

Our analysis is based on the one-dimensional continuous diffusion equation ∂C(x,t)/∂t = D ∂²C(x,t)/∂x², with boundary conditions ∂C/∂x (0,t) = ∂C/∂x (L, t) = 0. The general solution to this equation can be written as a Fourier series:

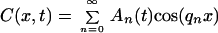1

where A_n(t) ≡ A _nexp(−q_n²Dt), and q_n ≡ 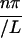, n = 1, 2, 3, … Here, C(x,t) is the concentration of GFP at position x and at time t, and D is the diffusion coefficient. We assume that fluorescence intensity is proportional to GFP concentration:

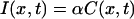2

To analyze the data, the Fourier amplitudes A_n(t) for each frame are determined from the data I(x,t) with the formula

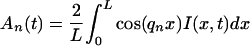3

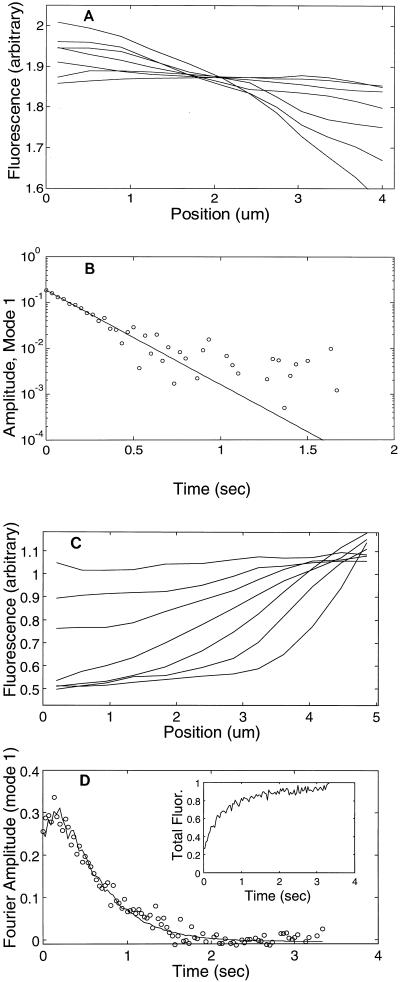
If the data solve the diffusion equation, A_n(t) will be proportional to exp(−q_n²Dt). Therefore, we perform a three-parameter fit of A_n(t) to the general exponential form Aexp(−Bt) + C. Here, C takes into account potential permanent intensity gradients that might arise from in homogeneities in cross-sectional area or uneven illumination intensity. We find C/A ≪ 1, indicating that such effects are small. D_a is determined by the decay rate, B, according to D_a = B/q_n². Fits were performed by a Levenberg-Marquardt algorithm, implemented in C (20). Figure 2A shows a typical sequence of one-dimensional profiles, I(x_i,t_j), and a plot of A₁(t) with a fitted exponential. Only lower-numbered terms in the series decay slowly enough to be followed with video-rate cameras; in this study we used modes n = 1 and n = 2 exclusively.

FIG. 2.

Analysis of photobleaching (A and B) and photoactivation (C and D) data. (A) Fluorescence intensity profiles at 0.03, 0.1, 0.17, 0.3, 0.5, 0.83, and 1.5 s after the end of photobleaching are shown for a DH5α cell expressing GFP. (B) For the same cell, temporal decay of first Fourier amplitude with time. Circles indicate data points; the solid line is a fit to the exponential function Aexp(−Bt) + C (see Materials and Methods). (C) Photoactivation intensity profiles are shown at the same time points as in panel A. (D) Temporal decay of first Fourier amplitude. The data are shown with circles, and a fit to an exponential decay corrected by the total cellular fluorescence enhancement is shown with a solid line (see Materials and Methods). The inset shows the total cellular fluorescence α(t). In panel B, the total intensity after photobleaching is constant (not shown).

GFP photoconverts to its red-emitting state with a time constant of ∼0.7 s (10), comparable to the diffusion time along the cell (see Fig. 2D, inset). Therefore, in photoactivation experiments, I(x,t) varies with time due to both photoconversion and diffusion, so the analysis procedure must be modified. If we assume that the rate of GFP conversion is independent of its position in the cell and local concentration, then I(x,t) is proportional to the product of the local fraction of newly photoactivated GFP, C*(x,t), and the total red fluorescence enhancement in the whole cell. That is, I(x,t) ∝ C*(x,t)[α(t)], where α(t) is the sum of the pixel intensities in the cell body at time t. We fit A_n(t), as defined in equation 3, to the three-parameter function A[α(t) − α₀] exp(−Bt) + C, where α₀ is α(t) evaluated just prior to the laser pulse. Since the parameter C remains small, the fit can alternatively be made to A[α(t) − α₀] exp(−Bt), resulting in differences in D_a of <3%. This procedure is insensitive to the shape of the photoactivation kinetics, α(t)−α₀, although in practice we find that the photoactivation kinetics are reasonably approximated by a single exponential.

To check for systematic analysis errors, GFP diffusion was simulated on a computer and simulations were analyzed like real data. We assumed exact diffusion of GFP in a one-dimensional geometry and allowed values for the apparent diffusion coefficient, cell length, signal intensity, noise, camera frame rate, and background bleaching rate to be set for each episode of photobleaching recovery. Analysis was performed “blind,” without knowledge of the correct answer. The error found upon comparison of “measured” values with “correct” values resulted primarily from overestimates of cell length (due to the difficulty of resolving cell ends). When cell lengths were corrected, errors of <5% remained. These simulations served to, first, verify the data analysis procedure; second, provide a limit of ∼5% on its accuracy; and third, suggest that cell length determination might be a major source of systematic error in the analysis of real data. We have no alternative measure of cell length with which to correct real data, but we found no significant correlation between D_a and L in a sample of 91 DH5α cells ranging in length from 3 to 5.5 μm. The relative magnitude of errors in L should be smaller for longer cells. Measurements on cephalexin-treated cells were consistent with measurements made on untreated, normal-length cells.

RESULTS

In vivo measurement of GFP diffusion.

We set out to measure diffusion of GFP in the cytoplasm of E. coli by photobleaching and photoactivation. In these experiments, we focused a laser through microscope optics to a small spot and used it to photobleach GFP near the pole of a single cell. Afterwards, we recorded the distribution of unbleached GFP throughout the cell with a video CCD camera. Use of the FRAP technique with image data in the small quasicylindrical geometry of the bacterial cell called for a method of analysis which considers the concentration of GFP throughout the cell rather than only in the photobleached region (see Materials and Methods).

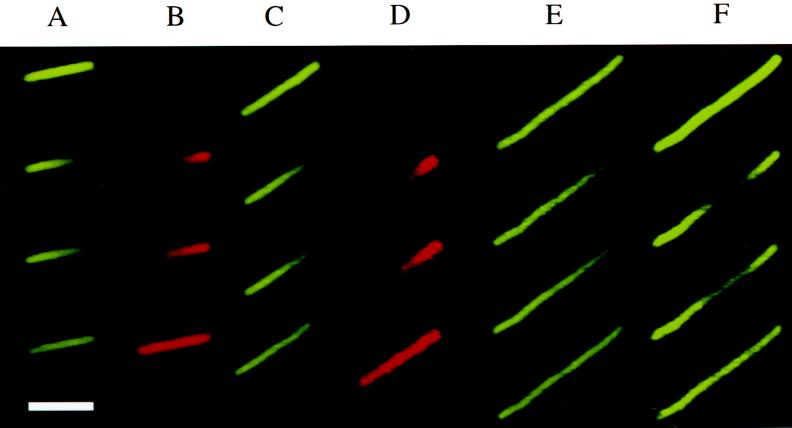
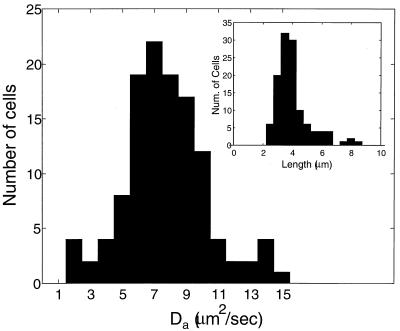
We first measured diffusion of the popular GFP variant GFPmut2 (7) in DH5α cells. Figure 1 (columns A and C) shows fluorescence images from two typical cells taken before and at various intervals after photobleaching. Figure 2A shows the one-dimensional intensity profile along the length of a cell at different times after photobleaching. The apparent diffusion coefficient was determined from the decay rate of the amplitude of the first Fourier mode (Fig. 2B; also see Materials and Methods). Diffusion was measured this way in 120 individual DH5α cells. The distribution of apparent diffusion coefficients is shown in Fig. 3. The value of D_a assigned to each cell is the average obtained from several successive laser pulses. The average value of D_a for all cells is 7.7 μm²/s, with a standard deviation (SD) of 2.5 μm²/s. Other common laboratory strains of E. coli showed similar behaviors (Table 1). However, strain AB1157, which expresses very high levels of GFP, has a D_a 43% lower than DH5α (4.4 μm²/s). Therefore, we increased the expression level of GFP in DH5α cells. When the concentration of inducer (IPTG) was increased from 100 to 500 μM, the apparent diffusion coefficient was indeed reduced to 4.8 μm²/s, and at 1 mM IPTG, D_a was further reduced to 3.6 μm²/s (Table 1). In addition to GFPmut2, we also performed experiments with the GFPuv (Clontech) variant, because it was previously found to exhibit modified diffusive behavior in eukaryotic cells (29). However, in bacteria, we observed no differences in its apparent diffusion coefficient.

FIG. 1.

Snapshots from photobleaching and photoactivation experiments. In each column the first row shows the cell before the laser pulse. The next three images show the cellular fluorescence distribution at subsequent times after the laser pulse. Columns A, C, E, and F show photobleaching (GFP filter set, false color green). Columns B and D show photoactivation (rhodamine filter set, false color red). Columns A to D show two different DH5α cells expressing GFP (A and B show cell 1; C and D show cell 2). Columns E and F show a cephalexin-treated DH5α cell, expressing GFP, being bleached first at the pole (E) and then at the center (F). Time points are as follows (t = 0 is set arbitrarily as the end of the laser pulse). (A) −0.42, 0.05, 0.18, 0.32, and 4.3 s. (B) −0.08, 0.08, 0.35, 0.62, and 4.7 s. (C) −0.5, 0.03, 0.10, 0.23, and 0.83 s. (D) −0.1, 0.03, 0.23, 0.63, and 1.7 s. (E) −0.57, 0.03, 0.43, 0.77, and 2.8 s. (F) −0.57, 0.03, 0.20, 0.37, and 1.8 s. Bar = 4 μm.

FIG. 3.

Histogram of apparent diffusion coefficients for 120 DH5α cells measured by photobleaching. (Inset) Distribution of cell lengths for the same data. There is no significant correlation between cell length and apparent diffusion coefficient.

TABLE 1.

Apparent diffusion coefficients for GFP and cMBP-GFP in E. coli

Strain or construct	Da (μm2/s)	SD	na
DH5α	7.7	2.5	120
AB1157	4.4	0.9	34
M15 + pREP4	7.6	1.4	22
MC1000	7.3	1.2	4
MC1061	8.2	1.3	21
MG1655	6.2	1.4	30
RP437	7.0	1.5	39
DH5α, 500 μM IPTG	4.8	0.9	5
DH5α, 1 mM IPTG	3.6	0.7	7
cMBP-GFP in DH5α	2.5	0.6	41
His6-GFP in DH5α	4.6	2.0	12

^an, number of cells measured. 

Photoactivation of red GFP.

In addition to FRAP, we used photoactivation of a red fluorescent state of GFP (10). This method allowed us to reduce the irradiation energy by a factor of 10. Time sequences from typical photoactivation experiments are shown in Fig. 1B and D. One-dimensional intensity profiles along the length of one cell are given in Fig. 2C at different times after the laser pulse. Photoactivation of GFP occurs slowly, with a half time of 0.7 s (10). Therefore, Fourier amplitudes were normalized according to the total fluorescence in the cell, as described in Materials and Methods. A typical fit to the normalized exponential decay function is shown in Figure 2D. In most cases, useful data were obtained from three successive pulses before photoactivation was complete. Then, we switched to the GFP-FITC filter set and performed the photobleaching experiment on the same cell. The average ratio of D_a measured by photoactivation to D_a measured by photobleaching (on the same cell) (± SD) was 1.1 ± 0.15 for 34 cells. This indicates that the two methods provide equivalent information.

Experiments with GFP fusion proteins.

In addition to ordinary GFP, we measured diffusion of a somewhat larger fusion protein, cMBP-GFP, which consists of MBP fused to the N terminus of GFP. This protein lacks a periplasmic signal peptide and is confined to the cytoplasm. Its molecular mass is 72 kDa, about 2.6 times larger than GFP alone. Its apparent diffusion coefficient is 3.1 times lower than that of GFP alone: 2.5 ± 0.6 μm²/s. In another experiment, we measured diffusion of a GFP construct with six histidine residues inserted at the N terminus of the protein. We obtained a broad distribution of values for this construct, centered at a value lower than that of GFP: 4.6 ± 2.0 μm²/s (Table 1).

Measurements with a histidine-tagged GFP–β-galactosidase fusion protein were also attempted. This protein is fluorescent and possesses a specific β-galactosidase activity approximately equal to that of β-galactosidase. Active β-galactosidase is known to be tetrameric. The predicted molecular mass of a tetramer of this fusion protein is ∼500 kDa. By fluorescence microscopy, cells appeared elongated and fluorescence was observed in approximately two-thirds of each cell (in the polar regions, but not in the center). When specific regions of the cell were photoactivated or photobleached, no motion of GFP was observed whatsoever, either between labelled regions or within a single labelled region. This indicates that this complex is essentially immobile in the cytoplasm.

FRAP and photoactivation of GFP were not phototoxic.

At very high laser power, photodamage occurs and no fluorescence recovery is seen in the photobleached spot. At the laser powers used here, diffusive recovery of the bleached region was complete and no visible signs of cell damage were detected. Nevertheless, we have tried to assess the unintended side effects of our laser treatment in three different ways.

The first indication that we caused only minimal perturbation to the cell is that the measured apparent diffusion coefficients with photobleaching and photoactivation were in close agreement even though the former experiments required 10-fold longer laser pulses.

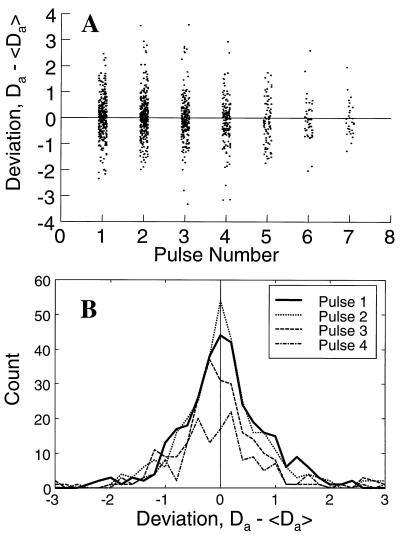
Second, in each photobleaching experiment a sequence of laser pulses was applied at the same site on a single cell. The measured values of D_a were compared with one another as a function of pulse number (see Fig. 5). Photoinduced cross-linking or other photodamage might be expected to progressively modify diffusive behavior. The absence of systematic variation in D_a with respect to pulse number implies that successive pulses did not cause accumulating mobility-altering photodamage to the cytoplasm.

FIG. 5.

Deviations of individual measurements of a single cell from their average values. For each cell, measurements of D_a were made several times. (A) Value of D_a obtained with a given measurement (“Pulse Number”) minus the average of all such measurements on the same cell as a function of the pulse number. There are fewer points at higher pulse numbers because fewer cells were subjected to a large (>3) total number of pulses. (B) Histograms of the data shown in panel A, showing the number of points as a function of deviation, for the first four pulses.

Third, as an indication of potential photodamage, we observed the response to irradiation of cells tethered by their flagella. The flagellar motor is powered by a proton gradient across the cell membrane; maintenance of a steady angular velocity indicates that the cell can sustain a steady proton motive force. We tethered GFP-expressing cells to coverslips by single flagella via antibodies to flagellin (24). The laser spot was focused on the stationary part of the rotating cell, and a series of laser pulses of the same power and duration as those used in the diffusion experiments were applied. We found reductions in angular velocity only after many more pulses or at energies greater than those used in actual experiments (data not shown).

These three types of experiments indicate that any potential damage to cells was minimal and did not substantially affect the diffusive behavior of GFP.

Ratio of decay rates for different diffusion modes.

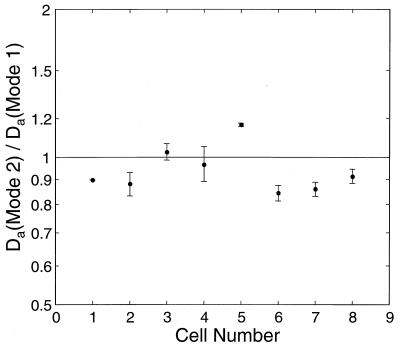
Since the diffusion time is proportional to L², long cells make higher decay modes accessible to measurement. To obtain the ratio of the decay rates of the first and second Fourier modes on the same cell, cells were treated with cephalexin, a drug which inhibits septation and causes cells to grow into long filaments. Eleven cells ranging in length from 7.5 to 11 μm were selected, and laser pulses were applied alternately at the cell pole and the cell center until GFP was completely photobleached. The first and second Fourier modes were analyzed from recovery data after photobleaching of the cell pole and center, respectively. An example of this experiment is presented in Fig. 1E and F. Values obtained for D_a were 7.2 ± 1.3 μm²/s (average ± SD; n = 8) for mode 1 and 6.8 ± 1.2 μm²/s for mode 2, consistent with the experiments done without cephelaxin on cells roughly half as long. On an individual cell the ratio of the two modes was close to unity, i.e., D_a(1)/D_a(2) = 1.06 with an SD of 0.11. Although a tendency toward ratios greater than 1 was observed (Fig. 4), this result indicates that the mobility-determining properties of the cytoplasm are not significantly compromised by cephalexin treatment and is an important consistency check on the analysis technique.

FIG. 4.

Ratio of apparent diffusion coefficients from Fourier modes 1 and 2 on single cephalexin-treated cells. Error bars indicate the SD of measurements over several laser pulses on the same cell. (For cells 1 and 5, only one pulse was made; therefore, there are no error bars.)

Sources of variation.

Errors and uncertainties in this measurement can be divided into at least three categories. First, there are “simple measurement errors” that affect measurements independently, whether they are made on the same cell or on different cells. Second, there are “cell errors,” random errors that affect different cells differently but have consistent effects when multiple measurements are made on the same individual. Third, there is “true variation,” which occurs if individuals possess different values of D_a from one another. Multiple measurements were made on each cell. A distribution of D_a values was thereby obtained for each individual. These distributions are, on average, symmetric about their average value and display no systematic trend with successive laser pulses (Fig. 5). For DH5α cells expressing GFP, the average SD of these distributions was 0.77 μm²/s (10% of the mean). This value is an estimate of the magnitude of the simple measurement error. A second estimate of the same statistic is obtained by assuming that GFP movement is diffusive and comparing the values of D_a obtained from the first and second Fourier modes on the same cell. In that case we obtain a similar value, 0.55 μm²/s (6% of the mean). The mean values of the single-cell D_a distributions form another distribution (Fig. 3). The width of this distribution is the cell-to-cell variation. It equals 2.5 μm²/s, which is more than three times larger than the measurement error. Its sources include cell errors, such as cell length estimation, and true variation, if it exists. Therefore, if natural variation of D_a exists in the population, the cell-to-cell variation places an upper limit of 2.5 μm²/s, or 32% of the mean, on its magnitude for GFP in DH5α cells.

DISCUSSION

We have performed FRAP and photoactivation experiments to measure the apparent diffusion coefficients of GFP and GFP fusion proteins in living E. coli cells. Differences with previous FRAP experiments used in other systems included the use of red GFP photoactivation, requiring 10 times less energy than photobleaching, and the analysis of recovery data throughout the cell rather than only in the irradiated spot. The apparent diffusion coefficient for GFP in bacterial cytoplasm is 7.7 ± 2.5 μm²/s, about 11 times lower than in water (87 μm²/s) (25, 26) and significantly lower than in eukaryotic cells (∼27 μm²/s) (25) and mitochondria (20 to 30 μm²/s) (19). Previously reported in vitro measurements suggest that background protein concentrations as high as 200 mg/ml (comparable to the total cellular protein concentration) reduce the mobility of tracer proteins (17 to 150 kDa) by factors of ∼3 (17). Therefore, direct effects of high total protein concentrations in the cell may not be sufficient to account for the low apparent diffusion coefficients observed here.

Low protein mobility might limit reaction times in some bacterial signal transduction systems. For example, in E. coli chemotaxis, cells change their swimming behavior in response to attractants or repellents. This response is mediated by diffusion of a 14 kDa protein, CheY, from its site of phosphorylation to the flagellar motor. The chemotactic response time has been measured to be 50 to 200 ms (15, 23). Based on our measurements for GFP, the expected time scale for diffusion of a small protein such as CheY through the cytoplasm would be on the order of 100 ms over a distance of 1 μm and thus comparable to the response time. These results are compatible with those of Segall et al., who previously estimated the rate of CheY diffusion to be about 10 μm²/s (22).

We observed no significant variations in the apparent GFP diffusion coefficients between common laboratory strains, suggesting that mobility is a property of the diffusing molecule (GFP) and generic structural properties of the cytoplasm, rather than the specific genetic background of the cell. In contrast, GFP concentration significantly influences GFP mobility, reducing the apparent diffusion coefficient of GFP twofold at high induction levels or in an overexpressing strain (Table 1). GFP reportedly dimerizes in solution at ionic strengths below 100 mM (28), and dimerization may contribute to the concentration-dependent effect. Modifications to GFP also caused quite significant changes in its diffusional mobility. Fusion to the much larger, tetramer-forming β-galactosidase protein essentially eliminates protein mobility and causes exclusion of GFP from the center of the cell. Addition of a cytoplasmically localized MBP domain (whose signal peptide has been deleted) reduced D_a by a factor of 3. This large reduction could in principle be due to viscous hydrodynamic effects related to the larger size and different shape of the fusion protein.

Surprisingly, however, a much smaller change to the protein, addition of a small six-histidine tag, commonly added to recombinant proteins for purification, reduced the apparent diffusion coefficient by as much as 40%. This effect is too drastic to be explained by viscosity and size alone. Slowing of the His-tagged protein could be due to nonspecific electrostatic interactions of the positively charged His tag with negatively charged nucleic acids. Regardless of the precise cause, however, this effect indicates that nongeometrical effects can exercise strong constraints on protein movement in vivo and demonstrates that even relatively small sequence changes may have large influences on protein mobility.

We have measured only an apparent diffusion coefficient here; the range of length scales to which it applies is not known. Substantial subdiffusive behavior, in which the average mean-squared displacement of a particle grows as a fractional power of time less than 1, i.e., <r²(t) > ∝ t^p, p < 1 (p of 1 corresponds to normal diffusion), has been observed in membranes by two-dimensional single-particle tracking experiments (11). It may occur as well in cytoplasm. FRAP experiments have difficulty distinguishing between normal diffusion with a fixed “immobile fraction” and subdiffusion (11). Direct signatures of subdiffusion are deviations from exponential temporal decay of the Fourier coefficients, which is difficult to detect, and disagreement of diffusion determinations made with different Fourier modes. We have been able to measure apparent diffusion in the lowest two modes in cephalexin-treated filamentous cells. This was found to be consistent with normal diffusion, with differences between the two modes averaging 6%, close to the limit of experimental precision (Fig. 4). This indicates that GFP transport is diffusive at least on the longest two length scales in the bacterium (the length and half-length of the cell). Because the cell length scale is long compared to the molecular scale, information on short-length diffusion inside cells, obtainable by other techniques, would complement these measurements and indicate whether GFP movement is truly diffusive.

In summary, the data presented here provide apparent diffusion rates for proteins expressed in E. coli. They also show that FRAP and photoactivation measurements must be interpreted with caution; in particular, one cannot assign an effective viscosity to the cytoplasm which would be applicable to all proteins inside it. Mobility depends sensitively on the protein under consideration, on its concentration, and on any genetic modification it may have undergone, such as His tagging. Thus, protein mobility must be seen not only as a property of the geometrical structure of cytoplasm and the background macromolecular concentrations alone but also as a characteristic of the diffusing species. Future work may elucidate the causes of the protein mobility variations observed here and show how they are tolerated, or compensated for, by cellular networks.