Evaluating differences between formulated dietary net energy values and net energy values determined from growth performance in finishing beef steers

Abstract

Based on principles of the California Net Energy System, the dry matter intake (DMI) by feedlot cattle can be subdivided into DMI required for maintenance and DMI required for gain. Thus, if DMI along with body weight at a compositional endpoint and shrunk weight gain are known, dietary concentrations of net energy for maintenance and gain (NEm and NEg, respectively) can be calculated from growth performance data. Close agreement between growth performance-predicted and tabular NEm and NEg values implies the system can be used to accurately predict growth performance and be used to evaluate marketing and management decisions. We used 747 pen means from 21 research studies conducted at Texas Tech University and South Dakota State University to assess the agreement between growth performance-predicted NEm and NEg values and those calculated from tabular energy values for feeds reported by the 2016 National Academies of Science, Engineering, and Medicine publication on beef cattle nutrient requirements. Regression of growth performance-predicted values on tabular values with adjustment for random effects of study indicated that the intercepts of the two regressions did not differ from zero, and the slopes did not differ from one. Residuals (tabular minus growth performance-predicted values) for NEm and NEg averaged −0.003 and −0.005, respectively. Nonetheless, the precision of growth performance-predicted values was low, with approximately 40.3% of performance-predicted NEm values and 30.9% of NEg values falling within 2.5% of the corresponding tabular value. Residuals for NEm were divided into quintiles to evaluate dietary, growth performance, carcass, and energetics variables that might help explain lack of precision in growth performance-predicted values. Among the variables considered, gain:feed ratio was the most discriminating, with differences (P < 0.05) among each of the quintiles. Despite these differences, however, gain:feed ratio did not explain important percentages of variation in components of growth performance-predicted NEm values like maintenance energy requirements (r² = 0.112) and retained energy (r² = 0.003). Further research with large datasets that include dietary composition, growth performance and carcass data, and environmental variables, along with fundamental research on maintenance requirements and energy retention, will be required to identify ways to improve the precision of growth performance-predicted NE values.

On average, dietary net energy values calculated from growth performance and carcass data agree with those calculated from tabular net energy values of feeds, but the precision of growth performance-predicted values is low. Further experimentation related to energy requirements of beef cattle as well as analysis of growth performance and carcass data could provide tools for improving the precision of growth performance-predicted net energy values.

Introduction

The California Net Energy System (CNES) was developed more than 50 yr ago and has been updated over the years to account for changes in cattle type and mature body weight at harvest. The CNES partitions energy into net energy for maintenance (NEm) and net energy for gain (NEg), both of which can be calculated for feedstuffs as a cubic function of dietary metabolizable energy (ME) concentration. For growing and finishing beef steers, the NEm required can be calculated from shrunk body weight (SBW), with energy available for gain (i.e., NEg) calculated from total dry matter intake (DMI) minus feed required to meet the NEm requirement. Likewise, shrunk weight gain (SWG) can be predicted from 13.91 × RE^0.9116 × EQSBW^−0.6837, where RE is retained energy (Mcal), which is equal to feed available for gain, and EQSBW is equivalent SBW (NASEM, 2016). Thus, if body composition can be reliably estimated relative to maturity, SWG and DMI can be used to calculate growth performance-predicted net energy values using a quadratic solution (Zinn and Shen, 1998). Evaluating observed vs. growth performance-predicted values of NEm and NEg enables nutritionists to better understand differences in maintenance energy requirements, efficiency of energy use, associative or antagonistic effects of feedstuffs, nutrient deficiencies, exogenous growth promotors, and environmental factors that affect growth performance (Owens and Hicks, 2019). Our objective was to use feedlot growth performance and carcass data from pens of cattle fed at three research locations at two universities to identify factors affecting residuals between dietary NEm and NEg values calculated from NASEM (2016) tabular data and growth performance-predicted NEm and NEg values. Our hypothesis was that analysis of residuals would provide an indication of key factors affecting the accuracy and precision of growth performance-predicted net energy values.

Materials and Methods

Data used in this paper were generated from 21 experiments previously conducted at Texas Tech University and South Dakota State University, which had been approved by the Institutional Animal Care and Use Committees at the two institutions. Thus, no live animals were used by the authors, and Institutional Animal Care and Use Approval was not necessary.

Performance and carcass dataset

Pen growth performance and carcass data from 747 pens of beef steers (typically British or British crossbred) were compiled in spreadsheet format. The complete dataset in spreadsheet format is available as Supplementary Material. Three hundred twenty-six pens were from seven different experiments conducted at the Texas Tech University Burnett Center from 2003 to 2012, with another 151 pens from three different experiments conducted at the Burnett Center from 2019 to 2020. Data from an additional 270 pens from 11 different studies conducted at the South Dakota State University Ruminant Nutrition Center (five experiments) or the Southeast Research Farm (six experiments) were conducted from 2019 to 2021. Experiments were initiated in all months of the year except July and August, and days on feed averaged 155 (range = 95 to 258 d). All experiments were conducted during the finishing phase except for one study from South Dakota that included both growing and finishing phases.

At Texas Tech University, cattle were housed in partially slotted-floor, concrete-surface pens (2.9 m × 5.6 m; 2.4 m of feed bunk space) with a heated water tank in each pen. The number of cattle per pen at Texas Tech University was generally 4, with 5 steers/pen in two experiments conducted in 2003. Pens at South Dakota State University Ruminant Nutrition Center were 7.62 m × 7.62 m with a concrete surface, fence-line feed bunks, and a heated water tank. The number of animals per pen was typically 8 (one study = 4 to 5). At the Southeast Research Farm pens were either open lots with a soil surface (13.7 m × 30.5 m with 6.1 m of feed bunk space) that housed 8 to 12 animals/pen or covered-barn pens with a concrete surface (4.9 m × 12 m total pen space with 4.9 m × 4.9 m of covered space and 4.8 m of feed bunk space) that housed 5 to 6 animals/pen. All pens had a heated water tank.

Corn was the primary grain in finishing diets, with steam-flaked corn used at Texas Tech University and dry-rolled or a 50:50 mixture of dry-rolled and high-moisture corn used at the South Dakota State University locations. Typical roughage sources were alfalfa hay and cottonseed hulls (Texas) and corn silage (South Dakota). Cattle at Texas Tech were fed once daily in the morning, as were cattle at the South Dakota State Southeast Research Farm and for one study conducted South Dakota State Ruminant Nutrition Center, whereas cattle in all other studies conducted at the South State Dakota Ruminant Nutrition Center were fed twice daily (50% of the daily allotment at each feeding).

Carcass data were collected in each of the 21 studies included in the dataset. Relevant data for the current analyses included hot carcass weight (HCW), fat thickness at the 12th rib, longissimus muscle area, marbling score, and quality grade. Carcass-adjusted final SBW was calculated as HCW divided by a dressing percent of 64% (0.64) and used along with initial SBW (4% shrink assumed) and days on feed to calculate SWG, with gain-to-feed ratio (G:F) calculated as SWG divided by DMI. Empty body weight (EBW) was calculated as 1.316 × HCW + 32.29 (Garrett, 1987). The percentage of estimated empty body fat (EBF) was calculated using the equation of Guiroy et al. (2001), which includes HCW, 12th rib fat, longissimus muscle area, and quality grade score (4 = Select, 5 = Choice⁻, 6 = Choice, 7 = Choice⁺, and 8 = Prime). The EBF value was then used to calculate BW adjusted to 28% EBF as per Guiroy et al. (2001), where adjusted final SBW, kg = (EBW, kg + (28 – EBF, %) × 14.26)/0.891. The 28% EBF adjusted final SBW was used in the calculation of average EQSBW ([478/adjusted final SBW, kg] × mean feeding SBW, kg) as per NASEM (2016), where mean feeding SBW was calculated as the average of initial SBW and carcass-adjusted final SBW.

Feed ingredient composition data for the diets in each study were used to determine the NASEM (2016) tabular NEm and NEg values. In cases where initial diets (start-up phase) differed from the finishing diet, or in the one experiment that included growing and finishing phases, overall NEm and NEg values used for data analyses were weighted by the days that a particular diet was fed. Measured values for crude protein and acid detergent fiber were available for all experiments. Dietary percentage of ether extract was available for all experiments except for one Texas Tech experiment, for which ether extract values were calculated from NASEM (2016) values.

Growth performance-predicted NEm and NEg values were calculated following the general quadratic solution approach of Zinn and Shen (1998) based on the relationship between dietary concentrations of NEm and NEg, average DMI, mean feeding SBW, and SWG. Specifically, daily DMI can be partitioned into DMI for maintenance and DMI for gain by dividing the respective NE requirement by the dietary concentration of NEm or NEg as follows:

DMI, kg/d = ([NEm required, Mcal/d] ÷ [Dietary NEm concentration, Mcal/kg]) + ([NEg required, Mcal/d] ÷ [Dietary NEg concentration, Mcal/kg])

The NEm (0.077 × mean feeding SBW^0.75) and NEg required (0.0557 × EQSBW^0.75 × SWG^1.097) can be calculated according to NASEM (2016) equations. The equation can then be reduced to only one unknown by replacing dietary NEg concentration with the equivalent NEm value reported by Zinn and Shen (1998; NEg, Mcal/kg = 0.877 × NEm, Mcal/kg – 0.41), allowing the resulting quadratic equation of the form ax² + bx + c = 0 to be solved by use of the general quadratic formula $\left(b^2\pm \sqrt{(b^2-4ac)}\right)/(2a)$. Once NEm concentration is determined, NEg concentration (Mcal/kg) is calculated from 0.877 × NEm, Mcal/kg – 0.41.

Statistical methods

Formulated vs. Growth Performance-Predicted Net Energy Values. The relationship between formulated and growth performance-predicted NEm and NEg concentrations was evaluated using the Mixed procedure of SAS (SAS Inst. Inc., Cary, NC; version 9.3). The model included a random intercept effect for study with an unstructured covariance structure. Study-adjusted growth performance-predicted values were created by adding the residuals from the mixed model to the model-predicted growth performance-predicted values as described by Galyean and Tedeschi (2014).

Analysis of Residuals. Residuals were defined as the difference between the formulated dietary NEm or NEg concentrations and the respective growth performance-predicted values. Specifically, the growth performance-predicted values were subtracted from the formulated values; hence, positive residuals reflect greater NE concentrations for formulated values, whereas negative residuals reflect greater NE concentrations for growth performance-predicted values.

To evaluate relationships between NEm residuals and aspects of growth performance and carcass data that might affect the relationship between formulated and growth performance-predicted NEm values, the Rank procedure of SAS was used to sort the data into quintiles of the NEm residuals. The Mixed procedure of SAS was then used to analyze the quintile data with a model that included fixed effects of quintile and treatment nested within study, and the random effect of study nested within quintile group. The treatment nested within study effect was not estimable for dietary NEm and NEg concentrations, so the overall effect of treatment replaced treatment nested within study. For dietary concentrations of crude protein and acid detergent fiber, the random effect of study nested within quintile group was not estimable; hence, a reduced model with the random effect eliminated was used. Quintile group least squares means were compared with the pdiff procedure of SAS. Because the growth performance-predicted NEg value is a linear function of the growth performance-predicted NEm value, quintile analyses were only conducted with NEm data.

Results and Discussion

Relationships between performance-predicted and formulated net energy values

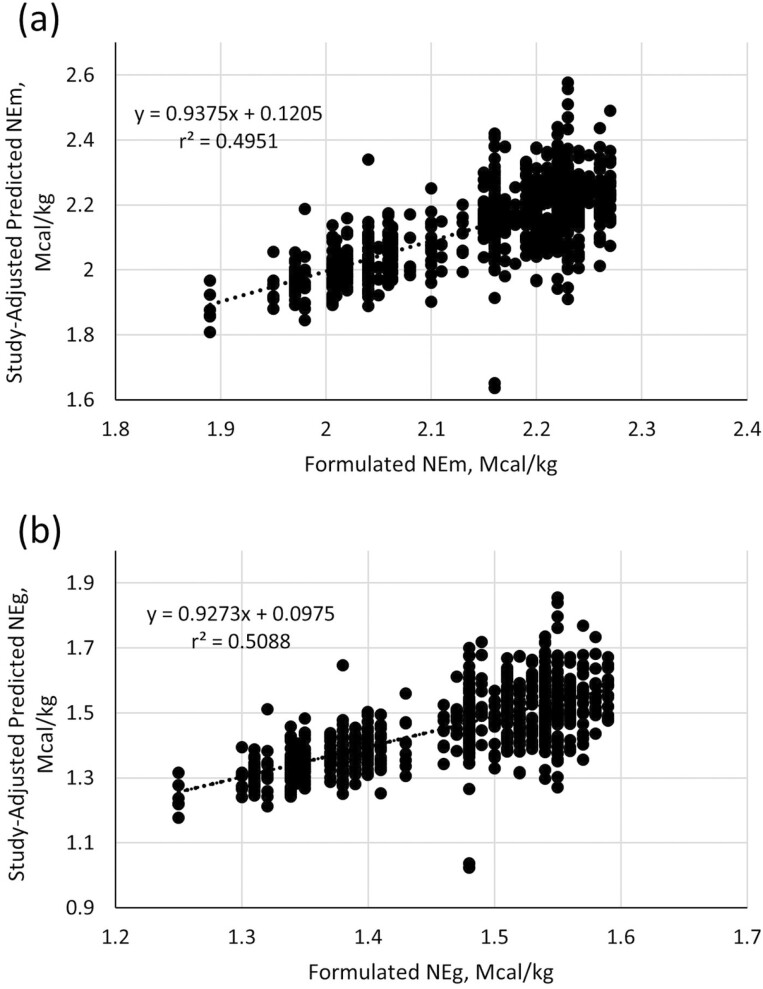
Overall means for growth performance and carcass variables, formulated and growth performance-predicted NE values, and variables related to calculation of predicted NE values are shown in Table 1. Both the formulated and growth performance-predicted NEm and NEg concentrations averaged 2.14 and 1.47 Mcal/kg, respectively, with corresponding NEm and NEg residuals of −0.003 and −0.005, respectively. In a summary of 23 research studies conducted in small pens with 40 different diets, Owens and Hicks (2019) reported that on average, growth performance-predicted NEg values were 101% of formulated values. For a commercial dataset with 2,245 pens of cattle fed similar diets, growth performance-predicted NEg values were 93.8% of formulated values. Relationships between formulated and study-adjusted growth performance-predicted NEm and NEg values in our dataset are depicted graphically in Figure 1. Based on the 95% confidence limits of the regressions of growth performance-predicted NEm and NEg concentrations on formulated NEm and NEg values, the intercepts of these two regression equations did not differ from 0, and the slopes did not differ from 1. This finding implies that “on average,” growth performance-predicted NE values agreed with formulated values.

Table 1.

Overall means for variables related to diet, growth performance, carcass, and components of net energy calculations in the dataset

Item1	Mean	Standard deviation	Minimum	Maximum
Diet NEm, Mcal/kg	2.14	0.096	1.89	2.27
Predicted NEm, Mcal/kg	2.14	0.174	1.72	2.65
NEm residual	−0.003	0.119	−0.421	0.442
Diet NEg, Mcal/kg	1.47	0.087	1.25	1.59
Predicted NEg, Mcal/kg	1.47	0.153	1.10	1.91
NEg residual	−0.005	0.104	−0.365	0.383
Diet crude protein, %	13.65	1.393	11.71	18.36
Diet ether extract, %	5.01	0.953	2.98	7.21
Diet acid detergent fiber, %	9.76	2.633	5.78	15.94
Initial SBW, kg	359.5	51.09	232.5	463.3
Carcass-adjusted final SBW, kg	610.9	42.88	500.0	737.1
Mean feeding BW, kg	485.3	36.42	366.3	591.0
Days on feed	154.9	35.93	96.0	258.0
Carcass-adjusted SWG, kg	1.63	0.225	1.02	2.57
Dry matter intake, kg	9.63	1.596	6.97	14.98
Gain:feed ratio	0.171	0.0186	0.113	0.223
Hot carcass weight, kg	391.0	27.44	320.0	471.7
12th rib fat, cm	1.38	0.349	0.53	2.68
Longissimus muscle area, cm2	89.4	6.84	67.3	110.2
Marbling score	576.1	61.18	415.0	810.0
Quality grade score	5.3	0.66	4.0	8.0
NEm required, Mcal/d	7.96	0.447	6.45	9.23
NEg required, Mcal/d	8.56	1.460	5.22	14.85
Estimated empty body fat, %	30.1	2.16	24.9	38.8
Empty BW, kg	546.8	36.11	453.4	653.1
Equivalent shrunk BW, kg	400.7	28.48	327.5	479.7
Adjusted final SBW, kg	580.1	39.32	450.3	695.4

¹Based on 747 pen observations. BW, body weight; SBW, shrunk BW; SWG, daily SBW gain. Predicted NEm and NEg values were calculated from performance data using the methods of Zinn and Shen (1998). Marbling score, where 500 = Small⁰, 600 = Modest⁰, 700 = Moderate⁰, etc. Quality grade score is derived from marbling score, where 5 = Choice−, 6 = Choice⁰, 7 = Choice⁺, etc.

Figure 1.

Study-adjusted NEm (a) and NEg concentrations (b) predicted from growth performance vs. NEm concentration calculated from dietary ingredients using NASEM (2016) tabular values. For predicted NEm concentration, the 95% confidence limits from the mixed-model analyses were −0.357 and 0.598 for the intercept and 0.726 and 1.149 for the slope. Comparable 95% confidence interval limits for predicted NEg were −0.222 and 0.417 for the intercept and 0.720 and 1.134 for the slope.

Despite agreement on average, the scatter of study-adjusted predicted NE values indicates that the precision of these estimates was disappointing. The standard deviation as a percentage of the mean was 8.1% for predicted NEm values and 6% for predicted NEg values, the latter value being similar to the values of 4.8% reported by Owens and Hicks (2019) for a commercial dataset with 2,245 feedlot pens fed a common diet and 7.5% for cattle fed 40 different diets in small-pen experiments. Using a data simulation approach, Vasconcelos and Galyean (2008) concluded that NE values calculated from growth performance data did not yield statistical advantages in sensitivity compared with the growth performance variables from which they were calculated, reflecting similar variation relative to the mean in growth performance-predicted NE values and underlying growth performance data.

Assuming a high-precision target for practical application of growth performance-predicted NE values is to be within 2.5% of the formulated value, in the current dataset, only 40.3% and 30.9% of growth performance-predicted NEm and NEg values would fall within the 2.5% target. If the target is moved to 5% of the formulated value, 66.7% and 57.6% of predicted NEm and NEg values would fall within the limits, whereas with a 10% of the mean target, 92.8% and 85.8% of predicted NEm and NEg values would be captured within the desired bounds. Thus, present results suggest that the probability of achieving close agreement between formulated dietary NE values and values based on growth performance is not as high as might be desired for practical application to prediction of cattle growth performance.

There are many reasons for variation and lack of agreement between growth performance-predicted NE values and formulated values. Tabular dietary NE values in NASEM (2016) are calculated from cubic equations based on dietary ME concentration, which in the NASEM (2016) model is computed from total digestible nutrients. Thus, the potential exists for tabular values to over- or under-estimate the actual NEm and NEg concentrations in feeds. Likewise, errors in feed mixing would affect the validity of tabular estimates. For growth performance-predicted values, lack of accuracy in measurements of BW, DMI, average daily gain (ADG), and body composition at harvest will affect accuracy and precision. Moreover, Owens and Hicks (2019) noted that nutrient deficiencies for some animals in a pen, environmental conditions like heat and cold stress, and feed selection and sorting by cattle in a pen would all affect agreement between performance-predicted and formulated NE values. Thus, practical utility of growth performance-predicted NE values requires careful attention to accuracy and precision of data collection methods, as well as fastidious monitoring of environmental and other external factors that can affect the quality of resulting estimates.

Quintile analyses of residuals

As noted previously, the data were sorted into quintiles based on the NEm residual for each pen. Quintile 1 represented pens of cattle for which the NEm residual was strongly negative (e.g., greater growth performance-predicted than formulated NEm value), whereas Quintile 5 represented pens of cattle for which the NEm residual was strongly positive (e.g., greater formulated than growth performance-predicted NEm value). Differences among mean values for the quintiles for variables related to diet, growth performance, carcass characteristics, and components of net energy calculations are shown in Tables 2 to 5. The key point of the quintile analyses was to elucidate differences among the quintiles that might shed light on factors influencing the precision of growth performance-predicted NE values. It should be noted that because quintile means are least-squares means adjusted for effects of treatment nested within quintile group and study nested within quintile group, they will differ from the unadjusted means shown in Table 1.

Table 2.

Quintile means for variables related to diet in the dataset

Item1	Quintile2					SEM3
	1	2	3	4	5
Number of pens	149	150	149	150	149	—
Diet NEm, Mcal/kg	2.20	2.19	2.19	2.19	2.20	0.015
Predicted NEm, Mcal/kg	2.27a	2.16b	2.11c	2.06d	1.97e	0.007
NEm residual	−0.159a	−0.046b	0.004c	0.057d	0.145e	0.0072
Diet NEg, Mcal/kg	1.52	1.51	1.51	1.51	1.51	0.014
Predicted NEg, Mcal/kg	1.58a	1.48b	1.44c	1.39d	1.32e	0.006
NEg residual	−0.143a	−0.043b	0.001c	0.047d	0.124e	0.0063
Diet crude protein, %	13.41	13.41	13.41	13.41	13.41	0.003
Diet ether extract, %	4.78	4.78	4.78	4.78	4.78	0.000
Diet acid detergent fiber, %	9.93	9.93	9.92	9.92	9.92	0.006

¹Predicted NEm and NEg values were calculated from performance data using the methods of Zinn and Shen (1998).

²Quintles are based on NEm residuals (formulated NEm minus growth performance-predicted NEm), where Quintile 1 has the most negative differences and Quintile 5 has the most positive differences.

³Standard error of quintile means. The largest SEM value is reported.

^a,b,c,d,eRow means that do not have the same superscript differ, P < 0.05.

Differences among the quintiles with respect to dietary variables are shown in Table 2. Formulated NEm and NEg values did not differ among the quintiles, but growth performance-predicted NEm and NEg values were different (P < 0.05) for each quintile, which is reflected in similar differences (P < 0.05) among the quintiles in NEm and NEg residuals. Dietary concentrations of crude protein, ether extract, and acid detergent fiber did not differ among quintiles, suggesting that despite important ranges in the concentrations of these components in the dataset (Table 1), these differences did not seem to be related to variation in performance-predicted NE values.

Among variables related to performance (Table 3), carcass-adjusted final SBW was greater (P < 0.05) for Quintiles 1, 2, and 3 than for Quintiles 4 and 5. Differences also were noted in mean feeding SBW, with greater (P < 0.05) values for Quintiles 1 and 3 than for Quintiles 4 and 5, but no difference between Quintile 2 and 4. Differences in SBW with similar days on feed among the quintiles resulted in differences for each quintile (P < 0.05) in carcass-adjusted ADG, with the exception of Quintiles 2 and 3, which did not differ from each other. Dry matter intake was less (P < 0.05) for Quintile 1 than for Quintiles 3, 4, and 5, which did not differ from each other or Quintile 2. Differences in ADG and DMI resulted in differences (P < 0.05) for each of the quintiles in G:F, with a nearly 17% decrease in G:F from Quintile 1 to 5. Thus, among growth performance variables, G:F seemed to provide the greatest ability to differentiate among the quintiles of NEm residuals.

Table 3.

Quintile means for variables related to growth performance measurements in the dataset

Item1	Quintile2					SEM3
	1	2	3	4	5
Number of pens	149	150	149	150	149	—
Initial SBW, kg	368.0	366.8	368.7	364.6	363.8	4.21
Carcass-adjusted final SBW, kg	629.5a	623.1a	621.9a	606.1b	597.5b	5.16
Mean feeding SBW, kg	498.4a	494.8a,b	495.4a	485.3b,c	480.6c	4.38
Days on feed	149.5	151.2	151.8	151.2	151.2	2.00
Carcass-adjusted SWG, kg	1.77a	1.72b	1.69b	1.62c	1.55d	0.014
Dry matter intake, kg	9.70a	9.95a,b	10.08b	9.99b	10.16b	0.103
Gain:feed ratio4	0.185a	0.174b	0.169c	0.163d	0.154e	0.0009

¹BW, body weight; SBW, shrunk BW; SWG, daily SBW gain.

²Quintles are based on NEm residuals (formulated NEm minus growth performance-predicted NEm), where Quintile 1 has the most negative differences and Quintile 5 has the most positive differences.

³Standard error of quintile means. The largest SEM value is reported.

⁴Carcass-adjusted SWG, kg/dry matter intake, kg.

^a,b,c,d,eRow means that do not have the same superscript differ, P < 0.05.

For carcass variables (Table 4), only HCW and 12th rib fat differed among the quintiles, with greater (P < 0.05) HCW for Quintiles 1, 2, and 3 compared with Quintiles 4 and 5. With 12th rib fat, the major difference was the higher (P < 0.05) value (1.52 cm) for Quintile 1 than for the average of the other quintiles (1.31 cm), although smaller differences were noted among these quintiles.

Table 4.

Quintile means for variables related to carcass measurements in the dataset

Item1	Quintile2					SEM3
	1	2	3	4	5
Number of pens	149	150	149	150	149	—
Hot carcass weight, kg	402.9a	398.8a	398.0a	387.9b	382.4b	3.30
12th rib fat, cm	1.52a	1.39b	1.34b,c	1.27c,d	1.24d	0.034
Longissimus muscle area, cm2	90.8	90.5	90.4	89.1	88.7	0.61
Marbling score	583.9	581.9	581.4	578.4	567.5	5.55
Quality grade score	5.4	5.4	5.3	5.3	5.1	0.07

¹Marbling score, where 500 = Small⁰, 600 = Modest⁰, 700 = Moderate⁰, etc. Quality grade score is derived from marbling score, where 5 = Choice−, 6 = Choice⁰, 7 = Choice⁺, etc.

²Quintles are based on NEm residuals (formulated NEm minus growth performance-predicted NEm), where Quintile 1 has the most negative differences and Quintile 5 has the most positive differences.

³Standard error of quintile means. The largest SEM value is reported.

^a,b,c,dRow means that do not have the same superscript differ, P < 0.05.

Among the variables related to calculation of growth performance-predicted NE values (Table 5), NEg required differed (P < 0.05) for each of the quintiles, except for Quintiles 2 and 3, which did not differ from each other. Greater NEg required is a reflection of greater carcass-adjusted ADG, which showed the same pattern of significant differences as NEg required. Estimated EBF was greatest for Quintile 1, greater (P < 0.05) for Quintile 2 than for Quintiles 4 and 5, but not different between Quintiles 2 and 3, Quintiles 3 and 4, and Quintiles 4 and 5. Empty BW was greater (P < 0.05) for Quintiles 1 through 3 than for Quintiles 4 and 5, and EQSBW had a similar pattern, although only Quintile 1 differed (P < 0.05) from the other four quintiles. Adjusted final SBW, which is calculated from EBW and estimated EBF did not differ among the quintiles.

Table 5.

Quintile means for variables related to net energy calculations in the dataset

Item1	Quintile2					SEM3
	1	2	3	4	5
Number of pens	149	150	149	150	149	—
NEm required, Mcal/d	7.84	7.86	7.86	7.75	7.71	0.104
NEg required, Mcal/d	9.48a	9.09b	8.89b	8.44c	7.99d	0.110
Estimated empty body fat, %	31.0a	30.3b	30.0b,c	29.6c,d	29.2d	0.21
Empty BW, kg	562.4a	557.1a	556.1a	542.7b	535.5b	4.35
Equivalent shrunk BW, kg	409.7a	403.0a,b	400.6b,c	397.4b,c	395.7c	2.79
Adjusted final SBW, kg	585.2	588.9	590.8	583.6	581.9	3.54

¹BW, body weight; SBW, shrunk BW.

²Quintles are based on NEm residuals (formulated NEm minus growth performance-predicted NEm), where Quintile 1 has the most negative differences and Quintile 5 has the most positive differences.

³Standard error of quintile means. The largest SEM value is reported.

^a,b,c,dRow means that do not have the same superscript differ, P < 0.05.

Applications

If pens of cattle with positive residuals (growth performance-predicted NEm < formulated NEm; Quintile 5) have increased maintenance requirements and decreased digestible energy (DE) and efficiency of converting DE to ME and ME to RE, and pens of efficient cattle (negative residuals; Quintile 1) have decreased maintenance requirements and a greater efficiencies of energy capture, adjusting NEm requirements and NEg available for gain (e.g., RE) accordingly would improve the precision of growth performance-predicted NE values. It is generally accepted that a static value for maintenance (NEm required, Mcal/d = 0.077 × shrunk BW^0.75) is not applicable to all cattle or production situations. For example, the NASEM (2016) model includes potential adjustments to maintenance requirements for breed, previous plane of nutrition, and sex (bulls vs. steers and heifers). Ferrell and Oltjen (2008) noted that adding variable maintenance requirements to the University of California-Davis growth model improved the precision of the model in terms of predicting RE and body fat. Cattle with a low residual feed intake (greater G:F) had a greater partial efficiency of growth (ADG/DMI available for gain) than cattle with a high residual feed intake (lesser G:F; Carstens and Tedeschi, 2006), suggesting differences in efficiency of energy use above ­maintenance between groups that differed in G:F, although maintenance requirements could have differed between groups as well. Similarly, de Assis Lage et al. (2019) reported that heifers classified as high efficiency tended (P = 0.06) to have an increased proportion of gross energy (GE) captured as DE, as well as a greater ME:GE ratio.

Overall, G:F was the most discriminating variable with respect to differences among the quintiles of NEm residuals. Pens of cattle that were more efficient had greater growth performance-predicted NEm or NEg values, whereas the least efficient pens of cattle had greater formulated than growth performance-predicted NE values. Given that G:F is strongly associated with differences among quintiles, might it be a tool to make such adjustments and improve the precision of growth performance-predicted predictions of NE values? In their analysis of performance-predicted NEg quartile data from commercial feedlot pens, Owens and Hicks (2019) noted that final SBW, ADG, and G:F differed (P < 0.05) among all the quartiles, with changes across the quartiles of 4.5%, 13.3%, and 12.5%, respectively. Although Owens and Hicks (2019) did not have access to carcass data to calculate an adjusted final SBW, their percent changes in predicted NEg were similar to ours for quintiles of NEm residuals (5.4%, 14.2%, and 20.1% for final SBW, ADG, and G:F, respectively). Using a simulation approach, Vasconcelos and Galyean (2008) noted that G:F was a more sensitive measure of treatment effects than growth performance-predicted NE values in cases where G:F increased as a result of increased ADG with no change in DMI, which is similar to the manner in which G:F increased in the current dataset.

Incorporating adjustments to NEm requirements, as well as adjusting RE for differences in efficiency among pens of cattle could offer the potential to improve the precision of growth performance-predicted NE estimates. Within contemporary feedlot growth performance data for cattle fed similar diets under similar environmental conditions, G:F might be a practical tool for making such adjustments. Nonetheless, G:F is a ratio of two key elements in the calculation of performance-predicted NEm values – ADG and DMI. As a result, G:F in our dataset was significantly associated with growth performance-predicted NEm (performance-predicted NEm, Mcal/kg = 0.755 + 8.115 × G:F; P < 0.001; r² = 0.745; root mean square error = 0.088). Differences among the quintiles in G:F reflect this relationship and thereby might not be particularly useful in explaining the underlying cause(s) of differences between formulated and growth performance-predicted NE values among the quintiles. In addition, increased G:F can result from different growth performance outcomes, including increased SWG with no change in DMI, increased SWG combined with increased DMI, and no change in SWG combined with decreased DMI, which could influence results. As noted previously, in our dataset, increased G:F was generally associated with no change or a small decrease in DMI and increased SWG.

To examine the potential value of differences in G:F to adjust growth performance-predicted NE values, we regressed NEm required on G:F (NEm required, Mcal/d = 9.335 – 8.050 × G:F; P < 0.001; r² = 0.112; root mean square error = 0.422). The negative slope of the relationship suggests lower maintenance requirements with increasing G:F, but the low r² and relatively high root mean square error (5.3% of the mean), suggest a lesser predictive value than might be desired to confidently alter maintenance requirements. Similarly, because RE is a key component of performance-predicted values, we regressed RE calculated from the NASEM (2016) equation (RE, Mcal/d = 0.0557 × EQSBW^0.75 × SWG^1.097) on G:F. The resulting regression equation (RE, Mcal/d = 7.793 + 4.497 × G:F; P > 0.11; r² = 0.003; root mean square error = 1.459) was not significant and would have essentially no value for adjusting RE for differences in G:F. Thus, we conclude that differences in G:F among the quintiles reflect its strong relationship to growth performance-predicted NE values but not an underlying explanation for the lack of precision in the values. The same conclusion most likely applies to the other growth performance and carcass variables evaluated in the quintile analyses, as in some way, all these variables are a component of predicted NE values.

In terms of growth performance-predicted NE values, variation could result from changes in energy requirements for both maintenance and gain associated with environmental factors that are not accounted for in the calculations (e.g., Wagner et al., 2008; Smerchek and Smith, 2020). Likewise, errors in measurement of DMI associated with feed delivery and bunk management and in ADG associated with body weight measurements would critically affect these variables, as could inaccurate estimates of body weight at the target endpoint (e.g., EQSBW and adjusted final SBW). On the formulated side of NE values, static tabular values do not account for variation in feed ingredient composition across time that is likely associated with different lots of ingredients that are used during long-term feeding trials. In addition, it is important to calculate NE values from diet formulations that have been adjusted for ingredient DM values measured regularly during the feeding period. Inaccurate feed mixing (e.g., lack of agreement between formulated vs. milled and delivered feed) also would affect estimates of formulated values, and feed sorting by cattle could result in differences among cattle in the same pen with respect to the actual NE concentration of consumed diets. With tabular values assumed to be fixed, such errors contribute to greater variation in residuals between formulated and growth performance-predicted NE values. Thus, given the many unknowns associated with both the feed and animal growth performance aspects of the calculations, as well as management factors, the potential to improve the precision of growth performance-predicted NEm and NEg values likely has limits.

Conclusions and Recommendations

If SBW and DMI are measured accurately and body composition, specifically body fat content at harvest, can be estimated, performance and carcass data can be used to estimate dietary NEm and NEg concentrations. Strong alignment between growth performance-predicted and formulated NEm and NEg values means that the CNES can be used to accurately predict growth performance, allowing producers to make better-informed management and marketing decisions. Our data suggest that on average, growth performance-predicted NE values agree with formulated values based on NASEM (2016) tabular data for feeds; however, the precision of these predicted values is low. As a result, in our data, the likelihood of performance-predicted values being within 2.5% of formulated values was approximately 40% or less.

Given our results, a logical question is “Should the CNES be completely revamped, or can we continue to adjust the system to make it more precise?” Because of the potential time and cost of completely revamping the CNES, an approach that focuses on adjustments to improve precision is probably the most reasonable course of action. As a means of improving precision, Owens and Hicks (2019) suggested that an international committee could work toward developing relationships between nutrient supply and cattle performance, including sensitivity analyses to evaluate results from the current version of the CNES as defined in NASEM (2016) against large datasets that include performance and carcass data from various geographic regions. If this approach is taken, including environmental data, animal health and production background information, and diet and feed ingredient nutrient profiles in such datasets would be an important component of data curation. ­Achieving such a goal will require a substantial commitment of finances, resources, and time by industry, university, and government partners.

Because maintenance requirements are an important component of growth performance predicted NE values, experimentation to better define biological variation in maintenance requirements (e.g., animal, management, and environmental effects) would seem to be a logical next step. In addition, further evaluation of the relationships between RE, SWG, and body composition at maturity, another important element of growth performance-predicted NE values, would seem to be an area where direct experimentation could be helpful. Such new data in combination with conclusions drawn from analyses of large datasets should provide a pathway to increase the precision and thereby the practical utility of the CNES.

Glossary

Abbreviations:

ADG

average daily gain

CNES

California net energy system

DE

digestible energy

DMI

dry matter intake

EBF

empty body fat

EBW

empty body weight

EQSBW

equivalent shrunk body weight

GE

gross energy (intake energy)

G:F

gain:feed ratio

HCW

hot carcass weight

ME

metabolizable energy

NEm

net energy for maintenance

NEg

net energy for gain

RE

retained energy

SBW

shrunk body weight

SWG

shrunk weight gain

TDN

total digestible nutrients

Conflict of interest statement

The authors declare no real or perceived conflicts of interest.