Coupled topological flat and wide bands: Quasiparticle formation and destruction

Abstract

Flat bands amplify correlation effects and are of extensive current interest. They provide a platform to explore both topology in correlated settings and correlation physics enriched by topology. Recent experiments in correlated kagome metals have found evidence for strange-metal behavior. A major theoretical challenge is to study the effect of local Coulomb repulsion when the band topology obstructs a real-space description. In a variant to the kagome lattice, we identify an orbital-selective Mott transition in any system of coupled topological flat and wide bands. This was made possible by the construction of exponentially localized and Kramers-doublet Wannier functions, which, in turn, leads to an effective Kondo-lattice description. Our findings show how quasiparticles are formed in such coupled topological flat-wide band systems and, equally important, how they are destroyed. Our work provides a conceptual framework for the understanding of the existing and emerging strange-metal properties in kagome metals and beyond.

Coupled topological flat and wide bands realize a metallic quantum critical point with a loss of quasiparticles.

INTRODUCTION

In flat electronic bands, Coulomb interactions are proportionally enhanced because of their reduced kinetic energy. As such, flat-band systems serve as a platform for strong correlation physics (1). Heavy fermion metals represent a canonical case of flat bands formed from highly localized atomic orbitals, and, indeed, they display rich correlation physics such as quantum criticality, strange metallicity, and unconventional superconductivity (2, 3). Studies here have led to the notion that quasiparticles are lost in strange metals (4–8). Another case, emerging in a growing list of materials, corresponds to flat bands formed by geometrical interference (9–13); such bands are often topological. These materials represent a playground to study both the strong correlations and topology (14–18) and have been found to show unusual properties such as exotic forms of charge density wave order (15, 19–23). Recently, experimental evidence for strange-metal behavior has emerged from correlated kagome metals (24, 25), which contains both flat and wide bands that intersect with each other. The observed behavior takes the form of a T-linear resistivity or a single-particle damping rate that is linear in frequency. This raises the question of how quasiparticles can be destroyed in such systems. The question is important not only for correlated kagome metals but also for related flat band settings such as moiré systems (26, 27).

Thus motivated, here we study the topological flat bands coupled to wide bands. Our work provides the first theoretical demonstration of an orbital-selective Mott transition in any system that involves coupled topological flat-wide bands. The orbital-selective Mott transition provides a framework to understand the quasiparticles’ formation and, equally important, their destruction. The latter allows for the understanding of the existing and emerging strange-metal properties of flat-band systems. Our work also connects the topological flat band systems to the orbital-selective physics of bulk correlated materials (28–30), in which the atomic orbitals exhibit different dispersions and yet [in contrast to models with fully decoupled orbitals (31)] are kinetically coupled with each other.

More specifically, the topological nature of the flat bands makes it difficult to describe them in terms of any localized orbitals. The band topology obstructs the formulation of exponentially localized and Kramers-doublet Wannier orbitals (32). This poses a challenge for treating the effect of sizable spatially local Coulomb repulsion and for connecting the behavior of the coupled topological flat-wide bands to the orbital-selective Mott physics.

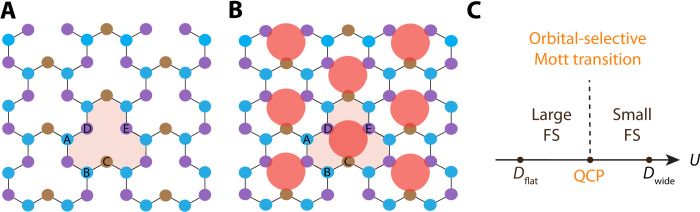
Here, we make progress by considering a lattice with a lower symmetry, which retains the central issue of topological obstruction while allowing—in a particularly transparent way—for the construction of exponentially localized and Kramers-doublet Wannier orbitals. The lattice, as illustrated in Fig. 1A, is a variant of the kagome lattice. We are able to construct the Wannier centers, which turn out to form a triangular lattice (Fig. 1B). When the effective local Coulomb repulsion is larger than the width of the flat band (D_flat) but smaller than that of the wide band (D_wide), we identify a continuous orbital-selective Mott transition [a quantum critical point (QCP)] (Fig. 1C). The two involved ground states respectively feature a “large” and a “small” Fermi surface (expanded form of FS); in an effective Kondo-lattice formulation that we construct, the large Fermi surface is Kondo driven; the small Fermi surface, then, develops from a Kondo destruction (6–8). By analogy with the phase diagram of heavy fermion metals (1–3), the existence of the phases with large and small Fermi surfaces (33–35) opens up a regime of amplified quantum fluctuations (6) for beyond-Landau quantum criticality and the accompanying strange-metal behavior (36). Thus, our work provides a conceptual framework to address the aforementioned strange-metal behavior in the flat band–based metals. The connection with a Kondo-lattice description is also being pursued in moiré systems (37–40). The approach taken here is expected to shed light on the quantum phases and their transitions in those systems.

Fig. 1. Lattice geometry and qualitative phase diagram.

(A) Lattice geometry. A, B, C, D, and E mark the five sites of a unit cell. (B) The Wannier orbitals we construct, which form a triangular lattice (the orange dots). (C) Illustration of the zero-temperature phase diagram that we determine, for the Hubbard interaction (U) that is larger than the width of the flat band (D_flat) and smaller than the width of the wide bands (D_wide), with the Fermi surface (FS) changing from large to small as the interaction U is increased across the orbital-selective Mott QCP.

RESULTS

The lattice contains five sublattices marked as A, B, C, D, E (Fig. 1A). The model is written as $\mathcal{H}={\mathcal{H}}_0+{\mathcal{H}}_1$, which contains the on-site Hubbard interactions

$${\mathcal{H}}_1=U{\displaystyle \sum _{r,i}}{n}_{\mathbf{r},i,\uparrow }^{\mathrm{\eta }}{n}_{{\mathbf{r}}^{\mathrm{\prime }},i,\downarrow }^{\mathrm{\eta }}$$ (1)

as well as the noninteracting Hamiltonian ${\mathcal{H}}_0$. Included in ${\mathcal{H}}_0$ are the nearest-neighbor tight binding hopping parameter t between two sites that are connected by a solid line in Fig. 1A, from an η electron (d_z² orbital) located at site r, sublattice i ∈ (A, B, C, D, and E) with spin σ, to its counterpart at r, j ∈ (A, B, C, D, and E) and spin σ; a chemical potential μ; a potential difference m between the sublattices C, D, and E and the sublattices A and B; and an additional potential difference γ between the sublattices D and E and the sublattice C (see Materials and Methods). To illustrate our case, we consider t = 1 = m without loss of generality.

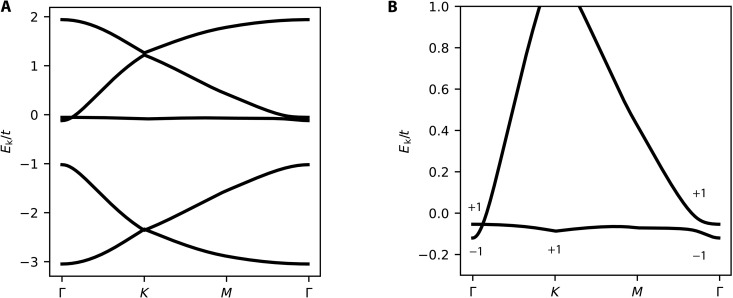
To analyze a more tractable model with a lower symmetry, we focus on the case of a nonzero γ. Here, a C_3z of the γ = 0 model (see Materials and Methods) is broken, and the middle band is not entirely flat, as seen in Fig. 2 (A and B). However, for small γ (which we illustrate with the case of γ = −0.1 t), the middle band remains relatively flat (the bandwidth is about 0.06 t) and, thus, will still be referred to as a flat band. Near Γ, there is a linear crossing between the flat and dispersive bands along the Γ − K line. The node is located near the Γ point and is protected by the M_x symmetry. When a spin-orbit coupling is further included (see the Supplementary Materials, fig. S1E), such a node would be gapped out, and the flat band acquires ±1 spin Chern number.

Fig. 2. Noninteracting band structure.

The full band structure (A) and zoomed-in band structure (B) at γ/t = −0.1 and μ/t = 1.02. In (B), we label the M_x-symmetry eigenvalues of the bands at the M_x-invariant momenta: Γ = (0,0) and K = (0,4π/3).

In this original lattice basis, the flat band comes from a linear superposition of the atomic states located in the five different sublattices. A single atomic–like representation of the flat band is needed to make progress, which we now turn to.

We will consider the Hubbard interaction U that is large compared to the width of the flat band but small compared to the width of the wide bands (Fig. 1C). Such a range is of interest to the experimentally studied systems mentioned earlier. Since there is an energy gap between the top three bands and the bottom two, we focus on the top three bands that include the flat band.

To express a band in terms of exponentially localized and Kramers-doublet Wannier orbitals, the Bloch states must have the same M_x-symmetry eigenvalue at all high-symmetry points (41, 42). In our case, the topological obstruction can be recognized by noticing that the different high-symmetry points of the flat band have different eigenvalues of the M_x symmetry. As shown in the Supplementary Materials (band 3 in table S1) and illustrated in Fig. 2B, the eigenvalue changes from +1 at K and M′ to −1 at γ. Similar changes of M_x-symmetry eigenvalues are also observed for the two wide bands (bands 1 and 2 in table S1). We therefore consider a combination of Bloch states so that the +1 eigenvalue portion of the flat band combines with the +1 eigenvalue portion of the wide band (band 2 in table S1 and illustrated in Fig. 2).

Through explicit construction, we indeed show the validity of the procedure. We find the exponentially localized Wannier functions, which are located on a triangular lattice (Fig. 1B), with the M_x-symmetry eigenvalue being +1. We call such a Wannier function a d orbital. The hopping integral of the two neighboring d orbitals is indeed weak in our construction: It turns out to be on the order of 0.03 t.

The remaining degrees of freedom can be represented by two Wannier orbitals with M_x-symmetry eigenvalue +1 and −1, respectively. These two orbitals mainly come from the top two dispersive bands, and we label them as c orbitals.

We have thus succeeded in constructing a single atomic–like state per unit cell to represent the flat band. The model takes the form of an effective multiorbital Hubbard model on a triangular lattice, which can also be viewed as an effective Anderson-lattice model. It is expressed in terms of the d and c orbitals, containing the kinetic term H₀ and the interaction term H_I.

The kinetic term, H₀, is given in detail in the Supplementary Materials. It involves two types of electrons, with $d_{\mathbf{R},\mathrm{\sigma }}^{†}$ creating a d electron (electron in the orbital d), which represents the flat band’s degrees of freedom, at site R with spin σ. Similarly, $c_{\mathbf{R},a,\mathrm{\sigma }}^{†}$ creates a conduction c electron (electron in orbital c), which represents the itinerant degrees of freedom, at site R with spin σ and orbital a = 1,2. H₀ contains the part H_d, describing the energy level (E_d) and their negligibly small hopping parameters; the part H_c, describing the inter-c-electron hopping parameters, $t_{\mathbf{R}-{\mathbf{R}}^{\mathrm{\prime }},a{a}^{\mathrm{\prime }},\mathrm{\sigma }}^c$ and the energy levels E_a (a = 1,2); and the part H_dc, the d-c hybridization term with matrix element V_{R−R′,a,σ}. These parameters are specified in the Supplementary Materials. As is seen there, the dominant hybridization is with one of the two conduction electron bands, a = 1. The corresponding hybridization is off-site because c_R,1,σ is mirror odd.

The most important interactions here include the Hubbard interactions of the d electrons (H_u), and the Hund’s coupling between the d and c electrons (H_Hund). The interactions are labeled u and J_1,2, respectively. The specific forms of the interactions are given in the Supplementary Materials.

In the limit of $u\gg \mid t_{\mathbf{R}-{\mathbf{R}}^{\mathrm{\prime }}}^d\mid$, the Hubbard interactions suppress the charge fluctuations of the d electrons and turn them into quantum spins. Correspondingly, the effective model acquires a representation in terms of a Kondo-lattice Hamiltonian on the same triangular lattice (see Materials and Methods). It contains two Kondo couplings J_K,a (a = 1,2) to two conduction c electron bands and an inter-moment exchange coupling J^H between the d spins. Both couplings are controlled by the parameter

$$\tilde{u}=4u{\mathrm{\varphi }}_0/3$$ (2)

with ϕ₀ being of order unity (see Materials and Methods and section SD).

For convenience in notation, we now treat $\tilde{u}$ of Eq. 2 as our tuning parameter (we note, however, that tuning $\tilde{u}$ is equivalent to varying the original Hubbard interaction U). At smaller $\tilde{u}$, the Kondo effect dominates. Increasing $\tilde{u}$ enhances the relative effect of the antiferromagnetic exchange interactions between the local moments, which favors the correlations between the local moments and is detrimental to the development of the Kondo effect.

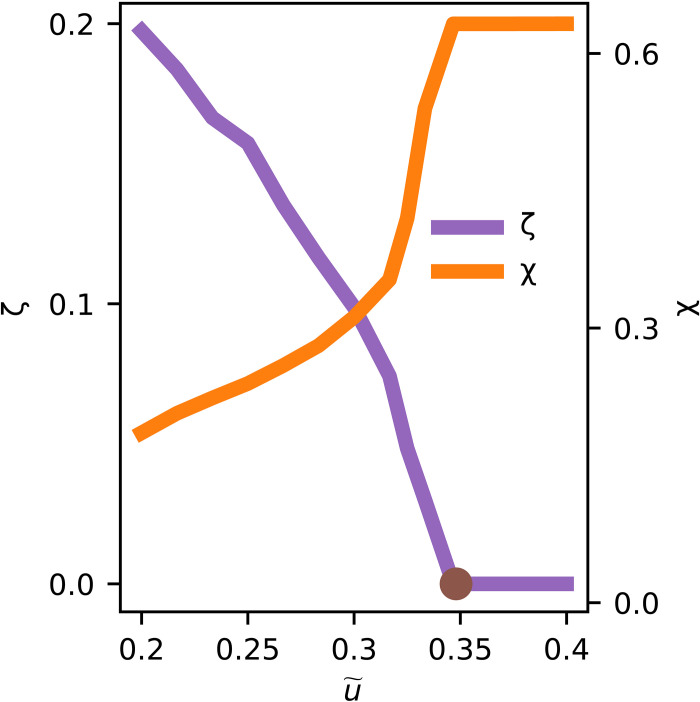
We have analyzed this competition through a set of saddle-point equations that are realized in a large-N limit (see Materials and Methods). We use a pseudo-fermion representation of the spin and solve the saddle-point equations in terms of the field ζ_R,R′a, which represents the hybridization of the Kondo-driven composite fermions and conduction-c fermions, and χ_R,R′, which characterizes the inter-moment spin singlets (43).

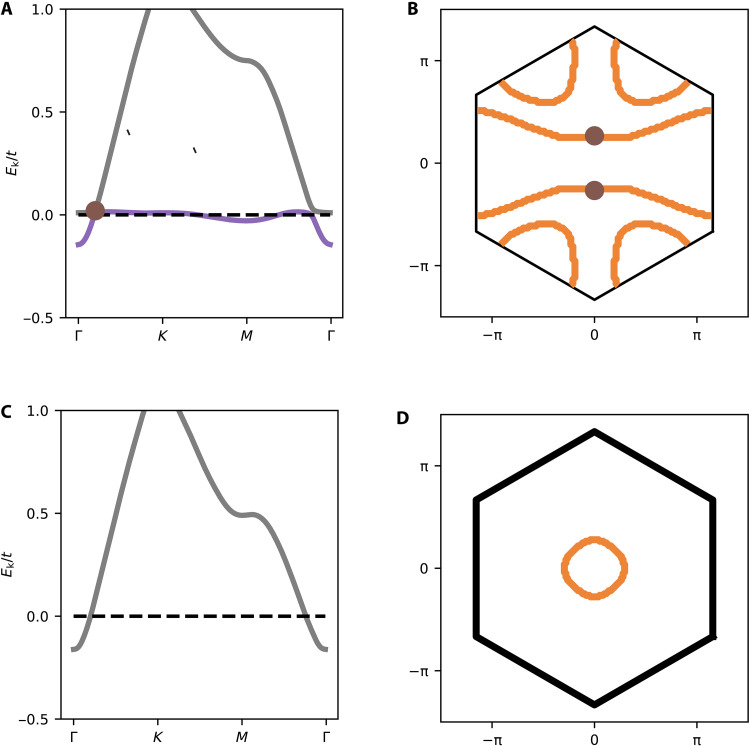
Figure 3 shows the resulting phase diagram. At small $\tilde{u}$, we realize a topological heavy Fermi-liquid phase via the condensation of the hybridization field ζ. The latter converts the local moments into composite fermions that are represented by the f fields, which hybridize with the conduction electrons. Furthermore, the nonzero hybridization ζ_R1a2 attaches a +1 M_x-symmetry eigenvalue to the composite fermion f field, which is the opposite to the eigenvalue of the dominantly hybridizing conducting c₁ band (see section SG). The correlated heavy bands are topological containing a Dirac node, as shown in Fig. 4A. The node is protected by M_x and the SU(2) symmetry: Because of the formation of the hybridized bands, the Fermi surface encloses the electrons residing on both the conduction and flat bands (44, 45). This is the large Fermi surface, which is shown in Fig. 4B.

Fig. 3. The zero-temperature phase diagram calculated in the large-N limit.

As the interaction $\tilde{u}$ is increased, η gradually decreases and goes to zero at $\tilde{u}=0.35$ (marked by the brown dot), which signals a continuous orbital-selective Mott transition between a Kondo-driven and Kondo-destroyed phases, with a large and a small Fermi surface, respectively.

Fig. 4. Quantum phases with large and small Fermi surfaces.

The band structure (A) and Fermi surface (B) in the phase with a large Fermi surface. Shown here are the results at $\tilde{u}=0.27$. For a larger value of $\tilde{u}=0.35$, the corresponding band structure (C) and Fermi surface (D) are shown for the phase with a small Fermi surface. In (A) and (B), the brown dots mark the Dirac nodes. The dashed line in (A) and its counterpart in (C) mark the Fermi energy. The orange lines in (B) and (D) denote the Fermi surface.

Increasing $\tilde{u}$ leads to a Kondo destruction (6–8): The local moments couple to each other, and they no longer form a Kondo singlet with the spins of the conduction electrons. Consequently, the Fermi surface is derived from the dispersion of the conduction electrons, plotted in Fig. 4C. It is shown in Fig. 4D and is small in the sense that the Fermi surface encloses only the conduction electrons. The frustrated nature of the effective lattice (Fig. 1B) has led to the Kondo-destroyed phase via the bond variables χ_R,R′. However, the physical mechanism leading to the Kondo destruction is more universal, as characterized by a global phase diagram for the competition between the Kondo and RKKY/Heisenberg interactions (1).

DISCUSSION

We have demonstrated the first realization of orbital-selective Mott transition in models of topological flat bands in the presence of coupling with wide bands. The large-Fermi surface state provides a proper description for the development of the strongly correlated d-electron quasiparticles. In turn, this sets the stage for the transition into the small-Fermi surface phase, which represents the destruction of the correlated quasiparticles. This orbital-selective Mott transition is in the same universality class as the Kondo-destruction quantum criticality of heavy fermion metals (4, 6–8, 46), associated with which strange metallicity develops. Our theoretical description, thus, provides the conceptual framework to understand the recently emerged experimental evidence for strange metal behavior in correlated kagome metals (24, 25).

We close with several remarks on the generality and implications of our results. First, our Wannier construction procedure works equally well for the case with a spin-orbit coupling. Accordingly, our Kondo-lattice construction and the results for the quasiparticle formation and destruction readily apply in this case. Second, by emphasizing the interplay and coupling between the flat and wide bands, our work brings out an analogy between the correlated quantum materials that host topological flat bands (10–12, 15, 22, 23) and moiré systems (37–40), in which the strange-metal behavior has also been indicated (26). Compared to the topology of the graphene-based moiré flat bands (38, 47), the bands in our case share the traits of being topological but have the distinction of being much simpler. This simplification represents a crucial advantage in allowing us to provide a proof-of-principle demonstration of both the emergence and destruction of the proper quasiparticles in systems with coupled topological flat-wide bands through the Kondo route. Our explicit construction of the Kondo lattice also sets the stage for the study of a global quantum-phase diagram (1) in such topological flat band–anchored systems. Third, the topological nature of the flat band makes our Kondo lattice topological. This topological feature distinguishes our current model from the conventional Kondo-lattice models where the bands are usually topologically trivial. This topological feature naturally makes the heavy Fermi-liquid phase topologically nontrivial, featuring a Dirac node. Beyond this, at the QCP and in the non–Fermi-liquid region, the incoherent electronic excitations could also show nontrivial topology. However, any such topological feature goes beyond the quasiparticle description and is left for future studies.

We now discuss the stability of the QCP and the corresponding non–Fermi-liquid behavior. First, at finite N, the Kondo destruction part of the phase diagram could contain a magnetically ordered phase. The stability of the Kondo destruction QCP and the corresponding non–Fermi-liquid behavior remain robust, as has been shown in the Kondo-lattice model (4, 46). Second, with a nonzero spin-orbit coupling, the SU(2) spin symmetry will be broken. However, the existence of the Kondo destruction critical behavior relies on the competition of local moment fluctuations and Kondo effect instead of the specific symmetry of the local moment (4, 46, 48). Therefore, the Kondo destruction QCP and the non–Fermi-liquid behavior that we found here are robust.

In conclusion, we have advanced a realistic model to study the effect of local Coulomb repulsion for a system of coupled topological flat and wide bands. By constructing exponentially localized and Kramers-doublet Wannier functions for these bands, we are able to formulate a Kondo-lattice description. This has allowed us to provide the first demonstration of an orbital-selective Mott transition in any system of coupled topological flat and wide bands. The orbital-selective Mott transition provides a characterization for both the development and destruction of quasiparticles, leading to quantum phases with large and small Fermi surfaces. Our work provides a conceptual framework to describe the amplified quantum fluctuations of multiband systems with topological flat bands, sets the stage to understand the strange-metal properties that are emerging in kagome metals and other flat-band systems, and uncovers a linkage between these systems and both the f and d electron–based correlated bulk materials.

MATERIALS AND METHODS

The Hubbard model, $\mathcal{H}={\mathcal{H}}_0+{\mathcal{H}}_1$, is defined on a variant of the kagome lattice defined in Fig. 1A, with the onsite interaction term, ${\mathcal{H}}_1$, given in Eq. 1. The noninteracting Hamiltonian is written as follows

$$\begin{array}{c}{\mathcal{H}}_0=\sum _{⟨\mathbf{r},\mathbf{r}\mathrm{\prime }⟩,i,j,\mathrm{\sigma }}t{\mathrm{\eta }}_{\mathbf{r},i,\sigma }^{†}{\mathrm{\eta }}_{\mathbf{r},j,\mathrm{\sigma }}-\mathrm{\mu }\sum _{\mathbf{r},i,\mathrm{\sigma }}{\mathrm{\eta }}_{\mathbf{r},i,\mathrm{\sigma }}^{†}{\mathrm{\eta }}_{\mathbf{r},i,\mathrm{\sigma }}\\ +\sum _{\mathbf{r},\mathrm{\sigma },i\in \{C,D,E\}}m{\mathrm{\eta }}_{\mathbf{r},i,\mathrm{\sigma }}^{†}{\mathrm{\eta }}_{\mathbf{r},i,\mathrm{\sigma }}+\sum _{\mathbf{r},\mathrm{\sigma },i\in \{D,E\}}{\mathrm{\gamma }\mathrm{\eta }}_{\mathbf{r},i,\mathrm{\sigma }}^{†}{\mathrm{\eta }}_{\mathbf{r},i,\mathrm{\sigma }}\end{array}$$ (3)

Here, ${\mathrm{\eta }}_{\mathbf{r},i,\mathrm{\sigma }}^{†}$ creates an electron at site r, sublattice i ∈ (A, B, C, D, E) with spin σ.

At γ = 0, the system has a C_3z rotational symmetry, an M_x mirror symmetry, and also an SU(2) spin rotational symmetry. This leads to a purely flat band as shown in the Supplementary Materials (fig. S1B). There is a quadratic band touching between the flat and a dispersive band at the center of the Brillouin zone, Γ = (0,0). The crossing is protected by both the M_x and C_3z symmetries. To analyze a more tractable model with a lower symmetry, we focus on the case of a nonzero γ, as described in the Results section.

In the limit of $u\gg \mid t_{\mathbf{R}-{\mathbf{R}}^{\mathrm{\prime }}}^d\mid$, the charge fluctuations of the d electrons are suppressed, and these electrons are turned into quantum spins. By integrating out the high-energy degrees of freedom [in the presence of the Hund’s coupling, (49, 50)], we reach a Kondo-Heisenberg model with the Hund’s coupling. The effective Kondo-lattice Hamiltonian on the triangular lattice is

$$\begin{array}{c}{H}_{KH}=H_c+H_H+H_K+H_{\mathrm{Hund}}\\ H_H={\displaystyle \sum _{\mathbf{R},{\mathbf{R}}^{\mathrm{\prime }}}}{J}_{\mathbf{R},{\mathbf{R}}^{\mathrm{\prime }}}^H{\overrightarrow{S}}_{\mathbf{R}}\cdot {\overrightarrow{S}}_{{\mathbf{R}}^{\mathrm{\prime }}}\\ H_K={\displaystyle \sum _{\mathbf{R},{\mathbf{R}}_1,a_1,{\mathbf{R}}_2,a_2}}{J}_{\mathbf{R},{\mathbf{R}}_1,a_1,{\mathbf{R}}_2,a_2}^K{\overrightarrow{S}}_{\mathbf{R}}\cdot c_{{\mathbf{R}}_1,a_1}^{†}\overrightarrow{\sigma }{c}_{{\mathbf{R}}_2,a_2}\end{array}$$ (4)

Here, ${\overrightarrow{S}}_{\mathbf{R}}$ is the emergent spin-1/2 local moment formed by the localized d electrons. In the large u limit, the hoppings of d electrons induce a Heisenberg interaction of strength $J_{\mathbf{R},{\mathbf{R}}^{\mathrm{\prime }}}^H=2{\mid t_{\mathbf{R},{\mathbf{R}}^{\mathrm{\prime }}}^d\mid }^2/\tilde{u}$, where $\tilde{u}$ is specified by Eq. 2. The nonlocal hybridization terms between the d and c electrons lead to nonlocal Kondo couplings of strength $J_{\mathbf{R},{\mathbf{R}}_1,{\mathbf{R}}_2,a_1,a_2}^K=4V_{\mathbf{R}-{\mathbf{R}}_2,a_2}^{\ast }{V}_{\mathbf{R}-{\mathbf{R}}_1,a_1}/\tilde{u}$. Here, the local moment of the d electron is Kondo coupled to a spin operator $c_{{\mathbf{R}}_1{a}_1}^{†}\overrightarrow{\mathrm{\sigma }}{c}_{{\mathbf{R}}_2{a}_2}$ that are formed by two electron operators from the sites R₁, R₂ and the orbitals a₁, a₂ respectively. Last, the Hamiltonians for the c electrons and for the Hund’s coupling remain unchanged from those given in the effective multiorbital Hubbard (i.e., the effective Anderson lattice) model. In particular, the Hund’s coupling acts between the d and c electrons of the same site (see section SC). To analyze the competition between the inter-moment and Kondo exchange couplings, we introduce the pseudo-fermion representation of the spin operators $S_{\mathbf{R}}^{x,y,z}=\frac{1}{2}{\sum }_{\mathrm{\sigma },{\mathrm{\sigma }}^{\mathrm{\prime }}}{f}_{\mathbf{R},\mathrm{\sigma }}^{†}{\mathrm{\sigma }}_{\mathrm{\sigma },{\mathrm{\sigma }}^{\mathrm{\prime }}}^{x,y,z}{f}_{\mathbf{R},\mathrm{\sigma }}$ and solve the model in the large-N limit [with a generalization of SU(2) to SU(N) and a suitable rescaling of the coupling constants in terms of 1/N; see section SF].

The ground state is characterized by the bond fields χ_R,R′ (43) and the hybridization fields ζ_R,R′a

$$\begin{array}{c}{\mathrm{\chi }}_{\mathbf{R},{\mathbf{R}}^{\mathrm{\prime }}}=\frac{1}{N}{\displaystyle \sum _{\mathrm{\sigma }}}⟨f_{\mathbf{R},\mathrm{\sigma }}^{†}{f}_{{\mathbf{R}}^{\mathrm{\prime }},\mathrm{\sigma }}⟩\\ {\mathrm{\zeta }}_{\mathbf{R},{\mathbf{R}}^{\mathrm{\prime }}a}=\frac{1}{N}{\displaystyle \sum _{\mathrm{\sigma }}}⟨f_{\mathbf{R},\mathrm{\sigma }}^{†}{c}_{{\mathbf{R}}^{\mathrm{\prime }},a,\mathrm{\sigma }}⟩\end{array}$$ (5)

and their maximum amplitudes ζ = max_R,R′,a{∣ζ_R,R′a∣} and χ = max_R,R′{∣χ_R,R′∣}. The results from solving the saddle-point equations have been given in the Results section. The Kondo destruction is captured by the suppression of the hybridization fields ζ, which appears not only in the SU(2)-symmetric setting but also in the cases with spin anisotropy (4, 46, 48).

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 and S2

Tables S1 and S2