Toward machine-assisted tuning avoiding the underestimation of uncertainty in climate change projections

Abstract

Documenting the uncertainty of climate change projections is a fundamental objective of the inter-comparison exercises organized to feed into the Intergovernmental Panel on Climate Change (IPCC) reports. Usually, each modeling center contributes to these exercises with one or two configurations of its climate model, corresponding to a particular choice of “free parameter” values, resulting from a long and often tedious “model tuning” phase. How much uncertainty is omitted by this selection and how might readers of IPCC reports and users of climate projections be misled by its omission? We show here how recent machine learning approaches can transform the way climate model tuning is approached, opening the way to a simultaneous acceleration of model improvement and parametric uncertainty quantification. We show how an automatic selection of model configurations defined by different values of free parameters can produce different “warming worlds,” all consistent with present-day observations of the climate system.

Automatic tuning is used to quantify parametric uncertainty of the climate change simulations provided in CMIP exercises.

INTRODUCTION

Physics-based global numerical models have played a leading role in warning about global warming. They have been used to demonstrate human responsibility in certain observed climate changes by means of detection-attribution simulations. They are also used to anticipate mitigation and adaptation policies. They are indeed the only tools able to integrate all the scales and processes involved in climate change and to provide physically consistent sequences of meteorological variables under modified climate (1). All global climate models agree on the fact that an increase in the concentration of greenhouse gases produces an increase of the global surface temperature. There is, however, a factor of typically three between the most and least sensitive models to this concentration increase. There is a particular concern in the community that the last generation of climate models, documented in the sixth phase of the “coupled model inter-comparison project” (CMIP6), was showing an even larger spread in the simulated climate sensitivity, with a set of state-of-the-art models being more alarmist than their previous versions, despite substantial improvement in their representation of the present-day climate (2). The range of equilibrium climate sensitivity (ECS), defined as the global mean surface air temperature change caused by a doubling of the atmospheric CO₂ concentration, was 1.8 to 5.6 K in CMIP6 simulations, compared with 2.1 to 4.7 K in CMIP5 (not far from the Charney’s report estimate of 1.5 to 4.5 K) (3). An extensive study of the ECS uncertainty was conducted recently, combining all the lines of evidence previously published (4). It underlined the fact that there is no direct relationship between ECS and the 20th-century warming, given the uncertainty of the aerosol forcing and the so-called “pattern effect.” This study increased the lower bound on the ECS from 1.5 to 2 K, compared to previous assessment and estimated an 18% chance of being above the previous upper value of 4.5 K.

A large part of the inter-model dispersion in the ECS is due to the choices made in the representation of cloud and convective processes, which occur at finer scale than the model grid mesh, through so-called parameterizations (5, 6). Ever since the first Atmospheric Model Intercomparison Project (AMIP) exercise (7), it is the quantification of the errors associated with modeling choices that has fundamentally motivated the climate “model inter-comparison projects” (MIPs), in which rigorous simulation protocols are shared across modeling groups. Providing climate change projections with an estimation of this modeling uncertainty is an essential role of the Coupled Model Intercomparison Project (CMIP) exercises, which are conducted about every 7 years, in advance of Intergovernmental Panel on Climate Change (IPCC) reports. The multi-model CMIP ensemble is used as an entry for so-called impact studies, often using physical and statistical downscaling approaches, and recent advances in Monte Carlo methods pave the way to a systematic use of the CMIP simulations ensembles in such studies (8).

However, the uncertainty quantification performed in CMIP is only partial. In practice, each modeling group provides numerical simulations performed with only one (or sometimes a few) model configuration, i.e., a specific choice of physical content, grids, and a particular set of values for the free parameters of the model. The free parameter values result from a long explicit or implicit calibration phase, often called tuning. Could other configurations of each model also simulate reasonable climates with other parameter settings? If so, how would this affect the range of ECS explored? What are the implications for the uncertainty of model-based climate change assessments and downstream impact studies? These issues are prompting some modeling teams to rerun “perturbed physics ensembles” (PPEs) with their particular model, in addition to CMIP multi-model ensembles, to more systematically explore the uncertainty in future climate projections to inform societal questions (9–12).

Although the issue of tuning was identified early in the history of climate modeling (13) and documented in some model reference publications (14–18), it has not been really considered as a scientific issue until recently and was not much publicized. Tuning was often seen as an unavoidable, technical, and dirty part of climate modeling. There was also probably a fear that climate change denialists may use the fact that models are tuned to cast a doubt on the reality of climate change projections. Nevertheless, the situation is changing fast and tuning is more and more discussed as a central aspect of climate modeling (19–23). The use of objective methods that explore the parameter space using fast surrogate models or emulators is also becoming common practice (19, 24, 25).

We show here how insights into model tuning and the use of objective methods can lead to systematic exploration of parametric uncertainty and accelerated model improvement. Contrary to previous studies based on PPEs, the ensemble produced here is reduced automatically to a subspace compatible with a priori defined tuning targets, thus making parametric exploration and model tuning two sides of the same exercise.

Tuning is usually seen as the search for an optimal set of parameters, with optimization approaches that typically minimize a cost function (19), and this idea is only gaining traction rather than losing credibility (26–28). Such a definition, however, automatically results in “overtuning,” i.e., forcing the model to find the best possible agreement with a set of metrics at the potential expense of inducing errors throughout the unused components of the climate state vector and model projections. With these approaches, adding or subtracting even just one metric can produce a completely different “best model” or distribution for the best model in the case of Bayesian methods (29), even when accounting for uncertainty in those metrics in the optimization (30).

The history matching approach (31) advocated here avoids parts of these defects. It defines tuning to be the identification of regions of parameter space within which a set of simulated metrics match their observed values to a given “tolerance to error” that includes, in principle, both the observational and model structural uncertainty. Because the structural uncertainty is generally not known a priori, this approach cannot fully guarantee against overtuning, but it both allows us to consider this problem directly and can help identify and even quantify specific structural errors in the model (32–34). While advocates of optimization approaches rightly point out that methods such as history matching require more simulations than a typical optimization, we advocate for the approach as it goes beyond finding a unique reference version of a model and allows us to explore the possible model worlds compatible with a set of observational constraints, given a model (physical and numerical) content and grid configuration.

To illustrate this, we start from the Institut Pierre-Simon Laplace (IPSL)–CM6A-LR (35) configuration (called IPSL-6A hereafter) of the IPSL coupled model (IPSL-CM) used for CMIP6 and obtained after a long and tedious phase of by-hand tuning (36). We revisit the tuning of the atmospheric component of the model, LMDZ-6A-LR (37), using history matching. We thus derive four coupled configurations with ECS values ranging from 3.7 to 5.4 K.

The IPSL-6A configuration itself shows an ECS of 4.6 K in the upper part of the very likely range given in the IPCC AR6 report: 2 to 5 K (38). However, 5 among the 33 members of an ensemble of historical simulations with this IPSL-6A version (that differed only by their initial state) showed climate trends over the 20th century compatible with observations (39). In these simulations, the warming over the past decades is in part compensated by a centennial oscillation of the coupled system. This centennial oscillation is quite strong in the IPSL model compared to others, but both the amplitude and the phase in the two particular members that match the 20th century the best were shown to be compatible with observations. Because of the unicity of the observed climate record, the part of the variability in the recent trend is however difficult to evaluate and should be taken into account as a major source of uncertainty.

There is a desire in the community to use so-called emergent constraints (40) or “multiple lines of evidence” (4) to further constrain ECS uncertainty and to select a subset of model configurations as a basis for future projections (38) [the extent to which emergent constraints accurately quantify uncertainty is discussed by Williamson and Sansom (41)]. Some modeling teams even provide simulations that target a given value of the ECS to the CMIP database (42) (calling into question any method that uses CMIP as a starting point for spanning ECS uncertainty). Given the importance of the question and the remaining sources of uncertainty in the most serious attempt to quantify it, we think that quantification rather than artificial reduction of the uncertainty of the ECS should be kept as one of the major targets of the future CMIP programs.

Carefully curated PPEs are a way to explore this uncertainty, and more precisely the uncertainty attributed to model free parameters for a given model configuration. The curation is important. By restricting our parametric exploration to a subset compatible with a series of predefined metrics on the present-day climate, we can meaningfully explore uncertainty induced by the model parameters among models that could reasonably be submitted to a CMIP exercise. Previous studies have used curated PPEs combined with CMIP to explore uncertainty in precipitation trends over continents and their relationship to the current climate representation (43, 44). In the most recent study, the authors use multi-objective optimization for a small collection of metrics important for emergent constraints. They identify a subset of the ensemble of simulations on a Pareto front to quantify the uncertainty in precipitation change. The authors present their approach as an alternative or a generalization of the emergent constraint approaches. Our approach shares similar motivations, but it deliberately avoids optimization, claiming that perhaps models that are not on the Pareto front could offer a better representation of climate (not only through the given metrics).

Among the four model configurations derived here, the two with the smallest and largest ECS represent the current climate with skill similar to IPSL-6A. Given the criteria adopted for model qualification, these two configurations could just as easily have been adopted by IPSL for CMIP6 production instead of the IPSL-6A version if the modeling team had stumbled upon them during the tuning phase. With only five configurations (the IPSL-6A configuration plus the four additional ones that we introduce here), we cover half of the CMIP multi-model ECS range, suggesting that the modeling uncertainty on the ECS might be underestimated by CMIP ensembles. We conclude that these results should prompt substantial redesign of CMIP exercises.

RESULTS

Translating “by-hand tuning” into numbers

Following a previous study (45), the targets of the by-hand tuning of the IPSL-6A configuration were translated into 14 scalar metrics. Among them, 11 relate to annual mean top-of-atmosphere (TOA) radiative fluxes, taking averages over the globe or specific regions and decomposing between solar and thermal radiation or clear sky fluxes and radiative effect of clouds, while three metrics relate to the distribution of rainfall (see fig. S1 and table S1). P = 18 parameters were considered unknown (see table S2), typically those modified during the tuning phase of the IPSL-6A configuration [table 3 in (37)]. The prior ranges for these parameters were set by expert judgment that did not account for knowledge of the values used by IPSL-6A configuration. A real advantage in applying objective methods like history matching is that it forces model developers to formalize their tuning choices through numbers. The choice of metrics and parameter ranges is obviously subjective (as it is with by-hand tuning) yet is made transparent by the process (23). Details are given in Materials and Methods and in section SI1.

All the radiative metrics but one were given a 1σ tolerance to error of ±5 W/m² for an observational uncertainty of about 4 W/m² for the CERES-EBAF L3b satellite product used as target (46). An exception was made for the TOA global imbalance, for which the value targeted was the global energy imbalance at TOA in the standard IPSL-6A configuration and the tolerance to error was set to 0.5 W/m², much smaller than the observational uncertainty. The rationale for targeting the value of a previous simulation rather than observation is the following. We know that with an imbalance value of 2.7 W/m² in stand-alone atmospheric mode with the 6A-LR tuning, the global mean sea surface temperature (SST) in coupled mode is close to the observed value by a few tenths of K [note that this global mean SST fluctuates by about 0.2 K on centennial time scales in IPSL-6A (39)]. This is partly due to an imperfect energy conservation in the global model (about 0.9 W/m² in the coupled IPSL-6A configuration, see table S3) and to the different mean states of the coupled and stand-alone atmospheric simulations modulating the energy fluxes at TOA. We also know from past experiments that a change of 1 W/m² of this imbalance would result in a change of about 1 K in the global near-surface temperature (about 0.7 K for the SST). By retuning the model in stand-alone configurations targeting the global energy imbalance of the IPSL-6A configuration, we in fact indirectly tune the global mean SST in the coupled model (known to a few tenths of a degree from observations). This strategy was already applied successfully to the by-hand tuning of the IPSL-6A configuration (36) (see section SI3 and table S3).

For rainfall, the three metrics retained are as follows: (i) the variability over ocean around the maritime continent (underestimated in the IPSL-6A version), with a target from The Tropical Rainfall Measuring Mission (TRMM) daily rainfall product (47) and a relative uncertainty of 10%; (ii) the annual mean rainfall over Sahel, with a target from the Global Precipitation Climatology Project (GPCP) monthly climatology (48) and a relative uncertainty of 50%; and (iii) the frequency of days with rainfall above 50 mm/day (to reduce the occurrence of so-called grid-point storms), targeting the TRMM product with a relative uncertainty of 50%.

History matching: How does it work?

History matching starts by generating a set of N = 250 (typically 10×P) parameter vectors λ of the P unknown parameters by randomly sampling the hypercube defined by the ranges of acceptable values (defined a priori) for each parameter. Parameters whose range span many orders of magnitude are first log-transformed before sampling the hypercube to ensure uniform sampling across the different orders of magnitude. For each parameter vector, we run a 2-year-long stand-alone atmospheric simulation forced by observed SST. The metrics are then computed on the second year of simulations, as was the case for the by-hand tuning (36). For each metric m(λ), the N simulations are used to fit an emulator or surrogate model using a Gaussian process (GP) (49). The GP treats any finite collection of a metric with different parameter choices as a multivariate normal distribution. Fitting a GP to a collection of simulations involves fitting a mean function, $\mathbb{E}[m(\mathbf{\text{λ}}\mathbf{)}\mathbf{]}$, and a covariance function Cov [m(λ), m(λ′)]. There are many methods and software for fitting different types of GP (49); we used the method and code detailed in (25). The emulators enable us to assess the match between observed and simulated metrics at thousands or millions of parameter vectors very quickly and to rule out those with poor skill. A parameter vector is ruled out if, for a fixed number of the metrics (usually 3 to avoid multiple testing), its implausibility

$$I(\mathbf{\text{λ}}\mathbf{)}\mathbf{=}\parallel \mathbb{E}\mathbf{[}{\mathbf{m}}_{\mathrm{EM}}\mathbf{(}\mathbf{\text{λ}}\mathbf{)}\mathbf{]}\mathbf{-}{\mathbf{m}}_{\mathrm{obs}}\parallel \mathbf{/}\sqrt{\{{\mathbf{\text{ϵ}}}_{\mathbf{m}}\mathbf{+}\mathrm{Var}\mathbf{[}{\mathbf{m}}_{\mathrm{EM}}\mathbf{(}\mathbf{\text{λ}}\mathbf{)}\mathbf{]}\}}$$ (1)

is larger than a threshold, fixed to 3 here. The choice of threshold can be made with the context that implausibility is a type of standardized distance between the observation and the model, where the standardization accounts for the observational and structural uncertainties, through ɛ_m, and the emulator uncertainty Var[m(λ)] (so our fixing to 3 says that 3 SDs is too many if it happens too often). The history matching procedure is then iterated on a number of “waves,” each time running N 2-year-long simulations and building an emulator for each metric.

In practice at wave W_i, a number 𝒩 (≫N) of parameter vectors is sampled in the original hypercube. The emulators from wave 1 to W_i are then applied iteratively for each metric to rule out some parameter vectors, keeping at each wave a subsample in the Not Ruled Out Yet (NROY) subspace. The sample of the N vectors for the following wave, W_i+1, is then randomly taken in the final NROY space. Note that we compute the emulator 𝒩 times for each metrics, while N/𝒩 needs to be larger than the NROY fraction (compared to the original hypercube), to have a sufficient sample in NROY space for building the next emulator. This means that the emulators must be extremely fast. The iteration progressively reduces the emulator variance while refining the sampling around the region in which the metrics match targets to a given tolerance to error. Note that, here, N was reduced to 200 for wave 2 and 180 for wave 3.

This iterative process is illustrated by showing the latitudinal variations of the short-wave radiative forcing (SW CRE) for the 250 + 200 + 180 simulations of the 3 history matching waves, among which 23 simulations (0 in wave 1, 9 in wave 2, and 14 in wave 3) showed a maximum value of the error/tolerance across the metrics smaller than 3 (Fig. 1A). Among those 23, we retained only 9 “BEST” simulations (red lines, Fig. 1A) for which the global TOA imbalance effectively departed by less than 0.5 W/m² from the imbalance in the control configuration with tuning of IPSL-6A (although the global TOA imbalance is one of the metrics used for tuning, the procedure does not warrant this constraint both because of the emulator uncertainty and because of the cutoff of three used on implausibility values).

Fig. 1. Illustration of the iterative procedure for history matching.

Both graphs display the latitudinal variations of the zonally averaged short-wave (SW) cloud radiative effect (CRE) computed as the difference between the total and clear-sky TOA SW radiation. The CERES-EBAF L3b observations are shown in black with error bars of ±4 W/m² (46). (A) SW CRE computed for the second year of an ensemble of 2-year forced-by-SST simulations for the three successive waves of the history matching procedure with 250, 200, and 180 simulations for waves 1, 2, and 3, respectively. The nine “BEST” simulations are shown in red and the gray line corresponds to a control simulation (CTRL) run with the parameters of the IPSL-6A configuration. (B) Ten-year average SW-CRE obtained in coupled ocean-atmosphere simulations in the multi-model ensemble of CMIP5 (yellow) and CMIP6 (orange) and in the control and four experiments retained from the history matching because of both their good behavior in present-day conditions [taken among the nine “BEST” configurations of (A)] and of their contrasted ECS (see the main text). For these last four experiments, we show the SW CRE obtained in both the coupled (thick line) and stand-alone (thin, 1-year average) atmospheric simulations that are almost superimposed.

Selecting atmospheric configurations with contrasted ECS

The reference method to evaluate the ECS of a climate model (50) involves abruptly quadrupling the CO₂ concentration, starting from a control coupled atmosphere-ocean simulation. The ECS is then estimated from a linear regression over the first 150 years of simulation, between the energy imbalance coming from the CO₂ increase, which progressively returns to zero, and the temperature difference between the control and perturbed experiment that progressively increases toward twice the ECS (see Materials and Methods).

To select a subset of configurations with contrasted ECS without running centennial simulations for all the BEST simulations, we compute an approximate ECS from the difference between the top of atmosphere energy budget obtained in two 10-year-long atmosphere-alone simulations, one with climatological SSTs and the second one with the same SSTs increased by 4 K (42, 51). This “clim+4K proxy” is thus only used here to identify simulations with low and high ECS (see Materials and Methods and SI2 for a discussion of this aspect).

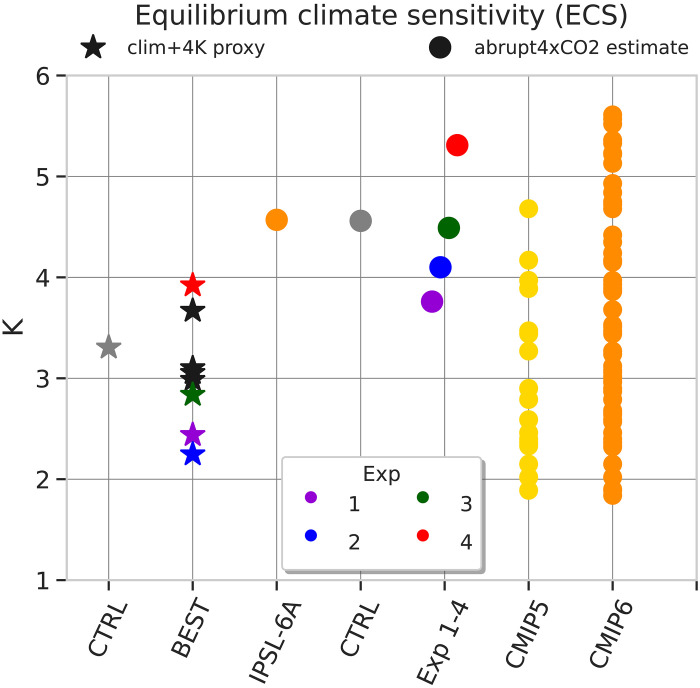
The abrupt4×CO₂ estimate of the ECS from the IPSL-6A and CTRL experiments (orange and gray dots in Fig. 2, respectively) show almost the same value of 4.6 K. The clim+4K proxy computed for the CTRL configuration (gray star in Fig. 2) shows a smaller value of 3.8 K. The clim+4K proxy computed for the nine “BEST” simulations varies from 2.7 to 4.6 K. Four configurations were retained among them for their contrasted ECS: one with an ECS increased by 1 K as compared to the CTRL configuration and three with an ECS decreased by more than 1 K.

Fig. 2. Estimation of ECS (K) for the various model configurations, including the CMIP5 (yellow) and CMIP6 (orange) multi-model ensembles.

The value of the standard IPSL-6A configuration (orange) is isolated from the other CMIP6 models to serve as a reference point for the work presented here. For the CTRL (with same parameters as IPSL-6A) and the four configurations selected (Exp 1 to 4), we show both the abrupt4×CO₂ ECS estimate (circles) computed from 150-year-long coupled ocean-atmosphere simulations and the clim+4K ECS proxy computed from forced by SST 10-year-long simulations (stars). This clim+4K proxy is shown as well for the five best simulations not selected to run coupled simulations (black stars).

Coupled simulation with contrasted ECS

For each of those four configurations, we then ran a pair of preindustrial and abrupt4×CO₂ experiments with the full coupled climate model. The four experiments were a posteriori labeled from Exp 1 to 4, from the smallest to the largest abrupt4×CO₂ ECS estimates. If the ranking is not exactly the same as for the clim+4K proxy, the range of amplitude is, however, similar (Fig. 2). The ECS estimates vary from 3.7 to 5.3 K for a value of 4.6 K for the IPSL-6A and CTRL configuration.

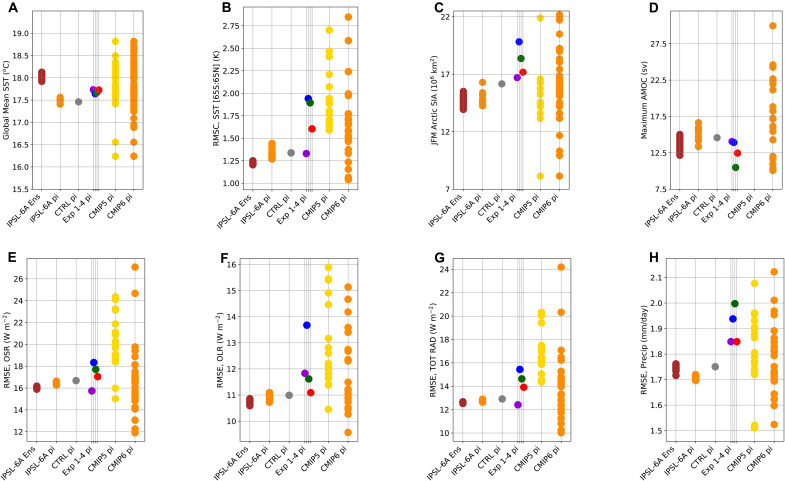
To assess the skill of the four configurations to represent the present-day climate, a series of metrics were computed on the corresponding coupled simulations (Fig. 3 and SI3). Note that the 14 metrics are not exactly those used for the tuning, but they are not independent either.

Fig. 3. Metrics computed on the CTRL and Exp 1 to 4 piControl coupled simulations.

The dispersion across those five configurations is compared with the multi-model spread for CMIP5 (yellow) and CMIP6 (orange) also computed from piControl simulations. It is compared as well with the multi-decadal variability in the IPSL-6A piControl simulation (one of the orange dots in the CMIP6 column), computed from 32 successive 30-year-long periods starting in 1850 (“IPSL-6A pi” column), and with the inter-member dispersion in the 33-member historical ensemble run with IPSL-6A for CMIP6 (“IPSL-6A Ens” column, brown). The period retained for the comparison of the historical simulations with observations is 1979–2005. The comparison of the IPSL pi and historical runs gives an estimate of the error, which is made by comparing with present-day observations simulations run in preindustrial rather than present-day conditions. (A) Global mean SST (°C). (B) Root mean square error computed on the mean seasonal cycle of the SST, between 65°N and 65°S to avoid sea ice dispersion, and after removing the mean bias (RMSC stands for centered root mean square). The mean bias is retrieved to minimize the impact of the global warming between 1850 and present day. (C) December-January-February-Marchmean sea ice extent. (D) Maximum intensity of the Atlantic Meridional Overturning Circulation (AMOC, Sv). (E to H) Root mean square error (RMSE) on the mean seasonal cycle of the Outgoing SW radiation [OSR, W/m² (E)], Outgoing LW radiation [OLR, W/m² (F)], total SW + LW Outgoing radiation [TOT RAD, W/m² (G)], and rainfall [Precip, mm/day (H)].

We first assess the success of the method that consists in targeting the global radiative imbalance of a previous configuration in stand-alone atmospheric simulations to adjust the global temperature of the coupled simulations (Fig. 3A). The five “worlds” generated with the model (CTRL and Exp 1 to 4) are all acceptable for the ensemble of metrics examined, if taking the CMIP6 ensemble as a measure of acceptability (Fig. 3, B to H). When looking in detail, Exp 1 (purple dots in Fig. 3) appears very close to IPSL-6A for most metrics, suggesting that we succeeded, with an automated procedure, to obtain one configuration with a very similar climate but with an ECS smaller by almost 1 K (see complementary diagnostics in SI3). In particular, it stands as IPSL-6A among the models with the smallest SST errors within the CMIP5 and CMIP6 ensembles (Fig. 3B). Both Exp 1 and 4 configurations also maintain a reasonable overturning oceanic circulation [Atlantic Meridional Overturning Circulation (AMOC), Fig. 3D, which is generally somewhat too weak in IPSL-CM] and a reasonable sea ice cover (Fig. 3C). They would probably have been qualified by the IPSL modeling group and retained for CMIP6 simulations if examined before fixing the parameter values of IPSL-6A during the tuning process. The intermediate simulations Exp 2 and 3 (blue and green dots, respectively) both suffer from more notable defects: Exp 2 is clearly missing clouds and underestimates the cloud radiative forcing in Fig. 1, which translate into degraded radiative metrics in Fig. 3 (E to G). Exp 3 has a very weak overturning oceanic circulation, which continues to decrease after 250 years of simulations. Those two configurations would probably have been rejected in the selection process.

Although showing contrasted ECS, the simulations do not seem to be that different in terms of simulation of climate change for a given global temperature change: the mean 2 m temperature change obtained for the standard configuration and for the Exp 1 and 4 simulations when reaching a global temperature change of 5.5 K (right column of Fig. 4) are much closer to each other than when comparing them at a given time of the simulation (after 30 years in the left column). The precipitation change in the three configurations looks also very similar at first glance for a temperature target of +5.5 K (left column in Fig. 5). Looking in detail, one can see some slight differences. For instance, the equatorial Africa warms less in Exp 1 than in IPSL-6A and Exp 4. The stronger warming in this region in Exp 4 compared to Exp 1 could be attributed to a larger increase in solar radiation reaching the surface (right column for Fig. 5), but it is not the case for IPSL-6A. Note also the large increase in surface radiation in Exp 4 compared to Exp 1 over South America, which does not translate into a significantly different temperature change, probably in part because of a larger evaporation in Exp 4 (see fig. S15). Other illustrations of these differences are shown in section SI4. Analyzing them in more detail is beyond the scope of the present paper.

Fig. 4. Two-meter temperature (K) change in coupled simulations CTRL (IPSL-6A configuration), Exp 1, and Exp 4.

The maps correspond to differences between the abrupt4×CO₂ and piControl simulations, averaged over 21 consecutive years. For the left column, this time is centered at year 30 of the simulations. For the right column, it is centered at the time when the global 2 m temperature has increased by 5.5 K, i.e., at year 33 for CTRL, year 65 for Exp 1, and year 17 for Exp 4.

Fig. 5. Surface evaporation (mm/day) and surface net solar radiation change (W/m²) in coupled simulations for a global temperature change of 5.5 K.

The maps correspond to differences between the abrupt4×CO₂ and piControl simulations, averaged over 21 consecutive years centered at year 33 for CTRL, year 65 for Exp 1, and year 17 for Exp 4.

DISCUSSION

Given the complexity of the climate “vast machine” (52) and the importance of the global warming issue, the quantification of the uncertainty in climate change projections is a question of prime importance. In view of this issue, the definition of the calibration problem as an optimization, producing one particular model configuration to the risk of compensation error, is more than questionable. History matching, by fundamentally defining the calibration process as the determination of the parameter subspace compatible with some metrics, to a given tolerance to error, offers an opportunity to reimagine the tuning process and the quantification of the parametric uncertainty as a single exercise. It also offers a framework for addressing the issues of error compensation and structural uncertainty quantification.

The slow improvement of climate models has raised questions whether coarse resolution global circulation models with parametrized physics may have become obsolete (1). The results presented here give real hope for an acceleration of the model development and improvement, providing an automatic way to return to an acceptable mean climate after adding new significant developments in the model physics. It should be reiterated that the alternate configurations of IPSL-CM were obtained after automatic calibration with the history matching procedure using 2-year-long stand-alone atmospheric simulations, ignoring the values of the IPSL-6A configuration, which were obtained after a long by-hand tuning phase.

The approach, of course, has a cost. About 800 2-year-long atmospheric simulations were needed to extract nine “acceptable” configurations. Although this number may seem large, it is in fact much smaller than the number of years simulated for the by-hand tuning of the IPSL-CM6 configuration (36, 37), not to mention the tremendous gain in human time. We showed in another study how preconditioning by a multi-wave tuning of a single-column version of the model against explicit high-resolution simulations of cloud scenes may significantly accelerate the tuning process (25, 45). The approach, not mature enough at the beginning of the present study, is since used routinely for the tuning of the IPSL model.

Four among those nine acceptable configurations were used to run coupled simulations. For all four, the standard metrics examined so far are in the spread of CMIP6 models. This success of the automated procedure benefited from the expertise gained in the team from decades of practice of by-hand tuning of the IPSL model (14, 17, 18, 37). In particular, the rather good score in simulating SST in IPSL-6A comes from the fact that we targeted on purpose some biases in the atmospheric fluxes that directly impact persistent temperature biases as the East-Tropical-Ocean (53) and Circum Antartica warm biases. These targets were thus included in the tuning procedure used here. This underlines that objective methods such as history matching cannot and should not replace the expertise and subjectivity inherent to the tuning process (23). The fact that this physical expertise and subjective choices are expressed in numbers, however, paves the way for it to be shared between modeling groups, with the aim of accelerating the improvement of climate models and gaining understanding in the behavior of the climate system.

The Exp 1 to 4 configurations not only compare well with the CMIP6 ensemble, but they also seem closer to IPSL-6A than to the other CMIP6 simulations. Does this reflect that the various configurations only differ by their parameter values while CMIP models also differ by their structural errors, linked to different choices in physics content and numerics? Is it due, in part, to the fact that the various configurations share the same unique parameter settings for models of continental surfaces and ocean? Might it also be due to the fact that the metrics selected for the automatic tuning of the atmospheric free parameters were mostly inherited from the by-hand tuning of the IPSL-6A version? The availability of objective methods such as history matching will enable us to explore these kinds of question for the first time. It would be enlightening to see, for instance, how applying the exact same tuning procedure, with the same metrics and tolerance to errors, to other CMIP models would reduce/increase the discrepancy in the aggregated metrics considered here.

All four configurations would have been available together with the IPSL-6A configuration at the time of the choice for CMIP6 simulations, probably one would have been discarded for an underestimation in cloud cover compared to IPSL-6A and another one for the rapid weakening of the AMOC intensity. Note that we are lacking so far expertise to ensure a reasonable tuning of important aspects of the coupled model such as sea ice cover or AMOC intensity, and specific work has to be done in this direction. It may indeed be by chance that three of the four selected experiments do not drift further in terms of AMOC. Gradually building a list of metrics that control more and more aspects of the simulated climate is a goal for future research. Note, however, that dealing with the long time constants of the deep ocean circulation can become computationally demanding, requiring large ensembles of multi-centennial simulations at each wave of the history matching process, unless proxies are identified in shorter simulations.

In the end, two configurations obtained automatically by history matching, Exp 1 and 4, could have been chosen instead of IPSL-6A because they show very similar results in terms of standard metrics. It turns out that these two configurations also show the most extreme ECS.

The range covered is about half that of the CMIP ensemble (Fig. 2). This means that part of the discrepancy in ECS observed in the CMIP ensembles might be the signature of the parametric uncertainty, not documented in the CMIP multi-model ensembles, and hence that the uncertainty in ECS might be underestimated by CMIP exercises. Although we used stand-alone atmospheric simulations to select configurations with contrasted ECS among the nine configurations selected in the history matching procedure, the exploration is of course very partial. A recent study tried to more systematically explore the range of possible ECS in the CNRM model under climatic constraints (54). On the basis of a PPE of stand-alone atmospheric simulations and using emulators, the authors derived 23 optimal configurations (that minimize some cost functions based on aggregate metrics), each one targeting an ECS value in the range spanned by the initial ensemble. However, unlike the work we present, there has been no attempt to confirm the results in coupled mode, either in terms of climate performance relative to CMIP or in terms of the range of ECS. It should be noted that a more systematic exploration of the ECS range could also be done with history matching, emulating the ECS in the last wave from our analysis and designing an ensemble that maximizes the range of ECS values according to that emulator.

There is an understandable temptation to use observed climate trends over the last decades to constrain the ECS and even tune it, as proposed by some groups (42), or to rule out some model configurations. However, this should only be done after a rigorous estimation of the uncertainty of the observations or of the emergent constraints used in the tuning or selection procedure (41), and by applying objective uncertainty quantification methods. This uncertainty quantification should also take into account the contribution of the multi-decadal internal climate variability which could significantly contribute to the recent climate trends (39). Until we carefully design CMIP simulations to capture all relevant uncertainties, users who consider the CMIP database as providing the uncertainty in future climate change for risk assessment will continue to be misled.

As expected, a decomposition of the model climate sensitivity in terms of clear sky versus cloud effect, in both LW and SW, points to a dominant role of the SW CRE (see SI2). Analyzing the origin of the dispersion of ECS in a larger ensemble of simulations may be a very powerful tool to get more insight into the processes that control the ECS. Note that compared to previous PPEs (9, 11), such an ensemble would be generated under the constraint of a series of global metrics, with some a priori tolerances and an automated procedure that could easily be shared among modeling groups. It would enable us to explore the parametric dispersion of ECS and radiative feedbacks not in general but under constraint given by a set of metrics with values of targets and tolerances to errors, i.e., for an acceptable representation of the present-day climate.

Despite the wide range spanned by ECS, the resemblance in the climate change simulated by the various configurations is more marked than their differences (Figs. 4 and 5). These results may advocate for working separately on the uncertainty quantification of the ECS and that of the climate change at a given global temperature change.

Finally, we would like to advocate the need to give more importance to quantifying the model intrinsic and parametric uncertainties in the forthcoming CMIP exercise, hence a reduction of the number of scenarios and protocols.

Sharing small parametric ensembles with various models, constrained by present-day observations to help quantify parametric and structural uncertainty in climate projections, would be a strong improvement for future CMIP exercises. We are willing to share the expertise and tools needed to build such ensembles. These ensembles could be combined with or complement those quantifying the uncertainty associated with decadal to centennial internal variability obtained by modifying the initial state of climate change simulations (55) and those quantifying the impact of various scenarios in the greenhouse gas trajectories, already provided in previous CMIP exercises.

The data used in tuning could be made available along with those flagship CMIP simulations, enabling users to build emulators that can propagate global climate uncertainties through to impacts using rigorous statistical frameworks (56) or to run physics-based impact models formulated within a statistical framework (57). This would lead to a step change in the types of uncertainty quantification that can be offered to those in society tasked with accounting for climate uncertainty on the outcomes of a decision or policy, whether for a single business or a region or whether it affects a whole country or continent.

The need for model calibration, for quantification of parametric uncertainty and for long spin-up simulations, will not disappear with global cloud resolving models. In these models, many aspects of the cloud physics (microphysics, subgrid scale heterogeneities, shallow convection, or the 3D radiative effects which are not accounted for so far) must still be parameterized. The same is true for many other aspects of the climate system. This constitutes a strong argument in favor of keeping a large part of the global climate modeling community working and investing on rather coarse resolution models. We must invest more on parameterizations, particularly for clouds and convection that are likely responsible for the majority of the spread in future climate projections for a given trajectory in greenhouse gas concentration.

MATERIALS AND METHODS

Climate simulations

The results presented here are based on analysis of climate simulations performed with global climate models. The models are run following well-established protocols that are summarized here.

The simulations are run either in full coupled mode between atmosphere, ocean, and continental surfaces, or in stand-alone atmospheric + continental surface mode, forced by imposed SSTs. The imposed SSTs are defined in the AMIP component of CMIP and consist of monthly averaged SSTs, interpolated in time with spline functions.

CMIP ensembles

To contextualize our results, we use the multi-model simulations of the two last CMIPs, CMIP5 and CMIP6. The outputs of the CMIP simulations are accessed through the Earth System Grid Federation (ESGF), which provides robust and effective data management. Details about ESGF are presented on the CMIP Panel website at https://wcrp-cmip.org/cmip-data-access/.

Preprocessed files will be made available with a DOI if the paper is accepted for publication, together with the scripts used to generate the figures.

We particularly use the following:

1. piControl simulations that are coupled simulations run with constant radiative forcing corresponding to preindustrial conditions.

2. abrupt4×CO₂ simulations in which the atmospheric concentration of CO₂ is abruptly multiplied by four as compared to the piControl simulation, starting from a state vector taken at a given time of the piControl simulation. The abrupt4×CO₂ and historical simulations are run with the exact same model configuration so that the climate sensitivity and climate change can be computed from the difference between the two simulations.

3. Historical simulations consisting in reconstructions of the past climate under observed and reconstructed external forcing. The latter include atmospheric concentration of anthropogenic greenhouse gases and aerosols, changes of surface land use, natural variations of the solar irradiance, and volcanic eruptions. The historical simulations start in 1850 and end in 2005 for CMIP5 and 2014 for CMIP6. The initial states are taken from the piControl simulation as well.

The IPSL coupled model IPSL-CM6A-LR

The tuning exercise and ECS exploration are done with IPSL-CM6A-LR (called IPSL-6A), the standard configuration of the IPSL coupled model designed for CMIP6 (35). It combines the LMDZ6 Atmospheric model (37), the ORCHIDEE land surface model (58), and the NEMO ocean model using the LIM3 sea ice model (59). The atmospheric model resolution is 144 × 143 points in latitude and longitude and 79 vertical layers (with a maximum height of about 80 km). The design of the IPSL-CM6A-LR configuration was the result of a long phase of improvements, bug corrections, and by-hand tuning (36).

The piControl, historical, and abrupt4×CO₂ simulations run with the IPSL model are used first as one member of the CMIP6 ensemble. In addition, to account for the natural variability in the assessment of the sensitivity experiments in Fig. 3, we use the 33-member ensemble of historical simulations run with the IPSL model for CMIP6 (39). The members differ only by their initial states, which correspond to different years in the piControl simulation. Each simulation of the ensemble follows the CMIP6 protocol for historical simulations (60) for the period 1850–2014.

Sensitivity experiments with IPSL-6A

The specific simulations run for this paper are done with a more recent model version, both for the atmospheric model and the other components. However, the changes are essentially technical and the grid configuration and physics content are the same as for the IPSL-6A configuration. To check that the results were not significantly affected by these technical changes, a CTRL configuration was rerun with exactly the same grid configuration and same values of the free parameters as for the CMIP6 standard simulations. The ensemble of tuning simulations as well as the coupled simulations Exp 1 to 4 were run by only changing the value of 18 atmospheric free parameters as compared to the CTRL simulation. As explained in "History matching: how does it work?", the atmospheric tuning is based on 2-year atmospheric simulations run with imposed climatological SSTs, computing metrics on the second year of the simulation. For CTRL and Exp 1 to 4 configurations, we run both piControl simulations and abrupt4×CO₂ experiments following the CMIP6 protocol for 250 and 150 years, respectively.

History matching

The principle of the history matching procedure, central to this work, is explained in "History matching: how does it work?". In practice, we use the High-Tune Explorer tool described in (25) at length. The application to the 3D global atmospheric component of the IPSL coupled model is very close to the description given in (45) with only two differences: (i) we do not use the preconditioning of the global tuning by 1D test cases; (ii) we add three precipitation metrics as explained in "History matching: how does it work?", in addition to the radiative metrics. The description of the metrics and the values of the metrics computed on the ensemble simulations of the successive waves of tuning are given in SI1.

Equilibrium climate sensitivity

By definition, the ECS is the change in global-mean near-surface air temperature (T_g) due to an instantaneous and uniform doubling of the atmospheric CO₂ concentration once the coupled ocean–atmosphere–sea ice system has achieved a statistical equilibrium (i.e., at the TOA, incoming solar shortwave radiation is balanced by reflected solar shortwave and outgoing thermal long-wave radiation). Computing this ECS with a coupled model requires to run the model for thousands of years to let the slowest component of the model adjust.

In practice, abrupt4×CO₂ simulations are preferred to abrupt2×CO₂ simulations because of a better signal-to-noise ratio (the noise corresponding here to the natural climate variability). In practice also, the ECS is computed from the relationship between the difference of the imbalance in the TOA global net radiative balance ΔR_net and the global atmospheric temperature difference ΔT_g computed from a pair of abrupt4×CO₂ and piControl simulations, to remove the common drift or common long-term variability of the two simulations. Although some models show a more complex behavior, the relationship is generally quite linear, and this extrapolation is deduced from a linear regression over the first 150 years, ΔR_net = aΔT_g + b, using yearly averages for ΔR_net and ΔT_g (50). The radiative forcing at equilibrium for a doubling of CO₂ is the intercept of the regression line with the y axis divided by 2 (ERF = b/2) while the ECS is the intercept with the x axis divided by 2 as well [ECS = −b/(2a)]. This regression is shown in fig. S7 of section SI2 for the CTRL and Exp 1 to 4 simulations.

Proxies of the ECS can be computed as well from simpler setups. Here, we use an effective ECS computed on stand-alone atmospheric simulations run on climatological SSTs (clim) and SSTs increased by 4 K (clim+4K). The ECS is computed as the ERF divided by the climate sensitivity, defined as the ratio of the change in global TOA radiation divided by the change in the global near-surface atmospheric temperature ECS^atm = ERF × ΔT_g/ΔR_net. Because the ERF is known only a posteriori, from the coupled simulations, we use a constant value of 4 W/m², somewhat overestimated compared to the effective values obtained in coupled simulations (fig. S7). For a number of reasons (51), this ECS^atm computation gives a rather poor estimate of the effective ECS of the coupled model. Although some propositions exist to account for the difference between ECS^cpl and ECS^atm (51), we prefer here to use the simplest estimate of ECS^atm, the proposed correction not affecting generally the ranking of the ECS values (see section SI2 and fig. S7).

Note that because the tuning was done with a more recent version of the model code, we run a control (CTRL) configuration with this version, but with the same parameter values as the IPSL-6A configuration, to check that they yield similar results.

Model evaluations

The most relevant way of comparing coupled simulations with observations of the past decades is to consider averages of the historical simulations for the same period. Here, we selected, for evaluation purposes, the period 1979–2005. However, since we did not run historical simulations for configurations Exp 1 to 4, most of the evaluation is done by comparing piControl simulation to present-day observations. To estimate both the part of the errors that comes from this choice as well as the possible contribution of the natural variability to the evaluation metrics in Fig. 3, we also include IPSL-6A 33-member ensemble of historical simulations (brown circles in Fig. 3).

Supplementary Materials

This PDF file includes:

SI1 to 4

Figs. S1 to S20

Tables S1 to S3