Abstract
The mechanics of vocal fold contact during phonation is known to play a crucial role in both normal and pathological speech production, though the underlying physics is not well understood. Herein, a viscoelastic model of the stresses during vocal fold contact is developed. This model assumes the cover to be a poroelastic structure wherein interstitial fluid translocates in response to mechanical squeezing. The maximum interstitial fluid pressure is found to generally increase with decreasing viscous dissipation and/or decreasing tissue elasticity. A global minimum in the total contact stress, comprising interstitial fluid pressure and elastic stress in the tissue, is observed over the studied dimensionless parameter range. Interestingly, physiologically reasonable estimates for the governing parameters fall within this global minimum region. The model is validated against prior experimental and computational work, wherein the predicted contact stress magnitude and impact duration agree well with published results. Lastly, observations of the potential relationship between vocal fold hydration and increased risk of tissue damage are discussed based upon model predictions of stress as functions of cover layer thickness and viscosity.
Keywords: Viscoelasticity, Contact stress, Viscous dissipation, Vocal fold hydration, Voiced speech modeling
1. Introduction
Voiced speech production is characterized by self-sustained oscillations of the vocal folds (VFs) that arise due to fluid-structure-acoustic coupling between the aerodynamic forces and viscoelastic tissue properties. Each phonatory cycle ends with the opposing VFs contacting one another along the medial surface, thus closing the glottis (Mittal et al. 2013). The dynamics of VF contact have been investigated in a number of theoretical (Titze 1994a), experimental (Jiang and Titze 1994; Alipour and Scherer 2000; Spencer et al. 2008), and computational VF models (Gunter 2003, 2004; Horacek et al. 2005, 2009; Bhattacharya and Siegmund 2012). Early work estimated that impact stresses were the most detrimental in terms of tissue damage (Titze 1994a). Subsequent work has shown that impact stresses during contact are on the order of one kilopascal (Hess et al. 1998; Verdolini et al. 1999), and that both the magnitude and duration of impact are indicators of epithelial damage, which can lead to phonotrauma (Tsuyoshi et al. 2014).
While VF closure is a hallmark of healthy voice production, excessive contact forces often lead to the formation of organic pathologies, such as VF nodules and polyps (Titze 1994b). First identified in 1866 (Türk 1886), VF lesions are believed to form as a result of some form of misuse or abuse (Hirano et al. 1980; Hillman et al. 1989). While lesions may develop due to acute trauma (Titze 1994b), they are often the result of subjecting the VF tissue to excessive repetitive mechanical stresses, as occurs during VF collision (Titze 1994a). It is believed that these collisions, and the resultant tissue stresses, give rise to structural modifications of the epithelium (Kojima et al. 2014) and underlying tissues in the superficial lamina propria (Gray and Titze 1988; Jiang et al. 1998; Gunter 2004), producing VF nodules (Rosen et al. 2000).
Particular interest lies in the ability to accurately resolve contact forces in low-order, simplified VF models (Erath et al. 2013), which, with their low computational cost, are suitable for long-duration investigations of cumulative contact damage. Prior modeling efforts have primarily considered contact using a spring-damper arrangement that relies upon ad hoc coefficients, as first suggested by Ishizaka and Flanagan (1972). More recent investigations have utilized Hertzian contact models (Horacek et al. 2005; Zañartu et al. 2007), which are still a simplification due to the nonlinearity of VF contact (Lin et al. 2009). Furthermore, while Hertzian approaches can incorporate a damping constant at collision, it is typically excluded in VF investigations, thereby neglecting the role of viscous dissipation within the tissue. Consequently, there is significant motivation for developing a low-order, physics-based representation of the viscoelastic nature of VF contact.
Higher-order, finite element approaches are capable of prescribing the layered, viscoelastic properties of the VF structure (Gunter 2003, 2004; Bhattacharya and Siegmund 2012, 2015), which includes the role of viscous dissipation (i.e., damping) during contact, as well as adhesion forces. Modeling viscous dissipation during contact is especially relevant as it is related to VF hydration, which is believed to play a crucial role in VF health by helping to mitigate excessive contact forces (Verdolini 1988; Verdolini et al. 1994; Tanner et al. 2007; Sivasankar and Leydon 2010). Zhang et al. (2008) developed a biphasic (solid-fluid) theory of the viscoelasticity of the lamina propria that prescribes the tissue as an elastic structure with viscosity arising from interstitial fluid migration when subjected to strain. They noted that dehydration results in the evacuation of interstitial fluid, which carries the bulk of the stress, and hence, would likely give rise to an increase in tissue stress, as the structure would be required to carry a greater percentage of the load. Still, the precise functional relationship between hydration and contact stresses remains unresolved.
Recent numerical investigations have also sought to determine the relationship between tissue viscoelasticity and contact stress. Tao et al. (2009) used a poroelastic model for the VFs, that is, a porous elastic solid with interstitial fluid (Mak 1986; Mow et al. 1993), to show that fluid migration within the VFs due to contact stresses can lead to increased contact pressure along the anterior–posterior midline, where VF lesions are most likely to occur. Similarly, Bhattacharya and Siegmund (2012) applied poroelasticity to a fully coupled, fluid-structure interaction, computational VF model in order to relate systemic hydration with the induced mechanical stresses that arise during VF collision. It was shown that VF collision produces an interstitial fluid flux that drives fluid away from the contact area, resulting in increased stress gradients. This effect is exacerbated in dehydrated tissue, producing a cascading effect that is postulated to be an important mechanism in the etiology of VF lesions. In this manner, it was shown that tissue stresses arising from VF contact can be directly related to VF hydration.
The importance of VF hydration relative to contact stresses can be further confirmed through clinical observations of systemically dehydrated patients on hemodialysis treatment (Fisher et al. 2001; Ori et al. 2006). In addition to noting that dehydration increased phonation threshold pressure (PTP) in post-dialysis patients, Ori et al. (2006) also measured the VF thickness of the study subjects, reporting that the ratio of the VF thickness in the medial-lateral direction to length in the anterior–posterior direction decreased on average by 10.9% due to systemic post-dialysis dehydration. This agrees with the relationship found by Titze (1988) that PTP is inversely proportional to VF thickness while also suggesting that hydration affects not just the viscosity of the VF tissue (Verdolini 1988; Verdolini et al. 1994; Chan and Tayama 2006) and is supported by the biphasic theory of lamina propria viscoelasticity developed by Zhang et al. (2008). These findings demonstrate a link between VF contact stresses and hydration, with the contact stresses being altered not only due to changes in the tissue properties, but also due to physical changes in the VF thickness. While Bhattacharya and Siegmund (2012) indirectly addressed this issue, noting that the flux of fluid out of the tissue gives rise to higher contact stresses, and Zhang et al. (2008) made similar observations, the precise dependence of contact pressure on VF cover thickness and tissue viscosity due to dehydration was not considered.
The objective of this manuscript is to (1) develop a low-order theoretical model of VF contact stresses that considers the influence of viscosity, elasticity, and thickness of the VF tissue to determine a functional relationship between contact forces and VF physiology, and (2) elucidate how hydration influences the physics of VF contact. A solution that is suitable for implementation into low-order numerical voiced speech models is pursued. The approach provides insight into the physical mechanisms of VF contact while also establishing a framework for implementing the solution into numerical modeling efforts for the investigation of accumulated damage as a function of contact stress.
The manuscript is organized by section as follows: Sect. 2 problem formulation; Sect. 3 general observations of model behavior; Sect. 4 model validation and discussion; and Sect. 5 conclusion.
2. Problem formulation
Herein, we aim to develop a quasi one-dimensional (1-D) viscoelastic contact model that captures the stress in the VF cover (epithelium, superficial lamina propria, and intermediate lamina propria) during collision by employing the biphasic assumption for the prescription of the viscoelastic behavior of the VF lamina propria (Zhang et al. 2008). The biphasic theory prescribes that the viscoelasticity of soft, hydrated tissues is well represented by treating the structure as an elastic, porous network with an interstitial flux of fluid. This approach, while not providing a prescription of viscoelasticity at the molecular level, does suitably capture the bulk, macroscopic behaviors (Oomens et al. 1987; Soltz and Ateshian 1998; Gray et al. 1999; Sun et al. 2004). In this manner, the superficial (cover) layer is modeled as a poroelastic fluid-filled layer with shear modulus . The remaining (body) layer is considered as an impermeable mass with shear modulus that is viscoelastically connected to the thyroid cartilage, represented as a rigid substrate (see Fig. 1). We presume that interstitial fluid motion is primarily confined to the VF cover layer during contact, while the body layer (deep lamina propria and muscle) provides the bulk of the VF inertia. The interstitial fluid is assumed initially at rest, consistent with the assumption that hydrostatic pressure drives the flux of the interstitial fluid (Bhattacharya and Siegmund 2012). Figure 1 shows a sketch of a coronal section of the VFs, with the cover and body layers identified (layers 1 and 2, respectively), in which portions of the opposing folds in the inferior–superior direction are in contact. This is the presumed VF configuration upon which the present model is based.
Fig. 1.
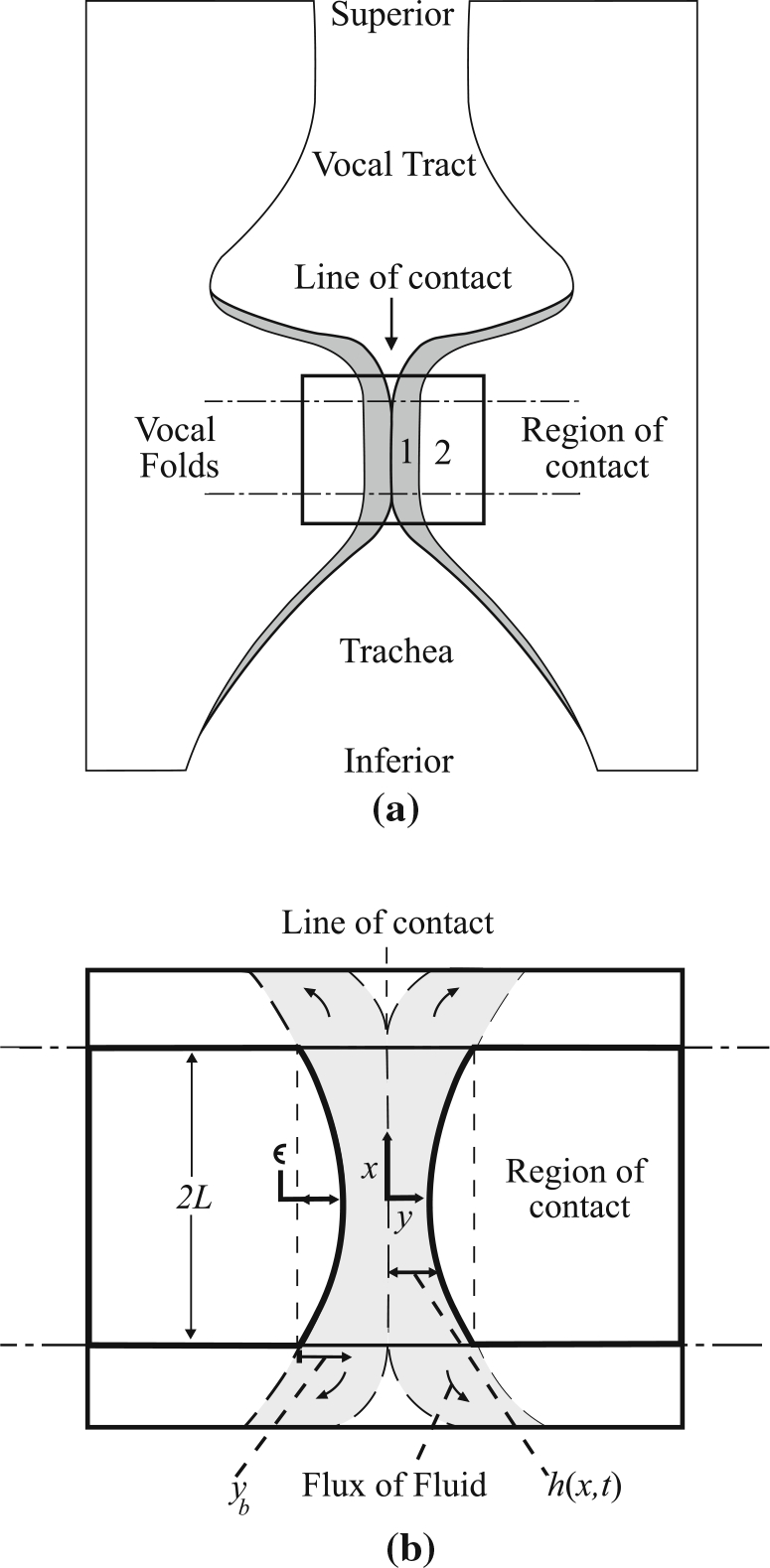
a Coronal section sketch of the problem being considered with the region of analysis indicated. The cover and body layers are labeled with 1 and 2, respectively. b Exploded view of the region of analysis shown in (a) with pertinent variable and coordinate system definitions. The shaded areas in both images demarcate the modeled cover layer
The VF motion is assumed to be symmetric about a common centerline, which is the line of contact between the opposing VFs illustrated in Fig. 1. A Cartesian coordinate system is fixed at the midpoint of the centerline, with the and axes oriented in the inferior–superior and medial-lateral directions, respectively. Herein, we assume that the VF tissue moves only in the -direction. The initial velocity of the VF mass is given as in the -direction, and the initial thickness of the cover layer is given as . The dimensions in the inferior–superior and anterior–posterior directions (into the page in Fig. 1) of the contact area are denoted by and , respectively.
The body stiffness is assumed to be much larger than the cover stiffness , such that deformation of the body mass during contact is small in comparison to that of the cover. This assumption is reasonable when the thyroarytenoid muscle is strongly contracted, for example (Story and Titze 1995; Zhang 2009). As such, we neglect deformation of the body and model the interface between the two layers, shown schematically in Fig. 1, as a fixed shape that translates as the mass moves. For simplicity, we presume a parabolic shape with maximum height . The curved interface accounts for mild curvature in the deep layers of the VF, which are presumed to remain undeformed, see Fig. 1. Under this assumption, the cover layer has thickness
| (1) |
where is time and is the distance of the interface between the cover and body layers from the centerline at . The locations correspond to the edges of the contacting regions of the VFs at the inferior and superior margins, see Fig. 1.
Contact initiates when the cover layers of the opposing folds first touch. The quasi 1-D viscoelastic contact model is initialized when a sufficient length of the medial surface is in contact such that this length is large in comparison with the initial cover layer thickness . As a rough estimation, the VF cover thickness is approximately 1/6 of the VF length, suggesting that this constraint is reasonably met for full VF contact. Upon initial contact, the cover layer is assumed to be at rest with respect to the fixed reference frame, with a moving boundary corresponding to the interface between the cover and body regions. Energy dissipation due to surface waves along the free surface of the cover upon the initial contact is neglected.
Viscoelasticity in the cover is modeled using a modified Kelvin–Voigt configuration consisting of elastic and viscous elements in parallel. Herein, viscous damping results from interstitial fluid motion within the superficial layer, akin to thin film lubrication, leading to nonlinear damping. As such, the cover is modeled as a viscous fluid with constant dynamic viscosity flowing through a poroelastic structure. Following Titze and Story (2002), we assume the cover to be transversely isotropic, completely compressible (Poisson’s ratio equal to zero), and that the elastic strain in the cover varies linearly across the cover thickness. Under such assumptions, the linear elastic component of the stress in the cover is given by
| (2) |
We note that under large strains, vocal fold tissue exhibits nonlinear elastic behavior (Titze 1994b). However, as the focus of this paper is on elucidating first-order effects primarily associated with fluid translocation and the associated viscous damping, we have neglected nonlinear elastic effects. This is generally a good assumption for small strains, and has been employed in several prior studies exploring VF contact (Gunter 2004; Tao and Jiang 2007; Zhang et al. 2008).
The fluid in the cover is assumed to be incompressible and Newtonian; as such the dynamics of the cover layer is governed by the Navier–Stokes equations. We note that it is assumed that the vast majority of the material in the cover is interstitial fluid, thus the VFs are essentially incompressible, despite the compressibility assumption used above in the reduced-order structural model development. The cover layer is assumed thin, and thus inertia of the fluid constituent in the cover is neglected. Recalling the assumption of impermeability of the body layer to the interstitial fluid in the superficial cover layer, the Navier–Stokes equations are simplified to a form of the thin film lubrication equation (Panton 1996). It is given as
| (3) |
where is the fluid dynamic viscosity, and is the fluid pressure, which is a function of both and . The constant on the right hand side is typically given as 1/12 in the thin film lubrication equation; however, in the present case, only half of the film is considered due to the symmetry of the problem (both VFs have their own cover; the boundary conditions at the interface are no velocity in the -direction and shear stress is zero), which results in a constant of 1/3. We also note that the assumption that the fluid is initially at rest, as described above, is not strictly true, as the fluid will be moving at the same speed as the rest of the cover prior to contact. However, since fluid inertia is negligible in the thin film approximation in comparison with the other forces, the analysis is simplified by merely assuming that the fluid is initially at rest.
For the proposed modified Kelvin–Voigt model, the total stress in the cover is given by a linear combination of the elastic stress and the fluid pressure , which is related to the viscous damping. That is,
| (4) |
The dynamics of the VF mass during contact is governed by
| (5) |
where a dot over a variable indicates differentiation with respect to time, and represents forces on the mass due to adhesion at the lateral boundaries to the thyroid cartilages. That is, the function comprises viscoelastic effects of the body layer and its coupling to the rigid cartilage substrate. We emphasize that this is the simplified governing equation during contact only, when there is no aerodynamic or other exogenous loading applied to the VFs. To recast Eq. (5) in terms of , we note that , where is the distance of the equilibrium position of the mass from the line of contact. Thus, Eq. (5) can be rewritten as
| (6) |
where is analogous to in Eq. (5). The boundary and initial conditions for Eqs. (3) and (6) are
| (7) |
where is a reference pressure in the cover fluid at the margins of the domain.
We are assuming that the pressure in the cover fluid is equal at the inferior and superior boundaries and that these pressures are constant, both of which are simplifications. As contact progresses, the high pressures in the region of contact will likely result in some deformation in the remainder of the cover due to fluid motion. This capacitive type effect may result in temporal variations in the boundary pressure and contact area. Furthermore, inferior–superior asymmetries in the flow of fluid in the cover may produce unequal boundary pressures. These effects are considered higher order in nature, and as such, are reasonably neglected in order to achieve the stated objective of providing a first-order investigation of how contact stresses in the VF cover are influenced by varying tissue properties. A first-order model is adopted to enable parametric evaluation of the variables of interest over relatively wide parameter ranges to gain physical insight into the problem. Future refinement may be accomplished using, for example, higher-fidelity numerical simulations.
The governing equations and their associated boundary and initial conditions can be nondimensionalized by letting , and . By substituting into Eq. (6) and employing this nondimensionalization scheme, Eqs. (1), (3), (6), and (7) become
| (8) |
| (9) |
| (10) |
and
| (11) |
where , and . The function governs the dynamics of the VF mass both during and outside of contact. The dimensionless parameters and are associated with the tissue elasticity and fluid damping in the cover, respectively, during the impact process, and as such, only have meaning during contact. Specifically, is the ratio of the elastic energy stored in the cover during contact to the kinetic energy of the VF, while represents the ratio between viscous dissipation in the fluid and the rate of change of kinetic energy of the VF mass.
For the remainder of the manuscript, all variables are assumed nondimensional unless otherwise noted. As such, from this point further the “hat” notation will be dropped for convenience.
3. General observations and model behavior
In this section, the general behavior of the quasi 1-D viscoelastic contact model is discussed for two cases: (i) a “flat” body/cover interface ; and (ii) a curved body/cover interface . For both cases, results are presented in terms of nondimensional parameters and to demonstrate how the physical interactions are dependent upon cover elasticity and viscous damping. In order to clearly illustrate the role of these governing contact parameters, we simplify the dynamics by decoupling the VF mass from the cartilages, that is, we set , resulting in contact forces being the only factor in the mass dynamics. This will generally lead to an overestimation of the stress, but our aim is not to provide quantitative data, but rather qualitative insight. These loads can be easily reinstated into fully self-oscillating VF studies; such studies incorporating the proposed contact model are left for future development.
Emphasis is initially placed on the dependency of the interstitial pressure in the cover on the nondimensional parameters, since the contribution of viscous dissipation to the total contact stress is manifest through this pressure, as noted from Eq. (4). Following this, the dependency of the total contact stress, including both viscous damping and tissue elasticity, is discussed as a function of and .
3.1. Planar VF contact;
The first case to be considered is a flat interface between the body mass and the cover layer, that is, . From here on, the subscript will be used to designate variables associated with the “flat” case, while a subscript will be used for the case when , see Sect. 3.2.
With , from Eq. (8) it is seen that is no longer a function of , and as such, Eq. (9) can be directly integrated twice to obtain the pressure distribution within the cover as a function of . Performing the integration and applying the pressure boundary conditions in Eq. (11) yields
| (12) |
The pressure distribution is parabolic1, and the peak pressure magnitude is a function of the VF cover thickness, the rate of change of the thickness, and the pressure in the cover fluid in the non-colliding region. We note that in the traditional Kelvin–Voigt model, the viscous damping is computed as a coefficient (the fluid viscosity) multiplied by the rate of strain in the material, which is in this case. In the present quasi 1-D viscoelastic contact model, the damping, embedded here in the cover fluid pressure, is still proportional to the rate of strain. In this case, however, the “coefficient” is nonlinearly dependent on the strain (the thickness ).
From Eq. (12), the maximum pressure occurs at . Furthermore, as the cover layer thins during contact, the pressure can increase drastically. Substituting Eq. (12) into Eq. (10) with and integrating yields
| (13) |
In the limiting case when and , this equation reduces to a separable first-order nonlinear differential equation, which can be solved directly. Separating, integrating, and applying the initial conditions from Eq. (11) yields
| (14) |
where . For , Eq. (13) can be numerically integrated.
Since is, in this simplified analysis, a constant that acts as a forcing function, and further, since a second constant forcing function exists in Eq. (13), we consider only the case where . For a given value of , the effect of a nonzero boundary pressure will be similar to the effect of an increase in . Note these are not completely equivalent, since is also on the left hand side of the equation. Detailed studies, not shown here for brevity, however, do indicate that increasing has similar behavior to increasing .
The thickness and rate of change of thickness of the cover layer as functions of time during contact for various values of and are presented in Fig. 2. In Fig. 2a, b, maintains a constant value of 0.1 with varying, while Fig. 2c, d displays the behavior for fixed over a range of values. We first consider the influence of with fixed and small , shown in Fig. 2a, b. For very small values of , corresponding physically to cases where the VF kinetic energy dominates the viscous energy dissipation in the cover layer, the VF body masses approach one another at essentially a constant velocity, equal to the initial velocity of , before abruptly stopping with the final resting position of the body masses being very close together ( very small). This is as if the cover layer was completely compressed. As increases, the masses slow down more gradually, resulting in more measured compression of the cover layer as it approaches its steady-state value. For large values of , corresponding to very high viscous dissipation, the kinetic energy of the mass is dissipated almost immediately, resulting in a minimum cover layer thickness very near the initial position , wherein the fluid-filled cover is virtually uncompressed.
Fig. 2.

Nondimensional thickness (a, c) and rate of change of thickness (b, d) of the cover layer as a function of nondimensional time. For (a) and (b), and varies from 10−4 to 10. For (c) and (d), and varies from 0 to 3
In the special case where , the cover layer thickness reaches a steady-state position at the minimum thickness (compressed). This steady-state thickness of the cover layer is , which is obtained by setting in the middle equality of Eq. (13) and solving for . In regards to the limits, if then , and if then . We note that since is small, but nonzero in Fig. 2a, b, the cover masses eventually begin to move away from one another (most easily observed by the velocity obtaining a small positive value), indicating a slight rebounding effect due to the cover layer elasticity. Were the cover mass coupled to the body, the additional springs would enhance the rebound, as would larger values of .
Figure 2c, d presents the influence of varying with fixed at 0.1. For small values of , the mass eventually comes to (or nearly to) rest, with the initial kinetic energy eventually damped by viscous dissipation as seen in Fig. 2a, b. As increases, however, more and more energy is stored in the tissue elasticity, which is eventually released, causing the VF mass to rebound. This is seen in Fig. 2c, d where the highest value of rebounds away from the centerline. We note the solution is only applicable during contact and, thus, is no longer valid when the cover thickness becomes greater than its initial value; that is, for , the cover has fully decompressed and regained its initial state.
As increases, the amount by which the cover mass compresses decreases, with the energy stored increasingly more in the tissue elasticity and relatively less being dissipated through viscous dissipation; recall that the dissipation is proportional to , and thus the relatively smaller degree of compression for a fixed value of is indicative of less viscous dissipation. As previously noted, having a nonzero value for the pressure boundary condition behaves similarly to inclusion of tissue elasticity. That is, for fixed values of and , increasing shows similar trends to those in Fig. 2c.
The impact of viscous damping during contact is elucidated by plotting the pressure in the cover layer during contact, as shown in Fig. 3. Figure 3a presents the peak pressure [corresponding to the pressure at from Eq. (12)] as a function of time for a fixed value of for values of ranging from 0 to 3. The peak pressure has an initial value of 3/2 at the start of contact . For small values of , the peak pressure rises as increases before reaching a maximum, then dropping off. The rise in pressure is initially slow, then ramps up quickly to the maximum value. As increases, the maximum value of the peak pressure waveform decreases, since more of the initial kinetic energy of the VF mass is absorbed by the tissue elasticity. The location of the maximum also shifts to later times. For the largest values of , the maxima is very small and shifts back to earlier times. Damping in these cases is minimal and most of the kinetic energy of the VF is converted directly into elastic strain energy.
Fig. 3.

a Nondimensional peak pressure as a function of nondimensional time for with varying ; and b the maximum pressure occurring during the interaction (i.e., the maxima of the waveforms in (a)) as a function of for varying
Figure 3b presents the maximum pressure during contact, that is, the maxima for each waveform in Fig. 3a, as a function of for various values of . For low values of , the maximum contact pressure increases with decreasing . Physically, this corresponds to the case where viscous damping and elasticity are both small in comparison with the initial kinetic energy of the folds. Thus, the contact is more of an impulse, with relatively little energy stored in the tissue elasticity, and minimal viscous damping until the cover compresses considerably, at which point damping increases rapidly, indicated by a sharp rise in interstitial fluid pressure, see Fig. 3a. As increases, viscous damping becomes more dominant and energy is removed more readily without the resulting spike in interstitial pressure. As increases, more and more energy is stored in the structure of the VF, thus the maximum fluid pressure reduces. For large values of the structure absorbs virtually all of the kinetic energy, regardless of the value of . In such cases, the cover compression is relatively small and rebound occurs rapidly, as shown in Fig. 2c.
The total stress in the cover layer , due to both interstitial fluid pressure (i.e., viscous damping) and tissue deformation, was introduced in dimensional form in Eq. (4). Nondimensionalizing, Eq. (4) becomes
| (15) |
Figure 4 presents , computed from Eq. (15), as a function of and with . In general, the maximum stress increases as and increase, simply by the nature of Eq. (15). The maximum stress also increases very rapidly for small values of and due to very high pressure occurring over this parameter range, as observed in Fig. 3. Interestingly, Fig. 4 indicates a region of minimum cover stress for approximately and . This minimum suggests a relationship between the system properties (, etc.) that minimizes the overall stress in the cover tissue, which should lead to minimum tissue damage during contact. This will be further discussed in Sect. 4.
Fig. 4.

Maximum nondimensional stress in the VF cover as a function of and
3.2. Non-planar VF contact;
The impact of a slightly curved body/cover mass interface on the pressure loading in the cover is now investigated by considering cases in which in Eq. (1) is greater than zero. In this configuration, the line of contact, however, remains planar, as discussed in Sect. 2 and shown in Fig. 1. As above, the influence of the boundary pressure will be neglected for clarity and simplicity. Substituting Eq. (8) into Eq. (9) and solving for the pressure distribution using the boundary conditions in Eq. (11) with yields
| (16) |
As mentioned in Sect. 2, the initiation of contact is not modeled; rather, this solution assumes that a region of the VFs are in contact, and models the subsequent dynamics. For the curved body/cover mass interface of this section, the cover region at has been in contact longer than the region at . We assume that is small in comparison with the size of the region in contact, however, and thus we ignore this slight inconvenience.
The pressure distribution along the body mass presented in Eq. (16) is plotted in Fig. 5 for various values of . The pressure is normalized by , such that the peak pressure for the case has a magnitude of unity. As increases, the pressure distribution deviates from the purely parabolic profile of the case, with the peak pressure becoming more pronounced.
Fig. 5.

Pressure distribution as a function of nondimensionalized position along the body mass for various values of . Pressure is normalized by the peak pressure for the case
Substituting Eq. (16) into Eq. (10) (with ) and integrating the pressure and elasticity distributions over the body mass yields
| (17) |
where .
The minimum cover thickness during contact for the curved case normalized by the minimum cover thickness in the flat case for various values of is presented in Fig. 6 as functions of and . For small values of , the dynamics of the cover mass is similar to the flat case, which is indicated in Fig. 6 by a horizontal line at . As increases, we find that the minimum cover mass thickness is larger than in the corresponding flat case; that is, the cover does not compress as much. Care should be taken in interpreting this result, however, since is the thickness of the cover at . The cover thickness at can be obtained by shifting each line in Fig. 6 down by its respective value. In so doing, we find that for larger values of and , the curved case results in a thinner cover at than in the flat case.
Fig. 6.

Nondimensional minimum thickness occurring during contact a as a function of for ; and b as a function of for for varying
Figure 7 presents the maximum pressure experienced during contact as a function of for various values of and , thereby elucidating how viscous damping during contact is influenced by geometric variations along the VF surface. The pressure is normalized by the maximum contact pressure for a flat case. As suggested by Fig. 7, for given values of and , the maximum contact pressure increases with increasing , leading to the reduced cover compression. As and increase, the impact of is mitigated. This is largely due to either the structure absorbing more of the energy, or the energy being rapidly dissipated through viscosity as these values increase.
Fig. 7.

Maximum pressure experienced during contact as a function of for a various values of at ; and b various values of at
Curvature in the base of the cover layer, either due to curvature of the thyroarytenoid muscle or some other geometric protuberance below the VF cover, produces a significant increase in the peak contact pressure. Were the protuberance due to growth of a lesion, a cascading feedback effect could occur; in such a case, the growth of the protuberance would lead to higher contact stresses, which may cause further tissue damage and growth of the organic pathology. This then would lead to even higher contact pressures. Increasing and mitigated the sensitivity of the contact pressure to the height of a protuberance, though the trend of increasing pressure with increasing protrusion height persisted.
4. Discussion
4.1. Comparison with prior work
The proposed quasi 1-D viscoelastic contact model can be validated by comparing the contact stress that it predicts with published data (Jiang and Titze 1994; Hess et al. 1998; Verdolini et al. 1999; Gunter 2003; Tao and Jiang 2007). Experimental and numerical investigations report a double peak in the temporal evolution of VF pressures during collision (Jiang and Titze 1994; Tao and Jiang 2007), with the initial pressure peak arising due to the contact mechanics, while the secondary peak occurs due to aerodynamic forces. Tao and Jiang (2007) utilized a layered, self-oscillating finite element VF model to investigate contact, decomposing the contact pressure into impact and aerodynamic pressures. The impact pressure was determined by specifying that when the VF surface overlapped the midline (i.e., contact occurred), a pressure was applied that was scaled with the penetration distance. In this manner, the reported impact pressure is analogous to the contact stress discussed herein (see Eq. 4), as opposed to the fluid pressure, which neglects the tissue elasticity. The time history of the impact pressure (stress) extracted from the experiments of Jiang and Titze (1994), as well as from the finite element models of Tao and Jiang (2007) and Bhattacharya and Siegmund (2012) are shown in Fig. 8. The overall pressure waveforms are qualitatively similar, with the pressure rising quickly to a maximum value, then returning back to 0 kPa over a duration of approximately 1ms. While the waveforms are similar, the maximum stress differs between the waveforms by up to a factor of approximately 2.5, which is consistent with the contact pressure ranges found in other studies (Hess et al. 1998; Verdolini et al. 1999).
Fig. 8.

Comparison of contact pressure (stress) extracted from experimental data (Jiang and Titze 1994) and finite element VF models (Tao and Jiang 2007; Bhattacharya and Siegmund 2012) with the maximum contact stress predicted by the current contact stress model as a function of time for the dimensional variables listed in Table 1
The contact stress predicted by the current model can be quantified to the first order in terms of the maximum impact stress, and the duration (time) of the impulse. Table 1 presents the relevant variables that are needed to compute the dimensional contact stress from the quasi 1-D viscoelastic contact model presented herein. Physiological measures that have been employed in prior works are reported in the third column (Value), while the fourth column (Approx.) provides the order of magnitude estimates that we use to compute the dimensional contact stress. The mass of the cover in the contact model was computed based on physiological measures of the volume and density. Nondimensional values of the time, stiffness parameter , and viscous dissipation , are also reported.
Table 1.
Dimensional VF properties, parameters and outcomes arising from contact
| Description | Variable | Value (units) | Approx. (units) |
|---|---|---|---|
|
| |||
| VF properties | |||
| Inferior–superior VF length | 3.0 (mm) (Scherer et al. 2001) | ||
| Anterior–posterior VF length | 12(mm) (Scherer et al. 2001) 15 (mm) (Hirano 1977) |
||
| Contact velocity | 0.7 (m/s) (Spencer et al. 2008) 1.6 (m/s) (Döllinger et al. 2005) |
||
| Shear modulus | 2.9–7.5 (kPa) (Chhetri et al. 2011) 2.0 (kPa) (Tao and Jiang 2007) |
||
| Cover layer thickness | 0.65 (mm) (Hirano 1977; Hirano et al. 1981) | ||
| Cover viscosity | 10−3–10−1 (Pa s) (Chan and Titze 2000) | ||
| Cover density | 1, 020 (kg/m3) (Perlman 1985) | ||
| Computed values | |||
| Mass of VF contact model | N.A. | ||
| Nondimensional time | N.A. | ||
| Nondimensional stiffness | N.A. | ||
| Nondimensional dissipation | N.A. | ||
| Measures of contact | |||
| Contact duration | ~1.5 (ms) (Jiang and Titze 1994) ~1 (ms) (Tao and Jiang 2007) |
||
| Peak contact stress | ~3 (kPa) (Jiang and Titze 1994) ~1 (kPa) (Tao and Jiang 2007) |
||
Included in Fig. 8 is the predicted stress in the cover layer from the viscoelastic model developed herein using the order of magnitude approximations from Table 1. The stress increases rapidly to a peak of just under 2 kPa before falling back to zero. We note that the initial stress from the predicted model is not zero since our model initiates once a sufficient length along the medial surface of the folds is in contact, as discussed in Sect. 2, which does not change in time as contact progresses. From Fig. 8 we observe that the present model is in good agreement with the other studies in terms of qualitative waveform shape, magnitude, and duration of the contact stress during impact. Specifically, the peak pressure predicted in the current model falls between the values from Jiang and Titze (1994) and Tao and Jiang (2007), with excellent agreement found with the values computed by Bhattacharya and Siegmund (2012). The total duration of contact in the present model is also within very good agreement, while the rise time in the contact stress falls within the range of values reported in prior work as well. We note that both the time of contact and the peak value are sensitive to the values of and , which can account for the variability in previously published measures of contact pressures.
Given the relative simplicity of the current model, the agreement with both higher-fidelity numerical simulations (Tao and Jiang 2007; Bhattacharya and Siegmund 2012) and experimental data (Jiang and Titze 1994) is very encouraging, suggesting that the pertinent physics is captured. Interestingly, based upon the physiological data from Table 1, we find that the ranges of and expected for speech fall roughly within the range of the minimal contact stress presented in the regime plot of the maximum contact stress shown in Fig. 4. This may be an evolutionary adaption that minimizes the stress experienced by the VFs and protects them from injury during normal speech.
4.2. Comments on the role of hydration on contact stress
It has been suggested that improved VF hydration reduces the viscosity of the mucosal layer (Chan and Tayama 2006), while also increasing the thickness of the cover layer (Ori et al. 2006; Zhang et al. 2008). In light of these two observations and the model results from Sect. 3, insights regarding the role of VF hydration on contact stresses can be obtained.
Figure 9, computed using the values from Table 1, demonstrates how the peak contact stress (dimensional) is influenced by both viscosity and cover thickness. Decreased cover thickness results in increased contact stress for all values of viscosity, with a sharp increase for below approximately 0.5mm. Increasing viscosity also produces a more modest rise in contact stress.
Fig. 9.

Maximum contact stress as a function of cover viscosity and thickness computed using the values listed in Table 1
These observations provide a direct relationship between decreased VF thickness and increased viscosity, both of which are directly related to VF hydration (Verdolini 1988; Verdolini et al. 1994; Chan and Tayama 2006; Ori et al. 2006), and a quantifiable rise in contact stress. The broader dependence of contact stress on tissue viscosity and cover thickness can be discerned by revisiting Fig. 4, where the same trends are presented, albeit in dimensionless form. The peak contact stress can be quantified in terms of the two nondimensional parameters and . As previously discussed, it is interesting to note that there is a clear localized minimum in the peak contact stress as functions of these dimensionless parameters, where deviation from this minimum can produce a precipitous rise in the contact stress. It is important to note that the order of magnitude estimations utilized herein preclude the comparison of these results to specific physiological cases. Nevertheless, the general trends and behaviors are physically sound. That is to say that on a patient-specific basis it is expected that there will be specific values for and that will minimize contact stress, although those specific values may not be the same as what is presented in Fig. 4. These findings suggest that restorative VF therapies following surgical intervention should focus not only on restoring the mucosal wave, as many approaches emphasize (Benninger et al. 1996), but also ensuring that the VF cover viscosity and thickness are restored.
The dependency of and on the cover viscosity and thickness (and the trends shown in Fig. 9) show that increasing viscosity and decreasing cover thickness produces an increase in and a decrease in (recall that , while ). As such, it is expected that the influence of relative to on the contact mechanics [observed by revisiting the order of each term of the governing equation for contact in Eq. (10)] will increase with increasing viscosity and decreasing cover thickness. That is, in this scenario, viscous dissipation becomes relatively more important in comparison with the tissue stiffness in determining the contact mechanics. Because increased tissue viscosity and decreased cover thickness are directly correlated with physical manifestations of VF dehydration (Chan and Tayama 2002; Ori et al. 2006), this indicates that contact stresses during VF dehydration become dominated by viscous damping (or the lack thereof), as opposed to tissue stiffness.
These findings provide insight into the physics of VF contact, illustrating a mechanism by which VF dehydration may give rise to increased contact stresses, and are in agreement with prior work noting that dehydrated VFs experience increased collision-induced stresses (Bhattacharya and Siegmund 2012). Furthermore, these findings agree with the biphasic theory developed by Zhang et al. (2008) that show that as tissue dehydrates and the volume of fluid decreases, the load is transferred from the fluid to the structure, where more damage is then likely to occur. The influence of interstitial fluid properties and cover thickness on contact stress may also have bearing on the use of gel implants injected into the mucosa in efforts to restore the mucosal wave and improve vocal function. Specifically, this study suggests it would be beneficial from a contact stress view point to inject sufficient gel (with low viscosity) such that the governing dimensionless groups fall within the contact stress minimum in Fig. 4.
While able to capture the pertinent physics of VF contact, the quasi 1-D viscoelastic contact model presented herein is also sufficiently tractable as to lend itself to implementation into lumped element modeling efforts (Erath et al. 2013). The proposed solution provides a relatively straightforward description of tissue damping that can be integrated into lumped element collision models to provide a physics-based representation of contact. The prescription of appropriate timescales that capture the relaxation history of VF tissue would facilitate investigation of functional relationships between tissue property degradation and damage measures by simply updating the boundary conditions in the current model following each contact event. This would thereby provide a platform for long time-frame modeling of the etiology of organic pathologies as a function of contact stress, where the magnitude and time of contact is known to cause increased degradation of the epithelial layer during VF collision (Tsuyoshi et al. 2014), and collision has been shown to produce a net flux of fluid away from the point of contact, thereby altering the structural properties of the VF cover (Bhattacharya and Siegmund 2012). This feature is especially relevant in scenarios such as ambulatory monitoring and numerical modeling of vocal hyperfunction (Mehta et al. 2012; Zañartu et al. 2014; Mehta et al. 2015). Including the accumulation of tissues damage as a function of the magnitude and duration of contact is a current avenue of research.
5. Conclusion
A quasi one-dimensional Kelvin–Voigt viscoelastic contact model has been proposed, wherein damping is derived from thin film lubrication theory. This model enables investigation of the relationship between viscous dissipation due to fluid motion through the cover, elasticity of the tissue, and VF contact stresses. The contact physics is shown to depend upon two nondimensional parameters; , which can be expressed as the ratio of the viscous tissue dissipation to the rate of change of kinetic energy in the VF mass, and , which is the ratio of elastic energy stored in the cover to the kinetic energy of the VF mass.
The spatial distribution of the interstitial pressure in the cover along the inferior–superior direction was shown to be parabolic. If the boundary conditions at the inferior and superior margins are equal, then the peak pressure occurs at the midline. During contact, this pressure generally increases in time until reaching a maximum, after which it rapidly decreases back to zero as the cover velocity goes to zero. The interstitial fluid pressures increase with decreasing values of both and . That is, if the structure absorbs less of the energy or less energy dissipates via viscosity, then the pressure within the cover layer increases. The peak contact stress, which is the combination of interstitial fluid pressure and elastic stress in the structure, was parametrized as a function of and , revealing a global minimum in contact stress over the investigated range of the two nondimensional parameters. Deviation from the minimum was found to result in a significant increase in the contact stress. Interestingly, when and are computed from published anatomical and physiological data, we find that they are within the range associated with the global minimum in contact stress, which may be a result of evolutionary adaptations in order to protect the VFs.
The relationship between contact stress and VF hydration was considered, providing a quantitative prescription of how VF thickness and viscosity influence contact stresses. This extended the scope of previous work that had shown that contact stresses can be directly related to hydration (Tao et al. 2009; Bhattacharya and Siegmund 2012), but did not provide a quantitative measure that explicitly related the behavior to measurable physiological variables. In short, the quasi 1-D viscoelastic contact model revealed that contact stresses increased with decreasing cover thickness and increasing viscosity of the VF cover in a nonlinear manner. The findings reported herein indicate that tissue thickness and viscosity, which may be altered by hydration, have a direct fundamental influence on contact forces. While hydration impacts these two parameters, there is also the possibility for other physiological variables, independent of hydration (e.g., anatomical variations), that may influence these parameters as well, thereby predisposing an individual to develop organic pathologies arising from excessive contact stress.
While the magnitude of contact stresses and duration of contact predicted by the model introduced herein agree well with published experimental and numerical data, it is important to keep in mind the limitations and assumptions of the model. As a lumped element model, the tissue mechanics are greatly simplified, with no inferior–superior excursion, for example. Furthermore, interstitial fluid motion is restricted to the inferior–superior direction, with no fluid motion into the body. This likely leads to higher interstitial fluid pressures in the present model. The fluid is also assumed to be Newtonian, which is not strictly true; hyaluronic acid, for example, is known to be shear thinning, which would alter the magnitude of viscous dissipation throughout the interaction. It is also assumed that the body is much stiffer than the cover, leading to a rigid interface. This is a good assumption in cases where the thyroarytenoid muscle is strongly contracted, but is less reasonable if the cricothyroid muscle is strongly contracted in the absence of thyroarytenoid contraction. The initial contact mechanics, including surface waves propagating away from the initial point of contact, is also neglected, as it is assumed that a significant length of the folds is already in contact when the model is initialized. As such, the energy dissipation and stresses arising from the initial contact are not captured. Despite these limitations, the simplicity of the proposed model enables incorporation into full reduced-order VF models for parametric studies, including studies on integrated tissue damage due to long time-scale voice use.
Acknowledgements
This work was funded in part by the Ontario Ministry of Research and Innovation through the Early Researcher Award program Grant ER13-09-269, the Natural Sciences and Engineering Research Council through Grant 386282-2010, and the Chilean CON-ICYT through Grants FONDECYT 1151077 and BASAL FB0008.
Footnotes
We note that the pressure distribution at is also parabolic, which is a consequence of neglecting the surface dynamics at the onset of contact.
References
- Alipour F, Scherer RC (2000) Dynamic glottal pressures in an excised hemilarynx model. J Voice 14:443–454 [DOI] [PubMed] [Google Scholar]
- Benninger MS, Alessi D, Archer S, Bastian R, Ford C, Koufman J, Sataloff RT, Spiegel JR, Woo P (1996) Vocal fold scarring: current concepts and management. Otolaryngol Head Neck Surg 115:474–482 [DOI] [PubMed] [Google Scholar]
- Bhattacharya P, Siegmund T (2012) A computational study of systemic hydration in vocal fold collision. Comput Methods Biomech Biomed Eng 17:1835–1852 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya P, Siegmund T (2015) The role of glottal surface adhesion on vocal folds biomechanics. Biomech Model Mechanobiol 14:283–295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chan RW, Tayama N (2002) Biomechanical effects of hydration in vocal fold tissues. Ann Otolaryngol Head Neck Surg 126:528–537 [DOI] [PubMed] [Google Scholar]
- Chan RW, Tayama N (2006) Biomechanical effects of hydration in vocal fold tissues. Otolaryngol Head Neck Surg 126:528–537 [DOI] [PubMed] [Google Scholar]
- Chan RW, Titze IR (2000) Viscoelastic shear properties of human vocal fold mucosa: theoretical characterization based on constituitive modeling. J Acoust Soc Am 107:565–580 [DOI] [PubMed] [Google Scholar]
- Chhetri DK, Zhang Z, Neubauer J (2011) Measurement of young’s modulus of vocal folds by indentation. J Voice 25:1–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Döllinger M, Berry DA, Berke GS (2005) Medial surface dynamics of an in vivo canine vocal fold during phonation. J Acoust Soc Am 117:3174–3183 [DOI] [PubMed] [Google Scholar]
- Erath BD, Zañartu M, Stewart KC, Plesniak MW, Sommer DE, Peterson SD (2013) A review of lumped-element models of voiced speech. Speech Commun 55:667–690 [Google Scholar]
- Fisher K, Ligon J, Sobeck J, Roxe D (2001) Phonatory effects of body fluid removal. J Speech Lang Hear Res 44:354–367 [DOI] [PubMed] [Google Scholar]
- Gray S, Titze I (1988) Histologic investigation of hyperphonated canine vocal cords. Ann Otol Rhinol Laryngol 97:381–388 [DOI] [PubMed] [Google Scholar]
- Gray SD, Titze IR, Chan R, Hammond TH (1999) Vocal fold proteoglycans and their influence on biomechanics. Laryngoscope 109:845–854 [DOI] [PubMed] [Google Scholar]
- Gunter H (2003) A mechanical model of vocal-fold collision with high spatial and temporal resolution. J Acoust Soc Am 113:994–1000 [DOI] [PubMed] [Google Scholar]
- Gunter H (2004) Modeling mechanical stresses as a factor in the etiology of benign vocal fold lesions. J Biomech 37:1119–1124 [DOI] [PubMed] [Google Scholar]
- Hess MM, Verdolini K, Bierhals W, Mansmann U, Gross M (1998) Endolaryngeal contact pressures. J Voice 12:50–67 [DOI] [PubMed] [Google Scholar]
- Hillman RE, Holmberg EB, Perkell JS, Walsh M, Vaughan C (1989) Objective assessment of vocal hyperfunction: an experimental framework and initial results. J Speech Lang Hear Res 32:373–392 [DOI] [PubMed] [Google Scholar]
- Hirano M (1977) Structure and vibratory behavior of the vocal folds. In: Sawashima M, Cooper FS (eds) Dynamics aspects of speech production. University of Tokyo, Tokyo, pp 13–27 [Google Scholar]
- Hirano M, Kurita S, Matsuo K, Nagata K (1980) Laryngeal tissure reaction to stress. In: Lawrence V (ed) Transcripts of the ninth symposium on care of the professional voice, part, 2 nd edn. The Voice Foundation, New York, pp 10–20 [Google Scholar]
- Hirano M, Kurita S, Makashima T (1981) The structure of the vocal folds. In: Stevens K, Hirano M (eds) Vocal fold physiology. University of Tokyo Press, Tokyo, pp 33–41 [Google Scholar]
- Horacek J, Sidlof P, Svec JG (2005) Numerical simulation of self-oscillations of human vocal folds with Hertz model of impact forces. J Fluids Struct 20:853–869 [Google Scholar]
- Horacek J, Laukkanen AM, Sidlof P, Murphy P, Svec JG (2009) Comparison of acceleration and impact stress as possible loading factors in phonation: a computer modeling study. Folia Phoniatr Logop 61:137–145 [DOI] [PubMed] [Google Scholar]
- Ishizaka K, Flanagan JL (1972) Synthesis of voice sounds from a two-mass model of the vocal cords. Bell Syst Tech J 51:1233–1268 [Google Scholar]
- Jiang JJ, Titze IR (1994) Measurement of vocal fold intraglottal pressure and impact stress. J Voice 8:132–144 [DOI] [PubMed] [Google Scholar]
- Jiang JJ, Diaz CE, Hanson DG (1998) Finite element modeling of vocal fold vibration in normal phonation and hyperfunctional dysphonia: implications for the pathogenesis of vocal nodules. Ann Otol Rhinol Laryngol 107:603–610 [DOI] [PubMed] [Google Scholar]
- Kojima T, VanDeusen M, Jerome WG, Garrett CG, Sivasankar MP, Novalesk CK, Rousseau B (2014) Quantification of acute vocal fold epithelial surface damage with increasing time and magnitude doses of vibration exposure. Plos One 9(e91):695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DC, Shreiber DI, Dimitriadis EK, Horkay F (2009) Spherical indentation of soft matter beyond the Hertzian regime: numerical and experimental validation of hyperelastic models. Biomech Model Mechanobiol 8:345–358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak AK (1986) The apparent viscoelastic behavior of articular cartilate - the contributions from intrinsic matrix viscoelasticity and interstitial fluid flows. J Biomech Eng 108:123–130 [DOI] [PubMed] [Google Scholar]
- Mehta DD, Zañartu M, Feng SW, Cheyne HA, Hillman RE (2012) Mobile voice health monitoring using a wearable acceleraometer sensor and a smartphone platform. IEEE Trans Biomed Eng 59:3090–3096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta DD, Van Starn JH, Zañartu M, Ghassemi M, Guttag VM, Espinosa JP, Cortés JP, Cheyne HA, Hillman RE (2015) Using ambulatory voice monitoring to investigate common voice disorders: research update. Front Bioeng Biotechnol 3:1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mittal R, Erath BD, Plesniak MW (2013) Fluid-dynamics of human phonation and speech. Ann Rev Fluid Mech 45:436–467 [Google Scholar]
- Mow VC, Kuei SC, Lai WM, Armstrong CG (1993) Biomechanics of diarthroidal joints: a review of twenty years of progress. J Biomech Eng 115:460–467 [DOI] [PubMed] [Google Scholar]
- Oomens CWJ, Van Campen DH, Grootenboer HJ (1987) A mixture approach to the mechanics of skin. J Biomech 20:877–885 [DOI] [PubMed] [Google Scholar]
- Ori Y, Sabo R, Binder Y, Weinstein T, Korzets A, Ori G, Chagnac A (2006) Effect of hemodialysis on the thickness of vocal folds: a possible explanation for postdialysis hoarseness. Nephron Clin Pract 103:144–148 [DOI] [PubMed] [Google Scholar]
- Panton RL (1996) Incompressible flow. Wiley, New York [Google Scholar]
- Perlman AL (1985) A technique for measuring the elastic propagation of vocal fold tissue. Ph.D. thesis, The University of Iowa, Iowa City, IA [Google Scholar]
- Rosen C, Lombard L, Murry T (2000) Acoustic, aerodynamic, and videostroboscopic features of bilateral vocal fold lesions. Ann Otol Rhinol Laryngol 109:823–828 [DOI] [PubMed] [Google Scholar]
- Scherer RC, Shinwari D, DeWitt KJ, Zhang C, Kucinschi BR, Afjeh AA (2001) Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees. J Acoust Soc Am 109:1616–1630 [DOI] [PubMed] [Google Scholar]
- Sivasankar M, Leydon C (2010) The role of hydration in vocal fold physiology. Curr Opin Otolaryngol Head Neck Surg 18:171–175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soltz MA, Ateshian GA (1998) Experimental verification and theoretical prediction of cartilage interstitial fluid pressurization at an impermeable contact interface in confined compression. J Biomech 31:927–934 [DOI] [PubMed] [Google Scholar]
- Spencer M, Siegmung T, Mongeau L (2008) Determination of superior surface strains and stresses, and vocal fold contact pressure in a synthetic larynx model using digital image correlation. J Acoust Soc Am 123:1089–1103 [DOI] [PubMed] [Google Scholar]
- Story BH, Titze IR (1995) Voice simulation with a body-cover model of the vocal folds. J Acoust Soc Am 97:1249–1260 [DOI] [PubMed] [Google Scholar]
- Sun DD, Guo XE, Likhitpanichkul M, Lai WM, Mow VC (2004) The influence of the fixed negative charges on mechanical and electrical behaviors of articular cartilages under unconfined compression. J Bomech Eng 126:6–16 [DOI] [PubMed] [Google Scholar]
- Tanner K, Roy N, Merrill R, Elstad M (2007) The effects of three nebulized osmotic agents in the dry larynx. J Speech Lang Hear Res 50:635–646 [DOI] [PubMed] [Google Scholar]
- Tao C, Jiang JJ (2007) Mechanical stress during phonation in a self-oscillating finite-element vocal fold model. J Biomech 40:2191–2198 [DOI] [PubMed] [Google Scholar]
- Tao C, Jiang JJ, Zhang Y (2009) A fluid-saturated poroelastic model of the vocal folds with hydrated tissue. J Biomech 42:774–780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titze IR (1988) The physics of small-amplitude oscillation of the vocal folds. J Acoust Soc Am 83:1536–1552 [DOI] [PubMed] [Google Scholar]
- Titze IR (1994a) Mechanical stress in phonation. J Voice 8:99–105 [DOI] [PubMed] [Google Scholar]
- Titze IR (1994b) Principles of voice production. Prentice Hall, Englewood Cliffs [Google Scholar]
- Titze IR, Story BH (2002) Rules for controlling low-dimensional vocal fold models with muscle activation. J Acoust Soc Am 112(3):1064–1076 [DOI] [PubMed] [Google Scholar]
- Tsuyoshi K, Van Deusen M, Jerome WG, Garrett CG, Sivasankar MP, Novaleski CK, Rousseau B (2014) Quanitfication of acute vocal fold epithelial surface damage with increasing time and magnitude doses of vibration exposure. PLOS One 9(e91):615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Türk L (1886) Klinik der Krankheiten des Kehlkopfes und der luftröhre (Clinical Diseases of the Trachea and Larynx). Maximillian Bresgen, Wien [Google Scholar]
- Verdolini K (1988) Practice good vocal health and prevent those voice disorders. Chorist Guild Lett 2:40–44 [Google Scholar]
- Verdolini K, Sandage M, Titze IR (1994) Effects of hydration treatments on laryngeal nodules and polyps and related voice measures. J Voice 8:30–47 [DOI] [PubMed] [Google Scholar]
- Verdolini K, Hess MM, Titze IR, Bierhals W, Gross M (1999) Investigation of vocal fold impact stress in human subjects. J Voice 13:184–202 [DOI] [PubMed] [Google Scholar]
- Zañartu M, Mongeau L, WG R, (2007) Influence of acoustic loading on an effective single-mass model of the vocal folds. J Acoust Soc Am 121:1119–1129 [DOI] [PubMed] [Google Scholar]
- Zañartu M, Galindo GE, Erath BD, Peterson SD, Wodicka GR, Hillman RE (2014) Modeling the effects of a posterior glottal opening on vocal fold dynamics with implications for vocal hyperfunction. J Acoust Soc Am 136:3262–3271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z (2009) Characteristics of phonation onset in a two-layer vocal fold model. J Acoust Soc Am 125(2):1091–1102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Czerwonka L, Tao C, Jiang JJ (2008) A biphasic theory for the viscoelastic behaviors of vocal fold lamina propria in stress relaxation. J Acoust Soc Am 123:1627–1636 [DOI] [PubMed] [Google Scholar]


