Abstract

Recently, lead halide perovskites have gained considerable attention by dint of their predominant physiochemical features and potential use in various applications with an improved power conversion efficiency. Despite the incredible technological and research breakthroughs in this field, most of those compounds present an obstacle to future commercialization due to their instability and extreme poisonousness. Because of this, it is preferable to replace lead with alternative stable elements to produce eco-friendly perovskites with equivalent optoelectronic qualities similar to lead-based perovskites. However, Pb-free perovskite-based devices have relatively low power conversion efficiency. Pressure might be considered an effective way for modifying the physical characteristics of these materials to enhance their performance and reveal structure–property correlations. The present study has been done to investigate the structural, electronic, optical, elastic, mechanical, and thermodynamic properties of nontoxic perovskite CsMgI3 under hydrostatic pressure by using density functional theory (DFT). At ambient pressure, the present findings are in excellent agreement with the available experimental data. Pressure causes the Mg–I and Cs–I bonds to shorten and become stronger. The absorption coefficient in the visible and ultraviolet (UV) zones grows up with the increase in pressure. Additionally, we have observed low reflectivity, a high-intensity conductivity peak, and a dielectric constant in the visible region of the electromagnetic spectrum. As pressure rises, the band gap keeps narrowing, facilitating an electron from the valence band to get excited easily at the conduction band. Furthermore, we analyze the mechanical, elastic, and thermodynamic properties under pressure, which suggests that this compound exhibit ductile behavior. The shrunk band gap and improved physical properties of CsMgI3 under hydrostatic pressure suggest that this material may be used in solar cells (for photovoltaic applications) and optoelectronic devices more frequently than at ambient pressure. In addition, this paper emphasizes the feasibility of hydrostatic pressure in the systematic modification of the optoelectronic and mechanical characteristics of lead-free halide perovskites.
1. Introduction
Over the past few decades, halide perovskites have captured the interest of researchers and experts worldwide. Perovskites are in spotlight due to their use in various commercial and technological applications, such as solar cells, lasers, X-ray detectors, catalysts, field effect transistors, light-emitting diodes (LEDs), photodetectors, and field effect transistors.1−8 These materials possess exceptional physical characteristics, such as tunable energy band gap, high absorption coefficient, low reflectivity, broad absorption spectrum, high photoconductivity, low exciton binding energy, strong charge carrier mobility, large diffusion lifetimes, long electron–hole diffusion lengths, and ferroelectricity.6−11 Perovskite-based technology is more affordable and effective than silicon-based technology due to its widespread existence in nature.9,12 Investigations of the structural, optical, elastic, and electronic properties as well as an appreciation of the system’s general characteristics are crucial for predicting any device application and treasure.13−16 In recent years, perovskite solar cell power conversion efficiency (PCE) has increased significantly, going from 3.8% to over 25%.17 For Pb-based perovskite (MAPbI3) solar cells, the highest recorded PCE is 25.2%.18 However, these materials exhibit instability at ambient conditions due to humidity, moisture, temperature, and ultraviolet (UV) light.19 Another concern is the presence of lead (Pb), which is poisonous and potentially hazardous to the environment.20 Furthermore, Pb-containing perovskites MAPbX3 (X = Cl, Br, and I) have low relative dielectric constants. Since the rate of charge recombination decreases with the increase in dielectric constant and improves the performance of solar cells, which is the main barrier to the application of solar cell devices.21 Because of this, it is critical to find Pb-free perovskites for solar cells and optoelectronic devices. Therefore, a new form of ABX3 has emerged, where A, B, and C are the monovalent cation, divalent cation, and halogen anion, respectively.
Ge-based inorganic perovskites become a possible alternative to Pb because of their better conductivity and absorption than Pb-based perovskites. Previously it was also claimed that the best Pb-free halide material is CsGeI3, though CsGeI3 shows brittle behavior and CsSnBr3 exhibits ductile behavior.22,23 It is generally known that high band gap values make halide perovskites inappropriate for use in photovoltaic devices. The likelihood of light absorption by perovskite materials increases when the band gap is reduced. The band gap can be tuned in several methods, including temperature-induced phase transitions,24,25 chemical alterations,26 metal doping, and hydrostatic pressure.27−30 Hydrostatic pressure is a simple, effective, and eco-friendly technique for changing the band gap of perovskite materials among the above techniques. As a result, the pressure has a major impact on the optical and electrical properties, which reveals promising qualities for photovoltaic (PV) and optoelectronic applications. Hydrostatic pressure has shown remarkable success in improving the physical characteristics of halide perovskites.27−30 Usually, hydrostatic pressure modifies the lattice parameters,31 displacement of cations and anions,32,33 rotation of octahedral cages,34 phase transitions,35,36 etc. As pressure is applied to metal halides, the volume of the unit cell and the lattice constants both drop.37,38 Recent studies have demonstrated that hydrostatic pressure can decrease the band gap in inorganic halide perovskites such as KCaCl3,39 RbYbF3,40 and CsGeI3,41 leading to an increase in conductivity. Moreover, the application of pressure can significantly improve the optical properties of halide perovskites, thereby enhancing their functionality in optoelectronic fields.
Here, we use DFT to investigate the pressure impact in metal halide perovskites to boost the efficiency of solar cells and other optoelectronic devices. The structural, mechanical, electronic, elastic, optical, thermodynamic, and lattice dynamic characteristics under various pressures are carefully studied using first-principles computations. A distinct band structure nature, appropriate change in absorption, conductivity, reflectivity in the visible region, and elastic behaviors are all investigated within the applied pressure range.
2. Computational Methods
Current simulations were run in the Cambridge Serial Total Energy Package (CASTEP) program employing the plane wave pseudopotential density functional theory (DFT).42 The generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE) functional for exchange-correlation interactions were used in the geometrical optimizations to get the stable form of the crystal.43 The Vanderbilt-type ultrasoft pseudopotentials were used to investigate the electron–ion interaction.44 The optimal configuration in the crystal structure of the halide perovskite was achieved using the BFGS (Broyden–Fletcher–Goldfarb–Shanno) optimization model with a density mixing approach.45 The cutoff energy for the plane wave of 520 eV and k-points for the sampling of the Brillouin zone of 6 × 6 × 6 was applied in all cases. The Monchorst–pack technique was used to choose the k-points over the first Brillouin zone.46 In this study, spin polarization was considered. The detailed convergence criteria are given in the Supporting Information. Phonon dispersion, phonon density of states, and lattice dynamic properties were calculated by using density functional perturbation theory (DFPT), as implemented in the CASTEP code.42
3. Results and Discussion
3.1. Structural Properties
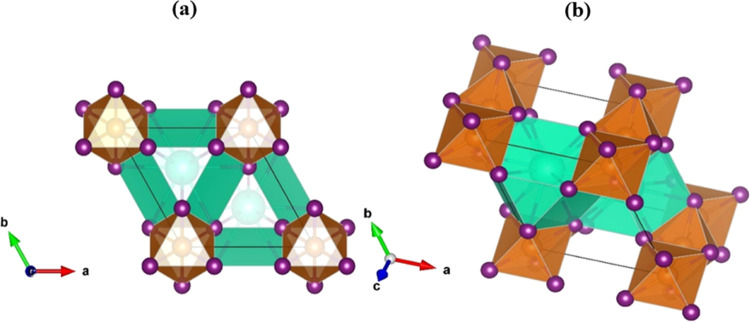
The all-inorganic metal halide perovskite CsMgI3 has a hexagonal structure with the space group P63/mmc and the structural parameters a = b = 8.414 Å and c = 7.123 Å.47 The unit cell has 10 atoms, two Cs atoms at the corner with 1a Wyckoff site and fractional coordinates (0.3333, 0.6667, 0.75), two Mg atoms at the body center with 1b Wyckoff site and fractional coordinates (0, 0, 0), and six I atoms at the face center with 3c Wyckoff position and fractional values (0.1618, 0.8382, 0.25).47 The optimized crystal structure of CsMgI3 is shown in Figure 1. Table S1 lists the pressure-dependent structural parameters of the CsMgI3 halide perovskite in the Supporting Information. The present findings reveal that DFT simulations are credible because the simulated results at 0 GPa are nearly the same as the existing experimental results.47 According to Figure 2a,b, as the applied pressure increases, the lattice constants and volume of the unit cell decrease, indicating that the distance between atoms decreases. This decrease in lattice properties under hydrostatic pressure suggests that bond length has decreased, as seen in Table S1. The calculated formation energy of CsMgI3 under pressure is displayed in Figure 2c. Moreover, the computed formation energy (Table S1) displays negative values under hydrostatic pressure, confirming the thermodynamic stability of the studied lead-free halide perovskite. Several halide perovskite AMX3 crystals have been fully characterized, and their ground-state structural characteristics are displayed in Table S2. The structural properties of CsMgI3 are remarkably similar to those of the halide perovskite AMX3. Clearly, CsMgI3 is structurally analogous to AMX3 systems that are magnetically coupled.
Figure 1.
Crystal structure of (a) 2D and (b) 3D view of the Pb-free CsMgI3 halide perovskite. The cyan, blue, and purple balls represent Cs, Mg, and I atoms, respectively.
Figure 2.
Pressure-induced structural distortion of (a) lattice parameter, (b) cell volume, and (c) formation energy of the CsMgI3 halide perovskite.
3.2. Optical Properties
The optical properties of a material provide essential information for the usage of optoelectronic applications. Reflectivity, dielectric function, refractive index, conductivity, absorption coefficient, and loss function are some optical parameters that can be used to characterize how a material reacts to incident electromagnetic radiation. The dielectric function explains how a material behaves when interacting with incoming radiation. It is referred to as the dielectric constant when the photon energy is zero. The dielectric constant greatly influences the rate of charge carrier recombination and the optoelectronic devices’ general effectiveness. As the rate of charge recombination decreases with an increase in dielectric constant, optoelectronic device efficiency increases.48 In the current investigation, we varied the hydrostatic pressure to get the high dielectric constant that enhances the performance or efficiency of the device. Figure 3a,c, respectively, illustrates the real and imaginary components of the CsMgI3 dielectric function as a function of photon energy at varying pressures. Lead-free halide CsMgI3 materials exhibit identical ε1 low energy at hydrostatic pressure; this energy increases in the infrared–visible area and decreases in the ultraviolet region. Additionally, CsMgI3 shows negative ε1 at energies between 7.5 and 11 eV. As can be seen in Figure 4a, the material exhibits high reflectivity in that energy region. Due to the decreased rate of charge recombination under 10 GPa pressure, the ε1 (0) is noticeably raised, making the material even more preferable for optoelectronic applications. At 0 GPa, the visible and early ultraviolet region’s ε2 is higher, suggesting a high level of absorption.49 But under high pressure, the ε2 spectrum moves to the low energy area. Integrated circuits is specifically proven by the higher ε1 and ε2 at low energy combined with smaller ε1 and ε2 at high-energy areas.50Figure 3b,d illustrates the wavelength-dependent dielectric function of CsMgI3 so as to facilitate comprehension of its dielectric function. As depicted in Figure 3b,d, superiority increases significantly under pressure. Except for some minor fluctuations, at high energies (over 18 eV), the imaginary part of the dielectric function tends to become zero. In contrast, the real part of the dielectric function reaches nearly one. Due to the low absorption of high-energy photons, the materials become transparent.
Figure 3.
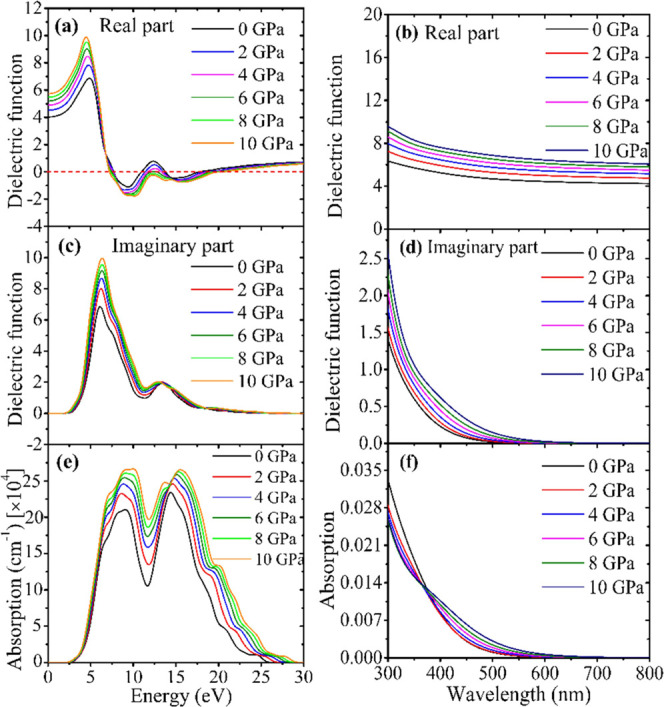
Simulated (a, b) real part of the dielectric function, (c, d) imaginary part of the dielectric function, and (e, f) absorption, all as a function of the energy and wavelength of the lead-free halide perovskite CsMgI3 at various hydrostatic pressures.
Figure 4.

Simulated (a, b) reflectivity, (c, d) loss function, and (e, f) real part of the refractive index, all as a function of the energy and wavelength of the lead-free halide perovskite CsMgI3 at various hydrostatic pressures.
Figure 3e shows the simulated optical absorption spectra of the lead-free CsMgI3 perovskite at various hydrostatic pressures based on photon energy. Between 2.5 and 30 eV, overall absorption is seen. In the visible spectrum, the light absorption significantly increased with rising pressure rather than ambient pressure. As is well known, solar cells and other photovoltaic applications significantly assist from the initial absorption peak. As a result, we saw that the absorption first peak in the visible zone grows as pressure rises, although the ambient pressure appears later. This makes the pressure effect crucial for solar cells and other optoelectronic devices since it increases absorption. The largest peak, at roughly 10.0 eV, is most impacted by the pressure effect. With increased pressure, it improved significantly. At 16.5 eV, a further peak in the UV region is visible, but the peaks in the high-energy range gradually diminish. The wavelength-dependent absorption coefficient is depicted in Figure 3f for a better understanding of the light absorption characteristic of CsMgI3 in the visible region. As shown in Figure 3f, the applied pressure enhanced the absorption spectra in the visible region relative to ambient pressure. Although absorption rises with pressure, band gap lowering is crucial for the applications of solar cells and optoelectronic devices.
The pressure-induced optical reflectivity, which is a crucial factor for materials used in photovoltaic applications, is depicted in Figure 4a. With the application of pressure throughout nearly all energy regions, the material’s light reflectivity increases. The low energy reflectivity becomes nearly constant at ambient pressure up to 2 eV. It is interesting to note that the reflectivity is at its highest when the real part of the dielectric function ε1(ω) dips below zero. More precisely, as shown in Figure 4a,b, the reflectance (with or without pressure) is low in the IR–visible region (0–5 eV), which suggests that, if the halides are employed in solar panels, they will allow sufficient visible spectra for generating photocurrent, considerably improving solar panel efficiency.51
The loss of energy as the initial electron travels through a material is explicitly expressed by the loss function, which is a crucial parameter.52Figure 4c shows the simulated photon energy-dependent loss function of the CsMgI3 compound. This indicates that the most significant peak at atmospheric pressure is situated at 19.1 eV. With the increase of pressure, the loss function spectrum expanded, peaking at 21.5 eV at 10 GPa. Due to more absorption in that region at lower energies under various hydrostatic pressures, the loss function of CsMgI3 was lowered. However, the plasma frequency53 is the energy that corresponds to the loss function’s most significant peak. If the frequency of incoming light exceeds the plasma frequency, the samples become transparent. When an electromagnetic wave travels through a substance, its refractive index indicates the wave’s phase velocity. The refractive index as a function of photon energy of our lead-free under study compounds under various hydrostatic pressures is shown in Figure 4e. The refractive index is prominent (high) at low energy and exhibits a fluctuating character at high energy. At 5.1 eV, the compound CsMgI3 exhibits the largest peak. The compound’s refractive index increases dramatically at 0 eV when 10 GPa pressure is applied. The refractive index drops at high energies because it is related to the dielectric constant.54 This suggests that CsMgI3, rather than other materials, should be preferred for optical components, including waveguides and photonic crystals.15
3.3. Electronic Properties
Analyzing a material’s band structure (BS) and density of states (DOS) is crucial to comprehend its electrical structure and adequately explaining its optical functions. The energy band, the total and partial density of states, and our findings regarding the pressure-induced electronic characteristics of CsMgI3 are discussed here. Figure 5a,b shows the electronic band structures of the CsMgI3 perovskite under hydrostatic pressure. The Fermi level (EF), marked by a red horizontal dashed line at the top of the valence band, is marked by a fixed value of 0 eV.
Figure 5.
Simulated pressure-induced (a, b) band structures and (c, d) density of states of lead-free halide perovskite CsMgI3.
Figure 5a,b shows that both the conduction band minimum (CBM) and valence band maximum (VBM) is located at the G point and do not overlap, indicating the direct band nature of the material. The observed band gap of CsMgI3 at 0 GPa is 3.172 eV, which agrees with the previous experimental finding (3.181 eV).47 According to Table S1, the band gap narrows as pressure increases (0–10 GPa), which means that there is a greater chance that an electron will jump from the valence band to the conduction band. However, our findings anticipate that pressure will enhance the physical performance of the CsMgI3 semiconductor.
The DOS plays an excellent role in understanding the properties of materials. Therefore, we have investigated the changes in the DOS of the CsMgI3 compound at different pressures (0–10 GPa). Figure 5c,d shows the computed total and partial densities of states of CsMgI3 at ambient and applied pressures. The sharp peaks progressively shift toward the EF as the pressure rises. The band gap under pressure, which also showed up in the band structures at the G point, is described concisely. To get a material’s atomic contribution for creating its band structure, however, PDOS is essential. The valence band close to the EF clearly originates mainly from the I-5s orbital, with minor contributions from the Mg-3s and Cs-5p orbitals, as seen in Figure 5c,d. Conversely, the conduction band arises from the states I-5p, Cs-5p, Cs-6s, and Mg-3s. As external pressure rises, the conduction bands shift closer to the EF, and the band gap narrows, promoting the hybridization of Mg-3s and I-5p. In addition, the Mg–I bond length reduction in response to pressure (Table S1) may enhance the hybridization of the Mg-3s and I-5p orbitals in the conduction band, resulting in a reduction in the CBM at the G point [Figure 5a,b]. Hence, the band gap of CsMgI3 reduces from 3.172 to 2.677 eV. The band gap and external pressure have an inverse relationship that increases the probability that an electron will move from the valence band to the conduction band, hence enhancing the conductive, absorptive, and other optical properties of the compound and improving potential advantages in optoelectronic applications.
3.4. Elastic Properties
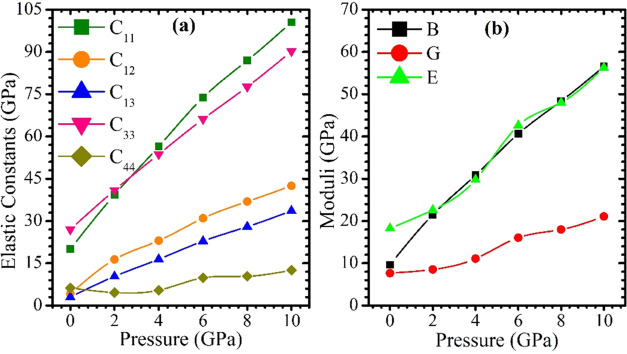
The elastic constants Cij greatly influence materials structural stability and mechanical properties. These constants link the dynamical and mechanical behavior of crystals and reveal how much a material deforms under stress and then regains its original shape after stress is removed. The hexagonal system has five unique elastic constants: C11, C12, C13, C33, and C44. These elastic constants for the CsMgI3 hexagonal perovskite was calculated using the finite strain theory,55 which is implemented in the CASTEP module. Table S3 lists the calculated values of the elastic constants Cij for the perovskite under various pressures. The elasticity in length is expressed by the elastic constants C11 and C33, and the elasticity in shape is connected to the additional constants C12, C13, and C44. Except for C44, the four elastic constants for the hexagonal CsMgI3 are observed to increase with pressure. C11 and C33 change under pressure quickly, C12 and C13 change under pressure gradually, and C44 starts to increase slightly under stress. Additionally, it can be observed that, at a given pressure, the elastic constant C11 is consistently smaller than its counterpart, C33, demonstrating that it is simpler to compress in the [100] direction than the [001] direction. The measured elastic constants of CsMgI3 at each investigated pressure (Table S3) satisfy the criteria, confirming the mechanical stability of CsMgI3.
As far as we are aware, neither experimental nor theoretical data on the elastic constants (Cij) of CsMgI3 compounds under pressure are available for comparison. Hence, we consider the current findings as prediction research that is currently awaiting experimental confirmation. Figure 6a illustrates the calculated elastic constants of CsMgI3 as a function of pressure. It is evident that the elastic constants C11, C12, C13, C33, and C44 almost rise with the applied pressure.
Figure 6.
Calculated (a) elastic constants and (b) elastic moduli as a function of pressure for CsMgI3.
3.5. Mechanical Properties
A material’s bulk modulus (B) assesses its resistance to volume deformation. The lower B value suggests their flexibility and softness. A material’s resistance to plastic deformation is indicated by its shear modulus (G). A lower G value denotes less rigidity and lower resistance to shape change in the material. The stiffness of materials is measured by Young’s modulus (E), and the higher its value, the stiffer the material. In Figure 6b, the modification of the elastic moduli for the material CsMgI3 with applied stress is graphically depicted. We find that during stress, the values of B, G, and E rise.
Here, the bulk modulus rises gradually as the stress increases, yet the shear and Young’s modulus variations are nearly identical to those of the bulk modulus variations for the chosen perovskite. According to these findings, the stiffness and shape change resistance both rise nonlinearly with pressure, while the volume change resistance rises (about) linearly. On the contrary, when pressure is applied, the compounds show increased resistance to fracture and plastic deformation and stiffness.
Figure 7a,b, respectively, depicts the pressure dependence of the B/G, Poisson’s ratio and Cauchy pressures for the lead-free material CsMgI3. We can assess the ductility and brittleness of materials using these parameters. Pugh’s rule54 states that ductile materials are distinguished from brittle ones by the critical value of B/G, which is 1.75. More specifically, materials with a Pugh’s ratio of more than 1.75 should behave ductility, while those with a Pugh’s ratio lower than 1.75 are thought to be brittle. Additionally, it is anticipated that ductile materials would have better thin films.56
Figure 7.
Calculated (a) Pugh’s and Poisson’s ratios and (b) Cauchy pressures as a function of pressure for CsMgI3.
Figure 7a demonstrates that CsMgI3 is brittle at ambient pressure but reveals that it is ductile under stress, i.e., the B/G value rises with pressure and is always more than 1.75 under the studied pressure range, with the only exception of ambient pressure. These suggest that CsMgI3 turns out more ductile under pressure. Since our considered perovskite is discovered to be brittle, the computed findings of Pugh’s ratio imply that the pressured material is suited for thin films. Poisson’s ratio can also be used to explain how ductile and brittle materials separate from one another. Poisson’s ratio for brittle materials is less than 0.26, and it is more than 0.26 for ductile materials, according to Poisson’s rule.57 As seen in Figure 7a, the Poisson’s ratio similarly rises with pressure and, with the exception of the ambient pressure, is always more than 0.26 in the pressure range under study. These also suggest that CsMgI3 becomes more ductile under pressure. Our computed Poisson’s ratio results agree with Pugh’s ratio, as shown in Figure 7a. The Cauchy pressure for the particular case of hexagonal crystals is defined as (C13– C44) for the [100] plane and (C12– C66) for the [001] plane.50 By confirming negative and positive values, this property distinguishes between two natures, such as brittle and ductile. The estimated value for this investigation at ambient pressure (Table S3) is consistent with its brittle character (negative). But the findings of the pressure application (Table S4) further support the ductile nature (positive). As a result, the optoelectronic sector offers hope for our investigated perovskite material. As can be seen from Figure 7a, pressure increases, indicating that the investigated compounds become more ductile. Interestingly, the B/G and v results match the data from Cauchy pressures exactly (Table S4).
According to elastic constants, plasticity, strain, ductility, strength, etc., hardness is a measure of the resistance to elastic deformation, plastic deformation, or failure under external force. Theoretically, eq S8(58) can be used to calculate the hardness (H) of polycrystalline materials. According to Table S4, it is evident that hardness roughly increases with pressure.
3.6. Thermodynamic Properties
Thermodynamic parameters are vital in understanding advanced solid-state physics and thermodynamic chemistry.59 Namely, the Debye temperature, ΘD is very closely related to many physical characteristics of materials, including melting temperature, bond nature, specific heat, thermal expansion, and elastic constants.60,61 It shows the crystal’s response to vibration. We calculate the Debye temperature of the CsMgI3 perovskite under pressure using optimized crystal parameters. In this procedure, ΘD can be computed directly by using the following equation62
| 1 |
where h is Plank’s constant, k is Boltzmann’s constant, n denotes the number of atoms per molecule, NA is the Avogadro number, ρ is the density of the solid, M is the weight of the molecule, and υm is the average sound velocity. The average sound velocity υm, in the crystal can be computed by using the following relation63
| 2 |
The transverse sound velocity υt and longitudinal sound velocity υl can be calculated by using the below relation
| 3 |
Table S5 shows the calculated values, υt, υl, and ΘD of the CsMgI3 perovskite under various external pressures. All of the computed Debye temperatures are not so high, which suggests that we will find lower melting points. The pressure-dependent behavior of ρ and ΘD for the compound is illustrated in Figure S3a,b, respectively. It is evident that when pressure increases, the value of ρ rises. In the meantime, the polycrystal’s value of υl rises as well, but υt decreases initially before rising with pressure. The results indicate that the anisotropy of sound velocity for CsMgI3 is significant and rises with pressure. In Figure S3b, we observed that Debye temperature increased gradually with pressure, indicating that the covalent bond length reduced and the compound became harder. It is the usual behavior because pressure strengthens the crystal increasing the Debye temperature.
3.7. Lattice Dynamics
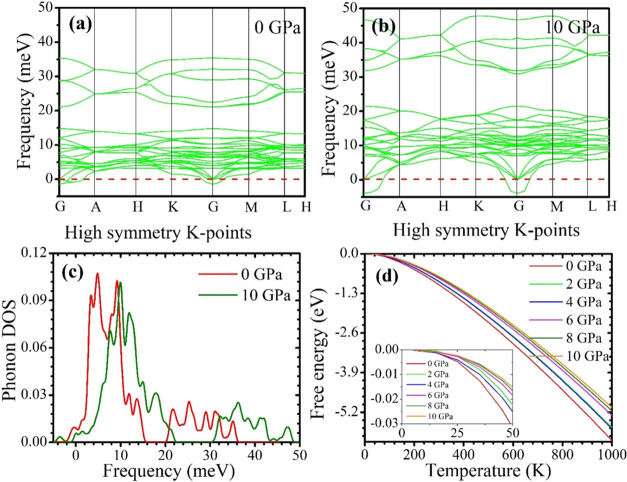
A material must have both mechanical and dynamic stability to be stable. We have already discussed mechanical stability in Section 3.4. To be dynamically stable, a compound’s crystal lattice must not change to be dynamically stable or soft phonon modes should not exist in the phonon dispersion. There is an imaginary (negative) frequency for soft phonon modes. So, a dynamically stable compound must have positive frequencies for each phonon. Our investigated phonon dispersion curves and phonon DOS of CsMgI3 at various pressure are shown in Figure 8a–c. The phonon dispersion curves have a negative frequency at the G point in Figure 8a,b. Consequently, positive frequencies are found at the A, H, K, M, and L points, revealing that they have stable nature.
Figure 8.
Calculated (a, b) phonon dispersion curves, (c) phonon density of states, and (d) free energy of CsMgI3 at various pressures. The zoomed view show the detailed variations of free energy.
Additionally, we explored the temperature-dependent thermodynamic stability of the CsMgI3 compound at various pressure. In this case, phonon modes were employed to compute the thermodynamic features, like free energy F, enthalpy H, and entropy S at various temperatures from the compound’s vibrational contribution according to the equations given in the Supporting Information.
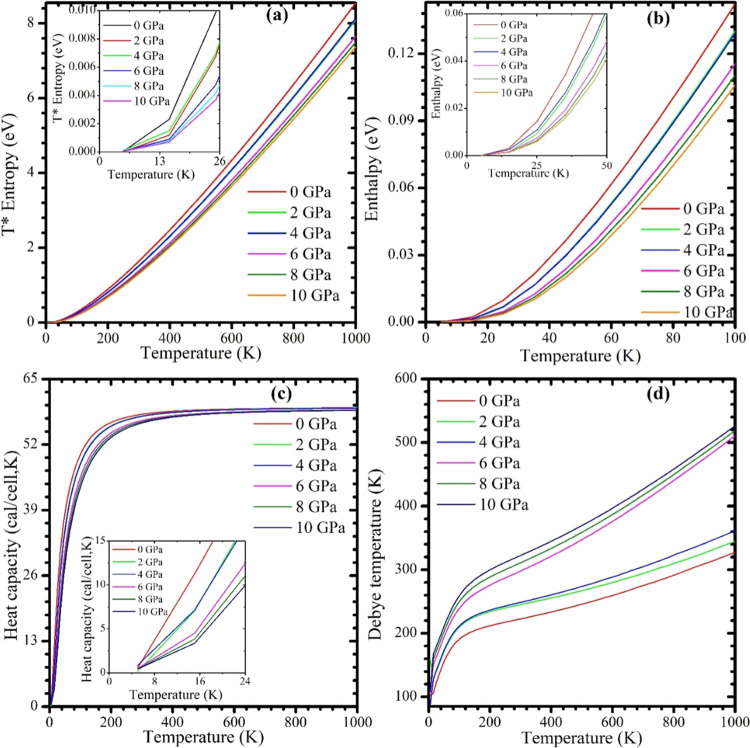
Figures 8c and 9a,b display the temperature-dependent free energy, T* entropy, and enthalpy, respectively, of the CsMgI3 perovskite under various pressure. These graphs demonstrate that when the temperature rises, entropy decreases but enthalpy and free energy increase. The evaluated value for each scenario supports the third law of thermodynamics, as the values of all of the terms for the CsMgI3 perovskites approach zero as the temperature approaches absolute zero. Figure 9c,d shows our analyzed heat capacity and Debye temperature of the CsMgI3 perovskite that we investigated at various temperatures under various pressures. As shown in Figure 9c, heat capacity approaches the Dulong–Petit limit at high temperatures. We predicted that our investigated sample would maintain phase stability at a pressure of 10 GPa.
Figure 9.
Temperature-dependent (a) T* entropy, (b) enthalpy, (c) heat capacity, and (d) Debye temperature of the CsMgI3 perovskite under various pressures. The zoomed view show the detailed variations of T* entropy, enthalpy, and heat capacity.
4. Conclusions
This paper presents the effects of pressure on the structure–property relationship and change in the physical properties of nontoxic metal halide perovskites CsMgI3 by using the DFT-based first-principles investigation. The simulated structural parameters match the existing studies at ambient pressure but decrease with the rise in pressure. Under pressure, the ionic/covalent bonds also become stronger. The band gap significantly reduces at increased pressure, which improves the optical properties (visible light absorption) and makes the compounds more preferable for solar cell applications and other optoelectronic devices. According to Pugh’s ratio, Cauchy pressure, and Poisson’s ratio, this compound exhibits brittle nature at ambient pressure, but it exhibits ductile nature under pressure and becomes more ductile with increasing pressure. The direction-dependent properties show that CsMgI3 exhibits anisotropic nature, which is also improved by applying pressure. Additionally, estimated elastic constants indicate that the substance is mechanically stable. Moreover, the obtained anisotropy, sound velocity, and Debye temperature for CsMgI3 rises with pressure. The studied compound is mechanically and dynamically stable, confirmed by the study of formation energy, elastic constants, and phonon dispersion. The present inspection offers an atomic-level knowledge of pressure-induced effects as a material design approach to tune the structure–property correlations of magnesium iodide perovskites.
Acknowledgments
The authors are grateful to the Pabna University of Science and Technology, Bangladesh, for partial financial support during this research work.
Data Availability Statement
The data sets generated and/or analyzed in this study are available from the corresponding author on reasonable request.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c01388.
Details of computational methods, structural stability and mechanical properties; simulated photon energy-dependent conductivity of (a) real, and (b) imaginary part of lead-free halide perovskite CsMgI3 semiconductors; anisotropic 3D representation of (a) Young’s modulus, (b) shear modulus, and (c) Poisson’s ratio of CsMgI3 at 0, 6, and 10 GPa pressure; calculated (a) mass density ρ and (b) Debye temperature ΘD as a function of pressure for CsMgI3 and ground-state structural parameters for the lead-free halide perovskite CsMgI3; ground-state structural parameters for other halide perovskite AMX3; elastic constants Cij (in GPa) of CsMgI3 under pressure up to 10 GPa; evaluated mechanical properties of CsMgI3 at both ambient and applied pressures; and calculated density ρ, transverse sound velocity νt, longitudinal sound velocity νl, average sound velocity νm, and Debye temperature ΘD of CsMgI3 (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Xiao Z.; Kerner R. A.; Zhao L.; Tran N. L.; Lee K. M.; Koh T. W.; Scholes G. D.; Rand B. P. Efficient perovskite light-emitting diodes featuring nanometre-sized crystallites. Nat. Photonics 2017, 11, 108–115. 10.1038/nphoton.2016.269. [DOI] [Google Scholar]
- Lanzani G.; Petrozza A.; Caironi M. Organics go hybrid. Nat. Photonics 2017, 11, 20–22. 10.1038/nphoton.2016.260. [DOI] [Google Scholar]
- Hwang J.; Rao R. R.; Giordano L.; Katayama Y.; Yu Y.; Shao-Horn Y. Perovskites in catalysis and electrocatalysis. Science 2017, 358, 751–756. 10.1126/science.aam7092. [DOI] [PubMed] [Google Scholar]
- Kim Y. C.; Kim K. H.; Son D. Y.; Jeong D. N.; Seo J. Y.; Choi Y. S.; Han I. T.; et al. Printable organometallic perovskite enables large-area, low-dose X-ray imaging. Nature 2017, 550, 87–91. 10.1038/nature24032. [DOI] [PubMed] [Google Scholar]
- Akyüz Ö; Scheffner M.; Cölfen H. Fluorescent Cadmium Chalcogenide Nanoclusters in Ubiquitin. Small Struct. 2021, 2, 2000127 10.1002/sstr.202170004. [DOI] [Google Scholar]
- Shahrokhi S.; Gao W.; Wang Y.; Anandan P. R.; Rahaman M. Z.; Singh S.; Wang D.; et al. Emergence of ferroelectricity in halide perovskites. Small Methods 2020, 4, 2000149 10.1002/smtd.202000149. [DOI] [Google Scholar]
- Bakr O. M.; Mohammed O. F. Powering up perovskite photoresponse. Science 2017, 355, 1260–1261. 10.1126/science.aam7154. [DOI] [PubMed] [Google Scholar]
- Chen J.; Zhou S.; Jin S.; Li H.; Zhai T. Crystal organometal halide perovskites with promising optoelectronic applications. J. Mater. Chem. C 2016, 4, 11–27. 10.1039/C5TC03417E. [DOI] [Google Scholar]
- Zhang Z.; Ghimire S.; Okamoto T.; Sachith B. M.; Sobhanan J.; Subrahmanyam C.; Biju V. Mechano-optical Modulation of Excitons and Carrier Recombination in Self-Assembled Halide Perovskite Quantum Dots. ACS Nano 2022, 16, 160–168. 10.1021/acsnano.1c04944. [DOI] [PubMed] [Google Scholar]
- Yin W. J.; Shi T.; Yan Y. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 2014, 26, 4653–4658. 10.1002/adma.201306281. [DOI] [PubMed] [Google Scholar]
- Kovalenko M. V.; Protesescu L.; Bodnarchuk M. I. Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science 2017, 358, 745–750. 10.1126/science.aam7093. [DOI] [PubMed] [Google Scholar]
- Sessolo M.; Bolink H. J. Perovskite solar cells join the major league. Science 2015, 350, 917–917. 10.1126/science.aad5891. [DOI] [PubMed] [Google Scholar]
- Rahaman M. Z.; Hossain A. M. A. Effect of metal doping on the visible light absorption, electronic structure and mechanical properties of non-toxic metal halide CsGeCl 3. RSC Adv. 2018, 8, 33010–33018. 10.1039/C8RA06374E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Islam M. A.; Rahaman M. Z.; Sen S. K. A comparative study of hydrostatic pressure treated environmentally friendly perovskites CsXBr3 (X = Ge/Sn) for optoelectronic applications. AIP Adv. 2021, 11, 075109 10.1063/5.0057287. [DOI] [Google Scholar]
- Hossain K. M.; Hasan M. Z.; Ali M. L. Narrowing bandgap and enhanced mechanical and optoelectronic properties of perovskite halides: Effects of metal doping. AIP Adv. 2021, 11, 015052 10.1063/5.0039308. [DOI] [Google Scholar]
- Rahman M. H.; Jubair M.; Rahaman M. Z.; Ahasan M. S.; Ostrikov K. K.; Roknuzzaman M. RbSnX 3 (X = Cl, Br, I): promising lead-free metal halide perovskites for photovoltaics and optoelectronics. RSC Adv. 2022, 12, 7497–7505. 10.1039/D2RA00414C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W. S.; Park B. W.; Jung E. H.; Jeon N. J.; Kim Y. C.; Lee D. U.; Seok S. I. Iodide management in formamidinium-lead-halide–based perovskite layers for efficient solar cells. Science 2017, 356, 1376–1379. 10.1126/science.aan2301. [DOI] [PubMed] [Google Scholar]
- National Renewable Energy Laboratory . Best Research-Cell Efficiency Chart, Photovoltaic Research, NREL 2019https://WWW.nrel.gov/pv/cell-efficiency.html.
- Correa-Baena J. P.; Saliba M.; Buonassisi T.; Grätzel M.; Abate A.; Tress W.; Hagfeldt A. Promises and challenges of perovskite solar cells. Science 2017, 358, 739–744. 10.1126/science.aam6323. [DOI] [PubMed] [Google Scholar]
- Lira-Cantú M. Perovskite solar cells: Stability lies at interfaces. Nat. Energy 2017, 2, 17115 10.1038/nenergy.2017.115. [DOI] [Google Scholar]
- Sun P. P.; Li Q. S.; Yang L. N.; Li Z. S. Theoretical insights into a potential lead-free hybrid perovskite: substituting Pb 2 + with Ge 2+. Nanoscale 2016, 8, 1503–1512. 10.1039/C5NR05337D. [DOI] [PubMed] [Google Scholar]
- Roknuzzaman M.; Ostrikov K.; Wang H.; Du A.; Tesfamichael T. Towards lead-free perovskite photovoltaics and optoelectronics by ab-initio simulations. Sci. Rep. 2017, 7, 14025 10.1038/s41598-017-13172-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brik M. G. Comparative first-principles calculations of electronic, optical and elastic anisotropy properties of CsXBr3 (X = Ca, Ge, Sn) crystals. Solid State Commun. 2011, 151, 1733–1738. 10.1016/j.ssc.2011.08.039. [DOI] [Google Scholar]
- Grote C.; Berger R. F. Strain tuning of tin–halide and lead–halide perovskites: a first-principles atomic and electronic structure study. J. Phys. Chem. C 2015, 119, 22832–22837. 10.1021/acs.jpcc.5b07446. [DOI] [Google Scholar]
- Knutson J. L.; Martin J. D.; Mitzi D. B. Tuning the band gap in hybrid tin iodide perovskite semiconductors using structural templating. Inorg. Chem. 2005, 44, 4699–4705. 10.1021/ic050244q. [DOI] [PubMed] [Google Scholar]
- Akkerman Q. A.; D’Innocenzo V.; Accornero S.; Scarpellini A.; Petrozza A.; Prato M.; Manna L. Tuning the optical properties of cesium lead halide perovskite nanocrystals by anion exchange reactions. J. Am. Chem. Soc. 2015, 137, 10276–10281. 10.1021/jacs.5b05602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y.; Wang L.; Ma Z.; Wang F. Pressure-induced band structure evolution of halide perovskites: A first-principles atomic and electronic structure study. J. Mater. Chem. C 2018, 123, 739–745. 10.1021/acs.jpcc.8b11500. [DOI] [Google Scholar]
- Coduri M.; Strobel T. A.; Szafrański M.; Katrusiak A.; Mahata A.; Cova F.; Bonomi S.; et al. Band gap engineering in MASnBr3 and CsSnBr3 perovskites: mechanistic insights through the application of pressure. J. Phys. Chem. Lett. 2019, 10, 7398–7405. 10.1021/acs.jpclett.9b03046. [DOI] [PubMed] [Google Scholar]
- Xiao G.; Cao Y.; Qi G.; Wang L.; Liu C.; Ma Z.; Yang X.; et al. Pressure effects on structure and optical properties in cesium lead bromide perovskite nanocrystals. J. Am. Chem. Soc. 2017, 139, 10087–10094. 10.1021/jacs.7b05260. [DOI] [PubMed] [Google Scholar]
- Ying Y.; Luo X.; Huang H. Pressure-induced topological nontrivial phase and tunable optical properties in all-inorganic halide perovskites. J. Phys. Chem. C 2018, 122, 17718–17725. 10.1021/acs.jpcc.8b06712. [DOI] [Google Scholar]
- Zhao Q.; Hazarika A.; Schelhas L. T.; Liu J.; Gaulding E. A.; Li G.; Zhang M.; et al. Size-dependent lattice structure and confinement properties in CsPbI3 perovskite nanocrystals: negative surface energy for stabilization. ACS Energy Lett. 2020, 5, 238–247. 10.1021/acsenergylett.9b02395. [DOI] [Google Scholar]
- Talanov M. V.; Shirokov V. B.; Talanov V. M. Phenomenological thermodynamics and the structure formation mechanism of the CuTi 2 S 4 rhombohedral phase. Phys. Chem. Chem. Phys. 2016, 18, 10600–10606. 10.1039/C6CP00387G. [DOI] [PubMed] [Google Scholar]
- King G.; Woodward P. M. Cation ordering in perovskites. J. Mater. Chem. 2010, 20, 5785–5796. 10.1039/b926757c. [DOI] [Google Scholar]
- Wang F.; Tan M.; Li C.; Niu C.; Zhao X. Unusual pressure-induced electronic structure evolution in organometal halide perovskite predicted from first-principles. Org. Electron. 2019, 67, 89–94. 10.1016/j.orgel.2019.01.003. [DOI] [Google Scholar]
- Ter-Oganessian N. V.; Sakhnenko V. P. Effect of pressure on the order–disorder phase transitions of B cations in AB′ 1/2B″ 1/2O3 perovskites. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2019, 75, 1034–1041. 10.1107/S2052520619013350. [DOI] [PubMed] [Google Scholar]
- Lin J.; Chen H.; Gao Y.; Cai Y.; Jin J.; Etman A. S.; Kang J.; et al. Pressure-induced semiconductor-to-metal phase transition of a charge-ordered indium halide perovskite. Proc. Natl. Acad. Sci. U.S.A. 2019, 116, 23404–23409. 10.1073/pnas.1907576116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan G.; Qin S.; Wu X.; Ding H.; Lu A. Pressure-induced phase transformation of CsPbI3 by X-ray diffraction and Raman spectroscopy. Phase Transitions 2018, 91, 38–47. 10.1080/01411594.2017.1357180. [DOI] [Google Scholar]
- Swainson I. P.; Tucker M. G.; Wilson D. J.; Winkler B.; Milman V. Pressure response of an organic– inorganic perovskite: methylammonium lead bromide. Chem. Mater. 2007, 19, 2401–2405. 10.1021/cm0621601. [DOI] [Google Scholar]
- Haq M. A.; Saiduzzaman M.; Asif T. I.; Shuvo I. K.; Hossain K. M. Ultra-violet to visible band gap engineering of cubic halide KCaCl 3 perovskite under pressure for optoelectronic applications: Insights from DFT. RSC Adv. 2021, 11, 36367–36378. 10.1039/D1RA06430D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ullah R.; Ali M. A.; Murad S.; Khan A.; Dar S. A.; Mahmood I.; Laref A. Structural, electronic and optical properties of cubic perovskite RbYbF3 under pressure: A first principles study. Mater. Res. Express 2019, 6, 125901 10.1088/2053-1591/ab540e. [DOI] [Google Scholar]
- Islam M. A.; Islam J.; Islam M. N.; Sen S. K.; Hossain A. K. M. Enhanced ductility and optoelectronic properties of environment-friendly CsGeCl3 under pressure. AIP Adv. 2021, 11, 045014 10.1063/5.0048849. [DOI] [Google Scholar]
- Clark S. J.; Segall M. D.; Pickard C. J.; Hasnip P. J.; Probert M. I.; Refson K.; Payne M. C. First principles methods using CASTEP. Z. Kristallogr. - Cryst. Mater. 2005, 220, 567–570. 10.1524/zkri.220.5.567.65075. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. 10.1103/PhysRevB.41.7892. [DOI] [PubMed] [Google Scholar]
- Fischer T. H.; Almlof J. General methods for geometry and wave function optimization. J. Phys. Chem. 1992, 96, 9768–9774. 10.1021/j100203a036. [DOI] [Google Scholar]
- Zaddach A. J.; Niu C.; Koch C. C.; Irving D. L. Mechanical properties and stacking fault energies of NiFeCrCoMn high-entropy alloy. JOM 2013, 65, 1780–1789. 10.1007/s11837-013-0771-4. [DOI] [Google Scholar]
- McPherson G. L.; McPherson A. M.; Atwood J. L. Structures of CsMgBr3, CsCdBr3 and CsMgI3—diamagnetic linear chain lattices. J. Phys. Chem. Solids 1980, 41, 495–499. 10.1016/0022-3697(80)90180-8. [DOI] [Google Scholar]
- Liu X.; Xie B.; Duan C.; Wang Z.; Fan B.; Zhang K.; Lin B.; et al. A high dielectric constant non-fullerene acceptor for efficient bulk-heterojunction organic solar cells. J. Mater. Chem. A 2018, 6, 395–403. 10.1039/C7TA10136H. [DOI] [Google Scholar]
- Ali M. L.; Rahaman M. Z. Investigation of different physical aspects such as structural, mechanical, optical properties and Debye temperature of Fe2ScM (M = P and As) semiconductors: A DFT-based first principles study. Int. J. Mod. Phys. B 2018, 32, 1850121 10.1142/S0217979218501217. [DOI] [Google Scholar]
- Pettifor D. G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. 10.1179/mst.1992.8.4.345. [DOI] [Google Scholar]
- Roknuzzaman M.; Alarco J. A.; Wang H.; Ostrikov K. K. Structural, electronic and optical properties of lead-free antimony-copper based hybrid double perovskites for photovoltaics and optoelectronics by first principles calculations. Comput. Mater. Sci. 2021, 186, 110009 10.1016/j.commatsci.2020.110009. [DOI] [Google Scholar]
- Parvin F.; Hossain M. A.; Ali M. S.; Islam A. K. M. A. Mechanical, electronic, optical, thermodynamic properties and superconductivity of ScGa3. Phys. B 2015, 457, 320–325. 10.1016/j.physb.2014.10.007. [DOI] [Google Scholar]
- Liu J.Optical Properties of Materials; Cambridge University Press, 2016; pp 22–65. [Google Scholar]
- Pugh S. F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. London, Edinburgh Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. 10.1080/14786440808520496. [DOI] [Google Scholar]
- Murnaghan F. D. Finite deformations of an elastic solid. Am. J. Math 1937, 59, 235–260. 10.2307/2371405. [DOI] [Google Scholar]
- Krishnamoorthy T.; Ding H.; Yan C.; Leong W. L.; Baikie T.; Zhang Z.; Sherburne M.; Li S.; Asta M.; Mathews N.; Mhaisalkar S. G. Lead-free germanium iodide perovskite materials for photovoltaic application. J. Mater. Chem. A 2015, 3, 23829–23832. 10.1039/C5TA05741H. [DOI] [Google Scholar]
- Mouhat F.; Coudert F. X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104 10.1103/PhysRevB.90.224104. [DOI] [Google Scholar]
- Chen X. Q.; Niu H.; Li D.; Li Y. Modeling hardness of polycrystalline materials and bulk metallic glasses. Intermetallics 2011, 19, 1275–1281. 10.1016/j.intermet.2011.03.026. [DOI] [Google Scholar]
- Hasnip P. J.; Refson K.; Probert M. I.; Yates J. R.; Clark S. J.; Pickard C. J. Density functional theory in the solid state. Philos. Trans. R. Soc., A 2014, 372, 20130270 10.1098/rsta.2013.0270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi L.; Jin Y.; Zhao Y.; Yang X.; Zhao H.; Han P. The structural, elastic, electronic properties and Debye temperature of Ni3Mo under pressure from first-principles. J. Alloys Compd. 2015, 621, 383–388. 10.1016/j.jallcom.2014.10.015. [DOI] [Google Scholar]
- Huang S.; Li R. Z.; Qi S. T.; Chen B.; Shen J. A theoretical study of the elastic and thermal properties of ScRu compound under pressure. Phys. Scr. 2014, 89, 065702 10.1088/0031-8949/89/6/065702. [DOI] [Google Scholar]
- Aydin S.; Simsek M. First-principles calculations of MnB 2, TcB 2, and ReB 2 within the ReB 2-type structure. Phys. Rev. B 2009, 80, 134107 10.1103/PhysRevB.80.134107. [DOI] [Google Scholar]
- Anderson O. L. A simplified method for calculating the Debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. 10.1016/0022-3697(63)90067-2. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data sets generated and/or analyzed in this study are available from the corresponding author on reasonable request.