Hybrid Controller Based on Numerical Methods for Chemical Processes with a Long Time Delay

Abstract

A hybrid control framework is proposed as an alternative for long time delays in chemical processes. The hybrid approach mixes the numerical methods in an internal mode control (IMC) structure, which uses the particle swarm optimization (PSO) algorithm to improve the adjustment of the controller parameters. Simulation tests are carried out on linear systems of high order and inverse response, both with dominant delay, and tests on a nonlinear process (chemical reactor). The performance of the proposed controller is stable and satisfactory despite nonlinearities in various operating conditions, set-point changes, process disturbances, and modeling errors. In addition, experimental tests were performed on a setup composed of two heaters and two temperature sensors mounted on an Arduino microcontroller-based board called the Temperature Control Laboratory (TCLab), with an additional software delay introduced. The merits and drawbacks of each scheme are analyzed using radar charts, comparing the control methods with different performance measures for set-point and disturbance changes. Furthermore, the new controller uses PSO to improve the tuning parameters.

1. Introduction

Chemical processes are multidimensional, with applications ranging from reaction engineering to biomedical, energy, materials, and green chemicals.¹ Originally used in the petrochemical and heavy chemical industries, chemical engineering has advanced rapidly with applications in various industries, including biomedicine, environmental systems, complex systems, new materials, and climate change.² Another example of a chemical process of great social importance is the development of antibiotics, vaccines, and immunology, which gives humanity better control over microbial diseases and allows for longer and healthier human lives.³ In addition, understanding semiconductor materials and their incredible precision in mass production is the foundation of modern microelectronics, computer science, and the World Wide Web.

A control system is required for chemical processes for one or both tasks: (1) Regulation consists of keeping the process at its set points and operating conditions. Many processes should work steadily or in a state that meets the industry’s needs, such as budget, output, safety, and other quality goals. (2) Tracking consists of moving the process from one state of operation to a new one. Sometimes, changing how a process works can be necessary for several reasons, including economics, product specifications, operational limitations, environmental regulations, consumer/customer specifications, and safety precautions, among others.⁴

Biological, chemical, and physical systems with nonlinear dynamics have an inherently nonlinear process constitution, which refers to the ability of a process or system to present nonlinear behavior independent of external influences. First, the inherent nonlinear nature of a process may result from the presence of nonlinear components, nonlinear interactions between components, or nonlinear input–output relationships;⁵ another, the nature of nonlinear processes can be difficult to model due to their complexity and the lack of knowledge of some process parameters. If the model is obtained, most process models relating the controlled and manipulated variables are of higher order, producing a controller difficult to implement. An efficient alternative method for process control is empirical models, which use low-order linear models with dead time. Most of the time, reduced-order models are suitable for process control analysis and design.^4,6

In addition, time delay is a common problem in industrial plants. It is caused by a variety of factors, such as the physical distance between the controller and the measuring instruments; the time required by actuators to produce a change, such as very heavy valves or gates; the intrinsic dynamic behavior of some plants, such as the time required by chemical reactions to produce the desired product in chemical reactors; the time required by sensors to achieve measurements; and the time necessary for the transmission of information in communication networks.^4,7

The control of time-delayed processes has been the subject of much research. Many industrial processes include inherent time delays, and time delays induce additional phase lag, making it difficult to control processes with significant time delays, as they can tend to cause closed-loop behavior instability; therefore, controlling a system with a time delay makes it more difficult to analyze and maintain adequate performance.^8,9

The design of adequate controllers for plants with dominating time delay is difficult because disturbances are not detected in time; the control action, which depends on reasonable measurement, does not occur properly; therefore, the plant response takes time to change. A delayed response of the plant to the control signal can result in a controller reaction that does not match the desired one, leading to a loss of system stability. From a classical control standpoint, the time delay introduces a negative phase, which reduces the critical frequency and phase margin, hence limiting the highest gain that can be used and the response speed of control systems. To ensure the stability of the closed-loop control system, readjusting the controller by decreasing the gain and increasing the integration constant is one of the methods used to mitigate the detrimental effect of time delay. However, this results in a relatively poor temporal response of the control system and a low rejection of disturbances, which is unsuitable in several situations.

However, the proportional integral derivative (PID) control algorithm is often used in chemical processes because it is simple, robust, and effective when put into practical use. However, when a process takes a prolonged time, also known as elevated dead time, the control performance that can be achieved using a PID controller is severely limited. As a result, the effectiveness of the PID controller has been found to decrease due to a significant increase in the amount of time spent on dead process time.⁶

On the other hand, in the case of long-delay systems, the most common control structure approach used is the Smith predictor (SP).¹⁰ It combines a PID controller with an inner loop that contains a process model to eliminate the long delay time in the system.¹¹ It aims to compare various SP configurations available in the literature to control inverse, integrating, stable, and unstable industrial processes with time delay. For example, ref (12) presents a new control strategy based on a modified SP. The main idea consists of representing the predictor model as a closed-loop observer, which considers only the estimated average value of the time delay, so no real-time measurement of the delay is required. Ref (10) focuses on an experimental comparison of three SP configurations. The three control systems are then applied to an Arduino-based Temperature Control Lab to test and assess their performance using various optimization strategies. Finally, they were evaluated under various conditions using many performance indicators. Ref (13) about a design method based on a modified SP structure and the direct synthesis approach. An integral proportional derivative (I-PD) control structure, a modification of the PID controller, where only the error will be integrated and the sum of the proportional and derivative parts of the output will be subtracted, is used on the side of the SP that tracks the set point. On the side that rejects disturbances, a PD controller in cascade with a lead–lag filter.

In contrast to other studies in the literature, simpler controllers make it possible to greatly reduce the number of math expressions that come up in the direct synthesis method. Thus, a model-based controller that is effective for processes with long dead times is sensitive to modeling errors.⁸ SP control is an excellent solution to the problem of controlling time-delay systems. However, it approaches improving system performance in real-time applications, and robustness is subject to modeling errors.^14,15 Furthermore, in the case of long-delay systems, the most common control structure approach used is the SP.¹⁰ It combines a PID controller with an inner loop that contains a process model to eliminate the long delay time in the system. Ref (11) aims to compare various SP configurations available in the literature to control inverse, integrating, stable, and unstable industrial processes with time delay. For example, ref (12) presents a new control strategy based on a modified SP. The main idea consists of representing the predictor model as a closed-loop observer, which considers only the estimated average value of the time delay, so no real-time measurement of the delay is required. Ref (10) focuses on an experimental comparison of three SP configurations. The three control systems are then applied to an Arduino Temperature Control Lab to test and assess their performance using various optimization strategies. Finally, they were evaluated under various conditions using many performance indicators. Ref (13) about a design method based on a modified SP structure and the direct synthesis approach. An I-PD controller structure is used on the side of the SP that tracks the set point. On the side that rejects disturbances, a PD controller in cascade with a lead–lag filter. In contrast to other studies in the literature, simpler controllers make it possible to greatly reduce the number of math expressions that come up in the direct synthesis method. Thus, a model-based controller that is effective for processes with long dead times is sensitive to modeling errors.⁸ SP control is an excellent solution to the problem of controlling time-delay systems. However, it approaches improving system performance in real-time applications, and robustness is subject to modeling errors.^14,15

Many control solutions have been created to mitigate the effect caused by long delays in industrial processes.¹⁶ We can mention model predictive controller (MPC), fuzzy logic controller (FLC), sliding mode control (SMC), robust control, internal model control (IMC), Smith predictor (SP) modifications, and combinations of them.^11,16−26 These control methods are useful for reducing the effects of long delays on stable and unstable systems.

This paper proposes a hybrid control framework as an alternative to previous approaches to treating long time delays in chemical processes. The hybrid approach mixes the numerical methods in an IMC structure, which uses the particle swarm optimization (PSO) algorithm to improve the adjustment of the controller parameters. PSO is a stochastic search method that is very efficient and effective in solving complex multiobjective problems where conventional optimization tools fail to work well,²⁷ and has been used for many applications, from parameter tuning to control problems.²⁸ Simulation tests are carried out on linear systems of high order and inverse response, both with dominant delay, and tests on a nonlinear process (chemical reactor) with a dominant delay. Finally, experimental tests were performed on a temperature system called TCLab with an additional software delay introduced so that it is considered a process with a dominant delay.

The contributions of this study can be summarized as follows:

• A hybrid control scheme is proposed for processes with a long delay, where the Smith predictor compensates for the time delay, and the approach based on numerical methods is used for reference tracking; an integral action is included to mitigate errors in modeling.

• The controller synthesis is proposed from a second-order plus delay (SOPDT) system, which is obtained by using the reaction curve and adjusted using the three-point method proposed by Stark.²⁹

• Tuning by optimization based on particle swarm is proposed for the controller parameters, where the function to be minimized is composed of the sum of the IAE (absolute integral error) and TVu (total variation of the control action) indices.

The remainder of this paper is organized as follows. Section 2 briefly presents the fundamental concepts. Section 3 shows how the hybrid controller is synthesized. Simulations using MATLAB/Simulink of three systems (two linear and one nonlinear) as an experiment using TCLab³⁰ for controller tests and their results and discussion are described in Section 4. Finally, Section 5 draws the concluding remarks of our paper.

2. Background

This section briefly describes the basic concept of the Smith predictor (SP), the linear algebra-based controller (LABC), and the identification model procedure.

2.1. Process Characterization Using a Second-Order Plus Dead Time Model

Information on the dynamic behavior of the process is necessary to design or adjust controllers, typically in the form of a reduced-order model (first order plus dead time (FOPDT) and second order plus dead time, SOPDT).³¹ The parameters of these models (gain, dead time, and time constants) can be identified from the open-loop process response to a step change in the input, called the process reaction curve.

There are several methods to determine these parameters based on the times required to reach two or three specific points based on the information from the process response.³¹ The three-point method proposed by Stark is considered,^29,32 where these points are the times that the process responds to 15% (t₁₅), 45% (t₄₅), and 75% (t₇₅) of the change in the output process (Δy) to a step change in input (Δu), as shown in Figure 1, to obtain an SOPDT model of the form

1

where 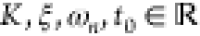are the static gain, damping factor, undamped natural frequency, and dead time, respectively.

Figure 1.

Reaction curve for the Stark method.

The following equations allow us to obtain the parameters K, ξ, ω_n, and t₀ of the model³³

2

also

3

If ξ ≤ 1.0, then

4

If ξ > 1.0, then

5

in addition

6

Moreover

7

8

Finally, the gain is given by the change in output (Δy) divided by the change in input (Δy)

9

2.2. Particle Swarm Optimization

PSO is one of the most well-known metaheuristic algorithms. It is inspired by a flying swarm of birds looking for food in nature, where each bird shares its discovery and helps the entire group get the best hunt.³⁴ That means each bird attempts to find the best personal solution in a high-dimensional space, and the best solution found by the swarm will be the optimal PSO solution.

Numerically, each bird is considered particle i in a space of dimensions d containing a velocity and position vector at time t of the form V_i = [v₁, v₂, v₃, ···, v_d] dimension and X_i = [x₁, x₂, x₃, ···, x_d], respectively. The PSO randomly initializes V_i and X_i. Then, the best position found by the particle (Pbest_i) and the whole swarm (Sbest) at each iteration guide particle i to update its velocity and position at the iteration t + 1,³⁵ according to eqs 10 and 11

10

11

where r₁ and r₂ are uniform random distributed numbers in the interval from 0 to 1, ω ∈ [0..1] is the inertia weight, which controls the particle’s search in terms of speed and direction, and the parameters c₁ and c₂ are the cognitive and social acceleration coefficients to control the weight of the particle’s search task and the recognition of the search result by the swarm. The update process of the particles runs iteratively until a stopping criterion is reached, for example, the total number of generations. It should be noted that the PSO local and global best solutions are based on minimizing or maximizing a given cost function (ϕ_d).

3. Design of the Hybrid Controller

This section develops a hybrid controller based on the combination of the Smith predictor and the numerical method approach.

3.1. Dead Time Compensation

Many industrial processes present nonlinear characteristics; however, these processes work around the point of operation. Therefore, a linear model can adequately represent the real behavior of processes. In practice, most chemical processes can be mathematically represented by an SOPDT model.³⁶⁻³⁸ Consider that a chemical process can be approximated by the SOPDT model, as presented in (eq 1).

The proposed hybrid control scheme is shown in Figure 2. It can be seen that a conventional internal model structure is used, such as the red Smith predictor (SP)³⁹ structure or dead time compensator (DTC), where y(t) is the output of the process, r(t) is the set point or reference, s) Gm(s) is the invertible part of the process model, y_m(t) is the output of the process model, and e_m(t) is the output modeling error. Therefore, the SP incorporates a process model and thus can predict its output. This allows the controller to be designed as if the system is delay-free, retaining the simple tuning features of PID controllers.⁴⁰

Figure 2.

Proposed hybrid control scheme.

Thus, the noninvertible and invertible parts of the Smith predictor structure are given by eqs 12 and13, respectively

12

13

Taking into account the modeling error (e_m ≈ 0), thus, the linear algebra-based controller observes the behavior of the process according to eq 13. However, to guarantee this consideration, the controller must assume the uncertainties in the modeling.

3.2. Controller Based on the Numerical Methods Approach

Numerical methods and linear algebra tracking control methods have been proven in many highly nonlinear systems. It began in underactuated mechanical systems, dynamic nonlinear systems controlled with a kinematic model for tracking and positioning control tasks for fast and slow dynamics systems such as mobile robots, then for chemical processes such as bioprocesses, and also for chemical reactors.⁴¹ Thus, to design a controller using a numerical method-based approach, eq 13 can be written as a differential equation

14

Taking into account the following state variables y₁(t) = y_m(t) and y₂(t) = ẏ₁, the systems described by eq 14 can be written as

15

where y₁(t) and y₂(t) are the controlled variables and their derivative, respectively, and u(t) is the input control.

The purpose is to establish a control law that is able to generate a control input u(t) so that the system variables follow the desired reference y_ref(t) with a minimum error.

Currently, controllers are being implemented in digital systems. One option is to express the system model in discrete time and, from this, determine the control law. Thus, the simplest approach is the Euler approximation

16

where T_s is the sampling time k ∈ {0, 1, 2, 3 ···}. An appropriate sampling time must be selected. For example, the T_s for the discrete controller will be in terms of ω_n and t₀ as: 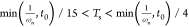.³⁹ It is assumed that all of the state variables can be measured for each sampling period. The application of numerical methods is used to transfer the variables from one sampling period to the next, where the real measurement of the variables is repeated, and there is no cumulative error. Therefore, the estimation of the sampling period range can guarantee the approximation by Taylor.

Now, the system variables y₁(t), y₂(t), and u(t) in discrete time are denoted by y_1,k, y_2,k, and u_k, respectively. Thus, the variables of the system are discretized by Euler’s approximation as follows

17

Using eq 17 in eq 15, a discretized system can be written in a compact form

18

eq 18 represents a system of linear equations that allows computing the control action at each sampling instant so that the system reaches the desired reference. Thus, to solve the reference tracking problem, it is necessary to specify the conditions that make Au_k = b have an exact solution.⁴¹⁻⁴³

It is seen that the system described by eq 18 has an exact solution, and the rows of b corresponding to the zero rows of A must be equal to zero. This implies that the variable y_2,k must satisfy

19

To improve the algorithm, it is necessary that the error decreases to zero considering y_1,k+1 – y_1,k + Δe₁ and y_2,k+1 – y_2,k + Δe₂. Then, we expect the error variation Δe₁ → 0 and Δe₂ → 0 for a huge 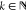, where Δe₁ = e_1,k+1 – e_1,k and Δe₂ = e_2,k+1 – e_2,k.

Thus, it is considered that

20

the error e_1,k+1 = y_1ref,k+1 – y_1,k+1 is replacing in eq 20, we have the following

21

where 0 < K₁ < 1, e_1,k = y_1ref,k – y_1,k, y_1ref is the desired reference, and K₁ is the adjustment parameter to calibrate the controller response. For a faster response, K₁ should be close to 0; for a lower response, K₁ is selected close to 1.

By replacing eq 19 with eq 21, we have the following

22

The variable y_2,k will be called y_2ez,k, and it is the necessary value to take y₂ to force the error tracking to zero. Thus, eq 22 is rewritten as

23

By solving eq 18, the control action is given by

24

where, for an analogous procedure, where eq 21 was obtained, y_2,k+1 is given by

25

with

Finally, eq 24, the control action can be written as

26

where y_1,k and y_2,k are the state variables y₁ and y₂, in the instant k, respectively.

To calculate the value of u_k, it is necessary to calculate y_2ez,k+1 because it is a value at a k later instant; for this purpose, the Taylor approximation is used

27

Here, is the complementary term; thus, for a short sampling time, y_2ez,k+1, it can be approximated by

28

or for a lower deviation, the following expression can be used

29

Now, substituting u_k from eq 24 to eq 18, the following expression is given

30

Finally, eq 22 in eq 30 and taking into account how the errors were defined, we have

31

where if 0 < K₁ < 1 and 0 < K₂ < 1, then e_1,k → 0, e_2,k → 0, k → ∞.

3.3. Controller Design with Integral Action

The model presented in eq 13 approximates the real process. Therefore, it is important to consider the presence of uncertainties in the design⁴⁴ and to guarantee zero error in the steady state. It is well known that adding an integral action can mitigate modeling uncertainties.

For the system presented in eq 14, a state-variable discrete model with additive term uncertainty E_k is introduced as

32

In this way, following the analogous procedure, we obtain eq 30, and the following expression can be determined

33

where E_k is considered unknown. The first-order uncertainty is defined as δE_k = E_k+1 – E_k. Furthermore, if constant uncertainty is considered, E_k = cte. Thus, δE_k = E_k+1 – E_k = 0. To mitigate the effect of uncertainty, an integral term is added to the control action in e₂. The action control is given by

34

where

3.4. Tuning of Controller Parameters Based on PSO

In this work, the PSO method is used to adjust the parameters of the proposed controller (K₁, K₂, K_i). The PSO algorithm is used for robust global optimization and is successfully used to adjust parameters in chemical processes. It is used to optimize the performance of the parameters.^45,46

This paper proposes an objective function to minimize, composed of a component depending on the error (ISE) and another depending on the control action (TVu), as indicated in eq 35. This function allows one to determine a compromise between the error and the control action, allowing the output variable to reach the reference as soon as possible with the least control effort

35

where 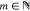, t_f is the total time of the experiment, and C₁ and C₂ are penalty coefficients.

The parameters of the proposed controller were tuned offline for which the MATLAB “particleswarm” function was used; the tests were carried out with MATLAB 2019b software on an Intel (R) Core (TM) i7–7500U@2.9 GHz PC on Windows 10. For the configuration of the PSO algorithm, an initial population of 30 particles and a maximum of 50 iterations were considered. Both the simulation and the experimental results were satisfactory, as presented in the next section.

4. Results and Discussion

This section presents two parts: the first is dedicated to the simulation of linear and nonlinear systems, and the second implements the controllers on a TCLab device.

All of the processes considered in this section present long dead time. When we talk about a short or long delay in process control, we are talking about the controllability ratio (t₀/τ). It is associated with the difficulty level in controlling a process,⁴⁷ also known as the normalized dead time or the normalized time delay.⁴⁸ Processes with a small (t₀/τ) are simple to regulate, and as a system gets bigger (t₀/τ), it can be considered more difficult to control. In this work, the ratio (t₀/τ) is greater than one, thus representing processes with a dominant time delay.

All controllers are compared and contrasted. Furthermore, radar charts with different performance indices are used as quantitative measures for controllers. These were normalized between 0 and 1, for which each performance index is divided by the maximum value.

4.1. Simulation Results

This section presents the performance of the proposed hybrid controller. This has been tested in high-order, inverse-response linear systems with a long time delay and in a nonlinear chemical reactor process with a long time delay. To design the proposed controller, the dynamics of the chemical reactor is approximated by an SOPDT model using the reaction curve method. Thus, the model is obtained using the Stark identification method. Furthermore, the parameters of the proposed controller were tuned using particle swarm-based optimization (PSO), as presented in Section 3.4.

The simulation results are performed with MATLAB 2019b software on an Intel (R) Core (TM) i7–7500U@2.9 GHz PC.

To measure controller performance, integral absolute error (IAE), integral square error (ISE), and total variation of the control action (TVu) are used.

4.1.1. High-Order Linear System

Using the fourth-order linear system proposed by Camacho et al.,³⁹ where the transfer function is given by

36

From the reaction curve identification method, the SOPDT model is obtained using the Stark method as follows

37

where ξ = 1.128, w_n = 1.458, K = 1, and t₀ = 10.33 (from eq 37). The controllability ratio is given by 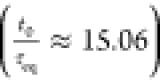, where 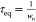.^4,6 Therefore, it is considered a long or dominant time-delay process.

The parameters of the three test controllers have been tuned as follows: first, the PID controller with the Smith predictor adapted by Kaya,⁴⁹ then the DTC-SMC controller tuned according to the methodology presented by Camacho et al.⁵⁰ The test controller tuning parameters are shown in Table 1.

Table 1. Controller Design Parameters for the High-Order Linear System.

parameter	proposed	Kaya-SP	DT-SMC
K1	0.6352
K2	0.0039
Ki	0.7122
Kp		2
Ti		1.2198
Td		0.1832
Ks			1.07
KD			0.164
δ			0.695
model-based	SOPDT	SOPDT	FOPDT

4.1.2. Reference Step Change Test for the High-Order System

In this test, two-step reference changes are made, the first from 0 to 1 and the second from 1 to 1.5. Also, from t = 100 s, a disturbance of a value of 0.2 is applied until the end of the simulation.

In Figure 3, the output responses of the process are presented, where the three controllers are able to follow the reference changes in the presence of disturbance. However, the DT-SMC controller has the slowest response. In addition, in the first reference change, the proposed controller and the Kaya-SP lead the system very fast toward the reference, but in the second reference change, only the proposed controller is able to achieve it.

Figure 3.

Process output response for the step change reference on the high-order system.

Control actions are shown in Figure 4, where the Kaya-SP controller displays larger peaks on the first reference change and when the disturbance starts. The proposed and DT-SMC controllers have a higher peak with the second reference change.

Figure 4.

Controller output for the step change reference on the high-order system.

To globally analyze the performance of the test controllers, a normalized radial chart is presented in Figure 5, where the proposed controller presents the lowest values in the IAE and ISE indices and presents a TVu value slightly higher than the DTC-SMC controller.

Figure 5.

Normalized radar chart for the reference of change in the high-order system.

4.1.3. Reference Variable Tracking Test for the High-Order System

In this test, a reference variable is applied to the system given by 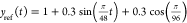is applied to the system. Furthermore, from t = 100 s, a disturbance of a value of 0.2 is applied until the end of the simulation.

Figure 6 shows the output responses when the reference is variable and when a disturbance is applied, where only the proposed controller is capable of leading the system to the reference (Figure 7).

Figure 6.

Process output response for the variable reference on a high-order system.

Figure 7.

Controller output for the variable reference on a high-order system.

Figure 13 shows the control actions for the variable reference tracking test on a high-order system where the Kaya-SP controller presents at the beginning of tracking and disturbance.

Figure 13.

Controller output for the variable reference on an inverse-response system.

Figure 8 shows a normalized radar chart, where it can be seen that the proposed controller presents the lowest values of the IAE and ISE indices and a slightly lower TVu value than the DT-SMC controller. Thus, the proposed controller presents the best global performance for this test.

Figure 8.

Normalized radar chart for the variable reference on a high-order system.

4.1.4. Inverse Response with the Long-Time-Delay System

The inverse response with a linear long-time-delay system is described in ref (51), where its transfer function is given by

38

The system described in eq 38 can be approximated by an SOPDT model as

39

where ξ = 1.455, w_n = 0.508, K = 1, and t₀ = 6.98 (from eq 37). The controllability ratio is given by , where τ_eq is defined as before. Therefore, it is considered to be a long time-delay process.

To analyze the performance of the designed controller, it is compared with the SMC and IMC-SMC controllers proposed by Camacho et al.⁵¹ The controller parameters are shown in Table 2.

Table 2. Controller Design Parameters for the Inverse-Response System.

parameter	proposed	IM-SMC	SMC
K1	0.6383
K2	0.2079
Ki	0.0833
λ		0.06
λ0			0.02
λ1			0.29
KD		0.93	0.43
δ		0.68	0.69
model-based	SOPDT	FOPDT	FOPDT

4.1.5. Reference Step Change Test for the Inverse-Response System

In this test, two-step reference changes are made; the first from 0 to 1 and the second from 1 to 0.6. Furthermore, from t = 100 s, a disturbance of a value of 0.2 is applied until the end of the simulation.

The output response of the process is shown in Figure 9, where all controllers can follow the reference changes with disturbances. However, the proposed controller allows the system to follow the reference quickly, although overshoots occur with reference changes. Additionally, the DTC-SMC controller has the slowest output response.

Figure 9.

Process output response for the step change reference on an inverse-response system.

Figure 10 shows the control actions where the proposed controller presents larger peaks.

Figure 10.

Controller output for the step change reference on an inverse-response system.

Figure 11 shows a normalized radar chart with performance indices and shows that the proposed controller displays lower IAE and ISE values. However, it presents a higher TVu value.

Figure 11.

Radar chart for step change on an inverse-response system.

4.1.6. Reference Variable Test for the Inverse-Response System

In this test, a reference variable given by 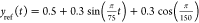is applied to the system. Furthermore, from t = 100 s, a disturbance of a value of 0.2 is applied until the end of the simulation. It can be seen (see Figure 12) that only the proposed controller brings the system quickly to the reference.

Figure 12.

Process output response for the variable reference.

Figure 13 shows the control actions for the variable reference follow-up test on the inverse-response system, where the proposed controller presents peaks at the beginning of the track and the disturbance.

Figure 14 shows a normalized radar chart of the performance indices, where it can be seen that the proposed controller presents lower IAE and ISE values. However, it presents the highest TVu value.

Figure 14.

Normalized radar chart for the variable reference on the inverse-response system.

4.1.7. Chemical Reactor with a Long Time Delay

To analyze the performance of the proposed controller, a continuous stirred tank reactor (CSTR) process taken from Camacho and Smith¹⁴ is used. The CSTR process is illustrated in Figure 15 and presents a modification in the location of the temperature transmitter.⁵²

Figure 15.

Chemical reactor process.

The chemical reactor is a continuous tank in which an exothermic reaction A → B takes place. Many processes are exothermic, including those used for the synthesis of ammonia⁵³ or for the free radical polymerization of acrylates.⁵⁴ To reduce the heat of the reaction, a coolant inlet is used, which circulates through the jacket surrounding the reactor. According to Figure 15, the outlet temperature T(t) is measured 50 m downstream of the reactor, introducing a transport delay that makes it difficult to control. The control objective is to maintain or change the reactor temperature T(t) within the operating range by manipulating the position of the valve m(t), varying the flow of the cover F_c(t). Furthermore, temperature T_i(t), flow F(t), and feed concentration C_A(t) are considered constant. To analyze the dynamics of the CSTR system, the following assumptions are taken into account.

• The reaction rate has a chemical kinetics of second order.

• Heat losses in the jacket surrounding the reactor are negligible.

• The densities and heat capacities of the reactants and products are constant.

• The heat of the reaction and the level of liquid in the reactor tank are constant.

• The reaction mixture and the reacted material are mixed uniformly.

For practical purposes, it should be considered that the temperature control is calibrated for the range from 80 to 100 °C, and the valve is managed in values from 0 to 1. Table 3 shows the steady-state values and parameters for the operation of the CSTR process.

Table 3. Operation Parameters and Steady-State Values.

variable	value	variable	value
CA	1.113 kgmol/m3	VC	1.82 m3
Cai	2.88 kgmol/m3	F(t)	0.45 m3/min
T	88 °C	Fcmax	1.2 m3/min
Ti	66 °C	Cpc	4184 J/kg·°C
Tci	27 °C	α	50
set point	88 °C	τT	0.33 min
ΔHR	–9.6e7 J/kgmol	k0	4.464 m3/min·kgmol
Cp	1.815e5 J/kgmol·°C	E	1.182e7 J/kgmol
U	2.13e5 J/min·m2·°C	TC	50.5 °C
ρc	1000 kg/m3	m	0.254 fraction CO
A	5.4 m2	V	7.08 m3
ρ	19.2 kgmol/m3	L	50.3 m
At	0.018636 m2	TO	0.4

The mathematical model of the CTRS process is described by the following equations.

Mole balance in reactant A

40

Energy balance in reactor contents

41

Energy balance in the jacket

42

Reaction rate coefficient

43

Pipe delay between the reactor and the sensor location

44

Transportation lag or delay time

45

Temperature transmitter

46

Equal percentage control valve (air to close)

47

where

C_A(t): concentration of the reactant in the reactor, kgmol/m³

C_ai: concentration of the reactant in the feed, kgmol/m³

T(t): temperature in the reactor, °C

T₁(t): equal to T(t) delayed by t₀, °C

T_i(t): temperature of the feed, °C

T_c(t): jacket temperature, °C

T_ci(t): coolant inlet temperature, °C

TO(t): transmitter signal on a scale from 0 to 1

F(t): process feed rate

k: reaction rate coefficient, m³/kgmol·s

ΔH_R: heat of the reaction, assumed constant, J/kgmol

ρ: density of reactor content, kgmol/m³

C_p: heat capacity of reactants and products, J/kgmol·°C

U: overall heat transfer coefficient, J/min·m²·°C

A: heat transfer area, m²

V_c: jacket volume, m³

ρ_C: density of the coolant, kg/m³

C_pc: specific heat of the coolant, J/Kg·°C

F_c(t): coolant rate, m³

τ_T: time constant of the temperature sensor, min

U(t): output signal on a scale from 0 to 1 (fraction CO)

F_Cmax: maximum flow through the control valve, m³/min

α: valve rangeability parameter

k₀: Arrhenius frequency parameter, m³/min·kgmol

R: activation energy of the reaction, 8314.39 J/kgmol·K

m(t): valve position on a scale from 0 to 1

A_t: pipe cross-section, m²

L: pipe length, m

4.1.8. Chemical Reactor Identification

To design the proposed controller, the dynamics of the chemical reactor are approximated by an SOPDT model using the reaction curve method. Thus, a change of 10% of the input to the system (m(t)) is made. Finally, the SOPDT model is expressed as follows:

48

where ξ = 1.1918, w_n = 0.1618, K = 1.67, and t₀ = 40. The controllability ratio is given by 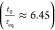. Thus, it is considered a long time-delay process.

4.1.9. Controller Parameter Tuning for CSTR

In this section, the parameter tuning of three test controllers is presented. The first test controller (PI) with the Smith predictor (SP) was tuned using the Kaya method for K_p and T_i,⁴⁹ as shown in Table 4. The second (SMC) was tuned using the procedure presented in ref (50), and the parameters of the proposed controller are shown in Table 4. Note that a control scheme based on an internal model is provided for the three test controllers.

Table 4. Controller Design Parameters for CTRS.

parameter	proposed	IM-SMC	Kaya-SP
K1	0.9665
K2	0.4575
Ki	0.1850
Kp			1.1976
Ti			8.9618
λ		0.0013
KD		0.1888
δ		0.6800
model-based	SOPDT	FOPDT	SOPDT

4.1.10. Reference Tracking Test for CSTR

Based on steady-state operating conditions, four reference changes are made for 500 min each. First, a ramp from 88 to 92 °C, the temperature remains at 92 °C, then another ramp from 92 to 96 °C, and finally, it remains constant at 96 °C.

The temperature response is shown in Figure 16, where the proposed controller leads the system very quickly and without overshooting to the desired reference. However, the kaya-SP and IM-SMC controllers cannot track the reference in the temperature-range sections. The IM-SMC controller is the slowest to track the reference and presents overshoots.

Figure 16.

Response of the temperature reactor T(t) for the reference tracking test.

Figure 17 shows the control actions, where it can be seen that the three controllers work within the operating limits for the input of the system (m(t)). However, when the reference changes, the proposed controller presents some peaks in the control action.

Figure 17.

Controller output m(t) for the reference tracking test on CSTR.

The results indicate that the proposed controller presents a lower cumulative error for the reference tracking test compared to PI-Kaya and IM-SMC, as shown in Figure 18.

Figure 18.

Cumulative error for the reference tracking test on CSTR.

A normalized radar chart is presented in Figure 19, where the performance indices ISE, IAE, and Tvu are used to give a general idea of the performance controllers. It can be seen that the proposed controller has the lowest ISE and IAE indices; however, it has the highest TVu index. Furthermore, the Kaya-SP controller presents performance indices lower than those of the IM-SMC.

Figure 19.

Normalized radar chart for the tracking reference on CTRS.

4.1.11. Disturbance Test for CSTR

In this test, a reference change at 92 °C is performed, then the feed F(t) is decreased from 0.45 to 0.4 m³/min at 200 s and then from 0.4 to 0.35 m³/min at 1000 s. The temperature responses are shown in Figure 20, where it can be seen that the proposed controller is capable of keeping the system at the reference in the presence of disturbances due to the change in feed flow. Also, the Kaya-SP controller is not able to keep the system on the reference from the second disturbance, and the IM-SMC has a very slow response.

Figure 20.

Response of the temperature reactor T(t) for the disturbance test.

Figure 21 shows the control actions where it can be seen that the proposed control and the IM-SMC work within the limits of the system input. However, the Kaya-SP controller presents high peaks and the control action saturates from the second disturbance.

Figure 21.

Controller output m(t) for the disturbance test on CSTR.

The IAE, ISE, and TVu performance indices are displayed using a normalized radar chart, as presented in Figure 22, where it can be seen that the proposed controller presents the best overall performance and the Kaya-SP controller shows the lowest performance.

Figure 22.

Normalized radar chart for the disturbance test on CTRS.

4.2. Experimental Results

In this section, we present the experimental results of the reference tracks. Then, the Temperature Control Laboratory (TCLab) analyzes the proposed controller’s performance. The TCLab is a portable, pocket-sized laboratory for control applications using MATLAB Simulink and Python software. This is an excellent tool for testing different control system design techniques.^10,30,55

The TCLab is made up of two heaters, two temperature sensors, a Leonardo Arduino board, and a power supply to feed the heaters, as shown in Figure 23.

Figure 23.

Temperature Control Laboratory (TCLab) setup.

The control maintains the outlet temperature at a desired reference by manipulating the power output of the heater,⁵⁶ where the thermal energy produced by the heater is transferred by conduction, radiation, and convection to the temperature sensor. This work uses only the single-input and single-output (SISO) configurations of the TCLab. Furthermore, the software introduces a time delay of 124 s at the TCLab input.

The experimental results are performed on MATLAB 2019b software on an Intel (R) Core (TM) i7–7500U@2.9 GHz PC using the ODE4 (Runge–Kutta) solver method with a sample time of T = 0.5 s.

4.2.1. TCLab Identification

The dynamics of the TCLab is approximated by an SOPDT model using the reaction curve method. To achieve this, a change of 60% of the input in the system (u(t)) is made, as shown in Figure 24. The model is obtained by Stakr’s identification method, where the parameters t₁₅ = 171.5 s, t₄₅ = 239.9 s, and t₇₅ = 359.9 s are determined. Thus, an SOPDT is expressed as follows:

49

where ξ = 1.5572, w_n = 0.0183, K = 1.091, and t₀ = 129. The controllability ratio is given by 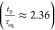, where 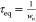. Thus, it is considered a long-time-delay process.

Figure 24.

TCLab reaction curve.

4.2.2. Controller Parameters Tuning for the TCLab

In this section, two test controllers are compared; the first is a PI controller with the SP, where its K_p and T_i parameters are tuned using the Kaya method.⁴⁹ The parameters of the proposed controller were tuned using PSO, as presented in Section 2. The parameters of both controllers are presented in Table 5.

Table 5. Controller Design Parameters for the TCLab.

parameter	proposed	Kaya-SP
K1	0.952
K2	0.9097
Ki	0
Kp		1.83
Ti		105.58
model-based	SOPDT	FOPDT

4.2.3. Reference Tracking Test for the TCLab

Three reference changes are made for the temperature of the initial operating conditions. First, the temperature remains around 20 °C, then increases from 20 to 60 °C, and finally remains constant at 60 °C. The response to the outlet temperature is shown in Figure 25, where the proposed controller quickly leads the TCLab to the desired reference. Unfortunately, the Kaya-SP controller cannot track the reference in the temperature ramp section.

Figure 25.

TCLab temperature response for the tracking reference.

According to Figure 26, the control actions u(t) of both controllers are kept within the allowed range of 0 to 90%. However, the proposed controller presents peaks in its control actions.

Figure 26.

TCLab controller output for the tracking reference.

In Figure 27, a normalized radar chart is presented, where the IAE and ISE performance indices are lower on the proposed controller than on the Kaya-SP controller. However, the TVu index is higher on the proposed controller.

Figure 27.

Normalized radar chart for the tracking reference on the TCLab.

5. Conclusions

A hybrid controller was designed using different concepts, numerical and internal mode control concepts, and the PSO algorithm to improve adjustments. Computer simulation examples indicated that the proposed controller performance is stable and satisfactory despite nonlinearities in various operating conditions, set-point changes, process disturbances, and modeling errors. Furthermore, it showed the improvement of the hybrid scheme for tracking and regulatory tasks. The same results are obtained in the experimental part. A comparative evaluation is performed to determine the performance of the proposal in four systems: linear, one nonlinear, and a reference device (TCLab) with a long delay. The merits and drawbacks of each scheme were analyzed using radar charts, comparing the control methods with different performance measures for set-point and disturbance changes. In summary, the controller synthesis is based on the approximation of the SOPDT model of the process to avoid the design from a complex model. Furthermore, the new controller uses PSO to improve the tuning parameters.

The proposed hybrid controller presents excellent reference tracking with high control effort, as explained in ref (42), when using discrete-time controllers, there is a trade-off between control accuracy and computational load, which increases with decreasing sampling period T_s. One advantage of a short sample period is that faults resulting from disturbances are detected earlier and the impact of disturbance can be reduced. Also, the control error is reduced for shorter sampling periods, but the control action is increased, and if the sampling period increases, thus the control actions are less.

When analyzing the time complexity of the PSO algorithm for the proposed method (approximately by measuring the rate of growth of the algorithm) using the big-O notation (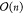),⁵⁷ the complexity is infinite (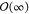) if the algorithm is analyzed from the point of view of mathematical optimization because it searches in the space of all possibilities. However, in our problem, we use an early stopping criterion (the combination of parameters that is less than a threshold) for a discrete parameter value space. Therefore, the PSO would incur as an algorithm with quadratic time complexity (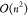). Therefore, due to the time execution and complexity, the algorithm for tuning parameters should be performed offline. Despite that, in future work, we would like to explore the feasibility of using PSO as a way to do online readjustment of the tuning parameters. We also plan to implement and validate the proposed controller in chemical processes with actual experimental data.

Author Contributions

O.C.: methodology, preparation of the first draft, and review of the final manuscript; M.H.: methodology, preparation of the first draft, simulations, and graphs; D.B.: preparation of the first draft and review of the final manuscript; N.P.: preparation of the first draft and review and help with the final manuscript; and A.d.T.: preparation of the first draft and methodology math review.

The authors declare no competing financial interest.