Abstract
Cyclone separation is an effective method for the treatment of oily wastewater from offshore oil production platforms. There is a lack of research on the impact of dispersion on the separation efficiency of current liquid–liquid separation hydrocyclones. A numerical simulation method was used to study the effect of the oil droplet characteristic parameters on the separation efficiency of a hydrocyclone oil removal device. An analysis of the trajectory of oil droplets revealed the oil removal mechanism of the hydrocyclone oil removal device: under the guidance of tangential velocity, the oil–water mixed fluid in the equipment generates different centrifugal forces due to the density difference, so oil and water adopt different flow paths to flow out. The effects of the particle diameter, velocity, and concentration of the inlet oil droplet on the separation efficiency were investigated. The droplet size had a positive effect on the separation efficiency, the oil concentration had a negative effect on the separation efficiency, and the speed of the oil drop was directly proportional to the separation efficiency within a certain range. These studies improved the basis for the efficient application of hydrocyclone oil removal devices.
Keywords: hydrocyclone oil removal device, oil droplet trajectory, oil drop characteristics, separation efficiency, numerical simulation
Introduction
Cyclone separation involves the realization of two-phase or multiphase separation by utilizing the centrifugal force generated by the high-speed rotation of liquids and the density difference between the two-phase or multiphase media.1,2 There are several types of hydrocyclones.3–6 They are widely used in petroleum, chemical, environmental protection, mineral processing, pharmacy, light, and many other industries because they can perform gas–liquid, liquid–liquid, liquid–solid, and gas–liquid–solid separation.7–10 Several researchers have conducted studies on the performance of hydrocyclones. For example, Dehdarinejad et al. summarized the numerical simulations of gas–solid cyclone separators with tangential inlets and evaluated the influence of nonuniform surface roughness on the cyclone performance and rate of erosion.11–14 Meng et al. investigated the effects of the fluid flow rate, gas flow rate, external pressure, and fluid viscosity on the separation efficiency in a gas–liquid cyclone separator. 15 Wang et al. investigated the effects of operating conditions, such as water cut, particle concentration at the inlet, and flow rate.16,17 Kuang et al. examined the liquid–gas–solid flow features in terms of the flow field, pressure drop, amount of water split into the underflow, and separation efficiency.10,18 In terms of liquid–liquid separation, Qian et al. studied the effect of the cone angle and inlet flow flux on the concentration distribution of droplets using a phase Doppler particle analyzer. 19 Motin et al. examined the effects of the parabolic and hyperbolic wall profiles of a hydrocyclone swirl chamber on the internal flow structures and separation efficiency based on numerical simulations. 20 Zhang et al. investigated the trajectory and residence time distribution in a liquid–liquid cyclone reactor. 21 Schütz et al. developed a population balance model to describe droplet coalescence and breakup during flow and separation processes. 22 Nascimento et al. proposed a new geometry for liquid–liquid hydrocyclones and numerically obtained the axial and tangential velocity profiles. 23 Delfos et al. developed a design tool for optimizing axial liquid–liquid hydrocyclones and designed a prototype de-oiling hydrocyclone separator using the design tool. 24
In recent years, the total amount of oilfield-produced water has increased with the rapid development of offshore oil production platforms, which has led to new requirements for the treatment capacity of the produced oily wastewater.25,26 Paradoxically, the actual production needs cannot be met by simply adding the traditional oily treatment equipment as the available space on offshore platforms is limited.27–29 With the development of cyclone separation technology, cyclone separators have been gradually introduced to separate oil and water in oil fields, but this is still insufficient for field applications.30,31 Hydrocyclones exhibit a series of problems, such as unstable separation performance and difficult debugging in field applications, which are affected by the periodic fluctuation of the physical parameters of the incoming liquid.32–34 In addition, adaptive adjustment of operating parameters according to changes in the physical parameters of the treated object cannot be realized in existing hydrocyclone products.35–39 In field applications, the separation performance and utilization rate of hydrocyclones are extremely low. Therefore, an in-depth study of the relationship between the characteristic parameters of oil droplets and the separation performance of hydrocyclones is of great significance for the further optimization and field application of hydrocyclones.
The impact of discrete phase characteristics on separation efficiency has not been investigated for the existing liquid–liquid cyclone separators. Therefore, computational fluid dynamics (CFD) software was used as a tool to carry out the numerical simulation of particle trajectory and oil droplet characteristics on separation efficiency of the oil–water phases in a cyclone separator and to explore the flow field structure and particle motion characteristics under the given equipment geometry. The results provide a basis for practical industrial applications and promote the development of cyclone separators. This study focuses on the application of cyclone separators for oil removal from oilfield sewage, and the results are expected to be applied on offshore platforms.
Mathematical model
Turbulence model
Continuity, momentum conservation, and energy conservation equation are the basic requirements to study a fluid flow. This study assumed that the oil removal hydrocyclone was an isothermal and incompressible (the oil and water phase densities were constant) two-phase flow; therefore, the energy conservation equation was not considered.
In the internal flow field of a hydrocyclone oil removal device, the continuity equation expressed in tensor form is 40
| (1) |
The momentum equation is as follows 41 :
| (2) |
A variety of turbulence models are produced according to different assumptions and treatment methods of the Reynolds stress term, such as the standard K-ε Model, RNG K-ε Model, Reynolds stress model (RSM), and large eddy model (LES). The RSM and LES are used to simulate the internal flow field of a hydrocyclone.42,43
The basic idea of the LES is to simulate the large-scale vortices in a turbulent flow field directly using the instantaneous N–S equation. 44 The LES has high requirements for mesh generation, and demands considerable computing time and cost. Further, its application in practical engineering simulations is still in its infancy. The minimum size of the grid that can be used is still larger than that of general small vortices because of the limited computing speed of computers. Thus, the effect of small-scale vortices on the flow field can only be calculated using an approximate model.
The development of the RSM occurred later than that of the two-equation mathematical model.45,46 It strictly considers streamline bending, vortex, rotation, and rapid changes in tension and has the potential to predict complex flows with higher accuracy.
The RSM model was selected for the turbulence calculation in this study, considering the accuracy and time cost of the simulation calculation.
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Discrete phase model (DPM)
The DPM is based on the Lagrange and Euler methods to simulate the fluid and particle phases.47–49 It uses the Euler method to describe the fluid motion and the Lagrange method to describe the particle motion. The DPM can also set different wall types for each wall and monitor the movement of oil droplets according to specific requirements. Therefore, the DPM was selected to simulate the oil droplet trajectory in the hydrocyclone oil removal device.
When the oil droplet moves in the device, it is mainly affected by the drag force FD caused by water, the additional mass force FV caused by the accelerated movement of water around the oil droplet, and the pressure gradient force FP generated by the pressure gradient in the flow field. The total force F is
| (10) |
| (11) |
Based on gravity, traction, pressure gradient force, and additional mass force received by the oil drop in the flow field, the motion equation trace of a single oil drop is as follows:
| (12) |
Eulerian model
Mixture and Eulerian models are suitable for mixing or separating multiphase flows. The Eulerian model treats each phase as a continuous phase full of the calculation area. The calculation accuracy of the Eulerian model is better than that of the mixture model considering the interaction between phases. The mixture model is suitable for applications in which the dispersed phase has a wide distribution, whereas the Euler model is suitable for applications in which the dispersed phase is concentrated in a certain region. Because oil droplets are mainly distributed along the axis when moving in a hydrocyclone, the Eulerian model was used to analyze the effect of inlet concentration on efficiency. The mass and momentum conservation equations of the model are as follows 50 :
| (13) |
| (14) |
| (15) |
Physical model and mesh discretization
Yang et al. 51 proposed a hydrocyclone oil removal device. Its structure is illustrated in Figure 1. The principle of oil–water auto-segregation of the device is the adoption of different flow paths because of the density difference between oil and water. Specifically, the oil–water mixed fluid flows spirally along the vortex section of the cylinder under the guidance of the tangential velocity after entering the device from the inlet. The fluid then descends under the action of gravity. When reaching the concentric reduction section, the oil moves toward the axis, and water moves toward the wall because of the shrinkage of the conical section and centrifugal force. When reaching the thin cone section, the small oil droplets converge along the axis to form an oil core because of the further contraction of the section and flow from the bottom of the device, whereas the water flows out of the water chamber.
Figure 1.
Hydrocyclone oil removal device (unit: mm).
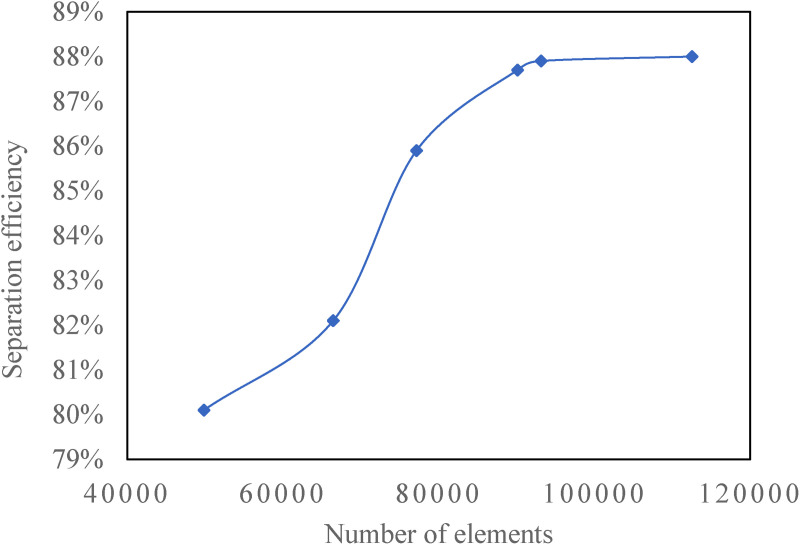
A mixed grid was used to divide the fluid model of the hydrocyclone oil-removal device, and the grids were densified and optimized. The network structure diagram is shown in Figure 2. In the verification of grid independence, the flow rate of the mixed fluid was 6 m/s, the oil droplet size was 30 um, and the oil content was 10%. For the calculation results, the separation efficiency was analyzed using six different numbers of elements. The number of elements was the independent variable, and the water outlet separation efficiency was the dependent variable, as shown in Figure 3. As shown in the figure, when the number of elements changed from 49846 to 112504, the separation efficiency increased rapidly. When the number of elements increased to 93132, the separation efficiency reached a stable state. Therefore, 93132 elements were used for the calculation grid. The Y + values for the various cases varied between 30 and 100.
Figure 2.
Mesh model.
Figure 3.
Mesh independence verification.
Boundary conditions and physical parameters
The RSM was used to simulate turbulence, and the DPM was used to simulate particle trajectories in the hydrocyclone oil removal device. The physical parameters of the fluid are listed in Table 1. The separation efficiency of the device was studied with inlet oil droplet diameters of 10, 20, 30, 40, 50, and 60 μm, oil droplet concentrations of 5%, 10%, 15%, 20%, 25%, and 30%, and droplet velocities of 2, 4, 6, 8, and 10 m/s.
Table 1.
Fluid physical parameters.
| Phase | Density | Viscosity |
|---|---|---|
| water | 1000 kg / m3 | 1 mPa·s |
| oil | 850 kg / m3 | 40 mPa·s |
Boundary conditions of water
The water and oil outlets were free outlets. All the walls of the hydrocyclone oil removal device were static and non-sliding. An unsteady calculation was performed. Oil droplets were introduced when the continuous-phase (water) flow field was stable.
Boundary conditions of oil droplet
An uncoupled calculation method was used. The effect of oil droplets on the water phase was ignored. First, a single jet source was selected to simulate the movement of the oil droplets. Three single jet sources with diameters of 20, 40, and 60 μm were set at the entrance. The entrance velocity of the oil drops was the same as that of water. The incident oil droplet coordinates were at the center of the entrance. Subsequently, the surface injection source was selected to investigate the relationship between the oil droplet size and separation efficiency. The inlet oil droplet sizes were set to 10, 20, 30, 40, 50, and 60 μm. The oil outlet of the device was set as a trap, the water outlet was set as an escape, and the wall was set as a reflection. The total number of captured oil droplets was determined after the simulation.
The pressure equation was discretized using PRESTO. The SIMPLE algorithm was used to couple pressure and velocity. A second-order upwind scheme was used for spatial discretization of the momentum, volume fraction, turbulent kinetic energy, dissipation rate, and Reynolds stresses. The convergence criteria for all the calculations were set so that the residual in the control volume for each equation was smaller than 10−5.
Validation
The separation efficiency of the oil–water mixture with an oil concentration of 10% was tested to verify the CFD simulation results. The density of the test oil was 850 kg/m3 and its viscosity was 40 mPa·s. The density of the water was 1000 kg/m 3 and its viscosity was 1 mPa·s. The oil was composed of diesel and crude oil. The inlet oil velocity was assumed to be equal to the water flow velocity during the experiments. The separation efficiencies at different flow rates are shown in Figure 4. The figure shows that the CFD simulation results are very close to the experimental values, and the error is within 5%, indicating that the CFD software can be used for the analysis and research of hydrocyclones.
Figure 4.
Comparison of simulated and experimental data of separation efficiency.
Results and discussions
Analysis of oil droplet trajectory
The separation of oil droplets can be observed directly by simulating the flow path of a single oil droplet in a hydrocyclone oil removal device. The trajectory of an oil droplet is highly complex and changes with its diameter. Simultaneously, an oil droplet is affected by randomness such as turbulent pulsation. Even if a unified oil droplet is released from the same position, its motion track can differ, as shown in Figures 5–7.
Figure 5.
Trajectory of 20 μm oil droplet in the hydrocyclone oil removal device.
Figure 7.
Trajectory of 60 μm oil droplet in the hydrocyclone oil removal device.
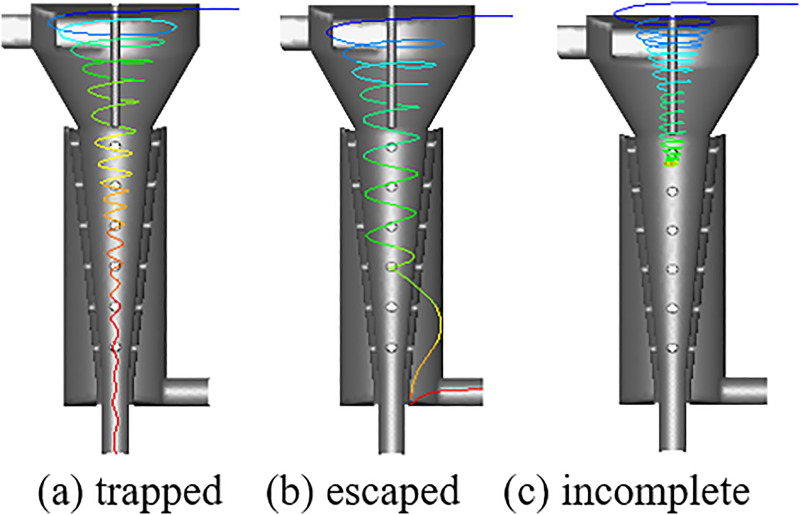
The oil droplets enter the outer swirling flow in the cylindrical section of the swirling field with the continuous phase water. Some oil droplets enter the inner swirl along the radial direction under the action of the fluid drag, inertial centrifugal force, and centripetal buoyancy force. Finally, they flow out through the oil outlet (Figures 5(a), 6(a), and 7(a)). Some oil droplets cannot flow into the inner swirl over time owing to the influence of turbulence pulsation and other factors and can only move from the diversion hole to the water outlet in the outer swirl (Figures 5(b), 6(b), and 7(b)). Some remain in the hydrocyclone (Figures 5(c), 6(c), and 7(c)) because the time required to enter the unit was too short to be separated.
Figure 6.
Trajectory of 40 μm oil droplet in the hydrocyclone oil removal device.
Figures 5–7 also present the influence of oil droplet size on the separation area. Generally, oil drops with a diameter of 60 μm can reach the internal swirl in the eddy current section of the cylinder. Oil drops with a diameter of 20 μm can reach the internal swirl only after flowing into the large cone segment or the upper part of the conic segment. For the separated oil droplets, the large oil droplets reach the inner swirl faster and shorter than the small oil droplets. If the oil droplet does not reach the inner swirl after flowing into the lower part of the conical segment, it would be difficult to separate. Even if it reaches the inner swirl in the lower part of the conic segment, the oil droplet may remain in the lower part of the conic segment and not flow out through the bottom because of the influences of the reduced swirl strength, weakened centrifugal force, turbulence, and other effects. If the droplet size is small, it may return to the outer swirl from the central area and flow out through the water outlet.
Effect of oil drop characteristics on separation efficiency
The separation efficiency is a key indicator of whether oil and water can be effectively separated. Several factors affect the separation efficiency of hydrocyclones. For the oil phase, the main factors are the particle size, speed, and concentration of oil droplets. Therefore, the following section discusses the impact of these three parameters on the separation efficiency of a hydrocyclone.
Oil droplet diameter
The oil-removal device was a hydrocyclone with a light-dispersed phase. The separation effect was measured based on separation efficiency. In this study, the separation efficiency of the device was expressed as the proportion of the volume flow of dispersed oil droplets at the water outlet to the volume flow of oil droplets at the inlet. Namely,
| (12) |
To simplify the calculation, a particle tracking method was used to calculate the oil separation efficiency. The oil droplets were tracked when they entered the oil–water separating device. The maximum tracking time step was set to 10,000 steps to ensure that the separated oil drops could flow out of the device for a long time. If the oil droplet reached the oil outlet, it was considered trapped, and the tracking was stopped. If the oil droplet reached the water outlet, it was considered to have escaped, and the tracking was stopped. If the oil droplet was neither trapped nor escaped within the set time step, the hydrocyclone oil removal device was considered unable to separate the oil droplet and tracking was stopped. Because of the random-track method, the number of oil droplets captured was slightly different when tracking oil droplets under the same working conditions. Oil droplet tracking was performed ten times under each working condition, and the average value was recorded.
Assuming that the number of oil droplets entering the hydrocyclone oil removal device with a particle size of di is ni and the maximum number of oil droplets captured with a diameter of di is nio, the classification efficiency E (di) and total separation efficiency Ea of the device can be expressed as follows:
| (13) |
| (14) |
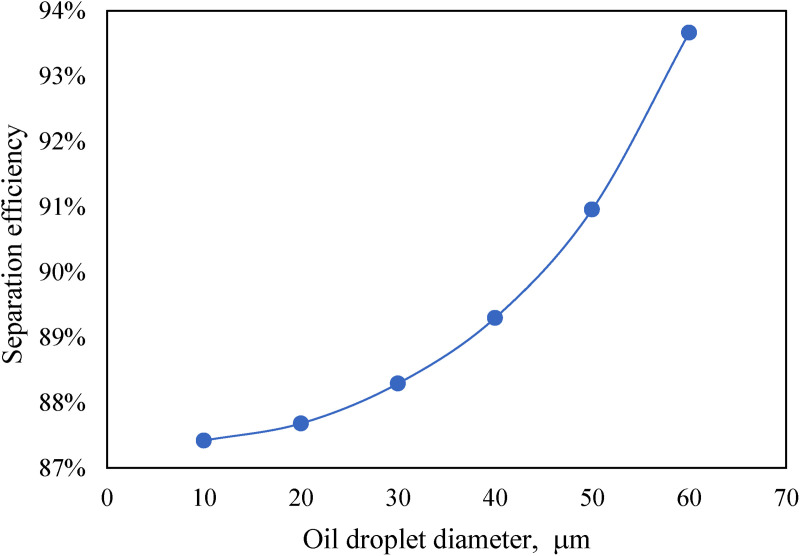
An oil–water mixture with the same flow rate, the same number of oil droplets, and different particle sizes were used for the simulation to evaluate the effect of oil droplet size on the separation performance of the oil removal device. The oil droplets were set as spherical particles without considering their deformation, polymerization, or fragmentation during the simulation. The simulation results are shown in Figure 8. The separation efficiency increased with increasing particle size. This is because the mass of oil droplets with large particle size is large, and the centrifugal force generated is greater at the same tangential velocity. Under the action of the centrifugal force, the oil droplets with large particle sizes were more likely to move toward the axis and gather in the axial area of the hydrocyclone oil removal device. Consequently, the probability of large-diameter oil droplets being captured by the bottom oil port was high; therefore, it provided a good separation effect. Oil droplets with small particle sizes were subjected to a small centrifugal force and were significantly affected by turbulent pulsation. They showed good follow-up to the continuous water phase. They entered the water chamber with the water phase from the diversion hole and then flowed out from the water outlet. Therefore, the separation effect was poor.
Figure 8.
Effect of oil droplet diameter on separation efficiency.
Oil droplet velocity
The velocity distribution of the fluid in the hydrocyclone oil removal device is shown in Figure 9. The axial velocity reflects the movement of the fluid toward the underflow port, as shown in Figure 9(a). The radial velocity represents the speed of fluid movement in the direction of the central axis, as shown in Figure 9(b). The greater the radial velocity, the faster the oil droplets migrate toward the central axis. The tangential velocity of the oil droplet is a key factor that affects whether the oil droplet can be effectively separated from the mixture. The larger the tangential velocity is, the greater the centrifugal force of the oil droplets and the easier their separation. If the tangential velocity is excessively low, the centrifugal force is too small to separate the oil from the wastewater. If the tangential velocity is too high, not only does the energy consumption of the oil removal device increase, but the oil droplets may also be broken into smaller droplets, and an emulsion phenomenon occurs, which reduces the separation efficiency. The tangential velocity distribution of the fluid flowing through the device is shown in Figure 9(c).
Figure 9.
a. Axial velocity (m/s). b. Radial velocity (m/s). c. Tangential velocity (m/s).
The velocity increased from the axis to the outside; however, the velocity near the wall of the hydrocyclone decreased. The reason for this phenomenon is that there was no relative sliding between the fluid and the wall of the hydrocyclone. The fluid velocity on the wall of the hydrocyclone was the same as that of the solid well, which is 0. The fluid velocity decreased gradually from top to bottom along the axis, and the highest velocity positions were in the cylindrical segment, large-cone segment, and upper part of the conic segment. This indicates that the oil–water separation mainly occurs at these three locations. Figure 9 also shows that the flow rate was negative near the outlet. This indicates that the direction of the flow rate changed because of the backflow of the fluid.
When studying the influence of the oil droplet speed on the separation efficiency, it was assumed that the oil droplet speed was the same as that of water. The calculation results are shown in Figure 10. The separation efficiency increases with an increase in the oil droplet speed with the same concentration of the mixed liquid. This occurs because an increase in the inlet fluid velocity results in an increase in the tangential velocity, and the centrifugal force and centrifugal effect of the fluid also increase. The liquid forms a vortex with high rotational speed in the hydrocyclone, and more small oil droplets can be separated from the mixed liquid. Thus, a high separation efficiency is obtained. When the inlet oil-droplet velocity reaches a certain value, a large amount of liquid quickly enters the oil-removal device. The liquid collides with the wall to produce an impact force that accelerates the rotation of the liquid. The oil droplets become smaller in particle size under the shear action of various external forces, which is not conducive to separation. Thus, the separation efficiency remains constant or even decreases.
Figure 10.
Effect of oil droplet inlet velocity on separation efficiency.
For oil droplets with the same velocity, the separation effect caused by a low concentration was better. For example, for a fluid with a flow rate of 2 m/s, the fluid separation efficiencies for the 15% and 5% fluids were 88.33% and 95.57%, respectively.
Oil droplet concentration
The droplet concentration is another parameter that has a significant influence on the separation efficiency. To study the effect of the oil concentration at the inlet on the separation efficiency, the distribution of oil droplets in the hydrocyclone oil removal device and the separation efficiency at different oil concentrations were simulated. The distribution of the oil-phase concentration is shown in Figure 11. The oil phase is primarily concentrated near the axis, whereas the water phase is primarily concentrated near the wall of the hydrocyclone. The mixture entering the hydrocyclone in the tangential direction rotates at a high speed, resulting in a vortex phenomenon. The difference in the densities of oil and water produces different centrifugal forces. The oil phase moves faster along the axis in the radial direction than the water phase. A stable oil core is eventually formed at the center of the hydrocyclone, and the oil droplets continue to move axially, as shown in Figure 12. Finally, most of the oil droplets flow out of the oil outlet and only a few enter the water chamber through the guide hole. The oil core decreases gradually from the cylinder eddy current section to the oil outlet, indicating that the separation effect of the oil droplets decreases gradually from the cylindrical segment to the lower half of the conical segment.
Figure 11.
Distribution of oil droplets.
Figure 12.
Oil core column.
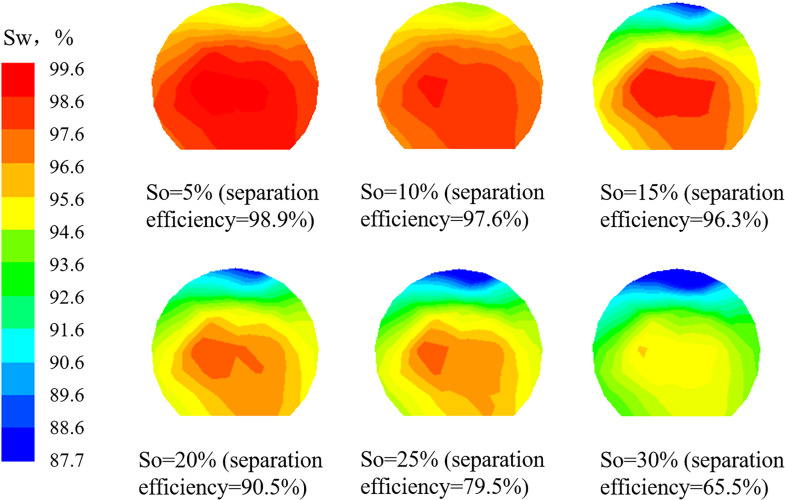
An inlet flow rate of 8 m/s was analyzed for the mixed liquids with different oil concentrations. The Eulerian model was used for the numerical calculations. The distribution of the water content at the water outlet, calculated using different concentrations, is shown in Figure 13. It can be observed from the figure that the oil concentration at the inlet is inversely proportional to the separation efficiency. As the oil concentration increases, the water content at the water outlet is obviously reduced and the corresponding separation efficiency gradually decreases. Therefore, one-time separation cannot achieve the purpose of separating a mixture with a high oil concentration. It is necessary to separate the mixed liquid several times to obtain satisfactory oil removal. The separation time can also be reduced by increasing the inlet velocity.
Figure 13.
Effect of inlet oil concentration on separation efficiency.
Conclusion
To compensate for the lack of research on the effect of dispersion on the separation efficiency in liquid–liquid hydrocyclones, the effects of oil droplet trajectory and droplet parameters on the separation efficiency of oil removal devices were considered using a CFD method. The DPM was applied to predict the oil droplet trajectory and the effect of oil droplet size on the separation efficiency. The Eulerian model was used to analyze the influence of oil droplet velocity and concentration on separation efficiency. The calculation results qualitatively and quantitatively illustrate the movement trajectory of the oil droplets in the hydrocyclone oil removal device and the influence of the oil droplet characteristics on the separation efficiency. The following conclusions were drawn:
Particle size affects the movement track of oil droplets in a hydrocyclone. Small oil droplets are significantly affected by turbulence pulsation; therefore, they remain in the hydrocyclone for a long time and are not easy to separate. The separation time can be reduced and the separation efficiency can be improved by increasing the particle size.
The tangential velocity is a key factor in the separation of oil droplets. Increasing the tangential velocity of the inlet can improve the separation efficiency; however, an increase in the tangential velocity will increase the energy consumption. An excessive tangential velocity may break the oil droplets into smaller droplets, thereby reducing the separation efficiency.
Oil droplets are mainly distributed along the axial center region of the hydrocyclone. The separation efficiency decreases with increasing oil concentration at the inlet. For oily wastewater with high oil content, the separation efficiency can be improved by multiple separations or the parallel use of hydrocyclones.
Glossary
Nomenclature
mean average velocity
- x
co-ordinates
mean average pressure
pulsating pressures i, j, k coordinate directions
- Dij
turbulent energy and molecular viscous diffusion
- Pij
shear stress generation
- Gij
buoyancy generation
- Φij
pressure strain
- εij
viscous discrete term
- Fij
system rotation generation
- μ
water viscosity
- Do
oil drop diameter
- ρ
density
- v
velocity
- vo
oil drop velocity
- t
time
pulsating velocity components
Reynolds stresses
- g
acceleration due to gravity
- θ
angle xk cartesian coordinate components
rotational angular velocity
- ε ikm, ε jkm
the Levi-Civita symbol
- m
mean
- CD
drag coefficient
- Re
relative Reynolds number
- mo
mass of single oil drop
- Qo
volume flow of oil droplets at the water outlet
- Qi
volume flow of oil droplets at the inlet
- α
volume fraction
- o, w
oil and water, respectively
- τ
shear stress
- CTD
turbulent dispersion coefficient
- FM
interphase momentum exchange or transfer term between the two phases
Author biographies
Mingjun Yang is a teacher of Sichuan University of Science and Engineering. She has studied water-control completion, water control device, separation machinery. She has published several papers on petroleum engineering. She holds BS, MS and PhD degrees from SWPU.
Rui Jiang is a teacher of Sichuan University of Science and Engineering. He has written and published several papers related to petroleum engineering. Jiang's research interests are well completion. He holds BS, MS and PhD degrees from SWPU.
Xinyuan Wu is a Senior Engineer at the Sichuan University of Science & Engineering. He has written and published several papers related to petroleum engineering. Wu's research interests are in Drill string mechanics, Development of Drilling and Completion Tools, Finite Element Simulation. He holds BS, MS, and PhD degrees from SWPU.
Yingchun Yue is a teacher at Mechanical Engineering institute of SUSE. His research interests include reservoir stimulation technique and new technology of oil production. He has published several papers on hydraulic fracturing, acidizing fracturing and fracturing completion. He holds BS, M.S., and Ph. D. degrees from SWPU, all in petroleum engineering.
Footnotes
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: This work was supported by the Science and Technology Department of Sichuan Province (grant numbers 2022NSFSC1154, 2021ZHCG0037, and 2020ZHCG0005).
ORCID iD: Mingjun Yang https://orcid.org/0000-0002-1986-2730
References
- 1.Gupta R, Kaulaskar MD, Kumar V, et al. Studies on the understanding mechanism of air core and vortex formation in a hydrocyclone. Chem Eng J 2008; 144: 153–166. [Google Scholar]
- 2.Zhou N, Gao Y, An Wet al. et al. Investigation of velocity field and oil distribution in an oil-water hydrocyclone using a particle dynamics analyzer. Chem Eng J 2010; 157: 73–79. [Google Scholar]
- 3.Hou D, Cui B, Zhang H, et al. Designing the hydrocyclone with flat bottom structure for weakening bypass effect. Powder Technol 2021; 394: 724–734. [Google Scholar]
- 4.Zhao L, Jiang M, Xu Bet al. et al. Development of a new type high-efficient inner-cone hydrocyclone. Chem Eng Res Des Trans Inst 2012; 90: 2129–2134. [Google Scholar]
- 5.Li Y, Liu C, Zhang T, et al. Experimental and numerical study of a hydrocyclone with the modification of geometrical structure. Can J Chem Eng 2018; 96: 2638–2649. [Google Scholar]
- 6.Liu M, Chen J, Cai X, et al. Oil–water pre-separation with a novel axial hydrocyclone. Chin J Chem Eng 2018; 26: 60–66. [Google Scholar]
- 7.Yang Q, Lv W, Shi Let al. et al. Treating methanol-to-olefin quench water by minihydrocyclone clarification and steam stripper purification. Chem Eng Technol 2015; 38: 547–552. [Google Scholar]
- 8.Bai Z, Wang H, Tu S. Dehydration of waste edible oil by hydrocyclones. Int J Green Energy 2009; 6: 184–191. [Google Scholar]
- 9.Silva DO, Vieira LGM, Barrozo MAS. Optimization of design and performance of solid-liquid separators: a thickener hydrocyclone. Chem Eng Technol 2015; 38: 319–326. [Google Scholar]
- 10.Kuang SB, Chu KW, Yu ABet al. et al. Numerical study of liquid-gas-solid flow in classifying hydrocyclones: effect of feed solids concentration. Miner Eng 2012; 31: 17–31. [Google Scholar]
- 11.Dehdarinejad E, Bayareh M. An overview of numerical simulations on gas-solid cyclone separators with tangential inlet. ChemBioEng Reviews 2021; 8: 375–391. [Google Scholar]
- 12.Dehdarinejad E, Bayareh M. Impact of non-uniform surface roughness on the erosion rate and performance of a cyclone separator. Chem Eng Sci 2022; 249: 117351. [Google Scholar]
- 13.Dehdarinejad E, Bayareh M, Ashrafizaadeh M. Impact of cone wall roughness on turbulence swirling flow in a cyclone separator. Chem Pap 2022; 76: 5579–5599. [Google Scholar]
- 14.Dehdarinejad E, Bayareh M. Performance improvement of a cyclone separator using spiral guide vanes with variable pitch length. J Braz Soc Mech Sci Eng 2022; 44: 1–19. [Google Scholar]
- 15.Zhang J, Meng XJ, Chen Get al. et al. Separation efficiency of gas-liquid cyclone separator in drilling fluid circular flow. Chem Eng(China) 2013; 41: 52–39. [Google Scholar]
- 16.Wang L, Zheng Z, Wu Y, et al. Numerical and experimental study on liquid-solid flow in a hydrocyclone. J Hydrodyn 2009; 21: 408–414. [Google Scholar]
- 17.Zhou H, Wang C, Wang Het al. et al. Eulerian-Lagrangian study of dense liquid-solid flow in an industrial-scale cylindrical hydrocyclone. Int J Miner Process 2016; 151: 40–50. [Google Scholar]
- 18.Zhao QG, Weiqing LI, Wei HE. Experimental study of pressure drop characteristics of a novel solid/liquid hydrocyclone. J Eng Thermophys 2010; 31: 61–63. doi: 10.3724/SP.J.1105.2010.10073. [DOI] [Google Scholar]
- 19.Qian P, Ma J, Liu Y, et al. Concentration distribution of droplets in a liquid-liquid hydrocyclone and ts application. Chem Eng Technol 2016; 39: 953–959. [Google Scholar]
- 20.Motin A, Bénard A. Design of liquid–liquid separation hydrocyclones using parabolic and hyperbolic swirl chambers for efficiency enhancement. Chem Eng Res Des 2017; 122: 184–197. [Google Scholar]
- 21.Zhang M, Zhang T, Wang Z, et al. Mixing and separation of liquid-liquid two-phase in a novel cyclone reactor of isobutane alkylation catalyzed by ionic liquid. Powder Technol 2017; 316: 289–295. [Google Scholar]
- 22.Schütz S, Gorbach G, Piesche M. Modeling fluid behavior and droplet interactions during liquid–liquid separation in hydrocyclones. Chem Eng Sci 2009; 64: 3935–3952. [Google Scholar]
- 23.Nascimento MRM, Bicalho IC, Mognon JL, et al. Performance of a new geometry of deoiling hydrocyclones: experiments and numerical simulations. Chem Eng Technol 2013; 36: 98–108. [Google Scholar]
- 24.Delfos R, Murphy S, Stanbridge D, et al. A design tool for optimising axial liquid–liquid hydrocyclones. Miner Eng 2004; 17: 721–731. [Google Scholar]
- 25.Liu Y, Lu H, Li Y, et al. A review of treatment technologies for produced water in offshore oil and gas fields. Sci Total Environ 2021a; 775: 145485. [DOI] [PubMed] [Google Scholar]
- 26.Lu H, Pan Z, Wang H, et al. Fiber coalescence treatment of oily wastewater: a new theory and application. J Hazard Mater 2021; 412: 125188. [DOI] [PubMed] [Google Scholar]
- 27.Liu Y, Li Y, Lu H, et al. A full-scale process for produced water treatment on offshore oilfield: reduction of organic pollutants dominated by hydrocarbons. J Cleaner Prod 2021: 296. Doi: 10.1016/j.jclepro.2021.126511 [DOI] [Google Scholar]
- 28.Montesantos N, Fini MN, Muff Jet al. et al. Proof of concept of hydrothermal oxidation for treatment of triazine-based spent and unspent h2 s scavengers from offshore oil and gas production. Chem Eng J 2022: 427. Doi: 10.1016/j.cej.2021.131020 [DOI] [Google Scholar]
- 29.Durdevic P, Yang Z. Dynamic efficiency analysis of an off-shore hydrocyclone system, subjected to a conventional pid- and robust-control-solution. Energies 2018; 11: 2379. [Google Scholar]
- 30.Wang LY, Zheng ZC, Guo J, et al. Investigation on separation efficiency of liquid/solid hydrocyclone. J Hydrodyn 2006; 18: 391–395. [Google Scholar]
- 31.Husveg T, Johansen O, Bilstad T. Operational control of hydrocyclones during variable produced water flow rates—fry case study. SPE Prod Oper 2007; 22: 294–300. [Google Scholar]
- 32.Noroozi S, Hashemabadi SH, Chamkha AJ. Numerical analysis of drops coalescence and breakage effects on de-oiling hydrocyclone performance. Sep Sci Technol 2013; 48: 991–1002. [Google Scholar]
- 33.Banerjee C, Chaudhury K, Majumder AKet al. et al. Swirling flow hydrodynamics in hydrocyclone. Ind Eng Chem Res 2015; 54: 522–528. [Google Scholar]
- 34.Liu L, Zhao LX, Liu HX, et al. Numerical simulation analysis of flow field characteristics for overflow-circle hydrocyclone. Chem Eng(China) 2017; 45: 48–53. [Google Scholar]
- 35.Knudsen BL, Bjørkhaug M, Johannesen B, et al. Field test of compact cyclonic technology for separation of gas/liquid and oil/water at the gullfaks field. In: Offshore Technology Conference, Houston, Texas, USA, May 2010; OTC 20748. doi: 10.4043/20748-MS. [DOI] [Google Scholar]
- 36.Bjørkhaug M, Johannesen B, Eidsmo GS. Flow induced inline separation(FIIS) de-watering tests at the gullfaks field. In: SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA, October 2011;SPE 146688. Doi: 10.2118/146688-MS. [DOI] [Google Scholar]
- 37.Westra RW, Knudsen BL, Bjartnes Het al. et al. Qualification of inline dewatering technology. In: SPE Offshore Europe Oil and Gas Conference and Exhibition, Aberdeen, UK, September 2013; SPE 166644. Doi: 10.2118/166644-MS. [DOI] [Google Scholar]
- 38.Tian J, Ni L, Song T, et al. Numerical study of foulant-water separation using hydrocyclones enhanced by reflux device: effect of underflow pipe diameter. Sep Purif Technol 2019; 215: 10–24. [Google Scholar]
- 39.Jiang L, Liu P, Yang X, et al. Effect of overflow pipe on the internal flow fields and separation performance of w-shaped hydrocyclones. Minerals 2020; 10: 29. [Google Scholar]
- 40.Huang L, Deng S, Guan J, et al. Separation performance of a novel liquid-liquid dynamic hydrocyclone. Ind Eng Chem Res 2018; 57: 7613–7623. [Google Scholar]
- 41.Vakamalla TR, Mangadoddy N. Numerical simulation of industrial hydrocyclones performance: role of turbulence modelling. Sep Purif Technol 2017; 176: 23–39. [Google Scholar]
- 42.Gomez JD. Doctoral Dissertation. In: Modelling of 75- and 250-mm hydrocyclones and exploration of novel designs using computational fluid dynamics. Utah, United States of America: The University of Utah, 2006. [Google Scholar]
- 43.Ghodrat M, Qi Z, Kuang SB, et al. Computational investigation of the effect of particle density on the multiphase flows and performance of hydrocyclone. Miner Eng 2016; 90: 55–69. [Google Scholar]
- 44.Jiang L, Liu P, Yang X, et al. Numerical analysis of flow field and separation characteristics in hydrocyclones with adjustable apex. Powder Technol 2019; 356: 941–956. [Google Scholar]
- 45.Sonawane U, Agarwal AK. Computational investigations of spray atomization and evaporation under cold-start conditions of a diesel engine. J Energy Res Technol 2022; 144: 112305. [Google Scholar]
- 46.Nourin FN, Blum BL, Amano RS. Evaluation of heat transfer enhancement on rotational gas turbine blade internal cooling channel with dimpled surface. J Energy Res Technol 2022; 144. doi: 10.1115/1.4054288 [DOI] [Google Scholar]
- 47.Sun W, Zhong W, Zhang Jet al. et al. Large eddy simulation on the effects of coal particles size on turbulent combustion characteristics and NO x formation inside a corner-fired furnace. J Energy Res Technol 2021; 143: 082302. [Google Scholar]
- 48.He Y, Xu Y, Tang Y, et al. Multi-phase rate transient behaviors of the multi-fractured horizontal well with complex fracture networks. J Energy Res Technol 2022; 144: 043006. [Google Scholar]
- 49.Shi X, Qian W, Liao Y, et al. Experimental and simulation analysis on spray characteristics of hydrous ethanol–gasoline blends. J Energy Res Technol 2022; 144: 112302. [Google Scholar]
- 50.Taghipour F, Ellis N, Wong C. Experimental and computational study of gas–solid fluidized bed hydrodynamics. Chem Eng Sci 2005; 60: 6857–6867. [Google Scholar]
- 51.Yang M, Jiang R, Wu X, et al. Numerical analysis of flow field and separation characteristics in an oilfield sewage separation device. Adv Powder Technol 2021; 32: 771–778. [Google Scholar]