Abstract
Rubber is the key component of a compression packer, which directly affects the success or failure of seals. Presently, the contact stress between the rubber and borehole walls is used as the main evaluation criterion for the sealing ability of the rubber of the compression packer. However, this evaluation criterion is imperfect. This study establishes the sealing performance and reliability evaluation system of a compression packer at 120°C. Considering the influence of time and temperature on the mechanical characteristics of rubber materials, the international advanced test technology was used to complete the uniaxial, planar and biaxial tensile tests and stress relaxation test for hydrogenated nitrile butadiene rubber (HNBR) of a compression packer under high temperature. Next, the hyperelastic and viscoelastic constitutive models of rubber materials based on high-temperature test data were established. Comprehensive sealing performance and reliability evaluation system for the compression packer rubber with compression rate, linear pressure, surface pressure and sealing performance coefficient were proposed. The evaluation system tested the rubber's stress relaxation effect on the rubber's sealing performance. The establishment of the evaluation system improved the shortcomings of the current packer-sealing performance evaluation system and provided a theoretical basis for the design and optimisation of the key structure of the packer-sealing system. Besides, based on the evaluation system, a platform for automatic structure simulation analysis and optimisation design of packer sealing system was developed and successfully applied to the actual design and optimisation process of packer. The system can effectively predict the sealing ability of the packer and guide field applications of the packer.
Keywords: compression packer, sealing performance, evaluation system, high-temperature test, stress relaxation, reliability
Introduction
Packers are important downhole tools in oil exploration and development. They are often used in drilling, water injection, water blocking and stratified oil production. 1 When it reaches the working position, packer rubber is axial compressed by setting pressure, comes into contact with the pipe wall or the open-hole wall to form a sealing annulus and divide the well. As the core-sealing component of the packer, the sealing performance of the rubber directly affects the sealing ability of the packer and oil and gas exploitation profits. 2 Therefore, improving the sealing performance of the packers has become a key research topic recently. Presently, improving the mechanical properties of the rubber material of the packer and structure of the rubber is the main ways to improve the sealing performance of the packer.
As sealing materials, rubber is soft, highly stretchable and elastic. 3 However, because of the different field requirements of the actual working conditions, rubber-sealing components often face extremely harsh working conditions, causing changes in the mechanical properties of the rubber materials, resulting in the failure of the sealing element. Therefore, to improve the mechanical properties of rubber materials, extensive experimental studies have been carried out. Hitchcock 4 indicated that the HNBR sample with carbon black filling had better compression resistance by normal and high-temperature uniaxial compressive tests. He 5 also found that the material strength increases as the carbon black filler content in the rubber material increases. Pervez 6 pointed out that prolonged exposure to sunlight and moisture reduced the flexibility and expansion capacity of the elastomers. In addition, studies have shown that if the rubber was in a corrosive medium for a long time, its tensile properties, hardness and sealing performance would be greatly affected.7–9 Ahmed 10 put forward that the sealing performance of EPDM and NBR would reduce when a mechanical defect was intentionally created and after exposure to carbon dioxide. Qamar 11 studied the mechanical properties of elastomers in different salinity solutions for self-expanding packers used in an oil field and found that the elastic and shear moduli of the rubber materials decreased by more than 90% in the first few days. Akhtar12,13 performed a one-month swelling test on the packer rubber sample and found that the contact pressure ( ) increased with the expansion of the rubber and that swelling in low-salinity brine produced higher .
However, it is difficult to simulate the complex downhole conditions by conventional test method. With the rapid development of computer technology, numerical simulation technology is more and more used in the study of rubber sealing performance. Li and Zhang13,14 analysed the sealing behaviour of the packer under sealed condition using the finite element (FE) software. The between the rubber and the well wall was used as an evaluation index of the sealing ability of the packer. Qu 15 studied the friction coefficient influence between the rubber and the well wall on the sealing performance of the packer. The results showed that the radial friction strongly influenced the sealing performance and that the fracturing of the sealing element could be avoided by reducing the surface friction coefficient. Li 16 used the strain gauge to investigate the circumferential strain of the casing wall and obtained the distribution of the casing along the axial direction. The result showed that the uniformity of the contact stress distribution of the packer rubber increased, and that the sealing effect was better under wet friction conditions. Hu 17 experimentally optimised the constitutive model of rubber materials and proposed evaluating the sealing performance of rubber with the maximum von Mises stress. Hu 18 and Ahmed 19 compared the visual experimental device results with the simulation results and obtained the relationship between the compressive deformation of rubber and the sealing performance.
Although extensive research activities have been conducted to improve the sealing performance of rubber and many outcomes have been achieved, the evaluation method of sealing performance used in numerical simulation lacks perfection yet. Hence, based on previous studies, this work proposes a rubber sealing performance evaluation system of a packer based on four parameters: compression rate, line pressure, surface pressure and sealing performance coefficient (K). In order to obtain exact hyperelastic constitutive model parameters of rubber, uniaxial tension test, planar tension test and equal biaxial tension test were conducted by samples. The stress relaxation behaviour of the rubber sample at high temperature was then added to consider. Then, numerical simulation analysis was used to evaluate the sealing performance of the packer. It provides a theoretical basis for the design of packer seal structure and field application.
Material tests
Hyperelastic constitutive model test
Study of the hyperelastic constitutive model of rubber materials mainly includes studying the elastic statistical theory, finite strain elastic theory and strain–energy function, and the strain–energy function is mostly used to describe the hyperelastic characteristics of rubber.20–22
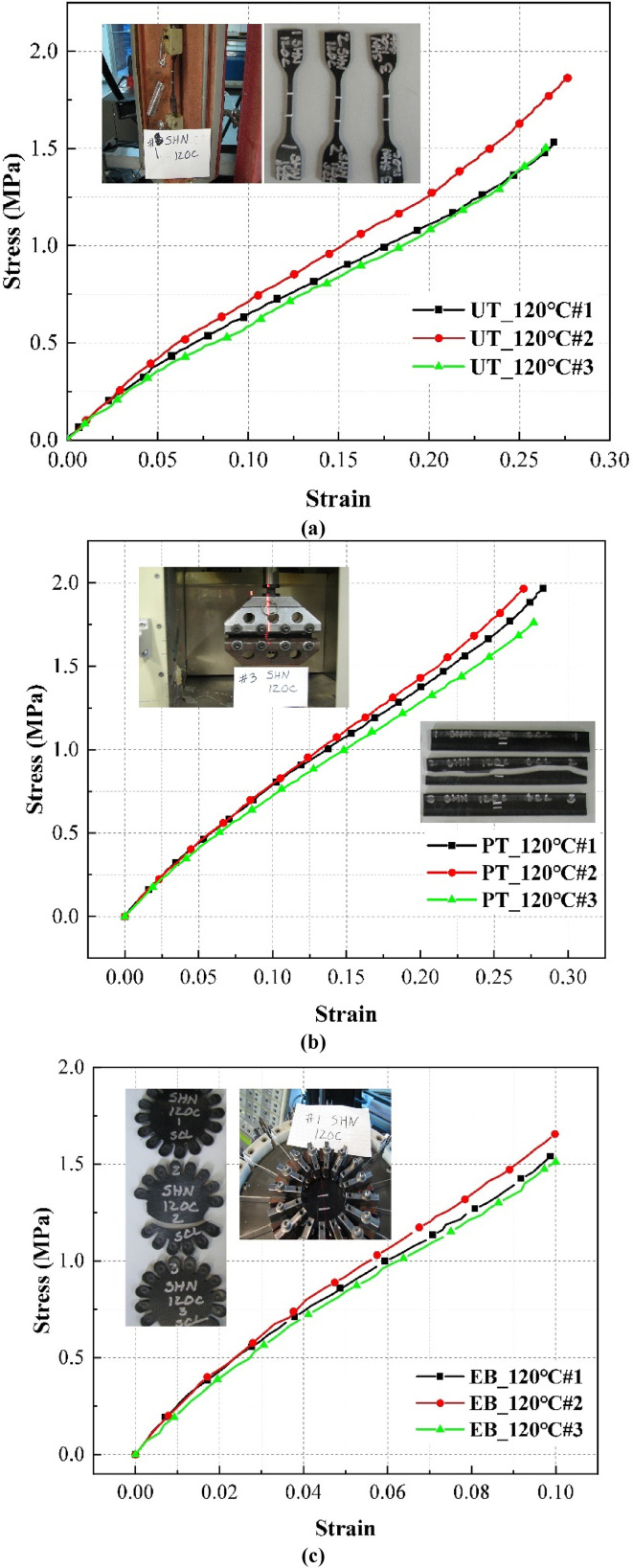
Therefore, the stress-strain data, tested by uniaxial tension test, planer tension test and equal biaxial tension test of HNBR samples at working temperature (120°C), was used to fit the parameters of rubber hyperelastic constitutive model, as shown in the Figure 1. In order to obtain accurately test data, all samples were prepared strictly according to the requirements of ATSM D412 23 and Abaqus. A contactless laser strain sensor was used to reduce the measuring error.
Figure 1.
(A) uniaxial tension test of HNBR samples at 120 °C; (b) planar tension test of HNBR samples at 120 °C; (c) equal biaxial tensile tests of HNBR samples at 120 °C.
The Mooney–Rivlin, Yoeh and Neo-Hookean models are the most used constitutive models of rubber materials based on the strain–energy function. 18 Based on the stress-strain relationship, the strain energy density function W of rubber can be described as
| (1) |
| (2) |
| (3) |
| (4) |
Usually, rubber is assumed to be isotropic and incompressible hyperelastic material, so that
| (5) |
When rubber is in the state of pure tension or pure shear, the value of approaching to zero.24,25 Therefore, the strain energy density function W of Mooney Rivlin (N = 2) constitutive model can be deduced 20
| (6) |
The strain energy density function W of Yoeh (N = 3) constitutive model can be deduced 25
| (7) |
And, the strain energy density function W of Neo-HooKean (N = 1) constitutive model can be deduced 26
| (8) |
The experimental data were fitted to the Mooney–Rivlin, Yoeh and Neo-Hookean constitutive models using the least-squares method (Figure 2). The strain rate of the packer rubber under the working conditions was 24%, which belongs to the small strain category. Thus, the Mooney–Rivlin constitutive model was selected as the constitutive model for subsequent numerical analysis combined with the fitting curve. Tables 1–3 listed the parameters of the fitting constitutive model.
Figure 2.
Fitting curve of the test data and constitutive model: (a) UT; (b) PT; (c) EB.
Table 1.
Fitting parameters of the Mooney–Rivlin constitutive model.
| C01 | C10 |
|---|---|
| 0.22 | 1.03 |
Table 2.
Fitting parameters of the Neo-Hookean constitutive model.
| C01 | C10 |
|---|---|
| 1.21 | / |
Table 3.
Fitting parameters of the Yoeh constitutive model.
| C10 | C20 | C30 |
|---|---|---|
| 1.40 | −2.23 | 5.30 |
Stress relaxation test
Rubber is a typical viscoelastic material with solid elasticity and liquid viscosity characteristics. Stress relaxation and creep are the main manifestations of viscoelastic properties of rubber. The conventional Maxwell model only describes a short relaxation time, however, the mechanical relaxation process of rubber has a complex relaxation time spectrum comprising multiple relaxation times. 27 Therefore, a generalised Maxwell (GM) model with multiple element combinations must simulate the stress relaxation phenomenon of the rubber material (Figure 3).
Figure 3.
Schematic of a GM model.
Based on previous research results, the energy storage model and dissipation model of a GM model are established. 27 The Prony series equation of a GM model is shown as follows: 28
| (9) |
| (10) |
Three HNBR samples were heated to 120°C in a temperature chamber. Then, the strain level of sample was stretched to 25% by universal electronic material testing machine. Keeping the strain level invariant, the relaxation curve of samples during 2000 s is shown in Figure 4.
Figure 4.
The stress relaxation curve of samples during 2000s.
Figure 5 shows the fitting curve of the generalised Maxwell model of the HNBR sample at 120 °C and the stress relaxation test data.
Figure 5.
Fitting curve of the stress relaxation test data and generalised Maxwell model of the HNBR sample at 120 °C.
From Figure 5, the determination coefficient of the fitting curve is 0.99947, approximately 1, indicating that the fitting results meet the requirements and can be used to simulate the stress relaxation phenomenon of HNBR. The Prony equations are used for parameterisation for the numerical analysis, and relevant parameters are listed in Table 4.
Table 4.
Fitting parameters of HNBR stress relaxation.
| gi | ki | τi |
|---|---|---|
| 0.033635 | 0 | 1.28918 |
| 0.05112 | 0 | 14.26533 |
| 0.070733 | 0 | 144.0569 |
| 0.088738 | 0 | 1860.04 |
Establishment of the FE analysis (FEA) model
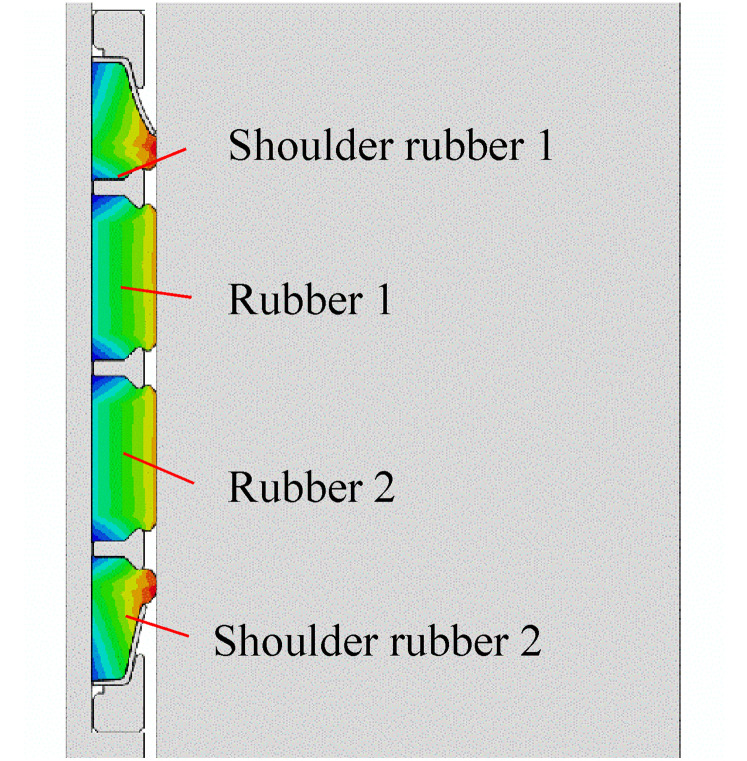
Y344 series packer is a kind of unsupported recoverable hydraulic packer that rely on hydraulic setting. The sealing part of the Y344 compression packer mainly comprises of four shoulder and four sealing rubbers. The rubber is compressed by the pressure of the pipe string or hydraulic load, forming a ring seal with the shaft wall (Figure 6).
Figure 6.
Y344 compression packer.
Herein, the sealing ability of the rubber was studied by ABAQUS software. In order to make the simulation model more targeted and scientific, there were some necessary assumptions carried out:
It was assumed that both the compression packer and open-hole wall were regular and uniform, so that it was feasible to simplify the model of packer into a two-dimensional axisymmetric model.
It was assumed that rubber was incompressible.
It was assumed that all the materials used in the model were homogeneous and isotropic.
So a simplified two-dimensional axisymmetric FEA model was established to improve the calculation efficiency and the analysis precision. The analysis model only contained the parts affecting the sealing pressure between the rubber and the open-hole wall, including the pressure cap, protective cap, shoulder rubber, spacer ring, rubber, centre tube and open-hole wall. The friction coefficient between the rubber and metal parts was 0.3, and the friction coefficient between the metal surfaces was 0.1. A working pressure difference of 14 MPa was applied in the axial direction and an 8 MPa internal and external pressure difference was applied to the inner wall of the central pipe (Figure 7).
Figure 7.
Total deformation of the sealant after applying pressure loads.
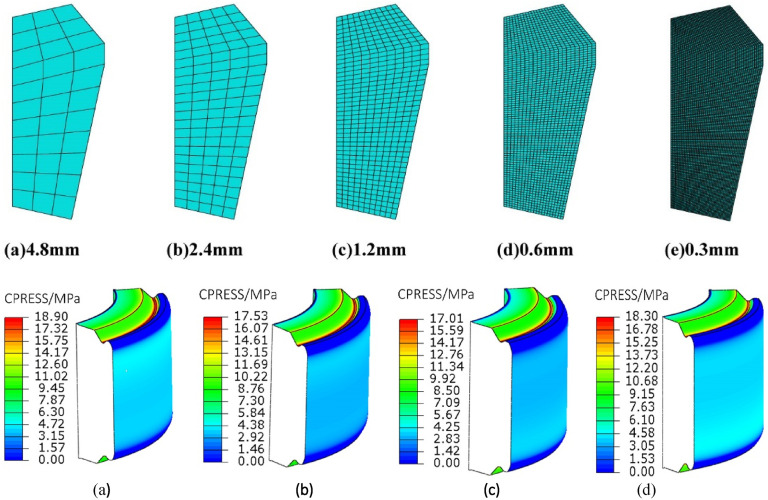
The setting process of the packer was stable and slow, which could be considered as a quasi-static process. So that the implicit solver of ABAQUS was used in this study. Due to rubber was a large deformation material, the CAX4H was used for mesh division of rubber, while the CAX4R and CAX3R were used for mesh division of the other components. Shoulder rubber 1 was taken as an example to carry out mesh sensitivity analysis (As it was showed in Figure 8). It was generally believed that when the deviation of the calculation results caused by the mesh is less than 5%, the convergence of the mesh was acceptable, and further refinement of the mesh on this basis would reduce the computational efficiency of the model. The finite element results showed that when the seed size was 0.6 mm, the computational results of the model meet the convergence requirements and the computational efficiency was the highest.
Figure 8.
Mesh division of shoulder rubber 1 with different seed size: (a) The default seed size was 4.8 mm; (b) The seed size was 2.4 mm; (c) The seed size was 1.2 mm; (d) The seed size was 0.6 mm; (e) The seed size was 0.3 mm.
In addition, owing to the hardness of open-hole wall was much bigger than rubber, it was considered as the rigid body. And mechanical parameters of the other packer components were listed in Table 5.
Table 5.
The mechanical parameters of the other packer components.
| Components | Materials | Passion ratio | Young's module/MPa |
|---|---|---|---|
| Pressure cap | 35CrMo | 0.286 | 213000 |
| Protect cap | T3 | 0.35 | 97625 |
| Space ring | 35CrMo | 0.286 | 213000 |
| Centre tube | 35CrMo | 0.286 | 213000 |
Evaluation system of the sealing performance of the packer rubber
The sealing performance of the packer directly determines the overall performance of the packer. The small and less contact between the rubber cylinder and the well wall, resulting in a liquid penetration, are common failure factors of the compression packer. Figure 8 shows the contact stress distribution states of rubber tubes 1–4 in the setting state. Due to the shoulder axon and stress concentration, the contact stress between the rubber and spacer ring increases significantly but does not contact the well wall. Figure 9 shows the state of the contact stress distribution with the wellbore after removing the shoulder axons and stress concentration. However, it is incomprehensive to evaluate the sealing performance of the packer only using contact stress. Therefore, to comprehensively evaluate the sealing performance and reliability of the packer-sealing system, the compression ratio (N), line pressure, surface pressure and sealing coefficient (K) are proposed based on the contact stress.
Figure 9.
Contact stress distribution between the rubber and well wall: rubbers (a) 1, (b) 2, (c) 3 and (d) 4.
(1) Compression ratio (N)
N is the ratio of the axial compression amount of the packer cylinder to the initial length of the rubber under normal working conditions.
| (11) |
Here, L0 is the initial axial length of rubber and L1 is the axial length of rubber after compression.
N is used to evaluate the seal performance and structural strength of the packer. The contact stress increases as N increases, and the structural strength decreases as the seal performance increases. Table 6 lists the N values of the packer.
Table 6.
Compression ratio of different rubbers.
| Components | Initial length/mm | Length after compression (mm) | Compression ratio (%) |
|---|---|---|---|
| Rubber 1 | 84 | 62.92 | 25.10 |
| Rubber 2 | 84 | 63.12 | 24.86 |
| Rubber 3 | 84 | 63.11 | 24.87 |
| Rubber 4 | 84 | 62.94 | 25.07 |
(2) Closed sealing curve (CSC)
The sealing surface between the packer rubber and the open-hole wall is actually a combination of many closed circular curves which is named closed sealing curve (CSC) in this paper (as shown in Figure 10.a). The value of maximum contact pressure of CSC indicates the ultimate sealing capacity between the packer rubber and the well wall.
Figure 10.
(a) Closed sealing curve; (b) Closed contact surface;(c) The contact pressure distribution of closed contact surface.
(3) Closed contact surface (CCS)
The closed contact surface (CCS) is contributed by an infinite number of closed sealing curves (Figure 10.b). Due to the distribution of contact pressure on the closed contact surface is not uniform (as shown in Figure 10.c), it is analysed and studied in section. What's more, the is the maximum contact stress on the contact surface.
The contact pressures of CSC and CCS are used to evaluate the sealability and reliability of the packer rubber structure, respectively. The structural sealability increases as the contact pressure of CSC increases. Similarly, the seal reliability increases as the contact pressure of CCS increases. The contact pressure of CSC and CCS ensures the sealed state of the packer.
In the two-dimensional axisymmetric model, the contact pressures of CSC and CCS are the contact pressure of a point and a line on the contact areas, respectively. The effective contact pressure and length describe the pressure effect of CCS. In the condition of the same effective contact stress, the sealing reliability increases as the effective contact length ( ) increases. Table 7 lists the contact pressure of CSC and CCS of different rubbers under working conditions.
Table 7.
Statistics of contact pressure of CSC and CCS of different rubbers.
| Components | Maximum contact pressure of CSC (MPa) | Contact pressure of CCS | |
|---|---|---|---|
| Effective contact pressure (MPa) | Effective contact length ( , mm) | ||
| Rubber 1 | 4.64 | ≥ 4 | 37.27 |
| ≥ 3 | 45.05 | ||
| ≥ 2 | 46.90 | ||
| Rubber 2 | 3.67 | ≥ 4 | - |
| ≥ 3 | 39.63 | ||
| ≥ 2 | 44.73 | ||
| Rubber 3 | 3.67 | ≥ 4 | - |
| ≥ 3 | 40.17 | ||
| ≥ 2 | 44.73 | ||
| Rubber 4 | 4.63 | ≥ 4 | 37.23 |
| ≥ 3 | 44.43 | ||
| ≥ 2 | 46.26 | ||
| ≥ 3 | 5.33 | ||
| ≥ 2 | 6.67 | ||
(4) Sealing coefficient (K)
The sealing coefficient K is an integral of contact pressure along the contact path. Since the contact between the packer rubber and the open-hole wall isn't necessarily continues, the equation for K can be derived as illustrated in Figure 10.c.
| (12) |
K is a comprehensive index for evaluating the sealability and reliability of the packer structure. The sealing performance increases as K increases. Table 8 lists the value of K of each rubber.
Table 8.
K values of each rubber of the packer.
| Components | Sealing coefficient K(MPa·mm) |
|---|---|
| Rubber 1 | 192.58 |
| Rubber 2 | 148.12 |
| Rubber 3 | 147.98 |
| Rubber 4 | 192.37 |
According to the symmetry principle of the packer geometry model and the loading form, the K values of rubber 1 and 2 should be close to that of rubbers 4 and 3, respectively. The same conclusion can be drawn from Table 5. Besides, Table 5 indicates that the sealing performances of rubbers 1 and 4 are superior to that of rubber 2 and 3, respectively.
Results and discussion
Due to the temperature and time dependence of the mechanical properties of the rubber material, the influence of the stress relaxation phenomenon of rubber materials on its sealing performance under working conditions for a long time and at high temperature is simulated. As shown in Figure 11, the packer is in a critical setting, working temperature and pressure of 120 °C and 14 MPa, respectively. Compared with the stress relaxation behaviour of the rubber material, the packer setting is transient, and thus the between the surface of the rubber and well wall reaches the maximum, and the sealing performance is optimal.
Figure 11.
Critical state of the setting.
After setting the packer, the stress relaxation behaviour of the rubber is simulated. Figures 12 and 13 show the changes in the contact stress of the shoulder rubber 1 and rubber 1 before and after stress relaxation.
Figure 12.
Changes in contact stress before and after stress relaxation between shoulder rubber 1 and the well wall: (a) before stress relaxation and (b) after stress relaxation.
Figure 13.
Changes in contact stress before and after stress relaxation between rubber 1 and the well wall: (a) before stress relaxation and (b) after stress relaxation.
The main functions of the end rubber cartridge are shoulder-protrusion prevention and protection of the seal rubber. However, it also has a weak sealing ability. Figures 12 and 13 show that the contact stress between the shoulder rubber 1 and the well wall is relatively small, 4.19 and 3.40 MPa before and after relaxation, respectively, with an 18.9% decrement rate. The contact stress between rubber 1 and the well wall decreased from 6.43 to 5.22 MPa after relaxation, with an 18.9% decrement rate. Both the contact stress of the shoulder rubber 1 and rubber 1 significantly reduced after the stress relaxation behaviour, affecting the sealing performance of the rubber (Figure 14).
Figure 14.
Change curves of contact stress of shoulder rubber 1 and rubber 1 before and after stress relaxation.
Figure 15 shows that the stress relaxation phenomenon causes the value of the maximum contact stress point of the shoulder rubber and the rubber to exhibit a downward trend like a logarithmic function. The downward trend is evident in the initial period, and the slope of the rear curve decreases and tends to stabilise over a long period. Table 9 lists the specific rate of change.
Figure 15.
Relaxation of the maximum contact stress point of the shoulder rubber and rubber.
Table 9.
Maximum contact stress change rate before and after the end of the rubber tube and barrel.
| Components | Contact stress (MPa) | |||
|---|---|---|---|---|
| Before relaxation | After relaxation | Change rate | ||
| Shoulder rubber 1 | 4.19 | 3.40 | 18.85% | |
| Rubber 1 | 6.43 | 5.22 | 18.82% | |
| Rubber 2 | 5.05 | 4.12 | 18.42% | |
| Shoulder rubber 2 | 1.09 | 0.91 | 16.51% | |
The maximum contact stress of the shoulder rubber and rubber changes before and after relaxation, and the rate of change exceeds 15%. The maximum contact stress between the shoulder rubber and the well wall and between the rubber and the well wall is reduced significantly by the stress relaxation, which significantly affects the sealing performance of the whole packer structure.
As shown in Figures 16–19, the stress relaxation property of HNBR reduces the line pressure of the packer. The line pressure influence of the rubber is > that of the shoulder rubber. When the surface pressure is ≥ 4 MPa, the stress relaxation property of the HNBR greatly influences the surface pressure, reducing the pressure of the packer rubber by 46.28%. When the surface pressure is ≥ 3 MPa, the stress relaxation of the HNBR rubber negligibly affects the surface pressure, reducing the pressure of the packer rubber by 6.70%. The stress relaxation property of the HNBR rubber significantly affects K, decreasing it by 18.09%. Thus, when considering the sealing performance of the packer, the stress relaxation effect on the sealing performance of the rubber should also be considered.
Figure 16.
Influence of stress relaxation on the line pressure.
Figure 17.
Influence of stress relaxation on the surface pressure (≥ 4 MPa).
Figure 18.
Influence of stress relaxation on the surface pressure (≥ 3 MPa).
Figure 19.
Influence of stress relaxation on K.
According to the above simulation results, rubber stress relaxation at high temperature will greatly reduce the sealing performance of packer rubber. Therefore, when designing the packer, the stress relaxation of the rubber material should be considered, and a stress relaxation safety factor should be set to ensure the reliability of the rubber seal.
In addition, the contact between the packer rubber and the borehole wall may actually be discontinuous, which cannot be described by the traditional single-value contact stress evaluation method. However,the sealing performance coefficient K proposed in this paper is the sum of the integral of multiple contact areas, which can perfectly describe the discontinuous contact state between the rubber and the borehole wall. What's more, it is more diversified to evaluate the sealing performance of rubber from the contact path, contact stress and contact area.
Application
Based on the new evaluation method of packer rubber sealing performance proposed in this paper, the multi-objective optimisation, process integration and knowledge encapsulation were used to develop Automation Structure Simulation Analysis and Optimisation Design Platform of Packer Sealing System, which not only help design engineers could quickly finish the simulation analysis and optimisation design for packer sealing system which greatly reduced technic threshold because only professional CAE engineers could do in the past, but also improved consistency and reliability of product design and analysis, improved product quality and efficiency and reduced the product cost.
The process call and intermediate data is encapsulated in front-end programme. Users can set calculation parameters in the form of web pages and send to the server for calculation. After the calculation, the web client is displayed to the user, which greatly reduces the user's work and improves the work efficiency. The login interface is illustrated in Figure 20 (a). After selecting the appropriate packer type, the packer rubber parameters are optimised (Figure 20(b)). The background programme is called for finite element analysis, and the evaluation method proposed in this paper was used to analyze and compare the sealing performance of different structures, as showed in Figure 20(c). This evaluation system has been used for the actual design and production of packers. According to the feedback from Daluhu oilfield, the sealing capacity of the packer rubber optimised by the platform is higher than 30% higher than that without the platform optimised design.
Figure 20.
Automation structure simulation analysis and optimization design platform of packer sealing system:(a) login interface;(b) structure optimisation of packer rubber;(c) evaluation and comparison of sealing performance.
Conclusions
The working performance of the packer-sealing system was studied in this work. Considering the temperature and time characteristics of the mechanical behaviour of the rubber material, the uniaxial, planar and biaxial tensile tests and stress relaxation tests were conducted on the HNBR material of the packer at high temperature. All tests were completed using an international advanced experiment facility and experimental methods. Furthermore, the hyperelastic and viscoelastic constitutive models of rubber materials based on high-temperature test data were established. Based on the highly nonlinear mechanical behaviour of the packer-sealing system, an FEA method for the packer-sealing system was established. The compression ratio, line pressure, surface pressure and sealing coefficient, as the index for evaluating the packer's sealing performance and reliability, were proposed. The evaluation system was used to analyse the stress relaxation effect on the sealing performance of the packer at high temperatures.
Based on the packer cartridge sealing performance evaluation system proposed in this paper, Automation Structure Simulation Analysis and Optimisation Design Platform of Packer Sealing System is developed. Designers can quickly and efficiently optimise the structure of the packer rubber. According to the feedback from Daluhu oilfield, the sealing capacity of the packer rubber optimised by the platform is higher than 30% higher than that without the platform optimised design.
Glossary
Nomenclature section
- HNBR
Hydrogenated Nitrile Butadiene Rubber
- EPDM
Ethylene Propylene Diene Monomer
- NBR
Nitrile Butadiene Rubber
- FEA
Finite element Analysis
- UT
Uniaxial tension test
- PT
Planar tension test
- EB
Equal biaxial tension test
Material constant parameter
Invariant of deformation tensor
The principal stretch ratio
- GM
Generalised Maxwell
Storage module
Loss module
Initial relaxation modulus
angular frequency, rad/s
A dimensionless expression for modulus,
The relaxation time corresponding to the ith Maxwell model unit
- CSC
Closed sealing curve
- CCS
Closed contact surface
- m
Number of contact surface
The nth contact pressure, MPa
The nth effective contact length, mm
The starting point of the nth contact path
The end of the nth contact path
Author biographies
Xu Zheng, School of Mechanical Engineering, Southwest Petroleum University, Chengdu, China Email:swpuzx123@126.com.
Bin Li, School of Mechanical Engineering, Southwest Petroleum University, Chengdu, China Email:swpu1958@126.com.
Gensheng Fei, Artificial Intelligence School, Wuchang University of Technology, Wuhan, China Email:13971672593@126.com.
Footnotes
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The work was supported by National Science and Technology Major Projects of China (2016ZX05038).
ORCID iD: Xu Zheng https://orcid.org/0000-0001-9007-3788
References
- 1.Li ZM, Liu JB, Ding YQ. Finite element analysis of the packer at fracturing. Applied Mechanics and Materials 2013; 385–386: 159–162. [Google Scholar]
- 2.Dorokhov M, Kostriba I, Biletskyi V. Experimental research on the sealing ability of borehole packers. Eastern-European Journal of Enterprise Technologies 2016; 4: 56–62. [Google Scholar]
- 3.AN G. Engineering with rubber. Engineering with Rubber 2012; I, III–XV, XVII–XVIII: 1–9. [Google Scholar]
- 4.Hitchcock GR, Akisanya AR, Thompson DS. The mechanical response and anti-extrusion characteristics of fibre-filled elastomers. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications 1999; 213: 37–46. DOI: 10.1177/146442079921300104 [DOI] [Google Scholar]
- 5.He X, Shi X, Hoch M, et al. Mechanical properties of carbon black filled hydrogenated acrylonitrile butadiene rubber for packer compounds. Polym Test 2016; 53: 257–266. https://www.sciencedirect.com/science/article/pii/S0142941816303579 [Google Scholar]
- 6.Pervez T, Qamar SZ, van de Velden M. Comparison between fresh and exposed swelling elastomer. J Elastomer Plast 2012; 44: 237–250. DOI: 10.1177/0095244311420530 [DOI] [Google Scholar]
- 7.Zeng D, Yang X, Zhu D, et al. Corrosion property testing of AFLAS rubber under the simulation modes of high acid Gas wells. Energy Procedia 2012; 16: 822–827. DOI: 10.1016/j.egypro.2012.01.132 [DOI] [Google Scholar]
- 8.Zeng D, Dong B, Qi Y, et al. On how CO2 partial pressure on corrosion of HNBR rubber O-ring in CO2–H2S–CH4 environment. Int J Hydrogen Energy 2021; 46: 8300–8316. DOI: 10.1016/j.ijhydene.2020.11.264 [DOI] [Google Scholar]
- 9.Dong B, Liu W, Cheng L, et al. Investigation on mechanical properties and corrosion behavior of rubber for packer in CO2-H2S gas well. Eng Fail Anal 2021; 124. DOI: 10.1016/j.engfailanal.2021.105364 [DOI] [Google Scholar]
- 10.Ahmed S, Salehi S, Ezeakacha C, et al. Experimental investigation of elastomers in downhole seal elements: implications for safety. Polym Test 2019; 76: 350–364. DOI: 10.1016/j.polymertesting.2019.03.041 [DOI] [Google Scholar]
- 11.Qamar SZ, Akhtar M, Pervez T, et al. Mechanical and structural behavior of a swelling elastomer under compressive loading. Mater Des 2013; 45: 487–496. DOI: 10.1016/j.matdes.2012.09.020 [DOI] [Google Scholar]
- 12.Akhtar M, Qamar SZ, Pervez T, et al. Performance evaluation of swelling elastomer seals. Journal of Petroleum Science and Engineering 2018; 165: 127–135. DOI: 10.1016/j.petrol.2018.01.064 [DOI] [Google Scholar]
- 13.Li B, Zhang SM. Contact pressure research of drill pipe and packer of rotating blowout preventer. Applied Mechanics and Materials 2011; 121–126: 3200–3204. [Google Scholar]
- 14.Zhang C, Zhang SM, Geng D, et al. FEM Analysis of plug packer based on the model of mooney-rivlin. Adv Mater Res 2011; 201–203: 326–331. [Google Scholar]
- 15.Qu BL. Effects of the friction coefficient on sealing performance of packer element. In: Yingying S, Guiran C, Zhen L. (eds) Proceedings Of the 2016 international conference on education, management, computer And society. Paris: Atlantis Press, 2016, pp.868–872. [Google Scholar]
- 16.Li ZM, Xu SY, Ren FS, et al. The effect of elastic modulus and friction coefficient on rubber tube sealing performance. In: Quan C, Qian K, Asundi A, et al. (eds) International conference on experimental mechanics 2014. Bellingham: Spie-Int Soc Optical Engineering, 2015. [Google Scholar]
- 17.Hu G, Zhang P, Wang G, et al. The influence of rubber material on sealing performance of packing element in compression packer. J Nat Gas Sci Eng 2017; 38: 120–138. DOI: 10.1016/j.jngse.2016.12.027 [DOI] [Google Scholar]
- 18.Hu G, Wang G, Li M, et al. Study on sealing capacity of packing element in compression packer. Journal of the Brazilian Society of Mechanical Sciences and Engineering 2018; 40: 438. journal article. DOI: 10.1007/s40430-018-1364-5 [DOI] [Google Scholar]
- 19.Ahmed S, Patel H, Salehi S. Numerical modeling and experimental study of elastomer seal assembly in downhole wellbore equipment: effect of material and chemical swelling. Polym Test 2020; 89. DOI: 10.1016/j.polymertesting.2020.106608 [DOI] [Google Scholar]
- 20.Mooney M. A theory of large elastic deformation. J Appl Phys 1940; 11: 582–592. [Google Scholar]
- 21.Rivlin RS, Saunders DW. Large elastic deformations of isotropic materials. VII. Experiments on the deformation of rubber. Philosophical Transactions of the Royal Society of London 1951; 243: 251–288. https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.1951.0004 [Google Scholar]
- 22.Treloar LRG. The physics of rubber elasticity. 2nd ed[M]The Clarendon Press, 1958. [Google Scholar]
- 23.ASTM Standards. Standard test methods for vulcanized rubber and thermoplastic elastomers -tension: D412-16[S]. West Conshohocken,PA: ASTM International, 2016.
- 24.Yeoh OH. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem Technol 1990; 63: 792–805. [Google Scholar]
- 25.Yeoh OH. Some forms of the strain energy function for rubber. Rubber Chem Technol 1993; 66: 754–771. [Google Scholar]
- 26.Dowaikh MA. On SH waves in a pre-stressed layered half-space for an incompressible elastic material. Mech Res Commun 1999; 26: 665–672. https://www.sciencedirect.com/science/article/abs/pii/S0093641399000762 [Google Scholar]
- 27.Xiao R, Sun H, Chen W. An equivalence between generalized Maxwell model and fractional Zener model. Mech Mater 2016; 100: 148–153. 10.1016/j.mechmat.2016.06.016 [DOI] [Google Scholar]
- 28.Jena RK, Chen X, Yue CY, et al. Rheological (visco-elastic behaviour) analysis of cyclic olefin copolymers with application to hot embossing for microfabrication. J Micromech Microeng 2011; 21. DOI: 10.1088/0960-1317/21/8/085029 [DOI] [Google Scholar]