Convective heat transfer for Peristaltic flow of SWCNT inside a sinusoidal elliptic duct

Abstract

A mathematical model is presented to analyse the flow characteristics and heat transfer aspects of a heated Newtonian viscous fluid with single wall carbon nanotubes inside a vertical duct having elliptic cross section and sinusoidally fluctuating walls. Exact mathematical computations are performed to get temperature, velocity and pressure gradient expressions. A polynomial solution technique is utilized to obtain these mathematical solutions. Finally, these computational results are presented graphically and different characteristics of peristaltic flow phenomenon are examined in detail through these graphs. The velocity declines as the volume fraction of carbon nanotubes increases in the base fluid. Since the velocity of fluid is dependent on its temperature in this study case and temperature decreases with increasing volumetric fraction of carbon nanotubes. Thus velocity also declines for increasing volumetric fraction of nanoparticles.

Introduction

Peristalsis is the study of transportation of fluid inside ducts having sinusoidally deformable walls. The applications of this peristaltic flow phenomenon include many physiological flow problems (i.e. movement of food inside digestive system, urine transport to bladder and blood circulation in small blood vessels etc). Moreover, there are plenty of engineering applications like transportation of noxious and corrosive fluids, aggressive chemicals and slurries. ¹ Many researchers have been interpreting the peristaltic flow problems for different geometries (tubes, rectangular duct, asymmetric channels etc) due to their variety of applications. Pozrikidis ² had provided a theoretical investigation for two-dimensional flow in channels having sinusoidally deformable walls. Yin and Fung ³ had analysed the peristaltic flow of a viscous Newtonian fluid inside cylindrical tubes. Srinivas and Kothandapani ⁴ had studied the combined effect of peristalsis and heat transfer inside an asymmetric geometry. Nadeem and Akram ⁵ had presented a mathematical investigation to study the peristaltic flow inside a duct having rectangular cross section. Further, some recent research articles that present the study of peristaltic flow inside different geometries is provided.^6–9 Moreover, a huge literature is available on study of peristaltic flow inside rectangular ducts, cylindrical and asymmetric channels. Recently, the analysis of fluid transport along with heat transfer inside ducts having elliptic cross-section and sinusoidally deformable walls has gained the interest of researchers. These elliptic duct peristaltic flow problems also have many applications in the field like the peristaltic flow problems for rectangular and circular ducts.

When compared to a circular duct, the elliptic duct is more practical to use if a better cooling effect is required for heat exchanger and the design has space as an important factor. The reason behind this advantage is that if an elliptic duct and a circular duct both have equal cross sectional area then the elliptic duct has a longer circumferential length as compared to circular duct. ¹⁰ The flow of heated Newtonian fluid inside a geometry with elliptic cross section was mathematically interpreted by Richardson. ¹¹ Abdel-Wahed et al. ¹² had presented the experimental analysis for heated and fully developed laminar fluid flow inside an elliptic duct. Some recent researches that include the flow in elliptic ducts with heat transfer are Sakalis et al., ¹³ Shariat et al., ¹⁴ and Ragueb and Mansouri. ¹⁵

Some fluids have low thermal conductivity and it restricts the analysis of heat transfer in many engineering problems. This issue can be resolved by adding a specific quantity of nano-sized particles in the base fluid. Since the addition of these nanoparticles play an important role to enhance thermal conductivity. ¹⁶ Thus, the analysis of fluid transport with nanoparticles has its role in different geometries used for fluid flow problems. Akbar et al. ¹⁷ had mathematically examined the peristaltic flow of nanofluids inside a vertical cylindrical duct. The fluid transport with single wall carbon nanotubes inside a curved cylindrical channel is mathematically modelled by Shahzadi et al. ¹⁸ Akbar ¹⁹ had provided the mathematical computations for the flow of carbon nanotubes across an asymmetrical channel. Ellahi et al. ²⁰ had interpreted mathematically the peristaltic flow of nanofluid inside a duct with rectangular cross section. Some researchers have also studied the nanofluid flow inside ducts having elliptic cross section.^21,22 Further, some of the recent researches that interpret the nanofluid flow with distinct applications of practical importance are referred as Ellahi et al., ²³ Maskeen et al., ²⁴ and Zeeshan et al.^25,26

All this literature review has revealed that the peristaltic flow of nanoparticles across a duct having elliptic cross section is not computed mathematically yet. We have mathematically computed the peristaltic flow of a heated Newtonian viscous fluid with single wall carbon nanotubes across a vertical duct having elliptic cross-section. In this study, water is considered as base fluid. The heat transfer analysis is explained by considering the constant heat absorption for base fluid. Exact mathematical computations are done to obtain velocity as well as temperature profile solutions. We have added some graphical results to explain the flow behaviour with heat transfer in detail. Further, different aspects of peristaltic flow are discussed with these graphical results. Streamlines depict the side view of this vertical elliptic duct peristaltic flow problem.

Mathematical model

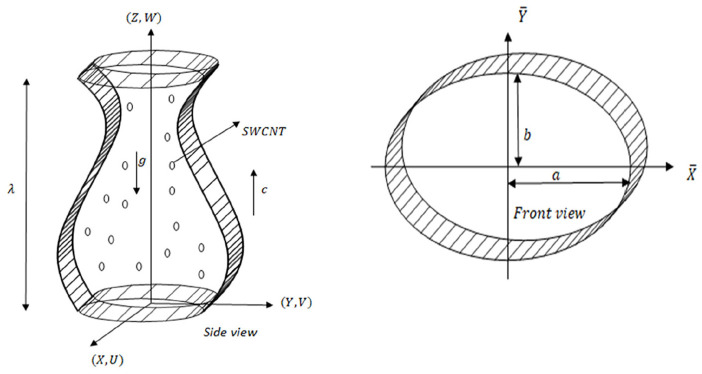
The peristaltic flow of a heated Newtonian viscous fluid inside a vertical elliptical duct is mathematically interpreted. The Cartesian coordinates $(\overline{X,}\overline{Y},\overline{Z})$ are used to interpret this problem mathematicall (See Figure 1).

Figure 1.

Geometrical model of the problem. ²⁷

The geometry of deformable walls is provided by the following sinusoidal equations

$$\begin{array}{c}\overline{a}(\overline{Z},\overline{t})=a_0+\mathrm{dSin}\left(\frac{2\pi }{\lambda }(\overline{Z}-c\overline{t})\right),\hfill \\ \overline{b}(\overline{Z},\overline{t})=b_0+\mathrm{dSin}\left(\frac{2\pi }{\lambda }(\overline{Z}-c\overline{t})\right),\hfill \end{array}$$ (1)

The mathematical equations governing the flow of this incompressible, Newtonian fluid are provided as ²⁷

$$\frac{\partial \overline{U}}{\partial \overline{X}}+\frac{\partial \overline{V}}{\partial \overline{Y}}+\frac{\partial \overline{W}}{\partial \overline{Z}}=0,$$ (2)

$${\rho }_{\mathrm{nf}}(\frac{\partial \overline{U}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{U}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{U}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{U}}{\partial \overline{Z}})=-\frac{\partial \overline{P}}{\partial \overline{X}}+{\mu }_{\mathrm{nf}}(\frac{{\partial }^2\overline{U}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{U}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{U}}{\partial {\overline{Z}}^2}),$$ (3)

$${\rho }_{\mathrm{nf}}(\frac{\partial \overline{V}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{V}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{V}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{V}}{\partial \overline{Z}})=-\frac{\partial \overline{P}}{\partial \overline{Y}}+{\mu }_{\mathrm{nf}}(\frac{{\partial }^2\overline{V}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{V}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{V}}{\partial {\overline{Z}}^2}),$$ (4)

$$\begin{array}{c}{\rho }_{\mathrm{nf}}(\frac{\partial \overline{W}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{W}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{W}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{W}}{\partial \overline{Z}})=-\frac{\partial \overline{P}}{\partial \overline{Z}}\hfill \\ +{\mu }_{\mathrm{nf}}(\frac{{\partial }^2\overline{W}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{W}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{W}}{\partial {\overline{Z}}^2})+{\left(\rho \beta \right)}_{\mathrm{nf}}g(\overline{T}-{\overline{T}}_w),\hfill \end{array}$$ (5)

$${\left(\rho C_p\right)}_{\mathrm{nf}}(\frac{\partial \overline{T}}{\partial \overline{t}}+\overline{U}\frac{\partial \overline{T}}{\partial \overline{X}}+\overline{V}\frac{\partial \overline{T}}{\partial \overline{Y}}+\overline{W}\frac{\partial \overline{T}}{\partial \overline{Z}})=k_{\mathrm{nf}}(\frac{{\partial }^2\overline{T}}{\partial {\overline{X}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Y}}^2}+\frac{{\partial }^2\overline{T}}{\partial {\overline{Z}}^2})+Q_0,$$ (6)

The dimensional form of the relevant boundary conditions is given as

$$\overline{W}=0,\overline{T}={\overline{T}}_w,\mathrm{for}\frac{{\overline{x}}^2}{{\overline{a}}^2}+\frac{{\overline{y}}^2}{{\overline{b}}^2}=1,$$ (7)

The two frames of reference (i.e. fixed frame and moving frame) are mathematically related by the following equations

$$\overline{x}=\overline{X},\overline{y}=\overline{Y},\overline{z}=\overline{Z}-c\overline{t},\overline{p}=\overline{P},\overline{u}=\overline{U},\overline{v}=\overline{V},\overline{w}=\overline{W}-c,$$ (8)

The useful dimensionless variables are provided by

$$\begin{array}{c}x=\frac{\overline{x}}{D_h},y=\frac{\overline{y}}{D_h},z=\frac{\overline{z}}{\lambda },t=\frac{c\overline{t}}{\lambda },w=\frac{\overline{w}}{c},p=\frac{D_h^2\overline{p}}{\mu \lambda c},\theta =\frac{\overline{T}-{\overline{T}}_w}{{\overline{T}}_b-{\overline{T}}_w},\delta =\frac{b_0}{a_0},\varphi =\frac{d}{b_0},\hfill \\ u=\frac{\lambda \overline{u}}{D_{h}c},v=\frac{\lambda \overline{v}}{D_{h}c},a=\frac{\overline{a}}{D_h},b=\frac{\overline{b}}{D_h},G_r=\frac{g({\overline{T}}_b-{\overline{T}}_w)D_h^2{\left(\rho \beta \right)}_f}{{\mu }_{f}c},\gamma =\frac{Q_0{D}_h^2}{({\overline{T}}_b-{\overline{T}}_w)k_f},\hfill \end{array}$$ (9)

The hydraulic diameter of ellipse is written as

$$D_h=\frac{\pi b_0}{E\left(e\right)},$$ (10)

The eccentricity of ellipse is $e=\sqrt{1-{\delta }^2},$ and the second kind elliptical integral $E\left(e\right)$ is written as ²⁸

Table 1 and 2 represents the numerical values and experimental formulas for thermo physical features of hybrid nanofluid respectively.

Table 1.

Thermo-physical properties of base fluid and CNT referred as Akbar et al. ²⁹

Physical properties	Water $\left({\mathit{H}}_2\mathit{O}\right)$	SWCNT
$C_p$	4179	425
$k$	0.613	6600
$\rho$	997.1	2600
$\beta \times {10}^{-5}$	21	1.5

Table 2.

Carbon nanotube model referred as Nadeem. ³⁰

Density	${\rho }_{\mathrm{nf}}=(1-\psi ){\rho }_f+\psi {\rho }_{\mathrm{CNT}}$ ,
Heat capacity	${\left(\rho C_p\right)}_{\mathrm{nf}}=(1-\psi ){\left(\rho C_p\right)}_f+\psi {\left(\rho C_p\right)}_{\mathrm{CNT}}$ ,
Viscosity	$\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}=\frac{1}{{(1-\psi )}^{2.5}},$
Thermal conductivity	$\frac{k_{\mathrm{nf}}}{k_f}=\frac{1-\psi +2\psi \left(\frac{k_{\mathrm{CNT}}}{k_{\mathrm{CNT}}-k_f}\right)\mathrm{Log}\left(\frac{k_{\mathrm{CNT}}+k_f}{2k_f}\right)}{1-\psi +2\psi \left(\frac{k_f}{k_{\mathrm{CNT}}-k_f}\right)\mathrm{Log}\left(\frac{k_{\mathrm{CNT}}+k_f}{2k_f}\right)},$
Thermal expansion coefficient and density relation	${\left(\rho \beta \right)}_{\mathrm{nf}}=(1-\psi ){\left(\rho \beta \right)}_f+\psi {\left(\rho \beta \right)}_{\mathrm{CNT}}$ .

$$E\left(e\right)=\underset{0}{\overset{\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{{\displaystyle \int }}}\sqrt{1-e^{2}Si{n}^2\alpha }d\alpha ,$$ (11)

The equations (3)–(6) are obtained in their non-dimensional form after using equations (8) and (9), then final simplified form of non-dimensional equations is obtained by applying lubrication theory, (i.e. λ $\to \infty$ ).

$$\frac{\partial p}{\partial x}=0,$$ (12)

$$\frac{\partial p}{\partial y}=0,$$ (13)

$$\frac{\mathrm{dp}}{\mathrm{dz}}=\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}(\frac{{\partial }^{2}w}{\partial x^2}+\frac{{\partial }^{2}w}{\partial y^2})+\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}{G}_r\theta ,$$ (14)

$$\frac{k_{\mathrm{nf}}}{k_f}(\frac{{\partial }^2\theta }{\partial x^2}+\frac{{\partial }^2\theta }{\partial y^2})+\gamma =0,$$ (15)

With non-dimensional boundary conditions

$$w=-1,\mathrm{for}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,$$ (16)

$$\theta =0,\mathrm{for}\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,$$ (17)

Where $a=\frac{E\left(e\right)}{\pi }[\frac{1}{\delta }+\varphi \mathrm{Sin}\left(2\pi z\right)],$ and $b=\frac{E\left(e\right)}{\pi }[1+\varphi \mathrm{Sin}\left(2\pi z\right)].$

Exact solution

Assume a polynomial form solution of temperature equation (15) given as

$$\theta (x,y)=C_1{x}^4+C_2{y}^4+C_3{x}^2{y}^2+C_4{x}^2+C_5{y}^2+C_6,$$ (18)

By using equation (18) in equation (15) and comparing coefficients of $x^2,y^2,x^0,y^0$ , we get these three equations given as

$$12C_1+2C_3=0,$$ (i)

$$2C_3+12C_2=0,$$ (ii)

$$2C_4+2C_5=-\frac{\gamma }{\raisebox{1ex}{$k_{nf}$}\!\left/ \!\raisebox{-1ex}{$k_f$}\right.},$$ (iii)

Now by using equation (18) in the relevant boundary condition for temperature given in equation (17) and by comparing coefficients of $x^4,x^2,x^0$ , we get these three equations

$$C_1{a}^4+C_2{b}^4-C_3{a}^2{b}^2=0,$$ (iv)

$$-2C_2{b}^4+C_3{a}^2{b}^2+C_4{a}^2-C_5{b}^2=0,$$ (v)

$$C_2{b}^4+C_5{b}^2+C_6=0,$$ (vi)

By solving equations (i)–(vi), we get values of constants $C_1,C_2,C_3,C_4,C_5,C_6$ given in equation (19) as follows

$$\begin{array}{c}{C}_1=0,C_2=0,C_3=0,C_4=-\frac{b^2\gamma }{2(a^2+b^2)\left(\frac{k_{\mathrm{nf}}}{k_f}\right)},\hfill \\ C_5=-\frac{a^2\gamma }{2(a^2+b^2)\left(\frac{k_{\mathrm{nf}}}{k_f}\right)},C_6=\frac{a^2{b}^2\gamma }{2(a^2+b^2)\left(\frac{k_{\mathrm{nf}}}{k_f}\right)},\hfill \end{array}$$ (19)

Now utilizing values of these constants in equation (18), we get an exact solution for temperature profile that satisfies both equation and boundary conditions exactly and is given as

$$\theta (x,y)=\frac{-a^2{b}^2(\frac{x^2}{a^2}+\frac{y^2}{b^2}-1)\gamma }{2(a^2+b^2)\left(\frac{k_{\mathrm{nf}}}{k_f}\right)},$$ (20)

The same procedure that is used to obtain temperature solution is used again to get an exact solution for velocity profile that satisfies both the momentum equation (14) and boundary condition given in equation (16). The exact solution for $w(x,y)$ is given as

$$\begin{array}{c}w(x,y)=\frac{1}{24{(a^2+b^2)}^2(a^4+6a^2{b}^2+b^4)\left(\frac{k_{\mathrm{nf}}}{k_f}\right)\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right)}\hfill \\ \left[b^8\{12\left(\frac{k_{\mathrm{nf}}}{k_f}\right)(\frac{\mathrm{dp}}{\mathrm{dz}}{x}^2-2\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right))+G_r{x}^4\gamma \left(\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}\right)\}\right)\hfill \\ +6a^2{b}^6\{2\left(\frac{k_{\mathrm{nf}}}{k_f}\right)(\frac{\mathrm{dp}}{\mathrm{dz}}(-b^2+7x^2+y^2)-16\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right))+G_r{x}^2(-b^2+x^2+y^2)\gamma \left(\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}\right)\}\hfill \\ +a^8\{-12\left(\frac{k_{\mathrm{nf}}}{k_f}\right)(\frac{\mathrm{dp}}{\mathrm{dz}}(b^2-y^2)+2\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right))+G_r(5b^4-6b^2{y}^2+y^4)\gamma \left(\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}\right)\}\hfill \\ +a^4{b}^4\{-84\left(\frac{k_{\mathrm{nf}}}{k_f}\right)(b^2\frac{\mathrm{dp}}{\mathrm{dz}}-\frac{\mathrm{dp}}{\mathrm{dz}}(x^2+y^2)+4\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right))\hfill \\ +G_r(5b^4+5x^4+12x^2{y}^2+5y^4-2b^2(16x^2+5y^2))\gamma \left(\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}\right)\}\hfill \\ +2a^6{b}^2\{6\left(\frac{k_{\mathrm{nf}}}{k_f}\right)(\frac{\mathrm{dp}}{\mathrm{dz}}(-7b^2+x^2+7y^2)-16\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right))\hfill \\ +G_r(13b^4+3y^2(x^2+y^2)-b^2(5x^2+16y^2))\gamma \left(\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}\right)\}]\hfill \end{array}$$ (21)

The mathematical result for dimensionless flow rate $q\left(z\right)$ is obtained by integrating the velocity solution $w(x,y)$ over the elliptic cross-section and given as

$$q\left(z\right)=\frac{-3\mathrm{ab}(a^2+b^2)\left(\frac{k_{\mathrm{nf}}}{k_f}\right)\pi (a^2{b}^2\frac{\mathrm{dp}}{\mathrm{dz}}+4(a^2+b^2)\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right))+a^5{b}^5{G}_r\pi \gamma \left(\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}\right)}{12{(a^2+b^2)}^2\left(\frac{k_{\mathrm{nf}}}{k_f}\right)\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right)}$$ (22)

The mathematical result of pressure gradient is evaluated from equation (22) as follows

$$\frac{\mathrm{dp}}{\mathrm{dz}}=-\frac{4(a^2+b^2)\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right)[-{\int }_0^1\mathrm{abdz}+\mathrm{ab}\pi +Q-\frac{a^5{b}^5{G}_r\pi \gamma \left(\frac{{\left(\rho \beta \right)}_{\mathrm{nf}}}{{\left(\rho \beta \right)}_f}\right)}{12{(a^2+b^2)}^2\left(\frac{k_{\mathrm{nf}}}{k_f}\right)\left(\frac{{\mu }_{\mathrm{nf}}}{{\mu }_f}\right)}]}{a^3{b}^3\pi },$$ (23)

The pressure rise expression over a single wavelength is calculated by

$$\Delta P=\underset{0}{\overset{1}{\int }}\frac{\partial p}{\partial z}\mathrm{dz},$$ (24)

Result and discussion

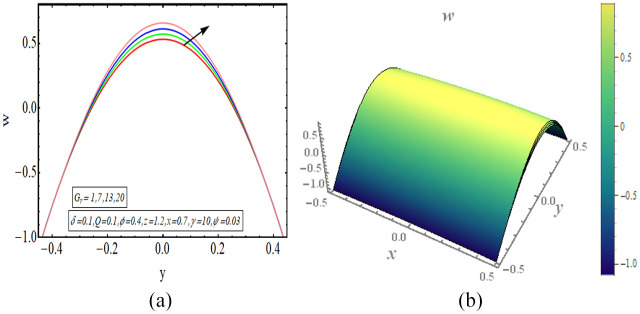
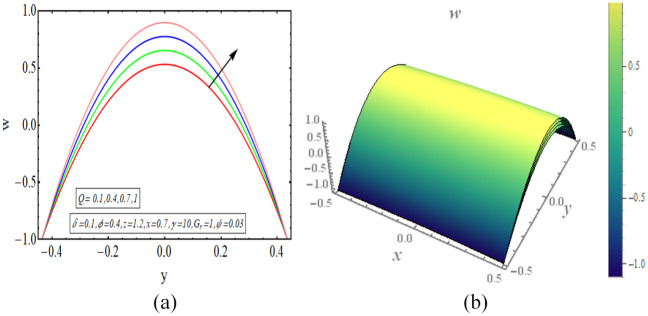
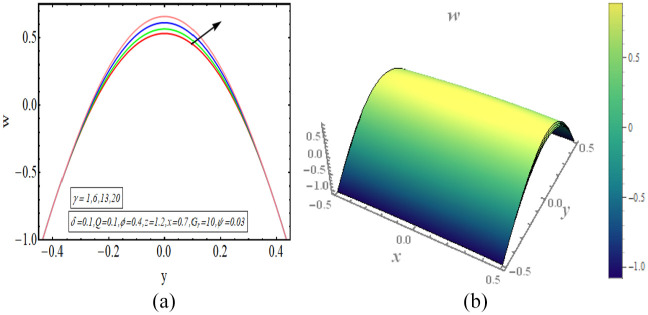
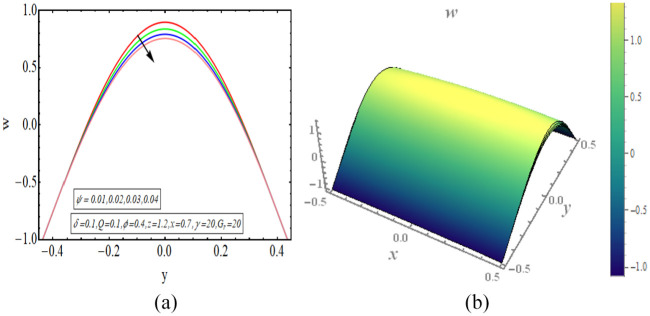
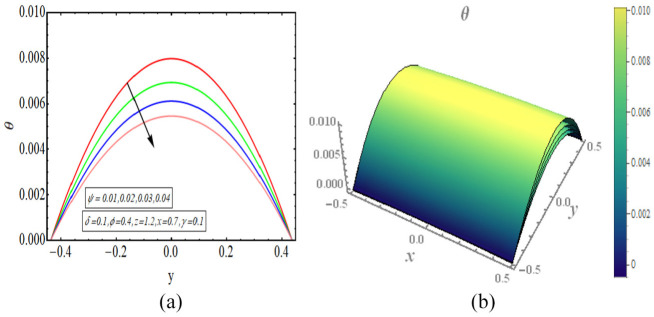
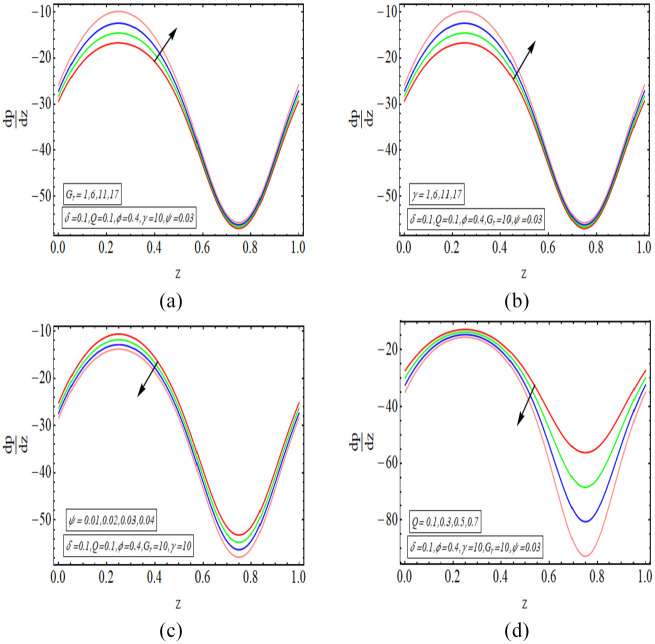
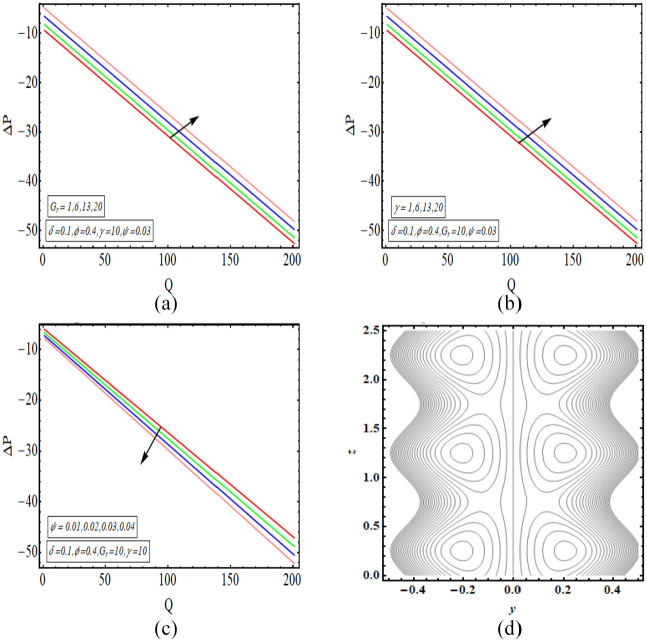
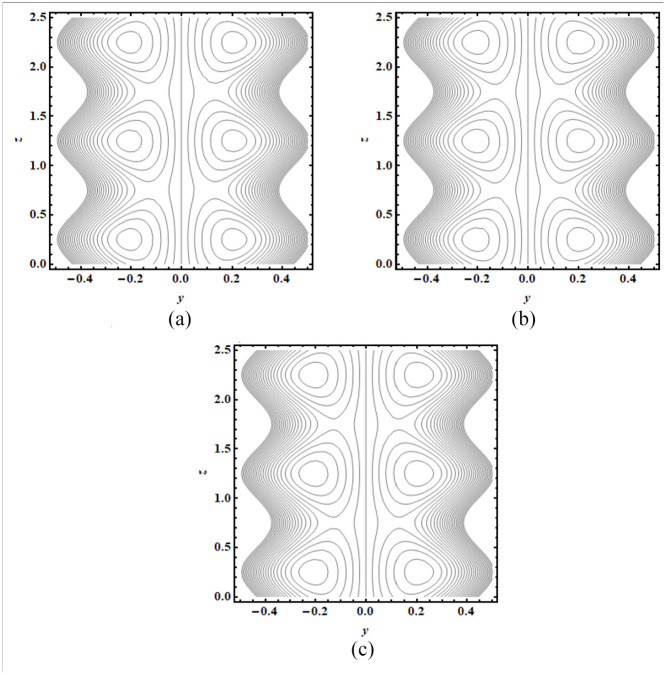
This segment provides a graphical assessment of the mathematical results that are obtained in the previous section. We have plotted some 2-dimensional as well as 3-dimensional graphs for both velocity and temperature profiles. The velocity of fluid is plotted for increasing value of different parameter as displayed in Figures 2 to 5. All these velocity graphs reveal that the velocity gains its highest value in the centre of elliptic duct and it declines toward the walls of duct. Also, an axial symmetry flow behaviour is revealed by these velocity graphs. Thus, we can conclude that the peristaltic flow in this vertical elliptic duct is an axially symmetric flow. Figure 2(a) gives a 2-dimensional graphical result of velocity for incrementing value of $G_r$ and it is revealed that velocity gains higher value with increasing values of $G_r$ . Figure 2(b) provides a 3-dimensional graph of velocity for incrementing value of $G_r$ and as a result velocity increases. The increasing value of $G_r$ implies the stronger buoyancy forces and as a result the flow is accelerated toward the axial direction. There is increase in the velocity for increasing values of $\gamma$ , displayed in Figure 3(a). Figure 3(b) depicts a 3-dimensional graph for rising value of $\gamma$ and the velocity of fluid increases with this rising value of $\gamma$ . Figure 4(a) depicts a decline in the velocity of fluid with increasing $\psi$ . A 3-dimensional graph of velocity for increasing value of $\psi$ is presented in Figure 4(b). The velocity decreases as the volume fraction of carbon nanotubes increase in the base fluid. Since the velocity of fluid is dependent on its temperature in this study case and temperature decreases with increasing value of volume fraction of carbon nanotubes. Thus velocity also declines for increasing volumetric fraction of nanoparticles. There is increase in velocity for incrementing value of flow rate as revealed in Figure 5(a). Figure 5(b) shows a 3-dimensional graphical result of velocity for increasing value of $Q$ and velocity enhances with incrementing values of flow rate. The temperature of this heated fluid is plotted against distinct physical parameters as shown in Figures 6 and 7. These temperature graphs show that the temperature has maximum value in the centre but declines toward the walls of duct. Also an axially symmetric behaviour is seen in these temperature graphs. Figure 6(a) depicts an increase in the temperature of fluid for increasing value of $\gamma$ . A 3-dimensional graph of temperature for increasing value of $\gamma$ is presented in Figure 6(b). The temperature of fluid increases as the value of heat absorption parameter increases. Figure 7(a) reveals a decline in temperature as the value of $\psi$ increases. Figure 7(b) depicts a 3-dimensional graph of temperature profile for increasing values of $\psi$ . The temperature of fluid declines with increasing the volume fraction of carbon nanotubes in the base fluid. The high value of thermal conductivity of carbon nanotubes is the main reason behind quick decline in the temperature of fluid. In Figure 8(a) to (d), the pressure gradient is plotted for different physical parameters against the axial coordinate of elliptic duct. The value of $\frac{\mathrm{dp}}{\mathrm{dz}}$ increases for increasing values of $G_r$ , as shown in Figure 8(a). Figure 8(b) shows an increasing behaviour in value of $\frac{\mathrm{dp}}{\mathrm{dz}}$ for increasing values of $\gamma$ . The value of $\frac{\mathrm{dp}}{\mathrm{dz}}$ decreases with increasing volume fraction $\psi$ of carbon nanotubes, displayed in Figure 8(c). Figure 8(d) depicts a decline in the value of $\frac{\mathrm{dp}}{\mathrm{dz}}$ for increasing values of $Q$ . In Figure 9(a) to (c), the pressure rise graphical result $\Delta P$ is plotted against the volumetric flow rate $Q$ . The value of $\Delta P$ increases for increasing value of $G_r$ , depicted in Figure 9(a). Figure 9(b) also shows increase in $\Delta P$ for increasing value of $\gamma$ . There is a decline in the value of $\Delta P$ with increasing value of $\psi$ . The streamlines for this peristaltic flow problem in a vertical duct having elliptic cross-section are provided in Figure 10(a) to (d). The graphs are plotted for enhancing values of flow rate. The trapping slightly increases in size with enhancing value of $Q$ . Further, the sinusoidally moving walls can be clearly seen in the streamline graph.

Figure 2.

(a) Velocity for $G_r$ (2-dimensional) and (b) velocity for $G_r$ (3-dimensional).

Figure 5.

(a) Velocity for $Q$ (2-dimensional) and (b) velocity for $Q$ (3-dimensional).

Figure 3.

(a) Velocity for $\gamma$ (2-dimensional) and (b) velocity for $\gamma$ (3-dimensional).

Figure 4.

(a) Velocity for $\psi$ (2-dimensional) and (b) velocity for $\psi$ (3-dimensional).

Figure 6.

(a) Temperature for $\gamma$ (2-dimensional) and (b) temperature for $\gamma$ (3-dimensional).

Figure 7.

(a) Temperature for $\psi$ (2-dimensional) and (b) temperature for $\psi$ (3-dimensional).

Figure 8.

(a) Pressure gradient for $G_r$ , (b) pressure gradient for $\gamma$ , (c) pressure gradient for $\psi$ and (d) pressure gradient for $Q$ .

Figure 9.

(a) Pressure rise for $G_r$ , (b) pressure rise for $\gamma$ and (c) pressure rise for $\psi$ .

Figure 10.

(a) Streamline for $Q=0.01$ , (b) streamline for $Q=0.02$ , (c) streamline for $Q=0.03$ and (d) streamline for $Q=0.04$ .

Conclusions

The flow of a heated Newtonian viscous fluid with single wall carbon nanotubes inside a vertical elliptical duct with sinusoidally deformable walls is mathematically interpreted. The main advantage of using carbon nanotubes in the base fluid is enhancement in the thermal conductivity. The major findings that appear in this work are given below

• The peristaltic flow in this vertical elliptic duct is an axially symmetric flow.

• An increment in the values of $G_r$ implies stronger buoyancy forces and as a result the flow is accelerated in the axial direction.

• An axially symmetric behaviour is seen in these temperature graphs.

• The temperature of fluid decreases with increasing the volume fraction of carbon nanotubes in the base fluid. The high value of thermal conductivity of carbon nanotubes is the main reason behind quick decline in the temperature of fluid.

• The trapping slightly increases in size with increasing values of flow rate $Q$ . Further, the sinusoidally moving walls can be clearly seen in these streamline graphs.

Author biographies

Salman Akhtar is a PhD research fellow at Quaid-i-Azam University, Islamabad, Pakistan. His field of research is applied mathematics and computational fluid mechanics. He has published many articles under the supervision of Prof. Sohail Nadeem.

Luthais B McCash is an Honorary Fellow at the University of Leicester. He was previously the Lead Data Scientist and Head of the Mathematical Modelling, Simulation & Computation at a Scottish Energy company. Although he is interested in Applied and Industrial Mathematics in general, Luthais’ current research focuses on quantum fluids, and applied PDEs. Currently he collaborates with colleagues in both Leicester and externally.

Sohail Nadeem is a Professor and chairman of department of Mathematics at Quaid-i-Azam University, Islamabad, Pakistan. His field of research is applied mathematics and computational fluid mechanics. His contribution to the field is recognized at national and international levels. He has produced a good number of PhD students. Also, he is serving as editor of various well reputed international journals.

Salman Saleem earned his PhD degree in mathematics and presently working as an Assistant professor at King Khalid University, Saudi Arabia. His area of research is computational fluid mechanics. He has published a good number of articles and serving as editor of Hindawi journals.

Alibek Issakhov is currently working Head of department at Alfarabi Kazkh National University, Kazakhstan. He is a scholar, researcher, and teacher per excellence. He has authored many research articles which show his excellence in the field.

Appendix

Notation

$(\overline{X,}\overline{Y},\overline{Z})$  Cartesian coordinate system

$(\overline{U},\overline{V},\overline{W})$  Velocity components

$a_0,b_0$  Ellipse half axes $(b_0<a_0)$

$d\left(m\right)$  Wave amplitude

$\lambda \left(m\right)$  wavelength

${\overline{T}}_w\left(K\right)$  Tube’s wall temperature

$c\left(m{s}^{-1}\right)$  Velocity of propagation

$D_h\left(m\right)$  Hydraulic diameter of ellipse

$\mu$ $\left(\mathrm{Ns}{m}^{-2}\right)$  viscosity

$k\left(\frac{W}{\mathrm{mK}}\right)$  Thermal conductivity

$C_p\left(\frac{J}{\mathrm{kg}.K}\right)$  Heat capacity

${\overline{T}}_b\left(K\right)$  Bulk temperature

$e$  Eccentricity of ellipse

$\delta$  Aspect ratio

$\varphi$  Occlusion

$\gamma$  Dimensionless heat absorption parameter

$G_r$  Grashof number

$\psi$  Volume fraction of SWCNT $\left(3\%\right)$

SWCNT Single wall carbon nanotubes

$\mathrm{nf}$  Nanofluid

$\rho \left(\frac{\mathrm{kg}}{m^3}\right)$  Density

$\beta \left(K^{-1}\right)$  Thermal expansion coefficient