Abstract
Introduction
The mode clamping mechanism is the most important part of forming section for the plastic injection molding machine. If this mechanism has double-toggle effects at the close position, it will get a larger clamping force and have higher safety. This study focuses on the optimal design of the Watt-chain mechanism with double-toggle effects at the close position.
Methods
The Watt-chain double-toggle mechanism is chosen to be the mold clamping mechanism by referring to the existing patents. Then, the kinematic characteristics of the Watt-chain double-toggle mechanism are analyzed by the vector loop method. Finally, based on the kinematic requirements and the proposed optimal design process according to the objective function, the optimal design on Watt-chain double-toggle mechanism is accomplished in this study.
Results
This study proposes an optimal design process on Watt-chain double-toggle mold clamping mechanism. By following the optimal design process, the optimal Watt-chain double-toggle mold clamping mechanism has a maximum acceleration 3418 mm/s2 (amax = 3418 mm/s2) and a force ratio is 2.24 (Fin/Fout = 2.24).
Discussion
According to the studies on the optimal designs of mechanisms, the optimal Watt-chain double-toggle mechanism, which is better than the multiple-joint double-toggle mold clamping mechanism in the existing patent by reducing 19.5% of acceleration and 30% of a driving force, is proposed. The results of this study could be the design reference in engineering when designing mold clamping mechanisms for plastic injection molding machines.
Keywords: Clamping force, driving force, double-toggle mechanism, maximum acceleration, Watt-chain mold clamping mechanism
Introduction
As the demand for plastic products is increasing dramatically, the improvement in production efficiency and product quality is more and more important from an engineering aspect. The requirements for the kinematic characteristics of plastic injection molding machines are more stringent than before. To improve production stability, it is necessary to reduce vibration and noise during the production process. The plastic injection molding machine includes forming section and injection section. The mode clamping mechanism is the most important part of forming section. Hence, a mold clamping mechanism with ideal kinematic characteristics is the goal pursued when designing the plastic injection molding machine. Therefore, the kinematic characteristics of the mold clamping mechanism must be analyzed first.
When the mold is at the close position, the mold clamping mechanism must have a toggle effect(s). If the mold mechanism has double-toggle effects at the close position, it will get a larger clamping force and have higher safety. This study focuses on the optimal design of the Watt-chain mechanism with double-toggle effects at the close position. First, by referring to the existing patents,1–11 the mold clamping mechanisms of two patents1,2 had double-toggle effects at the close position. The Watt-chain double-toggle mechanism is chosen to be the mold clamping mechanism of the injection molding machine. Then, according to the studies on the kinematics of mechanisms,12–19 the kinematic characteristics of the Watt-chain double-toggle mechanism are analyzed. The optimal design of the Watt-chain double-toggle mechanism is the purpose of this paper, according to the studies on the optimal designs of mechanisms,20–22 the optimal design process of the Watt-chain double-toggle mechanism is proposed. Finally, based on the design requirements of mold clamping mechanisms and the proposed optimal design process, the optimal design on Watt-chain double-toggle mechanism is accomplished in this study.
Toggle effect and toggle mechanism
Mechanism with toggle effect is called toggle mechanism. Figure 1 illustrates the fundamental principle of the toggle effect. For the 4 bar mechanism shown in Figure 1(a), if the lengths of links 2 and 3 are the same, the relationship of the forces acting on the joint a (Fa) and joint b (Fb) can be expressed as:
| (1) |
Figure 1.
Single toggle effect of 4-bar mechanism.
Based on equation (1), if β = 0°, links 2 and 3 are collinear (L1) as shown in Figure 1(b), we get:
| (2) |
According to equation (2), the clamping force Fb is infinitely large (Fb = ∞) for small force Fa. Figure 1(b) shows the toggle effect when links 2 and 3 are collinear (L1). A mechanism with a toggle effect is called a toggle mechanism.
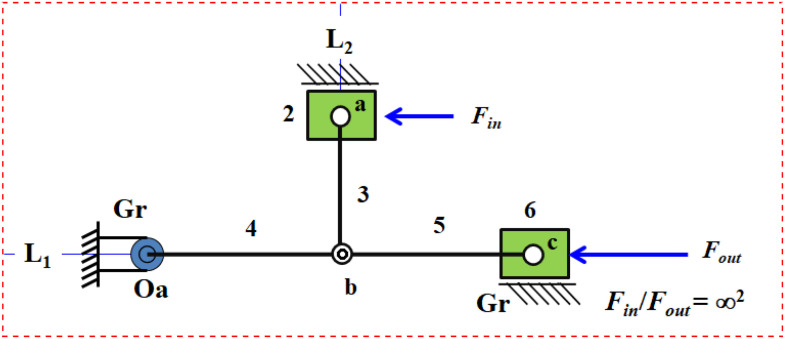
Figure 2(a) shows a molding mechanism with 6 links. Figure 2(b) to (d) shows the free body of joints a, c, and b, respectively. Where: Fin is driving force acting on input slider 2; Fout is clamping force acting on output slider 6; Ra is the force acting on input slider 2 by ground link 1; Rc is the force acting on input slider 6 by ground link 1; F3, F4, and F5 are the forces acting on links 3, 4, and 5.
Figure 2.
Double toggle effects of 6-bar mechanism.
According to Figure 2(b) and the theory of static balancing, we get:
| (3) |
According to Figure 2(c) and the theory of static balancing, we get:
| (4) |
According to Figure 2(d) and the theory of static balancing, we get:
| (5) |
| (6) |
According to equations (3) to (6), we get:
| (7) |
Then, based on equations (3) and (7), we get:
| (8) |
Based on equation (8), if α = 0° and β = 0°, links 2 and 3 are collinear (L2) and links 4 and 5 are also collinear (L1), as shown in Figure 3, we get:
| (9) |
Figure 3.
Double-toggle mechanism.
According to equation (9), the clamping force Fout is infinitely large (Fout = ∞2Fin). The mechanism, shown in Figure 3, with double-toggle effects (lines L1 and L2) is called the double-toggle mechanism.
Mold clamping mechanism
The mold clamping mechanism can be classified into two types: (1) input link with reciprocating linear motion and (2) input link with a reciprocating rocking motion. The mechanism discussed in this study is limited to the input link with reciprocating linear motion. In addition, the mechanism must have double-toggle effects at the close position in order to get a large clamping force.
The input link of the mold clamping mechanism in the patent, 1 shown in Figure 4, is the slider with reciprocating linear motion. Figure 5(a) and (b) shows the corresponding kinematic skeletons for the mold mechanism at the close and the open positions. The mechanism with two collinear lines (L1 and L2) has double-toggle effects at the close position as indicated in Figure 5(a).
Figure 4.
Mold mechanism for servo-drive type injection molding machine. 1
Figure 5.
Kinematic skeletons for patent 1 (r3 = 140 mm, r4 = 250 mm, and r5 = 250 mm).
The input link of the mold mechanism in the patent, 2 shown in Figure 6, is also the slider with reciprocating linear motion. Figure 7(a) and (b) shows the corresponding kinematic skeletons of the mold mechanism at the close and the open positions. According to Figure 7(a), the mechanism has two collinear lines (L1 and L2) which is a double-toggle mechanism, and also a Watt-chain mold mechanism with 6 links and 7 joints. Lastly, this study proposes the optimal design process based on Watt-chain mold mechanism with double-toggle effects.
Figure 6.
Driving device of controlling mold opening and closing for plastic molding machine. 2
Figure 7.
Kinematic skeletons for Watt-chain mechanism. 2
A mechanism with a toggle effect must have a collinear line; however, not all the mechanisms with collinear lines have toggle effects. In Figure 8(a), there are two collinear lines (L1 and L2) at the close position in this Watt-chain mechanism, but it only has a single toggle effect for the collinear line (L1). The collinear line (L2) does not have a toggle effect since the line L2 is not perpendicular with the vector of displacement Sin. On the other hand, Figure 8(b) shows the mold mechanism at the open position, which has the collinear line (L2), however, it does not have a toggle effect.
Figure 8.
The Watt-chain mold clamping mechanism.
Dimensional synthesis and kinematic analysis
Design requirements
According to the kinematic requirements and space constraints on mold clamping mechanism for injection machine, the design requirements are concluded as:
The displacement for the output slider (Sout) from close to the open position must be 250 mm (Sout = 250 mm) and completed the stroke in 1 s.
The horizontal dimension is identified to be 500 mm, that is, .
The vertical dimension (r2y) is constrained to be between 140 mm to 250 mm, that is, .
The displacement for the input slider (Sin) from close to the open position is constrained to be between 180 mm to 280 mm, that is, .
Multiple-joint mechanism
Figure 9(a) shows the kinematic skeleton at any position for the mold clamping mechanism in the patent, 1 and Figure 9(b) shows its corresponding vector coordinate system, which has two independent vector loops (vector loops I and II).
Figure 9.
Multiple-joint mold clamping mechanism in patent. 1
According to the research, 22 r2y = 140 mm, r3 = 140 mm, r4 = 250 mm, and r5 = 250 mm, we get:
(1). If θ4 = 0°, then θ3 = 270°, θ5 = 0°, r2x = 250 mm, and r6 = 500 mm. At this moment, the mechanism is at the close position with double-toggle effects. It can be referred to Figure 5(a) which shows the corresponding double-toggle mechanism (lines L1 and L2) at the close position.
(2). If θ4 = 60°, then θ3 = 33.12°, θ5 = 0°, r2x = 7.75 mm, and r6 = 500 mm. At this moment, the mechanism is at the open position without the toggle effect, as shown in Figure 5(b).
According to Figure 5(a) and (b), the displacement of the input slider is equal to 242.25 mm (Sin = 250 – 7.75 = 242.25 mm) and the displacement of the output slider is equal to 250 mm (Sout = 250 mm). The research 22 indicated that, if the input slider is pushed to move 242.25 mm in 1 s (β = 1 s) with MS (Modified Sine) motion, by the finite difference method, the corresponding velocity, acceleration, and force ratio (Fin/Fout) curves of output clamping mold are shown in Figure 10(a) to (c). For the output mold, the maximum velocity Vmax is 803 mm/s, the maximum acceleration amax is 4244 mm/s2, and the maximum force ratio (Fin/Fout)max is 3.2.
Figure 10.
The output characteristic curves of the mold. 22
In conclusion,
When the mold mechanism is at the close position, shown in Figure 5(a), the force ratio is 0 (Fin/Fout = 0), the mechanism has double-toggle effects.
When the mold mechanism is at the open position, shown in Figure 5(b), the force ratio is 3.2 (Fin/Fout = 3.2), which means the driving force (Fin) is 3.2 times of output load (Fout).
Watt-chain mechanism
When the mold clamping mechanism has the same output stroke as the research 22 but using the Watt-chain mechanism, the kinematic characteristics of the output mold would be adjusted. The skeleton for Watt-chain double-toggle mechanism is shown in Figure 7, and Figure 11(a) and (b) illustrates the kinematic skeleton and vector coordinate system of the Watt-type mold clamping mechanism. 2
Figure 11.
Watt-chain mold clamping mechanism. 2
According to Figure 11(b), the X- and Y-component equation from two independent vector loops (vector loops I and II) can be expressed as:
| (9) |
| (10) |
| (11) |
| (12) |
Assume the mechanical efficiency is 100%, the input power is equal to the output power, that is,
| (13) |
Initial design,
If r3 = 140 mm, r4a = r5 = 250 mm, r4b = 30 mm, and α = 900, then r2y = 160 mm, according to equations (9) to (13),
At the close position when θ4a = 0°, then θ4b = θ4a + π − α = 90°, θ3 = 270°, θ5 = 0°, r2x = 250 mm, and r6 = 500 mm. Figure 12(a) shows the corresponding kinematic skeleton for the Watt-chain double-toggle mechanism (Lines L1 and L2).
At the open position when θ4a = 60°, then θ4b = θ4a + π − α = 150°, θ3 = 210.77°, θ5 = 300°, r2x = −9.55 mm, and r6 = 250 mm. Figure 12(b) shows the corresponding kinematic skeleton for the Watt-chain mechanism without the toggle effect.
Figure 12.
Dimensions for initial design on Watt-chain mechanism.
Based on Figure 12, Sin = 250 + 9.55 = 259.55 mm. If the input slider is pushed to move 259.55 mm in 1 s (β = 1 s) with MS motion. Then, according to equations (9) to (13), by the finite difference method, the velocity, and acceleration, and force ratio curves of the output mold are drawn as Figure 13(a) to (c), respectively. The output mold maximum velocity Vmax is 778 mm/s, maximum acceleration amax is 3752 mm/s2, and maximum force ratio (Fin/Fout)max is 2.60.
Figure 13.
The output characteristic curves of the clamping mold (first design).
In conclusion,
At the close position shown in Figure 12(a), the force ratio is 0 (Fin/Fout = 0), the mechanism has double-toggle effects.
At the open position shown in Figure 12(b), the force ratio is 2.6 (Fin/Fout = 2.6), which means the driving force (Fin) is 2.6 times of output load (Fout).
For this Watt-chain double-toggle mechanism, the maximum acceleration for output mold is 3752 mm/s2 and the maximum force ratio at the open position is 2.6, which are better than the multiple-joint mechanism with a maximum acceleration of 4244 mm/s2 and a force ratio of 3.2. Therefore, the optimal design in the next section will use the Watt-chain double-toggle mechanism as the base model.
Optimal design on Watt-chain double-toggle mechanism
As the result of the analysis of both mechanisms in the previous section, the Watt-chain double-toggle mechanism is chosen for optimal design. Figure 14(a) and (b) shows the skeleton of the close and the open position on the Watt-chain mechanism.
Figure 14.
The skeleton for the Watt-chain double-toggle mechanism.
Optimal design process
The optimal design process on the Watt-chain double-toggle mechanism can be summarized as,
Step 1. Draw the skeleton of the Watt-chain mechanism at the close position with double-toggle effects, as shown in Figure 14(a), and decide the values of three design variables (r3, r4b, and α); then, values for r2y and r2x, c can be calculated.
Step 2. Draw the skeleton of the Watt-chain mechanism at the open position, as shown in Figure 14(b), and the value for r2x,o can be calculated. The stroke of the input slider is, Sin = r2x, c − r2x,o.
Step 3. Set the input slider to be pushed to move Sin in 1 s (β = 1 s) with MS motion, according to equations (9) to (13), the velocity, acceleration, and force ratio curves for the output clamping mold can be obtained.
Step 4. Change to other values for three design variables (r3, r4b, and α) and repeat steps 1 to 3 for the Watt-chain mechanism to get the optimal design.
Objective function
For the mechanism shown in Figure 13, r4a and r5 are identified to be 250 mm, that is, r4a = r5 = 250 mm. Here, the objective function Fo is defined as,
| (14) |
Where: W1 is the weight coefficient of amax identified as 1, and W2 is the weight coefficient of (Fin/Fout)max identified as 1000. According to equation (14), the objective function of the mechanism, shown in Figure 12, is . The result of the mechanism, shown in Figure 12, is shown in No. 1 of Table 1.
Table 1.
The design results based on the optimal design process.
| Design variables | Acceleration | Force ratio | Objective function | |||||
|---|---|---|---|---|---|---|---|---|
| No. | r3 (mm) | r4b (mm) | α | r2y (mm) | Sin (mm) | amax (mm/s2) | (Fin/Fout)max | Fo |
| 140 | – | – | 140.00 | 242.25 | 4244 | 3.20 | 7444 Multi-joint 22 | |
| 1 | 130 | 30 | 90° | 160.00 | 259.68 | 3752 | 2.60 | 6352 Initial design |
| 2 | 130 | 40 | 90° | 170.00 | 261.98 | 3597 | 2.66 | 6257 |
| 3 | 130 | 30 | 80° | 159.54 | 259.25 | 3700 | 2.57 | 6270 |
| 4 | 130 | 30 | 60° | 155.98 | 255.05 | 3667 | 2.6 | 6267 |
| 5 | 135 | 30 | 90° | 165 | 268.46 | 3670 | 2.47 | 6140 |
| 6 | 135 | 30 | 60° | 160.98 | 263.05 | 3612 | 2.49 | 6102 |
| 7 | 140 | 30 | 90° | 170.00 | 276.75 | 3615 | 2.36 | 5975 |
| 8 | 140 | 30 | 80° | 168.54 | 275.78 | 3586 | 2.36 | 5946 |
| 9 | 140 | 30 | 70° | 168.19 | 273.67 | 3574 | 2.37 | 5944 |
| 10 | 140 | 30 | 60° | 159.68 | 270.59 | 3576 | 2.40 | 5976 |
| 11 | 140 | 30 | 50° | 162.98 | 266.68 | 3593 | 2.45 | 6043 |
| 12 | 140 | 30 | 40° | 159.28 | 262.15 | 3618 | 2.51 | 6128 |
| 13 | 140 | 40 | 60° | 176.64 | 278.61 | 3476 | 2.28 | 5756 |
| 14 | 140 | 40 | 50° | 170.64 | 273.18 | 3497 | 2.34 | 5837 |
| 15 | 140 | 40 | 40° | 165.71 | 266.95 | 3525 | 2.42 | 5945 |
| 16 | 140 | 50 | 50° | 178.30 | 278.99 | 3428 | 2.26 | 5688 |
| 17 | 140 | 52 | 50° | 179.83 | 280.03 | 3418 | 2.24 | 5658 |
| 18 | 140 | 50 | 40° | 172.14 | 271.04 | 3464 | 2.35 | 5814 |
| 19 | 145 | 30 | 60° | 170.98 | 277.69 | 3553 | 2.33 | 5883 |
| 20 | 145 | 30 | 50° | 167.98 | 273.69 | 3568 | 2.38 | 5948 |
| 21 | 145 | 40 | 50° | 175.7 | 279.67 | 3486 | 2.29 | 5776 |
| 22 | 145 | 50 | 40° | 177.19 | 276.97 | 3467 | 2.31 | 5777 |
| 23 | 150 | 30 | 40° | 169.28 | 275.63 | 3579 | 2.38 | 5959 |
| 24 | 150 | 30 | 30° | 165.00 | 270.5 | 3607 | 2.44 | 6047 |
| 25 | 150 | 40 | 30° | 170.00 | 272.64 | 3550 | 2.40 | 5950 |
| 26 | 150 | 50 | 30° | 175 | 274.09 | 3510 | 2.37 | 5880 |
The bold value in Table 1 (No. 17) is the optimal value of the design, and No.1 is the initial design.
For the Watt-chain double-toggle mechanism shown in Figure 14, if the three design variables (r3, r4b, and α) are identified, based on equations (9) to (14), the values of r2y, Sin, amax, (Fin/Fout)max, and Fo can be calculated and shown in Table 1. According to Table 1, the three design variables with Min. value of Fo can be regarded as optimal design.
Optimal design
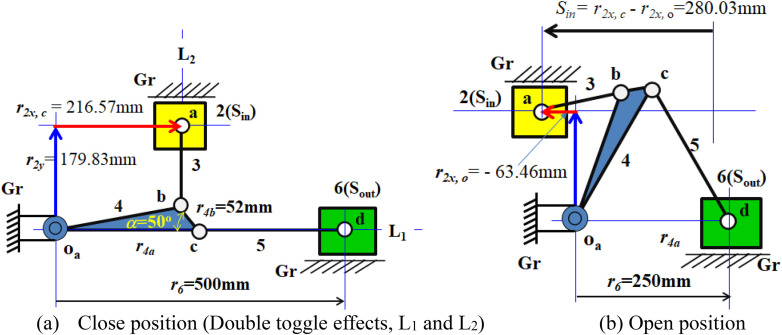
According to Table 1, design No. 17 is the optimal design out of 26 trials. For design No. 17, the design variables are, r3 = 140 mm, r4b = 52 mm, and α = 50°; the calculated values are, r2y = 179.83 mm and Sin = 280 mm which is at the upper limit. This mechanism skeleton of the close and open position is shown in Figure 15(a) and (b). This optimal design has amax = 3418 mm/s2, (Fin/Fout)max = 2.24, and Fo = 5658. Figure 16(a) to (c) shows the velocity, acceleration, and force ratio curves for the output mold based on the input slider being pushed to move 280 mm in 1 s (β = 1 s) with MS motion. The output mold maximum velocity Vmax is 733 mm/s, the maximum acceleration amax is 3418 mm/s2, and the maximum force ratio (Fin/Fout)max is 2.24 which has a significant improvement from the initial design.
Figure 15.
The optimal design for the Watt-chain mechanism (r3 = 140 mm, r4b = 52 mm, and α = 50°).
Figure 16.
The output characteristic curves of the clamping mold (optimal design).
According to the above results, it is concluded:
For this optimal design, the maximum acceleration for output mold is 3418 mm/s2 (amax = 3418 mm/s2), which is reduced by 19.5% from the multiple-joint mechanism in the patent. 1
For the mold mechanism at the open position as Figure 15(b), the force ratio is 2.24 (Fin/Fout = 2.24), the driving force (Fin) of the optimal design is reduced by 30% from the multiple-joint mechanism in the patent 1 (reduced from 3.2 to 2.24).
During the optimal design process, a trend can be referred to as the larger Sin is, the better kinematic characteristics will be on the Watt-chain double-toggle mechanism.
Conclusion
This Study proposes an optimal design process on Watt-chain double-toggle mold clamping mechanism. By following the optimal design process, the optimal design is accomplished. The optimal design on Watt-chain double-toggle mold clamping mechanism is better than the multiple-joint double-toggle mold clamping mechanism in the patent 1 by reducing 19.5% of acceleration and 30% of driving force. In summary, with the larger Sin, the kinematic characteristics on the Watt-chain double-toggle mold clamping mechanism would be better. The results of this study could be the design reference in engineering design mold clamping mechanisms of the plastic injection molding machines.
Footnotes
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The authors are grateful to Chum-power Machinery Co., Ltd for the support of this research under 108AF082.
ORCID iD: Tzu-Hsia Chen https://orcid.org/0000-0002-5379-1593
References
- 1.Lai GX, Su WF, Lin GX. The mold clamping mechanism of servo-drive type injection molding machine. Taiwan Patent 542097, Jul. 11, 2003.
- 2.Jiang FQ. Driving device of controlling mold opening and closing for plastic molding machine. Taiwan Patent M257273, Feb. 21, 2005.
- 3.Chang WT, Wu LY. Ten-link clamping mechanism with double dead-positions. Taiwan Patent I382913, Jan. 21, 2013.
- 4.Mathy JM, Oles PM, Fiorani DN. Modular clamp station. US Patent No.20130243898, 2013.
- 5.Li J, Li GW. All-electric plastic injection machine. Taiwan Patent M510231, Oct. 11, 2015.
- 6.Lin WY, Chang YC, Cheng Zet al. et al. New fast five-point locking mechanism with two dead-position configurations. Taiwan Patent M510233, Oct. 11, 2015.
- 7.Chen YY, Qin JC. Clamping device for mold. Taiwan Patent I537121, Jun. 11, 2016.
- 8.Lin WY, Chang YC, Xiao YJ. New five-point clamping mechanism with two dead-position configurations for injection molding machine. Taiwan Patent M54s1943, Mar. 21, 2017.
- 9.Taro O, Hiroshi M. Injection molding machine. Taiwan Patent I594867, Aug. 11, 2017.
- 10.Yang CK. Electric tooling locking apparatus for plastic injection machine. Taiwan Patent I600520, Oct. 01, 2017.
- 11.Sugahara K. Machine base for injection molding machine. US Patent No.20180168431, 2018.
- 12.Chen TH, Hsieh LC. The innovative design of the massage mechanisms for massage chair. Adv Technol Innov 2019; 4: 116–124. [Google Scholar]
- 13.Hsieh LC, Liu JY, Hsu MH. Systematic design of south pointing chariots with planetary gear trains. Trans Can Soc Mech Eng 1996; 20: 421–435. [Google Scholar]
- 14.Hsieh WH. Kinematic synthesis of cam-controlled planetary gear trains. Mech Mach Theory 2009; 44: 873–895. [Google Scholar]
- 15.Li H, Zhang Y. Seven-bar mechanical press with hybrid-driven mechanism for deep drawing; part 1: kinematic analysis and optimum design. J Mech Sci Technol 2010; 24: 2513–2160. [Google Scholar]
- 16.Hsieh WH, Tsai CH. On a novel press system with six links for precision deep drawing. Mech Mach Theory 2011; 46: 239–252. [Google Scholar]
- 17.Hsieh LC, Chen TH. The systematic design of planetary-type grinding devices for optical fiber ferrules and wafers. Trans Can Soc Mech Eng 2016; 40: 619–630. [Google Scholar]
- 18.Chen FC, Tzeng YF, Chen WR. On the mechanism design of an innovative elliptical exerciser with quick-return effect. Int J Eng Technol Innov 2018; 8: 228–239. [Google Scholar]
- 19.Chen TH, Hsieh LC. The design of mold clamping mechanisms with two dead-position configurations. Adv Technol Innov 2019; 5: 33–44. [Google Scholar]
- 20.Yuan ZF, Gilmartin MJ, Douglas SS. Optimal mechanism design for path generation and motions with reduced harmonic content. ASME Trans J Mech Des 2004; 126: 191–196. [Google Scholar]
- 21.Hsieh LC, Chen TH. The systematic design of link-type optical fiber polisher with single flat. J Adv Sci Lett 2012; 9: 318–324. [Google Scholar]
- 22.Hsieh LC, Chen TH, Lai PC. The kinematic design of mold clamping mechanism with minimal maximum acceleration. J Adv Mech Eng 2020; 12: 1–12. [Google Scholar]