Abstract
This work introduces a 4D flow magnetic resonance imaging (MRI) pressure reconstruction method which employs weighted least-squares (WLS) for pressure integration. Pressure gradients are calculated from the velocity fields, and velocity errors are estimated from the velocity divergence for incompressible flow. Pressure gradient errors are estimated by propagating the velocity errors through Navier-Stokes momentum equation. A weight matrix is generated based on the pressure gradient errors, then employed for pressure reconstruction. The pressure reconstruction method was demonstrated and analyzed using synthetic velocity fields as well as Poiseuille flow measured using in vitro 4D flow MRI. Performance of the proposed WLS method was compared to the method of solving the pressure Poisson equation which has been the primary method used in the previous studies. Error analysis indicated that the proposed method is more robust to velocity measurement errors. Improvement on pressure results was found to be more significant for the cases with spatially-varying velocity error level, with reductions in error ranging from 50% to over 200%. Finally, the method was applied to flow in patient-specific cerebral aneurysms. Validation was performed with in vitro flow data collected using Particle Tracking Velocimetry (PTV) and in vivo flow measurement obtained using 4D flow MRI. Pressure calculated by WLS, as opposed to the Poisson equation, was more consistent with the flow structures and showed better agreement between the in vivo and in vitro data. These results suggest the utility of WLS method to obtain reliable pressure field from clinical flow measurement data.
Keywords: Magnetic resonance imaging (MRI), pressure reconstruction, velocity error estimation, weighted least-squares
I. Introduction
Pressure measured from the cardiovascular system is widely used to diagnose disease. Many pressure-based clinical biomarkers, such as pulmonary wedge pressure [1], are single point measurements typically acquired by placing a pressure catheter in the region of interest [2]. However, this approach is invasive and still only provides a point measurement. Conversely, a spatial pressure distribution can provide a more complete view of the hemodynamics in the cardiovascular system. For example, the pressure distribution in the posterior communicating artery bifurcation has been explored and its correlation with the locations of the rupture of infundibulae or progression to aneurysms was established [3]. Further, such pressure distributions can be obtained noninvasively. One such noninvasive approach includes estimating the pressure difference from Doppler echocardiography and is typically employed for evaluating intra-ventricular pressure difference [4], [5]. However, conventional Doppler Ultrasound only measures one component of the velocity which limits the accuracy of the estimated pressure difference. Pressure fields can also be obtained using computational fluid dynamics (CFD) simulations, but fidelity of the simulation depends on the accuracy of segmentation and flow boundary conditions prescribed to the solver. These assumptions, as well as solver parameters have been shown to have a significant effect on the resulting flow field [6], [7]. In [8], the flow fields and flow-derived metrics were compared across cerebral aneurysm flow data obtained with in vivo 4D flow, in vitro PTV, and CFD. Minor flow field variations were found between modalities due to differences in the modeling assumptions and resolution limitations. High-resolution CFD simulations are also computationally expensive. Pressure reconstruction methods have become increasingly of interest with the development of flow measurement techniques such as 4D flow magnetic resonance imaging (MRI) which measures time-resolved velocity fields. However, several error sources and limitations inherent to in vivo 4D flow MRI result in unreliable pressure fields. The setting of velocity encoding (venc) parameter for a 4D flow acquisition is determined by the maximum velocity expected in the region of interest. Velocity greater than the venc leads to velocity aliasing, while higher venc settings lead to increased noise which affects 4D flow measurements in low velocity regions [9]. Artifacts such as concomitant gradient fields and eddy currents affect the accuracy of measured phase differences [10]. The partial volume effect and intravoxel dephasing are also common sources of systematic errors, especially for voxels near lumen boundaries [11]. For in vivo measurements, the limited scan time results in decreased spatiotemporal resolution and increased image artifacts [10]. Thus, a robust algorithm is needed to accurately reconstruct the pressure field from 4D flow MRI.
Several algorithms have been proposed to evaluate the pressure field from measured flow data. Most algorithms contain two major steps. The pressure gradient fields are first calculated from the velocity fields, which are then spatially integrated to obtain the instantaneous pressure fields.
For blood flow, the pressure gradient can be calculated using the incompressible Navier-Stokes momentum equation in the following form [12]-[16]:
| (1) |
where is pressure (Pa), is the spatial gradient operator such that is the pressure gradient (Pa/m), and are the density (kg/m3) and dynamic viscosity (Pa·s) of the fluid, respectively, is the velocity (m/s), and is time (s). represents viscous diffusion. and represent the local and convective accelerations (m/s2), respectively. The body force term has been ignored in (1) and in the following equations but it could be included.
With pressure gradients calculated from velocity data using (1), the pressure field can be reconstructed by spatially integrating the pressure gradient field. One approach to this reconstruction calculates the pressure at each point in the flow field by integrating the pressure gradient along one path or multiple paths [12], [17]. Path integration methods are rarely employed for 3D flow data due to the high computational cost. The most common approach for reconstructing pressure fields from 3D velocity data is by solving the pressure Poisson equation (PPE) in the following form [13]-[15], [18], [19]:
| (2) |
where is the pressure gradient field evaluated from the velocity field and is the divergence operator which evaluates the divergences from a vector field. This approach has been successfully applied to both engineering applications [13]-[15], [18], [19] and cardiovascular velocity measurements from phase-contrast MRI [20–24]. For incompressible flow, equation (2) is valid for both steady and unsteady conditions. Boundary conditions are required for solving (2), which can be Dirichlet boundary conditions with prescribed pressure values, Neumann boundary conditions with prescribed pressure gradient values, or a mix of the two types. As discussed in [25], both the path integration method and the method of solving the pressure Poisson equation can be regarded as global optimization formulations of the pressure-gradient spatial integration. Another method that falls into this category is a least-squares reconstruction method referred to as ordinary least-squares (OLS) reconstruction in this study [26]. For OLS, the pressure integration is performed by solving the following linear system:
| (3) |
where is the discrete gradient matrix, and is the unknown pressure field written as a column vector. Equation (3) is an over-determined linear system for 2D and 3D flow data. The OLS method solves the pressure field by minimizing the pressure gradient residuals in a least-squares sense as:
| (4) |
where is the L2 norm. In matrix form, equation (4) becomes:
| (5) |
As stated in [27], OLS reconstruction and Poisson share the same theoretical foundation, and solving the pressure Poisson equation with Neumann boundary conditions is mathematically equivalent to the solving the OLS formulation.
Due to the measurement inaccuracies in the in vivo 4D flow MRI, the calculated pressure gradient fields contain propagated errors. However, the above-mentioned pressure reconstruction methods do not have any way to account for or reduce the effect of such erroneous pressure gradient values. In order to improve the accuracy of reconstructed pressure fields, a weighted least-squares (WLS) reconstruction method for spatial integration of pressure gradients is introduced in this work. In this method, pressure fields are solved by minimizing the WLS of the pressure gradient residuals. The weights are determined based on estimated pressure gradient errors. To estimate such pressure gradient errors, velocity errors are calculated from the velocity divergence for incompressible flow and propagated through (1). Smaller weights are assigned to inaccurate pressure gradient values such that their effects are reduced during spatial integration. The performance of WLS was tested using synthetic velocity fields and in vitro Poiseuille flow measured using 4D flow MRI. The method was then applied to in vivo 4D flow MRI velocity data acquired for two aneurysms and in vitro PTV velocity data collected in patient-specific aneurysm models.
II. Methodology
A. Pressure reconstruction using weighted least-squares
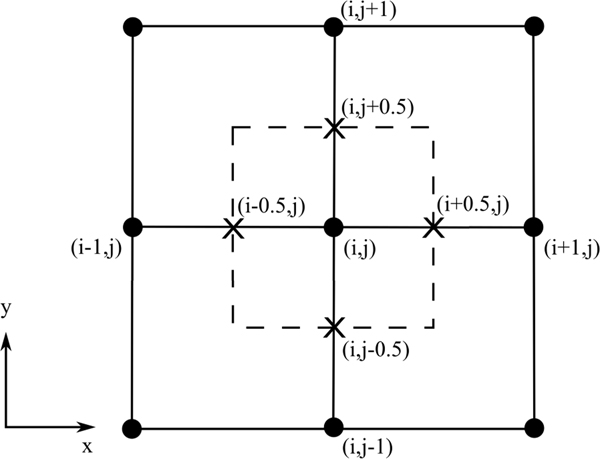
Pressure gradient fields were calculated from velocity fields using (1). Velocity data employed in this study were on Cartesian grids with velocity values located on grid nodes. A second order central (SOC) difference scheme was employed to evaluate the temporal and spatial derivatives of the velocity fields. Pressure gradient values were calculated on grid nodes, then linearly interpolated to the face centers of each grid cell. The SOC scheme and grid arrangement are demonstrated in Fig. 1. SOC computes the gradient at each point from its neighboring points, e.g., , where is the grid size. The reconstructed pressure values are on grid nodes.
Fig. 1.
Grid arrangement and SOC scheme demonstrated using a 2D Cartesian grid. The grid nodes are labeled by dots. A grid cell is drawn using dashed lines. Cell face centers are labeled by “X” marks.
The pressure field is obtained by solving
| (6) |
which gives the pressure result that minimizes the least-squares of pressure gradient residuals as
| (7) |
where is the weight matrix. is a diagonal matrix containing positive elements as weights for pressure gradient values . Greater weights are assigned to pressure gradient values anticipated to be more accurate. Unlike the Poisson equation, WLS reconstruction does not require boundary conditions to be explicitly assigned as the Poisson equation does. A minimum of one pressure reference point is needed. Pressure at the reference point can be obtained from direct measurement or a far-field pressure condition. If only the pressure differences between points in the flow field are of interest, the selection of reference point and reference pressure is arbitrary, e.g., zero pressure can be assigned at one point along the boundary.
B. Velocity error estimation from spurious divergence
For incompressible flow, the divergence of the true velocity field should be zero, expressed mathematically as:
| (8) |
where is the true velocity field. Because measured velocity data inevitably contain errors, the divergence of the measured velocity field is typically nonzero. The spurious divergence equals the divergence of the velocity error field as
| (9) |
where is the measured velocity field, is the velocity error field, and . Equation (9) forms an underdetermined linear system as there are less rows than columns in the discretized divergence operator . Thus, cannot be uniquely determined from (9). We estimate by finding the least-squares solution to (9) as
| (10) |
where is the estimated velocity error field. Previous studies have similarly employed the spurious velocity divergences to estimate the uncertainty of velocity data measured using tomographic particle image velocimetry (PIV) [28].
C. Generation of weight matrix
The pressure gradient error field is estimated by propagating through (1) as
| (11) |
where is the estimated pressure gradient error field and denotes evaluating (1) using the given velocity field.
Accuracy of the at each point from each time frame is determined from the weighted standard deviation (WSTD) of the estimated pressure gradient errors from neighboring points given as
| (12) |
where is an estimation of the pressure gradient uncertainty and is the number of points that are employed in the WSTD calculation. Weights for WSTD calculations are determined using a bivariate Gaussian function:
| (13) |
where and are the spatial and temporal separations from the neighboring points to the point of interest, respectively. and are the correlation lengths along the temporal and spatial dimensions which are determined by the numerical difference scheme. Based on the SOC scheme employed for calculation, neighboring values should not be correlated farther than spatially and temporally. Thus, the correlation lengths were chosen to be and . In addition, only points within the and neighborhood were employed in the WSTD calculation.
The weight matrix for WLS reconstruction is given by
| (14) |
where is the diagonal matrix generated from given diagonal elements. To avoid singularities due to zero weights, a lower bound of weights is given as 10−9 multiplied by the average of all weight elements.
D. Implementation of pressure reconstruction methods
The method of solving the PPE (denoted as ‘Poisson’ herein) was employed in this study to compare to the WLS method for evaluating its performance. The same formulation of PPE was employed in the present study as in [20–24] which considered both inertial and viscous effects of the blood flow. For the Poisson algorithm, pressure gradient fields were calculated from (1) by SOC and the grid arrangement described in section II-A. Divergence of the pressure gradients were calculated using SOC and employed as the source term for the pressure Poisson equation. At least one grid point along the boundary was prescribed with zero pressure as the Dirichlet boundary condition for both methods. Pressure gradients at all the other boundary points were employed as the Neumann boundary condition for solving the pressure Poisson equation. SuperLU, a general-purpose library for the direct solution of large, sparse, nonsymmetric systems of linear equations [29], was employed to solve (2) and (6) for the reconstructed pressure fields.
E. Synthetic flow fields
Two flow fields were used for validating and analyzing the pressure reconstruction methods. The first is a 2D Lamb-Oseen vortex ring flow field which consists of two counter-rotating vortices. Velocity of each vortex can be described by
| (15) |
where is the angular velocity, is the distance from the center of the vortex, is the distance where the maximum angular velocity is reached, and with . The constant was set to be 1.25643 according to [30]. The center points of vortices were separated by with . A free stream velocity component was added to make the flow steady as
| (16) |
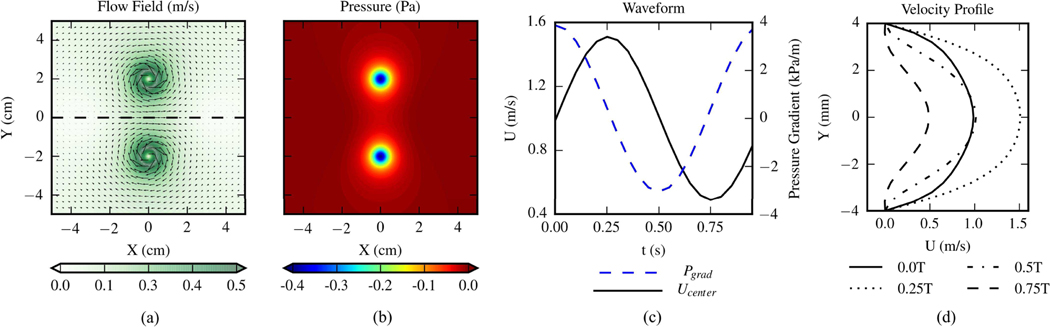
The exact velocity fields were generated on a uniform Cartesian grid with 652 grid points. The size of the domain was . The exact pressure field was obtained by numerically integrating the pressure gradients on a denser Cartesian grid with 1292 points. Fluid density was 1kg/m3 and the flow was inviscid. Fig. 2 (a) and (b) present the exact velocity and pressure field, respectively.
Fig. 2.
(a) Exact velocity field of the 2D Lamb-Oseen vortex ring. The vectors indicate the flow direction and color scale of the contours corresponds to velocity magnitude. The flow field is divided by the black dashed line into top and bottom halves. (b) Exact pressure field of the 2D vortex ring flow. (c) Waveforms of pressure gradient and centerline streamwise velocity within one cycle of the 2D pulsatile flow. (d) Streamwise velocity profiles at 4 time points in a cycle of the 2D pulsatile flow.
The second is 2D pulsatile flow between two parallel infinite plates driven by the unsteady pressure gradient given as
| (17) |
where the × direction is streamwise, is the ratio between the magnitude of the steady pressure gradient component and the amplitude of the oscillating pressure gradient component, K is the constant controlling the overall strength of the pressure gradient, and is the angular speed of the oscillating component. The velocity profile can be expressed as
| (18) |
with , where is the spanwise direction, is the channel half-width, and is the centerline velocity of the steady flow component. In this paper the flow field contains a 20 mm long channel with a of 4 mm. Blood-mimicking fluid properties were employed with of and of 0.0033 Pa·s. was set to be and the Womersley number of the flow was 5.75. was set to be 1m/s, and the other parameters were given as , , and . Fig. 2 (c) shows the waveforms of pressure gradient and centerline streamwise velocity component within one cycle. Fig. 2 (d) shows the streamwise velocity profile at 4 phases in a cycle. The flow fields were generated on a uniform Cartesian grid with a spatial resolution of 0.4×0.4 mm2, yielding 21×51 grid points in the field. This type of flow was employed in [16] to assess the performances of pressure reconstruction methods.
In order to test the robustness of the pressure reconstruction methods to errors in the velocity data, noise was added to the velocity fields in a manner similar to that done in [16], [31], which is designed to mimic experimental noise. Noise was added as a vector with a normally distributed magnitude and random direction at each point. The error magnitude can be expressed by
| (19) |
where is the error percentage level. For the vortex ring flow, two types of velocity noise distributions were considered which are referred to as ‘Uniform Noise Distribution (UND)’ and ‘Spatially Varying Noise Distribution (SVND)’ in this study. For UND, the measurement quality was uniform across the field, and was set to be consistent across the field. 26 UND test cases were generated with varying linearly from 1 to 51%. For SVND, the flow field was divided into a “top half” and “bottom half” with different values of applied to each half. A total of 7 cases were generated with varying exponentially from 8% to 64%, and set to 8% for all cases. For each test case with UND or SVND, 100 time frames were created with a sampling frequency of 50 Hz (). 0 Pa was assigned at the left end of the dashed horizontal line in Fig. 2(a) as the reference pressure. For the pulsatile flow, 26 UND test cases were generated with varying linearly from 1 to 51%. 1000 frames were created for a time span of 50 cycles, yielding 20 frames per cycle and a temporal resolution of 0.05 s. Dirichlet boundary condition with zero pressure was applied to the inlet of the 2D channel as the reference pressure.
F. In vitro 4D Poiseuille flow
Experimental measurements of steady, laminar Poiseuille flow in a circular pipe were acquired using 4D-flow MRI. The Poiseuille flow allowed the usage of an analytical pressure field as the benchmark to assess the accuracy of the reconstructed pressure. A blood mimicking water-glycerol solution with a density and viscosity of 1110 kg/m3 and 0.00372 Pa·s, respectively, was used as the working fluid. The volume ratio between water and glycerol was 60:40. A small amount (0.66 mg/mL) Gadolinium contrast was added to enhance the signalto-noise ratio (SNR) of the 4D flow MRI scan without altering the rheology of the fluid. A computer-controlled gear pump drove the working fluid at a steady flow rate of 7.6 mL/s. The diameter of the pipe was 12.7 mm and the length was sufficiently long prior to entering the MRI field of view to ensure a fully developed velocity profile. The 4D flow MRI scan was performed on a Siemens 3T PRISMA scanner at a spatial resolution of 0.85 × 0.85 × 0.8 mm3. A total of 12 time frames were collected. The venc of this 4D flow MRI scan (prospectively triggered time-resolved 3D PC MRI with 3-directional velocity encoding) was set to 16 cm/s, which is sufficiently high to avoid velocity wrapping. The echo time (TE) and repetition time (TR) were 5.87 ms and 8.60 ms, respectively. The yielded temporal resolution was 120.4 ms. The bandwidth was 455 kHz and flip angle was 15°. The 4D-flow MRI images were pre-processed (phase offset correction, noise filtering) using a customized Matlab-based software package, Velomap-Tool, developed at University Medical Center Freiburg [32].
The analytical velocity field of the Poiseuille flow is given by:
| (20) |
where is the axial (along z-axis) velocity component (m/s), is the radial distance from the pipe centerline (m) which equals to and is the axial pressure gradient (Pa/m). The velocity components along other axes ( and ) are 0. The axial pressure gradient is defined by:
| (21) |
where is the volumetric flow rate (m3/s). This yields a linear analytical pressure drop along the pipe. The analytical velocity and pressure fields were considered as the ground truth for error analysis.
G. In vivo and in vitro flow in cerebral aneurysms
In vivo flow data in a basilar tip aneurysm were acquired at San Francisco VA Medical Center and an internal carotid artery (ICA) aneurysm was imaged at Northwestern Memorial Hospital (NMH). Both aneurysms were acquired with 4D flow MRI on a 3T MRI scanner (Skyra, Siemens Healthcare, Erlangen, Germany). An ECG-gated RF spoiled 4D-flow MRI sequence (Siemens WIP sequence) was used with gadolinium contrast for imaging the basilar tip aneurysm, while no contrast was used for the ICA aneurysm. Aliasing, phase offsets, and noise were corrected. Velocity data from the in vivo measurements were obtained on Cartesian grids. The spatial resolution was 1.25×1.25×1.33 mm3 for the basilar tip aneurysm and 1.09×1.09×1.30 mm3 for the ICA aneurysm. The temporal resolutions were 40.5 ms (20 frames per cycle) and 44.8 ms (13 frames per cycle) for the basilar tip aneurysm and the ICA aneurysm, respectively.
In vitro PTV velocity data was obtained using a 1:1 scale models of the patient-specific aneurysms. To reproduce the in vivo flow field, the inflow was driven by a computer-controlled gear pump with the inlet flow based on the in vivo data. DaVis 10.0 (LaVision Inc.) was used to process the particle images. Shake the Box (STB), a particle tracking method, was used to compute the velocity fields. The unstructured STB velocity fields were interpolated to Cartesian grids. For the basilar tip aneurysm, the grid size was 0.3 mm and the temporal resolution was 2.5 ms. For the ICA aneurysm, the grid size was 0.4 mm and the temporal resolution was 1.5 ms. Blood mimicking fluids composed of water-glycerol-urea were employed with the details provided in Table I [33]. More details on the in vivo and in vitro measurements can be found in [8]. To mimic the in vivo 4D flow data, another dataset was created for each aneurysm by virtual spatial voxel averaging the in vitro PTV data, then temporally downsampling to the same frequency as the 4D flow measurement. Thus, the voxel-averaged and subsampled dataset (referred to as ‘PTV-voxavg’ herein) had the same spatial and temporal resolution as the corresponding in vivo 4D flow MRI dataset.
TABLE I.
Composition and properties of blood mimicking fluids used for in vitro measurements
| Geometry | Composition (%wt) | Density (kg/m3) | Kinematic Viscosity (m2/s) | ||
|---|---|---|---|---|---|
| Water | Glycerol | Urea | |||
|
| |||||
| Basilar tip | 44.8 | 32.8 | 22.4 | 1103 | 3.04×10−6 |
|
| |||||
| ICA | 45.3 | 29.7 | 25.0 | 1132 | 3.50×10−6 |
III. Results
A. Lamb-Oseen vortex ring
1). Velocity and pressure gradient error estimation:
To validate the error estimation algorithm employed in this study, the estimated velocity and pressure gradient errors were compared with the exact errors from all the Lamb-Oseen vortex cases. As a demonstration, the distributions of estimated and exact errors from the case with and being 8 and 32%, respectively, are shown in Fig. 3. Fig. 3(a) and (b) present the comparisons on velocity error magnitudes versus and pressure gradient error magnitudes versus respectively. Fig. 3(c) compares with the pressure gradient uncertainty evaluated as the root-mean-square (RMS) of from all time frames. For both estimated and exact errors, the magnitudes were greater in the top half of the field than in the bottom half, and greater in the vortices than in the ambient regions, as suggested by the spatial distributions. The estimated magnitudes were lower than the corresponding exact magnitudes as suggested by the medians from the histograms in Fig. 3. The median of was 5.5% while it was 6.0% for . The medians of and were 4.5% and 6.3%, respectively. The median of was 6.6% while it was 8.6% for . The error estimation algorithm performed consistently for all the cases.
Fig. 3.
Examples of the estimated error distributions compared with the exact error distributions from the SVND case with being 32% and being 8% for the 2D vortex ring flow. The first two columns are the spatial distributions. The last column shows histograms of error magnitudes. The dashed vertical lines represent the medians of the distributions. (a) Comparison between exact velocity error magnitudes and estimated velocity error magnitudes. (b) Comparison between exact pressure gradient error magnitudes and estimated pressure gradient error magnitudes. (c) Comparison between the pressure gradient uncertainties and the WSTD of the estimated pressure gradient errors.
2). Pressure error analysis:
The errors in the pressure fields reconstructed using Poisson and WLS were analyzed and compared. Pressure errors () were quantified as the deviation between the reconstructed pressure and the exact pressure. and were normalized by the RMS of the exact pressure field and velocity field, respectively. The distributions of velocity and pressure error magnitudes are shown in Fig. 4 for three cases with being 8% while being 8%, 32%, and 64%. The spatial distributions in Fig. 4 presents the RMS of normalized errors from all time frames. As suggested by both the spatial distributions and the histograms, the pressure error magnitudes for were lower than those for Poisson . The medians of and were 0.8% and 1.2%, respectively, with being 8%, 1.6% and 3.6% with being 32%, and 2.4% and 8.3% with being 64%.
Fig. 4.
The spatial distributions of normalized velocity error magnitudes (1st column), normalized pressure error magnitudes (2nd and 3rd columns), and the histograms of normalized pressure error magnitudes (last column) for three test cases of the 2D vortex ring flow. The errors were normalized by the RMS of the exact fields. The vertical dashed lines in the histograms are medians of the distributions. The vertical dotted lines are the lower and upper limits of pressure error magnitudes. (a) , . (b) , . (c) , .
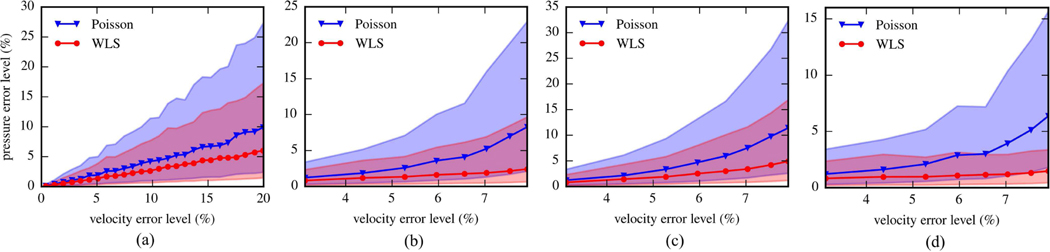
The performances of the pressure reconstruction methods are compared in Fig. 5(a) using results from all test cases with UND. The velocity error level for each case was determined as the median of the normalized velocity error magnitudes. As λ changed from 1 to 51%, the velocity error ranged from 0.39 to 19.9%. Similarly, the pressure error levels were determined as the median of the normalized pressure error magnitudes. For the noise level range used here, the pressure error for WLS increased from 0.10 to 6.0%, while it increased from 0.15 to 9.9% for Poisson. Thus, WLS maintained a 50% improvement on median pressure error over Poisson. Additionally, the lower and upper limits of the pressure errors were given as the 15.75th and 84.25th percentiles of the absolute error distribution, respectively. The upper limit for WLS increased from 0.28 to 17.3%, while it increased from 0.40 to 27.3% for Poisson. The lower limit for WLS increased from 0.025 to 1.44%, while it increased from 0.037 to 2.39% for Poisson.
Fig. 5.
The pressure error level versus velocity error level from the test cases of the 2D vortex ring flow. The error levels were determined as the medians of error magnitudes. The shaded areas are bounded by the upper and lower limits of pressure error magnitudes. (a) Results from UND cases with changing from 1% to 51%. (b) Results from SVND cases with changing from 8% to 64% and being 8%. (c) Pressure error levels in the top half of the flow fields shown as a function of velocity error levels for SVND cases. (d) Pressure error levels in the bottom half of the flow fields for SVND cases.
Fig. 5(b) compares the error levels for the two methods from all cases with SVND. As changed from 8 to 64% and stayed at 8%, the overall velocity error level increased from 3.1 to 7.9%. The pressure error for WLS increased from 0.8 to 2.4%, while the it increased from 1.2 to 8.3% for Poisson. The lower error limit ranged from 0.2 to 0.6% for WLS and from 0.3 to 2.1% for Poisson. The upper limit ranged from 2.4 to 9.7% for WLS and from 3.4 to 23.0% for Poisson. In addition to the overall pressure error level, the pressure error level within each half of the field was quantified and presented in Fig. 5(c) and 5(d), respectively. The pressure error level in the top half ranged from 0.8 to 4.9% for WLS and from 1.2 to 11.4% for Poisson, while that in the bottom half ranged from 0.8 to 1.4% for WLS and from 1.2% to 6.4% for Poisson.
B. 2D Pulsatile flow
The pressure fields were calculated from velocity fields for all cases using Poisson and WLS. Velocity and pressure errors were quantified by comparing to the analytical solutions. Fig. 6 (a) shows the pressure error levels as a function of the velocity error levels for results at 4 temporal phases. The velocity error level was evaluated as the median of the absolute velocity errors at all grid points normalized by . The pressure error level was the median of the absolute pressure errors at all grid points, and the pressure error limits were 15.75th and 84.25th percentiles. The pressure scale employed for the normalization was given as which was the dynamic pressure based on . As changed from 1 to 51%, the velocity error level increased from 0.3 to 15.3%. The ranges of pressure error levels were different at different phases. At peak systole (t/T=0.25), the pressure error level for Poisson increased from 0.6 to 40.6% and it increased from 0.7 to 20.1% for WLS. WLS reduced the pressure error level by around 100% for cases with velocity errors greater than 10%. At peak diastole, both methods accurately estimated the pressure fields as the pressure error levels were less than 3% for all cases.
Fig. 6.
(a) The pressure error level versus velocity error level from the test cases of 2D pulsatile flow at four time phases. The error levels were determined as the medians of normalized error magnitudes. The shaded areas are bounded by the upper and lower limits of pressure error magnitudes. (b) The normalized error distributions of velocity and reconstructed pressure fields as a function of y (spanwise) for the case of (velocity error level at 9.9%). (c) Histograms of the pressure error magnitudes for the two methods from the case of . The vertical dashed lines represent the medians and the vertical dotted lines are the error limits.
Fig 6 (b) shows the pressure and velocity error distributions as a function of Y (spanwise direction) for the case of with a velocity error level of 9.9%. WLS improved the pressure accuracy significantly in regions with lower velocity error level (near the walls). Fig 6 (c) compares the statistical distributions of the pressure error magnitudes by the two methods for the same case. The medians of and were 4.2% and 6.8%, respectively.
C. In vivo 4D Poiseuille flow
The analytical velocity field is shown in Fig. 7(a) together with a time frame from the measured velocity data. Fig. 7(b) compares the velocity errors () evaluated as the deviations between the analytical velocity and measured velocity with the velocity errors estimated based on velocity divergence (). The error magnitudes were normalized by the centreline velocity of the analytical field. For both and , the magnitudes were greater near the wall or close to the ends of the pipe.
Fig. 7.
(a) The velocity profiles of laminar pipe flow from analytical solution (left) and measurement (right). The velocity profiles are shown on x-y plane at z=0 mm and on x-z plane at y=0 mm. (b) The spatial distributions of normalized velocity errors shown as functions of r and z. (c) The spatial distributions of normalized pressure errors for Poisson and WLS. (d) Histograms of the pressure error magnitudes from the pressure fields reconstructed using Poisson and WLS.
Instantaneous pressure fields were reconstructed using Poisson and WLS from the measured velocity fields. The origin (r=0 mm, z=0 mm) was selected as the reference point with zero pressure. The pressure errors were evaluated as the deviation between analytical pressure and reconstructed pressure, then normalized by the analytical pressure drop across the measurement region (). Spatial distributions of the normalized pressure error magnitudes are presented as functions of r and z in Fig. 7(c). The pressure in the middle region of the pipe had significantly lower error when using WLS. To confirm this notion, the histograms of the relative pressure error magnitudes are shown in Fig. 7(d). The median of pressure error magnitude was 24.6 % for WLS and 35.6% for Poisson. The lower error limit was 7.8 % for WLS and 11.2% for Poisson. The upper error limit was 53.1% for WLS and 64.5% for Poisson.
D. Patient specific aneurysmal flow
The velocity fields at peak systole are presented using 3D pathlines in Fig. 8(a) and 2D contours with arrows in Fig. 8(b) for the in vivo4D flow and in vitro PTV data. The pressure fields reconstructed from the PTV data at peak systole using WLS are given in Fig. 8(c). Suggested by the 3D pathlines, the flow structures of the 4D flow and the PTV datasets are consistent for each aneurysm. For the basilar tip aneurysm, the inflow comes from the basilar artery and forms a vortical structure in the aneurysmal sac. For ICA aneurysm, the inflow comes from the curving ICA. Some of the flow enters the aneurysmal sac and forms the vortical flow structure inside before exiting through the distal ICA. The comparisons for the inflow rate and waveform were made across all modalities of the two aneurysms [8]. The flow rate values, and general waveform trends showed reasonable agreement. However, the PTV data was obtained with higher spatiotemporal resolution and was contaminated with less noise for both aneurysms. For the basilar tip aneurysm, the average flow rate error (difference between inflow and outflow flow rates normalized by the maximum flow rate for each modality) was 24.0% for the 4D flow data, and 6.9% for the PTV data. For the ICA aneurysm, the average flow rate errors were 17.3 and 3.6% for 4D flow and PTV, respectively. The lower average flow rate errors suggest better accuracy for PTV. The limited spatial resolution of the 4D flow MRI acquisition resulted in under-resolved velocity profiles and a lack of pathlines in the basilar and ICA aneurysms (Fig. 8a). As demonstrated in [34], at least 5–6 voxels across vessel diameter are required for accurate flow quantification. There were less than 4 image voxels across the basilar artery (Fig. 8b), which reduced the accuracy of velocity measurements and the subsequently computed flow metrics. In addition, a low MR signal region was identified in the ICA upstream of the aneurysmal sac, which also contributed to the discontinuity of the pathlines in Fig. 8(a) and the low velocity region in Fig. 8(b). These factors would cause greater errors in velocity fields as well as reconstructed pressure fields in those regions of 4D flow data.
Fig. 8.
(a) Velocity fields at peak systole represented using 3D pathlines from in vivo 4D flow MRI and in vitro PTV measurements for the basilar tip aneurysm and the ICA aneurysm. Shaded regions represent the geometries of the aneurysms. (b) Velocity fields on orthogonal slices represented using 2D contours with arrows. One arrow was drawn for each voxel from 4D flow data, while each arrow represents the velocity of 9 voxels for PTV data. (c) The pressure fields reconstructed using WLS method from PTV data. The planes correspond to the locations of the slices in (b).
As the flow structures are consistent, similar pressure fields are anticipated for the in vivo data and in vitro data. Thus, even given the noisy and under-resolved in vivo 4D-flow data, a robust pressure reconstruction method should be capable of obtaining similar pressure fields to those reconstructed from the in vitro PTV data. Pressure fields were reconstructed from each dataset using WLS and Poisson for each aneurysm. Fig. 9 compares the time series of pressure differences between several pairs of spatial points within the flow field. The locations of the points were labeled in Fig. 8(c). The discrepancies between the pressure differences of the three modalities were quantified for each pair of points and for each method. The RMS of the discrepancies was calculated and presented in Table II. WLS reduced the RMS discrepancies for most locations, with some reductions being more than 100%. The lower RMS discrepancies suggested better consistency between the pressure results from different modalities for WLS. The reduced signal in the 4D flow measurements of the ICA affected the calculated pressure difference between the inlet and sac shown in Fig. 9(b). Poisson overpredicted the pressure difference greatly, while WLS underestimated the pressure difference due to the low velocity caused by reduced signal in the ICA. WLS reduced the RMS discrepancy by 135% for this pair of locations. In general, WLS was more robust to velocity errors and the calculated pressure fields were more consistent with the measured flow field.
Fig. 9.
The time series of pressure differences between several points within the flow field. The pressure fields were reconstructed using the two methods from the datasets of basilar tip aneurysm (a) and ICA aneurysm (b). The locations of the points are given in Fig. 8(c).
TABLE II.
RMS discrepancies of pressure differences (Pa)
| Basilar tip | Locations | Inlet - tip | Inlet - center | Tip - center |
| Poisson | 9.1 | 13.3 | 6.3 | |
| WLS | 3.8 | 7.6 | 6.5 | |
|
| ||||
| ICA | Locations | Inlet - sac | Sac - outletl | Sac - outlet2 |
| Poisson | 16.7 | 13.2 | 18.3 | |
| WLS | 7.1 | 11.0 | 9.9 | |
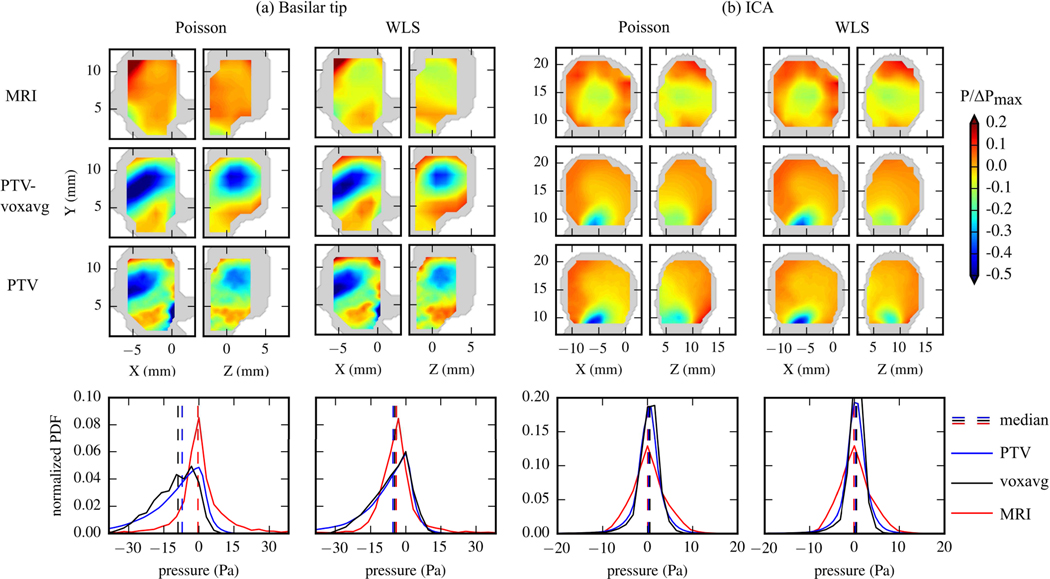
Fig. 10 compares the spatial distributions of pressure within the aneurysmal sacs from the in vivo 4D flow data and in vitro PTV and PTV-voxavg data. For 4D flow data, the pressure near the wall was not calculated due to the low signal intensity in near-wall voxels such that those measurements were less reliable. In addition, the pressure in the small branches were not calculated due to the insufficient number of voxels to perform the numerical differences. Thus, the pressure in these regions was not included in the following comparisons with pressure calculated from in vitro data. The spatial distributions were shown on the 2D planes whose locations were given in Fig 8(c). The pressure fields were normalized by the maximum pressure difference within the aneurysmal sac () from each modality. Additionally, the probability density function (PDF) histograms of the reconstructed pressure values in the aneurysmal sac from the entire cardiac cycle are shown in Fig. 10. For the basilar tip aneurysm given in Fig. 10(a), WLS showed better agreement across all datasets than Poisson in both the spatial distributions as well as the histograms. The median pressure values by Poisson were −0.4 Pa for 4D flow, −8.9 Pa for voxavg, and −7.1 Pa from PTV. The median values obtained using WLS were −4.1 Pa for 4D flow, −4.7 Pa for PTV-voxavg, and −5.5 Pa for PTV. The standard deviation of the medians was 3.7 Pa for Poisson and 0.6 Pa for WLS. This indicates that WLS maintained a tighter spread of the pressure values and more similarity across modalities, suggesting it is more robust to low-resolutions and high-noise velocity fields. To quantify the amount of change made by WLS compared to Poisson on the reconstructed pressure fields from each modality, the deviations between the pressure fields reconstructed by WLS and the pressure fields reconstructed by Poisson were quantified and normalized by . The total RMS of the normalized deviations was defined as the “effectiveness” of WLS on improving pressure reconstruction for each modality. The effectiveness was 28.7% for 4D flow, 17.9% for PTV-voxavg, and 8.7 % for PTV. For the ICA aneurysm given in Fig. 10(b), the median pressure value by Poisson was 0.06 Pa for 4D flow, 0.24 Pa for PTV-voxavg, and 0.52 Pa for PTV. The median by WLS was −0.07 Pa for 4D flow, 0.47 Pa for PTV-voxavg, and 0.25 Pa for PTV. The standard deviation of the medians was 0.19 Pa for Poisson and 0.22 Pa for WLS. The effectiveness of WLS was 34.2% for 4D flow, 6.8% for PTV-voxavg, and 11.9% for PTV.
Fig. 10.
Spatial and probability density distributions of pressure fields within the aneurysm sacs reconstructed using Poisson and WLS from each modality of the basilar tip aneurysm (a) and the ICA aneurysm (b). The spatial distributions are presented by the normalized pressure values on a x-y plane and a y-z plane cutting through the aneurysm sac at peak systole. Locations of the planes are given in Fig. 8(c). Shaded regions correspond to the geometry of the aneurysm. The probability distributions are evaluated using the values on all grid points at all cardiac phases within the aneurysm sac.
IV. Discussion and Conclusions
In this study we introduced a method which uses weighted least-squares for pressure integration. By assigning lower weights to less accurate velocity measurements and thus pressure gradient values, the WLS method reduces the effects of noisy measurements during the spatial integration, and improves the accuracy of the reconstructed pressure. Poisson and OLS can be seen as particular cases of WLS with uniform weights assigned to the pressure gradients. Compared to Poisson, the improvement made by WLS was a combination of the noise mitigation and the differences in the basic equations. However, the exact contribution of each aspect was not well understood, which is a limitation of this study. The accuracy of WLS relies on proper weight assignment. In this study, the weights were informed by the estimated velocity errors based on velocity divergence. Comparisons between exact velocity error and estimated velocity error demonstrated that the velocity error estimation algorithm used here was capable of recognizing high-error regions such that lower weights were assigned to the less accurate pressure gradients in these regions. Although the velocity and pressure gradient error magnitudes were found to be slightly underestimated by this algorithm, this is not expected to affect the performance of WLS. This is because underestimating the error magnitudes would have a similar effect as normalizing the weights by a constant greater than 1. Further, the weight matrix W appears on both sides of (6), therefore the weights can be normalized by any arbitrary nonzero, real constant while the pressure results remain the same. Thus, the spatial distribution of the estimated error is primarily what effects the accuracy of WLS as opposed to the error values themselves. It should also be noted that the weights can be informed by the pressure gradient reliabilities estimated using other algorithms. For velocity fields measured using PIV, there are algorithms to estimate the spatial distributions of velocity uncertainties [35],[36] and the pressure gradient uncertainties [37]. However, a corresponding algorithm for 4D-flow data has not been developed. The divergence-based algorithm employed in this study can be applied to velocity data measured from incompressible flows regardless of the measurement modality.
The WLS method reduces the spatial propagation of errors during pressure integration. From the spatial distributions of pressure errors for the synthetic Lamb-Oseen vortex flow in Fig. 4, it can be observed that WLS reduced pressure errors in the ambient regions as the greater errors were more confined to the vortices. In addition, in the bottom half of SVND cases was significantly less affected by the increase of as compared with . As observed in Fig. 5(d), as increased from 8% to 64% and stayed at 8%, the increase of the pressure error in the bottom half was 433% for Poison while only 75% for WLS. From the spanwise distributions of pressure errors for the 2D pulsatile flow in Fig. 6(b), WLS reduced pressure errors in the near-wall regions significantly as the greater errors were more confined around the centerline. This is also suggested by the spatial distributions of pressure errors from in vitro Poiseuille flow in Fig. 7(b) and (c). WLS confined the pressure errors to the regions with greater velocity errors (near the ends of the pipe) compared with Poisson. In previous studies, the spatial error propagation was reduced by segmenting the flow field into subdomains based on local velocity reliability, then reconstructing the pressure field in each subdomain sequentially in a descending order of reliability [26]. However, such an algorithm requires that the different levels of measurement reliability are spatially separable in the flow field such that the subdomains can be properly segmented. The WLS method proposed here does not require any segmentation, making it more usable across a larger variety of flow fields.
Improvement on pressure accuracy by WLS was more significant for velocity data with a greater range of errors. Results from synthetic Lamb-Oseen vortex flow fields demonstrated that the improvement by WLS was more significant for SVND cases with greater . Given in Fig. 5(b), the pressure error level for Poisson was 240% larger than that for WLS with of 64%, and 50% when was 8%. This was also reflected by the results from the aneurysmal flows. Among the three datasets of the basilar tip aneurysm, the in vivo 4D flow data contained the widest range of velocity errors. The pressure fields reconstructed from 4D flow data using WLS were more consistent with the observed flow structure compared with Poisson as suggested by Fig. 10(a). Specifically, the center of the aneurysmal sac was expected to be a low-pressure region given the vortical flow in that region, and the highpressure regions were expected to be near the inlet and the tip of the aneurysmal sac based on the flow deceleration. These anticipated distributions were observed using WLS, but not using Poisson. However, the pressure fields reconstructed from the in vitro datasets using the two methods were all consistent with the expected pressure distribution. The corresponding effectiveness of WLS was highest (28.7%) for 4D flow data compared with other datasets (17.9% for PTV-voxavg and 8.7% for PTV). For the ICA aneurysmal flow, the effectiveness of WLS was also higher (34.2%) for 4D flow data compared to other datasets (6.8% for PTV-voxavg and 11.9% for PTV). Overall, the analyses here suggest that WLS improved the pressure reconstruction from less accurate velocity data as compared to the Poisson method.
The improvement by WLS was more significant at time points with greater flow rates for pulsatile flows. Given in Fig. 6(a), WLS reduced the pressure error levels at peak systole by around 100% for 2D pulsatile flow cases with velocity errors greater than 10%, and the error reduction by WLS was not as significant at other phases. At peak diastole with the lowest flow rate, both methods were able to calculate the pressure accurately. This was also suggested by the results from the aneurysmal flows given in Fig. 9. WLS improved the pressure differences of 4D flow effectively at time points around peak systole (0.45 s for basilar tip aneurysm, 0.25 s for ICA aneurysm) reflected by the reduction in the discrepancy between the results across modalities.
A limitation of this study is that no benchmark pressure was available for the comparison between the pressure fields reconstructed from the aneurysm flow data and, therefore, the errors in the reconstructed pressure fields could not be quantified. A comparison of the reconstructed pressure to a direct pressure measurement would improve the WLS pressure accuracy assessment and will be explored in future work. Instead, we could only compare the pressure fields calculated from in vivo data and in vitro data based on the notion that the pressure fields should be similar as the flow structures are consistent. Although the in vivo and in vitro flow data were found to be in good agreement [8], they were not exactly the same and thus the pressure fields could maintain inherent differences. As given in Fig. 10 (b), the spatial distributions of pressure within the aneurysmal sac of the ICA aneurysm suggested a clear discrepancy between 4D flow and PTV.
There are also several limitations of the WLS pressure reconstruction method. The error estimation algorithm employed in this study can only be applied to incompressible flows as the divergence-free assumption is invalid for compressible flows. In addition, the algorithms for error estimation and pressure gradient calculation are only applicable to velocity data which fully resolves the gradients along all dimensions. For 3D flows, volumetric data with all 3 velocity components are required. 2D planar velocity data or 3 velocity components captured on a 2D plane measured from 3D flow would not be sufficient because the velocity gradient perpendicular to the measurement plane is not resolvable. However, this algorithm can be applied to 2D planar data if the flow is uniform along the perpendicular dimension, such as the 2D synthetic flows employed in this study. Another limitation of WLS is that the velocity data need to be temporally and spatially resolved to ensure accurate derivative evaluation. The pressure in small vessel branches (less than 3 voxels across the lumen diameter) cannot be estimated due to the insufficient number of voxels for numerical difference. However, this is a limitation for most pressure reconstruction methods.
Acknowledgments
This work was supported by the National Institutes of Health under grant NIH R21 NS106696.
Contributor Information
Jiacheng Zhang, School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907 USA..
Melissa C. Brindise, School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907 USA.
Sean Rothenberger, Weldon School of Biomedical Engineering, Purdue University, West Lafayette, IN 47907 USA..
Susanne Schnell, Feinberg School of Medicine, Northwestern University, Chicago, IL 60611 USA..
Michael Markl, Feinberg School of Medicine, Northwestern University, Chicago, IL 60611 USA.; McCormick School of Engineering, Northwestern University, Evanston, IL 60208, USA.
David Saloner, Department of Radiology and Biomedical Imaging, University of California San Francisco, CA 94143 USA..
Vitaliy L. Rayz, Weldon School of Biomedical Engineering, Purdue University, West Lafayette, IN 47907 USA. School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907 USA.
Pavlos P. Vlachos, School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907 USA. Weldon School of Biomedical Engineering, Purdue University, West Lafayette, IN 47907 USA
References
- [1].De Oliveira RKF, Ferreira EVM, Ramos RP, Messina CMS, Kapins CEB, Silva CMC et al. , “Usefulness of pulmonary capillary wedge pressure as a correlate of left ventricular filling pressures in pulmonary arterial hypertension,” J. Hear. Lung Transplant, vol. 33, no. 2, pp. 157–162, 2014. [DOI] [PubMed] [Google Scholar]
- [2].Wood EH, Leusen IR, Warner HR, and Wright JL, “Measurement of Pressures in Man by Cardiac Catheters,” Circ. Research, vol. 2, no. 4, pp. 294–303, 1954. [DOI] [PubMed] [Google Scholar]
- [3].Baek H, Jayaraman MV, and Karniadakis GE, “Wall Shear Stress and Pressure Distribution on Aneurysms and Infundibulae in the Posterior Communicating Artery Bifurcation,” Ann. Biomed. Eng, vol. 37, no. 12, pp. 2469–2487, 2009. [DOI] [PubMed] [Google Scholar]
- [4].Vlachos PP, Niebel CL, Chakraborty S, Pu M, and Little WC, “Calculating Intraventricular Pressure Difference Using a Multi-Beat Spatiotemporal Reconstruction of Color M-Mode Echocardiography,” Ann. Biomed. Eng, vol. 42, no. 12, pp. 2466–2479, 2014. [DOI] [PubMed] [Google Scholar]
- [5].Nagueh SF, Appleton CP, Gillebert TC, Marino PN, Oh JK, Smiseth OA et al. , “Recommendations for the Evaluation of Left Ventricular Diastolic Function by Echocardiography: An Update from the American Society of Echocardiography and the European Association of Cardiovascular Imaging,” Eur. Hear. J. – Cardiovasc. Imaging, vol. 17, no. 12, pp. 1321–1360, 2016. [DOI] [PubMed] [Google Scholar]
- [6].Berg P, Stucht D, Janiga G, Beuing O, Speck O, and Thé venin D, “Cerebral Blood Flow in a Healthy Circle of Willis and Two Intracranial Aneurysms: Computational Fluid Dynamics Versus Four-Dimensional Phase-Contrast Magnetic Resonance Imaging,” J Biomech Eng, vol. 136, no. 4, pp. 1–9, 2014. [DOI] [PubMed] [Google Scholar]
- [7].Voß S, Beuing O, Janiga G, and Berg P, “Multiple Aneurysms AnaTomy CHallenge 2018 ( MATCH )— Phase Ib?: Effect of morphology on hemodynamics,” PLoS One, vol. 14, no. 5, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Brindise MC, Rothenberger S, Dickerhoff B, Schnell S, Markl M, Saloner D. et al. , “Multi-modality cerebral aneurysm haemodynamic analysis: in vivo 4D flow MRI, in vitro volumetric particle velocimetry and in silico computational fluid dynamics,” J. R. Soc. Interface, vol. 16, no. 158, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Ha H, Kim GB, Kweon J, Kim Y, Kim N, Yang DH et al. , “Multi-VENC Acquisition of Four-Dimensional Phase-Contrast MRI to Improve Precision of Velocity Field Measurement,” Magn. Reson. Med, vol. 75, pp. 1909–1919, 2016. [DOI] [PubMed] [Google Scholar]
- [10].Dyverfeldt P, Bissell M, Barker AJ, Bolger AF, Carlhäll C, Ebbers T. et al. , “4D flow cardiovascular magnetic resonance consensus statement,” J. Cardiovasc. Magn. Reson, vol. 17, no. 72, pp. 1–19, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Nayak KS, Nielsen J, Bernstein MA, Markl M, Gatehouse PD, Botnar RM et al. , “Cardiovascular magnetic resonance phase contrast imaging,” J. Cardiovasc. Magn. Reson, vol. 17, no. 71, pp. 1–26, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Tronchin T, David L, and Farcy A, “Loads and pressure evaluation of the flow around a flapping wing from instantaneous 3D velocity measurements,” Exp. Fluids, vol. 56, no. 7, 2015. [Google Scholar]
- [13].de Kat R, van Oudheusden BW, and Scarano F, “Instantaneous Pressure Field Determination Around a Square-Section Cylinder Using Time-Resolved Stereo-PIV,” in 39th AIAA Fluid Dynamics Conference, 2009, no. 22–25 June, pp. 1–10. [Google Scholar]
- [14].Violato D, Moore P, and Scarano F, “Lagrangian and Eulerian pressure field evaluation of rod-airfoil flow from time-resolved tomographic PIV,” Exp. Fluids, vol. 50, no. 4, pp. 1057–1070, 2011. [Google Scholar]
- [15].De Kat R. and Van Oudheusden BW, “Instantaneous planar pressure determination from PIV in turbulent flow,” Exp. Fluids, vol. 52, no. 5, pp. 1089–1106, 2012. [Google Scholar]
- [16].Charonko JJ, V King C, Smith BL, and Vlachos PP, “Assessment of pressure field calculations from particle image velocimetry measurements,” Meas. Sci. Technol, vol. 21, no. 10, p. 105401, 2010. [Google Scholar]
- [17].Liu X. and Katz J, “Instantaneous pressure and material acceleration measurements using a four-exposure PIV system,” Exp. Fluids, vol. 41, no. 2, pp. 227–240, 2006. [Google Scholar]
- [18].Neeteson NJ, Bhattacharya S, Rival DE, Michaelis D, Schanz D, and Schröder A, “Pressure-field extraction from Lagrangian flow measurements: first experiences with 4D-PTV data,” Exp. Fluids, vol. 57, no. 6, pp. 1–18, 2016. [Google Scholar]
- [19].Schneiders JFG, Pröbsting S, Dwight RP, van Oudheusden BW, and Scarano F, “Pressure estimation from single-snapshot tomographic PIV in a turbulent boundary layer,” Exp. Fluids, vol. 57, no. 4, pp. 1–14, 2016. [Google Scholar]
- [20].Krittian SBS, Lamata P, Michler C, Nordsletten DA, Bock J, Bradley CP et al. “A finite-element approach to the direct computation of relative cardiovascular pressure from time-resolved MR velocity data,” Medical Image Analysis, vol. 16, no. 5, pp. 1029–1037, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Ebbers T, and Farnebäck G. “Improving computation of cardiovascular relative pressure fields from velocity MRI,” J. Magn. Reson. Imaging vol. 30, no. 1, pp. 54–61, 2009. [DOI] [PubMed] [Google Scholar]
- [22].Bock J, Frydrychowicz A, Lorenz R, Hirtller D, Barker AJ, Johnson KM et al. “In vivo noninvasive 4D pressure difference mapping in the human aorta: phantom comparison and application in healthy volunteers and patients,” Magn. Reson. Med vol. 66, no. 4, pp. 1079–1088, 2011. [DOI] [PubMed] [Google Scholar]
- [23].Lamata P, Pitcher A, Krittian S, Nordsletten D, Bissell MM, Cassar T. et al. “Aortic relative pressure components derived from four-dimensional flow cardiovascular magnetic resonance,” Magn. Reson. Med vol. 72, no. 4, 1162–1169, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Donati F, Nordsletten DA, Simith NP, and Lamata P, “Pressure mapping from flow imaging: enhancing computation of the viscous term through velocity reconstruction in near-wall regions,” Conf. Proc. IEEE Eng. Med. Biol. Soc. 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].van Oudheusden BW, “PIV-based pressure measurement,” Meas. Sci. Technol, vol. 24, no. 3, p. 032001, 2013. [Google Scholar]
- [26].Jeon YJ, Gomit G, Earl T, Chatellier L, and David L, “Sequential least-square reconstruction of instantaneous pressure field around a body from TR-PIV,” Exp. Fluids, vol. 59, no. 2, p. 27, 2018. [Google Scholar]
- [27].Wang CY, Gao Q, Wei RJ, Li T, and Wang JJ, “Spectral decomposition-based fast pressure integration algorithm,” Exp. Fluids, vol. 58, no. 7, pp. 1–14, 2017. [Google Scholar]
- [28].Azijli I. and Dwight RP, “Solenoidal filtering of volumetric velocity measurements using Gaussian process regression,” Exp. Fluids, vol. 56, no. 11, pp. 1–18, 2015. [Google Scholar]
- [29].Li XS, “An Overview of SuperLU?: Algorithms, Implementation, and User Interface,” ACM Trans. Math. Softw, vol. 31, no. 3, pp. 302–325, 2005. [Google Scholar]
- [30].Devenport BWJ and Rife MC, “The structure and development of a wing-tip vortex”, Journal of Fluid Mechanics, vol. 312, pp. 67–106, 1996. [Google Scholar]
- [31].Azijli I. and Dwight RP, “Solenoidal filtering of volumetric velocity measurements using Gaussian process regression,” Exp. Fluids, vol. 56, no. 11, pp. 1–18, 2015. [Google Scholar]
- [32].Bock J, Kreher BW, Hennig J, and Markl M, “Optimized preprocessing of time-resolved 2D and 3D phase contrast MRI data,” in Proc. Intl. Soc. Mag. Reson. Med, 2007, vol. 15, p. 3138. [Google Scholar]
- [33].Brindise MC, Busse MM, and Vlachos PP, “Density- and viscosity-matched Newtonian and non-Newtonian blood-analog solutions with PDMS refractive index,” Exp. Fluids, vol. 59, no. 11, pp. 1–8, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Hofinan MBM, Visser FC, van Rossum AC, Vink GQM, Sprenger M, and Westerhof N, “In Vivo Validation of Magnetic Resonance Blood Volume Flow Measurements with Limited Spatial Resolution in Small Vessels,” Magn. Reson. Med, vol. 33, no. 6, pp. 778–784, 1995. [DOI] [PubMed] [Google Scholar]
- [35].Xue Z, Charonko JJ, and Vlachos PP, “Particle image pattern mutual information and uncertainty estimation for particle image velocimetry,” Meas. Sci. Technol, vol. 26, no. 7, pp. 1–14, 2015. [Google Scholar]
- [36].Bhattacharya S, Charonko JJ, and Vlachos PP, “Particle image velocimetry ( PIV ) uncertainty quantification using moment of correlation ( MC ) plane,” Meas. Sci. Technol, vol. 29, pp. 1–14, 2018. [Google Scholar]
- [37].Azijli I, Sciacchitano A, Ragni D, Palha A, and Dwight RP, “A posteriori uncertainty quantification of PIV-based pressure data,” Exp. Fluids, vol. 57, no. 5, pp. 1–15, 2016. [Google Scholar]