An interpretable single-cell RNA sequencing data clustering method based on latent Dirichlet allocation

Abstract

Single-cell RNA sequencing (scRNA-seq) detects whole transcriptome signals for large amounts of individual cells and is powerful for determining cell-to-cell differences and investigating the functional characteristics of various cell types. scRNA-seq datasets are usually sparse and highly noisy. Many steps in the scRNA-seq analysis workflow, including reasonable gene selection, cell clustering and annotation, as well as discovering the underlying biological mechanisms from such datasets, are difficult. In this study, we proposed an scRNA-seq analysis method based on the latent Dirichlet allocation (LDA) model. The LDA model estimates a series of latent variables, i.e. putative functions (PFs), from the input raw cell–gene data. Thus, we incorporated the ‘cell-function-gene’ three-layer framework into scRNA-seq analysis, as this framework is capable of discovering latent and complex gene expression patterns via a built-in model approach and obtaining biologically meaningful results through a data-driven functional interpretation process. We compared our method with four classic methods on seven benchmark scRNA-seq datasets. The LDA-based method performed best in the cell clustering test in terms of both accuracy and purity. By analysing three complex public datasets, we demonstrated that our method could distinguish cell types with multiple levels of functional specialization, and precisely reconstruct cell development trajectories. Moreover, the LDA-based method accurately identified the representative PFs and the representative genes for the cell types/cell stages, enabling data-driven cell cluster annotation and functional interpretation. According to the literature, most of the previously reported marker/functionally relevant genes were recognized.

INTRODUCTION

Single-cell RNA sequencing (scRNA-seq) simultaneously determines gene expression levels for thousands of individual cells to better investigate cell-to-cell heterogeneity [1]. In the last decade, scRNA-seq has demonstrated a significant advantage in new cell type discovery and cell development studies and has been applied to various research areas, including tumours, immunity, neuroscience, microbes and developmental biology [2–4].

Unsupervised cell clustering is the most critical task in the scRNA data analysis workflow. In cell clustering, cells are grouped according to their gene expression patterns, enabling further downstream cell function recognition and cell-type annotation tasks. Dozens of cell clustering methods have been developed. Many of them are derived from generic clustering algorithms. pcaReduce implements an iterative strategy based on principal component analysis (PCA) and hierarchical clustering. After each merge or split operation, the method conducts dimensionality reduction to improve the scalability of the algorithm to large-scale scRNA-seq data [5]. SC3 was developed based on the k-means and PCA methods. It overcomes the greedy characteristic of k-means by repeatedly performing clustering under different initial conditions [6]. RaceID enhances the ability of k-means to identify rare cell types through outlier detection [7]. In addition to such generic clustering algorithm-based methods, community detection-based algorithms have been developed and broadly used. PhenoGraph adopts shared nearest-neighbour graphs and Louvain community detection to reduce the clustering time costs incurred on large-scale datasets [8]. Seurat integrates PCA, Louvain and many other methods, currently becoming the most popular tool for scRNA-seq analysis [9, 10].

The major obstacles to cell clustering are the high dimensionality, inherently high noise and rapidly increasing volume of scRNA-seq data [11]. The above state-of-the-art methods have made considerable efforts to solve the high dimensionality and large cell number problems. However, the high noise associated with data sparsity is still a major challenge.

The biological interpretation of cell clustering results, i.e. cluster annotation, is also essential for scRNA-seq data analysis. Because PCA-based dimensionality reduction is included, many scRNA-seq data analysis methods do not reserve biological significance during the clustering process. Genes are the key to annotating and interpreting cell clusters. There are two categories of automatic cell annotation methods. One category is the supervised methods, which require a labelled reference dataset. The gene expression patterns of the cell clusters are compared to the reference dataset. Clusters with similar expression patterns to a particular cell group in the reference dataset can be assigned its label [12]. The other category prioritizes genes for cells or cell clusters. For instance, Cell-ID employs a multivariate statistical method to extract gene signatures for each cell without a clustering process; the identified genes are considered to be informative for revealing cellular diversity and are capable of indicating cell functions [13]. Due to the complexity of biological systems, it is still difficult to build clear connections between the identified genes and cell functions. The cell annotation results are better supported by the literature.

Here, we incorporate latent Dirichlet allocation (LDA) into the scRNA-seq analysis workflow, aiming to discover latent and complex gene expression patterns with a built-in model approach and to obtain biologically meaningful results. LDA is a probabilistic topic model utilizing unsupervised learning that was initially proposed for text mining. It assumes that the reason we observe a specific set of words in a document is actually determined by a group of latent attributes in the document (topics) [14]. As a nonlinear method, LDA achieves outstanding performance on complex, sparse and noisy datasets [15]. In addition, LDA is considered interpretable because its parameters can be directly used to associate the input features with latent factors or target outcomes. In the bioinformatics field, LDA was applied to novel cancer mutation signature discovery [16], microbiome composition analysis [17, 18], substructure exploration in metabolomics [19] and pathway–drug relationships [20].

Similar topic models have also been applied in scRNA-seq data analysis [11, 21–25]. Hierarchical Dirichlet process (HDP) was adopted to conduct single-cell data clustering. This method does not require a cluster number parameter as input [21]. The cellTree tool focuses on producing tree structures outlining the hierarchical relationship between single-cell samples based on the LDA model. The method was implemented as an R/Bioconductor package [26].

The remainder of this article is organized as follows. First, we construct a scRNA-seq data analysis workflow based on LDA. Second, we compare the performance of LDA and several popular cell clustering methods using seven benchmark scRNA-seq datasets. Then, we analyse three public scRNA-seq datasets by using our methods in practice. Several biologically meaningful results are derived. Finally, we assess the robustness and computational efficiency of our multithreading LDA implementation on noisy and large-scale simulation datasets.

METHODS

Overview

The LDA model was originally developed for mining text from large-scale corpora, aiming for latent ‘topic’ recognition in massive observed documents. The LDA model assumes that each document is a mixture of multiple topics. The reason that specific words in a document are chosen is that the document is focused on the specific associated topics. Thus, mathematically, the document is described as a probabilistic distribution over its topics, and each topic is described as a probabilistic distribution over all possible words in the vocabulary.

More generally, the LDA model is applied to identify latent attributes that are difficult to directly observe from data. These datasets usually have two-layer structures, including data units and their unordered collections. The observed collection–unit relationship pattern is largely determined by the latent attributes. In many cases, recognizing the latent attributes is the main purpose of such a data analysis process.

According to the above idea, we incorporated the LDA model into the scRNA-seq data analysis process. In this study, the original LDA terms were mapped to the scRNA-seq data analysis context. ‘Document’ was mapped to ‘cell’. ‘Topic’ was mapped to ‘function’. ‘Word’ was mapped to ‘gene’ (Figure S1). Therefore, the basic assumption was that the reason we observe a specific gene expression profile in a cell is actually determined by the latent attributes of the cell, i.e. functions. In this context, cells were described as probabilistic distributions over functions, and functions were described as probabilistic distributions over genes.

In this study, we constructed an LDA-based scRNA-seq data analysis workflow (Figure 1). The input of the LDA model was a matrix containing the gene expression profiles of cells. Cells with irregular gene expression patterns were removed in advance. Then, the latent functions were identified by the LDA model parameter estimation procedure. Two estimated parameter matrices, i.e. the function distributions of cells and the gene distributions of functions, were used to characterize the putative functions (PFs) mined from the cell–gene expression data. Since latent function identification is a de facto dimensionality reduction technique imposed on the raw data, downstream analyses, including cell-type recognition, pseudo-time-series analysis and marker gene identification, could be conducted on the LDA results. In the above analysis, the Hellinger distance between the PF distributions of cells was used to measure cell similarity. The k-medoids algorithm was employed for cell clustering. The uniform manifold approximation (UMAP) algorithm was employed for pseudo-time-series analysis. Based on the two estimated parameter matrices, representative genes were prioritized for each PF, and major functions were assigned to each cell cluster. The LDA-based method yielded a built-in-model interpretation of the underlying biological mechanism.

Figure 1.

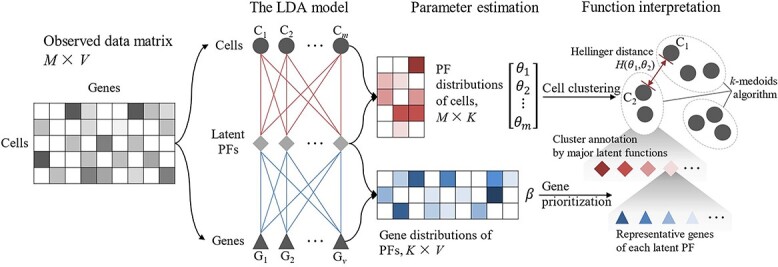
Overview of the workflow of the LDA-based method. Without explicit gene filtering, the LDA model inferred latent PFs from the cell–gene expression matrix. Two parameter matrices, i.e. the cell–function matrix ([θ₁, θ₂, …, θ_m]^T, M × K) and the function–gene matrix (β, K × V), were estimated. The cell–function matrix characterized the PF distributions over the cells. Cell-to-cell similarities were evaluated by the Hellinger distance between their PF distributions θ and further supported cell clustering. The function–gene matrix characterized the gene distributions over the PFs. Gene prioritization was conducted based on β. Genes with higher probabilities, i.e. the representative genes, enabled the biological interpretation of the latent variables (PFs) and cluster annotation.

The LDA model for scRNA-seq data analysis

In our method, LDA was used to discover the latent patterns contained in the gene expression profiles of a large-scale single-cell dataset. This approach assumes the gene expression of each of the M cells as follows:

(1) Choose N ~ Poisson (ξ).

(2) Choose θ ~ Dir (α).

(3) For each of the N transcripts w_n:

• (a) Choose a function z_n ~ multinomial (θ).

• (b) Choose a gene w_n from p (w_n | z_n, β), a multinomial probability conditioned on the function z_n.

Here, N denotes the distribution of the number of expressed transcripts in a cell and θ denotes the parameter of the multinomial distribution.

LDA assumes that the dimensionality K of the Dirichlet distribution, i.e. the dimensionality of the latent ‘function’ variable θ, is known and fixed. The gene probabilities for a function are parameterized by a K × V matrix β, where β_ij = p (w_j = 1 | z_i = 1) and V denotes the size of the complete set of all possible genes. The matrix β can be estimated through a machine learning process.

The number of cell transcripts N is not necessarily assumed to follow a Poisson distribution. Any realistic distribution can be used as needed, N is independent of all the other data generating variables (θ and z) and its randomness is thus usually ignored in LDA. In practice, the number of transcripts per million mapped reads (TPM) is used as a counting unit.

LDA can be solved by variational Bayesian expectation maximization or Gibbs sampling methods. Both the function–gene matrix (β, K × V) and the cell–function matrix ([θ₁, θ₂, …, θ_m]^T, M × K) were estimated. Each row of the function–gene matrix, i.e. the gene probability distribution, indicates the representative genes of a function; each row of the cell–function matrix, i.e. the function probability distribution, indicates the mixed function proportions of a cell transcriptome. Thus, the cell-to-cell similarity in terms of function could be represented by the Hellinger distance between the function probability distributions of the two cells.

Cluster annotation and function interpretation

Cluster annotation and function interpretation are completely data-driven processes. Based on the cell-to-cell Hellinger distances, the cells were clustered by the k-medoids algorithm. Then, the identified cell clusters were annotated using representative genes in a ‘cell-function-gene’ three-layer framework. In a cell cluster, each cell had a PF distribution characterizing the relevance of the functions to the cell. The major functions of each cell cluster were determined by its members’ representative PFs. Since the PFs were actually ‘defined’ by their representative genes, the interpretation of a PF was carried out by gene prioritization.

Representative PF identification for cell clusters

In the LDA model, the cells were characterized by their biological function components, which were mathematically estimated as the cell–function matrix ([θ₁, θ₂, …, θ_m]^T, M × K). Cells with close θ values were considered to be functionally similar and were clustered together. Although the cell clusters were formed on the basis of the functional similarity of the cells, there was no direct connection between the cell clusters and the PFs. Thus, we proposed a simple and intuitive method to assign representative PF to cell clusters using their members’ PF distributions.

Assuming that M cells are clustered into C clusters, C_i denotes the i-th cluster, |C_i| denotes the size of C_i, j denotes the cells in cluster C_i and Avg.P_ik denotes the average probability of a PF k of the C_i members,

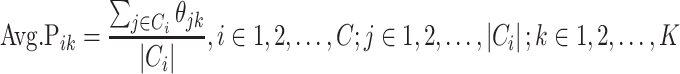(1)

Some PFs may be essential in more than one cell type and receive high probabilities in multiple clusters; thus, the Avg.P_ik values were normalized by the sum of the average probabilities of PF k in all clusters:

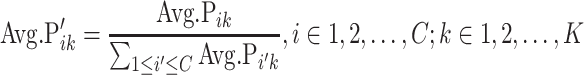(2)

For each cluster C_i, the normalized average probabilities of all PFs, i.e. Avg.P′_ik (k ∈ 1, 2, …, K), were sorted in descending order. Let k′ denote the descending rank of the PFs; then,

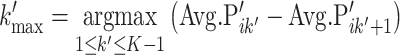(3)

As shown in Equation (3), we calculated the intervals between the adjacent Avg.P′_ik’, and the maximum interval was selected as the cut-off. The top k′_max PFs were assigned as the representative PFs for clustering C_i.

Gene prioritization and PF interpretation

In this study, the ‘PFs’ were latent patterns that learned from the data via the LDA model. Their actual biological meanings could only be interpreted by identifying their representative genes, i.e. by performing gene prioritization. Here, we proposed a balanced gene prioritization method considering both relevance and distinctiveness.

Each row of the estimated function–gene matrix (β, K × V) describes the relevance of all genes to a PF. In the hypothesized generation process of the LDA model, a PF chooses genes according to their probabilities. The higher the probability that the PF chooses a gene is, the more important the predicted gene is to the PF.

For each PF k, we sorted the genes in descending order by their probabilities. ‘Relevant genes’ were defined to be the smallest set of genes that contributed over 80% of the components to a putative function.

Let g′ denote the descending rank of the genes relative to the PFs; g′_min denotes the rank of the fewest number of top genes whose cumulative sum is greater than 0.8:

(4)

The top g′_min genes are the ‘relevant genes’ of the putative function k.

Furthermore, similar to cell–function relationships, some critical genes may have participated in multiple biological processes and were prioritized at the top of more than one PF. Thus, we introduced a normalized measurement process to determine a more distinct representative gene set for each PF.

Let β′_kg denote the normalized probability of a gene g to a PF k:

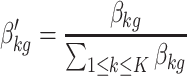(5)

For each PF k, we then sorted the genes in descending order again, except this time, we did so according to the normalized probability β′. Let g″ denote the descending rank of the genes in terms of β′.

For the ‘relevant genes’ of each PF, the rank sum of g′ and g″ was calculated. According to the rank sum, the top 10 genes were assigned as representative genes to the PF.

Cell cluster annotation

Cell cluster annotation was conducted by identifying both representative PFs and their representative genes.

For each cell cluster C_i, assuming there were k′_max representative PFs, let β_k′ denote the gene probabilities of a representative PF k′; then, the relevance vector δ_i from all genes to C_i could be defined as the average of β_k′ (1 ≤ k′ ≤ k′_max):

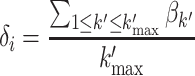(6)

By calculating the δ_i for all cell clusters, we obtained the cluster–gene matrix (δ = [δ₁, δ₂, …, δ_C]^T, C × V). Similar to β, the matrix δ describes the relevance of all genes to the cell clusters. Thus, the representative genes of the cell clusters could be identified by following the same strategy described above, except for replacing β with δ.

Benchmarking on gold-standard datasets

We compared the performance of LDA and four classic scRNA-seq clustering methods (Seurat, SC3, RaceID3 and clusterExperiment) and a similar model (HDP) to our method on seven human lung adenocarcinoma cell line datasets [27] (CEL-seq2_3cl, 10x_3cl, Drop-seq_3cl, 10x_5cl, CEL-seq2_5cl_p1, CEL-seq2_5cl_p2 and CEL-seq2_5cl_p3). Tian et al. [27] performed quality control without normalization. The authors claimed that there is no batch effect between the datasets. Detailed information about the seven datasets is shown in Table S1.

The performance of clustering against cell labels was evaluated by the adjusted Rand index (ARI), entropy of cluster accuracy (ECA) and entropy of cluster purity (ECP). ARI is calculated by measuring similarity or agreement between predictions and real labels. The ECA and ECP were observed to correlated with the ARI [28]. Cell annotation performance was assessed through ARI and three complementary metrics: precision, recall and F1 score, which is the harmonic mean between precision and recall. By employing these three complementary metrics, the overweighting of large clusters was avoided, and a greater contribution from rare cell types was allowed. The above metrics were calculated in R.

Tian et al. [27] also provided such metrics as along with the computation times for four clustering methods. Each method was normalized and imputed by different methods, and the top 1000 highly variable genes were selected. The normalization methods included Scran, Linnorm, Scone, DESeq2, BASiCS, Scnorm, Counts Per Million reads mapped (CPM) and Trimmed Mean of M values (TMM), and the imputation methods included SAVER, DrImpute and KNN-Smooth. Seurat_pipe takes raw Unique Molecular Identifier (UMI) counts as inputs and uses its default data preprocessing pipeline for normalization and gene selection. Most methods aside from Seurat have functions to help them choose the optimal number of clusters. Therefore, Seurat uses two resolutions, 1.6 (Seurat_1.6) and 0.6 (Seurat_0.6), to obtain more or fewer clusters, respectively.

The HDP study only mentioned that Gensim library was used for HDP modelling and did not provide any source code or implementation details [21, 29]. Therefore, we also employed the Gensim library to replicate its implementation method as much as possible. The HDP method does not require a predefined topic number, but tends to learn more topics from the data. Thus, following the instructions in the HDP article, we first labelled the topic with the highest membership probability as the cluster assignment for each cell, then grouped clusters with fewer than 15 cells as a separate single cluster.

In our method, the k-medoids algorithm was employed for cell clustering based on the ‘PF’ probabilities estimated from the LDA model. The parameter ‘K’ of k-medoids was directly set to be the number of cell types in the benchmark dataset. We chose the best metrics by enumerating the parameter ‘K’ of LDA, i.e. the number of ‘PFs’, from 2 to 20. For the other methods, we also chose their best performances for the comparison.

Robustness and computational efficiency evaluation on simulation datasets

Recently, the size of scRNA-seq datasets has been increasing fast. Noise and dropouts caused by various factors may also weaken algorithm performance [30–32]. It is necessary to evaluate the robustness and computational efficiency of our method on simulation datasets.

We used Splatter to simulate scRNA-seq data. The baseline parameters for Splatter were estimated using a scRNA-seq dataset including 1244 lung adenocarcinoma (A549) cells with 32 895 genes.

All simulation parameters were set to their default values. For each simulation, we fixed the number of genes at 15 000 and fixed the number of cell types at 5. For each of the five cell types, we simulated datasets with the probability of grouping (cell type) equal to 0.2 and set the probability of differentially expressed genes to 0.3, 0.1, 0.2, 0.01 and 0.1, among which the probabilities of downregulated genes were 0.1, 0.4, 0.9, 0.6 and 0.5.

For the robustness test, the size of the simulation datasets, i.e. the number of cells, was set to 10 000. The outlier probability parameter and dropout parameters were set to different values to control the data quality, and the specific parameter settings can be found in Table 3.

Table 3.

Robustness of the LDA-based method

Cells number	Genes number	Outlier probability	Dropouts midpoint	Dropouts shape	ARI	ECA	ECP
10 000	15 000	0.01	−5	−1.2	>0.999	8.3 × 10−4	8.6 × 10−4
10 000	15 000	0.01	−4	−1.2	>0.999	3.4 × 10−3	3.3 × 10−3
10 000	15 000	0.01	−3	−1.2	>0.999	1.7 × 10−3	1.7 × 10−3
10 000	15 000	0.01	−2	−1.2	>0.999	2.6 × 10−3	2.6 × 10−3
10 000	15 000	0.01	−1	−1.2	0.999	3.8 × 10−3	3.7 × 10−3
10 000	15 000	0.01	0	−1.2	0.998	7.9 × 10−3	7.8 × 10−3
10 000	15 000	0.01	1	−1.2	0.995	1.6 × 10−2	1.6 × 10−2
10 000	15 000	0.01	2	−1.2	0.979	5.4 × 10−2	5.3 × 10−2
10 000	15 000	0.1	−5	−1.2	>0.999	<10−5	<10−5
10 000	15 000	0.2	−5	−1.2	>0.999	<10−5	<10−5
10 000	15 000	0.3	−5	−1.2	>0.999	<10−5	<10−5
10 000	15 000	0.4	−5	−1.2	>0.999	<10−5	<10−5
10 000	15 000	0.5	−5	−1.2	>0.999	<10−5	<10−5
10 000	15 000	0.6	−5	−1.2	>0.999	<10−5	<10−5
10 000	15 000	0.7	−5	−1.2	>0.999	<10−5	<10−5

For the scaling test, the sizes of the simulation datasets were set to 1000, 2000, 5000, 10 000, 20 000, 50 000, 100 000, 200 000, 500 000 and 1 000 000 cells. We performed 10 simulations for sizes smaller than 100 000 and 1 simulation for larger sizes.

We evaluate our LDA-based method on the simulation datasets. The PF (topic) parameter of the LDA was set to 5. The number of threads was set to 48. We recorded the computation time and the highest CPU and memory usage during the model training process.

Method implementation and availability

In this study, the LDA-based scRNA-seq data processing workflow was packaged in an all-in-one Perl script, built upon MALLET (MAchine Learning for LanguagE Toolkit). MALLET is a JAVA-based toolkit for statistical natural language processing (NLP) that provides memory-efficient and multithreaded LDA modelling implementation [33].

The cluster annotation and function interpretation methods were provided as an R script. It takes the results of the LDA modelling and produces functional interpretations, such as cell clusters and their annotations, representative genes and PFs.

The source codes and test data are available at https://github.com/lrjuan/LDA_scRNAseq.

RESULTS

First, we benchmarked the LDA-based method with four classic scRNA-seq clustering methods on seven gold-standard datasets. Then, we analysed three public datasets used in practice, demonstrating the performance of our method on more complex data, as well as the capability of LDA to reconstruct cell development trajectories. The results showed that the PFs identified by our LDA-based method have significant biological implications. According to the literature, most previously reported marker/functionally relevant genes were recognized as representative genes of PFs or cell clusters. The mixtures of latent gene expression patterns were characterized. Finally, we investigated the computational efficiency of our method using simulation datasets.

Benchmarking of the LDA-based method

We compared the performance of our method with that of four classic scRNA-seq clustering methods and a similar model (HDP) to our method on seven benchmark datasets [27]. For each method and each dataset, we chose the best performance through the ARI for the comparison (Table S2). As described in the Methods section, the LDA model characterized the relevance of the genes to a PF using a multinomial distribution. The latent gene expression patterns were identified in a built-in model. Thus, for our method, there was no need to normalize or impute genes in advance. The number of clusters was directly assigned as the number of actual cell types in the given dataset. For the other clustering methods, the datasets were normalized and imputed by the recommended methods. Genes were filtered according to well-accepted parameters. The optimal numbers of clusters were chosen.

We compared the clustering performance of each method on all datasets with two metrics: accuracy (ECA) and purity (ECP). A lower ECA/ECP value indicated better performance. As shown in Figure S2, the LDA-based method performed best on the 10x_3cl, Drop-seq_3cl, CEL-seq2_3cl, 10x_5cl, CEL-seq2_5cl_p1 and CEL-seq2_5cl_p3 datasets and was close to the best method on the CEL-seq2_5cl_p2 datasets. Collectively, our method performed best, achieving a good balance between underclustering and overclustering across all datasets (Figure 2).

Figure 2.

Comparison between the LDA-based method and four scRNA-seq clustering methods and a similar model (HDP) to our method on seven benchmark datasets. The coordinates of each glyph are the ECP and ECA values for the top performing combinations of each method for different datasets. Colours denote different clustering methods. Seurat_pipe denotes the default pipeline. Seurat_1.6 and Seurat_0.6 denote 1.6 and 0.6 resolutions, which tend to obtain more or fewer clusters, respectively. Different types of glyphs indicate datasets with different protocols.

The performance of the HDP method was poor in the benchmarking. The ARI scores of the method were significantly lower than those of other methods. The HDP method achieved its best performance on the 10x_3cl dataset, with ECA and ECP reaching 0.24 and 0.61, respectively.

As shown in Figure 2, Seurat had a performance very close to LDA on the benchmark datasets. This may be because these cell line datasets are relatively simple, i.e. their gene expression patterns are significantly different from each other. Thus, both Seurat and our LDA-based method reached almost perfect performance. To demonstrate the capability of our method on complex datasets, we further conducted empirical analysis on three public datasets.

Empirical analysis of the LDA-based method

The performance of the LDA-based method on more complex data was examined using three public datasets. The first dataset, the ‘melanoma dataset’, was sequenced from 19 melanoma patients [34]. The second dataset, the ‘thymic development dataset’, included scRNA-seq data concerning the human thymus across the life span [35]. The third dataset, the ‘PBMC dataset’, was sequenced from peripheral blood mononuclear cells (PBMCs) of 29 samples [36].

Empirical analysis on melanoma dataset

The melanoma dataset included 1169 malignant cells from eight tumours and 2848 stromal cells obtained after the recommended cell selection process was carried out. In this study, the cells were grouped into 18 clusters, and 55 PFs were identified (Figure S3).

The cell clustering results of the LDA-based method were consistent with the cell labels annotated by Tirosh et al. [34] (Figure 3A and B). The malignant cells were grouped into eight clusters (C1~C8) according to the tumour origins of the patients. Among the stromal cells, four distinct clusters (C9~C12) were identified for B cells, macrophages, cancer-associated fibroblasts and endothelial cells. Moreover, our method divided tumour-infiltrating T cells and natural killer cells into six clusters, which was concordant with the supervised analysis of T cells conducted by Tirosh et al. [34] based on surface markers.

Figure 3.

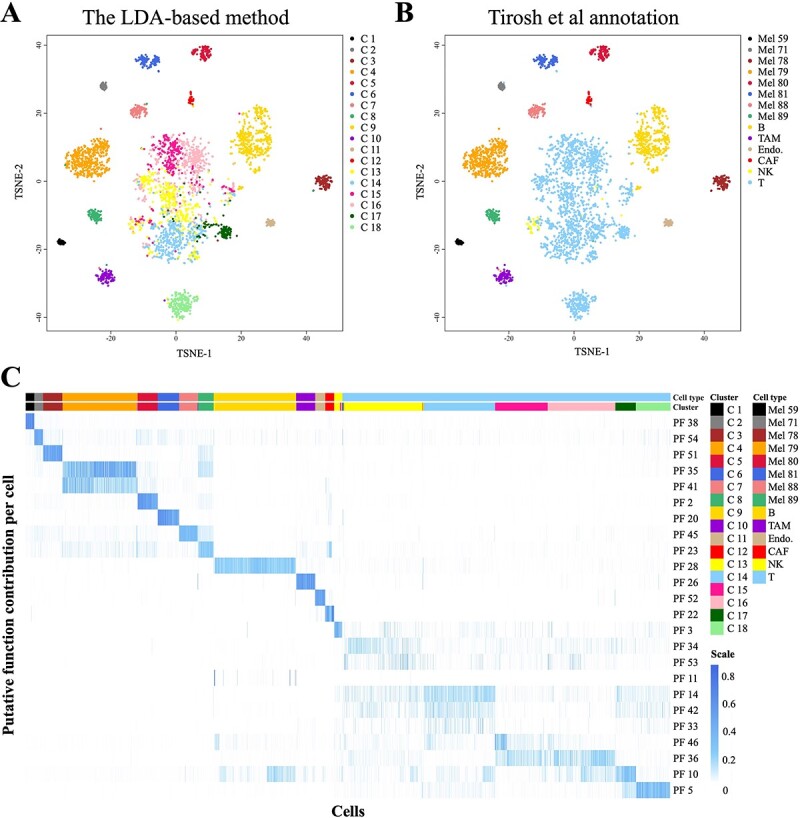
The analysis results obtained on the melanoma dataset. (A–B) The t-distributed stochastic neighbour embedding (t-SNE) plots based on the cell-to-cell Hellinger distances calculated from the θ parameters (PFs) estimated by the LDA model. As shown in (A), 18 clusters were identified by the downstream k-medoids algorithm. (B) shows the Tirosh et al. [34] annotations of the cells. (C) Heatmap based on the contribution of the PFs to each cell. Most of the identified clusters were significantly correlated to a PF, enabling further cluster annotation and functional interpretation (Table 1).

As shown in Figure 3C, the LDA-based method identified one to two representative PFs for most cell clusters. These representative PFs are actually core features in cell clustering and are capable of connecting further to biological implications.

Based on the representative PFs, the representative genes of the stromal cell clusters were identified using the method described in Section 2.3. The marker genes and the cell-type-specific genes of the stromal cells were significantly enriched in the 10 top-ranked representative genes of C9~C18 (Table 1). These genes were not only consistent with the results provided by Tirosh et al. [34] but also supported by a number of studies. Both the literature and an enrichment analysis demonstrated that these genes indicate the critical biological processes of the corresponding cell types. The details are shown in Table 1, Table S3 and Table S4.

Table 1.

Comprehensive validation of the top 10 representative genes in clusters 9 to 18 for the melanoma dataset

Cluster	Cell type	Putative function	Marker gene	Specific gene	Gene (experimental evidence)	Gene summary (experimental evidence)
C 9	B	PF 28	CD79B, CD79A, CD19	MS4A1, BANK1, VPREB3, IRF8	TCL1A, CD20, CD79A, CD79B, BANK1, CD19, IRF8, HLA.DOB	B-Cell receptor signalling pathway & activation & differentiation & proliferation
C 10	TAM	PF 26	CD14	C1QA, C1QC, C1QB, S100A9, LYZ, DAP12	C1QA, C1QB, C1QC, S100A8, S100A9, IL1B, LYZ, FCN1, CD14, DAP12	Macrophage activation & aggregation, regulation of inflammatory response
C 11	Endo.	PF 52	VWF	CCL14, CLDN5, FABP4, PLVAP, ECSM2, EGFL7	CLDN5, DARC, PLVAP, ECSM2, VWF, HP, EGFL7, CCL14, FABP4	Regulation of angiogenesis, endothelial cell protection & endocytosis, cell–cell junction assembly, anti-angiogenic and tumour inhibition effects
C 12	CAF	PF 22	DCN, COL1A1, COL3A1	LUM, COL3A1, CXCL14, TAGLN	CCL19, DCN, COL1A1, LUM, COL3A1, SFRP2, CXCL14, TAGLN	Extracellular structure organization, CAF growth and migration, tumorigenesis promotion, fibroblast ossification
C 13	T, NK	PF 34, PF 53, PF 3, PF 11	–	–	GNLY, GZMB, GZMH	NK cell-mediated cytotoxicity
C 14	T, NK	PF 33, PF 14, PF 42	–	CCL5, GZMK, CST7	CCL3, CCL4L1, CCL4L2, CCL4, CCL5, GZMA, GZMK, CST7	Regulation of NK cell cytotoxicity, NK cell-mediated cytotoxicity
C 15	T	PF 46	–	–	JUNB, DUSP2, TOB1, ZFP36L2	T-Cell development & differentiation, regulatory T-cell function suppression
C 16	T	PF 36	IL7R, CCR7	TCF-1	IL7R, CCR7, SELL, TXNIP, PIK3IP1, TCF-1, CD48	T-Cell differentiation & activation & immune response
C 17	T	PF 10	–	–	–	–
C 18	T	PF 5	CD8A, NKG2D, CD8B	CD8A, NKG2D	CD8A, CD8B, FCRL3, NKG2D, SLAMF7, KLRC3, STAT1	Regulation for NK cell maturation, T-cell activation & differentiation, cytotoxicity promotion, regulatory T-cell function suppression

Empirical analysis on thymic development dataset

The thymic development dataset included 3032 thymic T cells collected from different developmental stages. We reconstructed the T-cell differentiation trajectory based on the evaluated PFs provided by the LDA model. The number of PFs was varied from 6 to 20. A UMAP visualization suggested that 14 PFs best described the inherent differentiation structure of the T-cell development dataset. The reconstructed differentiation trajectory was consistent with the annotations of Park et al. [35].

As shown in Figure 4A, the trajectory started from CD4⁻CD8⁻ DN cells [DN(early)-DN(P)-DN(Q) stage], then became CD4⁺CD8⁺ DP cells [DP(P)-DP(Q) stage], and then transitioned through an αβT stage to diverge into mature CD4⁺ or CD8⁺ SP cells (CD4⁺ T and CD8⁺ T). The DN and DP cells were separated into two phases: proliferating (P) and quiescent (Q).

Figure 4.

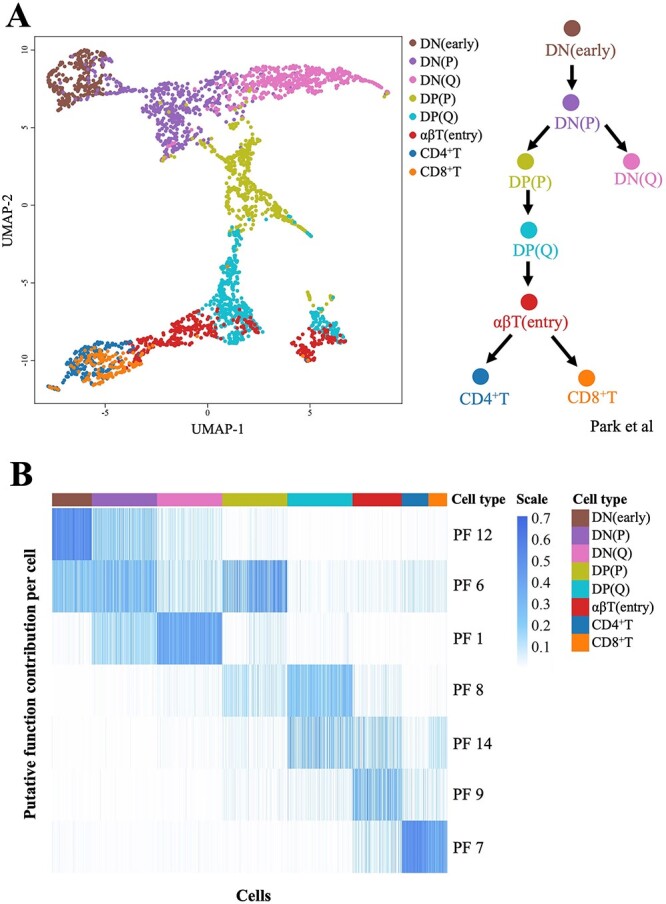
The analysis results obtained on the thymus development dataset. (A) The UMAP plot based on the cell-to-cell Hellinger distances calculated from the θ parameters (PFs) estimated by the LDA model, which was consistent with the annotations of Park et al. [35]. (B) Heatmap based on the PFs’ contributions to each cell. The identified PFs clearly characterized the shifts of dominant functions in T-cell development.

The LDA-based method provided PFs as a key to better understanding the T-cell differentiation mechanism. As shown in Figure 4B, seven representative PFs were observed to be successively dominant in T-cell development. The mixture of adjacent PFs manifested as cell types. Initially, PF12 and PF6 provided a mixture contribution to the DN (early) stage, and PF 12 dominated in the cells; then, PF1, PF6 and PF12 collaborated in the DN(P) stage, and PF6 slightly dominated. Moving through subsequent stages, the contribution of PF12 gradually decreased, those of PF1 and PF6 increased, PF1 dominated in the DN(Q) stage and PF6 dominated in the DP(P) stage. The PF annotations showed that the representative PF1 genes (e.g. PTCRA) included the pre-T-cell receptor alpha chain, while the representative PF6 genes were reported to be essential in cell proliferation (Table 2 and Table S5).

Table 2.

Comprehensive validation of the top 10 representative genes in the representative PFs for the thymus development dataset

Putative function	Marker gene	Gene (experimental evidence)	Gene summary (experimental evidence)
PF 12	IGLL1, SMIM24, AC002454.1, TPM4	–	–
PF 6	–	TUBA1B, H2AFZ, RAN, RANBP1, YBX1, HSPD1, FKBP4, FABP5, MCM7	Cell proliferation
PF 1	PTCRA, JCHAIN, ID1, MAL, SELL, FXYD2	PTCRA, ID1, CISH, CD99, MAL, SELL, JCHAIN	Pre-T-cell receptor alpha chain, T-cell receptor signalling pathway & differentiation
PF 8	SH3TC1, SMPD3, AQP3, CD1B, RAG1, RAG2, CD1E	RAG1, RAG2, TRBV20.1, DUSP1, CD1B, CD1E	V(D)J recombination, T-cell receptor beta chain, T-cell receptor signalling pathway
PF 14	LTB	TRBV2, TRBV4.2, TRBV6.1, TRBV6.5, TRBV7.9, LTB, LST1	T-Cell receptor beta chain, cell differentiation, MHC class III
PF 9	ITM2A, SATB1, CCR9	CCR9, JUN, ITM2A, SATB1, HSPA1B, ID3, TRBV5.1, TRBV6.6, TRBV10.3, TRBV12.4	Positive T-cell selection, T-cell receptor beta chain
PF 7	IFITM2, CCR7	HLA-A, HLA-B, HLA-C, HLA-E, FOS, IFITM1, IFITM2, B2M, CCR7	MHC class I of CD4+ T cells, CD4+ T-cell differentiation & activation, CD8+ T-cell anti-apoptosis

Then, PF8, PF9 and PF7 successively dominated in the DP(Q) stage, αβT(entry) stage and CD4⁺/CD8⁺ T stage, respectively. The representative PF8 genes (e.g. RAG1/2) participated in V(D)J recombination. The representative PF9 genes (e.g. ITM2A) participated in the positive selection of T cells. The representative PF7 genes (e.g. HLA) were involved in the major histocompatibility complex (MHC) synthesis of CD4⁺ T cells. The representative PF14 genes (e.g. TRBV) were components of the T-cell receptor beta chain.

Most of the representative PF genes coincided with the critical genes in T-cell development, providing good interpretations of these PFs (Table 2 and Table S5). The shifts in the dominant PFs for the different cell types were consistent with the T-cell development trajectory. Furthermore, the mixed contributions of multiple PFs to the cell types characterized the collaboration of PFs in certain T-cell developmental stages. The changes in this contribution proportion indicated the alterations of the cell states. The ‘cell-function-gene’ three-layer framework of our LDA-based method provides a proper tool to capture such subtle differences between cell types.

Empirical analysis on PBMC dataset

The PBMC dataset included 10 cell types: CD14⁺ monocyte, CD19⁺ B, CD34⁺, CD4⁺ T Helper2, CD4⁺/CD25 T Reg, CD4⁺/CD45RA⁺/CD25⁻ naive T, CD4⁺/CD45RO⁺ memory, CD56⁺ NK, CD8⁺ cytotoxic T and CD8⁺/CD45RA⁺ naive cytotoxic [36]. The dataset is well accepted as one of the most complex scRNA-seq benchmark datasets, with high pairwise correlations observed between the mean expression profiles of each cell population [37].

We performed additional benchmarking for our method with Seurat (Louvain) in terms of cell clustering, as well as Cell-ID and SCINA for marker-based cell annotation [10, 13, 38, 39]. The authors’ annotation was regarded as the ground-truth labels. There are two different annotation resolutions in the original study: the 6 major cell types and the 10 fine cell types. For each cell type, the reference marker genes were extracted from a blood cell marker collection from the XCell repository and a typical marker gene list provided by the original study [36, 40]. For our method, the cells were grouped into 6 clusters, and 19 PFs were identified in the major cell type resolution. In fine cell type resolution, the cells were grouped into 9 clusters, and 52 PFs were identified. For other methods, we also chose the best performance through the ARI for comparison.

For cell clustering, the performance of the LDA-based method is slightly better than Seurat (Louvain) on the PBMC dataset. The highest ARI is 0.628. Seurat (Louvain) achieved its best performance, 0.615, at resolution = 0.8. We also tested the Seurat (Leiden) method on this dataset; the best performance is almost the same as Seurat (Louvain). By comparing the ECA and ECP measures, we found that the LDA-based method tends to achieve better precision (0.49 versus 0.57), while Seurat prefers accuracy (0.46 versus 0.58).

For marker-based cell annotation, our method performed best in both major cell type resolution (Figure 5) and fine cell type resolution (Figure S4). In the major cell type resolution, the LDA-based method achieves a significant advantage in recall (Figure 5C), and the ARI reached 0.76, greater than both Cell-ID (0.71) and SCINA (0.55). In the fine cell type resolution, the performance of Cell-ID is actually very close to our method. Quite a few cell subtypes can only be annotated by either LDA or Cell-ID. The ARI of our method is 0.55, still greater than both Cell-ID (0.46) and SCINA (0.19).

Figure 5.

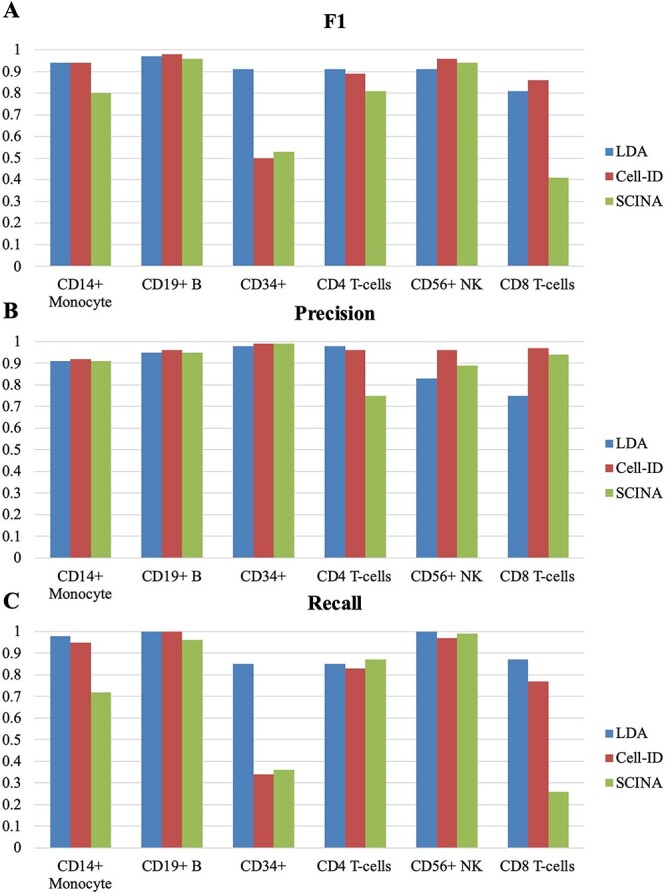
The performance comparison of marker-based cell annotation among the LDA-based method, Cell-ID and SCINA. The comparison was conducted on the PBMC dataset. The annotation precision and recall were evaluated in the major cell type resolution. (A) F1 score comparison among the three methods. (B) Precision comparison among the three methods. (C) Recall comparison among the three methods.

Robustness and computational efficiency of the LDA-based method

The above scRNA-seq analysis was conducted using a multithreading LDA implementation based on the MALLET package. We further investigated its robustness and computational efficiency across simulated datasets of different levels of noise/dropouts and sizes.

As shown in Table 3, the LDA-based method demonstrated excellent robustness on the simulated dataset. Splatter simulates dropouts following a logistic distribution, with the dropout probability determined by two parameters: dropout midpoint and dropout shape. By independently increasing the ‘outlier probability’ and the ‘dropout probability’, we observed that there was little influence on the model performance when outliers/noise were simulated, while the dropouts only had a very small effect on the model performance.

Simulation datasets ranging from 1000 to 200 000 cells were generated using Splatter [41]. Due to insufficient memory for Splatter to run, we produced 500 000-cell and 1 000 000-cell datasets by simply combining multiple 100 000-cell and 200 000-cell datasets, solely for testing the usability of our LDA implementation.

As the number of cells increased, the time consumption and memory usage of model training increased linearly (Table 4). Since the MALLET package was originally designed for training LDA models with massive documents in NLP area, benefiting from its efficient memory management strategy, our LDA implementation for scRNA-seq analysis is capable of processing up to the scale of 1 million cells. A typical 100 000-cell dataset took ~12 CPU hours on average, which could be completed in less than 15 min using an ~50-thread LDA implementation. Furthermore, the number of PFs may also affect the computational performance of our LDA implementation. The average time consumption is evaluated based on our Intel Xeon Gold 6326 CPU model (2.9G/3.5 GHz).

Table 4.

Computational performance of the LDA-based method

Cells number	Genes number	Topics (PFs) number	Threads number	Avg. memory (GB)	Avg. time (h)
1000	15 000	5	48	0.6	0.04
2000	15 000	5	48	1.0	0.06
5000	15 000	5	48	1.7	0.13
10 000	15 000	5	48	3.2	0.23
20 000	15 000	5	48	5.2	0.52
50 000	15 000	5	48	9.1	1.38
100 000	15 000	5	48	19.1	2.26 (1 time)
200 000	15 000	5	48	35.2	3.81 (1 time)
500 000	15 000	10	48	82.3	11.48 (1 time)
1 000 000	15 000	45	48	169.4	25.25 (1 time)

DISCUSSION

In this study, we proposed an LDA-based scRNA-seq analysis framework. Compared with four classic scRNA-seq clustering methods, the LDA-based method performed best on seven benchmark datasets. Then, by conducting an empirical analysis on three public datasets, our method was demonstrated to be able to capture the latent patterns of biological functions in multiple and complex cell types, and the results had good interpretability. Finally, we investigated the computational performance of the multithreading LDA implementation on large-scale datasets.

According to the results of the above analysis, our LDA-based scRNA-seq analysis method can not only cluster cells with high accuracy, but also possess strong capabilities for cell cluster annotation and marker gene identification. This is attributed to the unique advantages of LDA in scRNA-seq data analysis, which excels in its ability to discover latent gene expression patterns that exist in large-scale single cells.

In our method, the LDA model was employed to construct a cell-function-gene framework for scRNA-seq data analysis. Through a probabilistic generative process, LDA introduces latent variables into the observed cell–gene expression data. Although mathematically, the latent variables are distributions over all genes, only a few genes have been observed to contribute significant effects to each latent variable in practice. We use ‘representative genes’ to denote such genes. They provide insights for understanding the biological significance of the latent variables (topics) discovered by LDA, and are also the reason that the latent variables were named as ‘putative functions (PFs)’ in this study. Ultimately, the representative genes determine which functions of a cell are activated and further mark their cell types.

The cell-function-gene three-layer framework is capable of characterizing and precisely modelling complex biological mechanisms, which enables the LDA-based method to produce more meaningful results. This is the foundation of the data-driven cell annotation and functional interpretation method proposed in this study.

Furthermore, several intrinsic features of the LDA model make it well suited for scRNA-seq data analysis. For example, the latent topic identification process of LDA is a de facto dimensionality reduction technique imposed on the raw data. Information-intensive PFs were extracted from sparse gene expression profiles.

The LDA model is also capable of characterizing ‘mixtures’. In this study, cells were described as distributions over PFs, which means that each cell was understood as a state formed by the cooperation of multiple PFs. Thus, the LDA-based method could better distinguish between cell subtypes with subtle differences and more precisely model cells in intermediate states, which are common in development situations. The advantages of introducing the ‘mixture’ feature into single-cell analysis were first elucidated by duVerle et al. during the development of cellTree package [26]. Based on this insight, cellTree focuses on annotating the biological significance of LDA topics through a GO enrichment methodology.

Key Points

• An interpretable analysis framework for scRNA-seq data was constructed based on the Latent Dirichlet Allocation (LDA) model.

• A data-driven cell annotation and function interpretation method was proposed.

• Compared with classic methods, our method performed best onseven benchmark datasets.

• The LDA-based method is capable of capturing the latent patterns of biological functions in multiple and complex cell types, the results had good interpretability.

Author Biographies

Qi Yang graduated from School of Life Science and Technology, Harbin Institute of Technology. Her research interest is single-cell RNA sequencing data analysis method.

Zhaochun Xu is a graduate student of School of Life Science and Technology, Harbin Institute of Technology. His research interest is single-cell RNA sequencing data analysis method.

Wenyang Zhou graduated from School of Life Science and Technology, Harbin Institute of Technology. His research interest is immunological characteristic study based on scRNA-seq data.

Pingping Wang graduated from School of Life Science and Technology, Harbin Institute of Technology. Her research interest is disease study based on scRNA-seq data.

Qinghua Jiang is a professor of School of Life Science and Technology, Harbin Institute of Technology. His research focuses on immunoinformatics and bioinformatics.

Liran Juan is an associate professor of School of Life Science and Technology, Harbin Institute of Technology. His research focuses on computational methods and tools development for biological data analysis.

FUNDING

This work was supported by the Natural Science Foundation of China under grants [62072142, 62271175, 31601072].