Abstract
Computational analysis of RNA sequences constitutes a crucial step in the field of RNA biology. As in other domains of the life sciences, the incorporation of artificial intelligence and machine learning techniques into RNA sequence analysis has gained significant traction in recent years. Historically, thermodynamics-based methods were widely employed for the prediction of RNA secondary structures; however, machine learning-based approaches have demonstrated remarkable advancements in recent years, enabling more accurate predictions. Consequently, the precision of sequence analysis pertaining to RNA secondary structures, such as RNA–protein interactions, has also been enhanced, making a substantial contribution to the field of RNA biology. Additionally, artificial intelligence and machine learning are also introducing technical innovations in the analysis of RNA–small molecule interactions for RNA-targeted drug discovery and in the design of RNA aptamers, where RNA serves as its own ligand. This review will highlight recent trends in the prediction of RNA secondary structure, RNA aptamers and RNA drug discovery using machine learning, deep learning and related technologies, and will also discuss potential future avenues in the field of RNA informatics.
Keywords: RNA informatics, RNA secondary structure prediction, RNA-based therapeutics
INTRODUCTION
The central dogma posits that RNA functions solely as a conduit for the transfer of genetic information from DNA to proteins. Messenger RNAs (mRNAs) perform this role as information carriers. However, a number of exceptions to this paradigm have been discovered, involving RNA molecules participating in a diversity of functions. Transfer RNAs (tRNAs) function in the translation of the triplet codons of mRNAs into amino acids according to the genetic code. Ribosomal RNAs (rRNAs) constitute a primary component of ribosomes and catalyze protein synthesis as ribozymes. Micro RNAs (miRNAs) are involved in RNA silencing and post-transcriptional regulation of gene expression. Small nuclear RNAs (snRNAs) participate in the processing of pre-messenger RNAs within the nucleus. Long noncoding RNAs (lncRNAs), non-protein-coding RNAs with sequences longer than 200 bases, have been demonstrated to have various functions such as gene transcriptional regulation, translational regulation and epigenetic regulation [1]. The diversity of RNA species has been cataloged in databases such as Rfam [2–5] and RNAcentral [6], and the number of RNA species continues to grow.
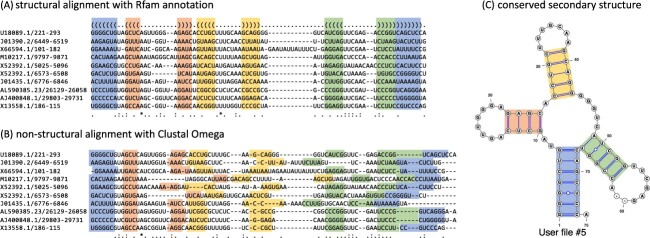
Many of these functional RNAs execute their functions by adopting tertiary structures that are evolutionarily conserved among RNA species. The experimental determination of RNA tertiary structures can be achieved through techniques such as X-ray crystallography, nuclear magnetic resonance (NMR) and cryo-electron microscopy (cryo-EM); however, these methods are both labor-intensive and cost-prohibitive for high-throughput analysis. As an alternative, RNA secondary structures are often targeted for structural and functional analysis of functional RNAs. An RNA secondary structure is defined as a set of base pairs with hydrogen bonds between two nucleotides, which makes a significant contribution to the tertiary structure in terms of free energy. This means that the folding of RNA is hierarchical in that tertiary interactions can be added without much distortion of the secondary structure [7]. It is well established that RNA secondary structures are also evolutionarily conserved among RNA species. For instance, a multiple sequence alignment of 10 tRNAs extracted from the Rfam database (Figure 1A), in which secondary structures are considered, yields the well-known and evolutionarily conserved cloverleaf shape (Figure 1C). In contrast, a multiple sequence alignment based on sequence identity alone, calculated using Clustal Omega [8], does not preserve the secondary structure at all, as shown in Figure 1B. This suggests that functional RNAs are evolutionarily conserved in their structures, rather than in their sequences and that structure correlates with function. Thus, RNA informatics has extensively studied RNA sequence analysis based on their secondary structures.
Figure 1.
Conserved secondary structures of transfer RNAs. (A) A multiple sequence alignment of 10 tRNAs extracted from the Rfam database is depicted, along with the annotated secondary structure. A string consisting of ‘.’, ‘(’ and ‘)’ at the top of the multiple alignment is the dot-bracket notation that represents the secondary structure. (B) A multiple sequence alignment based on sequence identity was calculated with Clustal Omega [8] for the 10 tRNAs. (C) The conserved secondary structure annotated by the Rfam database was visualized using VARNA [9]. Each colored region of base pairs corresponds to the acceptor stem (blue), D arm (red), anticodon arm (yellow) and T arm (green), respectively.
RNA secondary structure prediction, which has been a subject of study since the 1970s, constitutes a foundational technology in RNA sequence analysis. One of the pioneered works in this field was the Nussinov algorithm [10], which used dynamic programming to calculate the secondary structure with the maximum number of base pairs, under the assumption that the free energy of RNA structures decreases as base pairs are formed, thereby resulting in greater stability. Minimizing free energy using thermodynamic free energy parameters, such as Turner’s free energy parameters [11–13], is a widely used approach for predicting RNA secondary structures [11, 14–18]. However, these thermodynamics-based methods have a drawback in that they are limited by experimental technicalities in increasing the number and improving the quality of the free energy parameters. To address this issue, ‘assisted folding’ with high-throughput experiments involving chemical probing has been frequently employed. Selective 2’-hydroxyl acylation analyzed by primer extension (SHAPE) [19] and dimethyl sulphate (DMS) [20] are examples of high-throughput experiments that can induce chemical modifications on unpaired nucleotides, which can improve the accuracy of secondary structure prediction.
To address the drawback of the thermodynamics-based methods without wet-laboratory experiments, machine learning-based methods have been widely used. These methods learn their parameters from training data that include RNA sequences and their corresponding secondary structures, thus, more accurate models can be constructed by increasing the number of parameters if a sufficient amount of non-biased training data can be obtained. For example, compared with CONTRAfold [21, 22], which has approximately 300 parameters, ContextFold [23] learns a much richer parameter set of approximately 200k parameters from training data, resulting in the ability to predict RNA secondary structures with remarkable accuracy at the time. However, as discussed later, it has been shown that ContextFold’s rich parameterization can easily lead to low prediction accuracy due to overfitting to the training data [24, 25].
Another approach to further improve prediction accuracy is to incorporate evolutionary information from homologous sequences [26–31]. This approach is potentially very powerful, but it is a different problem from the de novo prediction from single sequences discussed in this review, because this approach incorporates much more information from homologous sequences. In addition, there are few RNA secondary structure prediction algorithms that incorporate evolutionary information in machine learning, and thus this category will not be addressed in this review.
Subsequent tasks include analyses utilizing the results of RNA secondary structure predictions, such as clustering [32, 33], family classification [34, 35], structural RNA detection [36, 37] and degradation prediction [38]. Machine learning techniques are frequently employed in these tasks as well.
With the aforementioned fundamental advancements in RNA informatics, the practical application of RNA research is also progressing at a rapid pace. One such application is RNA drug discovery, which is highly anticipated as a next-generation drug discovery modality. Research on RNA aptamers and mRNA vaccines, in which RNA itself serves as a therapeutic agent, and RNA-targeted drug discovery, in which RNA functions as an alternative drug target to proteins, is of particular interest. Additionally, the application of RNA bioinformatics research utilizing technologies such as machine learning and deep learning is required in these areas, and research is being conducted from various perspectives, including RNA structure.
In this review, we will present recent trends in the prediction of RNA secondary structures utilizing machine learning, deep learning and related technologies. Additionally, we will provide an overview of significant advancements in computational tasks that employ RNA secondary structure information, including the prediction of RNA–protein interactions and RNA drug discovery.
RNA SECONDARY STRUCTURE PREDICTION
What is RNA secondary structure prediction?
An RNA sequence is a sequence composed of four types of nucleotides: adenine (A), cytosine (C), guanine (G) and uracil (U). An RNA secondary structure is defined as a set of base pairs with hydrogen bonds between two nucleotides. Thus, the problem of RNA secondary structure prediction is to predict which two nucleotides in a given RNA sequence form base pairs. Typically, we consider only the Watson–Crick base pairs (A-U and G-C), which are the most prevalent, as well as the wobble base pairs (G-U), which are the next most common, in RNA secondary structure predictions. Other non-canonical base pairs are of great significance for tertiary structures, but they are much more challenging to model computationally, since each base is not guaranteed to form a base pair with at most one other base. An RNA secondary structure can be represented by a string in the dot-bracket notation, where two bases at the corresponding open and close brackets (‘(’ and ‘)’) form a base pair, while a base at the dot (‘.’) does not form a base pair with any base, as shown at the top of the multiple alignment in Figure 1A. A secondary structure that requires only one type of bracket for its dot-bracket notation, resulting in fully nested base pairs, is referred to as a pseudoknot-free secondary structure. Conversely, a substructure consisting of non-nested base pairs, as depicted in Figure 2, where the bases inside the loop form base pairs with the bases outside the loop, is called a pseudoknot. To describe a pseudoknot in the dot-bracket notation, two or more types of brackets (e.g. ‘[’ and ‘]’) are required. RNA secondary structure prediction including pseudoknots has been proven to be NP-hard for optimal solutions with no limitations on the complexity of pseudoknots [39, 40]. Therefore, approximations that restrict the complexity of pseudoknots or introduce heuristics are common approaches.
Figure 2.
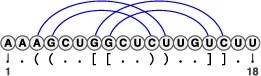
An RNA secondary structure with pseudoknots. The arcs connecting the two nucleotides represent base pairs. Since pseudoknot structures are non-nested, the arcs representing base pairs cross each other when the structure is drawn on a 2D plane.
Computational models
De novo computational modeling of RNA secondary structures can be broadly classified into three categories: nearest neighbor models, probabilistic generative models and deep learning models. This subsection provides an overview of these models and their implementations, along with a comparison of the three models. Figure 3 shows a schematic diagram of de novo RNA secondary structure prediction algorithms discussed in this subsection. Additionally, the datasets utilized for constructing models for predicting RNA secondary structures will be discussed.
Figure 3.
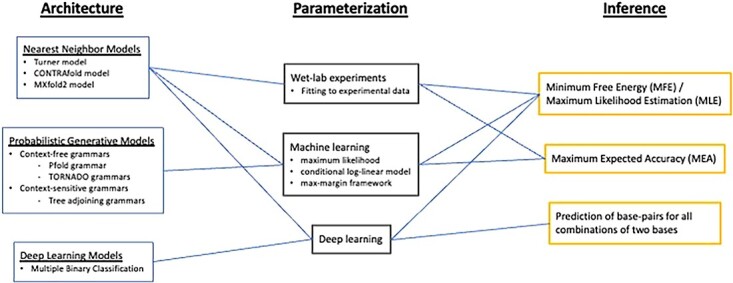
A schematic diagram of de novo RNA secondary structure prediction algorithms. Most RNA secondary structure prediction algorithms can be categorized by three aspects: ‘Architecture’, ‘Parameterization’ and ‘Inference’. Rivas et al. [25] added ‘Scoring scheme’ to these aspects, which is uniquely determined by ‘Parameterization’, and thus ‘Scoring scheme’ is omitted in this paper. From the ‘Architecture’ aspect, RNA secondary structure prediction algorithms can be categorized into nearest neighbor models, probabilistic generative models and deep learning models, depending on the RNA computational models. These are further sub-categorized according to their parameter assignment, fine-grainedness, grammatical rules etc. The ‘Parameterization’ aspect classifies RNA secondary structure prediction algorithms into three types, depending on how they find optimal parameter values for the parameter set defined in the ‘Architecture’: wet-lab experiments, machine learning and deep learning. Finally, the ‘Inference’ aspect classifies RNA secondary structure prediction algorithms according to how they use the models determined in the ‘Archtecture’ and ‘Parameterization’ to make secondary structure predictions.
Nearest neighbor models
The nearest neighbor model, which has been extensively utilized in the prediction of RNA secondary structures [11, 41–43], decomposes an RNA secondary structure into loop substructures with hairpin loops, stackings, bulge loops, internal loops, multi-branch loops and external loops, depending on the number of closing base pairs, as depicted in Figure 4. Each loop substructure is parametrized with several types of components, characterized by nucleotides in loops, the length of loops and other such factors, which are referred to as the energy parameters. The values assigned to each energy parameter are determined through either experimental methods or machine learning techniques. The free energy of each decomposed loop substructure is computed as the sum of the values of the energy parameters that characterize the loop substructure. The free energy of a given RNA secondary structure can be calculated as the sum of the free energies of the loop substructures that are decomposed from the given RNA secondary structure. Zuker et al. [44] established an efficient algorithm, known as the Zuker algorithm, which is based on the dynamic programming technique to find a secondary structure that minimizes the free energy among all possible secondary structures formed by a given RNA sequence. Many RNA secondary structure prediction methods that model RNA secondary structures without pseudoknots and employ the nearest neighbor model use the Zuker algorithm to find the minimum free energy (MFE) structures. The Zuker algorithm has a computational complexity of 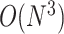 in time and
in time and 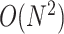 in space for an RNA sequence of length
in space for an RNA sequence of length 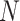 . Recently, the LinearFold algorithm [45] has been developed, which finds MFE structures accurately and approximately with
. Recently, the LinearFold algorithm [45] has been developed, which finds MFE structures accurately and approximately with 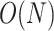 computational complexity in both time and space using the beam search technique. The key differences among the implementations of the Zuker algorithm or the LinearFold algorithm are the parametrization of the loop substructures and the determination of each value assigned to their energy parameters.
computational complexity in both time and space using the beam search technique. The key differences among the implementations of the Zuker algorithm or the LinearFold algorithm are the parametrization of the loop substructures and the determination of each value assigned to their energy parameters.
Figure 4.
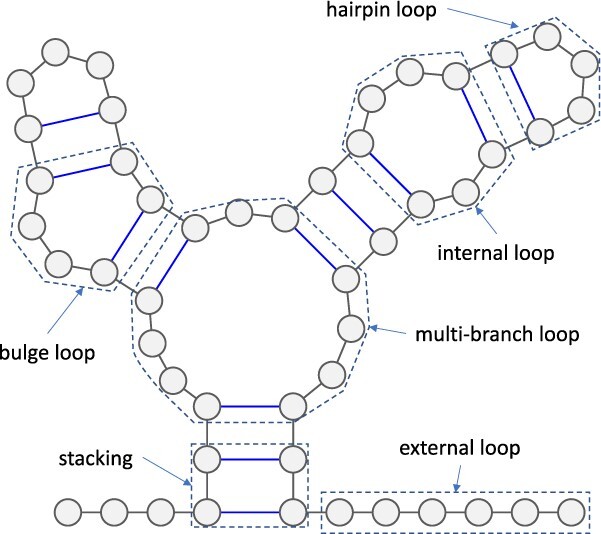
The nearest neighbor model decomposes RNA secondary structures into loop substructures. Hairpin loops are closed by a single base pair. Loop substructures that are closed by two base pairs with no unpaired bases are called stackings, those with unpaired bases on one strand are called bulge loops and those with unpaired bases on both strands are called internal loops. Multi-branch loops are loop substructures that are closed by three or more base pairs. Loop substructures closed by no base pairs are called external loops.
The methodology used to determine the energy parameters can be broadly classified into two approaches. The first approach involves determining the free energy parameters through wet-laboratory experiments, which is beyond the scope of this review; for further details, see the reference [46]. Examples of tools that fall under this approach include Mfold/UNAfold [14, 15], RNAfold in the ViennaRNA package [16, 17] and RNAstructure [11, 18]. Turner’s free energy parameters [11–13] are widely used in these thermodynamics-based approaches, and consist of up to approximately 12 700 parameters.
The second approach to determining energy parameters utilizes machine learning techniques to learn them from a large dataset of pairs of RNA sequences and their corresponding secondary structures. CONTRAfold [21, 22] used conditional log-linear models (CLLMs) to train approximately 300 parameters of the nearest neighbor model, resulting in high accuracy in predicting RNA secondary structures with significantly fewer parameters than Turner’s free energy parameters. Since the machine learning-based approach does not depend on wet-lab experiments, it allows for the development of a more comprehensive parametrization. For example, ContextFold [23] employed a fine-grained RNA secondary structure model with a parameter set of more than 200 000, resulting in the state-of-the-art prediction accuracy at the time. However, Rivas et al. [24, 25] pointed out that ContextFold had poor accuracy in predicting secondary structures for families not included in the training data, and was likely to fall into overfitting.
Several hybrid tools that combine both the thermodynamics- and machine learning-based approaches have been developed. SimFold [47, 48] modifies Turner’s free energy parameters to fit training data through the machine learning-based approach using training data including triplets of RNA sequences and their secondary structure as well as their free energies. MXfold [49] combines Turner’s energy parameters with rich-parametrized parameters trained by a max-margin framework, called structured support vector machines. It learns more precise parameters for substructures observed in the training data, reducing overfitting using thermodynamic parameters for unobserved substructures. MXfold2 [50], the successor of MXfold, utilizes deep learning to compute four types of scores for loop substructures: helix stacking scores, helix opening scores, helix closing scores and unpaired region scores, and combines them with Turner’s energy parameters, resulting in highly accurate and robust secondary structure prediction with a reduced risk of overfitting.
The majority of methods developed thus far predict RNA secondary structures based on the MFE under a given set of energy parameters. As the distribution of RNA secondary structures follows the Boltzmann distribution, the MFE is equivalent to the maximum likelihood estimation (MLE), which predicts a secondary structure with the maximum probability under the Boltzmann distribution. An alternative scheme, known as the maximum expected accuracy (MEA) approach, has been proposed, which predicts a secondary structure that maximizes the expected number of correctly predicted base pairs under the Boltzmann distribution, rather than predicting the MFE or MLE structure. The expected number of correctly predicted base pairs is calculated using the McCaskill algorithm [51], which is derived by replacing the ‘min’ operation of the Zuker algorithm with the ‘logsumexp’ operation. This scheme, first proposed in Knudsen et al.[52], is also implemented in various tools, such as CONTRAfold, RNAfold and RNAstructure. Additionally, Hamada et al.[53] have redefined MEA to be more compatible with the accuracy metrics for predicting RNA secondary structures, and developed CentroidFold [53, 54] using Turner’s parameters, CONTRAfold’s parameters and the Boltzmann likelihood parameters by Andronescu et al. [48].
The nearest neighbor model for pseudoknot-free structures was extended by incorporating additional parameters for pseudoknot substructures, and thus nearest neighbor models for pseudoknots, such as the Rivas–Eddy model [55], the Dirks–Pierce model [56] and the Cao–Chen model [57], were developed to model RNA secondary structures that include pseudoknots. Algorithms to compute exact minimum free energies on these models through dynamic programming have been implemented as PKNOTS [55] and NUPACK [56], with a significant computational cost of 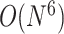 time for PKNOTS,
time for PKNOTS, 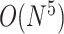 time for NUPACK, and
time for NUPACK, and 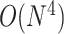 space for both for the limited complexity of pseudoknotted structures. For more accurate prediction of secondary structures including pseudoknots, further efforts were made to use machine learning techniques to estimate more accurate energy parameters. Andronescu et al. [58] used HotKnots [59], which can rapidly predict pseudoknotted structures through heuristics on the Dirks–Pierce model, to train its parameters from training data using the same methodology as SimFold. In contrast, IPknot [60, 61] utilizes the results of learning the parameters of the nearest neighbor model for pseudoknot-free structures, such as CONTRAfold, from training data and forcibly predicts pseudoknotted structures through a heuristic using integer programming.
space for both for the limited complexity of pseudoknotted structures. For more accurate prediction of secondary structures including pseudoknots, further efforts were made to use machine learning techniques to estimate more accurate energy parameters. Andronescu et al. [58] used HotKnots [59], which can rapidly predict pseudoknotted structures through heuristics on the Dirks–Pierce model, to train its parameters from training data using the same methodology as SimFold. In contrast, IPknot [60, 61] utilizes the results of learning the parameters of the nearest neighbor model for pseudoknot-free structures, such as CONTRAfold, from training data and forcibly predicts pseudoknotted structures through a heuristic using integer programming.
Probabilistic generative models
The use of stochastic context-free grammars (SCFGs) as a probabilistic generative model for modeling RNA secondary structures without pseudoknots was first proposed by Eddy and Durbin [62] and Sakakibara et al. [63]. A variant of this approach, known as covariance models, has been applied to the popular RNA homology search tool, Infernal [64]. Building covariance models requires highly accurate RNA multiple sequence alignments, which enable accurate and robust homology searches due to the evolutionary information provided by the alignment. Pfold [52, 65] is a method for RNA secondary structure prediction that utilizes simple context-free grammars. Dowell et al. [66] compared nine lightweight grammars for RNA secondary structure prediction, including the Pfold grammar. Sato et al. [67] proposed a method for learning RNA grammars with appropriate complexity using a non-parametric Bayesian approach. TORNADO [24] is a flexible framework that can describe a variety of RNA grammars, allowing SCFGs to emulate the nearest neighbor model with Turner’s parameters or CONTRAfold, and demonstrated prediction accuracy comparable with their counterparts.
Since RNA secondary structure prediction including pseudoknots is beyond the capacity of context-free grammars, context-sensitive grammars, such as tree-adjoining grammars [68, 69] and multiple context-free grammars [70], are alternatively used for predicting pseudoknotted structures. However, due to their large computational complexity, it is impractical to use them for secondary structure prediction including pseudoknots.
Deep Learning models
Deep learning techniques have been leveraged to achieve groundbreaking advancements in a plethora of fields, including the life sciences, and have been applied to the prediction of RNA secondary structures. A majority of deep learning-based methods for RNA secondary structure prediction make no assumptions about the structures themselves, such as the nearest neighbor model and probabilistic generative models. Instead, these methods perform secondary structure prediction by solving multiple binary classification problems for all combinations of two bases in a given RNA sequence, determining whether each of the two bases form a base pair or not. In order to address the constraints that RNA secondary structures must satisfy, such as the restriction that each base can only form a base pair with at most one other base, methods such as E2Efold [71] and UFold [72] utilize linear programming, while Akiyama et al. [73] employ integer programming, originated from IPknot [60, 61]. SPOT-RNA [74] did not aim to solve such constraints, instead attempting to predict base triplets, and employed ensemble of multiple networks with different hyperparameters to mitigate overfitting. UFold, on the other hand, aimed to reduce overfitting by utilizing data augmentation, through the random generation of a large number of artificial RNA sequences and their secondary structures predicted by CONTRAfold, as additional training data.
Unlike other deep learning-based approaches, MXfold2 [50] employs deep learning to infer the energy of decomposed loop substructures within the nearest neighbor model, subsequently utilizing the Zuker algorithm to predict RNA secondary structures. To mitigate overfitting, MXfold2 introduces thermodynamic regularization, ensuring that the energy of the secondary structure calculated by MXfold2 does not deviate significantly from the free energy calculated using Turner’s parameters.
It has been acknowledged that the utilization of deep learning for RNA secondary structure prediction can easily result in overfitting, owing to the high number of parameters that require training. This implies that the accuracy of secondary structure prediction for structurally dissimilar RNA sequences from the training data is not particularly high if no efforts are taken to prevent overfitting [50, 73, 75, 76]. For example, E2Efold [71] was not designed against overfitting, and in their benchmark experiments, the training and test datasets were created by randomly splitting a single dataset. Consequently, overfitting could not be detected because structurally similar sequences were included in training and test datasets. This resulted in very low prediction accuracy of E2Efold for families not included in the training data, which is unfortunately not practical.
Comparison of the three computational models
Table 1 summarizes the de novo RNA secondary structure prediction tools presented in this review that are currently available. The nearest neighbor model is based on the knowledge of RNA secondary structures, which has been extensively studied for a long time. To date, the mainstream approach for predicting RNA secondary structures has been to conduct wet-lab experiments or employ machine learning techniques to determine the energy parameters of the nearest neighbor model. Probabilistic generative models, on the other hand, provide a framework for describing RNA structure modeling through the use of formal grammars. As demonstrated by Rivas et al. [24], the nearest neighbor model can be articulated by SCFGs, with prediction accuracy that is comparable with that of its nearest neighbor model counterpart. However, to date, no RNA grammar has been developed that surpasses the prediction accuracy of the nearest neighbor model.
Table 1.
List of de novo RNA secondary structure prediction tools presented in this paper that are currently available.
The column labeled ‘Model’ indicates the category to which the method belongs (NN: nearest neighbor model, PG: probabilistic generative model, DL: deep learning-based model). The ‘TM’ column indicates whether the method uses thermodynamic parameters. The column labeled ‘ML’ indicates whether the method can train its parameters using machine learning, and if so, which training method is used (MLE: maximum likelihood estimation, CG: constraint generation, CLLM: conditional log-linear models, BL: Boltzmann likelihood, MM: max-margin framework, DL: deep larning). The ‘MEA’ column indicates whether the method predicts secondary structure by default (✓) or optionally (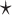 ) with the maximum expected accuracy. The column labeled ‘PK’ indicates whether the method can predict pseudoknotted structures.
) with the maximum expected accuracy. The column labeled ‘PK’ indicates whether the method can predict pseudoknotted structures.
Conversely, full deep learning methods, with the exception of MXfold2, do not rely on knowledge of RNA secondary structures, thereby allowing for a high degree of freedom in model construction. This can lead to improved fitting of the training data, and thus high prediction accuracy for RNA sequences with structures similar to those in the training data. However, this also increases the risk of overfitting and poor prediction accuracy for structurally dissimilar sequences. The problem of overfitting is a prevalent issue not only in deep learning but also in other machine learning techniques with rich parametrization; it is particularly acute in deep learning as models can easily be scaled to an enormous number of parameters [75, 78].
Datasets for building models
Frequently employed benchmark datasets for RNA secondary structure prediction are summarized in Table 2, which include RNA STRAND dataset [79], Archive II dataset [80] and RNAStralign dataset [81]. These benchmark datasets were constructed by compiling RNA sequences with known and reliable secondary structures from various databases such as Comparative RNA Web (CRW) Site [83], tmRNA database [84], Sprinzl tRNA Database [85], RNase P Database [86], SRP Database [84] and others. These benchmark datasets, however, are limited in their diversity of RNA secondary structures, containing only 8–10 RNA families. More recently, a more comprehensive dataset, bpRNA-1m dataset [82], has been constructed by incorporating RNA sequences with secondary structure annotations from Rfam 12.2 [4] in addition to RNA sequences derived from the aforementioned databases, comprising 102 318 sequences from approximately 2600 RNA families.
Table 2.
Benchmark datasets commonly used in recent machine learning- and deep learning-based methods.
| # fam. | # seq. | Length | Ref. | |
|---|---|---|---|---|
| RNA STRAND | 172 | 4666 | 4 ~ 4381 | [79] |
| TORNADO dataset | [24] | |||
| TrainSetA | 11 | 3166 | 10 ~ 734 | |
| TestSetA | 11 | 697 | 10 ~ 768 | |
| TrainSetB | 22 | 1094 | 27 ~ 237 | |
| TestSetB | 22 | 430 | 27 ~ 244 | |
| Archive II | 10 | 3975 | 28 ~ 2968 | [80] |
| RNAStralign | 8 | 30 451 | 30 ~ 1851 | [81] |
| bpRNA-1m |
 2600
2600 |
102 318 | 2 ~ 4381 | [82] |
| bpRNAnew |
 1500
1500 |
5401 | 33 ~ 489 | [50] |
# fam.: the number of families. # seq.: the number of sequences.
In many previously conducted benchmark experiments for RNA secondary structure prediction methods, these datasets have been randomly partitioned into training and test data for cross-validation. This means that the test data may not contain highly homologous sequences to those in the training data, but structurally similar sequences from the same families.
Rivas et al. [24, 25] have highlighted that accuracy evaluations utilizing ‘sequence-wise cross-validation’ cannot detect overfitting, and subsequently established TrainSetA, TestSetA, TrainSetB and TestSetB. TrainSetA and TestSetA were compiled from literature sources [21, 47, 48, 66, 85, 87], while TrainSetB and TestSetB, comprising 22 families with 3D structure annotations, were extracted from Rfam 10.0 [3]. The sequences in Train/TestSetB share less than 70% sequence identity with the sequences in TrainSetA. It is worth mentioning that the literature-based TrainSetA and Rfam-based TestSetB share no families and are structurally dissimilar, while TrainSetA and TestSetA exhibit some structural similarity. By conducting ‘family-wise cross-validation’, in which training is performed using TrainSetA and subsequently testing with TestSetB, Rivas et al. [24, 25] demonstrated that ContextFold, which exhibits an extremely high prediction accuracy in sequence-wise cross-validation, is prone to overfitting. Similar trends have been reported for deep learning-based methods by Szikszai et al. [75].
To further perform family-wise cross-validation on models trained from a bpRNA-1m-based dataset, Sato et al. [50] constructed bpRNAnew dataset from approximately 1500 families newly discovered and registered with Rfam since the release of Rfam version 12.2 (January 2017), on which bpRNA-1m dataset is based.
In general, machine learning and deep learning algorithms operate under the assumption that training data are randomly and uniformly sampled from the population. However, this assumption is often invalidated, even in large datasets such as bpRNA-1m dataset, as novel RNA families continue to be discovered to this day. If prior knowledge of the family of a sequence of interest is available, a homology search tool such as Infernal [64] can be more accurate in predicting its structure. However, when no knowledge of the family is available, it is necessary to make RNA secondary structure predictions solely from the sequence in order to perform structural and functional analyses. Therefore, it is crucial to evaluate prediction accuracy in such situations through the use of family-wise cross-validation, avoiding methods with significantly lower accuracy for unknown families.
APPLICATIONS OF RNAs TO THERAPEUTICS
Currently, the majority of pharmaceuticals consist of small molecules that target disease-associated proteins in small molecule drug discovery. However, the limitations of this approach are well known, and there is a pressing need for alternative drug modalities. To address these limitations, synthetic and natural RNAs have garnered significant attention as potential drug candidates and targets, respectively. This section outlines the use of machine-learning and deep-learning techniques in the discovery and development of RNA-based drugs, including the use of synthetic RNAs as drugs and natural RNAs as targets for drug discovery. We will also discuss the importance of RNA structures in these approaches (Figure 5B).
Figure 5.
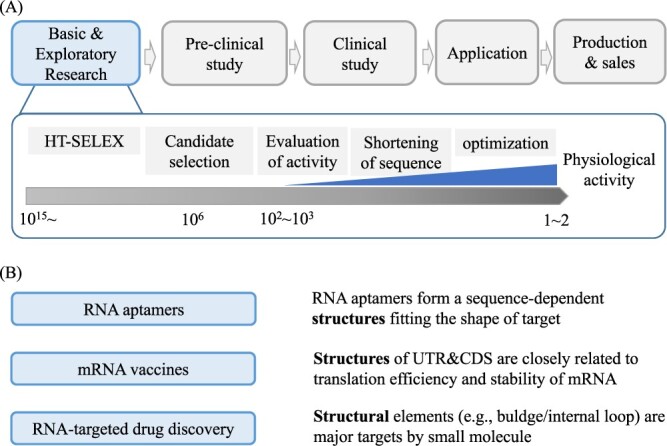
(A) Schematic representation of the RNA aptamer development process and (B) the significance of RNA structure in each RNA therapeutic approach. (A) The basic and exploratory research comprises multiple stages, encompassing HT-SELEX, candidate identification from the HT-SELEX output, assessment of the selected candidates’ activity and sequence truncation/optimization. (B) The importance of RNA structure (right) in three RNA-based therapeutics (left) that have been highlighted in this review.
RNA drug discovery—making RNAs into drugs
RNA aptamers
RNA aptamers are single-stranded RNA molecules that range in length from 20 to 50 bases and form specific three-dimensional structures based on their nucleotide sequence. These structures allow RNA aptamers to fit into the shape of target substances, such as disease-related proteins, and act as drugs; it is therefore important to consider RNA structures in aptamer design. RNA aptamers have several advantages over traditional drugs, including high affinity and specificity, the ability to be designed for a wide range of target molecules, including membrane proteins, and low immunogenicity. As a result, RNA aptamers are considered to be potential next-generation drugs. As of February 2022, only one RNA aptamer, Macugen® (pegaptanib), has been approved for the treatment of age-related macular degeneration.
The process of creating RNA aptamers follows a similar path to traditional drug development, comprising several stages such as basic and exploratory research, preclinical study, clinical study, application and production and distribution (Figure 5A). Many computational studies on RNA aptamers focus on the initial stage of basic and exploratory research, which is further divided into several steps. The first step involves obtaining candidate aptamer sequences using a technique called SELEX (Systematic Evolution of Ligands by EXponential enrichment) [88]. This process involves repeatedly binding and amplifying RNA sequences that bind strongly to the target from a pool of random sequences, enriching for aptamers with high binding activity. High-throughput sequencing techniques, known as HT-SELEX (High-Throughput SELEX), enable comprehensive measurement of the sequence information in the enriched sequence pool at each round, generating a large amount of sequence data in each round of HT-SELEX.
A number of computational approaches have been proposed to improve the identification of aptamers from HT-SELEX data [89–91], including sequence/structure clustering-based methods [92–94], motif-based methods [95, 96], scoring-based methods [97, 98] and so forth. Here, we review some of these approaches that utilize machine learning and deep learning and discuss their effective utilization.
Bashir et al. [99] proposed a machine learning (ML)-guided Particle Display methodology (MLPD), which integrates physical experiments and machine learning. They used particle display (PD) to partition aptamer libraries according to affinity and used these data to train machine learning models. This method allows for the in silico prediction of aptamer affinity, and the authors were able to successfully identify novel aptamers with enhanced affinity.
RaptGen [100] employs a combination of a variational autoencoder (VAE) and a profile hidden Markov model (HMM) to effectively model aptamers with local motifs that contain substitutions and indels. The latent spaces learned by RaptGen are used for several purposes: (i) visualizing SELEX data and generating novel aptamers, (ii) optimizing aptamers using Bayesian optimization with additional information, such as detailed affinity scores obtained through surface plasmon resonance experiments and (iii) designing shortened (truncated) aptamers, which is realized using shorter profile HMM in RaptGen model. While the current version of RaptGen does not take structural information of RNA into account, this can be addressed using a profile stochastic context grammar (SCFG; see the previous section) instead of a profile HMM.
Di Gioacchino et al. [101] created a restricted Boltzmann machine (RBM) model using SELEX data for thrombin, which is a probabilistic generative model capable of generating novel aptamer sequences (similar with RaptGen). They demonstrated that the log-likelihood of sequences correlates with their fitness (i.e. binding ability to the target).
Recently, Andress et al. [102] proposed a method called Daptev, which combines a deep generative model (VAE) and molecular simulation (molecular docking). As both data-driven and simulation-based approaches (considering tertiary structures of aptamers) can be useful for in silico aptamer design, this may be a promising approach.
Note that the above-mentioned approaches, such as RaptGen and MLPD, assume a target protein with experimental data (e.g. SELEX). More general (and difficult) problem setting that predicts pairs of aptamer-protein is introduced. AptaNet [103] uses a multi-layer perceptron (MLP) to predict aptamer–protein pairs, taking a pair of RNA and amino acid sequences as input. The training dataset for this model was compiled from Aptagen and Aptamer Base and consists of 850 positive and 2554 negative instances. In Torkamanian-Afshar et al. [104], a classifier for aptamer–protein pairs was trained using the sequential and structural properties of known aptamer–protein complexes, utilizing positive and negative data from RPINBASE [105]. This classifier was then used to select target-binding RNA sequences as a potential biomarker for aminopeptidase N (CD13). These sequences were utilized as the starting population for a genetic algorithm (GA) to generate new aptamers that exhibit higher selectivity for binding to CD13 compared with the original ones.
In contrast, a wealth of data on RNA sequences that bind to various natural RNA-binding proteins (RBPs) have been accumulated, and research utilizing these data through machine learning and deep learning methods is ongoing [106]. For example, Yamada et al. [107] proposed a BERT (Bidirectional Encoder Representations from Transformers)-based model for predicting RNA–protein interactions with biological implications, and Kashiwagi et al. [108] introduced a max-margin model for predicting residue-level contact in RNA–protein interactions. These studies on natural RBPs could potentially inform the design of artificial RNA aptamers that target proteins; for further details, see the reference [109].
As previously mentioned, beneficial machine learning techniques for in silico aptamer design have been developed in recent years and are anticipated to aid in the expansion of aptamer drug discovery in the future. Furthermore, the refinement of RNA structure prediction contributes significantly to the development of highly effective RNA aptamers.
mRNA vaccines
Since 2020, the development of coronavirus disease 2019 vaccines such as BNT162b2 (Pfizer/BioNTech) and mRNA-1273 (Moderna) has been active, and the drug discovery modality of mRNA medicine has garnered significant attention [110–112]. mRNA vaccines have also been proposed as a potential therapeutic approach for cancer [113]. To facilitate the rapid production of mRNA vaccines, computational design of mRNA sequences is crucial, involving the comprehensive design of 5’ untranslated region (UTR), coding sequence (CDS) and 3’UTR sequences.
The sequence of the 5’UTR is closely correlated with translation efficiency. A study by Sample et al. [114] developed a convolutional neural network (CNN) model to predict Mean Ribosome Load (MRL), a measure of ribosome association, for given 5’UTR sequence. The authors used MRL measurements from 280 000 random 5’UTRs as a training dataset for the model. Utilizing this CNN model and a GA, the authors were able to generate 5’UTR sequences with a desired MRL value. These comprehensive data will be beneficial for 5’UTR design in the development of mRNA vaccines.
The sequence of CDS also impacts the abundance of translation. iCodon [115] is a tool designed to optimize coding regions that contain synonymous codon substitutions in order to increase mRNA stability and protein expression (e.g. designing high-expression reporters) or de-optimize sequences containing synonymous codon substitutions (e.g. designing sequences with reduced expression). The prediction model of mRNA stability is proposed in Medina-Muñoz et al. [116]. Zhang et al. [117] proposed an efficient method, named LinearDesign, for mRNA design by reducing it to a problem in computational linguistics. The optimal mRNA is analogous to finding the most probable sentence among similar-sounding alternatives. The algorithm takes 11 min for the Spike protein and can optimize stability and codon usage concurrently.
According to Leppek et al. [118], a method for optimizing the structure, stability and translation of mRNA through combinatorial means was introduced. Initially, viral and cellular UTRs mined from literature were procured, followed by structure-informed CDS design in which Eterna (crowdsourced) [77] and the LinearDesign were utilized as efficient design tools.
RNA-targeted drug discovery—making RNAs into drug target
Another challenge in drug discovery is the depletion of potential drug targets. Currently, disease-related proteins are the primary targets for drug discovery. Recent research has shown that lncRNAs play a vital role in a variety of intracellular regulatory processes in eukaryotes, including humans [119, 120]. Moreover, many lncRNAs have been found to be associated with serious diseases such as cancer and neurodegenerative disorders, making them potential new drug targets [121–123].
A strategy for RNA-targeted drug discovery is to design small molecules (i.e., traditional drugs) that bind to RNA structures in lncRNAs [124–126] and ribo-switches [127], indicating that the consideration of RNA structures is essential in this kind of researches. Although there exists limited studies for RNA–target drug discovery using machine learning [128], we will introduce a few studies in the following.
RNAmigos [129] is a tool that constructs and encodes network representations of RNA structures and predicts potential ligands for novel binding sites. It employs a graph convolutional neural network (GCN) to represent RNA structures as an Augmented Base Pairing Network (ABPN), including both canonical and non-canonical base-pairs. The training data were sourced from the RNA–ligand pairs in the RCSB PDB Data Bank [130].
A recent study by Yazdani et al. [131] that analyzed data from screening experiments suggests that there may be a correlation between the properties of RNA and the properties of small molecule ligands that bind to RNA. Using machine learning methods to analyze their own library of RNA-bound small molecules, the authors found that general chemical properties of RNA-bound small molecule compared with protein-bound small molecules and FDA-approved drugs.
Stefaniak et al. [132] developed AnnapuRNA, a machine-learning statistical scoring function, to accurately predict the structure of RNA-ligand complexes. Their program utilizes a coarse-grained representation for both the RNA and small molecule ligands involved in the interaction. On the other hand, Chhabra et al. [133] used a distance-dependent fingerprint to characterize the binding pose of a ligand in an RNA binding pocket (RNAPosers). They trained a machine-learning algorithm using data from 80 experimentally determined RNA–ligand complexes and used it to score docking poses.
Grimberg et al. [134] sought to design novel small molecule inhibitors that would bind to the RNA hairpin within the ribosomal peptidyl transferase center (PTC) of Mycobacterium tuberculosis through the use of computational optimization models integrating CNNs with classical machine learning regression and decision tree models, using approximately 800 training data points [135]. Upon synthesizing the 10 small molecules identified by these computational means, functional validation was conducted, revealing that four of the molecules were potent inhibitors targeting hairpin 91 in the ribosomal PTC of M. tuberculosis, thereby inhibiting translation. This study demonstrates the potential for optimizing RNA-binding drugs with sufficient training data.
It should be noted that all of the aforementioned methods assume targeted RNA elements of relatively small size. However, it is crucial to identify specific RNA elements (such as structures, modifications and binding sites of other biomolecules) that are suitable for drug targeting, as lncRNAs are lengthy and the location of functional elements can be challenging to determine. To this end, various approaches have been proposed, including infoRNA [136]. While machine learning-based approaches in this direction are limited, these approaches may prove useful in identifying functional elements in lncRNAs in the future if sufficient data are available.
CHALLENGES AND OPPORTUNITIES
The accuracy of RNA secondary structure prediction has considerably improved in recent years due to the utilization of machine learning and deep learning techniques. One potential avenue for further enhancement in prediction accuracy is the incorporation of evolutionary information from homologous sequences, which can be achieved through methods such as common secondary structure prediction from multiple sequence alignments [26, 27], probabilistic consistency transformation of base-pairing probabilities from homologous sequences [28, 29], MSA transformers [137] and the utilization of pre-trained large language models, such as BERT [107, 138, 139].
Additionally, high-throughput experiments such as selective 2’-hydroxyl acylation analyzed by primer extension (SHAPE) [19] and dimethyl sulphate (DMS) [20], which can stochastically induce chemical modifications on unpaired nucleotides, have been shown to improve the accuracy of secondary structure predictions. The incorporation of pseudo-free energy calculated using the reactivity of chemical probing from high-throughput experiments has also been shown to substantially enhance the accuracy of thermodynamics-based RNA secondary structure prediction [140]. However, despite the potential benefits, few machine learning methods have been developed to predict RNA secondary structures from RNA sequences with chemical reactivity due to a lack of a large amount of training data including not only RNA sequences and their structure, but also their chemical reactivities. EternaFold [77] augmented the accuracy of secondary structure prediction by refining the parameters of the nearest neighbor model via multitask learning with high-throughput experimental data that lack secondary structure annotations, thereby demonstrating the potential of using high-throughput experimental data in machine learning-based RNA secondary structure prediction. Currently, the accuracy of RNA secondary structure prediction is still insufficient for long RNA sequences longer than 500 bases. One of the reasons for this is that the number of long RNAs with known secondary structures is small, and models that can handle long sequences cannot be sufficiently trained by machine learning or deep learning. If secondary structure prediction models can be trained from high-throughput experimental data, which are easily available even for long sequences, the accuracy of secondary structure prediction for long sequences is expected to improve.
RNA modifications play a significant role in various biological processes including splicing, translation, cell development and disease [141, 142]. In mRNA vaccines, all uridines are modified to N1-methylpseudouridines, which enables them to bypass the Toll-like receptors (TLRs) that detect RNA viruses and thus produce viral proteins [143]. Due to the need for modified free energy parameters and potential alteration of base pairing partners, the development of RNA secondary structure prediction methods that can consider RNA modifications is limited [144]. However, as RNA modifications are more prevalent in vivo than previously thought, and the increasing demand for mRNA vaccine stability prediction and other applications make the development of highly accurate RNA modification-aware RNA secondary structure prediction by machine learning an urgent task. However, this is a challenging task due to the scarcity of data of RNA sequences containing modified bases with secondary structures available.
It is highly demanding to establish high-throughput methods for determining RNA 3D structures, not only for RNA structural and functional analysis, but also for RNA drug discovery and RNA-targeted drug discovery. AlphaFold2 [145] has achieved highly accurate protein 3D structure prediction comparable with experimental structure determination. Inspired by AlphaFold2, similar deep learning approaches have been applied to tackle RNA 3D structure prediction and have been reported to perform well on their datasets [146–148]. However, in the competition for RNA 3D structure prediction held at the most recent CASP 15 (https://predictioncenter.org/casp15/), these deep learning-based RNA 3D structure prediction methods were not at all comparable with conventional approaches. The number of 3D structures registered in Protein Data Bank (PDB) [149] is 173 649 for proteins, but only 1682 for RNAs (December 2022). Therefore, highly accurate RNA 3D structure prediction without falling into overfitting is presumed to be challenging with fully deep learning-based approaches like AlphaFold2.
CONCLUSION
In recent years, there has been a growing interest in structure-based RNA analysis, as it is believed that the function of many RNAs is closely related to their structures. In this paper, we have reviewed the latest advancements in RNA secondary structure prediction, which is a fundamental technique for structure-based RNA analysis, particularly in methods that utilize machine learning and deep learning. We have also discussed the use of machine learning and deep learning in RNA drug discovery and RNA-targeted drug discovery, which are among the most notable applications of structure-based RNA analysis in recent times. It is important to note that compared with proteins, there are orders of magnitude fewer known samples of RNA structures and interactions with other molecules. Therefore, when applying machine learning and deep learning techniques to analyze RNAs, it is essential to be cognizant of the fact that the training data may be small, biased or both, and to implement various strategies to enhance generalization capabilities.
Key Points
In this review, we have outlined the field of RNA secondary structure prediction, focusing particularly on methods that utilize machine learning and deep learning.
It is important to note that, in order to maintain the prediction accuracy of these methods, the test data used for benchmarking must be carefully constructed to detect any potential overfitting.
Fundamental technologies of RNA informatics are applicable to the development of RNA-based therapeutics.
We provided a review of RNA drug discovery and RNA–target drug discovery, in which various machine learning and deep learning approaches are effectively utilized.
ACKNOWLEDGMENTS
The authors thank the organizers and the attendees of the RNA Informatics Dojo 2022 in Miyazaki, Japan for fruitful discussions.
Author Biographies
Kengo Sato is a professor at Tokyo Denki University, Japan. He received his Ph.D. in Computer Science from Keio University, Japan, in 2003. His research interests include bioinformatics, computational linguistics and machine learning.
Michiaki Hamada is a professor at Waseda University in Japan, and is concurrently appointed at National Institute of Advanced Industrial Science and Technology (AIST) and Nippon Medical University. He obtained his Ph.D. in Science from the Tokyo Institute of Technology in 2009. His research interests encompass RNA bioinformatics, drug discovery and artificial intelligence.
Contributor Information
Kengo Sato, School of System Design and Technology, Tokyo Denki University, 5 Senju Asahi-cho, Adachi-ku, Tokyo 120-8551, Japan.
Michiaki Hamada, Department of Electrical Engineering and Bioscience, Faculty of Science and Engineering, Waseda University, 55N-06-10, 3-4-1, Okubo, Shinjuku-ku, Tokyo 169-8555, Japan; Computational Bio Big-Data Open Innovation Laboratory (CBBD-OIL) , National Institute of Advanced Industrial Science and Technology (AIST), 3-4-1, Okubo, Shinjuku-ku, Tokyo 169-8555, Japan; Graduate School of Medicine, Nippon Medical School, 1-1-5, Sendagi, Bunkyo-ku, Tokyo 113-8602, Japan.
FUNDING
This work was partially supported by a Grant-in-Aid for Scientific Research (B) (No. 22H03689) from the Japan Society for the Promotion of Science (JSPS) to K.S., and by JST CREST (grant nos. JPMJCR1881 and JPMJCR21F1), AMED (Nos. 21479280, JP22ama121055) and JSPS KAKENHI (Nos. 22H04925, 20H00624, 17K20032) to M.H.
REFERENCES
- 1. Mattick JS, Amaral PP, Carninci P, et al. Long non-coding RNAs: definitions, functions, challenges and recommendations. Nat Rev Mol Cell Biol 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Griffiths-Jones S, Moxon S, Marshall M, et al. Rfam: annotating non-coding RNAs in complete genomes. Nucleic Acids Res 2005;33(Database issue):D121–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Gardner PP, Daub J, Tate J, et al. Rfam: Wikipedia, clans and the “decimal” release. Nucleic Acids Res 2011;39(Database):D141–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Nawrocki EP, Burge SW, Bateman A, et al. Rfam 12.0: updates to the RNA families database. Nucleic Acids Res 2015;43(Database issue):D130–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Kalvari I, Nawrocki EP, Ontiveros-Palacios N, et al. Rfam 14: expanded coverage of metagenomic, viral and microRNA families. Nucleic Acids Res 2021;49(D1):D192–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. RNAcentral Consortium . RNAcentral 2021: secondary structure integration, improved sequence search and new member databases. Nucleic Acids Res 2021;49(D1):D212–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Tinoco I, Jr, Bustamante C. How RNA folds. J Mol Biol 1999;293(2):271–81. [DOI] [PubMed] [Google Scholar]
- 8. Sievers F, Wilm A, Dineen D, et al. Fast, scalable generation of high-quality protein multiple sequence alignments using clustal omega. Mol Syst Biol 2011;7(1):539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Darty K, Denise A, Ponty Y. VARNA: interactive drawing and editing of the RNA secondary structure. Bioinformatics 2009;25(15):1974–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Nussinov R, Jacobson AB. Fast algorithm for predicting the secondary structure of single-stranded RNA. Proc Natl Acad Sci U S A 1980;77(11):6309–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Mathews DH, Sabina J, Zuker M, et al. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J Mol Biol 1999;288(5):911–40. [DOI] [PubMed] [Google Scholar]
- 12. Mathews DH, Disney MD, Childs JL, et al. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc Natl Acad Sci U S A 2004;101(19):7287–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Turner DH, Mathews DH. NNDB: the nearest neighbor parameter database for predicting stability of nucleic acid secondary structure. Nucleic Acids Res 2010;38(Database issue):D280–2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res 2003;31(13):3406–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Markham NR, Zuker M. UNAFold: software for nucleic acid folding and hybridization. Methods Mol Biol 2008;453:3–31. [DOI] [PubMed] [Google Scholar]
- 16. Hofacker IL. Vienna RNA secondary structure server. Nucleic Acids Res 2003;31(13):3429–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Lorenz R, Bernhart SH, Höner Zu Siederdissen C, et al. ViennaRNA package 2.0. Algorithms Mol Biol 2011;6:26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Reuter JS, Mathews DH. RNAstructure: software for RNA secondary structure prediction and analysis. BMC Bioinform 2010;11:129. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
19.
Lucks JB, Mortimer SA, Trapnell C, et al. Multiplexed RNA structure characterization with selective 2
 -hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq). Proc Natl Acad Sci U S A 2011;108(27):11063–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
-hydroxyl acylation analyzed by primer extension sequencing (SHAPE-Seq). Proc Natl Acad Sci U S A 2011;108(27):11063–8. [DOI] [PMC free article] [PubMed] [Google Scholar] - 20. Ding Y, Tang Y, Kwok CK, et al. In vivo genome-wide profiling of RNA secondary structure reveals novel regulatory features. Nature 2014;505(7485):696–700. [DOI] [PubMed] [Google Scholar]
- 21. Do CB, Woods DA, Batzoglou S. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics 2006;22(14):e90–8. [DOI] [PubMed] [Google Scholar]
- 22. Do CB, Foo CS, Ng AY. Efficient multiple hyperparameter learning for log-linear models. In: Platt JC, Koller D, Singer Y et al. (eds). Advances in Neural Information Processing Systems 20. Curran Associates, Inc., 2007, 377–84. [Google Scholar]
- 23. Zakov S, Goldberg Y, Elhadad M, et al. Rich parameterization improves RNA structure prediction. J Comput Biol 2011;18(11):1525–42. [DOI] [PubMed] [Google Scholar]
- 24. Rivas E, Lang R, Eddy SR. A range of complex probabilistic models for RNA secondary structure prediction that includes the nearest-neighbor model and more. RNA 2012;18(2):193–212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Rivas E. The four ingredients of single-sequence RNA secondary structure prediction. A unifying perspective. RNA Biol 2013;10(7):1185–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Bernhart SH, Hofacker IL, Will S, et al. RNAalifold: improved consensus structure prediction for RNA alignments. BMC Bioinform 2008;9:474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Hamada M, Sato K, Asai K. Improving the accuracy of predicting secondary structure for aligned RNA sequences. Nucleic Acids Res 2011;39(2):393–402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Hamada M, Sato K, Kiryu H, et al. Predictions of RNA secondary structure by combining homologous sequence information. Bioinformatics 2009;25(12):i330–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Hamada M, Yamada K, Sato K, et al. CentroidHomfold-LAST: accurate prediction of RNA secondary structure using automatically collected homologous sequences. Nucleic Acids Res 2011;39(Web Server issue):W100–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Will S, Reiche K, Hofacker IL, et al. Inferring noncoding RNA families and classes by means of genome-scale structure-based clustering. PLoS Comput Biol 2007;3(4):e65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Sato K, Kato Y, Akutsu T, et al. DAFS: simultaneous aligning and folding of RNA sequences via dual decomposition. Bioinformatics 2012;28(24):3218–24. [DOI] [PubMed] [Google Scholar]
- 32. Saito Y, Sato K, Sakakibara Y. Fast and accurate clustering of noncoding RNAs using ensembles of sequence alignments and secondary structures. BMC Bioinform 2011;12(Suppl 1):S48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Heyne S, Costa F, Rose D, et al. GraphClust: alignment-free structural clustering of local RNA secondary structures. Bioinformatics 2012;28(12):i224–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Sato K, Mituyama T, Asai K, et al. Directed acyclic graph kernels for structural RNA analysis. BMC Bioinform 2008;9:318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Amin N, McGrath A, Chen YPP. Evaluation of deep learning in non-coding RNA classification. Nat Mach Intell 2019;1(5):246–56. [Google Scholar]
- 36. Washietl S, Hofacker IL, Stadler PF. Fast and reliable prediction of noncoding RNAs. Proc Natl Acad Sci U S A 2005;102(7):2454–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Gruber AR, Findeiß S, Washietl S, et al. RNAz 2.0: improved noncoding RNA detection. Pac Symp Biocomput 2010;69–79. [PubMed] [Google Scholar]
- 38. Wayment-Steele HK, Kladwang W, Watkins AM, et al. Deep learning models for predicting RNA degradation via dual crowdsourcing. Nat Mach Intell 2022;4(12):1174–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Akutsu T. Dynamic programming algorithms for RNA secondary structure prediction with pseudoknots. Discrete Appl Math 2000;104(1):45–62. [Google Scholar]
- 40. Lyngsø RB, Pedersen CN. RNA pseudoknot prediction in energy-based models. J Comput Biol 2000;7(3–4):409–27. [DOI] [PubMed] [Google Scholar]
- 41. Borer PN, Dengler B, Tinoco I, Jr, et al. Stability of ribonucleic acid double-stranded helices. J Mol Biol 1974;86(4):843–53. [DOI] [PubMed] [Google Scholar]
- 42. Xia T, SantaLucia J, Jr, Burkard ME, et al. Thermodynamic parameters for an expanded nearest-neighbor model for formation of RNA duplexes with Watson-crick base pairs. Biochemistry 1998;37(42):14719–35. [DOI] [PubMed] [Google Scholar]
- 43. Bloomfield VA, Crothers DM, Tinoco I, Jr. Nucleic acids: structures, properties and functions. University Science Books, 2000. [Google Scholar]
- 44. Zuker M, Stiegler P. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res 1981;9(1):133–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
45.
Huang L, Zhang H, Deng D, et al. LinearFold: linear-time approximate RNA folding by 5
 -to-3
-to-3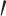 dynamic programming and beam search. Bioinformatics 2019;35(14):i295–304. [DOI] [PMC free article] [PubMed] [Google Scholar]
dynamic programming and beam search. Bioinformatics 2019;35(14):i295–304. [DOI] [PMC free article] [PubMed] [Google Scholar] - 46. Mathews DH. Revolutions in RNA secondary structure prediction. J Mol Biol 2006;359(3):526–32. [DOI] [PubMed] [Google Scholar]
- 47. Andronescu M, Condon A, Hoos HH, et al. Efficient parameter estimation for RNA secondary structure prediction. Bioinformatics 2007;23(13):i19–28. [DOI] [PubMed] [Google Scholar]
- 48. Andronescu M, Condon A, Hoos HH, et al. Computational approaches for RNA energy parameter estimation. RNA 2010;16(12):2304–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Akiyama M, Sato K, Sakakibara Y. A max-margin training of RNA secondary structure prediction integrated with the thermodynamic model. J Bioinform Comput Biol 2018;16(6):1840025. [DOI] [PubMed] [Google Scholar]
- 50. Sato K, Akiyama M, Sakakibara Y. RNA secondary structure prediction using deep learning with thermodynamic integration. Nat Commun 2021;12(1):941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. McCaskill JS. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers 1990;29(6–7):1105–19. [DOI] [PubMed] [Google Scholar]
- 52. Knudsen B, Hein J. Pfold: RNA secondary structure prediction using stochastic context-free grammars. Nucleic Acids Res 2003;31(13):3423–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Hamada M, Kiryu H, Sato K, et al. Prediction of RNA secondary structure using generalized centroid estimators. Bioinformatics 2009;25(4):465–73. [DOI] [PubMed] [Google Scholar]
- 54. Sato K, Hamada M, Asai K, et al. CENTROIDFOLD: a web server for RNA secondary structure prediction. Nucleic Acids Res 2009;37(Web Server issue):W277–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Rivas E, Eddy SR. A dynamic programming algorithm for RNA structure prediction including pseudoknots. J Mol Biol 1999;285(5):2053–68. [DOI] [PubMed] [Google Scholar]
- 56. Dirks RM, Pierce NA. A partition function algorithm for nucleic acid secondary structure including pseudoknots. J Comput Chem 2003;24(13):1664–77. [DOI] [PubMed] [Google Scholar]
- 57. Cao S, Chen SJ. Predicting RNA pseudoknot folding thermodynamics. Nucleic Acids Res 2006;34(9):2634–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Andronescu MS, Pop C, Condon AE. Improved free energy parameters for RNA pseudoknotted secondary structure prediction. RNA 2010;16(1):26–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59. Ren J, Rastegari B, Condon A, et al. HotKnots: heuristic prediction of RNA secondary structures including pseudoknots. RNA 2005;11(10):1494–504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Sato K, Kato Y, Hamada M, et al. IPknot: fast and accurate prediction of RNA secondary structures with pseudoknots using integer programming. Bioinformatics 2011;27(13):i85–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Sato K, Kato Y. Prediction of RNA secondary structure including pseudoknots for long sequences. Brief Bioinform 2022;23(1):bbab395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Eddy SR, Durbin R. RNA sequence analysis using covariance models. Nucleic Acids Res 1994;22(11):2079–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Sakakibara Y, Brown M, Hughey R, et al. Stochastic context-free grammars for tRNA modeling. Nucleic Acids Res 1994;22(23):5112–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Nawrocki EP, Eddy SR. Infernal 1.1: 100-fold faster RNA homology searches. Bioinformatics 2013;29(22):2933–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Knudsen B, Hein J. RNA secondary structure prediction using stochastic context-free grammars and evolutionary history. Bioinformatics 1999;15(6):446–54. [DOI] [PubMed] [Google Scholar]
- 66. Dowell RD, Eddy SR. Evaluation of several lightweight stochastic context-free grammars for RNA secondary structure prediction. BMC Bioinform 2004;5:71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Sato K, Hamada M, Mituyama T, et al. A non-parametric Bayesian approach for predicting RNA secondary structures. J Bioinform Comput Biol 2010;08(04):727–42. [Google Scholar]
- 68. Uemura Y, Hasegawa A, Kobayashi S, et al. Tree adjoining grammars for RNA structure prediction. Theor Comput Sci 1999;210(2):277–303. [Google Scholar]
- 69. Matsui H, Sato K, Sakakibara Y. Pair stochastic tree adjoining grammars for aligning and predicting pseudoknot RNA structures. Bioinformatics 2005;21(11):2611–7. [DOI] [PubMed] [Google Scholar]
- 70. Kato Y, Seki H, Kasami T. RNA pseudoknotted structure prediction using stochastic multiple context-free grammar. IPSJ Digital Courier 2006;2:655–64. [Google Scholar]
- 71. Chen X, Li Y, Umarov R, et al. RNA secondary structure prediction by learning unrolled algorithms. In Proceedings of the 8th International Conference on Learning Representations. 2020.
- 72. Fu L, Cao Y, Wu J, et al. UFold: fast and accurate RNA secondary structure prediction with deep learning. Nucleic Acids Res 2022;50(3):e14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73. Akiyama M, Sakakibara Y, Sato K. Direct inference of base-pairing probabilities with neural networks improves prediction of RNA secondary structures with pseudoknots. Genes 2022;13(11):2155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74. Singh J, Hanson J, Paliwal K, et al. RNA secondary structure prediction using an ensemble of two-dimensional deep neural networks and transfer learning. Nat Commun 2019;10(1):5407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75. Szikszai M, Wise M, Datta A, et al. Deep learning models for RNA secondary structure prediction (probably) do not generalize across families. Bioinformatics 2022;38(16):3892–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76. Flamm C, Wielach J, Wolfinger MT, et al. Caveats to deep learning approaches to RNA secondary structure prediction. Front Bioinform 2022;2:835422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77. Wayment-Steele HK, Kladwang W, Strom AI, et al. RNA secondary structure packages evaluated and improved by high-throughput experiments. Nat Methods 2022;1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78. Qiu X. Decisive roles of sequence distributions in the generalizability of de novo deep learning models for RNA secondary structure prediction. 2022; bioRxiv:2022.06.29.498185. [DOI] [PMC free article] [PubMed]
- 79. Andronescu M, Bereg V, Hoos HH, et al. RNA STRAND: the RNA secondary structure and statistical analysis database. BMC Bioinform 2008;9:340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Sloma MF, Mathews DH. Exact calculation of loop formation probability identifies folding motifs in RNA secondary structures. RNA 2016;22(12):1808–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81. Tan Z, Fu Y, Sharma G, et al. TurboFold II: RNA structural alignment and secondary structure prediction informed by multiple homologs. Nucleic Acids Res 2017;45(20):11570–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82. Danaee P, Rouches M, Wiley M, et al. bpRNA: large-scale automated annotation and analysis of RNA secondary structure. Nucleic Acids Res 2018;46(11):5381–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83. Cannone JJ, Subramanian S, Schnare MN, et al. The comparative RNA web (CRW) site: an online database of comparative sequence and structure information for ribosomal, intron, and other RNAs. BMC Bioinform 2002;3:2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84. Andersen ES, Rosenblad MA, Larsen N, et al. The tmRDB and SRPDB resources. Nucleic Acids Res 2006;34(Database issue):D163–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Sprinzl M, Vassilenko KS. Compilation of tRNA sequences and sequences of tRNA genes. Nucleic Acids Res 2005;33(Database issue):D139–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86. Brown JW. The ribonuclease P database. Nucleic Acids Res 1999;27(1):314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87. Lu ZJ, Gloor JW, Mathews DH. Improved RNA secondary structure prediction by maximizing expected pair accuracy. RNA 2009;15(10):1805–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88. Stoltenburg R, Reinemann C, Strehlitz B. SELEX–a (r)evolutionary method to generate high-affinity nucleic acid ligands. Biomol Eng 2007;24(4):381–403. [DOI] [PubMed] [Google Scholar]
- 89. Hamada M. In silico approaches to RNA aptamer design. Biochimie 2018;145:8–14. [DOI] [PubMed] [Google Scholar]
- 90. Sun D, Sun M, Zhang J, et al. Computational tools for aptamer identification and optimization. TrAC Trends Anal Chem 2022;157:116767 ISSN 0165-9936. [Google Scholar]
- 91. Buglak AA, Samokhvalov AV, Zherdev AV, Dzantiev BB. Methods and applications of in silico aptamer design and modeling. Int J Mol Sci 2020;21(22). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92. Kramer ST, Gruenke PR, Alam KK, et al. FASTAptameR 2.0: a web tool for combinatorial sequence selections. Mol Ther Nucleic Acids 2022;29:862–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93. Hoinka J, Berezhnoy A, Sauna ZE, et al. AptaCluster - a method to cluster HT-SELEX aptamer pools and lessons from its application. Res Comput Mol Biol 2014;8394:115–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Kato S, Ono T, Minagawa H, et al. FSBC: fast string-based clustering for HT-SELEX data. BMC Bioinform 2020;21(1):263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Dao P, Hoinka J, Takahashi M, et al. AptaTRACE elucidates RNA sequence-structure motifs from selection trends in HT-SELEX experiments. Cell Syst 2016;3(1):62–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96. Caroli J, Forcato M, Bicciato S. APTANI2: update of aptamer selection through sequence-structure analysis. Bioinformatics 2020;36(7):2266–8. [DOI] [PubMed] [Google Scholar]
- 97. Song J, Zheng Y, Huang M, et al. A sequential multidimensional analysis algorithm for aptamer identification based on structure analysis and machine learning. Anal Chem 2020;92(4):3307–14. [DOI] [PubMed] [Google Scholar]
- 98. Ishida R, Adachi T, Yokota A, et al. RaptRanker: in silico RNA aptamer selection from HT-SELEX experiment based on local sequence and structure information. Nucleic Acids Res 2020;48(14):e82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99. Bashir A, Yang Q, Wang J, et al. Machine learning guided aptamer refinement and discovery. Nat Commun 2021;12(1):2366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100. Iwano N, Adachi T, Aoki K, et al. Generative aptamer discovery using RaptGen. Nat Comput Sci 2022;2(6):378–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101. Di Gioacchino A, Procyk J, Molari M, et al. Generative and interpretable machine learning for aptamer design and analysis of in vitro sequence selection. PLoS Comput Biol 2022;18(9):e1010561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. Andress C, Kappel K, Cuperlovic-Culf M, et al. Daptev: deep aptamer evolutionary modelling for covid-19 drug design. bioRxiv 2022. https://www.biorxiv.org/content/early/2022/11/30/2022.11.30.518473.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Emami N, Ferdousi R. AptaNet as a deep learning approach for aptamer-protein interaction prediction. Sci Rep 2021;11(1):6074. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Torkamanian-Afshar M, Nematzadeh S, Tabarzad M, et al. In silico design of novel aptamers utilizing a hybrid method of machine learning and genetic algorithm. Mol Divers 2021;25(3):1395–407. [DOI] [PubMed] [Google Scholar]
- 105. Torkamanian-Afshar M, Lanjanian H, Nematzadeh S, et al. RPINBASE: an online toolbox to extract features for predicting RNA-protein interactions. Genomics 2020;112(3):2623–32. [DOI] [PubMed] [Google Scholar]
- 106. Pan X, Yang Y, Xia CQ, et al. Recent methodology progress of deep learning for RNA-protein interaction prediction. Wiley Interdiscip Rev RNA 2019;10(6):e1544. [DOI] [PubMed] [Google Scholar]
- 107. Yamada K, Hamada M. Prediction of RNA–protein interactions using a nucleotide language model. Bioinformatics. Advances 2022;2(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108. Kashiwagi S, Sato K, Sakakibara Y. A max-margin model for predicting Residue-Base contacts in protein-RNA interactions. Life 2021;11(11):1135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109. Wei J, Chen S, Zong L, et al. Protein-RNA interaction prediction with deep learning: structure matters. Brief Bioinform 2022;23(1):bbab540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110. Sahin U, Karikó K, Türeci Ö. mRNA-based therapeutics–developing a new class of drugs. Nat Rev Drug Discov 2014;13(10):759–80. [DOI] [PubMed] [Google Scholar]
- 111. To KKW, Cho WCS. An overview of rational design of mRNA-based therapeutics and vaccines. Expert Opin Drug Discov 2021;16(11):1307–17. [DOI] [PubMed] [Google Scholar]
- 112. Rohner E, Yang R, Foo KS, et al. Unlocking the promise of mRNA therapeutics. Nat Biotechnol 2022;40(11):1586–600. [DOI] [PubMed] [Google Scholar]
- 113. Beck JD, Reidenbach D, Salomon N, et al. mRNA therapeutics in cancer immunotherapy. Mol Cancer 2021;20(1):69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114. Sample PJ, Wang B, Reid DW, et al. Human 5’ UTR design and variant effect prediction from a massively parallel translation assay. Nat Biotechnol 2019;37(7):803–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115. Diez M, Oz SG, Castellano LA, et al. iCodon customizes gene expression based on the codon composition. Sci Rep 2022;12(1):12126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116. Medina-Muñoz SG, Kushawah G, Castellano LA, et al. Crosstalk between codon optimality and cis-regulatory elements dictates mRNA stability. Genome Biol 2021;22(1):14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117. Zhang H, Zhang L, Lin A, et al. Algorithm for optimized mRNA design improves stability and immunogenicity. Nature 2020. [DOI] [PMC free article] [PubMed]
- 118. Leppek K, Byeon GW, Kladwang W, et al. Combinatorial optimization of mRNA structure, stability, and translation for RNA-based therapeutics. Nat Commun 2022;13(1):1536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119. Statello L, Guo CJ, Chen LL, et al. Gene regulation by long non-coding RNAs and its biological functions. Nat Rev Mol Cell Biol 2021;22(2):96–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120. Mattick JS, Amaral PP, Carninci P, et al. Long non-coding RNAs: definitions, functions, challenges and recommendations. Nat Rev Mol Cell Biol 2023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121. Mercer TR, Munro T, Mattick JS. The potential of long noncoding RNA therapies. Trends Pharmacol Sci 2022;43(4):269–80. [DOI] [PubMed] [Google Scholar]
- 122. Winkle M, El-Daly SM, Fabbri M, et al. Noncoding RNA therapeutics - challenges and potential solutions. Nat Rev Drug Discov 2021;20(8):629–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123. Zhu Y, Zhu L, Wang X, et al. RNA-based therapeutics: an overview and prospectus. Cell Death Dis 2022;13(7):644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124. Childs-Disney JL, Yang X, Gibaut QMR, et al. Targeting RNA structures with small molecules. Nat Rev Drug Discov 2022;21(10):736–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125. Ursu A, Childs-Disney JL, Andrews RJ, et al. Design of small molecules targeting RNA structure from sequence. Chem Soc Rev 2020;49(20):7252–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126. Aguilar R, Spencer KB, Kesner B, et al. Targeting Xist with compounds that disrupt RNA structure and X inactivation. Nature 2022;604(7904):160–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127. Panchal V, Brenk R. Riboswitches as drug targets for antibiotics. Antibiotics (Basel) 2021;10(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128. Bagnolini G, Luu TB, Hargrove AE. Recognizing the power of machine learning and other computational methods to accelerate progress in small molecule targeting of RNA. RNA 2023;29(4):473–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129. Oliver C, Mallet V, Gendron RS, et al. Augmented base pairing networks encode RNA-small molecule binding preferences. Nucleic Acids Res 2020;48(14):7690–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130. Berman HM, Westbrook J, Feng Z, et al. The protein data Bank. Nucleic Acids Res 2000;28(1):235–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131. Yazdani K, Jordan D, Yang M, et al. Machine learning informs RNA-binding chemical space. bioRxiv 2022. https://www.biorxiv.org/content/early/2022/08/01/2022.08.01.502065.full.pdf. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132. Stefaniak F, Bujnicki JM. AnnapuRNA: a scoring function for predicting RNA-small molecule binding poses. PLoS Comput Biol 2021;17(2):e1008309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133. Chhabra S, Xie J, Frank AT. RNAPosers: machine learning classifiers for ribonucleic acid-ligand poses. J Phys Chem B 2020;124(22):4436–45. [DOI] [PubMed] [Google Scholar]
- 134. Grimberg H, Tiwari VS, Tam B, et al. Machine learning approaches to optimize small-molecule inhibitors for RNA targeting. J Chem 2022;14(1):4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135. Tam B, Sherf D, Cohen S, et al. Discovery of small-molecule inhibitors targeting the ribosomal peptidyl transferase center (PTC) of M. Tuberculosis. Chem Sci 2019;10(38):8764–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136. Disney MD, Winkelsas AM, Velagapudi SP, et al. Inforna 2.0: a platform for the sequence-based design of small molecules targeting structured RNAs. ACS Chem Biol 2016;11(6):1720–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137. Rao R, Liu J, Verkuil R, et al. MSA transformer. Proceedings of Machine Learning Research. 2021;139:8844–56. [Google Scholar]
- 138. Akiyama M, Sakakibara Y. Informative RNA base embedding for RNA structural alignment and clustering by deep representation learning. NAR Genom Bioinform 2022;4(1):lqac012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139. Chen J, Hu Z, Sun S, et al. Interpretable RNA foundation model from unannotated data for highly accurate RNA structure and function predictions. 2022; arXiv:2204.00300.
- 140. Deigan KE, Li TW, Mathews DH, et al. Accurate SHAPE-directed RNA structure determination. Proc Natl Acad Sci U S A 2009;106(1):97–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141. Incarnato D, Oliviero S. The RNA epistructurome: uncovering RNA function by studying structure and post-transcriptional modifications. Trends Biotechnol 2017;35(4):318–33. [DOI] [PubMed] [Google Scholar]
- 142. Helm M, Motorin Y. Detecting RNA modifications in the epitranscriptome: predict and validate. Nat Rev Genet 2017;18(5):275–91. [DOI] [PubMed] [Google Scholar]
- 143. Karikó K, Buckstein M, Ni H, et al. Suppression of RNA recognition by toll-like receptors: the impact of nucleoside modification and the evolutionary origin of RNA. Immunity 2005;23(2):165–75. [DOI] [PubMed] [Google Scholar]
- 144. Tanzer A, Hofacker IL, Lorenz R. RNA modifications in structure prediction - status quo and future challenges. Methods 2019;156:32–9. [DOI] [PubMed] [Google Scholar]
- 145. Jumper J, Evans R, Pritzel A, et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021;596(7873):583–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146. Feng C, Wang W, Han R, et al. Accurate de novo prediction of RNA 3D structure with transformer network. 2022; bioRxiv:2022.10.24.513506. [DOI] [PMC free article] [PubMed]
- 147. Pearce R, Omenn GS, Zhang Y. De novo RNA tertiary structure prediction at atomic resolution using geometric potentials from deep learning. 2022; bioRxiv: 2022.05.15.491755.
- 148. Shen T, Hu Z, Peng Z, et al. E2Efold-3D: end-to-end deep learning method for accurate de novo RNA 3D structure prediction. 2022; arXiv:2207.01586.
- 149. wwPDB consortium . Protein data bank: the single global archive for 3D macromolecular structure data. Nucleic Acids Res 2019;47(D1):D520–8. [DOI] [PMC free article] [PubMed] [Google Scholar]