A hybrid physics-based and data-driven framework for cellular biological systems: Application to the morphogenesis of organoids

Summary

How cells orchestrate their cellular functions remains a crucial question to unravel how they organize in different patterns. We present a framework based on artificial intelligence to advance the understanding of how cell functions are coordinated spatially and temporally in biological systems. It consists of a hybrid physics-based model that integrates both mechanical interactions and cell functions with a data-driven model that regulates the cellular decision-making process through a deep learning algorithm trained on image data metrics. To illustrate our approach, we used data from 3D cultures of murine pancreatic ductal adenocarcinoma cells (PDAC) grown in Matrigel as tumor organoids. Our approach allowed us to find the underlying principles through which cells activate different cell processes to self-organize in different patterns according to the specific microenvironmental conditions. The framework proposed here expands the tools for simulating biological systems at the cellular level, providing a novel perspective to unravel morphogenetic patterns.

Graphical abstract

Highlights

• •Framework combining agent-based modeling and deep learning
• •Deep learning manages cell decisions of biological functions in the agent-based model
• •Model reproduces morphogenetic patterns from image data metrics
• •Simulates organoid development, unraveling cell coordination

Biological sciences; Developmental biology; Biophysics; Biocomputational method; Neural networks

Introduction

Organ morphogenesis can be studied in situ through the analysis of stained tissue sections taken at different phases of embryonic development. This provides relevant, albeit static, information about the evolution of the morphology and the interactions between the elements of the developing organ. Morphogenesis can also be studied using 2D in vitro models built from stem cells properly stimulated with growing factors and/or cocultured cells. These models replicate some of the cellular interactions that occur during organ development, providing important information about the signaling pathways involved in normal organ formation. 2D culture models, however, lack a key element of organ morphogenesis, namely, the complex ensemble of three-dimensional spatial interactions that occur during the developmental process. These interactions, which determine the successful series of events that end with the formation of a mature organ, include not only interactions between cells but also, very importantly, interactions between the cells and their local microenvironment. This has caused the birth of a growing trend in the study of morphogenesis, which is the use of 3D in vitro cellular models or organoids that recreate in vitro the process of organ formation.^1,2,3 Some organotypic models have also been developed that replicate the growth and development of tumors (tumor organoids) from cancer stem cells and the appropriate stimulation of growth factors and biomechanical cues.^4,5 These complex models replicate the interactions that exist between cancer cells and with other cells of the tumor microenvironment, most relevantly the cells of the immune system. Tumor organoids can be of different complexity, from simple spheroids made of one or a few cell types suspended in medium enriched with the appropriate growth factors⁶ to more complex models comprising several cell types embedded in a biomimetic hydrogel. Finally, more advanced models are being developed based on microfabrication-bioprinting and microfluidic technologies that allow the simulation of interstitial flows.⁷ Tumor organoids are becoming invaluable tools to study the response of tumors to therapies, including those that stimulate the host immune system.

There are also different approaches to simulate morphogenesis in silico. On the one hand, continuum models permit the simulation of large cell populations at the tissue level. This is the case for reaction-diffusion systems based on partial differential equations (PDEs)⁸ or positional information (PI).⁹ However, these methods neglect the individuality of cells in favor of larger scales, disregarding the important role played by cell-to-cell interactions and the phenotypic diversity of the biological system. Consequently, these methods struggle to reproduce the way cell communities develop into complex structures, especially in three dimensions. On the other hand, discrete approaches with agent-based modeling consider cells as autonomous entities that interact among themselves and with the microenvironment.¹⁰ These methods are usually classified into lattice models, in which cell positions are fixed within a spatial grid,¹¹ and lattice-free models, which allow continuous cell positioning in space.¹² Based on the way the cell shape is represented in lattice-free models, there are center-based models, in which cells are represented as spheres and are described by their centers and radii,¹³ and deformable cell models and vertex models, which account for the cell shape and deformability.^14,15 These models have been widely employed, for instance, to simulate tumor growth in vitro,¹⁶ to study the role of extracellular matrix density in cell migration within tumor spheroids,¹⁷ collective cell migration,¹⁸ or tissue regeneration.¹⁹ These approaches seem appropriate to simulate morphogenesis, it being a process that evolves from a single cell, and the emerging pattern emerges from cell interactions, cell heterogeneity, and cell processes.^20,21 Furthermore, agent-based modeling focuses on the cell level; therefore, it very flexibly simulates in vitro experiments. However, these models have some challenges related to the designation of rules and fitting parameters that govern decision-making heuristics and the behavior of cells.^20,21 In addition, they usually have a large number of parameters compared to continuous models, especially when considering molecular events per cell,²² which makes their calibration difficult.

Data-driven models are widely used to predict the behavior of complex physical systems.^23,24 They can unravel unknown phenomena and reduce the degree of abstraction of computational models. In computational biology, there are examples of data-driven models used to find the optimal parameter values in gene regulatory networks to reproduce the growing limb bud²⁵ or Bayesian inference of agent-based cellular automaton to study kidney branching morphogenesis.²⁶ These methods combining data-driven and computational models aim to obtain the required parameters of the computational model, which is an optimization method that lacks generalization, as in the case of the data changing, the parameters must change as well. In the context of data-driven methods, there is an increasing use of artificial intelligence and, in particular, machine learning and deep learning algorithms.²⁷ However, data-driven models are considered black boxes and are difficult to relate to physical interpretations, because they are mainly focused on finding input-output relationships.

In this work, we propose a hybrid approach that combines deep learning and agent-based models as a novel computational framework to simulate cellular biological systems. In other approaches, the coordination between cells is fixed beforehand and then adjusted to reproduce a certain behavior. On the one hand, in continuum models, cell processes are included in constitutive equations and these cell functions are performed at the same time.^28,29 Then, they are adjusted through a sensitivity analysis to obtain the fitting solution. However, there is no competition between cell functions, because they occur simultaneously. On the other hand, in stochastic models, cells change between cell states through cell state rules, Boolean circuits, gene regulatory circuits (GRNs), and biochemical reactions from the more abstract to the more detailed.^30,31 These relationships between cell states are complex to establish and describe.³² Both approaches are usually made to simulate one particular case or median cases from experiments. However, it is difficult to reproduce different cases since their parameters are adjusted to reproduce one observed behavior and the variability is obtained by the introduction of noise. Moreover, they usually fail to reproduce dynamical processes because of the intricacy of recreating distinct behaviors temporarily with fixed parameters and even more taking into account the variability between cells. In this new work, we do not determine how cells behave before defining the relationships between cell states to perform a sensitivity analysis to find the parameters that allow us to reproduce an observed behavior. Instead, we eliminate all the parameters in the physics-based model that preestablish the behavior of cells and incorporate the mechanical cell interactions and biological cell functions in an agent-based model that uses a neural network to drive the cellular decision-making of the agents during the simulation, replicating how cells make decisions and behave in vivo. This deep learning algorithm coordinates cell decision-making by evaluating the simulation in real time and comparing it with metrics that define the final architecture of the morphogenetic pattern extracted from cell-level images of real organoids or in vivo data.

To validate and illustrate this framework, we show three different applications. First, we explain how to particularize this approach to simulate the formation and growth of tumor organoids from a mouse pancreatic adenocarcinoma cell line grown in a 3D biometric Matrigel matrix. These organoids form cystic structures, namely, an organized architecture of cells around a fluid-filled space called the lumen. Then, we show the simulations of these experiments. In addition, we show the application of the approach to simulate the formation and growth of solid tumor organoids from other mouse pancreatic adenocarcinoma cell lines grown in a 3D biometric Matrigel matrix, which consists of dense aggregates of cells. Finally, we apply this framework to simulate a theoretical case of the evolution of solid tumor organoids with time-dependent quantitative data.

Results

Hybrid physics-based and data-driven framework

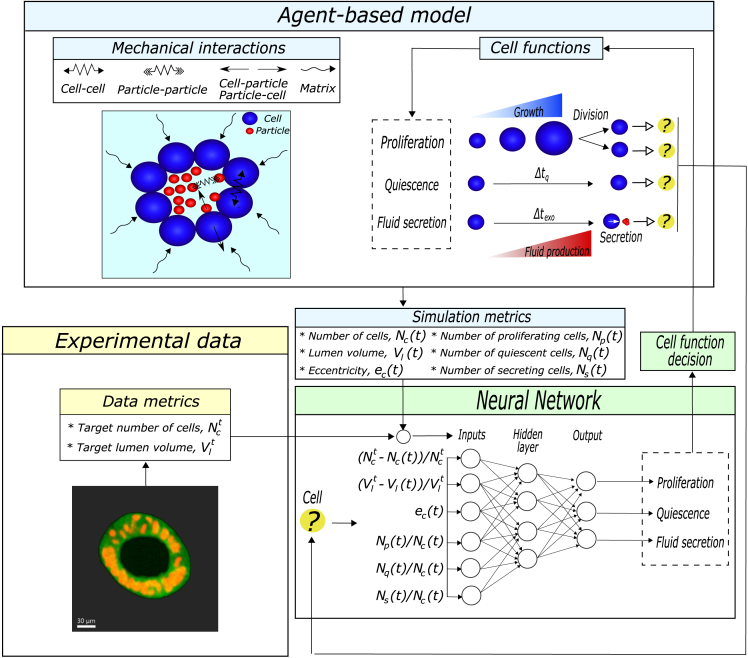
We present a novel hybrid physics-based and data-driven framework that combines agent-based modeling and deep learning to simulate morphogenetic patterns (Figure 1). The purpose of the physics-based model is to replicate a specific morphogenetic pattern. The data-driven algorithm in turn coordinates, through a neural network, the cell functions required in the physics-based model to achieve that pattern (Figure 1A). Thus, the physics-based part consists of an agent-based model that couples mechanical interactions and the cell biological functions that are decisive in the morphogenetic process, namely, proliferation, quiescence, secretion, migration, cell death, etc. The selection of these cell functions depends on the morphogenetic process being simulated.

Figure 1.

Framework of the hybrid physics-based and data-driven model

(A) Schematic overview of the hybrid data-driven and physics-based algorithm. It consists of an agent-based model that incorporates mechanical interactions and cell biological functions. To orchestrate the cell functions within the simulation, the agent-based model employs a data-driven algorithm. Thus, to determine which function the cell has to perform, the agent-based model goes into the data-driven algorithm. The data-driven algorithm extracts from the desired morphogenetic pattern data metrics that characterize the pattern, which are introduced, together with simulation metrics, into the neural network as inputs. The neural network evaluates the inputs and determines the cell function that the cell must perform. This process is repeated until the simulation time of the agent-based model reaches ($t_{sim}$). Finally, a fitness value is given to the simulation by comparing the simulated and desired morphogenetic patterns.

(B) Schematic overview of the training algorithm of the neural network. The training starts with the creation of a random generation (Gen) composed of a population (Pop) of ten neural networks. Then, the physics-based algorithm performs a simulation with each neural network, following a similar methodology as (A). Finally, the genetic algorithm selects the two best populations based on their fitness and creates a new generation through crossover and mutation algorithms. The training is concluded when the number of generations reaches the specified number of generations ($Ge{n}_{\mathit{max}}$).

The physics-based model coordinates the biological behavior of cells to form a specific pattern, which also requires the appropriate mechanical interactions. For that coordination, instead of using parameters that fix the relationships between them, we introduce a data-driven algorithm that performs the cellular decision-making of the cell functions. Therefore, during the simulation of the agent-based model, the neural network determines which cell function each cell has to perform (Figure 1A). To this end, given a morphogenetic pattern, we first define the data metrics that characterize the pattern and establish target values. These data metrics set the objective of the simulation. Then, when a cell needs to decide which function to perform, the neural network receives as inputs the predefined data metrics and the simulation metrics from the agent-based model that evaluates the actual state of the simulation. In this way, the neural network compares the simulation with the target values and makes a decision (see the data-driven box in Figure 1A). Each node of the output layer is related to one cell function; therefore, the activated node determines the biological function that the cell will perform. This decision is fed to the agent-based model, which initiates the corresponding cell function for that cell. This process is repeated during the predefined time of simulation every time a cell finishes the biological function that it was performing. When the simulation finishes, a fitness value is reported, which indicates how close the simulated morphogenetic pattern is compared to the desired morphogenetic pattern. Therefore, the result depends on how well the neural network evaluates the simulation and coordinates cell functions through adequate decision-making.

Learning by the neural network framework

To simulate the morphogenetic pattern, the neural network needs to learn how to evaluate the simulation and, depending on the target values, decide which biological function the cell has to perform. To make the neural network learn, we propose a learning methodology based on a genetic algorithm (Figure 1B). Initially, the genetic algorithm creates a random population of ten neural networks with different weight values assigned, i.e., a generation. Then, we perform a simulation of the agent-based model with each neural network of the generation. When the simulation finishes, we obtain a simulated pattern for each population. Subsequently, each neural network of the generation is given a fitness value, which represents how well they performed in the simulation. Finally, it selects from the current generation the two fittest neural networks and obtains, through a genetic algorithm (further details are included in learning algorithm in STAR Methods), the next generation of neural networks. This process is repeated for a predefined number of generations.

Application of the physics-based framework to the simulation of cystic organoids

To show the potential of our approach, we simulated cystic tumor organoids, i.e., organoids formed by an outer shell made of cancer cells surrounding a lumen (Figure 2). Lumen morphogenesis implies the development of an organized architecture of cells around a fluid-filled space. This inner space, called the lumen, is found in many parts of metazoan organisms and allows them to perform specific functions. The development of a lumen requires sophisticated coordination of several cell processes. Specifically, three basic mechanisms are crucial³³: Initially, cells proliferate and polarize to determine the landmark where the lumen will be initiated. Next, cells secrete fluid into that central site and generate luminal hydrostatic pressure that makes the lumen enlarge.^34,35,36,37 To preserve the overall cystic structure, a balance between strong cell-cell junctions and spatially controlled cell mitosis is needed. Finally, the stiffness of the extracellular matrix (ECM) plays an important role³⁸ by balancing the luminal hydrostatic pressure and providing physical cues that regulate cell behavior.³⁹

Figure 2.

Particularization of the framework for organoids with lumen

The physics-based model consists of an agent-based model that integrates mechanical interactions and cell functions. Cells are biological entities, and the particles simulate the lumen fluid. Three cell functions are considered: proliferation, quiescence, and fluid secretion. $\Delta t_q$ is the minimum period of time that a cell remains quiescent and $\Delta t_{exo}$ is the fluid production time.

To simulate the morphogenesis of the lumen, we built a three-dimensional agent-based model. This physics-based model is based on a previous three-dimensional lattice-free, center-based model.⁴⁰ Here, we use the structure of that model, but we eliminate the parameters that coordinate the relationships between cell functions, the effect of the cell net forces on the cell cycle, and multiluminal polarization mechanisms. To reproduce the morphogenesis of organoids composed of cells enclosing a fluid-filled lumen, we consider two types of agents: cells, which are the biological entities, and particles, which are secreted by cells and simulate the lumen fluid. The mechanical equilibrium between cells anchored to the ECM and the luminal pressure ensures the maintenance of the luminal architecture (further details are included in agent-based modeling in STAR Methods). To model this mechanical equilibrium, we use agents that interact mechanically to generate and maintain the lumen. Thus, cells interact among themselves based on pairwise potential functions in an adhesive-repulsive manner. The repulsion between agents mimics cell resistance to deformation when their membranes touch, and the attractive forces are the result of the cell junctions exerted through specialized protein complexes. Moreover, particles also interact via pairwise potential functions and interact with cells in a repulsive manner. This interaction mimics the luminal hydrostatic pressure generated by the cells’ fluid secretion, and it is responsible for the movement of cells and generation of the luminal space. Finally, agents interact with the extracellular matrix by means of a friction coefficient that represents the dynamic viscosity of the matrix (Figure 2 top left).

Three decisive cell functions are considered to achieve the cystic morphogenetic pattern: proliferation, quiescence, and fluid secretion (Figure 2 top right). First, we define a mathematical model for simulating the cell cycle that regulates cell proliferation. Overall, it consists of a growth phase, in which the cell progressively increases its volume as a result of DNA replication, and a mitosis phase, in which the cell divides into two daughter cells (see cell division in STAR Methods). In addition, we include a quiescent state in which the cell remains inactive for a period of time ($\Delta t_q$). Finally, cells can produce fluid during a period of time ($\Delta t_{exo}$) and then secrete it inside the lumen, increasing the lumen volume. To simulate this process, we assume that cells generate particles that simulate the lumen fluid (further details are included in characterization of the lumen fluid in STAR Methods). Consequently, the lumen is in a state of hydrostatic pressure because of this cell secretion.

Application of the data-driven framework to the simulation of cystic organoids

In the data-driven framework, we first define the metrics that characterize the pattern using target values. In the case of organoids with lumen, we defined the target number of cells ($N_c^t$) and target lumen volume ($V_l^t$) to describe the morphology of the organoid (Figure 2 middle). We also define several simulation metrics that are updated when a cell has to decide its next cell function. Specifically, these simulation metrics are the total number of cells, the lumen volume, the eccentricity between the cells center of mass and the lumen fluid center of mass (see eccentricity in STAR Methods), and the number of proliferating, quiescent and secreting cells. These values are given as inputs to a neural network (Figure 2 bottom right). We assume that each cell can only perform one cell function at a time. Hence, the neural network determines the appropriate cell function that cells must perform. The neural network consists of an input layer with six nodes, one hidden layer with four nodes and a hyperbolic tangent activation function, and a layer with three outputs and a sigmoid activation function. Each node of the output layer identifies the function that the cell must perform: proliferation, quiescence, or fluid secretion.

Learning of the neural network to simulate cystic organoids

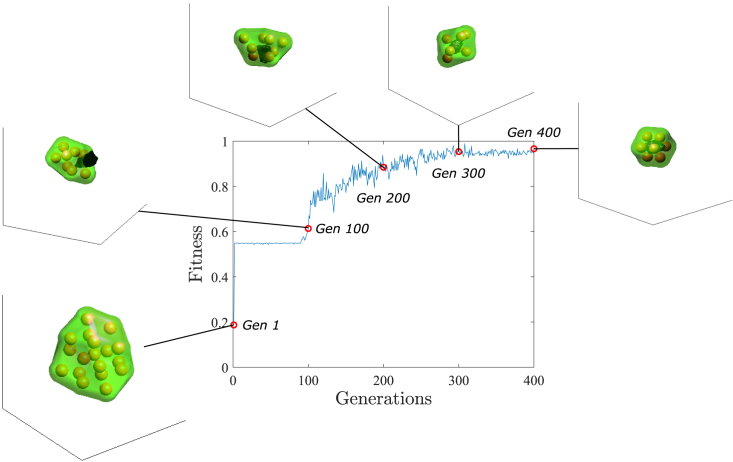
The success of the morphogenetic pattern depends on how well the neural network coordinates cell functions during the simulation. To make the neural network learn to form organoids with a lumen, we trained the neural networks for 400 generations. For this purpose, we did not use any of the experimental data; instead, we used a synthetic pattern consisting of an organoid with 8 cells and a lumen of 1000 $\mu m^3$. To illustrate this process, we show the increase in performance for each generation of neural networks (Figure 3). As shown, the first generation of neural networks did not coordinate the cell functions properly, because the fitness (see fitness function in STAR Methods) of this generation was 0.1869. In fact, the neural network only allowed cells to proliferate, thus generating an organoid without a lumen. Then, the performance increased to 0.6136 in generation 100, because cells were also secreted to generate the lumen. However, the fluid of the lumen leaked because of the poor coordination between proliferation and secretion. In generation 200, the fitness increased to 0.8846, and better coordination than in generation 100 was found, in that lumen fluid did not leak, but the organoid was too asymmetrical. Generation 300 achieved a symmetrical organoid with lumen with a better approximation of the number of cells and lumen volume. Finally, in generation 400, an organoid composed of 7 cells and a lumen volume of 1245 $\mu m^3$ was achieved.

Figure 3.

Learning of the neural network

The fitness value represented corresponds with the highest fitness of the population within the generation. Snapshots of the achieved organoid inserted in a cube with 100 μm sides featuring one population at generations 1, 100, 200, 300, and 400 are represented. The spheres represent the nuclei of cells with radius $R_c/2$ and the green hull is an estimation of the cell membrane through alpha shapes of the cells with $\alpha =2R_c$.⁴¹ The lumen fluid is represented in black through the alpha shapes of particles with the smallest alpha that produces an alpha shape enclosing all of the particles.

Simulation of pancreatic cystic tumor organoids

We simulated 3D cultures of murine pancreatic ductal adenocarcinoma cells grown in a biomimetic matrix made of Matrigel (4 $mg/ml$). Real 3D cultures of PDAC93-GFP cells were generated and incubated for 5 days. In the experimental setup, we generated a randomly distributed population of organoid seeds ranging from single cells to small clusters of 2–3 cells (Figure S2). Then, multiphoton microscopy images of the grown organoids were segmented and quantified to characterize their morphology. In particular, we obtained the number of cells in the organoid and the lumen volume, which were used as target values for the simulation. We chose organoids of different sizes to test the generalization potential of the methodology (Table 1). Specifically, we used two intermediate-size samples (organoids #1 and #2), one small-size sample (organoid #3), and one large-size sample (organoid #4). We initiated the simulations with one cell and ran the simulations for 7 days. Although the PDAC93-GFP cells were incubated for 5 days, we extended the simulation time to 7 days to prove that the model was able to reach steady-state patterns. The parameter values used in the simulations are described in Table S1.

Table 1.

Experiment and simulation of pancreatic tumor organoids with lumen

Organoid	Experiment		Simulation
	$N_c^t$	$V_l^t\left(\mu m^3\right)$	$N_c$	$V_l\left(\mu m^3\right)$
1	29	11263	30	11330
2	37	13233	41	14097
3	13	1985	14	2174
4	59	42762	59	43239

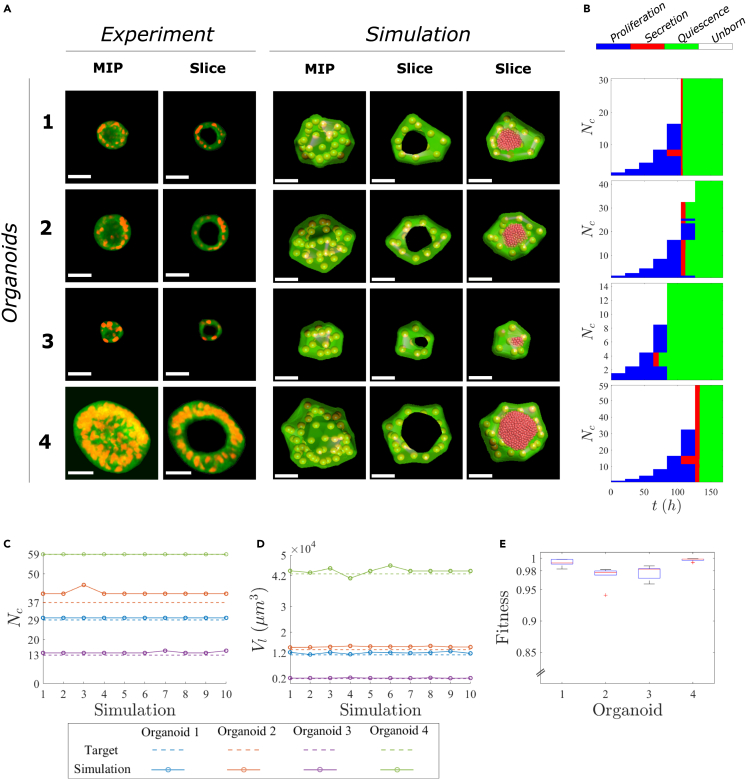
We show images of the experimental organoids used as targets of the simulation, the achieved solution of one of the simulations performed, and the coordination of cell functions (Figure 4) corresponding to the organoids in Table 1. As shown, sophisticated coordination of cell functions is required to form an organoid with a lumen (Figure 4B). In our simulations, cells first proliferated, generating a closed volume. Then, some cells started secreting fluid, whereas other cells continued proliferating to create more luminal space to secrete and prevent fluid leakage. In organoid #1, 2 out of 16 cells (13%) started secreting after 84 h, and then at 105 h, the rest of the cells also contributed to lumen enlargement by producing and secreting fluid (Video S1). In the case of organoid #2, 23 out of 32 cells (72%) were secreting at 105 h, whereas 9 cells continued proliferating. After these 9 cells finished proliferating, the target lumen volume was already reached, so no more fluid secretion was needed (Video S2). In organoid #3, cells started secreting earlier (63 h) than in organoids #1, #2 and #4. In this situation, only two cells were secreting over approximately 8 h since the lumen volume of this organoid was small (Video S3). In the case of organoid #4, 5 cells out of 32 cells (16%) started secreting at 105 h, and 21 h later, the remaining cells that initially were proliferating were also secreting. Finally, cells entered a quiescent state in all four organoids when they achieved the final pattern.

Figure 4.

Simulation of experimental pancreatic tumor organoids with lumen

(A) Image of in vitro organoids and a slice view. Maximum Intensity Projection (MIP). Snapshots of the full view, a slice of the simulated organoids, and a slice of the simulated organoids with the lumen particles representation. The spheres represent the nuclei of cells with radius $R_c/2$ and the green hull is an estimation of the cell membrane through alpha shapes of the cells with $\alpha =2R_c$. The lumen fluid is represented in black (fourth column) through the alpha shapes of particles with the smallest alpha that produces an alpha shape enclosing all of the particles. All scale bars are 30 $\mu m$.

(B) Coordination of cell functions, in which blue represents proliferation, red represents secretion, green represents quiescence, and white represents an unborn cell.

(C) Target number of cells ($N_c^t$) and the number of cells ($N_c$) in the 10 simulations for each organoid.

(D) Target lumen volume ($V_l^t$) and lumen volume ($V_l$) in the 10 simulations for each organoid.

(E) Boxplot of the fitness value of the 10 simulations for each organoid.

To demonstrate the robustness of the neural network to properly coordinate cell functions, we performed 10 simulations with the same neural network for each organoid. Both the number of cells (Figure 4C) and the lumen volume (Figure 4D) obtained in the simulations consistently approximated the target data. The fitness of the simulations was evaluated similarly to the fitness function used for the training of the neural network but neglected the penalization of the eccentricity, since we were not aiming to approximate the eccentricity of the in vitro experiments, because it was not used as input data (Figure 4E). The minimum median value of the fitness was 0.978 for organoid #2. The median values for organoids #1, #3, and #4 were all above 0.983.

Moreover, a sensitivity analysis was performed to investigate the influence of the main parameters of the model on the coordination of cells. For that purpose, organoid #1 was simulated in situations where the cell cycle time was decreased and increased by 20% from 30 h to 24 h and 36 h respectively (Figure S7). Originally, the cells finished proliferating after 105 h. A cell cycle time reduction makes cells proliferate faster; therefore, cells finished proliferating after 84 h. Conversely, cells proliferate slower when the cell cycle time increases, thus requiring approximately 125 h to finish proliferation. In addition, a similar sensitivity analysis for the fluid production time $\left(\Delta t_{exo}\right)$ was performed (Figure S8). When the fluid production time was 15 min, cells secreted during 23 h. A reduction of the fluid production time to 6 min caused cells to secrete during 21 h, only 2 h less than in the previous case. However, in this case, only two cells were secreting, since they were able to produce more fluid over the same time period. Finally, when the fluid production time increased to 60 h, cells were secreting over 34 h. Although the variation in these parameters produced changes in the temporal evolution of the process, neither the variation in the cell cycle time nor the differences in the fluid production time altered the coordination of cell functions. Therefore, there might exist a specific organization of cell functions independent of cell type.

Finally, an analysis of the effect of the noise on the parameters was performed. Accordingly, the cell cycle time and fluid production time parameters varied ±20%. Thus, every time a cell is set to perform either proliferation or fluid secretion, a random variation of the parameter for that individual cell is made between [-20, +20] % of the value from Table S1 and assigned for its cell cycle time or fluid production time. To determine how this variation could affect the results, we simulated an intermediate cystic organoid (organoid #2). Thus, we performed 10 simulations of this organoid to determine the effect of the fluctuation of the parameter. We found that the coordination of cell functions when the parameters are variable is similar to the case without any variability (Figure S9). However, there is a desynchronization between cells in terms of cell functions caused by the variability of the duration of their functions. To better compare the coordination of the cell functions, we represented the evolution of the normalized number of proliferating cells, secreting cells, and quiescent cells over time (Figure S9C). In the three cases, the evolution of the functions performed by the cells in the case with variable parameters was aligned with the case without variation. Despite the introduction of this noise, the median value of the fitness of the ten simulations was 0.9956, and the minimum was 0.9537 (Figure S9D).

Application of the framework to solid tumor organoids

To illustrate the possibility of applying this framework to other morphogenetic patterns, we applied our methodology to simulate the formation of solid tumor organoids (Figure S10). These solid tumor organoids consist of dense spherical aggregates of cells. To simulate the formation of this pattern, we considered two cell functions: proliferation and quiescence. Furthermore, we consider cell-cell mechanical interactions based on pairwise potential functions and the interaction of cells with the extracellular matrix by means of a friction coefficient. In the data-driven part of the model, we employed the target number of cells ($N_c^t$) as the metric that defines the size of the organoid and fixes the objective of the simulation. We also extracted some simulation metrics, which are the total number of cells, the number of proliferating cells, and the number of quiescent cells. The neural network consists of an input layer of three nodes, a hidden layer of two nodes, and an output layer of two nodes, which represents either proliferation or quiescent states of the cell. Therefore, the neural network coordinates both processes to achieve the target size of the organoid.

Simulation of solid tumor organoids

We simulated the corresponding experiments of 3D cultures of PM12500-GFP tumor cells grown also in a biomimetic matrix (Matrigel 4 $mg/ml$). This cell line is characterized by the formation of organoids composed of aggregates of cells that do not form a lumen. Here, real 3D organoids of PM12500-GFP tumor cells were also generated and incubated for 5 days. Then, their morphology was segmented and quantified from multiphoton microscopy images of the grown organoids. In this case, we obtained the number of cells to quantify the size of the organoids. Different-size organoids were chosen again to prove the adaptive response of the computational-based methodology to the data. In particular, we used one small sample (organoid #1), one intermediate sample (organoid #2), and two large samples (organoids #3 and #4) (Table 2). The simulations were initiated with one cell and run for 7 days to prove that the model is able to reach steady-state patterns. The parameters of the simulations can be found in Table S2.

Table 2.

Experiment and simulation of solid tumor organoids

Organoid	Experiment	Simulation
	$N_c^t$	$N_c$
1	23	23
2	34	34
3	53	53
4	60	60

We show images of the experimental organoids, the simulation of the organoids, and the coordination of cell functions (Figure 5), which represent the organoids in Table 2. The simulated organoids matched the target number of cells of the experimental data by day 5. Here, precise coordination between proliferative and quiescent cells is needed, because the organoids approximate the target number of cells (Figure 5B). In organoid #1, after 67 h, 7 cells continued proliferating, and 9 cells entered quiescence, reaching the target number of cells at 84 h. In organoid #2, most of the cells (93.75%) became quiescent at 84 h, whereas 2 cells continued proliferating to finally form the target pattern at 101 h. In organoid #3. Twenty-two cells (68.75%) were proliferating after 84 h to increase the number of cells up to 53 at 101 h. Organoid #4 was the case in which more cells continued proliferating after 84 h, 28 out of 32 (87.5%).

Figure 5.

Simulation of experimental solid tumor organoids

(A) Image of in vitro organoids. Snapshots of the simulated organoids. The spheres represent the nuclei of cells with radius $R_c/2$ and the green hull is an estimation of the cell membrane through alpha shapes of the cells with $\alpha =2R_c$. All scale bars are 30 $\mu m$.

(B) Coordination of cell functions, in which blue represents proliferation and green represents quiescence.

Application of the framework to the evolution of solid organoids

To demonstrate not only the application of the methodology to other patterns but also the possibility to mimic the temporal evolution of patterns, we show an extrapolation of our methodology to simulate the evolution of solid organoids without lumen, which consists of dense spherical aggregates of cells (Figure S11). With this methodology, we aim to reproduce the growth of solid organoids so that the evolution of this organoid matches the target evolution. To do that, target data is specified at different time points (${\mathit{t}}^t$). In this case, the target data consisted of the number of cells (${\mathit{N}}_c^t$). In the agent-based framework, we consider cell mechanical interactions and the cell interactions with the extracellular matrix. Moreover, cells can either proliferate or stay in a quiescent state during a period of time ($\Delta t_q$). When a cell finishes the cell function that it is performing, the neural network decides the next cell function that the cell has to perform. Thus, we extract some simulation metrics (number of cells, number of proliferating cells, number of quiescent cells, and the simulation time) that characterizes the state of the simulation. Then, we obtain from the target time (${\mathit{t}}^t$) the target time immediately superior to the simulation time (t) and the number of cells (${\mathit{N}}_c^t$) corresponding to that target time. These data are transferred to the input layer of the neural network in the following manner: the first node receives the comparison between the target number of cells and the number of cells of the simulation ($\left({\mathit{N}}_c^t-N_c\left(t\right)\right)/{\mathit{N}}_c^t$); the second node receives the normalized number of quiescent cells, and the third node receives the normalized number of proliferating cells. Finally, the neural network determines the next function to perform.

Simulation of the evolution of solid organoids

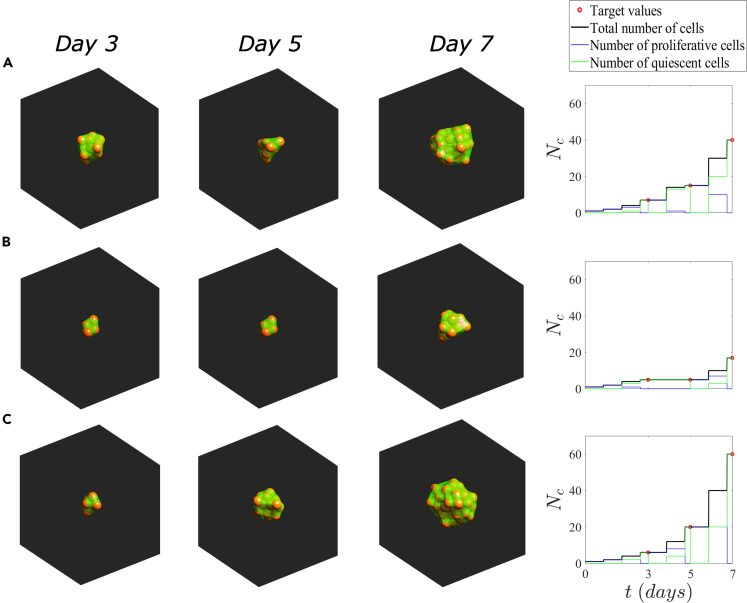
To show the possibilities of the methodology, we consider three synthetic cases of solid organoids with different temporal evolutions (Table 3). Organoid A represents a proliferative organoid. Case B represents an organoid that proliferates, then remains quiescence between day 3 and day 5, and proliferates again between day 5 and 7. Finally, case C corresponds to a proliferative organoid with a higher proliferation rate than case A. The parameters used for the simulation are collected in Table S3.

Table 3.

Target data for the evolution of solid organoids

Organoid	Target number of cells $\left(N_{\mathit{c}}^{\mathit{t}}\right)$
	Day 3	Day 5	Day 7
A	7	15	40
B	5	5	17
C	6	20	60

The simulations matched the evolution of the number of cells in the three cases (Figure 6), adapting to the changes in input data over time. In organoid A, as cells proliferate, they become quiescent whereas some cells still proliferate to match the target values (Figure 6A and Video S4). In the case of the organoid B, cells proliferate until day 3, and between day three and five they enter into a quiescent state to finally proliferate after day 5 (Figure 6B and Video S5). In organoid C, cells have a higher proliferative capacity than organoids A and B, so cells tend to proliferate against quiescence (Figure 6C and Video S6). Also, we simulated the evolution of a larger solid tumor organoid to demonstrate that the model works for any size. In this case, the target number of cells was established to 100 cells on day 7 and 500 cells on day 10 (Table S5). The simulation matched the evolution of the number of cells (Figure S12). Thus, this methodology is also able to mimic the temporal evolution of morphogenetic patterns of any size as long as the final result is feasible to achieve.

Figure 6.

Simulation of the evolution of solid organoids

Snapshots at days 3, 5, and 7 of the temporal evolution of the solid organoids inserted in a cube of 200 $\mu m$ side and the evolution of their number of cells. The spheres represent the full cell volume, and the green hull is an estimation of the cell membrane through alpha shapes of the cells with $\alpha =2R_c$.

(A) Organoid A.

(B) Organoid B.

(C) Organoid C.

Discussion

We present a novel hybrid physics-based and data-driven approach that combines agent-based modeling and deep learning for the simulation of developmental biology at the cellular level. Thus, we hypothesized that the different patterns that cells form are consequences of the distinct spatial and temporal coordination of their cellular functions. The following question is then how cells determine which cellular function to perform, since if we are able to replicate the decision-making of cells, we can reproduce the coordination of cell functions to achieve any pattern. Thus, we built a novel computational framework in which a neural network manages the decision-making of biological cell functions within a physics-based model to achieve an objective morphogenetic pattern. To accomplish the simulation of morphogenetic patterns, we do not fix the relationships between cell functions beforehand; instead, we consider cell functions as independent processes that cannot occur simultaneously, and the deep learning algorithm decides for each cell which cellular function they will be performing during the developmental process, properly coordinating all cellular functions for pattern formation. Thus, this artificial intelligence-based method learns the intrinsic mechanisms of the morphogenetic process and, therefore, is capable of reproducing similar morphogenetic patterns with different dynamical processes without optimizing the parameters ad hoc just by changing the target data about the pattern transferred to the input of the neural network. Therefore, with this approach, we can understand how cells must behave both spatially and temporarily to form different patterns.

In this work, we showed how to integrate a physics-based model with a deep learning algorithm to simulate morphogenetic patterns in 3D organoids. This modular framework offers a wide flexibility to change and adapt the physics-based and the data-driven models involved. On the one hand, in the physics-based part, agent-based modeling offers a broad range of types of models: from center-based models to deformable or vertex models.¹⁰ This allows us to take advantage of a chosen model to better adapt to a specific application. On the other hand, regarding the data-driven part of the framework, different types of neural networks and activation functions can be considered. Indeed, the architecture of the neural network could be simplified to reduce the computational cost of the learning process or incremented to unravel complex features, trying to find the optimal conditions for each case depending on the type of morphogenetic pattern, the quantity of input data, and the different cell states considered.⁴² In addition, there exist different learning algorithms that can be integrated into this approach (genetic algorithm, gradient descent, conjugate gradient, Levenberg-Marquardt algorithm, among others⁴³) for different computational speeds and memory requirements given a set number of parameters of the chosen neural network. Therefore, our framework is scalable with different types of models and permits modification to improve the computational cost and to better capture the specific biological process.

To evaluate the potential of the approach, we showed two applications mimicking in vitro data of the final pattern of organoids and one application reproducing synthetic time-lapse data. Thus, one advantage of this approach is that it requires little information about the morphogenetic processes, being able to undertake pattern formation using just final morphological information about the pattern extracted visually. In pattern formation, generally, the information is obtained from the observed final pattern (in general image data), and the efforts move to unravel how it was formed. In particular, time-lapse experiments could alter the viability of cell cultures by inducing cellular damage (e.g., imaging-induced phototoxicity, leading to cell-cycle arrest or cell death⁴⁴). However, it is possible not only to obtain the coordination from the data of the final pattern but also to reproduce the temporal evolution of patterns. This permits us to mimic the exact evolution of the pattern formation when having time-lapse data, since it matches the known temporal constraints.

Regarding the simulation of in vitro data of lumen morphogenesis in PDAC organoids, physiologically, the generation of a cystic organoid requires the orchestration of proliferation, fluid secretion, and quiescence. On the one hand, if cells secrete fluid too early, the preapical patch, which is the closed volume necessary to secrete fluid, will not be formed, resulting in fluid leakage. On the other hand, if cells secrete too much fluid, the hydrostatic pressure excessively increases, and the lumen opens. In addition, if cells proliferate too much, they will not fit in the monolayer around the lumen, and cystic structures will not be formed. In contrast, if cells do not proliferate, they will not create enough inner space for the fluid, resulting in leakage. Only if cell functions are coordinated in a sophisticated manner will cystic structures form. In particular, first cells must proliferate to create an inner volume and then secrete fluid while continuing to proliferate to create more inner space as the fluid increases, before finally entering into a quiescent state. Therefore, the success of lumen generation depends on the proper coordination between cell proliferation, cell secretion, and quiescence. In fact, what the neural network learns is that if it generates too much pressure through fluid secretion with an insufficient number of cells, it leaks. In addition, it learns that cells must first proliferate to generate the organoid and, as the organoid reaches its final size, enter into a quiescent state. Despite the great biological variability in terms of the final size of in vitro experiments (Figure S13), we were able to obtain the developmental process to finally predict their size in each case. This quantitative validation with in vitro data proves that this approach does not produce ad hoc solutions and confirms that the different coordination of processes determines the final pattern. This is very suitable to simulate biological systems, which display variability and fluctuations around a solution. In the case of solid tumor organoids, the neural network coordinates proliferation and quiescence to achieve the final size of the organoid. This regulation of the dynamics of the population of cells is a helpful tool that could be used in many types of simulations. This permits the integration of data into simulations to determine cell proliferation, which is sometimes a difficult task, especially when the dynamics of the population of cells change over time. Therefore, our model is designed to predict the order in which cells behave to achieve a specific pattern.

Moreover, from a biological perspective, we found in our simulations that some cells are predisposed to perform a specific function over others. This is the case for the initial cell or first cells, which tend to proliferate more than daughter cells (Figure 4B). These initial precursor cells might have a higher proliferative potential, and as they divide, the daughter cells are more specialized with a higher differentiation grade. Inside an organoid, there exists heterogeneity of cellular functions, and we hypothesize that the cellular functions that cells perform in a morphogenetic process are not governed by the maturation of cells but by the stimuli to which they are exposed when they determine which function to perform. This implies that some cells are more specialized in division and others in secretion within the organoid. We also found that the final size of the organoid depends on the morphological characteristics of the organoid when the lumen is initiated. In our simulations, the initiation of the lumen, determined by the beginning of the fluid secretion, was different for each case, being earlier the smaller the final size of the organoid was (Figure 4B). We were able to establish that, initially, cells have a less differentiated phenotype and have a higher proliferative capacity. Then, as they proliferate, the daughter cells adopt a higher differentiation grade and specialize into secretory cells because of the stimuli that they are exposed when they are born. Thus, when they start secreting, the proliferative capacity of the organoid is reduced, so the final size of the organoid is limited by its size at the lumen initiation time. Therefore, we hypothesize that the proliferation capacity of cells may be hindered by the initiation of lumen formation and that the final size can be predicted at the initiation of lumen formation. These hypotheses could be validated by performing cell culture immunostaining with a mitotic cell marker to determine the number of proliferative cells in the biological system.⁴⁵

Another potential of this approach is that once the neural network has learned how to orchestrate cells to form the morphogenetic pattern, the parameters of the physics-based model can be modified to study the morphogenetic process under different scenarios. This allows the simulation of morphogenesis with different extracellular matrix properties, cell cycle times, or even organ-specific morphogenesis. In the case of morphogenesis, similar patterns are found in many parts of the organism, but the dynamic process differs in each organ since cell cycle time phases vary considerably between different types of cells and secretory cells may require different amounts of time to produce fluid. This implies that similar morphogenetic patterns can result in different sizes and require different lengths of time to achieve the final shape. However, although morphogenesis depends on cell type and the dynamics of the process vary, the requirements of the morphogenetic process are conserved among similar patterns. To this aim, we conducted a sensitivity analysis (Figures S7 and S8) varying the cell cycle time and fluid production time for the pancreatic cystic tumor organoids. This variation in these two parameters represents either the fluctuation of the behavior between the same type of cells or other types of cells that can also form cystic organoids. We also performed an analysis of the influence of the introduction of noise in the cell cycle and fluid secretion parameters (Figure S11), showing that the model is robust in forming the patterns and that the neural network can orchestrate cells despite the fluctuations of these parameters. With these analyses, we showed that in addition to the alteration of the dynamical processes of cells, the coordination to form the same pattern with the same morphological features (in this case, the number of cells and lumen volume) is conserved.

The potential of the proposed framework combining physics-based and data-driven modeling opens the door to a novel way of performing biological simulations at a cellular level, understanding how cell functions must coordinate to generate morphogenetic patterns by replicating how cells make decisions and adapting dynamically their responses to the variability found in biology.

Limitations of the study

In the applications shown in this work, some simplifications have been assumed. First, we employed a center-based lattice-free model to simulate the formation and growth of organoids, which entails some simplifications. The most important one is that cells are assumed to be nondeformable spheres, and their shape was not represented accurately. This simplification allowed us to approximate the size of the organoids through their number of nuclei with a reduced computational cost. Since the deformation of cells is not simulated, there are differences between the volume of the simulated organoids and the experiments (Figure 5A). However, this simplification does not influence the coordination that cells must follow to form morphogenetic patterns. Here, we did not aim to reproduce the exact shape and volume of the organoids; instead, we focused on showing the potential of the framework to unravel the orchestration of cell functions from a morphogenetic pattern, which is independent of the cell shape and volume. Second, we represented the lumen fluid through a particle-based model comparable to other works.^40,46 Although this representation is a simplification, we showed that our approach accurately reproduces the expected velocity and shear stress profiles for a Newtonian fluid, similar to water (see the characterization of the lumen fluid in STAR Methods). This confirms the capability of our method to model real fluids, serving as a minimal model that aims to recapitulate certain features such as mass conservation and momentum exchange. However, it does not rigorously reproduce bulk-scale physical properties. Furthermore, our approach enables us to simulate the interaction between cells and the fluid during a morphogenetic process, in which the lumen initiates de novo and grows through a fluid deposition process by cells, thus evolving the interface between cells and fluid over time. In addition, we investigated the influence of particle radius on the rheological properties of the fluid (further details are included in particle radius influence on the rheological properties of the fluid in STAR Methods). We have justified the choice of the particle radius and demonstrated that the rheological properties of the fluid play a crucial role in cystic organoid morphogenesis (see particle radius influence on fitness in STAR Methods).

Another limitation of the approach relates to the selection of cell functions and the question of whether the hypothesized functions are sufficient to generate the specific pattern. In our model, the decision-making possibilities are limited to the cell functions considered, which in this work were proliferation, secretion, and quiescence. Indeed, there are many cellular functions and processes that could be simulated. However, including more cell functions does not guarantee that all of them might be activated to reach a specific morphogenetic pattern. This allows us to underestimate them and reduce the complexity of the neural network and the number of outputs. Furthermore, in this first work, we created this data-driven approach with a neural network that receives the quantitative data as inputs. However, the neural network aims to reproduce the cell signaling through which cells sense, receive, and transduce external factors from their microenvironment (such as pressure, chemical signals, nutrients, etc.), or even internal factors (such as cell damage and cell deformation). Therefore, this approach permits the introduction of those factors as inputs of the neural network to enrich cell signaling and response. The final concern is related to finding the optimal neural network architecture for each specific application. Although some rules help to select the number of nodes and hidden layers, trial and error are commonly used. The neural network architecture determines the capacity to solve the problem and must be appropriate for the application. Moreover, the choice of the fitness function is fundamental to make the neural network learn. The fitness function evaluates the neural network performance depending on how close the simulated pattern is compared to the objective pattern. Therefore, this interplay between the neural network and the fitness function regulates the learning of the morphogenetic pattern. Despite the simplifications made in the applications of this framework, it allowed us to reproduce the morphogenetic patterns of organoids, understating how cells orchestrate their cellular functions to achieve those patterns.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, peptides, and recombinant proteins
Advanced DMEM F12	Gibco	12634-010
HEPES	Lonza	17-737E
GlutaMax	Gibco	35050-038
Penicillin/Streptomycin	Gibco	15140-122
A83-01	TOCRIS	2939
EGF	Life Technologies	PMG8041
FGF	Peprotech	100-26
Gastrin I	TOCRIS	3006
Noggin	Peprotech	250-38
Y-27632	Sigma	Y0503
N-acetylcysteine	Sigma	A9165
Nicotinamide	Sigma	N0636
B-27	Life Technologies	17504-044
Experimental models: Cell lines
Mouse ductal pancreatic cancer organoids	Boj, et al.47	https://doi.org/10.1016/j.cell.2014.12.021
Deposited data
Original data and code	Github, Zenodo	https://github.com/daniel-camacho-gomez/AIOrganoids https://doi.org/10.5281/zenodo.8019619
Software and algorithms
StarDist 3D	Weigert, et al.48	https://github.com/stardist/stardistl
ImageJ	Schneider, et al.49	https://imagej.nih.gov/ij/
MATLAB	MathWorks	https://es.mathworks.com/products/matlab.html

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Maria Jose Gomez-Benito (gomezmj@unizar.es).

Materials availability

This study did not generate unique reagents.

Experimental model and study participant details

Murine PDAC cells culture and maintenance

Cystic organoids formed from PDAC93-GFP and solid organoids formed from PM12500-GFP pancreatic ductal adenocarcinoma (PDAC) cells derived from Pdx1-Cre; Kras+/LSL-G12D; Trp53+/LSL-R172H male mice (KPC) were kindly donated by Dr. Mariano Ponz and Dr. Silvestre Vicent. Authentication of cell lines was not required. The cell line used to generate the organoids was a primary line donated by a collaborator, generated from a transgenic mouse model of pancreatic cancer. It is not a commercial line, thus authentication is not possible. The organoid cell line was tested for mycoplasma contamination using MycoAlert® Mycoplasma Detection Kit (Lonza). Cells were thawed from frozen stock in 50 ml Falcon tubes containing 10 ml of DMEM and centrifuged to remove any traces of the cryoprotectant DMSO. Then, the cells were incubated in T75 flasks (TC treated; Nunc EasyFlask, Thermo Scientific) containing 10 ml of DMEM supplemented with 10% FetalClone III (SH30109.02, Cytiva) at 37 °C and 5% CO2. Once cells reached 90% confluence, cell cultures were passed to a new T75 flask using 0.05% Trypsin-EDTA (25300-096, Gibco) followed by centrifugation and resuspension in 10 ml of fresh DMEM supplemented with serum and subsequent incubation at 37 °C and 5% CO2.

3D cultures of murine PDAC cells in matrigel

PDAC93-GFP and PM12500-GFP cells were grown in T75 flasks (TC treated; Nunc EasyFlask, Thermo Scientific) containing 10 ml of DMEM supplemented with 10% FetalClone III (SH30109.02, Cytiva). Once the cells reached 90% confluence, they were detached using 0.05% trypsin-EDTA (25300-096, Gibco), centrifuged, and resuspended in 1 $ml$ of fresh DMEM supplemented with serum. Then, the cell suspensions were embedded in 4 mg/ml growth factor reduced (GFR) Matrigel at a final concentration of 300,000 cells/ml. A total of 20 $\mu l$ of this cell-hydrogel mixture was added to individual 5 mm diameter wells of a homemade PDMS device followed by a 15 min incubation at 37 °C to complete the Matrigel gelation process. Finally, 800 $\mu l$ of organoid feeding media (a detailed description of the cell culture media used is available in Table S4) was added to the organoid culture device, and the 3D cell culture was incubated at 37 °C and 5% $C{O}_2$ as needed.

Method details

Learning algorithm

In order to make the neural network learn, we employed a genetic algorithm based on selection, crossover, and mutation algorithms. For the sake of simplicity, we illustrate how the weights of one node of the neural network are updated.

Selection

selection is how the progenitors are chosen from the generation. Thus, the two fittest progenitors of the actual generation are chosen as parents of the next generation. Let A be the best of its generation and B the second best. These two are also selected as offspring (parent A = off.1 and parent B = off.2). Then, the rest of the offspring (off.3, off.4, …, off.10) are obtained through crossover and mutation algorithms.

Crossover

parent A and parent B are mixed to obtain the offspring. Four-different crossover algorithms are implemented:

single point crossover: beginning with one parent ending with other:

$$\begin{array}{ccc}\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}①\\ ②\\ 3\\ 4\end{array}\right]}}+& \stackrel{ParentB}{\overbrace{\left[\begin{array}{c}5\\ 6\\ ⑦\\ ⑧\end{array}\right]}}=& \stackrel{Off.3}{\overbrace{\left[\begin{array}{c}1\\ 2\\ 7\\ 8\end{array}\right]}}\end{array}\begin{array}{ccc}\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}1\\ 2\\ ③\\ ④\end{array}\right]}}+& \stackrel{ParentB}{\overbrace{\left[\begin{array}{c}⑤\\ ⑥\\ 7\\ 8\end{array}\right]}}=& \stackrel{Off.4}{\overbrace{\left[\begin{array}{c}5\\ 6\\ 3\\ 4\end{array}\right]}}\end{array}$$

two point crossover: first and final values are chosen from one parent and middle values from the other parent:

$$\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}①\\ 2\\ 3\\ ④\end{array}\right]}}+\stackrel{ParentB}{\overbrace{\left[\begin{array}{c}5\\ ⑥\\ ⑦\\ 8\end{array}\right]}}=\stackrel{Off.5}{\overbrace{\left[\begin{array}{c}1\\ 6\\ 7\\ 4\end{array}\right]}}\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}1\\ ②\\ ③\\ 4\end{array}\right]}}+\stackrel{ParentB}{\overbrace{\left[\begin{array}{c}⑤\\ 6\\ 7\\ ⑧\end{array}\right]}}=\stackrel{Off.6}{\overbrace{\left[\begin{array}{c}5\\ 2\\ 3\\ 8\end{array}\right]}}$$

arithmetic crossover: sum of parents:

$$\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\right]}}+\stackrel{ParentB}{\overbrace{\left[\begin{array}{c}5\\ 6\\ 7\\ 8\end{array}\right]}}=\stackrel{Off.7}{\overbrace{\left[\begin{array}{c}6\\ 8\\ 10\\ 12\end{array}\right]}}$$

uniform crossover: offspring values are randomly copied from A or B parent:

$$\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}1\\ 2\\ ③\\ 4\end{array}\right]}}+\stackrel{ParentB}{\overbrace{\left[\begin{array}{c}⑤\\ ⑥\\ 7\\ ⑧\end{array}\right]}}=\stackrel{Off.8}{\overbrace{\left[\begin{array}{c}5\\ 6\\ 3\\ 8\end{array}\right]}}$$

Mutation

The purpose of mutation is to introduce diversity into the sampled population, avoid local minima and get faster to the solution ($rand\left(-\mathrm{1,1}\right)$ is a function that chooses the value -1 or 1 and $mu{t}_{rate}$ is a parameter):

$$off.9=\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\right]}}+mu{t}_{rate}·\left[\begin{array}{cccc}rand\left(-\mathrm{1,1}\right)& rand\left(-\mathrm{1,1}\right)& rand\left(-\mathrm{1,1}\right)& rand\left(-\mathrm{1,1}\right)\end{array}\right]·\stackrel{ParentA}{\overbrace{\left[\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\right]}}$$ (Equation 1)

$$off.10=\stackrel{ParentB}{\overbrace{\left[\begin{array}{c}5\\ 6\\ 7\\ 8\end{array}\right]}}+mu{t}_{rate}·\left[\begin{array}{cccc}rand\left(-\mathrm{1,1}\right)& rand\left(-\mathrm{1,1}\right)& rand\left(-\mathrm{1,1}\right)& \mathit{ran}d\left(-\mathrm{1,1}\right)\end{array}\right]·\stackrel{ParentB}{\overbrace{\left[\begin{array}{c}5\\ 6\\ 7\\ 8\end{array}\right]}}$$ (Equation 2)

Agent-based modeling

Mechanical interactions between agents make them move and change their positions. To describe these interactions we follow our previous work.⁴⁰ We illustrate how the cell position ${\mathit{x}}_c$ and particle position ${\mathit{x}}_p$ are calculated. Let ${\mathbf{N}}_c$ be the set of cells ${\mathbf{N}}_c=\left\{1,\dots ,N_c\right\}$, and let ${\mathbf{N}}_p$ be the set of particles ${\mathbf{N}}_p=\left\{1,\dots ,N_p\right\}$. First, the velocity of each i-cell ${\mathit{v}}_{c_i}$ and each k-particle ${\mathit{v}}_{p_k}$ are calculated from the balance of forces:

$$m_{c_i}\frac{d{\mathit{v}}_{c_i}}{dt}=\sum _{j\in {\mathbf{N}}_c}\left({\mathit{F}}_{c_i{c}_j}\right)+\sum _{j\in {\mathbf{N}}_p}\left({\mathit{F}}_{c_i{p}_j}\right)+{\mathit{F}}_{c_{i_{drag}}}\approx 0\text{,}$$ (Equation 3)

$$m_{p_k}\frac{d{\mathit{v}}_{p_k}}{dt}=\sum _{j\in {\mathbf{N}}_p}\left({\mathit{F}}_{p_k{p}_j}\right)+\sum _{j\in {\mathbf{N}}_c}\left({\mathit{F}}_{p_k{c}_j}\right)+{\mathit{F}}_{p_{k_{drag}}}\approx 0\text{.}$$ (Equation 4)

Here, $m_{c_i}$ and $m_{p_k}$ are the cell and particle masses, respectively, ${\mathit{F}}_{c_i{c}_j}$ represents cell-cell interaction force, ${\mathit{F}}_{c_i{p}_j}$ indicates the cell-particle interaction force, ${\mathit{F}}_{p_k{p}_j}$ is the particle-particle interaction force, ${\mathit{F}}_{p_k{c}_j}$ denotes the particle-cell interaction force and ${\mathit{F}}_{c_{i_{drag}}}$ and ${\mathit{F}}_{p_{k_{drag}}}$ are the friction of the cell and particle with the extracellular matrix, respectively. The inertial terms $m_{c_i}\frac{d{\mathit{v}}_{c_i}}{dt}$ and $m_{p_k}\frac{d{\mathit{v}}_{p_k}}{dt}$ are neglected because $Re\ll 1$. The drag forces ${\mathit{F}}_{c_{i_{drag}}}$ and ${\mathit{F}}_{p_{k_{drag}}}$ are obtained from Stoke’s law:

$${\mathit{F}}_{c_{i_{drag}}}=-6\pi \eta R_{c_i}{\mathit{v}}_{c_i}\text{,}$$ (Equation 5)

$${\mathit{F}}_{p_{k_{drag}}}=-6\pi \eta R_p{\mathit{v}}_{p_k}\text{,}$$ (Equation 6)

where η is the dynamic viscosity of the extracellular matrix, $R_{c_i}$ is the radius of the i-cell, $R_p$ is the radius of the particle and ${\mathit{v}}_{c_i}$ and ${\mathit{v}}_{p_k}$ are the velocities of the i-cell and k-particle.

Cell-cell interaction forces are usually modeled as repulsive-attractive forces. The repulsion between cells arises from cell resistance to deformation when their membranes touch, and the attractive forces are the result of the junctions that cells form between themselves through specialized protein complexes (⁵⁰). In the case of particles, the repulsive-attractive forces represent the intermolecular forces in fluids. Accordingly, we modeled the interaction forces ${\mathit{F}}_{{\delta }_i{\gamma }_j}$ (both subindexes δ and γ denote c or p, depending on whether the i and j agents are cells (c) or particles (p)) following,¹² as follows:

$${\mathit{F}}_{{\delta }_i{\gamma }_j}=F_{\delta \gamma }\frac{{\mathit{r}}_{ij}}{\Vert {\mathit{r}}_{ij}\Vert }$$ (Equation 7)

where:

$${\mathit{r}}_{ij}={\mathit{x}}_{{\gamma }_j}-{\mathit{x}}_{{\delta }_i}\text{,}$$ (Equation 8)

and:

$$F_{\delta \gamma }=\{\begin{array}{ll}{F}_{re{p}_{\delta \gamma }}\chi {\left(-s\right)}^{3/2},s<0\left(\text{repulsion}\right)\text{,}& \\ -F_{ad{h}_{\delta \gamma }}\chi \left\{\left(s+s_0\right)e^{-\lambda {\left(s+s_0\right)}^2}-v_0{e}^{-\lambda s^2}\right\},s\ge 0\left(\text{adhesion}\right)\text{.}& \end{array}$$ (Equation 9)

Consequently, χ, s, $x_0$ and $v_0$ are defined as:

$$\chi =\frac{R_{{\delta }_i}}{2}\left(\frac{1}{R_{{\delta }_i}}+\frac{1}{R_{{\gamma }_j}}\right),s=\frac{d-mi{n}_{dist}}{R_{{\delta }_i}}\text{,}$$ Equation (10)

$$x_0=\sqrt{\frac{1}{2\lambda }},v_0=x_0{e}^{-\lambda x_0^2}\text{.}$$ (Equation 11)

$F_{re{p}_{\delta \gamma }}$ and $F_{ad{h}_{\delta \gamma }}$ are the strengths of the adhesive and repulsive forces, respectively. ${\mathit{r}}_{ij}$ is the distance between the centers of the agents, and $R_{{\delta }_i}$ and $R_{{\gamma }_j}$ are the radii of the corresponding agents. $x_0$, $v_0$ and λ are matching constants, and χ is a geometric correction factor. The value of $mi{n}_{dist}=-0.1R_{{\delta }_i}$ is chosen such that the equilibrium state where the adhesive and repulsive forces are balanced is slightly less than zero, following,¹² and $d=\Vert {\mathit{r}}_{ij}\Vert -R_{{\delta }_i}-R_{{\gamma }_j}$ is the distance between the agents’ surfaces.

Since cells do not present any attraction towards the lumen fluid, the interaction force between cells and particles is only repulsive ($F_{ad{h}_{cp}}=F_{ad{h}_{pc}}=0$).

Finally, the velocity of the i-cell and the k-particle at time t can be calculated explicitly:

$$\frac{d{\mathit{x}}_{c_i}\left(t\right)}{dt}={\mathit{v}}_{c_i}\left(t\right)=\frac{1}{6\pi \eta R_{c_i}}\left(\sum _{j\in {\mathbf{N}}_c}\left({\mathit{F}}_{c_i{c}_j}\right)+\sum _{j\in {\mathbf{N}}_p}\left({\mathit{F}}_{c_i{p}_j}\right)\right)\text{,}$$ (Equation 12)

$$\frac{d{\mathit{x}}_{p_k}\left(t\right)}{dt}={\mathit{v}}_{p_k}\left(t\right)=\frac{1}{6\pi \eta R_p}\left(\sum _{j\in {\mathbf{N}}_p}\left({\mathit{F}}_{p_k{p}_j}\right)+\sum _{j\in {\mathbf{N}}_c}\left({\mathit{F}}_{p_k{c}_j}\right)\right)\text{.}$$ (Equation 13)

Cell functions

To reproduce the biological characteristics of tumor pancreatic organoids with lumen, three cell functions are considered within the agent-based model: proliferation, quiescence, and fluid secretion. Proliferation is modeled by a growth phase, in which the cell progressively increases its volume as a result of DNA replication, and by a mitosis phase, in which the cell divides into two daughter cells. Thus, we track the volume of each cell $V_i\left(t\right)$ and calculate the volume growth from⁴⁰:

$$\frac{d{V}_i\left(t\right)}{dt}=\alpha V_i\left(t\right)\text{,}$$ (Equation 14)

where $\alpha =1/T_c$ is the growth rate, which is related to the cell cycle time $T_c$. When the volume of the cell reaches twice its initial volume, DNA replication is concluded, and the cell divides. In this regard, cell division is performed using a random cleavage plane that contains the line that passes through the cell center and the lumen center of mass.

Quiescent cells remain inactive for 6 minutes ($\Delta t_{bio}$) and do not perform any cell function.

Finally, through the fluid secretion function, cells generate particles inside the lumen after fluid production time $\Delta t_{exo}$. First, when the lumen does not yet have any fluid, the cell secretes into the cell’s center of mass. Then, when another cell secretes, some random particles are duplicated to recreate the increment in the fluid volume.

Cell division

When the volume of the cell reaches twice the value of its initial volume, DNA replication is concluded, and the cell divides. A spatially controlled division is a fundamental condition to maintain the lumen architecture and to enhance its growth by enlarging the lumen volume. In this regard, a complex molecularly controlled process regulates the spindle orientation, so mitosis occurs in the plane of the monolayer.^{51,52,53,54,55,56} Here, we distinguish the division between nonpolarized cells and polarized cells. Nonpolarized cells are those that have not yet formed a lumen, and polarized cells are those that belong to a lumen and face it. In the case of nonpolarized cells, the division direction is chosen randomly. Polarized cell division is performed using a random cleavage plane that contains the line that passes through the cell center and the lumen center of mass. The position of the two daughter cells $\left({\mathit{x}}_{daughters}\right)$ are calculated similarly to other models^57,58 from the center of the parent cell ${\mathit{x}}_{parent}$ at:

$${\mathit{x}}_{daughters}={\mathit{x}}_{parent}\pm \left(R_c-\frac{1}{\sqrt[3]{2}}{R}_c\right)\mathit{n}\text{,}$$ (Equation 15)

where $R_c$ is the radius of the parent cell and $\mathit{n}$ is the unit orientation vector. When a nonpolarized cell divides, the unit orientation vector $\mathit{n}$ is chosen randomly. However, when a polarized cell divides, the unit orientation vector $\mathit{n}$ is normal to the random cleavage plane that contains the line that passes through the cell center and the lumen center of mass.

Fitness function

The fitness function is an objective function that assesses neural network performance. When the simulation finishes, a fitness value is given to the neural network depending on how close the obtained result is with respect to the target solution. Let $N_c^t$ and $V_l^t$ be the number of cells and lumen volume target values. The fitness function for cystic organoids is formed by three components: the first relates to the number of cells, the second to the lumen volume and the third is a penalty term for the eccentricity. Therefore, the fitness is evaluated through this equation:

$$Fitness\left(N_c,V_l,d_{cm}\right)=0.5·{100}^{-\frac{{\left(N_c-N_c^t\right)}^2}{2{\left(N_c^t\right)}^2}}+0.5·{100}^{-\frac{{\left(V_l-V_l^t\right)}^2}{2{\left(V_l^t\right)}^2}}-250{\left(\frac{e_c}{\left(V_l^t/10\right)}\right)}^2\text{,}$$ (Equation 16)

where $N_c^t$ is the target number of cells, $V_l^t$ is the target lumen volume and $e_c$ is the eccentricity (the distance between the cells’ center of mass and the lumen’s center of mass). Thus, the better the neural network approximates the target number of cells and target lumen volume, the better the solution. However, the higher the eccentricity $e_c$ is, the worse the solution. In the case of the fitness function for solid organoids, the fitness function is only dependent on the number of cells.

Eccentricity

In the process of the generation of a cystic organoid, fluid secretion, proliferation, and quiescence must be orchestrated. If cells secrete fluid too early, the preapical patch, which is the closed volume necessary to secrete fluid would not form, so the fluid would leak. Also, if cells secrete too much the lumen would open. Also, if they do not proliferate, they would not create more inner space for the fluid and it would leak. To maintain the structure, there is competition between these processes. Therefore, to make the neural network understand that these cell functions must coordinate to preserve the structure, we introduce a metric called eccentricity that permits us to take into account the structure. This metric refers to the distance between the cells’ center of mass and the lumen’s center of mass. The lower this value is, the more spherical the organoid is (Figure S1A). Conversely, the higher this value is, the less spherical the organoid is, reaching a certain moment that it opens (Figure S1B). Therefore, the neural network uses this metric to evaluate the state of the cystic structure.

Characterization of the lumen fluid

We conducted a shear test to validate that our approach represents an actual fluid. In this regard, we used a bulk domain consisting of fluid particles with a radius $R_p=2\mu m$ (Figure S3) The top layer of particles (depicted in black in Figure S3) was subjected to a velocity u in the X direction, while the bottom layer (depicted in blue in Figure S3) had fixed displacements in the X and Y directions.

Then, to obtain the steady flow curve to assess the behavior of particles, we set the shear stress experiment with a time duration of $t_{\mathit{exp}}=30$ min and varied the velocity of the top layer within the values $u=\left[0.01,0.05,0.1,0.2,0.5\right]/t_{\mathit{exp}}\mu m/\mathit{min}$. Finally, we were able to determine the viscosity of the fluid $\left(\eta \right)$ by measuring the shear stress $\left(\tau \right)$ as the sum of the reaction forces ($F_x$) of the particles forming the bottom $XY$-plane of the cube of side length l in the X direction $\left(\tau =\frac{\sum F_x}{l^2}\right)$ for each shear rate $\left(\dot{\gamma }=\partial v/\partial z\right)$.

$$\eta =\frac{\tau }{\frac{\partial v}{\partial z}}\text{.}$$ (Equation 17)

We show the linear regression of the shear stress on the deformation rate (Figure S4). We obtained that the shear stress is linearly proportional to the shear strain, resulting in a constant viscosity of $1.072·{10}^{-3}$ Pa.s, with an R-Squared value of 0.9996. Therefore, this analysis confirms that our approach accurately reproduces the expected velocity and shear stress profiles for a Newtonian fluid similar to water ($\sim {10}^{-3}$ Pa.s) and demonstrates the capability of our method to model real fluids, serving as a minimal model that aims to recapitulate certain features such as mass conservation and momentum exchange. However, it does not rigorously reproduce bulk-scale physical properties.

Particle radius influence on the rheological properties of the fluid

The particle radius in a particle-based model has a great influence on the mechanical and rheological properties of the fluid. Viscosity is a physical property of a fluid that describes its resistance to deformation or flow. In particle-based approaches, the viscosity coefficient is typically calculated from the smoothing length and the particle spacing and depends on the strength of the interaction forces between neighboring particles.

Reducing the particle radius while keeping all other properties constant, results in a change in the mechanical and rheological properties of the fluid. Therefore, to maintain the rheological properties of the fluid while changing the particle radius it is necessary to modify other parameters such as the interaction forces between the particles to maintain a consistent viscosity coefficient so that the macroscopic behavior of the fluid remains the same. On the one hand, if the particle radius is reduced for a given volume, the number of particles increases. Consequently, the fluid becomes more viscous than when the particle radius is greater since more particles oppose the shear stress. On the other hand, increasing the particle radius reduces the viscosity of the fluid. Thus, it is necessary to adjust the interacting forces so that the behavior remains the same when integrating the response of the fluid to deformation.

We have modified the interacting forces between particles for particle radii of $1,4$ and 6 μ m, through the optimization of the parameters $F_{re{p}_{pp}}$ and $F_{ad{h}_{pp}}$ in Equation 9 so we obtain the same response of the rheological properties of the fluid as for the particle radius of $R_p=2$ μ m (Figure S5A). In this case, the mean value of the viscosity obtained for all particle sizes is $1.078·{10}^{-3}$ Pa.s with a standard error of $1.210·{10}^{-5}$. Finally, we show a comparison between the interacting forces for $R_p=2$ μ m and the modified interacting forces for particle radii of $1,4$ and 6 μ m to obtain the same response (Figure S5B). Since the number of particles increases when the particle radius decreases, the interacting forces reduce so when integrating the contribution of the particles to the viscosity it is equivalent across different particle sizes.

Particle radius influence on fitness

We analyze the effect of the variation of the particle radius. For this purpose, we simulated an intermediate-size cystic organoid (organoid 2 from Table 1 of the manuscript) with different particle radii to determine how it affects the results. We show the influence of particle radii on the fitness value and computation time while keeping the interacting forces the same as for the case of $R_p=2$ μ m (Figure S6A). We found that increasing the particle radius from 1 $\mu m$ to 2 $\mu m$ causes an absolute decrease of the fitness value of 0.15% and a relative decrease in the computation of 96.02% (from 1029 min to 41 min). An increase of the particle radius from 2 $\mu m$ to 4 $\mu m$ entails an absolute worsening of the fitness of the approximation of 4.16% and a relative improvement of the computing time of 93.88% (from 41 to 3 min). Therefore, this analysis shows that the rheological properties of the fluid are important in the cystic morphogenetic process and require proper interaction to develop the organoid correctly. In particular, making the fluid less viscous (increasing the particle radius) entails a worsening of the simulated organoid. Then, we studied the influence of the particle radii on the fitness value and computation time with the interacting forces obtained in Figure S5B to have the same viscosity as water. In this case (Figure S6B) the fitness is above 0.91 for all particle sizes simulated. However, increasing the particle radius results in a slight decrease in fitness due to a higher increase in lumen volume per fluid secretion compared to smaller particle sizes, leading to a reduced sensitivity in the secretion process. Therefore, a particle radius of 2 μ m is optimal for maintaining low computational costs while having sufficient sensitivity in the fluid secretion process.

Multiphoton microscopy of PDAC organoids

3D cultures of PDAC93-GFP and PM12500-GFP cells were generated and incubated for 5 days as described in the previous section. Then, samples were fixed with 4% paraformaldehyde in DPBS solution at 37 °C for 30 minutes and washed thoroughly with DPBS followed by cell nuclei staining with a 5 $\mu g/ml$ solution of Hoechst 33342 for 16 h at room temperature. Image acquisition was performed using a Zeiss LSM 880 AxioObserver inverted confocal microscope equipped with a 25x LD LCI Plan-Aprochomat 0.8 NA W objective. A total sample volume of approximately 1065x1065x200 $\mu m^3$ was acquired using a Mai Tai® DeepSee™ Ti:Sapphire laser sequentially set to 740 nm and 920 nm for multiphoton microscopy of stained nuclei and endogenous cytoplasmic GFP, respectively.

Quantification of 3D PDAC organoid morphology

Nuclei and cytoplasmic GFP segmentation masks were generated using StarDist 3D⁴⁸ and the Trainable Weka Segmentation 3D⁵⁹ plugin for Fiji, respectively. The StarDist 3D model was trained from scratch for 50 epochs on 45 paired image patches (patch size: (72,72,32), batch size 1, number of rays: 32, augmentation: true),⁶⁰ accelerated using an NVIDIA Quadro P1000 GPU. Afterward, the generated masks were analyzed using a homemade script for Fiji. Briefly, cytoplasmic GFP masks were preprocessed using a GPU-accelerated 3D median filter and binary closing available in the CLIJ2 library⁶¹). Then, each individual organoid was labeled, and the intersection between the cytoplasmic GFP mask and the nuclear mask was calculated using a logical AND operator. The number of nuclei and morphological descriptors, such as the organoid volume or sphericity, were quantified using MorpholibJ.⁶²

Quantification and statistical analysis

Statistical analyses and figure generation were performed using MATLAB (MathWorks). The exact number of simulations conducted to test the robustness in Figure 4 was indicated in the legend. The R-squared values of the linear regressions in Figures S4 and S5 were also specified in the legend.

Published: June 19, 2023

Data and code availability

• •All data reported in this paper will be shared by the lead contact upon request.
• •Original codes are available on request to the corresponding authors and are also publicly available at https://github.com/daniel-camacho-gomez/AIOrganoids. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.