Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Jul 10;145(28):15162–15170. doi: 10.1021/jacs.3c01576

Engineering Robust Metallic Zero-Mode States in Olympicene Graphene Nanoribbons

Ryan D McCurdy †, Aidan Delgado †, Jingwei Jiang ‡,§, Junmian Zhu †, Ethan Chi Ho Wen †, Raymond E Blackwell †, Gregory C Veber †, Shenkai Wang †, Steven G Louie ‡,§,*, Felix R Fischer †,§,∥,⊥,*
PMCID: PMC10360063  PMID: 37428750

Abstract

graphic file with name ja3c01576_0006.jpg

Metallic graphene nanoribbons (GNRs) represent a critical component in the toolbox of low-dimensional functional materials technology serving as 1D interconnects capable of both electronic and quantum information transport. The structural constraints imposed by on-surface bottom-up GNR synthesis protocols along with the limited control over orientation and sequence of asymmetric monomer building blocks during the radical step-growth polymerization have plagued the design and assembly of metallic GNRs. Here, we report the regioregular synthesis of GNRs hosting robust metallic states by embedding a symmetric zero-mode (ZM) superlattice along the backbone of a GNR. Tight-binding electronic structure models predict a strong nearest-neighbor electron hopping interaction between adjacent ZM states, resulting in a dispersive metallic band. First-principles density functional theory-local density approximation calculations confirm this prediction, and the robust, metallic ZM band of olympicene GNRs is experimentally corroborated by scanning tunneling spectroscopy.

Introduction

Graphene nanoribbons (GNRs) are representatives of an emerging class of bottom-up synthesized designer quantum materials whose electronic structure can be tuned with atomic precision by deterministic chemical designs. Their structures exhibit unusual and some never before realized physical properties that extend far beyond the parent 2D graphene. Highly tunable band gaps,1−3 photoemission,4 magnetic spin chains,5 and even symmetry-protected topological states6−9 can all be tailored by real space structural parameters including, among others, width, symmetry, edge termination, and substitutional doping.10−13 A dominant electronic feature common to almost all GNRs is the opening of a sizeable band gap imposed by laterally confining a 2D graphene sheet to a quasi-1D GNR (width < 2 nm). This quantum confinement effect has emerged as a veritable challenge to the design of intrinsically metallic band structures. Bottom-up access to a family of robust metallic GNRs not only represents a critical component in the development of advanced nanographene-based logic circuits,14 e.g., as covalent interconnects capable of electronic and quantum transport, but could serve a versatile and highly tunable platform to explore emergent physical phenomena such as Luttinger liquids,15−18 plasmonics,19−22 charge density waves,23−26 and superconductivity in 1D.27−30

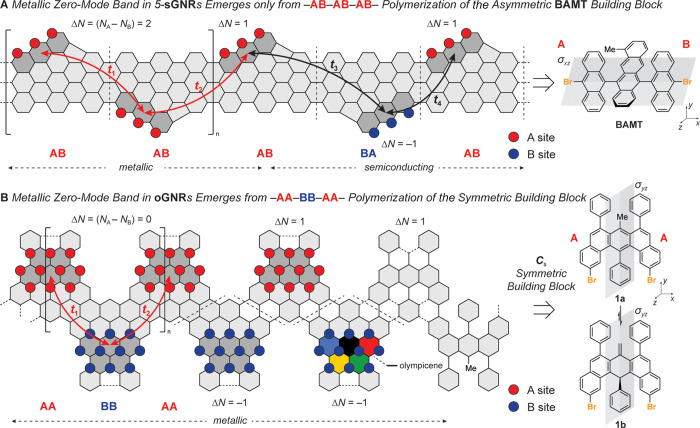
We recently reported a general approach for accessing metallic GNRs by embedding a superlattice of localized zero-mode (ZM) states along the backbone of a bottom-up synthesized sawtooth GNR (sGNR).31,32 A key ingredient to this approach was the design of a molecular building block, 6,11-bis(10-bromoanthracen-9-yl)-1-methyltetracene (BAMT in Figure 1), that introduces a sublattice imbalance (ΔN = NA – NB) between carbon atoms occupying the A and the B sublattice sites of graphene, respectively. The concept is reminiscent of Lieb’s theorem,33 a surplus of carbon atoms on sublattice A versus sublattice B will lead to ΔN eigenstates at E = 0 eV, or ZMs, localized on the majority sublattice. Application of a simple tight binding model, the Su–Schrieffer–Heeger (SSH) dispersion relationship,34 that describes the interaction between these local ZM states gave rise to two distinctive bands defined by an intracell hopping amplitude t1 and an intercell hopping amplitude t2. The energy gap enclosed by these bands is ΔE = 2||t1| – |t2||. If the absolute magnitude of the two hopping amplitudes is equal, i.e., |t1| = |t2|, as illustrated for the evenly spaced ZM states in sGNR (Figure 1A), the energy gap vanishes and the 1D electronic structure becomes metallic.35,36 The presence of a metallic ZM band at the Fermi level (EF) in sGNRs could be visualized by scanning tunneling spectroscopy (STS) and was further corroborated by density functional theory-local density approximation (DFT-LDA) calculations. This method, however, suffered from a Stoner-type instability for narrow bands that could open up a spin-splitting gap. To overcome this, we had to introduce an effective sublattice mixing (e.g., introduction of 5-membered rings in 5-sGNRs) to facilitate the hopping between the localized zero modes.

Figure 1.

Figure 1

Open in a new tab

Bottom-up design and ZM engineering of metallic GNRs. (A) Metallic band in 5-sGNRs emerges only if the orientation of the monomers along the axis of polymerization (x-axis) follows a regioregular −AB–AB–AB– pattern. (B) Presence of a σyz mirror plane in 1a/b normal to the axis of polymerization (x-axis) ensures that either of two possible orientations of a monomer during the radical step-growth polymerization gives rise to a metallic ZM band in oGNRs.

A major shortcoming inherent to the design of 5-sGNRs is the requirement that all bonds formed between molecular precursors as part of the on-surface radical step-growth polymerization have to follow a strict head-to-tail pattern (−AB–AB–AB– in Figure 1A) to ensure that the intracell hopping amplitude |t1| remains equal in magnitude to the intercell hopping amplitude |t2|. The statistical probability that this specific arrangement is adopted for a single C–C bond-forming step on the surface is only ∼50%. Were the molecular building blocks to fuse in the undesirable head-to-head (−BA–AB−) or tail-to-tail (−AB–BA−) configuration, the ZM bands would split (|t3| ≠ |t4|) and give rise to a semiconductor rather than a metal.31,32 The probability of producing a metallic sGNR segment from n monomers is therefore Pn = (0.5)n or less than 1% for n > 7, severely limiting the use of metallic sGNRs at length scales necessary for applications as device interconnects. While sGNRs served as a successful proof of concept for our general approach to access metallic phases in GNRs, designs that ensure regioregularity and an efficient sublattice mixing of ZM states are needed to obtain uniform samples of extended GNRs with persistent, intrinsically metallic ZM bands.

Here, we report the design and on-surface synthesis of metallic olympicene GNRs (oGNRs) derived from Cs symmetric molecular building blocks 1a,b (Figure 1B) (herein, 1a and 1b represent two discrete constitutional isomers that interconvert through a tautomerization equilibrium). Rather than relying on a statistical distribution of bond-forming events that dictated the band structure in sGNRs, the molecular building blocks for oGNRs feature a σyz mirror plane perpendicular to the x-axis, the main axis of polymerization, ensuring that oGNRs arising from 1a,b will always be metallic. This could be achieved by placing the carbon atom contributing to the sublattice imbalance ΔN, the methyl group in 1a or the methylene in 1b, along the σyz mirror plane of the building block. The arrangement of any two monomers forming the oGNR unit cell ensures that the position of the ZM state alternates between the A and the B sublattice sites. The efficient sublattice mixing that gives rise to a robust metallic ZM band is built into the design. Atomically precise oGNRs were synthesized from molecular precursors on a Au(111) surface and characterized in ultrahigh-vacuum (UHV) by low-temperature scanning tunneling microscopy (STM) and STS. Experimental results are further corroborated by first-principles calculations, revealing a robust metallic band that spans across EF emerging from the interaction of ZM states along the backbone of oGNRs.

Results and Discussion

Synthesis of Molecular Precursors for oGNRs

The synthesis of the molecular precursor 1b for oGNRs is depicted in Figure 2. Double Suzuki cross-coupling of 2,6-dibromo-4-methyl-1,1′-biphenyl (2) with 2 equiv of 2-(5-methoxy-2-(phenylethynyl)phenyl)-4,4,5,5-tetramethyl-1,3,2-dioxaborolane (3) yielded the diyne 4. Treatment of 4 with Barluenga’s reagent in TfOH successfully induced the sterically demanding benzannulation to give the benzo[m]tetraphene core 5. The two aryl iodide groups in 5 were removed by lithium-halogen exchange with s-BuLi followed by protonation with MeOH to yield 6. With the assembly of the characteristic carbon backbone of the monomer building block completed, the task shifted to converting the methoxy groups in 6 to aryl halides that serve as thermally labile chemical handles during the on-surface GNR growth. A well-precedented route involves deprotection of aryl-methyl ethers to reveal the free alcohols followed by conversion into aryltriflates which serve as versatile handles for further diversification.111H and 13C NMR revealed that deprotection of 6 under Lewis/Brønsted acidic (e.g., BBr3, AlBr3, TMSI, HBr, HI, and TfOH) or nucleophilic (e.g., NaSEt and LiI) conditions induced a tautomerization of the benzo[m]tetraphene core to yield predominantly the 7-methylene-7,14-dihydrobenzo[m]tetraphene 7b rather than the tautomeric species 7a. Following the synthetic route outlined above, treatment of 7b with Tf2O gave access to the triflate 8b. Single crystals suitable for X-ray diffraction were grown by slow diffusion of MeOH into a saturated solution of 8b in CH2Cl2. The crystal structure of 8b revealed that the central ring of the dihydrobenzo[m]tetraphene core, ring c in Figure 2, adopts a boat-like conformation placing the methylene group at C7 and the phenyl group at C14 at angles of 35.0° and 76.0° above the base plane spanned by the remaining four carbon atoms (C6a, C7a, C13b, and C14a) of ring c, respectively. While this conformation comes at the cost of breaking the extended aromatic ring system of a benzo[m]tetraphene core into two isolated naphthalene units, the boat conformation adopted by ring c significantly reduces the A1,3 strain between the exocyclic methylene group and the two phenyl substituents at C6 and C8. To complete the synthesis, the triflates in 8b were converted into the diboronic ester 9b before treatment with excess CuBr2 yielded the 2,12-dibromo-7,14-dihydrobenzo[m]tetraphene 1b, the molecular building block for oGNRs. Single crystals of 1b suitable for X-ray diffraction and surface-assisted oGNR growth were obtained by diffusion of MeOH into a saturated solution of 1b in CH2Cl2. In close analogy to the conformation adopted by 8b, the ring c in dihydrobenzo[m]tetraphene 1b adopts a boat-like conformation. The included angles between the methylene group at C7 and the phenyl substituent at C14 with the base plane of ring c are 37.5° and 75.0°, respectively.

Figure 2.

Figure 2

Open in a new tab

Synthesis of molecular precursor 1b for oGNRs. Single X-ray crystal structures of 8b and 1b. Thermal ellipsoids are drawn at the 50% probability level. Color coding: C (gray), O (red), F (green), S (yellow), Br (orange). Hydrogen atoms are placed at calculated positions.

Surface-Assisted Growth and Electronic Structure Characterization of oGNRs

Samples of metallic oGNRs were prepared following an established surface-assisted bottom-up GNR synthesis. Molecular precursor 1b was sublimed in UHV from a Knudsen cell evaporator onto a Au(111) surface held at 25 °C. Figure 3A shows a representative topographic STM image of self-assembled islands of 1b on an atomically flat Au(111) terrace. Step-growth polymerization of 1b was induced by annealing the molecule-decorated surface first to 180 °C for 15 min followed by a second annealing step at 350 °C for 15 min to complete the cyclodehydrogenation. Topographic images of a high coverage sample, Figure 3B, reveal extended GNRs featuring a characteristic alternating pattern of protrusions along the backbone of the GNR and lengths ranging up to 30 nm (Supporting Information Figure S1). Bond-resolved STM (BRSTM) with CO-functionalized tips reveals that the radical step-growth polymerization proceeds concurrently with the partial cyclodehydrogenation of the oGNR backbone (Figure 3C,D). At 180 °C, the [4]-helicene fragments lining the edges of oGNRs have partially fused to form 5-membered rings (Figure 3E, Supporting Information Figure S1C). A second annealing step (350 °C for 15 min) merely completes the process, giving rise to a uniform edge termination in 5-oGNRs (Figure 3C,D, Supporting Information Figure S2).

Figure 3.

Figure 3

Open in a new tab

Bottom-up synthesis of 5-oGNRs. (A) STM topographic image of a self-assembled island of molecular precursor 1b on Au(111) (Vs = 0.05 V, It = 20 pA). (B) STM topographic image of a high coverage sample of 5-oGNRs following annealing to 350 °C (Vs = 0.05 V, It = 20 pA). (C and D) BRSTM and Laplace-filtered BRSTM image of a 5-oGNR segment showing the 5-membered rings resulting from the fusion of [4]helicene groups along the oGNR edges (Vs = 0.01 V, It = 400 pA). (E) Schematic representation of the stepwise thermally induced cyclodehydrogenation that gives rise to 5-oGNRs.

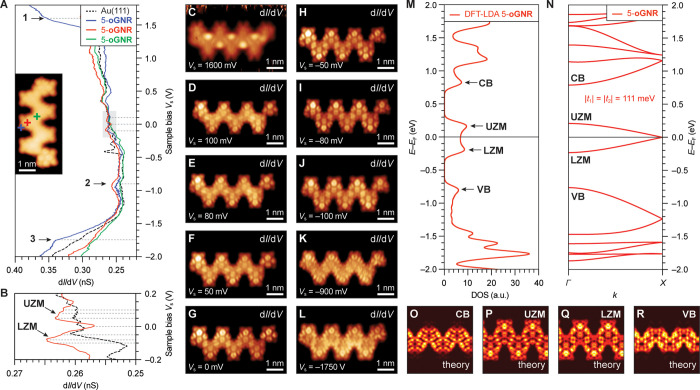
Having resolved the chemical structure of 5-oGNRs, we shifted our focus to the characterization of its local electronic structure using differential tunneling spectroscopy. Figure 4A shows typical dI/dV point spectra for a 5-oGNR recorded with a CO-functionalized STM tip at the positions highlighted in the inset. Three spectral features can clearly be seen in the range of −2.00 V < Vs < +1.80 V. Two shoulders at Vs = +1.60 V (Peak 1) and Vs = −1.75 V (Peak 3) dominate the spectrum, along with a broad peak centered at Vs = −0.90 V (Peak 2). The signal intensities of Peaks 1 and 3 are strongest when the STM tip is placed close to the convex protrusions lining the edge of the ribbon (blue line in Figure 4A), whereas Peak 2 is prominently featured in both spectra recorded above the center of an olympicene unit (red line in Figure 4A, Supporting Information Figure S3) and along the edge of the ribbon. Figure 4B shows dI/dV spectra taken over a narrower bias range −0.20 V < Vs < +0.20 V. Most prominent here is a U-shaped feature anchored by two peaks in the differential conductance spectrum at Vs = −0.08 V and Vs = +0.05 V when the STM tip is placed above the center of the olympicene unit. Differential conductance maps recorded over a bias range of Vs = +0.10 V to Vs = −0.10 V (Figure 4D–J, Supporting Information Figure S3H–P) show characteristic wavefunction patterns associated with two degenerate low-bias states that intersect at Vs = +0.00 V. The peak at Vs = −0.08 V can thus be assigned to the bottom edge of the lower ZM (LZM) of two ZM bands contributing to the metallic state in 5-oGNRs, while the peak at Vs = +0.05 V captures the top edge of the upper ZM (UZM) band. The U-shaped local density of states (LDOS) spanning across EF is the signature of van Hove singularities associated with the flat band edges of the LZM and UZM bands.

Figure 4.

Figure 4

Open in a new tab

Electronic structure of 5-oGNRs. (A and B) STS dI/dV spectra recorded on a 5-oGNR at the positions marked in the inset STM topographic image with a red, blue, and green cross (spectroscopy: Vac = 11 mV, f = 455 Hz; imaging: Vs = 50 mV, It = 20 pA, CO-functionalized tip). (C–L) Constant height dI/dV maps recorded at the indicated biases (spectroscopy: Vac = 11 mV, f = 455 Hz). (M) DFT-LDA-calculated DOS of 5-oGNR (spectrum broadened by 10 meV Gaussian). Features associated with the CB, UZM, LZM, and VB are indicted by arrows. (N) DFT-LDA-calculated band structure of a freestanding 5-oGNR. A tight binding fit to the DFT-LDA band structure yields the hopping parameters |t1| = |t2| = 111 meV. (O–R) Calculated DFT-LDA LDOS maps evaluated at the edge of the bulk CB, at the UZM and LZM bands, and at the edge of the bulk VB.

First-Principles Calculation of the 5-oGNR Electronic Structure

We further explored the metallic band structure of 5-oGNRs using ab initio DFT. Figure 4M,N shows the theoretical DOS and the band structure of a 5-oGNR calculated using an LDA to the exchange-correlation potential. Two highly dispersive bands, labeled LZM and UZM, span across the energy scale from E–EF = −0.25 V to E–EF = +0.25 V. The LZM and UZM bands cross EF at k = X, giving rise to a robust metallic band with a width of EZM ∼ 0.5 eV. Both the upper and lower edges of the ZM bands show a flattening as they approach k = Γ. The corresponding calculated DOS (Figure 4M) faithfully reproduces the U-shaped signature of the metallic band identified in the experimental LDOS (Figure 4A,B). DFT-LDA LDOS projections evaluated at the energy of the UZM and LZM edges (Figure 4P,Q) show the characteristic nodal pattern observed in the corresponding dI/dV maps (Figure 4D–J). At energies above and below E–EF = ±0.25 V, the calculated metallic ZMB gives way to minigaps, narrow regions of vanishing DOS, that span the energy window separating the ZMB from the bottom of the CB and the top of the VB, located at E–EF = +0.80 V and E–EF = −0.75 V, respectively. Both LZM and UZM bands can be fit to an SSH tight binding model

graphic file with name ja3c01576_m001.jpg 1

with the intra- and intercell hopping amplitudes |t1| = |t2| = 111 meV and δ = 0 (δ is the relative phase between t1 and t2). Supercell calculations further show that the rigid GNR backbone renders oGNR virtually impervious to mechanical deformations usually associated with strong electron–phonon coupling along the main x-axis of the ribbon that would otherwise induce spontaneous metal–insulator transitions (i.e., Peierls distortion). A decisive advantage of oGNRs over the first-generation metallic sGNRs is that the Cs symmetric molecular precursor 1b features a σyz mirror plane perpendicular to the axis of polymerization. This plane of symmetry ensures a uniform, predictable monomer sequence that exclusively gives rise to a metallic band structure. Besides this key structural design feature, the family of oGNRs has one last trick up its sleeve.

Robust metallicity in sGNRs required the fusion of [4]helicene fragments along the sawtooth edge to induce an effective mixing of sublattice spin-polarized ZM states. The resulting broadening of the metallic ZMB (i.e., a reduced DOS at EF) proved sufficient to circumvent Mott insulator or Stoner magnetic phase transitions. In contrast, an efficient hopping between ZM states localized on the A and B sublattice sites is already built into the design of oGNRs. The −AA–BB–AA– polymerization places ZM states on alternating sublattice sites, ensuring that the hopping amplitudes t1 and t2 between adjacent states are dominated by the nearest-neighbor hopping term rather than the much smaller second nearest-neighbor hopping (Figure 1B). The sublattice mixing resulting from the fusion of [4]helicene fragments along the edges of 5-oGNRs is small and has a negligible effect on the width of the metallic ZMB (Supporting Information Figure S4A). Band structure calculations using the local spin density approximation (LSDA) show no sign of magnetic phase transitions for the disperse metallic ZM bands in 5-oGNRs (Supporting Information Figure S4B).

Conclusions

We herein demonstrate the versatility of ZM engineering for introducing robust metallicity in 1D GNRs. A Cs symmetric molecular building block undergoes a regiocontrolled on-surface polymerization to yield homogeneous samples of 5-oGNRs featuring a symmetric superlattice of ZM states along the GNR backbone. Guided by elementary tight-binding analysis, we pioneer the design of 5-oGNRs around a strong nearest-neighbor hopping interaction between electrons in adjacent ZM states, giving rise to a large ZM bandwidth that is insensitive to Peierls and Stoner metal–insulator transitions. First-principles DFT-LDA calculations and STS corroborate the emergence of metallic ZM bands in 5-oGNRs. The design and synthesis of robust, metallic GNRs pave the way toward the realization of energy-efficient integrated circuit architectures based on low-dimensional carbon materials that are capable of high-speed electronic37,38 and quantum information processing.39,40

Experimental Section

Materials and Instrumentation

Unless otherwise stated, all manipulations of air- and/or moisture-sensitive compounds were carried out in an oven-dried glassware under an atmosphere of N2. All solvents and reagents were purchased from Alfa Aesar, Spectrum Chemicals, Acros Organics, TCI America, and Sigma-Aldrich and were used as received unless otherwise noted. Organic solvents were dried by passing through a column of alumina and were degassed by vigorous bubbling of N2 through the solvent for 20 min. Flash column chromatography was performed on SiliCycle silica gel (particle size 40–63 μm). Thin layer chromatography was carried out using SiliCycle silica gel 60 Å F-254 precoated plates (0.25 mm thick) and visualized by UV absorption. All 1H and 13C{1H} NMR spectra were recorded on a Bruker AV-600 spectrometer and are referenced to residual solvent peaks (CD2Cl21H NMR = 5.32 ppm, 13C{1H} NMR = 53.84 ppm). ESI mass spectrometry was performed on a Finnigan LTQFT (Thermo) spectrometer in positive ionization mode. X-ray crystallography was performed on a Rigaku XtaLAB P200 equipped with a MicroMax 007HF dual-source rotating anode and a Pilatus 200 K hybrid pixel array detector. Data were collected using Mo-Kα (λ = 0.71073 Å) radiation. Crystals were kept at 100 K throughout the collection using an Oxford Cryostream 700 for 1b and 8b. Data collection was performed with CrysAlisPro.41 Data was processed with CrysAlisPro and includes a multi-scan absorption correction applied using the SCALE3 ABSPACK scaling algorithm within CrysAlisPro. Crystallographic data was solved with ShelXT, refined with ShelXL and finalized in Olex1.5.

2-(5-Methoxy-2-(phenylethynyl)phenyl)-4,4,5,5-tetramethyl-1,3,2-dioxaborolane (2)

A 50 mL Schlenk flask was charged under N2 with 2-bromo-4-methoxy-1-(phenylethynyl)benzene (0.500 g, 1.75 mmol), bis(pinacolato)diboron (0.670 g, 2.63 mmol), and potassium acetate (0.515 g, 5.25 mmol) in dry dioxane (10 mL). The reaction mixture was degassed by sparging with N2 for 20 min before [1,1′-bis(diphenylphosphino)ferrocene]dichloropalladium(II) (0.07 g, 0.09 mmol) was added under N2. A reflux condenser was attached, and the reaction mixture was stirred under N2 for 18 h at 80 °C. The reaction mixture was concentrated on a rotary evaporator. Column chromatography (SiO2; CH2Cl2) yielded 2 (0.570 g, 1.7 mmol, 97%) as a colorless solid. 1H NMR (600 MHz, CD2Cl2) δ = 7.55 (d, J = 8.0 Hz, 2H), 7.49 (d, J = 8.0 Hz, 1H), 7.38–7.33 (m, 3H), 7.29 (d, J = 2.0 Hz, 1H), 6.97 (dd, J = 8.0 Hz, J = 2.0 Hz, 1H), 3.85 (s, 3H), 1.39 (s, 12H) ppm; 13C {1H} NMR (151 MHz, CD2Cl2) δ = 159.5, 134.4, 131.8, 128.9, 128.3, 124.8, 120.6, 117.1, 91.1, 90.0, 84.6, 83.8, 55.9, 25.3 ppm; HRMS (ESI-TOF) m/z: [C21H24O3B1]+ calcd [C21H24O3B1] 335.1813; found 335.1815.

2,6-Dibromo-4-methyl-1,1′-biphenyl (3)

A 250 mL Schlenk flask was charged under N2 with N,N-diisopropylethylamine (2.0 g, 20 mmol) in dry THF (140 mL). The reaction mixture was cooled to −78 °C and stirred for 20 min. n-BuLi (6.2 mL, 15.5 mmol, 2.5 M in hexanes) was added dropwise and stirred for 5 min. 3,5-Dibromotoluene (3.75 g, 15 mmol) was added dropwise, and the reaction mixture was stirred for 20 min. ZnCl2 (2.10 g, 15.5 mmol) was added, and the reaction mixture was stirred for 2.5 h at 24 °C. Iodobenzene (1.00 g, 5 mmol) and tetrakis(triphenylphosphine)palladium(0) (0.82 g, 0.71 mmol) were added, and the reaction mixture was stirred for 18 h at 24 °C. The reaction mixture was concentrated on a rotary evaporator, diluted with H2O (200 mL), and extracted with CH2Cl2 (300 mL). The combined organic phases were washed with H2O (100 mL) and saturated aqueous NaCl (100 mL), dried over MgSO4, and concentrated on a rotary evaporator. Column chromatography (SiO2; hexane) yielded 3 (1.60 g, 4.9 mmol, 98%) as a colorless crystalline solid. 1H NMR (600 MHz, CD2Cl2) δ = 7.49 (s, 2H), 7.47–7.41 (m, 3H), 7.20 (d, J = 8.0 Hz, 2H), 2.36 (s, 3H) ppm; 13C {1H} NMR (151 MHz, CD2Cl2) δ = 141.7, 141.3, 140.4, 133.0, 130.0, 128.7, 128.5, 124.4, 20.8 ppm; HRMS (EI-TOF) m/z: [C13H10Br2]+ calcd [C13H10Br2] 325.9129; found 325.9125.

5-Methoxy-3′-(5-methoxy-2-(phenylethynyl)phenyl)-5′-methyl-2-(phenylethynyl)-1,1′:2′,1″-terphenyl (4)

A 1000 mL Schlenk flask was charged with 2 (1.45 g, 4.3 mmol), 3 (6.48 g, 19.4 mmol), and K2CO3 (3.57 g, 25.8 mmol) in dioxane (250 mL) and H2O (40 mL). The reaction mixture was degassed by sparging with N2 for 20 min before tetrakis(triphenylphosphine)palladium(0) (0.50 g, 0.43 mmol) was added under N2. A reflux condenser was attached, and the reaction mixture was stirred under N2 for 18 h at 100 °C. The reaction mixture was concentrated on a rotary evaporator, diluted with H2O (200 mL), and extracted with CH2Cl2 (300 mL). The combined organic phases were washed with H2O (100 mL) and saturated aqueous NaCl (100 mL), dried over MgSO4, and concentrated on a rotary evaporator. Column chromatography (SiO2; 3:2 hexane/CH2Cl2) yielded 4 (1.75 g, 3.0 mmol, 70%) as a light-yellow solid. 1H NMR (600 MHz, CD2Cl2) δ = 7.45 (s, 2H), 7.36 (d, J = 8.0 Hz, 2H), 7.30–7.06 (m, 10H), 6.97–6.86 (m, 5H), 6.70 (d, J = 8.0 Hz, 2H), 6.58(m, 2H), 3.58 (s, 6H), 2.53 (s, 3H) ppm; 13C{1H} NMR (151 MHz, CD2Cl2) δ = 159.4, 146.7, 140.7, 140.0, 138.1, 136.2, 133.5, 131.6, 128.8, 128.2, 127.2, 126.3, 124.4, 116.6, 115.7, 113.7, 91.7, 90.1, 55.8, 21.5 ppm; HRMS (ESI-TOF) m/z: [C43H33O2]+ calcd [C43H33O2] 581.2475; found 581.2477.

5,9-Diiodo-2,12-dimethoxy-7-methyl-6,8,14-triphenylbenzo[m]-tetraphene (5)

A 500 mL Schlenk flask was charged in the dark under N2 with bis(pyridine)iodonium tetrafluoroborate (2.25 g, 6.0 mmol) in dry CH2Cl2 (240 mL). Trifluoromethane sulfonic acid was added dropwise, and the reaction mixture was stirred for 15 min at 24 °C. The reaction mixture was cooled to −40 °C before 4 (1.00 g, 1.7 mmol) was added as a solution in CH2Cl2 (60 mL). The reaction mixture was stirred for 30 min at −40 °C before being warmed to 24 °C over 1.5 h. The reaction mixture was diluted with saturated aqueous Na2S2O3 (200 mL) and extracted with CH2Cl2 (300 mL). The combined organic phases were washed with H2O (100 mL) and saturated aqueous NaCl (100 mL), dried over MgSO4, and concentrated on a rotary evaporator. The crude solid was dissolved in a minimum amount of CH2Cl2, filtered over a short pad of SiO2, and precipitated by trituration with MeOH, yielding 5 (0.971 g, 1.17 mmol, 68%) as a yellow solid. 1H NMR (600 MHz, CD2Cl2) δ = 8.19 (d, J = 8.0 Hz, 2H), 7.55 (d, J = 8.0 Hz, 2H), 7.51–7.47 (m, 3H), 7.30–7.29 (m, 6H), 7.14–7.13 (m, 4H), 6.96 (dd, J = 8.0 Hz, J = 2.0 Hz, 2H), 6.76 (d, J = 2.0 Hz, 2H), 3.23 (s, 6H), 1.37 (s, 3H) ppm; 13C{1H} NMR (151 MHz, CD2Cl2) δ = 157.1, 148.8, 144.9, 141.7, 135.2, 134.1, 133.5, 133.4, 132.4, 131.8, 131.4, 130.7, 130.0, 129.1, 128.4, 128.3, 127.9, 117.7, 111.7, 108.5, 55.5, 23.2 ppm; HRMS (ESI-TOF) m/z: [C43H30O2I2]+ calcd [C43H30O2I2] 832.0330; found 832.0331.

2,12-Dimethoxy-7-methyl-6,8,14-triphenylbenzo[m]tetraphene (6)

A 500 mL Schlenk flask was charged under N2 with 5 (0.95 g, 1.14 mmol) in dry THF (120 mL). The reaction mixture was cooled to −78 °C and stirred for 20 min. s-BuLi (16.3 mL, 22.8 mmol, 1.4 M in cyclohexane) was added dropwise, and the reaction mixture was stirred for 5 min at −78 °C. The reaction mixture was quenched by rapid addition of MeOH (10 mL). The reaction mixture was concentrated on a rotary evaporator, diluted with H2O (200 mL), and extracted with CH2Cl2 (300 mL). The combined organic phases were washed with H2O (100 mL) and saturated aqueous NaCl (100 mL), dried over MgSO4, and concentrated on a rotary evaporator. The crude solid was dissolved in a minimum amount of CH2Cl2, filtered over a short pad of SiO2, and concentrated on a rotary evaporator. The crude solid was sonicated in a minimum amount of pentane, filtered, and washed with a minimum amount of pentane, yielding 6 (0.450 g, 0.77 mmol, 68%) as a yellow solid. 1H NMR (600 MHz, CD2Cl2) δ = 7.66 (d, J = 8.0 Hz, 2H), 7.60 (m, 2H), 7.55 (m, 2H), 7.50 (m, 3H), 7.31 (m, 8H), 7.26 (m, 2H), 6.96 (dd, J = 8.0 Hz, J = 2.0 Hz, 2H), 6.81 (d, J = 2.0 Hz, 2H), 3.24 (s, 6H), 1.78 (s, 3H) ppm; 13C{1H} NMR (151 MHz, CD2Cl2) δ = 156.5, 146.0, 145.8, 136.3, 134.7, 134.0, 132.7, 131.8, 131.4, 130.8, 130.5, 129.5, 129.1, 129.1, 128.8, 128.4, 127.7, 127.0, 117.1, 112.2, 55.3, 25.1 ppm; HRMS (ESI-TOF) m/z: [C43H32O2]+ calcd [C43H32O2] 580.2397; found 580.2389.

7-Methylene-6,8,14-triphenyl-7,14-dihydrobenzo[m]tetraphene-2,12-diol (7b)

A 100 mL Schlenk flask was charged under N2 with 6 (0.375 g, 0.65 mmol) in dry DMF (16 mL). NaSEt (0.540 g, 6.5 mmol) was added under N2 as a solid in one portion. The reaction mixture was stirred under N2 for 3 h at 153 °C. The reaction mixture was quenched with 1 M HCl, causing the crude product to precipitate. The crude solid was isolated by filtration and washed with 1 M HCl (50 mL) and H2O (100 mL). The crude solid was dissolved in a minimum amount of CH2Cl2 and precipitated by trituration with hexanes, yielding 7b (0.200 g, 0.36 mmol, 56%) as a colorless solid. 1H NMR (600 MHz, CD2Cl2) δ = 7.95 (d, J = 2.0 Hz, 2H), 7.81 (d, J = 8.0 Hz, 2H), 7.67 (s, 2H), 7.46 (m, 4H), 7.40–7.35 (m, 6H), 7.33–7.30 (m, 2H), 7.16 (dd, J = 8.0 Hz, J = 2.0 Hz, 2H), 7.07–7.02 (m, 3H), 6.74 (s, 1H), 5.55 (s, 2H), 4.89 (s, 2H) ppm; 13C{1H} NMR (151 MHz, CD2Cl2) δ = 155.0, 143.6, 143.1, 139.8, 136.4, 135.6, 134.7, 132.1, 131.4, 130.6 (2C), 128.8, 128.6, 128.5, 128.5, 127.0, 127.0, 125.8, 118.4, 106.9, 42.9 ppm; (ESI-TOF) m/z: [C41H27O2]+ calcd [C41H27O2] 551.2017; found 551.2009.

7-Methylene-6,8,14-triphenyl-7,14-dihydrobenzo[m]tetraphene-2,12-diyl bis(trifluoromethanesulfonate) (8b)

A 100 mL Schlenk flask was charged under N2 with 7b (0.190 g, 0.34 mmol) in dry CH2Cl2 (34 mL). The reaction mixture was cooled to 0 °C. Et3N (0.425 g, 4.2 mmol) was added dropwise under N2, and the reaction mixture was stirred at 0 °C for 15 min. Trifluoromethanesulfonic anhydride (0.593 g, 2.1 mmol) was added dropwise under N2. The reaction mixture was warmed to 24 °C and stirred for 1.5 h at 24 °C. The reaction mixture was concentrated on a rotary evaporator. The crude solid was dissolved in a minimum amount of 1:1 hexanes/CH2Cl2, filtered over a short pad of SiO2, and concentrated on a rotary evaporator, yielding 8b (0.277 g, 0.34 mmol, 99%) as a colorless solid. 1H NMR (600 MHz, CD2Cl2) δ = 8.50 (d, J = 2.0 Hz, 2H), 8.01 (d, J = 8.0 Hz, 2H), 7.84 (s, 2H), 7.49–7.36 (m, 14H), 7.13–7.06 (m, 3H), 6.70 (s, 1H), 5.04 (s, 2H) ppm; 13C{1H} NMR (151 MHz, CD2Cl2) δ = 148.8, 142.8, 142.2, 140.2, 138.9, 136.1, 132.3, 132.2, 130.9 (2C), 130.4, 129.3, 128.7, 128.6, 127.8, 127.6, 127.6, 120.6, 120.5, 118.5, 116.2, 43.9 ppm; (ESI-TOF) m/z: [C43H27O6F6S2] + calcd [C43H27O6F6S2] 817.1148; found 817.1152.

2,2′-(7-Methylene-6,8,14-triphenyl-7,14-dihydrobenzo[m]-tetraphene-2,12-diyl)bis(4,4,5,5-tetramethyl-1,3,2-dioxaborolane) (9b)

A 50 mL Schlenk flask was charged under N2 with 8b (0.130 g, 0.16 mmol), bis(pinacolato)diboron (0.254 g, 0.96 mmol), and KOAc (0.300 g, 2.88 mmol) in dry dioxane (15 mL). The reaction mixture was degassed by sparging with N2 for 20 min before [1,1′-bis(diphenylphosphino)-ferrocene]dichloropalladium(II) (0.013 g, 0.02 mmol) was added under N2. A reflux condenser was attached, and the reaction mixture was stirred under N2 for 18 h at 80 °C. The reaction mixture was concentrated on a rotary evaporator. Column chromatography (SiO2; CH2Cl2) yielded 9b (0.096 g, 0.12 mmol, 78%) as a colorless solid. 1H NMR (600 MHz, CD2Cl2) δ = 9.24 (s, 2H), 7.89–7.85 (m, 4H), 7.77 (s, 2H), 7.53 (d, J = 8.0 Hz, 4H), 7.43 (t, J = 8.0 Hz, 4H), 7.38–7.34 (m, 4H), 7.28 (s, 1H), 7.08–7.01 (m, 3H), 4.90 (s, 2H), 1.49 (s, 24H) ppm; 13C{1H} NMR (151 MHz, CD2Cl2) δ = 144.3, 143.1, 139.8, 139.6, 137.0, 135.0, 134.7, 132.7, 131.1, 130.7, 130.5, 130.2, 129.1, 128.6, 128.5, 128.4, 127.2, 126.8, 125.7, 84.6, 42.7, 25.5, 25.4 ppm; (ESI-TOF) m/z: [C53H51O4B2]+ calcd [C53H51O4B2] 773.3968; found 773.3961.

2,12-Dibromo-7-methylene-6,8,14-triphenyl-7,14-dihydrobenzo-[m]tetraphene (1b)

A 25 mL sealable Schlenk tube was charged under N2 with 9b (0.040 g, 0.05 mmol) and CuBr2 (0.070 g, 0.31 mmol) in THF (1 mL), MeOH (2 mL), and H2O (2 mL). The reaction mixture was degassed by sparging with N2 for 20 min. The reaction mixture was sealed under N2 and stirred for 18 h at 120 °C. The reaction mixture was concentrated on a rotary evaporator, diluted with H2O (10 mL), and extracted with CH2Cl2 (30 mL). The combined organic phases were washed with H2O (10 mL) and saturated aqueous NaCl (10 mL), dried over MgSO4, and concentrated on a rotary evaporator. Column chromatography (SiO2; 4:1 hexane/CH2Cl2) yielded 1b (0.034 g, 0.05 mmol, 96%) as a colorless solid. 1H NMR (600 MHz, CD2Cl2) δ = 8.78 (s, 2H), 7.79–7.73 (m, 4H), 7.63 (d, J = 8.0 Hz, 2H), 7.47–7.26 (m, 12H), 7.11–7.05 (m, 3H), 6.82 (s, 1H), 4.93 (s, 2H) ppm; 13C{1H} NMR (151 MHz, CD2Cl2) δ = 142.9, 142.6, 139.2, 139.1, 135.9, 135.1, 132.0, 131.7, 131.1, 130.8, 130.4, 130.1, 129.0, 128.6, 128.5, 127.4, 127.2, 126.8, 126.7, 121.7, 42.8 ppm; HRMS (EI-TOF) m/z: [C41H26Br2]+ calcd [C41H26Br2] 678.0381; found 678.0381.

5-oGNR Growth on Au(111) Surfaces

5-oGNRs were grown on Au(111)/mica films under UHV conditions. Atomically clean Au(111) surfaces were prepared through iterative Ar+ sputter/anneal cycles. A sub-monolayer coverage of 1b on atomically clean Au(111) was obtained by sublimation at crucible temperatures of 453–473 K using a Knudsen cell evaporator. After deposition, the surface temperature was slowly ramped (≤2 K min–1) to 453 K and held at this temperature for 15 min to induce the radical step-growth polymerization and then ramped slowly (≤2 K min–1) to 623 K and held there for 15 min to induce cyclodehydrogenation.

Scanning Tunneling Microscopy and Spectroscopy

All STM experiments were performed using a commercial OMICRON LT-STM operating at T = 4 K using PtIr STM tips. STM tips were optimized for STM using an automated tip conditioning program.42 dI/dV measurements were recorded with CO-functionalized STM tips using a lock-in amplifier with a modulation frequency of f = 455 Hz and a modulation amplitude of Vac = 11 mV. dI/dV point spectra were recorded under open feedback loop conditions. dI/dV maps were collected under constant height conditions. Peak positions in dI/dV point spectroscopy were determined by fitting the spectra with Lorentzian peaks. Each peak position is based on an average of ∼10 spectra collected on various GNRs with different tips, all of which were first calibrated to the Au(111) Shockley surface state.

Calculations

First-principles DFT calculations in the LDA and LSDA approximations were implemented using the Quantum Espresso package.43 We used Norm-conserving pseudopotentials with a 60 Ry energy cut-off and 0.005 Ry Gaussian broadening. To ensure the accuracy of our results, a sufficiently large vacuum region was included in the supercell calculation. All of the dangling bonds at the edge of the carbon skeleton were hydrogenated. The structures were first fully relaxed until all components of the force were smaller than 0.01 eV/Å.

Acknowledgments

This work was primarily funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), Materials Sciences and Engineering Division under contract DE-AC02-05-CH11231 (Nanomachine program KC1203) (molecular design, tight-binding studies, topological states analysis) and contract DE-SC0023105 (surface growth). Research was also supported by the Office of Naval Research under award N00014-19-1-2503 (STM characterization) and the National Science Foundation under grant nos. CHE-2203911 (STS analysis) and DMR-1926004 (DFT calculations). Part of this research program was generously supported by the Heising-Simons Faculty Fellows Program at UC Berkeley. STM instruments are supported in part by the Office of Naval Research under award N00014-20-1-2824. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility operated under Contract No. DE-AC02-05CH11231. Computational resources were also provided by the NSF TACC Frontera and NSF through ACCESS resources at the NICS (stampede2). E.C.H.W. acknowledges support from the Croucher Foundation through a Croucher Scholarship for Doctoral Study. We thank Dr. Hasan Çelik and the UC Berkeley NMR facility in the College of Chemistry (CoC-NMR) for assistance with spectroscopic characterization. Instruments in the CoC-NMR are supported in part by the National Institutes of Health (NIH) award no. S10OD024998.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.3c01576.

  • Experimental details, STM/BRSTM images, additional spectroscopic data on 5-oGNRs, calculations, and 1H and 13C NMR spectra for all compounds (PDF)

Author Contributions

All authors have given approval to the final version of the manuscript. R.D.M., A.D., and J.J. contributed equally.

The authors declare no competing financial interest.

Supplementary Material

ja3c01576_si_001.pdf (8.1MB, pdf)

References

  1. Son Y. W.; Cohen M. L.; Louie S. G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803 10.1103/PhysRevLett.97.216803. [DOI] [PubMed] [Google Scholar]
  2. Cai J. M.; Ruffieux P.; Jaafar R.; Bieri M.; Braun T.; Blankenburg S.; Muoth M.; Seitsonen A. P.; Saleh M.; Feng X. L.; Müllen K.; Fasel R. Atomically precise bottom-up fabrication of graphene nanoribbons. Nature 2010, 466, 470–473. 10.1038/nature09211. [DOI] [PubMed] [Google Scholar]
  3. Chen Y. C.; de Oteyza D. G.; Pedramrazi Z.; Chen C.; Fischer F. R.; Crommie M. F. Tuning the Band Gap of Graphene Nanoribbons Synthesized from Molecular Precursors. ACS Nano 2013, 7, 6123–6128. 10.1021/nn401948e. [DOI] [PubMed] [Google Scholar]
  4. Senkovskiy B. V.; Usachov D. Y.; Fedorov A. V.; Haberer D.; Ehlen N.; Fischer F. R.; Gruneis A. Finding the hidden valence band of N = 7 armchair graphene nanoribbons with angle-resolved photoemission spectroscopy. 2D Mater. 2018, 5, 035007 10.1088/2053-1583/aabb70. [DOI] [Google Scholar]
  5. Mishra S.; Catarina G.; Wu F. P.; Ortiz R.; Jacob D.; Eimre K.; Ma J.; Pignedoli C. A.; Feng X. L.; Ruffieux P.; Fernandez-Rossier J.; Fasel R. Observation of fractional edge excitations in nanographene spin chains. Nature 2021, 598, 287–292. 10.1038/s41586-021-03842-3. [DOI] [PubMed] [Google Scholar]
  6. Cao T.; Zhao F. Z.; Louie S. G. Topological Phases in Graphene Nanoribbons: Junction States, Spin Centers, and Quantum Spin Chains. Phys. Rev. Lett. 2017, 119, 076401 10.1103/PhysRevLett.119.076401. [DOI] [PubMed] [Google Scholar]
  7. Rizzo D. J.; Veber G.; Cao T.; Bronner C.; Chen T.; Zhao F. Z.; Rodriguez H.; Louie S. G.; Crommie M. F.; Fischer F. R. Topological band engineering of graphene nanoribbons. Nature 2018, 560, 204–208. 10.1038/s41586-018-0376-8. [DOI] [PubMed] [Google Scholar]
  8. Groning O.; Wang S. Y.; Yao X. L.; Pignedoli C. A.; Barin G. B.; Daniels C.; Cupo A.; Meunier V.; Feng X. L.; Narita A.; Mullen K.; Ruffieux P.; Fasel R. Engineering of robust topological quantum phases in graphene nanoribbons. Nature 2018, 560, 209–213. 10.1038/s41586-018-0375-9. [DOI] [PubMed] [Google Scholar]
  9. Jiang J.; Louie S. G. Topology Classification using Chiral Symmetry and Spin Correlations in Graphene Nanoribbons. Nano Lett. 2021, 21, 197–202. 10.1021/acs.nanolett.0c03503. [DOI] [PubMed] [Google Scholar]
  10. Yang L.; Park C.-H.; Son Y.-W.; Cohen M. L.; Louie S. G. Quasiparticle energies and band gaps in graphene nanoribbons. Phys. Rev. Lett. 2007, 99, 186801 10.1103/PhysRevLett.99.186801. [DOI] [PubMed] [Google Scholar]
  11. Ruffieux P.; Wang S. Y.; Yang B.; Sanchez-Sanchez C.; Liu J.; Dienel T.; Talirz L.; Shinde P.; Pignedoli C. A.; Passerone D.; Dumslaff T.; Feng X. L.; Mullen K.; Fasel R. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 2016, 531, 489–492. 10.1038/nature17151. [DOI] [PubMed] [Google Scholar]
  12. Blackwell R. E.; Zhao F. Z.; Brooks E.; Zhu J. M.; Piskun I.; Wang S. K.; Delgado A.; Lee Y. L.; Louie S. G.; Fischer F. R. Spin splitting of dopant edge state in magnetic zigzag graphene nanoribbons. Nature 2021, 600, 647–652. 10.1038/s41586-021-04201-y. [DOI] [PubMed] [Google Scholar]
  13. Wen E. C. H.; Jacobse P. H.; Jiang J.; Wang Z. Y.; McCurdy R. D.; Louie S. G.; Crommie M. F.; Fischer F. R. Magnetic Interactions in Substitutional Core-Doped Graphene Nanoribbons. J. Am. Chem. Soc. 2022, 144, 13696–13703. 10.1021/jacs.2c04432. [DOI] [PubMed] [Google Scholar]
  14. Wang W. L.; Yazyev O. V.; Meng S.; Kaxiras E. Topological Frustration in Graphene Nanoflakes: Magnetic Order and Spin Logic Devices. Phys. Rev. Lett. 2009, 102, 157201 10.1103/PhysRevLett.102.157201. [DOI] [PubMed] [Google Scholar]
  15. Voit J. One-Dimensional Fermi Liquids. Rep. Prog. Phys. 1995, 58, 977–1116. 10.1088/0034-4885/58/9/002. [DOI] [Google Scholar]
  16. Bockrath M.; Cobden D. H.; Lu J.; Rinzler A. G.; Smalley R. E.; Balents L.; McEuen P. L. Luttinger-liquid behaviour in carbon nanotubes. Nature 1999, 397, 598–601. 10.1038/17569. [DOI] [Google Scholar]
  17. Mastropietro V.; Mattis D. C.. Luttinger model: the first 50 years and some new directions; World Scientific: New Jersey; London; Singapore; Beijing; Shanghai; Hong Kong; Taipei; Chennai, 2014; p xiii, 297 pages. [Google Scholar]
  18. Wang S.; Zhao S. H.; Shi Z. W.; Wu F. Q.; Zhao Z. Y.; Jiang L. L.; Watanabe K.; Taniguchi T.; Zettl A.; Zhou C. W.; Wang F. Nonlinear Luttinger liquid plasmons in semiconducting single-walled carbon nanotubes. Nat. Mater. 2020, 19, 986–991. 10.1038/s41563-020-0652-5. [DOI] [PubMed] [Google Scholar]
  19. Goni A. R.; Pinczuk A.; Weiner J. S.; Calleja J. M.; Dennis B. S.; Pfeiffer L. N.; West K. W. One-Dimensional Plasmon Dispersion and Dispersionless Intersubband Excitations in Gaas Quantum Wires. Phys. Rev. Lett. 1991, 67, 3298–3301. 10.1103/PhysRevLett.67.3298. [DOI] [PubMed] [Google Scholar]
  20. Lin M. F.; Shung K. W. K. Plasmons and Optical-Properties of Carbon Nanotubes. Phys. Rev. B 1994, 50, 17744–17747. 10.1103/PhysRevB.50.17744. [DOI] [PubMed] [Google Scholar]
  21. Kataura H.; Kumazawa Y.; Maniwa Y.; Umezu I.; Suzuki S.; Ohtsuka Y.; Achiba Y. Optical properties of single-wall carbon nanotubes. Synth. Met. 1999, 103, 2555–2558. 10.1016/S0379-6779(98)00278-1. [DOI] [Google Scholar]
  22. Fei Z.; Goldflam M. D.; Wu J. S.; Dai S.; Wagner M.; McLeod A. S.; Liu M. K.; Post K. W.; Zhu S.; Janssen G. C. A. M.; Fogler M. M.; Basov D. N. Edge and Surface Plasmons in Graphene Nanoribbons. Nano Lett. 2015, 15, 8271–8276. 10.1021/acs.nanolett.5b03834. [DOI] [PubMed] [Google Scholar]
  23. Monceau P.; Ong N. P.; Portis A. M.; Meerschaut A.; Rouxel J. Electric-Field Breakdown of Charge-Density Wave-Induced Anomalies in NbSe3. Phys. Rev. Lett. 1976, 37, 602–606. 10.1103/PhysRevLett.37.602. [DOI] [Google Scholar]
  24. Gruner G.; Zawadowski A.; Chaikin P. M. Non-Linear Conductivity and Noise Due to Charge-Density-Wave Depinning in NbSe3. Phys. Rev. Lett. 1981, 46, 511–515. 10.1103/PhysRevLett.46.511. [DOI] [Google Scholar]
  25. Brazovskii S.; Brun C.; Wang Z. Z.; Monceau P. Scanning-Tunneling Microscope Imaging of Single-Electron Solitons in a Material with Incommensurate Charge-Density Waves. Phys. Rev. Lett. 2012, 108, 096801 10.1103/PhysRevLett.108.096801. [DOI] [PubMed] [Google Scholar]
  26. Xie H.; Gao J. H.; Han D. Z. Excited spin density waves in zigzag graphene nanoribbons. New J. Phys. 2018, 20, 013035 10.1088/1367-2630/aa9fa0. [DOI] [Google Scholar]
  27. Little W. A. Possibility of Synthesizing Organic Superconductor. Phys. Rev. 1964, 134, 1416–1424. 10.1103/PhysRev.134.A1416. [DOI] [Google Scholar]
  28. Little W. A. Superconductivity of Organic Polymers. J. Polym. Sci., Part C: Polym. Sym. 1967, 3–12. 10.1002/polc.5070170103. [DOI] [Google Scholar]
  29. Tang Z. K.; Zhang L. Y.; Wang N.; Zhang X. X.; Wen G. H.; Li G. D.; Wang J. N.; Chan C. T.; Sheng P. Superconductivity in 4 angstrom single-walled carbon nanotubes. Science 2001, 292, 2462–2465. 10.1126/science.1060470. [DOI] [PubMed] [Google Scholar]
  30. Takesue I.; Haruyama J.; Murata N.; Chiashi S.; Maruyama S.; Sugai T.; Shinohara H. Superconductivity in entirely end-bonded multi-walled carbon nanotubes. Phys. C 2007, 460, 111–115. 10.1016/j.physc.2007.03.286. [DOI] [PubMed] [Google Scholar]
  31. Rizzo D. J.; Veber G.; Jiang J.; McCurdy R.; Cao T.; Bronner C.; Chen T.; Louie S. G.; Fischer F. R.; Crommie M. F. Inducing metallicity in graphene nanoribbons via zero-mode superlattices. Science 2020, 369, 1597–1603. 10.1126/science.aay3588. [DOI] [PubMed] [Google Scholar]
  32. Sun Q.; Yao X. L.; Groning O.; Eimre K.; Pignedoli C. A.; Mullen K.; Narita A.; Fasel R.; Ruffieux P. Coupled Spin States in Armchair Graphene Nanoribbons with Asymmetric Zigzag Edge Extensions. Nano Lett. 2020, 20, 6429–6436. 10.1021/acs.nanolett.0c02077. [DOI] [PubMed] [Google Scholar]
  33. Lieb E. H. Two Theorems on the Hubbard-Model. Phys. Rev. Lett. 1989, 62, 1201–1204. 10.1103/PhysRevLett.62.1201. [DOI] [PubMed] [Google Scholar]
  34. Su W. P.; Schrieffer J. R.; Heeger A. J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698–1701. 10.1103/PhysRevLett.42.1698. [DOI] [Google Scholar]
  35. Su W. P.; Schrieffer J. R.; Heeger A. J. Soliton Excitations in Polyacetylene. Phys. Rev. B 1980, 22, 2099–2111. 10.1103/PhysRevB.22.2099. [DOI] [Google Scholar]
  36. Kundu R. Tight-Binding Parameters for Graphene. Mod. Phys. Lett. B 2011, 25, 163–173. 10.1142/S0217984911025663. [DOI] [Google Scholar]
  37. Fang J. T.; Chen S. M.; Vandenberghe W. G.; Fischetti M. V. Theoretical Study of Ballistic Transport in Silicon Nanowire and Graphene Nanoribbon Field-Effect Transistors Using Empirical Pseudopotentials. IEEE Trans. Electron. Dev. 2017, 64, 2758–2764. 10.1109/TED.2017.2695960. [DOI] [Google Scholar]
  38. Hills G.; Lau C.; Wright A.; Fuller S.; Bishop M. D.; Srimani T.; Kanhaiya P.; Ho R.; Amer A.; Stein Y.; Murphy D.; Arvind; Chandrakasan A.; Shulaker M. M. Modern microprocessor built from complementary carbon nanotube transistors. Nature 2019, 572, 595–602. 10.1038/s41586-019-1493-8. [DOI] [PubMed] [Google Scholar]
  39. Liu X. L.; Hersam M. C. 2D materials for quantum information science. Nat. Rev. Mater. 2019, 4, 669–684. 10.1038/s41578-019-0136-x. [DOI] [Google Scholar]
  40. Wasielewski M. R.; Forbes M. D. E.; Frank N. L.; Kowalski K.; Scholes G. D.; Yuen-Zhou J.; Baldo M. A.; Freedman D. E.; Goldsmith R. H.; Goodson T.; Kirk M. L.; McCusker J. K.; Ogilvie J. P.; Shultz D. A.; Stoll S.; Whaley K. B. Exploiting chemistry and molecular systems for quantum information science. Nat. Rev. Chem. 2020, 490–504. 10.1038/s41570-020-0200-5. [DOI] [PubMed] [Google Scholar]
  41. CrysAlisPro, 1.171.40.82a, 1.171.41.116a; Oxford Diffraction/Agilent Technologies UK Ltd.: Oxford, UK, 2015. [Google Scholar]
  42. Wang S. K.; Zhu J. M.; Blackwell R.; Fischer F. R. Automated Tip Conditioning for Scanning Tunneling Spectroscopy. J. Phys. Chem. A 2021, 125, 1384–1390. 10.1021/acs.jpca.0c10731. [DOI] [PubMed] [Google Scholar]
  43. Giannozzi P.; Baroni S.; Bonini N.; Calandra M.; Car R.; Cavazzoni C.; Ceresoli D.; Chiarotti G. L.; Cococcioni M.; Dabo I.; Dal Corso A.; de Gironcoli S.; Fabris S.; Fratesi G.; Gebauer R.; Gerstmann U.; Gougoussis C.; Kokalj A.; Lazzeri M.; Martin-Samos L.; Marzari N.; Mauri F.; Mazzarello R.; Paolini S.; Pasquarello A.; Paulatto L.; Sbraccia C.; Scandolo S.; Sclauzero G.; Seitsonen A. P.; Smogunov A.; Umari P.; Wentzcovitch R. M. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 2009, 21, 395502 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja3c01576_si_001.pdf (8.1MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES