Abstract
Heat transfer takes place in every aspect of our daily life. Many situations, such as energy conversion plants, heating devices, and cooling systems, focus on heat transfer. One of the subjects in heat transfer is the boundary layer of the laminar flow problem. Well-known exploratory algorithms are used to solve for the flow on a flat plate in this study. The algorithms used are genetic algorithm (GA), particle swarm optimization (PSO), simulated annealing (SA), ant colony optimization for continuous domains (ACOR), artificial bee colony (ABC), and firefly algorithm (FA). The three properties, the layer thickness of the laminar boundary, heat flux, and the distance of the leading edge, are optimized. Each property is determined in three conditions; minimum, maximum, and target. The results showed that PSO, SA, ABC, and FA algorithms were more suitable than GA and ACOR algorithms. It has also been determined that the processing times are long in the FA and SA algorithms. The findings show that heuristic algorithms can find global results or results close to global results in heat transfer problems.
Keywords: Particle swarm optimization, Artificial bee colony, Heat transfer, Flat plate, Optimization, Laminar boundary layers
1. Introduction
Heat transfer is the local displacement of energy due to temperature differences. Heat transfer, which is also a sub-branch of thermodynamics, appears in many places in our daily life. Many events, such as heating the indoor environments using radiators in winter, keeping the tea temperature in the thermos, using heaters used in the open areas of cafes or restaurants, and increasing the daytime temperature by the sun, can be considered examples of heat transfer. Heat transfer has become essential in today's climate conditions with global warming [1]. In recent years, intensive studies have been carried out on heat transfer, aiming to use energy more efficiently. The materials, approaches, and geometric models used here have gained importance.
Heat transfer can occur in three ways. These are convection, conduction, and radiation. Heat conduction is applied in the processor's radiators, building insulation, or heatsink. The fan on the CPU cooler is an example of heat transfer. Conversely, the best example of heat radiation is sun rays.
Thermal insulation materials involved in heat convection are used in many areas in practice [1]. They are used in pipe ducts, cylindrical surfaced heat exchangers in coolers, chemistry, power plants, steam, and hot water pipelines, to prevent heat loss in furnaces [2]. Heat convection is not only used for insulation purposes but also heat transmission, ensuring the lowest energy loss. Transferring the stove's heat fired in the room to the environment with a chimney, heating the environment with radiators, and taking the heat over the processor using coolers are also examples of heat convection. Heat convection aims transfer heat to another environment quickly and ensure that heat is kept in place located with minimal loss. The two situations mentioned vary according to the properties of the materials.
Various studies have been conducted to solve heat transfer problems using optimization techniques. In one of these studies, conducted by Li and Chow [3], cost and efficiency analysis is studied. This research compares two methods against freezing water pipes in regions under cold weather conditions: pipe insulation and electrical heating. The lowest possible value of the tube walls is analyzed. The authors also studied determining the appropriate insulation thickness when selecting the insulation material [1]. The thermal economic analysis of pipes insulated using different composite materials was studied by Zaki and Al-Turki [4]. In the study, in which a nonlinear external cost function is used, annual energy loss and insulation investment costs are taken as a basis. A set of different thicknesses of insulating materials are used for inequality restrictions. Furthermore, the outside surface temperature of the insulating material is considered for safety [2]. The Hook and Jeeves search method determines the lowest yearly cost under boundary conditions with optimum thickness. Also, a comparison of the calculation results with the optimum insulation is made, and it is stated that the cost decreased significantly [2]. Ozdemir and Parmaksizoglu [5] tried to find the hot water installation's optimum pipe and duct insulation thicknesses. They compared the results with regulations and standards [5]. To maximize heat flux under laminar refrigerant stream conditions, Fabbi modified the side profile of the longitudinal fins in the circular channels [1]. A finite element model is used in the study to determine the velocity and temperature distributions on the circular channel section, and a global heat transfer coefficient is derived. For the wings, a polynomial lateral profile is studied. The blade geometry is adjusted at a specific amount of material and a given hydraulic resistance to allow the best heat transmission. Finally, optimal wing profiles produced using a genetic algorithm for various scenarios are demonstrated [3]. Joe and Karava [6] showed optimization of the hydronic radiant floor systems of the workplace using predictive control. They prepared a grey-box model with a state-space condition for building and solved the optimization problem using the mathematical framework [6]. In the study conducted by Tuncer [7], a model is proposed to optimize the building insulation material thickness for heating and cooling. The total annual insulation cost minimization determines the optimum insulation thickness. The model is determined using various materials and regions [7]. Gunal et al. [8] determined insulation parameters and optimized them [9]. In Siavashi et al. [10], particle swarm optimization (PSO) was used to find the optimal condition of multi-layered foams in a heat exchanger. Gunal et al. [11] used several optimization algoritmhs over a plate. Sathish and Mohanavel [12] found the results of porous insert configurations for heat transfer using computational fluid dynamics, and they used the inertia weight firefly algorithm to optimize optimum porosity distributions. Hetmaniok et al. [13] presented a numerical solution to the reverse heat conduction problem using ant colony optimization. Other studies use artificial intelligence tools such as least squares support vector machine (LSVM), adaptive neuro-fuzzy inference systems (ANFIS), and artificial neural networks (ANN) [14]. In Ref. [14], the models were used to predict the Nusselt number for heat transfer performance of carbon nanotubes and water nanofluid flows. Li et al. [15] evaluated the heat transfer of a micro heat exchanger cooling in an experimental setup. Uncertainty was found using measurements and calculations of equations. In Hassanpour et al. [16], neural network types, multi-layer perceptron, radial basis function, general regression, and cascade feedforward were used to estimate the heat transfer coefficient in water-based nanofluids. They compared experimental results with estimations, and models showed exceptional estimations. In addition to the research described above, there are several studies concerning heat flux optimization [[17], [18], [19], [20], [21]]. In heat transfer, numerical optimization solutions and optimization approaches are significantly utilized. Regarding the study topic, research on laminar flow issues is mostly theoretical.
Additionally, there are several studies on different topics for optimization algorithms. The genetic algorithm expedited the polarity mining process in natural language processing. A hybrid genetic algorithm and ontology-based 3-tier natural language processing framework were developed [22]. Another example of the use optimization algorithm is forecasting. PSO, ABC, and genetic algorithm (GA) were used to optimize the parameters of the neural network while modeling forecast intraday stock prices [23]. PSO and ABC-optimized models were the best models according to parameter estimations. Query optimization is another topic that GA was used to analyze decision support system (DSS) queries [24]. GA approaches were compared using runtime, quality of solution, and total cost. Another study used PSO, GA, and ACO algorithms to optimize wind farm layouts with 25 scenarios [25]. Finding a suitable turbine layout with maximum efficiency is a complex problem. In Ref. [26], the exploitation of gene selection is obtained with ABC and exploration with GA. The proposed algorithm in the study applied six gene expression datasets. Erdogmus [27] solved nonlinear equation systems with the help of grey wolf optimization (GWO). GWO, PSO, and GA algorithms were used for seven problems. In two cases, PSO, ABC, and ACOR were used to determine damages for large-scale spatial trusses [28]. They changed vibrations, and their responses and the goal function were selected as natural frequency and modal assurance criteria [29,30]. Given different subjects, it is also presaged that optimization algorithms will be used in psychiatric disorder diagnosis in the future [31]. In 2022, metaheuristic techniques that are swarm intelligence-based were reviewed. It is expressed that these methods were widely used in wireless sensor networks, disease diagnosis, image segmentation, weather forecasting, optimal power flow, air pollution forecasting, drug design, transport, and routing [32].
Literature studies have shown that optimization algorithms are used in different subjects for which it is challenging to find a global solution. Optimization algorithms have been applied in a wide area, from biology to medicine, from decision support systems to language processing solutions, and from engineering problems to solutions of mathematical problems. The authors studied recent metaheuristic algorithms in previous studies [9]. However, well-known optimization algorithms are not applied in solving the laminar flow problem in heat transfer. Objectives of the study are as follows.
-
-
The results will show the usability of well-known optimization algorithms in laminar flow layer problems.
-
-
The reproducibility of the results was tested by running the same algorithms ten times again.
The most suitable one of the six optimization algorithms was determined with a detailed evaluation of the results obtained.
This research uses well-known optimization algorithms to solve a heat transfer problem. Various parameters of the laminar flow problem are investigated, and the results are evaluated.
The boundary layer thickness is evaluated for conditions where.
-
-
the airflow characteristics are constant, and the radiation is ignored,
-
-
the plate and air temperatures are constant on the plate.
The study's primary goal is to demonstrate the applicability of the heuristic algorithms in heat flux problems that require optimization.
The following part of the study gives definitions and information about basic optimization and optimization algorithms. In the third section, laminar boundary layer modeling for thermal flow over a flat plate, an example, and the model flow diagram are explained. The fourth section gives the results by repeating the problems ten times with six different algorithms with the same features, average, and error percentages. In the fifth section, the conclusion is given, along with the evaluation of results and recommendations.
2. Mathematical backgrounds
2.1. Optimization
Optimization is finding the largest and smallest values of an objective function under certain constraints [33]. It chooses the most appropriate one within the desired framework (constraint) from the results obtained from the problem. Since it is difficult or even impossible to solve problems with many unknowns and constraints by derivatives, the importance of optimization algorithms that usually give the objective function value in a suitable or close to the mathematical result has increased. Optimization is not always that simple. E.g., If land needs to be selected for a factory, criteria such as land unit price, transportation alternatives, proximity to raw materials, proximity to the market, and personnel alternatives affect the selection. Criteria prioritization must be done, and the most suitable ones must be determined. After that, the best choice, in other words, the optimum choice, can be made. A solution is an optimal solution only if it satisfies all constraints. People unconsciously optimize many of the choices in their lives that begin with birth and continue.
The reasons, why optimization is popular in the literature are as follows.
-
-
Ease of implementation and success;
-
-
Does not require gradient (derivative) knowledge;
-
-
Ability to skip local minimum and maximum points;
-
-
It applies to a wide range of issues and addresses many problems [33].
2.2. Optimization algorithms
There are various algorithms in optimization. The literature divides optimization algorithms into stochastic and deterministic [34]. Deterministic methods consist of two parts computational methods and gradient methods. Computational methods do not need slope information. It is a time consuming and costly method. Gradient-based methods implement the slope as an objective function. With deterministic methods, it is difficult or even impossible to solve high-dimensional problems with no slope [34].
On the other hand, heuristic algorithms aim to find the optimum solution with a certain number of random solutions, improvement, and iteration steps. Metaheuristic means more heuristic. Heuristic methods aim to scan the search area dynamically and iteratively. These methods do not always ensure finding a global solution [35], but they are pretty helpful. The main reason is that they can effectively solve large-scale and complex problems [35]. In optimization, exploration is the global search capacity, and exploitation is the local search capacity around the optimal solution. The main difference between the developed algorithms lies in balancing the exploitation and exploration approach [34]. While heuristic optimization algorithms give results in a specific neighborhood to the desired result, deterministic (non-heuristic) optimization algorithms give precise results. Information about the optimization methods applied in the study is provided in this section.
2.2.1. Particle swarm optimization algorithm (PSO)
The particle swarm optimization (PSO) algorithm is developed to mimicking swarm intelligence. It is used in engineering optimization problems [36,37]. In the algorithm, the herd members move within their region to communicate and update others about events such as danger or food. Here, the structure is created by the particle merger (moving together), where particles are called a swarm [38]. Each particle has a specific location and speed. The particle's new location consists of a vectorial combination of certain parts of the particle velocity, the swarm's best position vector, and its global best vector. The length of the vectors to be used is obtained by multiplying the vectors by the randomly generated number [39]. The combination of these three vectors always approximates the global best. It is checked whether the position found in each iteration is more suitable for the target function. Whether the output is better than the best of the swarm is determined by comparing it with the global best.
The algorithm includes the following steps [40].
-
1)
An initial swarm is created with randomly generated initial positions and speeds.
-
2)
Whether all the particles in the swarm are within limits and the objective function values are calculated.
-
3)
The local best value for the current cycle is found for each particle.
-
4)
The global best is selected from the local best.
-
5)
Positions and velocities are updated using Equation (1) and Equation (2).
| (1) |
| (2) |
In both equations, is the location, is the speed, and values are randomly generated numbers. Inertia weight in the equation is w and , are scaling values. Until the maximum cycle is reached, 2,3,4, and 5 steps are repeated [40].
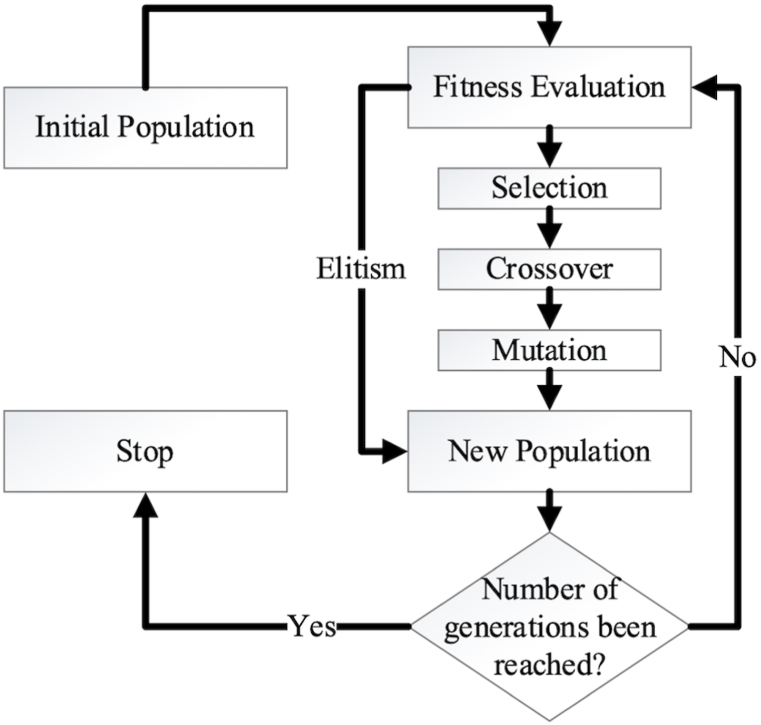
2.2.2. Genetic algorithm (GA)
A search and optimization technique called the Genetic Algorithm (GA) uses Darwin's theory of evolution and natural selection [41,42]. It is used in engineering optimization problems [36,43]. This method was first introduced by John Holland et al. Biological background and expressions in genetic processes are listed below (Fig. 1).
-
-
The smallest structure is called a gene. They are the building blocks of the elements that make up the gene chromosomes (sequences) in the specified intervals.
-
-
Chromosome (Individual) is the sequence formed by more than one gene coming together. Each of the chromosomes is a candidate solution.
-
-
The structure formed by the chromosomes is called the population. Population fitness is found by applying maximization or minimization processes according to the determined constraints. Natural selection transfers the sequences whose fitness value is above the determined average to the next generation, thus creating better generations [42].
-
-
Crossover is the formation of two new chromosomes by replacing the pre- and post-parts of a randomly selected place from two chromosomes [44]. In this way, it helps to approach the best by facilitating the coexistence of chromosomes with good characteristics [42].
-
-
In creating a new generation, the generations begin to repeat themselves after a certain period of time, and mutation is done to prevent this. The mutation ensures population diversity and avoids sticking to local outcomes [44].
Fig. 1.
Genetic algorithm flow diagram.
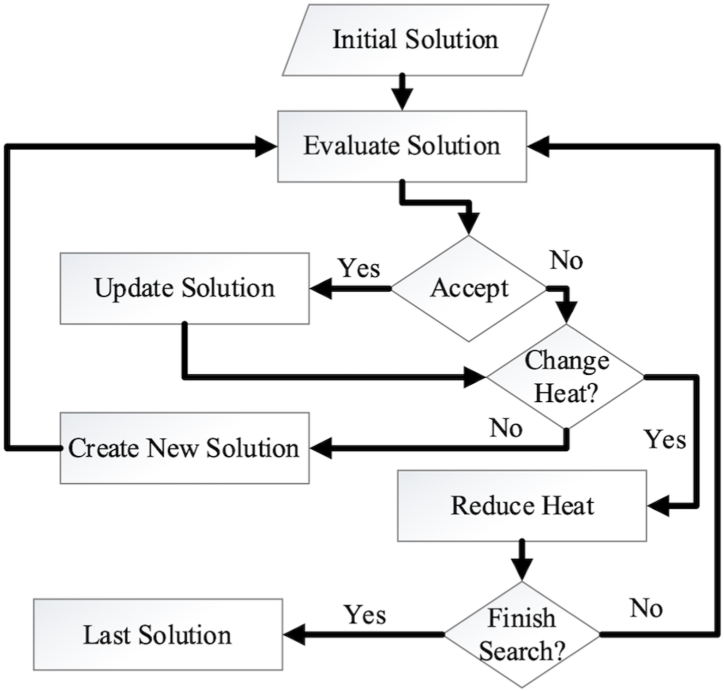
2.2.3. Simulated annealing (SA)
One optimization technique that simulates hot metal cooling is simulated annealing (SA) [45]. Metropolis et al. developed the annealing simulation design for solid metals. It is used in engineering optimization problems [[46], [47], [48]]. Rao [49] altered the Metropolis method for optimization operations. The annealing simulation steps are as follows.
-
-
Annealing is the process of heating the metal for a certain time (according to its properties) and cooling it slowly. It is the general name of the heat treatment carried out to soften the metal and make it useful.
-
-
Heat treatment is the process of reducing the temperature of the metal after raising it to a maximum determined degree.
Boltzmann's probability distribution is used while making solutions (Equation (3)). The function that gives the acceptance probability of a lambda change in the objective function is called the acceptance function [45]. The acceptance of the motion in the neighborhood is determined randomly. In this equation, P is the probability, lambda (Δ) is the difference between the neighboring and the current solution, and T is the temperature.
| (3) |
Fig. 2 shows the process diagram of the annealing simulation algorithm. There are various decisions of the algorithm [45]. These decisions determine the starting temperature, the temperature change values, the number of cycles to be performed at each temperature, and the stopping criterion.
Fig. 2.
The flow diagram of the annealing simulation.
2.2.4. Ant colony optimization for continuous domains (ACOR)
ACOR algorithm is used in many engineering problems [50,51]. The continuous domains optimization problem was solved using ant colony optimization in Socha and Dorigo [52]. The authors developed the ACOR algorithm, which is based on the ant colony algorithm, without any modifications. The model is built on the ant's food-seeking behavior. The ACOR flowchart is shown by Chen et al. [53].
The steps of the algorithm.
-
-
Population and appropriate parameters are created.
-
-
The problem size and the number of generations are defined.
-
-
Random routes are generated for weight matrix generation and selection probabilities.
-
-
Pheromones are updated. Weight matrices are created for each ant's route.
-
-
The selection possibilities for each are updated. The best solutions are taken.
-
-
The most appropriate Tau (τ) value is updated.
-
-
Function results are compared. If the value found is better, the objective function is updated.
-
-
According to the problem, a global minimum or global maximum is obtained as a result of an iteration.
2.2.5. Artificial bee colony (ABC)
Another optimization technique is the Artificial bee colony (ABC), developed by mimicking bee behaviors by Karaboga and Basturk [54]. It has several usages in optimization [[55], [56], [57]]. The colony has three kinds of bees.
-
-
Workers: They carry the food from the source to the hive.
-
-
Scouts: They look for food by hovering randomly.
-
-
Onlookers: The number of them is equal to employed bees.
Onlooker bees learn the location of food from dancing bees once scout bees find it. Onlooker bees select a source based on the incoming information. When the resources run out, the worker bee transforms into a scout bee, and scout bees search for new sources randomly.
Fig. 3 shows the flow diagram of the artificial bee colony algorithm. The steps are as follows.
-
1.
Creation of a food resource zone for a start.
-
2.
Directing the worker bees to the source, calculating the number of resources.
-
3.
Calculating probabilities for the selection of onlooker bees.
-
4.
Onlooker bees choose the source area according to the calculated probabilities.
-
5.
Separation from source criterion: number of onlooker and scout bees production.
-
6.
If not the Maximum cycle, go to Step 2.
Fig. 3.
The flow diagram of the artificial bee colony algorithm. Source: [54].
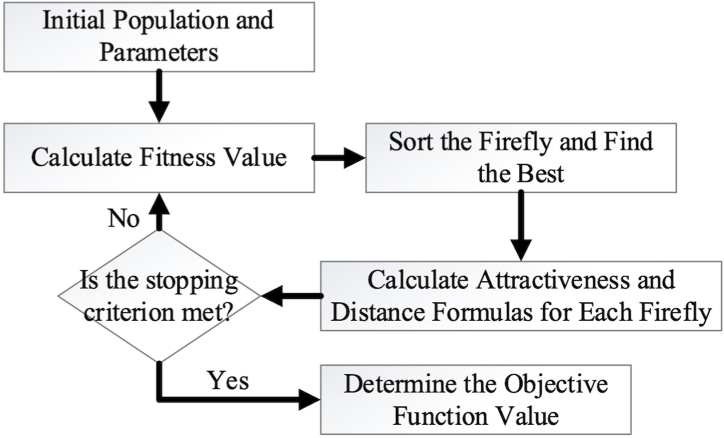
2.2.6. Firefly algorithm (FA)
The firefly algorithm (FA) implements the fireflies’ brightness logic developed by Yang [58,59]. It is used in engineering optimization problems [60,61]. The less bright fireflies tend to spread light similar to the bright fireflies in the swarm. The principles of the firefly algorithm are as follows.
-
-
They can affect each other by being considered genderless.
-
-
The brighter firefly appeals the less bright.
-
-
The objective function value determines being the brightest.
All fireflies have elements up to the specified size. The size is first randomly determined according to the constraints. The flowchart of the firefly algorithm is shown in Fig. 4.
Fig. 4.
Firefly algorithm flowchart.
2.3. Modeling
The region above a surface where the temperature varies noticeably in the direction perpendicular to the surface is referred to as the thermal boundary layer [62]. As the flow direction progresses parallelly, the thermal boundary layer thickness increase. Details of the modeling are given in Ref. [11]. This section applies optimization algorithms to calculate the thickness of the boundary layer for a steady-state laminar zone airflow with constant characteristics, no irradiation, and constant plate and air temperatures.
If the condition is satisfied, laminar flow occurs. The free flow velocity, the distance from the leading edge, and kinematic viscosity of the fluid are used to find Re number [62]. Reynold and Prandtl numbers are required to find Nusselt number [62]. Prandtl number is calculated using specific heat capacity, thermal conductivity, kinematic viscosity, and density [63]. Inside temperature and is the outside temperature are used to find heat transfer coefficient [62,63]. Thermal boundary layer thickness is calculated using Reynold number, and distance from the leading edge. At the end, hydrodynamic boundary layer thickness is found using thermal boundary layer thickness and Prandtl number. If is satisfied, the laminar flow changes to turbulent flow as shown in Fig. 5.
Fig. 5.
Heat flow model.
2.3.1. Linear flow sample problem
Assume air at 56.5 °C and under 1 bar pressure flow on a slab at 4.5 m/s velocity, 124.5 °C temperature, and 1 × 0.8 m length. In this problem.
-
a.
The average heat transfer coefficient of the plate and the local heat transfer coefficients at two different locations from the starting point of the plate.
-
b.
The summation of heat transfer amount from the plate to the air;
-
c.
The thickness of the thermal boundary layer and the velocity at the end of plate's are solved.
The solution can be found as follows [63]:
Firstly; Equations (4), (5)) are valid for flow on the plate
| (4) |
| (5) |
Using the information provided in Table 1 at 80 °C and 100 °C air, calculations are done. The following list states the problem's assumptions.
-
-
Regime is continuous.
-
-
Radiation is ignored.
-
-
The plate and air have constant properties and temperatures.
Table 1.
values at and temperature.
| Parameters | Units | Air at | Air at | 90.5 °C |
|---|---|---|---|---|
| Density | ||||
| Kinematic viscosity | ||||
| Thermal conductivity coefficient | ||||
| Air heat |
The average film temperature in the problem is as follows in Equation (6):
| (6) |
Table 1 variables are calculated using linear interpolation and given in the last column of the table. The Pr value is then determined as shown in Equation (7);
| (7) |
Equations (4), (5)) are used to calculate Re and Nu numbers to find the coefficient of heat transfer at and , in order to answer option a. Calculations of Re are given in Equations (8), (9)).
| (8) |
| (9) |
The first connection is found since the result of equations (8), (9)) is . In Equations (10), (11)), Nu value is calculated for x = 0.4 m. In Equations (12), (13)), the Nu value is calculated for x = 0.8 m.
| (10) |
| (11) |
And
| (12) |
| (13) |
Option a requires the , which is determined using Equation (14).
| (14) |
Option b requires the calculation of the amount of heat transfer coefficient from the plate to the air by convection, which is determined by Equation (15).
| (15) |
The result is obtained in equation (16), when h, A, and temperature values are replaced in the formula.
| (16) |
The solution of option c is given in Equations (17), (18)) for δ and δT at the plate end ( = 0.8 m), respectively;
| (17) |
| (18) |
The calculations found δ and δT at the end of the plate, which are 9.9 mm and 10.8 mm, respectively.
2.3.2. Laminar flow sample cases
The study addresses the critical thickness problem of the thermal boundary layer for laminar flow by optimizing scenarios, which are listed below.
-
1.
Objecting the thermal boundary layer thickness ().
-
2.
Objecting the heat flux (Q).
-
3.
Objecting the distance (x) from the edge.
The first scenario is shown as “Case 1”. The objective, in this case, is to ascertain the thermal boundary layer () maximum, minimum, and target (19.6 mm) thicknesses. The constraints of this scenario are the parameters Re () and Q (140 W ≤ Q ≤ 190 W). Additionally, x, which represents the proximity from the edge (0.2 m ≤ x ≤ 1 m), and T, which represents the temperature (80 °C ≤ T ≤ 130 °C), are the model's design variables. The design variables of x = 1 m, and T = 1 °C are optimization algorithms' starting values.
The second scenario is shown as “Case 2”. The objective, in this case, is to ascertain the maximum, minimum, and target (160.43 W) heat fluxes (Q). In the second scenario, the number of constraints is one, and the number of design variables is three. The constraint of this scenario is the parameter Re (). Additionally, x, which represents the proximity from the edge (0.2 m ≤ x ≤ 1 m), T, which represents the temperature (80 °C ≤ T ≤ 130 °C), and δt, which represents the thermal boundary layer thickness (0,01 mm≤ ≤20 mm), are the model's design variables. The design variables of x = 1 m, and T = 1 °C, = 1 mm are the optimization algorithms' starting values.
The third scenario is shown as “Case 3". The objective, in this case, is to ascertain the maximum, minimum, and target (0.61 m) distance (x) from the leading edge. The constraints of this scenario are the parameters Q (140 W ≤ Q ≤ 190 W) and δt (0,01 mm≤ ≤20 mm). Additionally, Re number (), and T, which represents the temperature (80 °C ≤ T ≤ 130 °C), are the model's design variables. The design variables of Rex = 1, and T = 1 °C are the initial states of the optimization algorithms.
In each of the three scenarios, six optimization methods are applied. All algorithms, ten random tests are run with 100 populations and 100 iterations, where the initialization parameters are the same.
In the random tests, the boundary layer thickness given in Equation (11) is the objective function of Case 1. Optimization techniques calculate , T, Q, and x values that allow the objective function to give the best outcome according to the chosen state (minimum-maximum-target value), and the optimum function (δt) value is discovered.
The heat flow given in Equation (10) is the objective function of Case 2 in the random tests. Optimization techniques calculate , T, , x values that allow the objective function to give the best outcome according to the chosen state (minimum-maximum-target value), and the optimum function (Q) value is discovered.
The objective function of Case 3 in the random tests is the distance from the edge (x), which is given in Equation (4). Equation (19) is the related formula of Equation (4), where ν is the kinematic viscosity of the fluid. Linear interpolation is used to find kinematic viscosity by applying Table 1 on Equation (20).
| (19) |
| (20) |
Optimization methods are used to calculate , T, and Q values to enable the best result to be created for a specific objective function cases (min-max-target value), and the optimum function value (x) is discovered.
3. Numerical results
Laminar heat flow is essential in heat transfer. This paper addresses the laminar flow problem using GA, PSO, SA, ACOR, ABC, and FA optimization techniques. Three scenarios are created for the problem. In Case 1, the boundary layer thickness's maximum, minimum, and target values are estimated. In an engineering problem, the boundary layer thickness is important because it indicates the thermal layer at a certain distance from the leading edge. In Case 2, the heat flow's maximum, minimum, and target values are estimated. Heat flux is another important variable. In the insulation problem, engineers require less heat flux. Computer hardware designers, on the contrary, want more heat transfer. Thus, the cooling on the hardware will be more. The distances from the laminar flow edge are estimated in maximum, minimum, and target values in Case 3. Another critical issue in heat flow is turbulence, which is generally undesirable. Therefore, in Case 3, the laminar region is maximum, minimum, and target value has been determined depending on other variables.
Three scenarios for three parameters are created to solve the problem and run ten times. Tests are run at considerable intervals to prevent bias from the cache. The software environment is MATLAB R2020a. This section presents the research results.
The optimization algorithms’ parameters are also important in obtaining the results. In the ABC algorithm, the colony size is 100, the abandonment limit parameter (Trial Limit) is 60, and the acceleration coefficient upper limit is 1. The ACOR algorithm takes a population size of 100, the sample size of 20, an intensification factor (selection pressure) of 0.5, and a deviation-distance ratio of 1. In the FA algorithm, the number of fireflies (swarm size) is taken as 100, gamma (light absorption coefficient) 1, beta (attraction coefficient base value) 2, alpha (mutation coefficient) 0.2, alpha damp (mutation coefficient dumping ratio) 0.98. In the GA algorithm, the crossover percentage is 100%, mutation 0.05, gamma 0.6, and sigma 0.1. The PSO algorithm takes the swarm size (population) as 100, inertia weight 1, inertia weight dumping ratio 0.99, personal learning coefficient 1.5, and global learning coefficient 2.0. The SA algorithm takes the population size as 100, the maximum number of sub-iterations as 2, the initial temperature as 0.5, the temperature reduction rate as 0.99, the number of neighbors per individual value as 5, and the mutation rate as 0.5. The number of iterations in all algorithms is 100.
3.1. Case 1 numerical results
In Case 1, optimization algorithms are used to determine the boundary layer thickness's maximum, minimum, and target values (Table 2). The region where the minimum thermal boundary layer was found close to each other in all six optimization algorithms (Tables 2a–7.07 mm). The x and T design variable values at which the boundary layer is determined are the same in all six optimization algorithms. Except for GA, all optimization algorithms gave the same result for Q and Re constraint values. It is seen that GA, which takes the different point as the optimum point in the constraint value, finds this point close to the optimum global point. The FA time is the highest in the processing times, while the lowest is in the GA. The maximum thermal boundary layer is determined to be the same in all cases except for ACOR, which yielded a value of 25.12 mm, as shown in Table 2b. In the same condition, although the Q value in GA is 0.15 W lower than the optimization algorithms other than ACOR, the Re number is slightly higher. While the ACOR algorithm found the value of 25.01 mm in 10 trials, Q, T, Re, and x values are quite similar in each trial. In the case where the thermal boundary layer is 19.6 mm as the target value (Table 2c), it is seen that all algorithms found the target value (Table 2c).
Table 2.
Case 1 optimization results. (a) δt Minimum value, (b) δt Maximum value, (c) δt Target value (19.6 mm).
| Test | x | T | Rex | δt | Q | Time(s) | Error |
|---|---|---|---|---|---|---|---|
| (a) | |||||||
| PSO | 0.08445 | 80.00000 | 3842.811 | 7.07210 | 190.00000 | 1.67490 | 0.000% |
| GA | 0.08499 | 80.00000 | 3867.200 | 7.09448 | 189.40385 | 1.35629 | 0.316% |
| SA | 0.08445 | 80.00000 | 3842.982 | 7.07233 | 189.99578 | 4.92237 | 0.003% |
| ACOR | 0.08445 | 80.00000 | 3842.811 | 7.07210 | 190.00000 | 4.39949 | 0.000% |
| ABC | 0.08445 | 80.00000 | 3842.821 | 7.07218 | 189.99984 | 1.68618 | 0.001% |
| FA |
0.08445 |
80.00000 |
3458.916 |
7.07210 |
189.99999 |
30.53532 |
0.000% |
| (b) | |||||||
| PSO | 1.00000 | 116.75120 | 41,347.866 | 25.12140 | 190.00000 | 1.64163 | 0.000% |
| GA | 1.00000 | 116.70901 | 41,352.204 | 25.12052 | 189.85007 | 4.51513 | 0.004% |
| SA | 1.00000 | 116.75081 | 41,347.907 | 25.12140 | 189.99868 | 5.06173 | 0.000% |
| ACOR | 0.89023 | 106.73642 | 37,723.299 | 25.40680 | 163.65026 | 5.39199 | 1.136% |
| ABC | 1.00000 | 116.75120 | 41,347.866 | 25.12140 | 190.00000 | 1.73180 | 0.000% |
| FA |
1.00000 |
116.74995 |
41,347.998 |
25.12140 |
189.99546 |
31.64163 |
0.000% |
| (c) | |||||||
| PSO | 0.62630 | 100.18815 | 27,009.626 | 19.60000 | 164.66976 | 1.54420 | 0.000% |
| GA | 0.62762 | 99.05883 | 27,145.582 | 19.60165 | 159.27969 | 4.52280 | 0.008% |
| SA | 0.62872 | 97.95012 | 24,559.568 | 19.60000 | 154.01459 | 4.97925 | 0.000% |
| ACOR | 0.62608 | 100.39927 | 21,528.209 | 19.60000 | 165.67466 | 4.08306 | 0.000% |
| ABC | 0.62650 | 99.72617 | 27,063.723 | 19.60002 | 162.47003 | 1.74641 | 0.000% |
| FA | 0.62465 | 101.71371 | 26,831.764 | 19.60000 | 171.93269 | 29.85310 | 0.000% |
It is observed that the design variables and constraints are different in all optimization algorithms. Among these three cases, the average processing time of FA is the highest, with 30 s. While the average minimum processing time is 1.62 s in the PSO algorithm, it is 1.72 s for ABC algorithms, which is very close to this value. In the remaining three algorithms, GA, SA, and ACOR, processing times average less than 5 s.
Convergence curves are prepared to visualize the training process of six algorithms (Fig. 6). The algorithms solutions were determined in the first 20 iterations in minimum (Fig. 6a) and maximum thicknesses (Fig. 6b). The target thickness solution was obtained in 25 iterations (Fig. 6c). There was fine-tuning in the subsequent iterations. Additional iterations did not affect the duration, and it was helpful to run it.
Fig. 6.
Plots of convergence curve for Case 1 (a) minimum, (b) maximum, (c) target values.
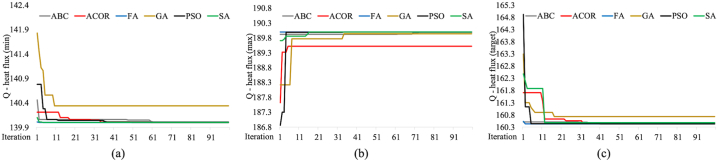
3.2. Case 2 numerical results
In Case 2, optimization algorithms are used to determine the heat flow's maximum, minimum, and target values (Table 3). The region where the maximum heat flow is found close to each other in all six optimization algorithms (Tables 3a–140 W). The values of the design variables x, T, and δt, used for heat flow, are different in all six optimization algorithms. The Re value is the highest in the FA algorithm, with 34,067.5, and the lowest in the ABC algorithm, with 18,866.9. Again, the T values of FA and ABC algorithms are very close and are found to be around 95 °C. When the experiments in all algorithms are examined in detail, it is seen that the design variables and constraints differ significantly from each other. In addition, the results of the design variables found by the six algorithms in the heat flow are different. Design variable results show that the solution space is large, with many close global results. In determining the case where the heat flow is maximum, the results are very close to each other and the same, except for ACOR (189.52 W) (Table 3b–∼190 W). In the same situation, the Re value is the lowest at 18,263.8 in GA, while it is the highest at 29,597.8 in ACOR. The highest T value is 103.32 °C in the ABC algorithm, and the lowest temperature is 94.05 °C in the SA algorithm. For the case where the thermal flow is 160.43 W as the target value (Table 3c), all algorithms found the target value. It has been observed that the design variables and constraints differ in all optimization algorithms. It is also observed that the constraints and design variables are different in all optimization techniques. In all scenarios, the average processing time of FA is the highest at 42.94 s. The average minimum processing time is 2 s in the ABC algorithm. In the PSO and GA algorithms, this value is 2.07 and 2.6 s, respectively, close to the ABC value. On average, the processing times for the remaining two algorithms, SA and ACOR, are less than 13 s.
Table 3.
Case 2 optimization results. (a) Q Minimum value, (b) Q Maximum value, (c) Q Target value (160.43 mm).
| Test | x | T | Rex | δt | Q | Time(s) | Error |
|---|---|---|---|---|---|---|---|
| (a) | |||||||
| PSO | 0.56209 | 88.23896 | 23,810.267 | 15.08936 | 140.00001 | 2.06804 | 0.000% |
| GA | 0.68403 | 91.57782 | 29,136.058 | 17.26953 | 140.34339 | 1.60931 | 0.245% |
| SA | 0.46223 | 87.68731 | 20,583.889 | 14.72154 | 140.00111 | 6.04936 | 0.001% |
| ACOR | 0.74587 | 88.15312 | 33,278.632 | 15.03215 | 140.00000 | 6.39504 | 0.000% |
| ABC | 0.42944 | 95.75970 | 18,866.932 | 15.17322 | 140.01345 | 2.03140 | 0.010% |
| FA |
0.49915 |
95.33843 |
34,067.453 |
19.82131 |
140.00000 |
42.63396 |
0.000% |
| (b) | |||||||
| PSO | 0.58691 | 96.09353 | 25,573.342 | 14.97603 | 189.99996 | 2.03954 | 0.000% |
| GA | 0.43280 | 99.53710 | 18,263.772 | 16.67329 | 189.93656 | 4.71640 | 0.033% |
| SA | 0.47139 | 94.05170 | 20,699.414 | 13.97348 | 189.99680 | 5.93625 | 0.002% |
| ACOR | 0.68237 | 97.19713 | 29,597.808 | 16.96797 | 189.51620 | 7.17532 | 0.255% |
| ABC | 0.48797 | 103.32119 | 20,964.783 | 16.24127 | 189.98741 | 1.96457 | 0.007% |
| FA |
0.57919 |
99.95795 |
23,111.229 |
16.87395 |
189.99954 |
42.97571 |
0.000% |
| (c) | |||||||
| PSO | 0.50773 | 95.82307 | 22,142.225 | 17.57906 | 160.43003 | 2.10864 | 0.000% |
| GA | 0.47429 | 93.84061 | 20,418.737 | 16.39765 | 160.72842 | 1.45927 | 0.186% |
| SA | 0.51949 | 92.58451 | 22,779.495 | 15.69151 | 160.47869 | 26.53560 | 0.030% |
| ACOR | 0.38726 | 95.12689 | 16,906.831 | 17.17410 | 160.43000 | 6.13038 | 0.000% |
| ABC | 0.64898 | 98.83050 | 28,231.721 | 15.99615 | 160.45468 | 2.00924 | 0.015% |
| FA | 0.49059 | 99.94421 | 10,050.855 | 19.97608 | 160.43001 | 43.21707 | 0.000% |
The convergence curves of the algorithms are shown in Fig. 7. Most of the algorithms determined the optimum solution in the first twelve iterations. ABC in determining minimum (Fig. 7a) and GA in determining maximum values (Fig. 7b) were higher than 60 iterations. FA found target heat flux in the third iteration (Fig. 7c), which is comparably faster than the other algorithms. There was fine-tuning in the subsequent iterations.
Fig. 7.
Plots of convergence curve for Case 2 (a) minimum, (b) maximum, (c) target values.
3.3. Case 3 numerical results
For the last scenario, Case 3, optimization algorithms were utilized to determine the maximum, minimum, and target values of the distance from the laminar flow edge, as shown in Table 4. The same result was found in the six optimization algorithms for the region where the flow distance from the edge is minimum (Tables 4a–0.08 m). The values of the design variables Re and T, in which the distance from the edge of the laminar flow is determined, are the same in all five optimization algorithms and are 3842 and 80 °C, respectively. In GA, the temperature value is 80 °C, the same as the other algorithms, while the Re number is determined as 4271. Except for GA, all algorithms produced the same result in Q (190 W) and δt (7.07 mm) constraints. In GA, Q, and δt values were 180.22 W and 7.46 mm, respectively. FA has the longest processing time, while GA has the shortest. The region where the maximum flow distance from the edge is the same in all five optimization algorithms (Tables 4b–1.23 m). This value is higher than the others in ACOR, as 1.25 m. Apart from ACOR, temperature, Re number, thermal boundary layer thickness, and heat flow are similar in other optimization algorithms. In ACOR, all constraints and design variables have lower values. For the case where the laminar flow edge distance is 0.61 m as the target value (Table 4c), all algorithms were able to determine the target value. T, Re, δt, and Q have the lowest values in the PSO algorithm. SA algorithm has the highest T, Q, and δt except for Re. Although the Re value is not the highest in the SA algorithm, it is very close to the highest value.
Table 4.
Case 3 optimization results. (a) X Minimum value, (b) x Maximum value, (c) x Target value (0.61 m).
| Test | x | T | Rex | δt | Q | Time(s) | Error |
|---|---|---|---|---|---|---|---|
| (a) | |||||||
| PSO | 0.08445 | 80.00000 | 3842.811 | 7.07210 | 190.00000 | 1.70131 | 0.000% |
| GA | 0.09386 | 80.00000 | 4271.165 | 7.45590 | 180.22080 | 1.37934 | 11.148% |
| SA | 0.08445 | 80.00000 | 3843.006 | 7.07230 | 189.99520 | 4.88419 | 0.006% |
| ACOR | 0.08445 | 80.00000 | 3842.811 | 7.07210 | 190.00000 | 4.28200 | 0.000% |
| ABC | 0.08445 | 80.00000 | 3842.820 | 7.07220 | 189.99980 | 1.73802 | 0.001% |
| FA |
0.08445 |
80.00000 |
3842.817 |
7.07220 |
189.99990 |
29.13008 |
0.001% |
| (b) | |||||||
| PSO | 1.22659 | 122.52594 | 50,000.000 | 27.96016 | 189.98236 | 5.22242 | 0.001% |
| GA | 1.22660 | 122.53093 | 50,000.000 | 27.96040 | 189.99718 | 80.20104 | 0.000% |
| SA | 1.22660 | 122.53181 | 50,000.000 | 27.96050 | 189.99955 | 21.08328 | 0.000% |
| ACOR | 1.24910 | 118.75625 | 49,256.225 | 27.53398 | 180.14272 | 104.38318 | 1.834% |
| ABC | 1.22660 | 122.53109 | 50,000.000 | 27.96045 | 189.99760 | 5.90879 | 0.000% |
| FA |
1.22656 |
122.50602 |
50,000.000 |
27.95894 |
189.92382 |
7.89300 |
0.003% |
| (c) | |||||||
| PSO | 0.61000 | 96.66315 | 24,145.583 | 19.28457 | 150.30341 | 5.11667 | 0.000% |
| GA | 0.61332 | 97.51306 | 26,633.790 | 19.35116 | 153.87966 | 4.53231 | 0.545% |
| SA | 0.61000 | 103.47060 | 26,084.444 | 19.39819 | 182.14272 | 20.49119 | 0.000% |
| ACOR | 0.61000 | 101.59221 | 26,210.239 | 19.36688 | 173.40599 | 86.34984 | 0.000% |
| ABC | 0.61000 | 99.24683 | 26,369.785 | 19.32768 | 162.43662 | 5.43169 | 0.000% |
| FA | 0.61001 | 100.24184 | 26,302.294 | 19.34431 | 167.08834 | 1.70427 | 0.001% |
The convergence curves of the algorithms for Case 3 are shown in Fig. 8. While minimum values are determined in the first 41 iterations (Fig. 8a), maximum values were determined in ten iterations (Fig. 8b). Target values are found in the first 15 iterations (Fig. 8c).
Fig. 8.
Plots of convergence curve for Case 3 (a) minimum, (b) maximum, (c) target values. Source: [64].
Among three cases, the ACOR algorithm performs the optimization in the longest time at the maximum and target value, while the FA algorithm performs the optimization in the longest time at the minimum value. The algorithm with the lowest processing time is the PSO technique for the maximum and minimum value and the FA algorithm for the target value. The average processing time of PSO and ABC algorithms is under 5 s. SA and FA algorithms' average processing time is under 16 s. The GA technique processed in 28.7 s, while the ACOR technique's processing time is 65 s on average.
Statistical tests are used to compare the results obtained from different algorithms. One of these tests is the one-way analysis of variance (ANOVA), and it is used to determine whether the model results obtained in each algorithm deviate from the mean [28]. Tukey's post-hoc test determines whether the results obtained differ from the means. The hypothesis of the results (null hypothesis); the mean of the values obtained by heuristic algorithms is equal. In the alternative hypothesis, not all means of the values obtained by all algorithms are equal. The significance level is 0.05, and equal variances are assumed for the analysis. Accordingly, means of GA in determining the minimum values for all three cases and the means of ACOR in determining the maximum values differ from other algorithms. At the target value, the mean of the GA in determining the heat flux is different compared to the other target value cases. For heat flux (Case 2), the null hypothesis is rejected in all three conditions. For the target values of δt (Case 1) and x (Case 3), all algorithms failed to reject the null hypothesis, and their averages are the same. Obtained results are shown in Table 5.
Table 5.
Analysis of variance hypothesis test results with Tukey's pairwise comparison.
| Minimum |
Maximum |
Target |
||||
|---|---|---|---|---|---|---|
| F value | p value | F value | p value | F value | p value | |
| δt - thermal layer thickness | 5.338235 | 0.000466 | 8.63 × 1027 | 0 | 0 | 1 |
| Tukey Pairwise |
GA |
ACOR |
– |
|||
| Q - heat flux | 18.36997 | 1.3 × 10−10 | 12.83823 | 3.09 × 10−8 | 7.074588 | 3.77 × 10−5 |
| Tukey Pairwise |
GA |
ACOR |
GA |
|||
| x – distance from the edge | 7.788 × 1029 | 0 | 1.46 × 1028 | 0 | 0 | 1 |
| Tukey Pairwise | GA | ACOR | – | |||
4. Discussion
Optimization algorithms were used in several types of research. The algorithms GA, PSO, and ACOR were used to place wind turbines [25]. It was found that PSO was the worst algorithm. GA and ACOR performances were similar from the point of fitness function view. Also, ACOR performance was found to be poorer compared to GA. The PSO, GA, and ABC algorithms with NN were used to forecast the intraday stock price [23]. This study placed the highest accuracy for different split training-test datasets in PSO, ABC, and GA. In Ebrahimi and Khamehchi [35], 26 benchmark problems were tested, and PSO performance was better than GA. Also, it is mentioned that PSO usually gives better results due to its higher search capability in continuous space. A civil engineering study used PSO, ACOR, and ABC to identify vibration response damages of changes in large-scale spatial trusses [28]. None of them is suitable for finding damages. The breast cancer classification's ordered performance from best to worst was GA, ACOR, PSO, and ABC, respectively [65]. A heat transfer study used a genetic algorithm to optimize the location of discrete heat sources [18]. GA converged global optimum solution. In another heat transfer problem [13], ACOR was used to determine and compare the heat transfer coefficient with the ABC algorithm. They mentioned that ACOR had better coverage.
This study tried finding minimum, maximum, and target values in three cases with six optimization algorithms. In finding the minimum values, the errors of the GA algorithm were the highest for all 3 cases. Afterward, SA and ABC algorithms had errors in all 3 cases, but SA errors were higher than ABC. FA and ACOR algorithms had errors in only one case. The PSO algorithm produced no errors. In finding the maximum value, the errors of the ACOR algorithm were the highest in all 3 cases. Afterward, GA, PSO, FA, and SA algorithms had errors in both cases. The second-highest error occurred in GA among these algorithms. The ABC algorithm produced an error value in only one case. The highest error in finding the target values was also in the GA algorithm and for 3 cases. While one case was wrong in SA and PSO algorithms, 2 cases were wrong in ABC and FA algorithms. No errors were found in the ACOR algorithm.
When the maximum, minimum, and target value errors of all algorithms are added to 3 cases, it is seen that the highest error total is 24.643% in GA. The second highest algorithm is the ACOR algorithm, with a 5.314% error. That result was supported by Aggarwal et al. [25] because GA and ACOR performances were similar in their study. While the SA algorithm has the third highest error with 0.081%, the ABC algorithm has the fourth highest error with 0.067%. Opposite to Aggarwal et al. [25], the total error of the PSO algorithm was 0.002%, and it was the best performance. Also, Chandar [23] found that ABC and PSO algorithms had the highest accuracy. The second best was the FA algorithm, with an error of 0.011%. It was found the opposite results with comparing breast cancer classification, which was found that GA and ACOR were the best algorithms [65]. According to the same study, PSO and ABC results were worse than GA and ACOR. In order to solve the laminar heat flow problem, the study examined the minimum, maximum, and target values of three distinct variables using six optimization techniques. The effectiveness of optimization techniques in resolving heat transfer problems is evaluated. The results showed that ACOR and GA could not find the best value in minimum and maximum cases compared to other optimization algorithms. The ACOR algorithm gave better results than other algorithms in determining the target values. In addition, when the results are examined based on the optimization times, it is seen that the operations of the FA and SA algorithms take a long time. The algorithms with the shortest processing times are PSO and ABC. Although the ACOR algorithm had average processing times in the first two cases, it achieved very high optimization times in Case 3. The processing time of GA is in the middle among all algorithms. When the results obtained are compared with [55], it is seen that the environment in which the algorithm is coded is very effective in the processing time. In addition, the GA results in the related study are close to the GA results in this study.
5. Conclusion
Heat transfer, one of the critical sustainability concerns, is one of today's current issues. For example, insulation materials and geometries are being developed to prevent building heat loss. On the other hand, different materials and geometries are obtained to transmit the heat faster and without heat loss. These two cases are optimization problems with minimum and maximum heat conduction. Determining the optimum geometry, material, and condition are essential issues in heat transfer. Although differential equations are used to determine the optimum solution in the classical approach, today's complex and many variable conditions make the solution difficult. Here, the finite element method and heuristic algorithms establish the solution. This research studied the layer thickness problem for laminar flow as a heat transfer problem. In the study, maximum, minimum, and target values of thermal boundary layer thickness (δt), heat flux (Q), and distance (x) from the edge variables were tried to be determined using PSO, GA, SA, ACOR, ABC, and FA algorithms. The results of the study revealed that PSO, SA, ABC, and FA algorithms were more suitable for solving the problem than GA and ACOR algorithms. It was also found that FA and SA algorithms were relatively longer processing times compared to other algorithms. The study confirmed that all six optimization algorithms were capable of addressing heat transfer problems. Future studies will aim to test different optimization algorithms in more complex heat transfer problems addressing insulation and conduction.
Funding
The authors received no financial support for this article's research, authorship, and/or publication.
Author contribution statement
Özen Günal: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Mustafa Akpinar: Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Data availability statement
Data will be made available on request.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
Not applicable.
References
- 1.Fabbri G. Heat transfer optimization in finned annular ducts under laminar-flow conditions. Heat Tran. Eng. 1998;19(4):42–54. doi: 10.1080/01457639808939935. [DOI] [Google Scholar]
- 2.Kulkarni M. Introduction of a new crossover radius for radial heat conduction, part ı: cylindrical systems. J. Therm. Envelope Build. Sci. 1998;22(1):72–88. doi: 10.1177/109719639802200106. [DOI] [Google Scholar]
- 3.Li Y., Chow W. Optimum ınsulation-thickness for thermal and freezing protection. Appl. Energy. 2005;80(1):23–33. doi: 10.1016/j.apenergy.2004.02.009. [DOI] [Google Scholar]
- 4.Zaki G., Al-Turki A. Optimization of multilayer thermal insulation for pipelines. Heat Tran. Eng. 2000;21(4):63–70. doi: 10.1080/01457630050144514. [DOI] [Google Scholar]
- 5.Ozdemir M., Parmaksizoglu I. Mekanik tesisatta ekonomik yalıtım kalınlığı. Tesisat Mühendisliği Dergisi. 2006;91(1):39–45. [Google Scholar]
- 6.Joe J., Karava P. A model predictive control strategy to optimize the performance of radiant floor heating and cooling systems in office buildings. Appl. Energy. 2019;245:65–77. doi: 10.1016/j.apenergy.2019.03.209. [DOI] [Google Scholar]
- 7.Tuncer M. M. S. Thesis. Yildiz Technical University; Yıldız: 2007. The optimization of the thermal insulation in the heating and cooling residences. [Google Scholar]
- 8.Gunal O., Akpinar M., Ovaz Akpinar K. 2022 International Conference on Decision Aid Sciences and Applications (DASA) IEEE; Chiangrai, Thailand: 2022. Determination of ınsulation parameters with optimization algorithms; pp. 1711–1714. [DOI] [Google Scholar]
- 9.Gunal O., Akpinar M., Ovaz Akpinar K. Optimization of laminar boundary layers in flow over a flat plate using recent metaheuristic algorithms. Energies. 2022;15(14):5069. doi: 10.3390/en15145069. [DOI] [Google Scholar]
- 10.Siavashi M., Talesh Bahrami H., Aminian E. Optimization of heat transfer enhancement and pumping power of a heat exchanger tube using nanofluid with gradient and multi-layered porous foams. Appl. Therm. Eng. 2018;138:465–474. doi: 10.1016/j.applthermaleng.2018.04.066. [DOI] [Google Scholar]
- 11.Gunal O., Akpinar M., Ovaz Akpinar K. 2022 8th International Conference on Information Technology Trends (ITT) IEEE; Dubai, UAE: 2022. Performance evaluation of metaheuristic optimization techniques in ınsulation problem; pp. 205–209. [DOI] [Google Scholar]
- 12.Sathish T., Mohanavel V. IWF based optimization of porous ınsert configurations for heat transfer enhancement using CFD. J. Appl. Fluid Mech. 2018;11:31–37. doi: 10.36884/jafm.11.si.29414. [DOI] [Google Scholar]
- 13.Hetmaniok E., Słota D., Zielonka A. In: Parallel Processing and Applied Mathematics. PPAM 2011, Lecture Notes in Computer Science. Wyrzykowski R., Dongarra J., Karczewski K., Waśniewski J., editors. Springer; Berlin, Heidelberg: 2012. Determination of the heat transfer coefficient by using the ant colony optimization algorithm. [DOI] [Google Scholar]
- 14.Baghban A., Kahani M., Nazari M., Ahmadi M., Yan W. Sensitivity analysis and application of machine learning methods to predict the heat transfer performance of CNT/water nanofluid flows through coils. Int. J. Heat Mass Tran. 2019;128:825–835. doi: 10.1016/j.ijheatmasstransfer.2018.09.041. [DOI] [Google Scholar]
- 15.Li Z., Khaled U., Al-Rashed A., Goodarzi M., Sarafraz M., Meer R. Heat transfer evaluation of a micro heat exchanger cooling with spherical carbon-acetone nanofluid. Int. J. Heat Mass Tran. 2020;149 doi: 10.1016/j.ijheatmasstransfer.2019.119124. [DOI] [Google Scholar]
- 16.Hassanpour M., Vaferi B., Masoumi M. Estimation of pool boiling heat transfer coefficient of alumina water-based nanofluids by various Artificial İntelligence (AI) approaches. Appl. Therm. Eng. 2018;128:1208–1222. doi: 10.1016/j.applthermaleng.2017.09.066. [DOI] [Google Scholar]
- 17.Karami A., Rezaei E., Shahhosseni M., Aghakhani M. Optimization of heat transfer in an air cooler equipped with classic twisted tape inserts using imperialist competitive algorithm. Exp. Therm. Fluid Sci. 2012;38:195–200. doi: 10.1016/j.expthermflusci.2011.12.007. [DOI] [Google Scholar]
- 18.Madadi R., Balaji C. Optimization of the location of multiple discrete heat sources in a ventilated cavity using artificial neural networks and micro genetic algorithm. Int. J. Heat Mass Tran. 2008;51(9–10):2299–2312. doi: 10.1016/j.ijheatmasstransfer.2007.08.033. [DOI] [Google Scholar]
- 19.Rao R., More K. Optimal design of the heat pipe using TLBO (teaching–learning-based optimization) algorithm. Energy. 2015;80:535–544. doi: 10.1016/j.energy.2014.12.008. [DOI] [Google Scholar]
- 20.Velichkin V., Zavyalov V. vol. 317. IOP Publishing; Bristol: 2018. Optimization of thermal object nonlinear control systems by energy efficiency criterion. (IOP Conference Series: Materials Science and Engineering). [DOI] [Google Scholar]
- 21.Yang J., Lourenço M., Estefen S. Thermal insulation of subsea pipelines for different materials. Int. J. Pres. Ves. Pip. 2018;168:100–109. doi: 10.1016/j.ijpvp.2018.09.009. [DOI] [Google Scholar]
- 22.Sharma M., Singh C., Singh R. Design of GA and ontology based NLP frameworks for online opinion mining. Recent Pat. Eng. 2019;13(2):159–165. doi: 10.2174/1872212112666180115162726. [DOI] [Google Scholar]
- 23.Chandar S.K. Hybrid models for intraday stock price forecasting based on artificial neural networks and metaheuristic algorithms. Pattern Recogn. Lett. 2021;147(1):124–133. doi: 10.1016/j.patrec.2021.03.030. [DOI] [Google Scholar]
- 24.Sharma M., Singh G., Singh R., Singh G. Analysis of DSS queries using entropy based restricted genetic algorithm. Appl. Math. Inf. Sci. 2015;9(5):2599–2609. doi: 10.12785/amis/090544. [DOI] [Google Scholar]
- 25.Aggarwal S.K., Saini L.M., Sood V. Large wind farm layout optimization using nature inspired meta-heuristic algorithms. IETE J. Res. 2021 doi: 10.1080/03772063.2021.1905082. in press. [DOI] [Google Scholar]
- 26.Aziz R.M. Nature-inspired metaheuristics model for gene selection and classification of biomedical microarray data. Med. Biol. Eng. Comput. 2022;60(1):1627–1646. doi: 10.1007/s11517-022-02555-7. [DOI] [PubMed] [Google Scholar]
- 27.Erdogmus P. A new solution approach for non-linear equation systems with grey wolf optimizer. Sakarya Univ. J. Comput. Inf. Sci. 2018;1(3B2):1–11. [Google Scholar]
- 28.Mishra M., Barman S.K., Maity D. Performance studies of 10 metaheuristic techniques in determination of damages for large-scale spatial trusses from changes in vibration responses. J. Comput. Civ. Eng. 2020;34(2) doi: 10.1061/(ASCE)CP.1943-5487.0000872. [DOI] [Google Scholar]
- 29.Ermakov V., Safonov V., Dogadkin D. Characteristic features of molybdenum, copper, tungsten and rhenium accumulation in the environment. Innov. Infrastruct. Solut. 2021;6:104. doi: 10.1007/s41062-021-00481-5. [DOI] [Google Scholar]
- 30.Ventsova I., Safonov V. Biochemical criteria for the development mechanisms of various reproduction disorders in dairy cows. Biodiversitas J. Biol. Divers. 2021;22(11):4997–5002. doi: 10.13057/biodiv/d221135. [DOI] [Google Scholar]
- 31.Sharma M., Romero N. Future prospective of soft computing techniques in psychiatric disorder diagnosis. EAI Endorsed Trans. Pervasive Health Technol. 2018;4(15):e1. doi: 10.4108/eai.30-7-2018.159798. [DOI] [Google Scholar]
- 32.Monga P., Sharma M., Sharma S.K. A comprehensive meta-analysis of emerging swarm intelligent computing techniques and their research trend. J. King Saud Univ. – Comput. Inf. Sci. 2022;34(10B):9622–9643. doi: 10.1016/j.jksuci.2021.11.016. [DOI] [Google Scholar]
- 33.Mirjalili S. SCA: a sine cosine algorithm for solving optimization problems. Knowl. Base Syst. 2016;96:120–133. doi: 10.1016/j.knosys.2015.12.022. [DOI] [Google Scholar]
- 34.Sörensen K. Metaheuristics-the metaphor exposed. Int. Trans. Oper. Res. 2013;22(1):3–18. doi: 10.1111/itor.12001. [DOI] [Google Scholar]
- 35.Ebrahimi A., Khamehchi E. Sperm whale algorithm: an effective metaheuristic algorithm for production optimization problems. J. Nat. Gas Sci. Eng. 2016;29:211–222. doi: 10.1016/j.jngse.2016.01.001. [DOI] [Google Scholar]
- 36.Yun Y., Gen M., Erdene T.N. Applying GA-PSO-TLBO approach to engineering optimization problems. Math. Biosci. Eng. 2023;20(1):552–571. doi: 10.3934/mbe.2023025. [DOI] [PubMed] [Google Scholar]
- 37.Ray T., Saini P. Engineering desıgn optimization using a swarm with an intelligent information sharing among individuals. Eng. Optim. 2001;33(6):735–748. doi: 10.1080/03052150108940941. [DOI] [Google Scholar]
- 38.Kennedy J., Eberhart R. Particle swarm optimization. Proc. ICNN'95 - Int. Conf. Neural Netw. 1995;4:1942–1948. doi: 10.1109/icnn.1995.488968. IEEE, Perth, WA. [DOI] [Google Scholar]
- 39.Demirci H., Yurtay N. Effect of the chaotic crossover operator on breeding swarms algorithm. Sakarya Univ. J. Comput. Inf. Sci. 2021;4(1):120–130. doi: 10.35377/saucis.04.01.796903. [DOI] [Google Scholar]
- 40.Ozsaglam M., Cunkas M. Particle swarm optimization algorithm for solving optimization problems. J. Polytech. 2008;11(4):299–305. [Google Scholar]
- 41.Özger Y., Akpınar M., Musayev Z., Yaz M. Electrical load forecasting using genetic algorithm based holt-winters exponential smoothing method. Sakarya Univ. J. Comput. Inf. Sci. 2019;2(2):108–123. doi: 10.35377/saucis.02.02.600620. [DOI] [Google Scholar]
- 42.Taşkın Ç., Emel G. first ed. Alfa Aktuel; Bursa: 2009. Sayısal Yöntemlerde Genetik Algoritmalar. [Google Scholar]
- 43.Gandomi A.H., Yang X.S., Alavi A.H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013;29:17–35. doi: 10.1007/s00366-011-0241-y. [DOI] [Google Scholar]
- 44.Carr J. Whitman College; Walla Walla, WA: 2014. An Introduction to Genetic Algorithms. [Google Scholar]
- 45.Nabiyev V. fourth ed. Seçkin Yayınları; Ankara: 2012. Yapay Zeka. [Google Scholar]
- 46.Huri D., Mankovits T. Surrogate model-based parameter tuning of simulated annealing algorithm for the shape optimization of automotive rubber bumpers. Appl. Sci. 2022;12:5451. doi: 10.3390/app12115451. [DOI] [Google Scholar]
- 47.Huang Q., Sheng Z., Fang Y., Li J. 2nd International Conference on Consumer Electronics and Computer Engineering (ICCECE) IEEE; Guangzhou: 2022. A simulated annealing-particle swarm optimization algorithm for UAV multi-target path planning; pp. 906–910.https://10.1109/ICCECE54139.2022.9712678 [Google Scholar]
- 48.Lim K.C.W., Wong L.P., Chin J.F. Simulated-annealing-based hyper-heuristic for flexible job-shop scheduling. Eng. Optim. 2022 doi: 10.1080/0305215X.2022.2106477. in press. [DOI] [Google Scholar]
- 49.Rao S. fourth ed. John Wiley & Sons, Inc.; New Jersey: 2009. Engineering Optimization: Theory and Practice. [Google Scholar]
- 50.Milenkovic B., Krstic M., Jovanovic D. Applying ant colony optimization algorithm to solve gear box design. Process Eng. 2022;4(1):63–68. doi: 10.24874/PES04.01.009. [DOI] [Google Scholar]
- 51.Liang X. Multiobjective optimization management of construction engineering based on ant colony algorithm. J. Control Sci. Eng. 2022;2022 doi: 10.1155/2022/2397246. [DOI] [Google Scholar]
- 52.Socha K., Dorigo M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008;185(3):1155–1173. doi: 10.1016/j.ejor.2006.06.046. [DOI] [Google Scholar]
- 53.Chen Z., Zhou S., Luo J. A robust ant colony optimization for continuous functions. Expert Syst. Appl. 2017;81:309–320. doi: 10.1016/j.eswa.2017.03.036. [DOI] [Google Scholar]
- 54.Karaboga D., Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial Bee Colony (ABC) algorithm. J. Global Optim. 2007;39(3):459–471. doi: 10.1007/s10898-007-9149-x. [DOI] [Google Scholar]
- 55.Adak M., Akpinar M. A hybrid artificial bee colony algorithm using multiple linear regression on time series datasets. 2018 3rd Int. Conf. Smart Sustain. Technol. (SpliTech) 2018:1–5. Split, Croatia. [Google Scholar]
- 56.Akpinar M., Adak M.F., Yumusak N. 2017 International Conference on Computer Science and Engineering (UBMK) IEEE; Antalya: 2017. Time series forecasting using artificial bee colony based neural networks; pp. 554–558. [DOI] [Google Scholar]
- 57.Yan G., Li C. An effective refinement artificial bee colony optimization algorithm based on chaotic search and application for pid control tuning. J. Comput. Inf. Syst. 2011;7(9):3309–3316. [Google Scholar]
- 58.Yang X. Stochastic Algorithms: Foundations and Applications. Springer; Berlin, Heidelberg: 2009. Firefly algorithms for multimodal optimization; pp. 169–178. [DOI] [Google Scholar]
- 59.Yang X. first ed. Luniver Press; Frome, U.K: 2010. Nature-Inspired Metaheuristic Algorithms. [Google Scholar]
- 60.Marannano G., Ricotta V. In: Design Tools and Methods in Industrial Engineering II. ADM 2021. Lecture Notes in Mechanical Engineering. Rizzi C., Campana F., Bici M., Gherardini F., Ingrassia T., Cicconi P., editors. Springer; Cham: 2022. Firefly algorithm for structural optimization using ANSYS. [DOI] [Google Scholar]
- 61.Kasdirin H.A., Yahya N.M., Tokhi M.O. Hybridizing firefly algorithm with invasive weed optimization for engineering design problems. 2015 IEEE Int. Conf. Evolving Adapt. Intell. Syst. (EAIS) 2015:1–6. doi: 10.1109/EAIS.2015.7368801. Douai, France. [DOI] [Google Scholar]
- 62.Holman J. tenth ed. McGraw Hill; New York: 2002. Heat Transfer. [Google Scholar]
- 63.Halıcı F., Gündüz M. Sakarya University; Sakarya: 2001. Ӧrneklerle Isı Gecİşİ. [Google Scholar]
- 64.Akpınar M. Application of genetic algorithm for multi-objective optimizing of heat-transfer parameters. Sakarya Univ. J. Sci. 2019;23(6):1123–1130. doi: 10.16984/saufenbilder.500643. [DOI] [Google Scholar]
- 65.Stephan P., Stephan T., Kannan R., Abraham A. A hybrid artificial bee colony with whale optimization algorithm for improved breast cancer diagnosis. Neural Comput. Appl. 2021;33:13667–13691. doi: 10.1007/s00521-021-05997-6. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.