Effects of activation overpotential in photoelectrochemical cells considering electrical and optical configurations

Abstract

Photoelectrochemical cells (PECs) are a promising option for directly converting solar energy into chemical energy by producing hydrogen (H₂) gas, thus providing a clean alternative to consuming fossil fuels. H₂ as fuel is free from any carbon footprints and negative environmental impacts. Therefore, the H₂ production, especially directly using sunlight in PECs, is critically important for the rapidly growing energy demand of the world. Although promising, PECs are inefficient and must overcome a few inherent losses in producing H₂—the most important being the activation overpotential (${\eta }_{\mathrm{a}}$) required for splitting water. This work analyzes the impact of ${\eta }_{\mathrm{a}}$ on solar-to-fuel efficiency (${\eta }_{\mathrm{STF}}$) and H₂ production rate (HPR). This work also discusses choosing appropriate photo-absorbing materials based on their energy bandgaps and suitable electrode pairs to achieve desired ${\eta }_{\mathrm{STF}}$ and HPR for different electrical and optical PEC configurations. Significant changes are observed in ${\eta }_{\mathrm{STF}}$ and HPR when ${\eta }_{\mathrm{a}}$ is considered in water splitting.

1. Introduction

Photoelectrochemical cells (PECs) produce hydrogen (H₂) gas by splitting water using solar energy and suitable photo-absorbing semiconductors [1], [2], [3], [4]. In PECs, light energy dissociates water molecules into H₂ and oxygen (O₂) [5], [6]. Conventional energy sources, such as fossil fuels, are limited. Fossil fuels cause irreparable environmental damage by producing greenhouse gases, such as carbon dioxide (CO₂). Therefore, reducing CO₂ emissions is the most urgent need of time to save the earth's climate. In addition, fossil fuels will not last long and are estimated to be depleted by 2100 if burning continues at the present rate [7]. In the recent UN climate change conference (COP26) in Glasgow, world leaders proposed to reduce the carbon footprint rate to zero by the year 2050 [8]. Therefore, fossil fuel dependency needs to be reduced, and alternative solutions must replace fossil fuels in applications soon. The best alternative energy solutions lie with renewable sources. Among the renewable energy sources, solar energy is drawing significantly more attention [9], [10], [11], [12]. Solar energy can be converted into chemical energy by splitting water and producing H₂ gas. Renewable solar H₂ gas is a clean and green alternative to fossil fuels, especially for its applications in the automotive sector. When burned in fuel cells, H₂ produces only water [13], [14], [15], [16].

The initial reports on electrochemical photolysis drew attention to finding new anode and cathode materials for water splitting [17], [18], [19], [20], [21], [22], [23], [24]. Initial research initiatives also aimed to increase the obtainable voltage and current by exploring different optical and electrical configurations [25]. Significant research has also been conducted to obtain appropriate anode and cathode materials in PECs [2], [5], [26], [27], [28], [29], [30]. Several mixed transition metal oxides have been used in the last two decades for efficient photoelectrochemical H₂ production [4]. Due to their exceptional photoelectrochemical stability, low cost, suitable band-edge locations, and widespread bandgap dispersion, metal oxides have drawn much attention. Significant advancements in creating metal oxide nanoparticles for PEC water splitting have been made during these decades. To name a few, TiO₂, ZnO, WO₃, and Fe₂O₃ have been thoroughly investigated for PEC water splitting [31]. Recently, semiconductor and carbon quantum dots (QDs) have been increasingly used due to their suitable shapes, sizes, compositions, tunable absorption spectrum, ease of surface functionalization, and outstanding electron transfer efficiency [32], [33], [34]. Their large surface area relative to their volume improves QD's ability to absorb light. In addition to serving as electron reservoirs to support photo-generated electrons with much reduced electron-hole recombination, the newly discovered QDs might also function as photosensitizers to improve solar light harvesting, resulting in significantly improved PEC performance. To date, QD-based photocatalysts, ZnO, Cu₂ZnGeS₄, CuInSSe/ZnS, Zn-CuInSe₂/CuInS₂, Cd_xZn${}_{1-x}$S have been extensively investigated for photocatalytic applications [34], [35], [36].

Although experimental reports of PEC performances are common in literature, a detailed theoretical treatment of this topic is still lacking. In addition, to date, theoretical analyses report solar-to-fuel efficiency (${\eta }_{\mathrm{STF}}$) and H₂ production rate (HPR) considering only ideal PECs, where ${\eta }_{\mathrm{STF}}$ and HPR are not affected by any losses [37], [38], [39]. However, losses are inherent to PECs, and realistic implementations of efficient PECs are impossible without considering the losses incurred [40], [41], [42], [43].

The efficiency of an ideal PEC for water splitting will be greater than a PEC working in a practical scenario. In practice, several losses pertinent to the electrodes, electrolyte, and junctions, such as overpotential, shunt losses, resistance losses of the contacts, charge carrier transportation losses, junction losses, thermodynamic and radiative recombination losses, and polarization losses, impact the performance of a PEC. Due to these losses, ${\eta }_{\mathrm{STF}}$ does not reach the desired level. Among the losses incurred, the overpotential loss within the electrode and the resistance loss within the electrolyte are the primary concerns [13], [44], [45], [46], [47], [48], [49], [50], [51]. The overpotential is the excess potential applied to an electrode to initiate electron transfer from the electrode to the electrolytic solution in an electrochemical cell. The value of ${\eta }_{\mathrm{STF}}$, considering the overpotential loss, can be less than half of that when considering an ideal situation [52]. Also, the selection of electrodes is critical due to the losses [53], and the studies of losses due to electrode materials is a crucial issue. The electrode materials should be selected based on high exchange current density, low overpotentials, strong conductivity, and good stability.

Photo-absorbing materials can be used as electrodes in PECs in addition to absorbing light and generating electric potential [5], [54]. In this case, materials must have both photo-absorbing characteristics and those required for water splitting, making it challenging to meet both. For effective light harvesting and electron transfer, photo-absorbing materials should have the following qualities: a bandgap that matches the required potential, a high absorption coefficient, a large surface area to maximize the number of active sites, and stability. For a single photo-absorber, obtaining the required electric potential for water splitting is met only by a single $E_{\mathrm{g}}$. For double or triple photo-absorber, the standard potential of ${\mathrm{H}}^{+}/{\mathrm{H}}_{\mathrm{2}}$ and ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ would be achieved by $E_{\mathrm{g}}$s of all photo-absorbing materials. Therefore, different materials are often used for electrodes and photo-absorbers. In this case, photo-absorbing materials are only used to generate the open-circuit voltage ($V_{\mathrm{oc}}$) and short-circuit current density ($J_{\mathrm{sc}}$) by absorbing the solar irradiance spectrum, as used in this work. Separate electrodes and photo-absorbers offer a negligible loss at the electrode–photo-absorbing material junction, considered an ohmic contact in PEC [55], [56].

The structural designs of PECs may vary in optical and electrical configurations. The optical configuration focuses on efficiently harvesting light, and the electrical configuration is for transporting photo-excited charge carriers. Both optical and electrical configurations may be series, parallel, and a combination of series and parallel. The positions of electrodes depend on the branches of an electrical configuration. Different current densities flow through different branches in a mixed electrical configuration. Hence, ${\eta }_{\mathrm{STF}}$ and overpotential losses (η) also vary depending on the PEC configuration. Furthermore, the positions of electrodes in an electrical configuration cause current density (J) to vary from branch to branch. Therefore, ${\eta }_{\mathrm{a}}$ also varies for different PEC configurations. The variation of ${\eta }_{\mathrm{STF}}$ leads to significant changes in H₂ production.

To date, there are no detailed reports on the effects of ${\eta }_{\mathrm{a}}$ on ${\eta }_{\mathrm{STF}}$ and HPR for H₂ generation. This work investigates how ${\eta }_{\mathrm{a}}$ depends on bandgap energy $(E_{\mathrm{g}})$ and $J_{\mathrm{sc}}$ considering different electrode pairs. This work also investigates the effects of ${\eta }_{\mathrm{a}}$ on ${\eta }_{\mathrm{STF}}$ and HPR for different photo-absorbing and electrode materials. Libraries of photo-absorbing and electrode materials have been created. PEC ${\eta }_{\mathrm{STF}}$ and HPR are analyzed for several combinations of photo-absorbing and electrode materials. The bandgaps of photo-absorbing materials are determined for optimized ${\eta }_{\mathrm{STF}}$ and HPR for several electrical and optical configurations considering the impact of ${\eta }_{\mathrm{a}}$. Also, this work analyzes the impact of electrode positions in electrical branches and discusses the selection of compatible electrode pairs considering ${\eta }_{\mathrm{a}}$. Due to ${\eta }_{\mathrm{a}}$, choosing compatible photo-absorbers is a difficult task for any PEC configuration as a slight variation of ${\eta }_{\mathrm{a}}$ causes a significant change in J. The values of ${\eta }_{\mathrm{STF}}$ and HPR change significantly when ${\eta }_{\mathrm{a}}$ is considered in the calculation. Finally, this work illustrates PEC designs considering the material parameters, electrical and optical configurations, and the number of electrolyzers.

2. Theoretical modeling

At standard conditions, the Gibbs free energy, $\mathrm{\Delta }G=237.2$ kJ/mol, changes when H₂ and 1/2O₂ are obtained from a H₂O molecule. The change in free energy indicates $\mathrm{\Delta }{E}^0=1.23$ eV per electron transferred according to the Nernst equation [5]. Therefore, the photo-absorbing material must absorb photon irradiance with energy >1.23 eV and convert it into H₂ and O₂. Here, a photon with >1.23 eV has a wavelength ≤1000 nm [57]. However, due to losses in a practical scenario, there is a need for an additional $\gtrsim 0.4\text{–}0.6$ eV for water splitting [29], [52]. A PEC water splitting system must generate two electron-hole pairs per molecule of H₂ or four electron-hole pairs per molecule of O₂.

A single semiconductor material can drive the H₂ (HER) and O₂ evolution reactions (OER) using electrons and holes generated under illumination. The material must have an $E_{\mathrm{g}}$ greater than that required to split water and conduction ($E_{\mathrm{cb}}$) and valence band-edge energies ($E_{\mathrm{vb}}$) that straddle the electrochemical potentials $E^0$(${\mathrm{H}}^{+}/{\mathrm{H}}_2$) and $E^0$(${\mathrm{O}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$) [57]. If a single semiconductor material does not meet the required potential for water splitting, multiple semiconductor materials can be used in tandem, providing sufficient electrochemical potential for HER and OER. Tandem cells are a stack of multiple photo-absorbing materials on top of each other, effectively capturing solar energy. They are classified into two categories: (1) type A tandem cells have two terminals, one connected to the top of the cell and the other to the bottom, and (2) type B tandem cells have multiple terminals, separate connections with each photo-absorber. Band alignment is not a problem for type B cells. However, band alignment is crucial for type A cells for which the conduction band of the photo-absorbing material at the anode side is more negative than the valence band at the cathode side, and the band gap of the photo-absorber should be sufficient for ${\mathrm{H}}^{+}/{\mathrm{H}}_{\mathrm{2}}$ or ${\mathrm{O}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ standard potential for HER and OER [58]. The HER and OER can be written as

$${\mathrm{H}}_{\mathrm{2}}\mathrm{O}\to \frac{\mathrm{1}}{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+{\mathrm{H}}_{\mathrm{2}}\mathrm{\Delta }G=+237.2\text{kJ/mol},$$ (1a)

$$\mathrm{2}{\mathrm{H}}^{+}+\mathrm{2}{\mathrm{e}}^{-}\to {\mathrm{H}}_{\mathrm{2}}(\mathrm{HER}),$$ (1b)

$${\mathrm{H}}_{\mathrm{2}}\mathrm{O}+\mathrm{2}{\mathrm{h}}^{+}\to \frac{\mathrm{1}}{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{2}{\mathrm{H}}^{+}(\mathrm{OER}).$$ (1c)

Electron transfer processes are critically important to drive the HER and OER given in Eq. (1a), (1b), (1c). The electron transfer processes at the electrode–liquid junctions incur losses due to the concentration and kinetic overpotentials. The overpotential is the difference between the experimentally and theoretically observed values of the required voltages for water splitting in PECs. Among the mechanisms responsible for overpotential, ${\eta }_{\mathrm{a}}$ is the most critical and must be accounted for in HER and OER [59], [60].

2.1. Modeling of activation overpotential

Activation overpotential (${\eta }_{\mathrm{a}}$), the most significant overpotential loss, is the potential difference above the equilibrium potential required to overcome the activation energy of the cell reaction to generate a specified current density. Basically, ${\eta }_{\mathrm{a}}$ causes a slow electrode reaction and is associated with the charge transfer between the electrode and the electrolytic solution. Therefore, it depends on the concentration of the electrolytic solution. The overpotential is measured from the difference between an electrode's equilibrium and operating potentials—the difference between the solid and dashed lines in Fig. 1. At an electrode–electrolytic solution junction, opposite polarity charges are accumulated, as shown in Fig. 1. The positive charge polarity exists in the electrolytic solution's inner Helmholtz plane. However, both positive and negative polarity charges exist in the outer Helmholtz plane. An electron participates in the initial reaction after passing through the inner Helmholtz plane. After coming out of the outer Helmholtz plane, the reaction between the electron and H⁺ completes [61].

Figure 1.

Schematic illustration of the electric double layer (EDL) with Helmholtz plane between an electrode and electrolytic solution and the corresponding cell potential.

Considering the half-cell reactions of cathode and anode, the HER and OER can be written as

$$\mathrm{2}{\mathrm{H}}^{+}+\mathrm{2}{\mathrm{e}}^{-}\to {\mathrm{H}}_{\mathrm{2}},$$ (2a)

$${\mathrm{O}}^{\mathrm{2}-}\to \frac{\mathrm{1}}{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}+\mathrm{2}{\mathrm{e}}^{-}.$$ (2b)

If the equilibrium concentrations of H⁺ and O²⁻ are denoted as $C_{{\mathrm{H}}^{+}}$ and $C_{{\mathrm{O}}^{\mathrm{2}-}}$, and the non-equilibrium concentrations of H⁺ and O²⁻ are denoted as $C_{{\mathrm{H}}^{+}}^{⁎}$ and $C_{{\mathrm{O}}^{\mathrm{2}-}}^{⁎}$, the Butler-Volmer equation (BVE) for the current density (J), due to the reactions in Eq. (2a), (2b), can be written as [62]

$$J=J_0[\frac{C_{{\mathrm{H}}^{+}}}{C_{{\mathrm{H}}^{+}}^{⁎}}\exp \frac{-\beta nF\eta }{RT}-\frac{C_{{\mathrm{O}}^{\mathrm{2}-}}}{C_{{\mathrm{O}}^{\mathrm{2}-}}^{⁎}}\exp \frac{(1-\beta )nF\eta }{RT}].$$ (3)

In Eq. (3), $J_0$ is the exchange current density between the electrode and the electrolytic solution in equilibrium condition, n is the number of transferred electrons in HER, F is the Faraday constant, and R is the universal gas constant. Also, β is the symmetry factor of the electrode, which is usually assumed as 0.5 [5], [63]. In PECs, $J_0$ can be defined as the equilibrium current density flowing equally in both directions at a reversible potential.

If the mass transfer coefficient between the electrode surface and the bulk electrolytic solution is greater than the HER rate, the concentration difference of H⁺ is negligible between these two. In such a scenario, the mass transfer of ions between the electrolytic solution and the outer Helmholtz plane is much faster than the rate at which the ions react at the electrodes [64], [65], [66]. Therefore, we can write $C_{{\mathrm{H}}^{+}}=C_{{\mathrm{H}}^{+}}^{⁎}$, $C_{{\mathrm{O}}^{\mathrm{2}-}}=C_{{\mathrm{O}}^{\mathrm{2}-}}^{⁎}$, and $\eta ={\eta }_{\mathrm{a}}$. Hence, the BVE becomes

$$J=J_0[\exp \frac{-\beta nF{\eta }_{\mathrm{a}}}{RT}-\exp \frac{(1-\beta )nF{\eta }_{\mathrm{a}}}{RT}].$$ (4)

The BVE given in Eq. (4) is not used at anode and cathode simultaneously. The properties of the anode and cathode materials and corresponding $J_0$ are not the same. Also, ${\eta }_{\mathrm{a}}$ is different for different electrochemical cells. Hence, it is simplified for two significant cases at the conditions during electrolysis related to (1) large overpotentials, when $|{\eta }_{\mathrm{a}}|>100$ mV, and (2) small overpotentials, $|{\eta }_{\mathrm{a}}|<10$ mV. The large overpotential approximation is used for water electrolysis as the optimum current density level is required to meet the minimum requirement of the redox potential. Therefore, the large cathodic or anodic overpotential is expected for water splitting [5], [67].

For large cathodic activation overpotential (${\eta }_{\mathrm{a},\mathrm{c}}$), the second term of the BVE can be neglected as the sign of ${\eta }_{\mathrm{a}}$ is negative. When $J_0=J_{\mathrm{0},\mathrm{c}}$ is the cathodic exchange current density, Eq. (4) reduces to

$${\eta }_{\mathrm{a},\mathrm{c}}=\frac{RT}{\beta nF}\ln \left|\frac{J}{J_{\mathrm{0},\mathrm{c}}}\right|.$$ (5)

In contrast, for large anodic activation overpotential (${\eta }_{\mathrm{a},\mathrm{a}}$), the first term of the BVE can be neglected as the sign of ${\eta }_{\mathrm{a}}$ is positive. When $J_0=J_{\mathrm{0},\mathrm{a}}$ is the anodic exchange current density, Eq. (4) reduces to

$${\eta }_{\mathrm{a},\mathrm{a}}=\frac{RT}{(1-\beta )nF}\ln \left|\frac{J}{J_{\mathrm{0},\mathrm{a}}}\right|.$$ (6)

This work used Eqs. (5) and (6) to determine ${\eta }_{\mathrm{a},\mathrm{c}}$ and ${\eta }_{\mathrm{a},\mathrm{a}}$. The total ${\eta }_{\mathrm{a}}$ is the summation of ${\eta }_{\mathrm{a},\mathrm{c}}$ and ${\eta }_{\mathrm{a},\mathrm{a}}$.

2.2. STF efficiency

Photo-absorbing materials generate $V_{\mathrm{oc}}$ by absorbing solar irradiance spectrum in a PEC. If the number of electrolyzers ($N_{\mathrm{elec}}$) is one, the voltage required for water splitting from photo-absorbing materials is the sum of water redox potential ($E_{\mathrm{rxn}}$) and ${\eta }_{\mathrm{a}}$. However, if there are multiple electrolyzers in a PEC, the minimum required voltage from a cell is $V_{\mathrm{oc}}=N_{\mathrm{elec}}(E_{\mathrm{rxn}}+{\eta }_{\mathrm{a}})$.

The ${\eta }_{\mathrm{STF}}$ of a single electrolyzer system is given by ${\eta }_{\mathrm{STF}}={\eta }_{\mathrm{f}}J{E}_{\mathrm{rxn}}/P_{\mathrm{solar}}$, where ${\eta }_{\mathrm{f}}$ is the Faradaic efficiency and $P_{\mathrm{solar}}$ is the power density of the solar irradiance spectrum. Faradaic efficiency defines the efficiency of photo-excited electron transfers between the electrode and electrolytic solution in electrochemical cells. Consequently, ${\eta }_{\mathrm{STF}}=J{E}_{\mathrm{rxn}}/P_{\mathrm{solar}}$ for a water splitting process with 100% charge transfer efficiency, i.e., ${\eta }_{\mathrm{f}}=1$. If there are $N_{\mathrm{elec}}$ electrochemical cells in series, each will have the same J, and ${\eta }_{\mathrm{STF}}$ will be given by

$${\eta }_{\mathrm{STF}}=\frac{J\times N_{\mathrm{elec}}\times E_{\mathrm{rxn}}}{P_{\mathrm{solar}}}.$$ (7)

This work takes a “detailed balance” approach to calculate J by using the standard ideal diode equation and the assumptions that (1) each cell is planar with an abrupt absorption threshold, (2) all photons with an energy greater than the bandgap are absorbed, and (3) there is no multiplication of carriers at the ambient condition and from radiative emission from other cells [40], [47], [68], [69]. Therefore, one photon excites one electron, i.e., the PEC has a unity quantum efficiency [70]. Now, the current-voltage relationship of a single photo-absorber is given by

$$J=J_{\mathrm{L}}-J_{\mathrm{s}}[\exp (k{V}_{\mathrm{oc}}/k{T}_{\mathrm{a}})-1],$$ (8a)

$$J_{\mathrm{L}}=q\underset{E_{\mathrm{g}}}{\overset{\infty }{\int }}{b}_{\text{AM}1.5\text{G}}dE,$$ (8b)

$$J_{\mathrm{s}}=\frac{2f_{\mathrm{g}}q\pi }{h^3{c}^2}\underset{E_{\mathrm{g}}}{\overset{\infty }{\int }}\frac{E^2}{\exp (E/k{T}_{\mathrm{a}})-1}dE,$$ (8c)

where $J_{\mathrm{L}}$ is the light-induced current density, $J_{\mathrm{s}}$ is the reverse saturation current density, and $b_{\text{AM}\mathrm{1.5 G}}$ is the solar photon flux normal on the earth surface per energy interval dE. The constants q, h, c, and k are the elementary charge, Planck's constant, speed of light, and the Boltzmann constant, respectively.

Two kinds of losses occur when photo-absorbing materials absorb light: The radiative emission and the non-radiative transition [71]. The non-radiative transition is not considered here. The radiative emission is included as a geometric factor $(f_{\mathrm{g}})$, which is equal to one when the radiative emission is limited to the front side, i.e., the photo-absorber has a perfect back reflector. In addition, $f_{\mathrm{g}}=2$ if the radiative emission can leave from both the front and back sides. Finally, unless stated otherwise, AM 1.5 G spectrum (ASTM G173), as shown in Fig. 2, and $T_{\mathrm{a}}=298.15$ K have been considered in this work [72].

Figure 2.

AM 1.5 G terrestrial solar irradiance spectrum on the earth-surface.

2.3. Hydrogen production rate

HPR is an important performance parameter of an electrochemical cell. HPR depends on ${\eta }_{\mathrm{STF}}$ and the intensity of the solar irradiance spectrum ($P_{\mathrm{total}}$) and can be calculated using [73]

$$\mathrm{HPR}(\text{mol}{\text{H}}_2/{\text{cm}}^2\text{sec})=\frac{N_{\mathrm{ph}}\times {\eta }_{\mathrm{STF}}\times P_{\mathrm{total}}({\text{W}\text{cm}}^{-2})}{\mathrm{\Delta }{G}^0},$$ (9)

where $N_{\mathrm{ph}}$ is the number of photo-absorbers. The HPR given in Eq. (9) is in per unit area of each photo-absorber. The total H₂ amount can be obtained by multiplying HPR by a single photo-absorber's effective photo-absorbing area. This work assumes that the effective photo-absorption area of each photo-absorber is the same. The unit of HPR is modified to mL H₂/cm² hour considering ambient temperature ($T_{\mathrm{a}}$), pressure (P), and molar gas constant (R) by

$$\mathrm{HPR}(\mathrm{mL}{\mathrm{H}}_{\mathrm{2}}/{\text{cm}}^2\text{hour})=\frac{\text{mol}{\text{H}}_2/{\text{cm}}^2\text{sec}\times R\times T_{\mathrm{a}}\times 1\text{hour}\times 1000}{P}.$$ (10)

3. Simulation model

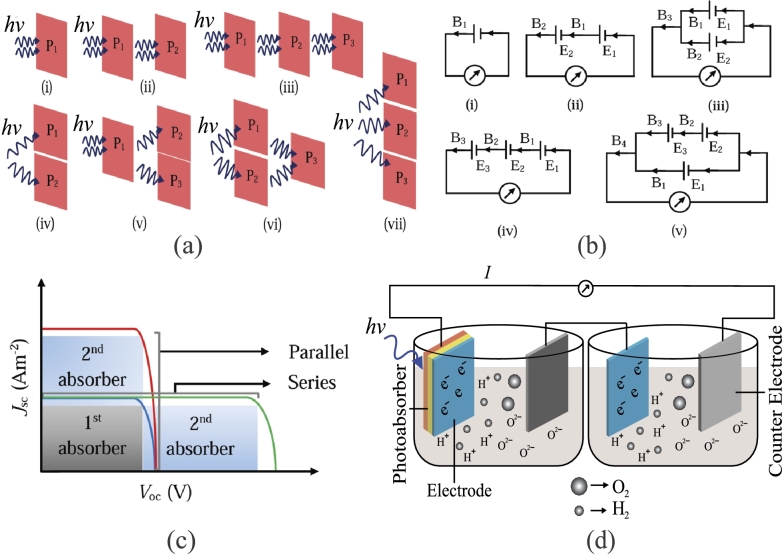
We have investigated several electrical and optical PEC configurations, such as electrically series or parallel, optically series or parallel, and mixed series and parallel. Figs. 3(a) and 3(b) show several electrical and optical PEC configurations. In an optically parallel configuration, photo-absorbing materials are positioned parallelly and not optically connected, thus splitting the solar light equally to each photo-absorber. The effective area of each photo-absorber is assumed to be the same, and the total effective area of all parallel photo-absorbers is calculated by summing up the effective areas of photo-absorbers. In contrast, light propagates from one photo-absorber to another for an optical series configuration. Hence, the effective area of every photo-absorbing material is considered one.

Figure 3.

(a) Different types of optical configurations: (i) single photo-absorbing material, (ii) series-connected double photo-absorbing materials, (iii) series-connected triple photo-absorbing materials, (iv) parallel-connected double photo-absorbing materials, (v, vi) mixture of series- and parallel-connected photo-absorbing materials, (vii) parallel-connected triple photo-absorbing materials. (b) Different types of electrical configurations: (i) single photo-absorbing material, (ii) series-connected double photo-absorbing materials, (iii) parallel-connected double photo-absorbing materials, (iv) series-connected triple photo-absorbing materials, (v) mixture of series- and parallel-connected photo-absorbing materials. (c) J_sc vs. V_oc characteristics of series and parallel photovoltaic cell. (d) Schematic diagram for double photo-absorbing materials with double electrolyzers in an optically series and electrically series configuration.

In an electrical configuration, the series connection increases $V_{\mathrm{oc}}$, and the parallel connection increases $J_{\mathrm{sc}}$. Different electrical configurations for PECs are shown in Fig. 3(b). Fig. 3(d) shows a PEC system where double photo-absorbing materials with double electrolyzers are connected optically and electrically in series.

We have calculated $P_{\mathrm{solar}}$ by integrating the solar irradiance spectrum considering wavelengths from 280 nm to 4000 nm. The simulations depend on the number of photo-absorbing materials and electrolyzers and the optical, electrical, and electrode configurations. The simulation parameters are given in Table 1. Additionally, we have assumed unity efficiency for the electrolyte to specifically focus on the impact of activation overpotential on the efficiency of PEC devices. Since J and ${\eta }_{\mathrm{a}}$ are related to each other, as given in Eqs. (5) and (6), we have solved them iteratively. We have calculated the initial J and V without ${\eta }_{\mathrm{a}}$ using Eq. (8a), (8b), (8c) and estimated the initial ${\eta }_{\mathrm{a},\mathrm{c}}$ and ${\eta }_{\mathrm{a},\mathrm{a}}$ using Eqs. (5) and (6). Finally, J, V, ${\eta }_{\mathrm{a},\mathrm{c}}$ and ${\eta }_{\mathrm{a},\mathrm{a}}$ are determined from Eqs. (5), (6), and (8a), (8b), (8c) using the numerical convergence method. Here, the total activation overpotential is ${\eta }_{\mathrm{a}}={\eta }_{\mathrm{a},\mathrm{c}}+{\eta }_{\mathrm{a},\mathrm{a}}$. Consequently, ${\eta }_{\mathrm{STF}}$ and HPR are calculated using Eqs. (7) and (10).

Table 1.

Input parameters for the simulation model.

Name	Value	Name	Value
Temperature (Ta)	298.15 K	Pressure (P)	1 atm
Solar irradiance spectrum	AM 1.5 G	Faradaic efficiency (ηf)	1
Standard redox potential (Erxn)	1.23 V	Geometric factor (fg)	1 or 2

3.1. Electrode material library

Electrode materials used in this work for H₂ production and their corresponding $J_0$ are shown in Table 2. Ten materials are used as cathodes and five materials are used as anodes. The $J_0$ values given in Table 1 are constant considering $T_{\mathrm{a}}$ of 298.15 K and 1 N H₂SO₄ electrolytic solution [74], [75]. This work utilized these materials to calculate ${\eta }_{\mathrm{a}}$ for different PEC configurations.

Table 2.

Electrode materials with their J₀ at T_a of 298.15 K in 1N H₂SO₄ solution.

Cathode	$J_{\mathrm{0},\mathrm{c}}(\mathrm{A}{\mathrm{m}}^{-\mathrm{2}})$	Cathode	$J_{\mathrm{0},\mathrm{c}}(\mathrm{A}{\mathrm{m}}^{-\mathrm{2}})$	Anode	$J_{\mathrm{0},\mathrm{a}}(\mathrm{A}{\mathrm{m}}^{-\mathrm{2}})$
Palladium (Pd)	10	Titanium (Ti)	7.00 × 10−4	PtFe/C	2.15 × 10−3
Platinum (Pt)	8	Lead (Pb)	1.00 × 10−8	PtW2C/C	4.70 × 10−4
Nickel (Ni)	0.07	Cadmium (Cd)	1.50 × 10−7	RuxSey	2.22 × 10−4
Gold (Au)	0.04	Manganese (Mn)	1.30 × 10−7	RuxFeySez	4.47 × 10−4
Tungsten (W)	0.013	Mercury (Hg)	5.00 × 10−10	Pt	1.00 × 10−5

3.2. Photo-absorbing material library

Photo-absorbing materials used in this work for H₂ production and their corresponding $E_{\mathrm{g}}$ values are shown in Table 3 [5], [76]. This work analyzes the state of H₂ production in different PEC combinations using these 30 materials with $E_{\mathrm{g}}$ varying from 0.52 eV to 3.08 eV.

Table 3.

Photo-absorbing materials and their corresponding bandgap energy (E_g).

Photo-absorber	Eg (eV)	Photo-absorber	Eg (eV)	Photo-absorber	Eg (eV)
C-Si/CuSnS4	0.52	p-GaAs/Cu2MnSnS4	1.4	Cu4SiS4	1.95
Ge	0.67	Cu2ZnSnSe4	1.48	Cu3SbSe3	2.01
BaSi2	0.72	Cu2BaSnSSe3	1.59	Cu2O	2.06
Cu2ZnSnSe4	0.9	CuBiS2	1.61	Cu2ZnGeS4	2.08
CuSbTe2	0.92	Cu2BaSnSe4	1.68	Cu3SbS3	2.13
CuSbSe2	1.05	Cu2FeSnS4	1.71	n-Fe2O3	2.2
Cu4GeS4	1.15	Cu2BeSnS4	1.76	p-GaP	2.3
CuBiSe2	1.18	Cu2BaSnS4	1.8	Cd0.6Zn0.4S	2.47
p-InP	1.3	Cu2SrSnS4	1.81	Penta-C20/Cu2ZnSiS4	2.89
CuSbS2	1.37	Cu3BiS3	1.88	ZnO-Ce	3.08

4. Results and discussion

4.1. Activation overpotential in PECs

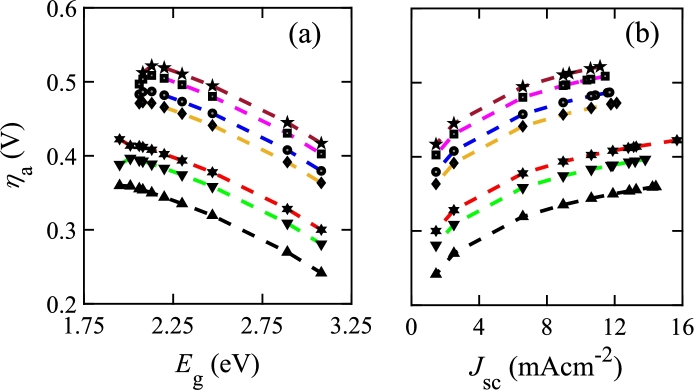
In PECs, ${\eta }_{\mathrm{a}}$ critically depends on $J_{\mathrm{sc}}$, which is calculated from $E_{\mathrm{g}}$ of the photo-absorbing material. In addition, different electrode pairs show a significant variation of ${\eta }_{\mathrm{a}}$ due to the difference of $J_0$ among them. Fig. 4 shows ${\eta }_{\mathrm{a}}$ vs. $E_{\mathrm{g}}$ and $J_{\mathrm{sc}}$ of a photo-absorber for various electrode pairs. Fig. 4(a) shows that ${\eta }_{\mathrm{a}}$ decreases as the photo-absorber $E_{\mathrm{g}}$ increases, which is attributed to increasing $V_{\mathrm{oc}}$ and decreasing $J_{\mathrm{sc}}$ as $E_{\mathrm{g}}$ increases, as shown in Fig. 3(c). By contrast, ${\eta }_{\mathrm{a}}$ increases with $J_{\mathrm{sc}}$, as shown in Fig. 4(b).

Figure 4.

Activation overpotential (η_a) vs. bandgap (E_g) and short circuit current density (J_sc) for various electrode pairs. Electrode pairs are denoted by different markers: ★ indicates Au cathode and PtW₂C/C anode, ■ indicates Ni cathode and PtW₂C/C anode, ● indicates Pt cathode and Pt anode, ◆ indicates Ni cathode and PtFeC/C anode, ✶ indicates Pt cathode and Ru_xSe_y anode, ▼ indicates Pt cathode and PtW₂C/C anode, and ▲ indicates Pt cathode and PtFe/C anode.

The smallest ${\eta }_{\mathrm{a}}$ values are found for Pt cathode and PtFe/C anode with the variation of $E_{\mathrm{g}}$. On the other hand, the greatest ${\eta }_{\mathrm{a}}$ values are found for the Au cathode and PtW₂C/C anode. The Pt and PtFe/C electrode pair has a greater $J_0$ than Au and PtW₂C/C electrode pair. Hence, the charge transfer kinetics of the Pt and PtFe/C electrode pair is faster than the other.

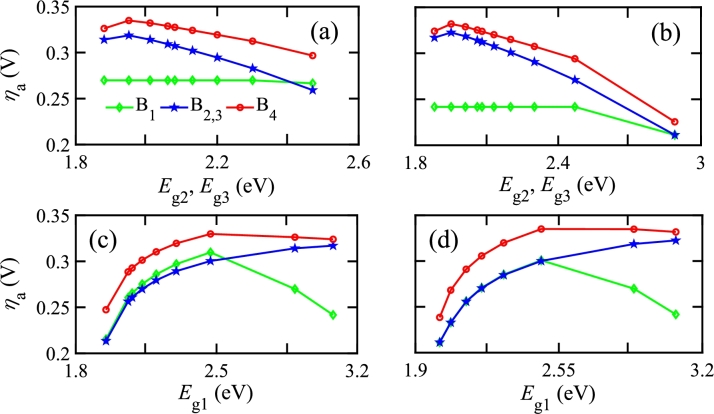
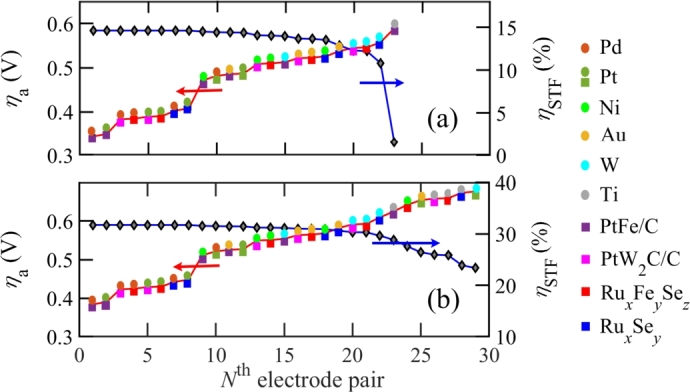
Electrical configurations can have photo-absorbers in different branches along with the electrodes. Different electrical configurations are possible for electrodes placed on different branches, as shown in Fig. 3(b). Fig. 5 shows that there are significant changes in ${\eta }_{\mathrm{a}}$ based on the electrode position due to the change in $J_{\mathrm{sc}}$ from branch to branch. Therefore, ${\eta }_{\mathrm{STF}}$ and HPR also vary with the electrode position, making the electrode pair configuration a critical design parameter for H₂ production.

Figure 5.

η_a vs. energy bandgaps of photo-absorbers for optical series and electrical series configuration of single photo-absorbing material with parallel-connected double photo-absorbing materials. Electrodes are located in different branches (B₁, B₂, B₃, and B₄) of the electrical configuration. (a) E_g2 and E_g3 are varied while E_g1 is constant at 3.08 eV, (b) E_g2 and E_g3 are varied while E_g1 is kept constant at 2.88 eV, (c) E_g1 is varied while E_g2 and E_g3 are kept constant at 1.88 eV, and (d) E_g1 is varied while E_g2 and E_g3 are kept constant at 1.95 eV.

This work analyzed the impacts of electrical series and parallel configurations by considering a mixed PEC configuration, as shown in Fig. 3(b)(v), where four electrical branches are present. Fig. 5 shows ${\eta }_{\mathrm{a}}$ against $E_{\mathrm{g}}$ of photo-absorbers in different branches. The bandgaps $E_{\mathrm{g2}}$ and $E_{\mathrm{g3}}$ of photo-absorbers are the same due to optically parallel connection. In Figs. 5(a) and (b), $E_{\mathrm{g2}}$ and $E_{\mathrm{g3}}$ are varied equally, while keeping $E_{\mathrm{g1}}$ fixed. In all cases, ${\eta }_{\mathrm{a}}$ is maximum at branch 4 and minimum at branch 1 since ${\eta }_{\mathrm{a}}$ is proportional to $J_{\mathrm{sc}}$. Therefore, ${\eta }_{\mathrm{a}}$ is less in branch 1 as $J_{\mathrm{sc}}$ is the smallest in branch 1 among all branches. The same feature is also observed in branches 2 and 3 where $J_{\mathrm{sc}}$ is greater than that of branch 1. Since $J_{\mathrm{sc}}$ of branch 4 is the summation of $J_{\mathrm{sc}}$ of branches 1, 2, and 3, the maximum ${\eta }_{\mathrm{a}}$ occurs at branch 4. In Figs. 5(c) and (d), $E_{\mathrm{g1}}$ is varied while keeping $E_{\mathrm{g2}}$ and $E_{\mathrm{g3}}$ fixed, and a similar change in $J_{\mathrm{sc}}$ has been obtained. The features shown in Fig. 5 show the electrical branch where the electrode should be placed so that the optimized ${\eta }_{\mathrm{STF}}$ and HPR are found.

${\eta }_{\mathrm{a}}$ impacts ${\eta }_{\mathrm{STF}}$ of any PEC significantly. Due to the presence of ${\eta }_{\mathrm{a}}$, a higher potential is needed to split water than in an ideal situation. Eventually, $J_{\mathrm{sc}}$, on which ${\eta }_{\mathrm{STF}}$ depends proportionally, decreases. Therefore, ${\eta }_{\mathrm{STF}}$ decreases as well with ${\eta }_{\mathrm{a}}$. Fig. 6 shows ${\eta }_{\mathrm{STF}}$ against $E_{\mathrm{g}}$ and $J_{\mathrm{sc}}$ with and without ${\eta }_{\mathrm{a}}$. In both cases, the PEC consists of a single photo-absorbing material and a single electrolyzer. The electrolyzer uses Pt as the cathode and PtFe/C as the anode. When ${\eta }_{\mathrm{a}}=0$, ${\eta }_{\mathrm{STF}}$ can be up to 30%. However, ${\eta }_{\mathrm{STF}}$ drops to 18% when ${\eta }_{\mathrm{a}}$ is considered. Notably, ${\eta }_{\mathrm{STF}}=0$ for $E_{\mathrm{g}}=1.59\text{–}1.96$ V if ${\eta }_{\mathrm{a}}$ is considered, although ${\eta }_{\mathrm{STF}}\gg 0$ if ${\eta }_{\mathrm{a}}$ is not considered. Fig. 6(b) shows that a higher ${\eta }_{\mathrm{STF}}$ is achieved for a smaller $E_{\mathrm{g}}$ since $J_{\mathrm{sc}}$ increases when $E_{\mathrm{g}}$ decreases. Since $J_0$ is fixed for a particular electrode pair, ${\eta }_{\mathrm{a}}$ varies with $J_{\mathrm{sc}}$ following Eqs. (5) and (6).

Figure 6.

η_STF against E_g for a single photo-absorbing material in a single electrolyzer (a) without and (b) with considering η_a. In each case, Pt is used as the cathode and PtFe/C is used as the anode. η_a values are shown in (b) beside corresponding data points.

4.2. Choice of electrode materials

In this work, PEC performances are analyzed for different electrode pairs. The choice of the proper electrode pair is essential as ${\eta }_{\mathrm{a}}$ depends on it. A greater ${\eta }_{\mathrm{STF}}$ with a suitable $E_{\mathrm{g}}$ is obtained for an electrode pair if ${\eta }_{\mathrm{a}}$ is less. Fig. 7 shows ${\eta }_{\mathrm{STF}}$ for different electrode pairs considering ${\eta }_{\mathrm{a}}$. Fig. 7(a) shows ${\eta }_{\mathrm{STF}}$ for different pairs of electrode materials for a single photo-absorber, while Fig. 7(b) shows that for double photo-absorbers connected in series both electrically and optically. Here, $E_{\mathrm{g}}=2.13$ eV is used for the single photo-absorber, and $E_{\mathrm{g}}=1.4$ eV and 0.72 eV are used in double photo-absorbers. Fig. 7 shows that ${\eta }_{\mathrm{a}}$ and ${\eta }_{\mathrm{STF}}$ depend inversely on each other. If ${\eta }_{\mathrm{a}}$ increases, ${\eta }_{\mathrm{STF}}$ decreases for any pair of cathode and anode. As a result, for the anode and cathode materials considered, the bottom left pairs of Fig. 7 can be preferable for any PECs as they have a smaller ${\eta }_{\mathrm{a}}$ due to larger $J_0$. Fig. 7(b) shows that ${\eta }_{\mathrm{STF}}$ depends more sensitively on the choice of electrode materials for double photo-absorbers than a single photo-absorber in a PEC configuration.

Figure 7.

η_a and η_STF for (a) single photo-absorber with E_g = 2.13 eV and (b) double photo-absorbers with E_g1 = 1.4 eV and E_g2 = 0.72 eV. Symbols ● and ■ indicate cathode and anode, respectively. Electrode materials are given as legends.

4.3. PEC configurations

HPR and ${\eta }_{\mathrm{STF}}$ are calculated considering ${\eta }_{\mathrm{a}}$ utilizing photo-absorbing and electrode materials from the libraries. ${\eta }_{\mathrm{STF}}$ depends on different optical and electrical configurations of PEC. ${\eta }_{\mathrm{STF}}$ also depends on the number of photo-absorbers, number of electrolyzers, and different electrode pairs. Increasing the number of photo-absorbers increases the absorption of solar energy. Although ${\eta }_{\mathrm{a}}$ increases when more electrolyzers are added to the system, the negative gradient of H₂ concentration decreases, offering convenient H₂ collection. This work compares ${\eta }_{\mathrm{STF}}$ of each photo-absorbing material utilizing several electrolyzers and electrode pairs.

4.3.1. Single photo-absorber

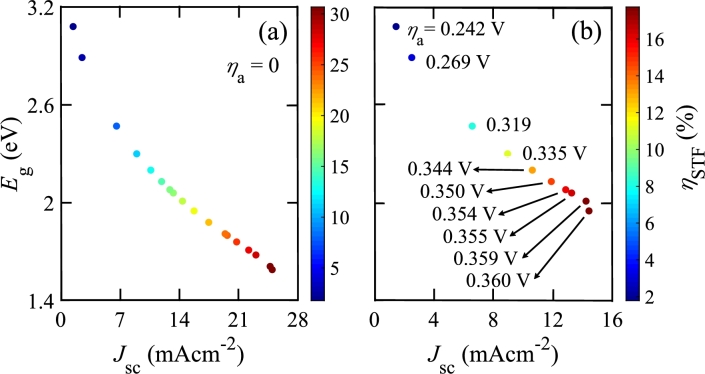
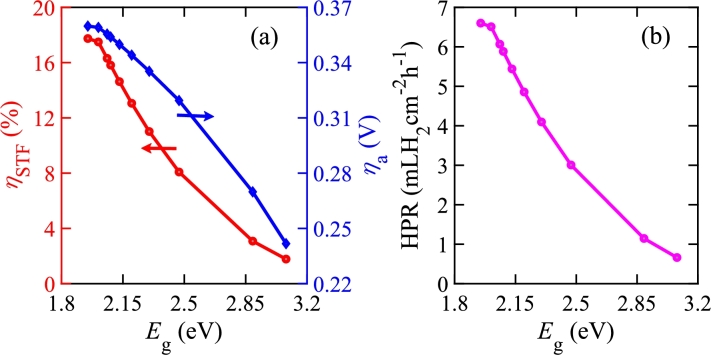
Fig. 8 shows ${\eta }_{\mathrm{STF}}$, ${\eta }_{\mathrm{a}}$, and HPR for a PEC that has a single photo-absorber in an electrolyzer. This PEC has a Pt cathode and a PtFe/C anode. We vary the photo-absorber $E_{\mathrm{g}}$ as given in Table 3. In this case, Fig. 8(a) shows that the maximum ${\eta }_{\mathrm{STF}}$ is 17.743% when the photo-absorber $E_{\mathrm{g}}=1.95$ eV and its corresponding ${\eta }_{\mathrm{a}}$ is 0.35982 V. Murphy et al. also reported that the required minimum $E_{\mathrm{g}}$ is almost 2 eV by utilizing AM 1.5 G for single photo-absorber [77]. If ${\eta }_{\mathrm{a}}$ is not considered, ${\eta }_{\mathrm{STF}}=19.337\text{\%}$ for the same $E_{\mathrm{g}}$, as also reported in Ref. 37. We note that ${\eta }_{\mathrm{STF}}=0$ for $E_{\mathrm{g}}<1.9$ eV if ${\eta }_{\mathrm{a}}$ is considered. However, ${\eta }_{\mathrm{STF}}$ can be obtained for smaller $E_{\mathrm{g}}$ values if ${\eta }_{\mathrm{a}}$ is neglected. For example, when $E_{\mathrm{g}}=1.59$ eV, ${\eta }_{\mathrm{STF}}$ is 30.68% without including ${\eta }_{\mathrm{a}}$. However, ${\eta }_{\mathrm{STF}}=0$ for the same bandgap, i.e., $E_{\mathrm{g}}=1.59$ eV, when ${\eta }_{\mathrm{a}}$ is considered in the calculation as the photo-absorber $E_{\mathrm{g}}$ does not meet the required potential for water splitting. Figs. 8(a) and (b) show that ${\eta }_{\mathrm{STF}}$ and HPR decrease when $E_{\mathrm{g}}$ increases. This is because ${\eta }_{\mathrm{STF}}$ is proportional to $J_{\mathrm{sc}}$, which decreases with increasing $E_{\mathrm{g}}$. Since HPR is proportional to ${\eta }_{\mathrm{STF}}$, it has a similar trend. On the other hand, ${\eta }_{\mathrm{a}}$ decreases when $E_{\mathrm{g}}$ increases as it also depends proportionally on $J_{\mathrm{sc}}$.

Figure 8.

(a) η_STF and η_a vs. E_g and (b) HPR vs. E_g of a PEC with a single photo-absorber in an electrolyzer.

4.3.2. Double photo-absorbers

We have also analyzed the impact of ${\eta }_{\mathrm{a}}$ on ${\eta }_{\mathrm{STF}}$ for double photo-absorbing materials in a PEC. Four PEC configurations are possible with double photo-absorbers, as shown in Figs. 3(a) and (b). This work investigated only the optical series-electrical series (OS-ES) and optical parallel-electrical series (OP-ES) PEC configurations for double photo-absorbers. Other configurations, such as optical series-electrical parallel (OS-EP) and optical parallel-electrical parallel (OP-EP) are discussed with triple photo-absorbers.

Fig. 9 shows the impact of ${\eta }_{\mathrm{a}}$ on ${\eta }_{\mathrm{STF}}$ for OS-ES PEC configuration with double photo-absorbers. While Figs. 9(a) and (b) illustrate ${\eta }_{\mathrm{STF}}$ and ${\eta }_{\mathrm{a}}$ with $E_{\mathrm{g}}$ for single electrolyzer, Figs. 9(c) and (d) illustrate those for double electrolyzers. For the single electrolyzer, Pt is used as the cathode and PtFe/C is used as the anode. In Figs. 9(a) and (c), the maximum ${\eta }_{\mathrm{STF}}$ is observed in the left-bottom portion of the range of the bandgaps, showing the maximum power point (MPP), where the cell outputs the maximum net power at a certain $V_{\mathrm{oc}}$ and $J_{\mathrm{sc}}$. As $E_{\mathrm{g}}$ increases, $V_{\mathrm{oc}}$ also increases but $J_{\mathrm{sc}}$ decreases. As a result, at a certain combination of the bandgaps, the MPP is achieved with the maximum ${\eta }_{\mathrm{STF}}$. In most cases, ${\eta }_{\mathrm{STF}}$ does not change significantly. $J_{\mathrm{sc}}$ is approximately a constant till the MPP, however, it decreases significantly as the operating point crosses the MPP. Therefore, the output power ($P_{\mathrm{out}}$) and ${\eta }_{\mathrm{STF}}$ decreases according to

$$V_{\mathrm{oc}}=V_{\mathrm{oc1}}+V_{\mathrm{oc2}},P_{\mathrm{out}}=V_{\mathrm{oc}}{J}_{\mathrm{sc}},{\eta }_{\mathrm{STF}}=\frac{P_{\mathrm{out}}}{P_{\mathrm{in}}}.$$ (11)

Figure 9.

Optimized η_STF and corresponding η_a for double photo-absorbing materials with optical and electrical series configuration for (a,b) single electrolyzer and (c,d) for double electrolyzers.

In the double-photo-absorber configuration, $V_{\mathrm{oc}}=V_{\mathrm{oc1}}+V_{\mathrm{oc2}}$, according to Eq. (11). However, $V_{\mathrm{oc1}}$ of $E_{\mathrm{g1}}$ acts as the main driver. When $E_{\mathrm{g2}}$ increases linearly, keeping $E_{\mathrm{g1}}$ constant, change of ${\eta }_{\mathrm{STF}}$ is also shown in Figs. 9(a) and (c). ${\eta }_{\mathrm{STF}}$ sharply decreases as $E_{\mathrm{g2}}$ increases for $E_{\mathrm{g1}}\le 2.6$ eV. However, when $E_{\mathrm{g1}}>2.6$ eV, ${\eta }_{\mathrm{STF}}$ does not change much when $E_{\mathrm{g2}}$ increases.

We note that $E_{\mathrm{g1}}$ and $E_{\mathrm{g2}}$ used in Fig. 9 are chosen from the photo-absorber library given in Table 3. Here, an increase in $E_{\mathrm{g}}$ means an increase in $V_{\mathrm{oc}}$. Keeping $E_{\mathrm{g1}}$ constant means keeping $V_{\mathrm{oc1}}$ constant for the first photo-absorber, and an increase in $E_{\mathrm{g2}}$ will not impact ${\eta }_{\mathrm{STF}}$ as $J_{\mathrm{sc}}$ remains constant initially, as shown in Fig. 3(c). When $E_{\mathrm{g2}}$ continues to increase, it eventually overcomes the constant value of $E_{\mathrm{g1}}$, and as a result, $J_{\mathrm{sc}}$ decreases. Consequently, ${\eta }_{\mathrm{STF}}$ decreases as well. These phenomena are observed in Fig. 9(a). ${\eta }_{\mathrm{a}}$ values for the variations of $E_{\mathrm{g1}}$ and $E_{\mathrm{g2}}$ are shown in Fig. 9(b). Fig. 9(c) shows ${\eta }_{\mathrm{STF}}$ for the same configuration as before, except for a PEC with double electrolyzers. Fig. 9(c) also shows that ${\eta }_{\mathrm{STF}}$ values are right-shifted compared to that in Fig. 9(a) due to high $V_{\mathrm{oc}}$ required for water splitting in double electrolyzers. Hence, the $E_{\mathrm{g}}$ range for double electrolyzers is smaller than that of a single electrolyzer. The second electrode pair of the double electrolyzers consists of Ni as the cathode and PtW₂/C as the anode. Corresponding ${\eta }_{\mathrm{a}}$ is shown in Fig. 9(d), where the values of ${\eta }_{\mathrm{a}}$ are higher than single electrolyzer values due to double electrolyzer.

Fig. 10 presents ${\eta }_{\mathrm{STF}}$ and ${\eta }_{\mathrm{a}}$ for OP-ES connection of double photo-absorbers in a single electrolyzer. The electrode pair consists Pt as the cathode and PtFe/C as the anode. The bandgap of each photo-absorber must be the same for an optically parallel connection. Fig. 10 shows that ${\eta }_{\mathrm{STF}}$ decreases as $E_{\mathrm{g}}$ increases. For double electrolyzers, higher bandgaps are required for water splitting to obtain ${\eta }_{\mathrm{STF}}$ along with decreasing ${\eta }_{\mathrm{a}}$.

Figure 10.

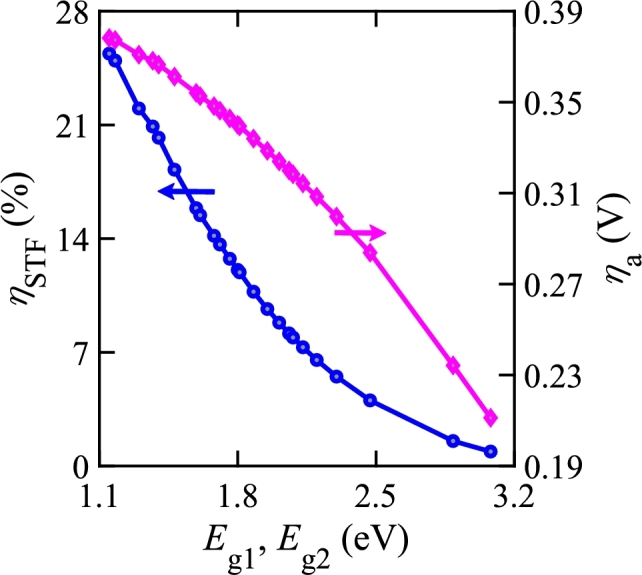
η_STF and η_a vs. bandgaps for optical parallel and electrical series configuration with double photo-absorbing materials in a single electrolyzer.

4.3.3. Triple photo-absorbers

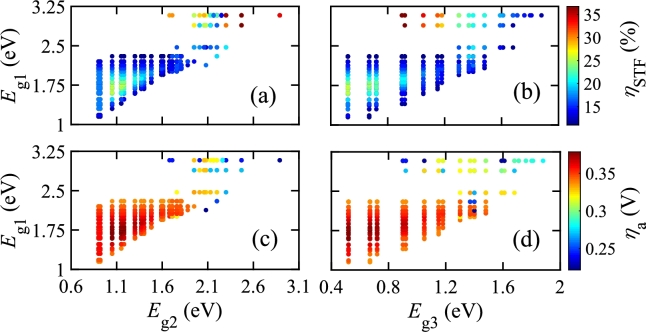
Fig. 11 is a scatter plot of ${\eta }_{\mathrm{STF}}$ and ${\eta }_{\mathrm{a}}$ for OS-ES PEC configuration with triple photo-absorbing materials in a single electrolyzer. Figs. 11(a,b) and 11(c,d) are illustrations of ${\eta }_{\mathrm{STF}}$ and ${\eta }_{\mathrm{a}}$ against $E_{\mathrm{g}}$, respectively. The electrode pair consists of Pt as the cathode and PtFe/C as the anode. We note that ${\eta }_{\mathrm{STF}}\ge 30\text{\%}$ when $E_{\mathrm{g1}}\ge 2.89$ eV, $2.3\le E_{\mathrm{g2}}\le$2.89 eV, and $0.9\le E_{\mathrm{g3}}\le 1.18$ eV. Fig. 11 also gives an idea of ${\eta }_{\mathrm{STF}}$ for any compatible bandgaps of triple photo-absorbing materials compared to the color from the color bar. The advantage of using triple photo-absorbing materials rather than single or double photo-absorbing materials is that the lower bandgap values can be utilized, and a greater ${\eta }_{\mathrm{STF}}$ can be obtained in the presence of ${\eta }_{\mathrm{a}}$. For a PEC with double electrolyzers, although the range of bandgaps for photo-absorbers increases, ${\eta }_{\mathrm{a}}$ increases as well.

Figure 11.

Optimized η_STF in (a,b) and corresponding η_a in (c,d) are shown for triple photo-absorbing materials with optical series and electrical series configuration.

For the OP-ES PEC configuration of triple photo-absorbing materials, ${\eta }_{\mathrm{STF}}$ and ${\eta }_{\mathrm{a}}$ follow a similar trend as in the OP-ES PEC configuration of double photo-absorbing materials. However, smaller bandgap materials can be used in triple photo-absorbing materials.

We also investigated a mixed configuration to obtain a detailed analysis of EP PEC configuration. For the mixed configuration of triple photo-absorbing materials, we used the optical configuration from Fig. 3(a)(v) and the electrical configuration from Fig. 3(b)(v). $J_{\mathrm{sc}}$ will increase in the EP configuration, whereas $V_{\mathrm{oc}}$ will increase in the ES configuration. There are four branches in this mixed configuration. One branch is external, and the rest are internal. The mixed configuration will work fine when an electrolyzer is located in the external branch according to the connections of Fig. 3(b)(v). However, when an electrolyzer is located in the internal branch, then another electrolyzer should be placed in the external branch. Otherwise, the external connection must be open to make the circuitry work, and opening the external connection will eventually make the mixed configuration an ES configuration.

We analyzed ${\eta }_{\mathrm{STF}}$ and ${\eta }_{\mathrm{a}}$ with $E_{\mathrm{g}}$ for the mixed configuration where a single electrolyzer is located in the external branch, as shown in Fig. 12. ${\eta }_{\mathrm{STF}}$ and ${\eta }_{\mathrm{a}}$ show a similar trend where larger values of them are obtained on the top-left portion of the Figs. 12(a) and (b) with $E_{\mathrm{g1}}\ge 2.2$ eV and $E_{\mathrm{g2}}$, $E_{\mathrm{g3}}\le 2.2$ eV. The results we obtained here are also applicable for the EP PEC configuration where $E_{\mathrm{g1}}$ is connected in parallel with series connected $E_{\mathrm{g2}}$ and $E_{\mathrm{g3}}$.

Figure 12.

(a) Variation of η_STF with bandgap for the mixed configuration analyzed in this paper. (b) Corresponding η_a for same PEC configuration.

Table 4 is a summary of the optimized ${\eta }_{\mathrm{STF}}$ and HPR for different PEC configurations, as shown in Figs. 3(a) and 3(b). For each PEC configuration with several electrolyzers, the optimized cathode, anode, and photo-absorbing materials are found from the photo-absorbing and electrode material libraries based on ${\eta }_{\mathrm{STF}}$ given in Table 4. Corresponding HPR and ${\eta }_{\mathrm{a}}$ are also given in Table 4.

Table 4.

Optimized η_STF and HPR including η_a for different PEC configurations of Fig. 3(a,b).

Configuration	Nelec	Cathode	Anode	Eg (eV)	ηSTF (%)	HPR	ηa (V)
Fig. 3(a)(i), 3(b)(i)	1	Pt	PtFe/C	1.95	17.74	6.60	0.359
Fig. 3(a)(ii), 3(b)(ii)	1	Pt	PtFe/C	1.59, 0.92	31.75	23.62	0.389
	2	Pt, Ni	PtFe/C, PtW2C/C	2.3, 1.81	21.891	16.28	0.831
	3	Pt, Ni, Au	PtFe/C, PtFe/C, PtW2C/C	3.08, 2.47	5.23	3.89	1.017
Fig. 3(a)(iv), 3(b)(ii)	1	Pt	PtFe/C	1.15, 1.15	25.39	18.89	0.378
	2	Pt, Ni	PtFe/C, PtW2C/C	2.01, 2.01	16.51	12.28	0.802
	3	Pt, Pt, Ni	PtFe/C, PtFe/C, PtW2C/C	2.89, 2.89	4.621	3.44	0.863
Fig. 3(a)(iii), 3(b)(iv)	1	Pt	PtFe/C	3.08, 2.47, 0.90	36.75	41.02	0.242
	2	Pt, Ni	PtFe/C, PtW2C/C	2.01, 1.48, 1.05	35.30	29.40	0.880
	3	Pt, Ni, Au	PtFe/C, PtFe/C, PtW2C/C	2.47, 2.06, 1.76	24.24	27.06	1.255
Fig. 3(a), 3(b)(iv)	1	Pt	PtFe/C	0.92, 0.92, 0.92	21.28	23.75	0.369
	2	Pt, Ni	PtFe/C, PtW2C/C	1.48, 1.48, 1.48	23.97	26.75	0.840
	3	Pt, Pt, Ni	PtFe/C, PtFe/C, PtW2C/C	1.95, 1.95, 1.95	17.57	19.61	1.069
Fig. 3(a)(v), 3(b)(v)	1	Pt	PtFe/C	2.47, 1.95, 1.95	10.95	12.22	0.335

5. Conclusion

This work is critical to calculating ${\eta }_{\mathrm{STF}}$ and HPR in realistic PECs. This work includes ${\eta }_{\mathrm{a}}$ in calculating ${\eta }_{\mathrm{STF}}$ and HPR for different configurations and finds photo-absorber and electrode materials for desired PEC performances. It is found that the ${\eta }_{\mathrm{STF}}$ and HPR are significantly affected when ${\eta }_{\mathrm{a}}$ is considered in the calculation. An idea is obtained for selecting appropriate photo-absorbers and electrode pairs for PEC configurations to achieve a desired ${\eta }_{\mathrm{STF}}$ and HPR. The proper design of electrical branches and the positions of electrodes in branches can be determined based on the optimized ${\eta }_{\mathrm{STF}}$ and HPR calculated in the presence of ${\eta }_{\mathrm{a}}$. However, it is important to note that this work considers a constant temperature and pressure. This work also does not consider losses due to electrolytes. The results will vary slightly when the impacts of temperature, pressure, and electrolytic losses are considered.

CRediT authorship contribution statement

Abdul Ahad Mamun, Asif Billah: conceived and designed the experiments; performed the experiments; analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; and wrote the paper.

Muhammad Anisuzzaman Talukder: conceived and designed the experiments; performed the experiments; analyzed and interpreted the data; and wrote the paper.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

Data will be made available on request.