Growth Feedback Confers Cooperativity in Resource-Competing Synthetic Gene Circuits

Abstract

Modularity is a key concept in designing synthetic gene circuits, as it allows for constructing complex molecular systems using well-characterized building blocks. One of the major challenges in this field is that these modular components often do not function as expected when assembled into larger circuits. One of the major issues is caused by resource competition, where multiple genes in the circuit compete for the same limited cellular resources, such as transcription factors and ribosomes. In addition, the mutual inhibition between synthetic gene circuits and cell growth results in growth feedback that significantly impacts its host-circuit dynamics. However, the complexity of the gene circuit dynamics under intertwined resource competition and growth feedback is not fully understood. This study developed a theoretical framework to examine the dynamics of synthetic gene circuits by considering both growth feedback and resource competition. Our results suggest a cooperative behavior between resource-competing gene circuits under growth feedback. Cooperation or competition is non-monotonically determined by the metabolic burden threshold. These two diverse effects could lead to the activation or deactivation of one circuit by the other. Lastly, the cooperativity mediated by growth feedback can attenuate the winner-takes-all resource competition. These findings show that coupling growth feedback and resource competition plays a crucial role in the dynamics of the host-circuit system, and understanding its effects helps control unexpected gene expression behaviors.

1. Introduction

Synthetic gene circuits usually need multiple modules to achieve complicated functions. Ideal modularity could greatly facilitate the construction process of multi-module gene circuits. However, these well-characterized modules in isolation could be undesirably connected by indirect context-dependent interactions [1, 2, 3, 4, 5, 6, 7], such as resource competition and growth feedback. Resource competition exists between circuit modules where one module exploits the limited resources in the host cells for its transcription and translation at the expense of other modules [8, 9, 10]. Growth feedback is found between the synthetic circuit and host cell growth, where the expression of synthetic gene circuits inhibits the growth rate by causing a metabolic burden to the host and in return is affected by cell growth-mediated dilution [11, 12, 13, 14]. These indirect interactions between modules can lead to unexpected outcomes if the whole circuit design is under any assumption of ideal modularity.

Previous works have studied the implications of resource competition on the deterministic and stochastic behavior of synthetic gene circuits [8, 9, 15, 10, 16]. For example, Qian et al. found that the intended monotonically increasing dose-response curve of an activation cascade circuit was found to be biphasic or monotonically decreasing due to resource competition [9]. Zhang et al. found that the resource competition of a synthetic gene circuit with two bistable switch modules led to a winner-takes-all outcome instead of the expected co-activation [10]. That is, one of the modules takes most of the resources, making it hard to activate the other module and coactivate the system. Feedback and feedforward control strategies have been proposed to mitigate the effects of resource competition and allow the system to achieve the co-activation of two modules [17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27].

On the other hand, growth feedback creates another layer of complexity in the circuit-host system. For example, Zhang et al. demonstrate that growth feedback could affect circuit memory depending on the network topology [28]. In addition, growth feedback can lead to the emergence of unexpected qualitative states [29, 30] or oscillations [31]. However, the combined effects of growth feedback and resource competition on a circuit-host system have not been elucidated.

Here, we studied how growth feedback could affect the dynamics of multi-module gene circuits under resource competition. We developed a mathematical modeling framework incorporating both resource competition and growth feedback. First, we found that coupling modules through growth feedback could lead to cooperativity between them and thus counteract the effects of resource competition. We demonstrated the existence of the cooperativity between two simple genes under growth feedback and characterized the mathematical conditions that allow cooperative behavior. In addition, we analyzed the cooperativity of a system with one inducible gene module and one self-activating module. We found that an inducible gene can activate or deactivate the latter module. Similarly, a self-activation gene circuit’s bistability could lead to a bistable competition or cooperation behavior in a constitutive expressing gene. Lastly, we found that the growth feedback could buffer the winner-takes-all effect caused by resource competition. Thus, the resource competition between gene circuits and their interaction with growth feedback could significantly impact the dynamics of synthetic gene circuits involving multiple modules.

2. Results

2.1. Modeling Framework for Synthetic Gene Circuit by Considering Both Resource Competition and Growth Feedback

Different host-circuit mathematical models have been developed in previous works to describe the growth feedback [28] or resource competition [10]. Here we incorporated the resource competition between multiple modules in circuits based on the theoretical framework developed by Zhang et al. [10]. In addition, we added the dilution rate and metabolic burden based on the modeling framework from [28]. The general ordinary differential equations for synthetic circuits with multiples genes are given by:

$$\frac{d{x}_i}{dt}=\stackrel{\text{production rate under Resource competiton}}{\overbrace{\frac{v_i{R}_i}{\underset{k=1}{\overset{n}{\Sigma }}\frac{R_k}{Q_k}+1}}}-\underset{\text{Degradation rate}}{\underbrace{d_i{x}_i}}-\stackrel{\text{Dilution rate under Metabolic burden}}{\overbrace{\frac{k{g}_0{x}_i}{\underset{k=1}{\overset{n}{\Sigma }}\frac{R_k}{J_k}+1}}}$$ (1)

where x_i is the expression level of gene-i, and v_i is the overall gene expression rate of gene-i. R_i is the concentration of active promoters for gene-i bound by transcription factors,and d_i is the degradation rate constant of the gene-i product. Q_i is the overall capacity of limited resources in the host cell available for gene-i expression. Therefore, the maximum production rate is v_i R_i, and the effect of the resource competition is given by $1/({\sum }_{k=1}^n\frac{R_k}{Q_k}+1)$. The cell growth rate effect without metabolic burden is kg₀, and the maximum dilution rate is kg₀ * x_i. The growth attenuation by metabolic burden is given by $1/({\sum }_{k=1}^n\frac{R_k}{J_k}+1)$, where J_i is the metabolic burden threshold for gene-i expression. This framework is suitable for analyzing the system’s steady state in the exponential growth phase.

2.2. Two Competing Circuits Could Cooperate under Growth Feedback

First, we studied the synthetic gene circuit with one module with inducible promoter x₁ (Module 1) and one constitutive expressing module x₂ (Module 2). We analyzed how expression levels of gene 1 and 2 (x_1ss and x_2ss) and growth rate change with module 1 inducer, R₁ under conditions without (1A, top) and with (1B, top) growth feedback. By increasing the values of R₁, we expect an increase on x_1ss. Accordingly, x_2ss with a fixed value of R₂ is expected to decrease due to the resource competition from x₁. Figure 1A (bottom) shows a linear decrease of steady-state values of x₂ (blue line) with the increase of x₁ for a system without considering the growth feedback. Given that the metabolic burden caused by synthetic genes was not considered, the system’s growth rate (orange line) is not affected by gene expression. In addition, model analysis reveals that this phenomenon can occur for any positive parameter value set (See supplementary material, proposition 1). This idea case is consistent with previous works [8].

Figure 1:

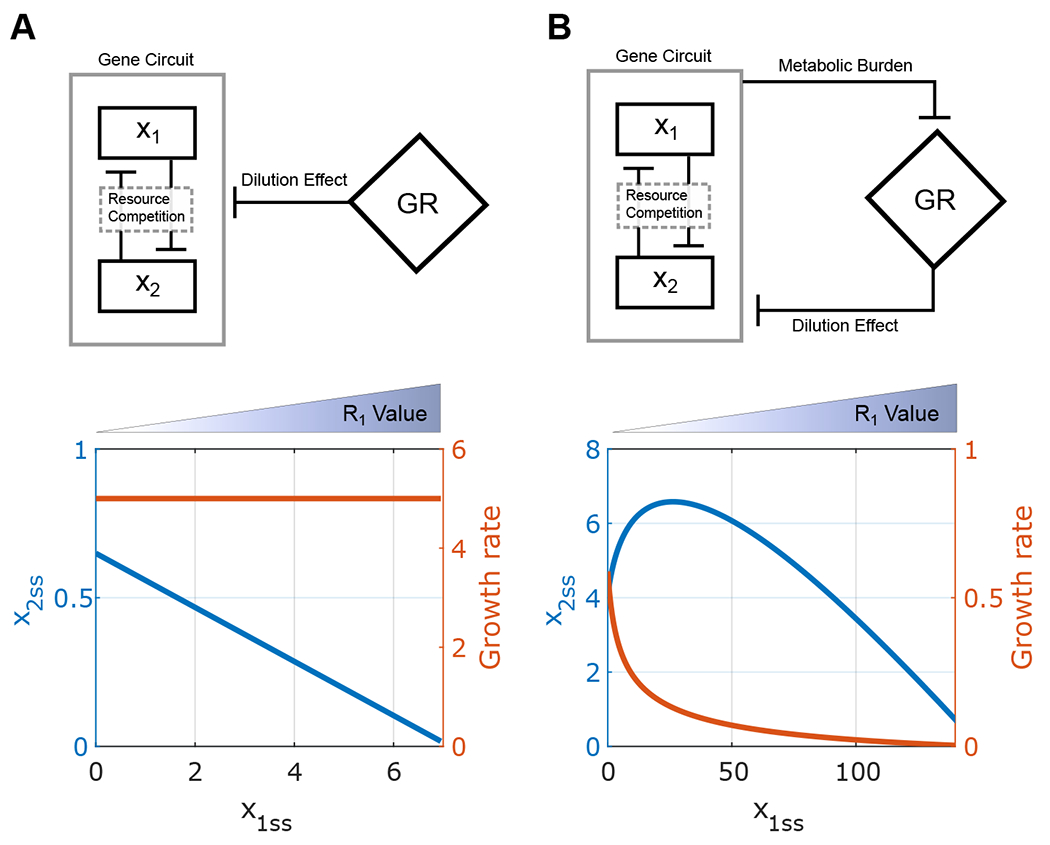
Analysis of the synthetic gene circuit with one constitutive expressing module and one module with the inducible promoter. (A-B) Diagram of interactions between a synthetic gene circuit by considering resource competitive only (A, Top), or both resource competition and growth feedback (B, Top). The level of x₂ (blue line) and growth rate (orange line) with the increase of x₁ under the context with and without growth feedback, respectively(Bottom).

Next, we incorporated the growth feedback into the system by considering the growth rate reduction caused by the metabolic burden from the gene circuit (1B, top). Now the growth rate decreases with an increase of x_1ss (Figure 1B, Bottom). Interestingly, x_2ss first increases simultaneously with x₁, then decreases. The increment of x_2ss implies some cooperativity between the two modules, different from the competitive effect due to resource competition. An increase of x₁ expression decreases the growth rate and the growth-mediated dilution of x₂ and thus benefits the x₂ expression. When x₂ increases, it also causes additional metabolic burden and a decrease in the growth rate, which ultimately leads to an further increase in x₂. With a further increase of x₁, the resource competition between modules starts to be significant, which decreases x₂ after reaching a maximum level. Therefore, two competing genes can cooperate with each other under growth feedback under some conditions.

2.3. Cooperation between Two Circuits is non-monotonically Controlled by Metabolic Burden Threshold

We further analyzed the model to find the condition that allows the system to show the cooperative behavior revealed in Figure 1B (bottom). Here, the cooperativity is quantified by the increment of Module 2 expression (x_2ss ) with respect to an increment of Module 1 expression (x_1ss ). Through analysis (see more detail in Supplementary Material 2.1), we found the following parameter condition:

$$\frac{1}{Q_1}\frac{Q_2}{(Q_2+R_2)}\le \frac{1}{J_1}\frac{J_2}{(J_2+R_2)}\frac{J_2}{J_2+R_2\left(\frac{d_2}{d_2+k{g}_0}\right)}\frac{k{g}_0}{k{g}_0+d_2}$$ (2)

The system shows a cooperative relation if the above condition is satisfied for a bounded range of R₁. On the other hand, a parameter set that does not follow the above condition shows only competitive behavior. Each term in the parameter condition is interpreted as follows: 1/Q₁ represents the load of x₁ using resources available for the synthetic genes circuit. Q₂/(Q₂ + R₂) is the fraction of resource that x₂ takes from the limited resource for synthetic gene circuits. 1/J₁ is the factor modifying the host’s metabolic burden caused by x₁. J₂/(J₂ + R₂) is the fraction of the metabolic burden generated by x₂. The kg₀/(kg₀ + d₂) and d₂/(d₂ + kg₀) represent the fraction of the loss rate for Module 2 driven by dilution and degradation, respectively. To find the parameter condition of cooperativity, the left-hand side term of the condition should be as low as possible and the right-hand side term should be as greater as possible.

From the above condition, we can see that the Q_i and J_i are the important parameters for the cooperativity. This is reasonable as they represent the strength of the growth feedback and resource competition. To demonstrate the dependence of the cooperativity on them, we analyzed the mathematical model for the case where the two modules have equal values for Q and J, that is, Q₁ = Q₂ = Q and J₁ = J₂ = J.

We used two characteristics to measure the intensity and robustness of the cooperativity between the two competing modules (Figure 2A), the maximum relative increment (MRI), and the competition relief range (CRR). MRI quantifies the extent of increment of one module expression because of the expression of the competing module. MRI is calculated as the maximum relative change between the expression level of module 2 with and without module 1 expression. That is, MRI is defined as 100*|x_2ss − x₂₀|/x₂₀, where x_2ss and x₂₀ are the module 2 expression level with and without x₁ expression respectively. MRI corresponds to the intensity of cooperativity. CRR describes the total range of one module induction where the other module expression increases. CRR is defined as the range of module 1 expression level x_1ss where the module 2 expression is enhanced. That is, in CRR, x_2ss are higher than the expected expression without module 1 expression x₂₀. CRR indicates the robustness of the cooperativity between the competing genes.

Figure 2:

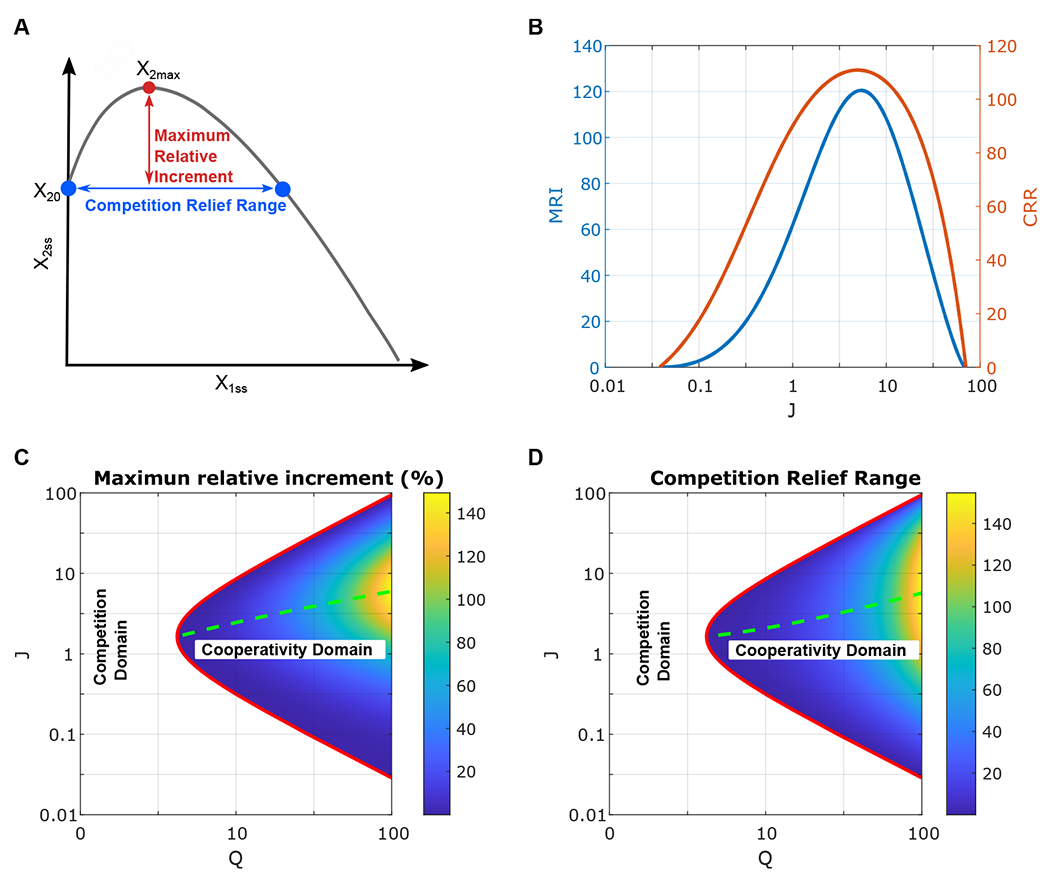
Analysis of the condition for the cooperativity between two competing modules. (A) Diagram of the two features to quantify the cooperative behavior. The maximum relative increment (MRI) is the maximum relative change between the expression level of module 2 with and without module 1 expression. The competition relief range (CRR)represents the range of x_1ss where the module 2 expression is enhanced by expressing module 1. (B) The dependence of MRI (left) and CRR (right) on J with fixed (Q = 75.14). Colormaps of MRI (C) and CRR (D) in the space of Q and J. Red lines represent the parameter condition (see the inequality equation 3).

Figure 2B shows the dependence of MRI (blue line) and CRR (orange line) on J with a fixed value of Q. Interestingly, both MRI and CRR first increase before reaching their maximum and then decrease with metabolic burden threshold J, showing a nonmonotonic dependence. Low or high values of J do not show cooperative behavior. For a fixed value of Q, a maximum level of cooperativity can be found with an optimal value of J. In the previous section, we show that the cooperativity in competing genes is driven by growth feedback. It is reasonable for the low level of cooperativity under a large value of J since the metabolic burden caused by one module is insufficient to significantly change the dilution rate of the other module. For a small value of J, the metabolic burden is significant that both modules could be expressed at high levels with highly reduced dilution rate, which also leads to a high level of resource competition and diminishes the level of cooperativity.

To understand the system’s condition with competition relief, we estimated the value of MRI and CRR for in the space of J and Q (Figure 2 C and D). Cooperativity cannot be achieved with high competition (low values Q). Within this white region, we expect that the system behaves like the one is shown in Figure 1A (competition domain). Increasing the Q value decreases the competition between two modules, and thus gives the system the chance to have cooperativity and increase the MRI and CRR value . That is, a decrease in competition between gene modules creates a higher level of cooperativity.

Interestingly, both MRI and CRR first increase and then decreases with parameter J, showing a nonmonotonic dependence on the metabolic burden threshold. For a fixed value of Q, a maximum level for cooperativity can be found with an optimal value of J (Figure 2C–D; dashed green lines on the colormap). Interestingly, the optimal value of J for the maximum cooperativity increases with Q (Figure 2C–D; dashed green lines), which is largely due to the opposite effects from growth feedback and resource competition. Remarkably, the boundary between competition and cooperative domains is defined by the parameter condition discussed above for J = J₁ = J₂ and Q = Q₁ = Q₂, and is given by:

$$\frac{1}{(Q+R_2)}\le \frac{1}{(J+R_2)}\frac{J}{J+R_2\left(\frac{d_2}{d_2+k{g}_0}\right)}\frac{k{g}_0}{k{g}_0+d_2}$$ (3)

2.4. Activation and Deactivation of One Self-activating Circuit by one Resource-Competing Circuit

To explore the implication of the cooperativity phenomenon on a more complicated circuit, here, we developed and analyzed a mathematical model for a system with a gene with an inducible promoter (x₁) and a self-activation (x₂) module (Figure 3A). For this system, R₂ is defined as follows:

$$R_2=(k_{02}+\frac{(I_{SA}\cdot x_2{)}^2}{{(I_{SA}\cdot x_2)}^2+1})\cdot N_{cp2}$$

where N_cp is the plasmid copy number, and the I_SA is the induction parameter of the self-activation. k₀₂ is the parameter that represents a basal production for the self-activation module.

Figure 3:

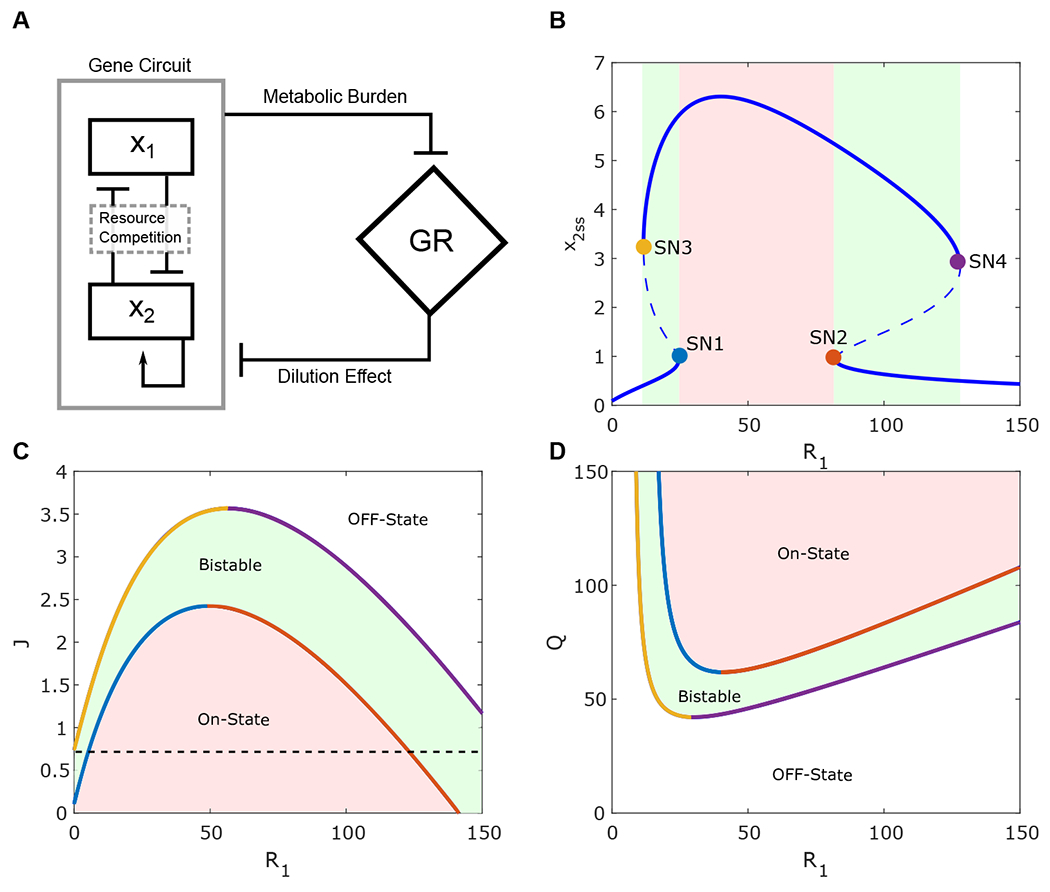
Analysis of the synthetic gene circuit with a gene with an inducible promoter and a self-activation module. (A) Diagram of interaction between a synthetic gene circuit with a gene with an inducible promoter (x₁) and self-activation (x₂) modules and growth rate. (B) The bifurcation diagram of x₂ with respect to R₁. Solid and dashed lines correspond to stable and unstable steady state points. Solid circles denote the saddle-node bifurcation points (blue, orange, yellow, and purple for SN1-4, respectively). (C-D) Two-parameter bifurcation diagram shows the dependence of the saddle-nodes (SN1-4) on J (Q in (D)) and R₁. SN1 (blue line), SN2 (orange line), SN3 (yellow line), and SN4 (purple line) correspond to the saddle-node bifurcation points. The red region represents the ON-state of x₂ Module, the green region corresponds to the system bistability, and the white region represents the OFF-state of the x₂ module

We first performed a one-parameter bifurcation analysis to understand how one competing gene cooperates with the self-activation module. As shown in Figure 3B, four saddle nodes (SN1-4) were found in the bifurcation diagram of x₂ with respect to R₁. The four saddle nodes represent the value of R₁ where an x₂ steady state appears or vanishes. It is noted that for low values of R₁, the system is monostable with low expression level of x₂ due to the high dilution rate. However, an increase of R₁ above SN1 (blue circle) activates the switch due to the cooperativity. That is, the expression of module 1 causes metabolic burden and decreases the host cell growth rate and, thus, the dilution of module 2. Module 2 with reduced dilution, is able to be activated. Activated module 2 can be maintained at the ON state even if the R₁ value is reduced until SN3 (yellow circle). The system shows bistability with values of R₁ between SN1 and SN3. An increase of R₁ to larger values makes the competition between the two modules significant and thus leads to the decrease of x₂. Thus, module 1 turns off the self-activation switch at another saddle-node bifurcation point SN4 (purple circle). That is, another bistable region appears between SN2 and SN4, which is driven by competition. Finally, x₂ stays in the OFF state for values of R₁ greater than SN4. Hence, a simple gene module can turn a self-activation switch module on or off by creating a cooperative or competitive environment.

It is noted that for low values of R₁, the system is monostable with a low expression level of x₂ because the self-activation circuit is not strong enough to be activated under the condition with a high dilution rate. However, an increase of R₁ above SN1 (Figure 3B, blue circle) attenuates the growth rate significantly enough to activate the self-activation switch. Activated module 2 can be maintained at the ON state with the high metabolic burden caused by itself even if the R₁ value is reduced until SN3 (Figure 3B, yellow circle). That is, the system shows bistability with values of R₁ between SN1 and SN3 due to the cooperativity between a SA and an inducible gene circuit. This implies a mechanism by which some signaling pathways are activated due to a change in growth rate by any other factors. A similar phenomenon has been seen in natural systems. Kueh et at. report that the feedback between the cell cycle and regulatory factor PU.1 could regulate myeloid differentiation [32].

We further performed a two-parameter bifurcation analysis with respect to R₁ versus J and Q, which shows the dependence of the R₁ values of the saddle nodes with respect to the J and Q value (Figure 3 C and D). Figure 3 C shows that by increasing the values of J (decrease of the metabolic burden), SN1 (blue curve) and SN2 (orange curve) merge where the monostable ON-state region (red region) vanishes. In this region, the monostable ON-state of x₂ module can be turned off by increasing or decreasing the value of R₁. Further, increasing J could lead to the vanishing of SN3 and SN4, leading to the loss of cooperativity between the two modules and the non-activation of module 2. On the other hand, with low values of J (high metabolic burden, below the dashed line in Figure 3C), SN3 vanishes. That is, the module 2 switch can be turned on by module 1, but can only be turned off by the resource competition from x₁ (increasing R₁). Figure 3D shows the two-parameter bifurcation with respect to R₁ and Q. The monostable ON-state region between SN1 and SN2 expands with decreasing the resource competition between genes (increasing Q). Meanwhile, the SN1 and SN2 merge by increasing module resource competition (decreasing Q). Under this condition, module 2 cannot turn on by changing R₁. Lowering the values of Q (increasing the competition) makes module 1 suppress the switching capacity of module 2, leading to a monostable OFF-state where x₁ dominates. Under the non-fair resource competition parameter set (Q₁ ≠ Q₂ and J₁ ≠ J₂), we expect a similar outcome with respect to J₁ and Q₁ (Figure S1 A and B). The change in J₁ and Q₁ provoked a similar change seen in Figures 3 C and D. Therefore, under certain parameter conditions, an inducible gene expression could activate or deactivate a self-activation circuit.

2.5. Emergent Bistability in one Constitutively Expressing Circuit induced by One Bistable Resource Competitor

In the last section, we analyzed how the dynamics of one self-activation circuit could be perturbated by expressing one resource-competing circuit using one constitutively expressing circuit as one example. One bistable self-activation circuit could lead to two states with different cell growth rates and resource levels, significantly affecting the dynamics of other circuits in the same cell. Here we explore how the bistable behavior of one self-activation circuit affects the expression of one constitutively expression (CE) gene circuit.

First, we performed a one-parameter bifurcation analysis with respect to the SA circuit inducer dose (I_SA) with different Q values (Figures 4 A–B). Increasing I_SA activates the SA circuit at threshold SN2, and decreasing I_SA deactivates it at threshold SN1. That is, the SA circuit is bistable between SN1 and SN2. Interestingly, the CE circuit also becomes bistable with the same thresholds. However, the CE circuit bistable behavior depends on the Q values. For a small Q value, the resource competition between the SA and CE circuits is significant. Thus, the SA circuit’s activation leads to the CE circuit’s deactivation (Figure 4A). However, with a large Q value, the SA circuit activation leads to the CE circuit’s further expression at higher level (Figure 4B) due to the reduced resource competition and dilution effect. That is, high resource availability (Q) for synthetic genes promotes stronger cooperation from self-activation to constitutive gene circuit. Taken together, when the cooperativity between two circuits is dominant, the emergent bistable behavior of the CE circuits aligns with the SA circuit while running in the opposite direction when the resource competition dominates.

Figure 4:

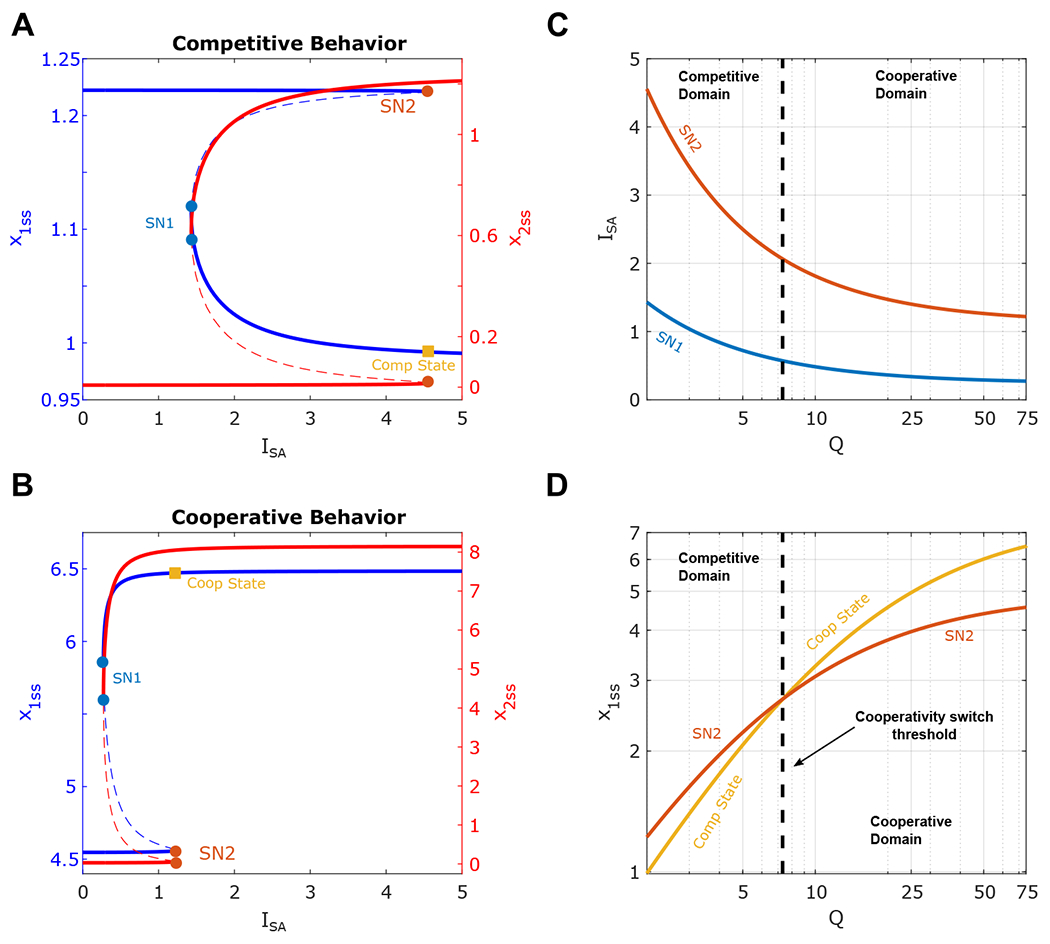
Analysis of the dynamics of one Constitutively Expressing (CE) Circuit upon induction of One Bistable SA Circuit . (A-B) One-parameter bifurcation diagram of x₁ (blue) and x₂ (red) with respect to I_SA. Solid and dashed lines correspond to stable and unstable steady states, respectively. Solid circles denote the saddle-node bifurcation points ( SN1-2, respectively). Q = 75 in A and Q = 2 in B. (C) Two-parameter bifurcation diagram shows the dependence of the saddle-node bifurcation (SN1-2) on Q value. (D) The expression levels of the CE circuit at the ON/OFF states around the activation threshold of the SA circuit (SN2) . The dashed black line at the intersection of two curves indicates the boundary of the competitive domain (left) and cooperative domain (right).

It is noted that the saddle-node points shift to the left when the Q value increases (Figure 4A–B). This is reasonable given that the Q value indicates the level of available resources to the circuits in the host cell. Thus, with a large Q value, the basal level at the OFF state for SA Circuit becomes larger. In addition, the resource-mediated inhibition from the CE circuit becomes smaller. All these factors lead to the reduced activation threshold for the SA circuit. This is confirmed by our two-parameter bifurcation result, which shows that increasing the value of Q decreases the I_SA values at the saddle nodes (Figure 4C). Hence, increasing the resource availability for synthetic circuits changes not only the emergent bistable of the CE circuit but also decreases the deactivation and activation thresholds. To further understand how the effect of the SA circuit on the CE circuit depends on the resource availability, the expression levels of the CE circuit at the ON/OFF states around the threshold SN2 as a function of the Q value are shown in Figure 4D. We found that the two curves intersect at Q ≈ 7.3 (the dashed line in Figure 4D), separating the system into the competitive (left) and cooperative domain (right). Our results suggest that one circuit could become bistable because of a bistable circuit in the same host cell, and it could switch on or off upon the activation of the bistable circuit, depending on resource availability.

2.6. Cooperativity Could be Used to Remediate Winner-Take-All Resource Competition

In the previous section, the model analysis revealed how constitutive gene modules could switch on and off a self-activation module based on cooperativity or competition with a bistable circuit. Following, we studied the gene circuit system with two self-activation modules (Figure 5A). For this system, R₁ and R₂ are defined as

$$R_1=\left(k_{01}+{\frac{(I_{SA1}\cdot x_1{)}^2}{{(I_{SA1}\cdot x_1)}^2+1}}^2\right)\cdot N_{cp1}$$

$$R_2=\left(k_{02}+{\frac{(I_{SA2}\cdot x_2{)}^2}{{(I_{SA2}\cdot x_2)}^2+1}}^2\right)\cdot N_{cp2}$$

Figure 5:

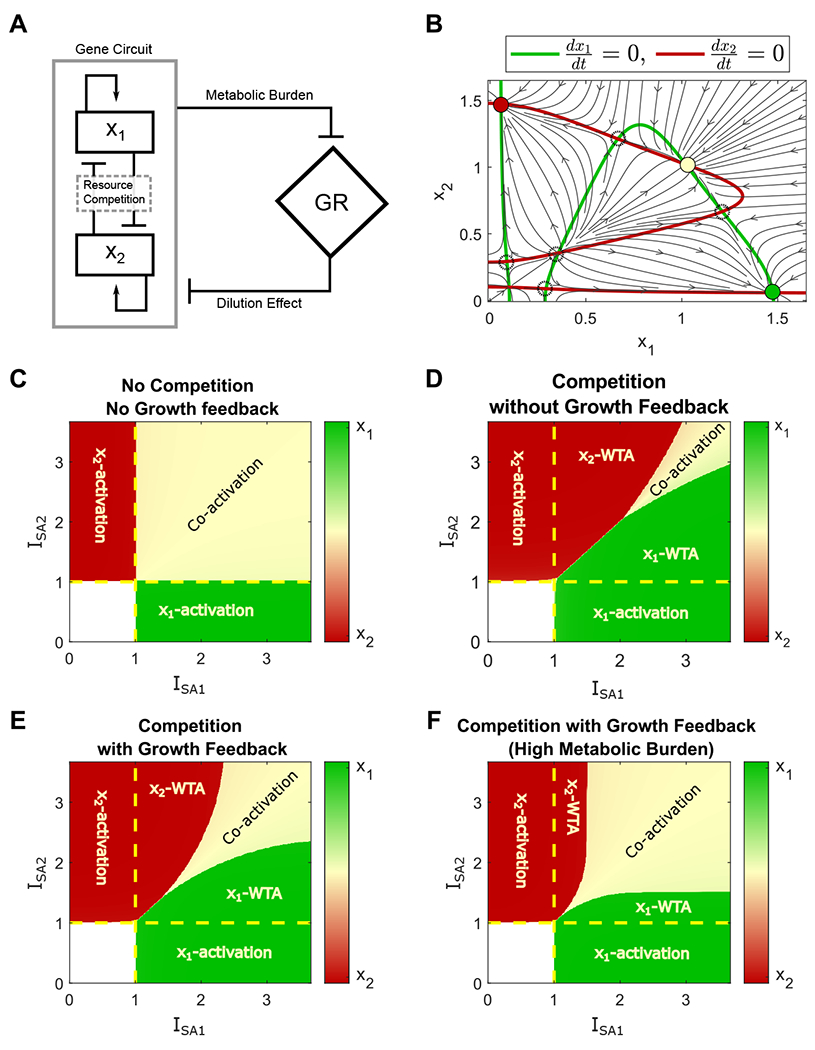
Cooperativity induced by the Growth feedback remediates the winner-take-all (WTA) competition of two self-activation modules. (A) Diagram of interaction between a synthetic gene circuit with two self-activation modules and growth rate. (B) Nullcline analysis. Green and red lines represent the nullcline (dx₁/dt = 0, dx₂/dt = 0) for x₁ and x₂, respectively. Solid and dashed circles represent stable and unstable steady states. Black arrows represent the directional field of the system. (C-F) Cell fates in the space of inducer I_SA1 and I_SA2, starting from the OFF-OFF state, normalized with respect to the switch activation thresholds under conditions with neither competition nor growth feedback (C), with resource competition and no growth feedback (D); competition with metabolic burden (E)(J₁ = J₂ = 15), and high metabolic burden (F)(J₁ = J₂ = 4).

where N_cpi is the plasmid copy number, and I_SAi is the inducer dose of the self-activation. k_0i is a basal production rate for the self-activation module. i ∈ {1, 2} denotes the module index. Figure 5B shows the nullcline (green and red curves) and direction field (black arrows) of the system, where nine steady states were found at the intersections between the nullclines (circles). The directional field reveals four stable steady states (solid color circles), including the low expression (OFF-OFF state), activation of module 1 only (ON-OFF state), activation of module 2 only (OFF-ON state), and co-activation of both modules (ON-ON state). That is, the co-activation of competing self-activation modules could exist even if a high resource competition between the modules (low values of Q₁ and Q₂) was used. The reason is that the incorporation of growth feedback in the model could lead to some level of cooperation to counteract resource competition.

We further analyzed how co-activation is affected by the cooperativity induced by the growth feedback. Figure 5 C–F shows the final steady states of the system in the space of the normalized inducer doses of two modules starting from an OFF-OFF state, under conditions with no normal and high metabolic burden, respectively. The red and green regions represent the activation of module 1 or module 2, respectively. The white region represents the OFF-OFF state, and the yellow region represents the co-activation state. Without neither resource competition nor growth feedback, the two modules are independent, so the activation of one module does not affect the other, leading to the ideal modularity (Figure 5C). Figure 5D shows that a high level of resource competition leads to a significantly reduced co-activation region (yellow area) and a large winner-take-all (WTA) region in the system without growth feedback. This provides an alternative strategy to mitigate the Winner-Takes-All resource competition in addition to the proposed negative feedback and feedforward controllers in the previous works [24, 25]. Incorporating the growth feedback into the system (figure 5E) expands the co-activation region and reduces the winner-take-all region. In addition, a system with a higher metabolic burden could further reduce the WTA behavior and expand the activation region to close the ideal case (Figure 5E). The non-normalized heat map (Figure S2) shows that the activation threshold is reduced under growth feedback. This is consistent with a change in the activation threshold of the self-activation circuit reported in the previous studies [30, 28]. It also implies that the change in the activation threshold of bistable switch by growth feedback does not depend on resource competition. Thus, the growth feedback contributes to cooperativity, which leads to the robustness of the co-activation of two competing self-activation modules system.

3. Conclusion

Growth feedback and resource competition are two most critical context-dependent factors that could significantly affect the robustness of our synthetic gene circuits [29, 28, 33, 34, 35]. While the effects of growth feedback on synthetic gene circuits and the consequences of resource competition on multi-module circuits have been extensively studied separately [10, 36], the combined impact of both factors in the same system is not fully understood. Here we present an effort to investigate the perturbation of the host-circuit system behavior by coupling these two factors. Our general modeling framework approach provides a theoretical tool for future studies of designing multi-module gene circuits, where both resource competition and growth feedback are important. Moreover, our analysis suggests that it is important to consider both in one system. Our results reveal unexpected phenomena of multiple-module gene circuits arising from the interplay between growth feedback and resource competition. A new phenomenon, cooperative behavior between two competing modules, was found through growth feedback. Our model analysis uncovers the parameter condition that ensures the cooperativity of the system. This parameter condition provides a qualitative design principle for the future design of multi-module synthetic gene circuits in a competitive or cooperative way. This cooperativity is a consequence of two factors, the attenuation of cell growth-mediated dilution by high metabolic burden and the weak mutual inhibition induced by competing for limited resources. Thus, two gene modules could benefit from the presence of each other under the circumstance where the resource competition is not severe and the metabolic burden caused by the circuit is significant. This could be plausible if the host cell growth is susceptible to exogenous gene plasmid.

The cooperativity and competition induced by the host-circuit interactions could be utilized to tune the synthetic circuit dynamics. For example, our analysis suggests that a monostable resource-competing circuit could activate (by cooperation) or deactivate (by competition) a self-activating circuit. This phenomenon implies that one circuit could be used to tune the dynamics of the other circuit bidirectionally. Interestingly, bistable module cooperation could generate bistability in a non-bistable circuit in the presence of growth feedback and other competing circuits. Manipulating gene circuits’ state by cooperativity and competition could bring an alternative way to control circuit functionality under host-circuit interactions. Additionally, the emergence of cooperativity in competing gene modules under growth feedback brings new insight for mitigating resource competition in addition to negative feedback and feedforward controllers. Here we demonstrated how cooperativity could mitigate WTA resource competition. Previously, Zhang et al. showed that two competing modules exhibit a winner-takes-all behavior where only one of the two modules dominates the limited resources and highly expresses itself only [10]. However, in the context where the modules generate a sufficiently high metabolic burden, the resulting growth feedback could improve the robustness of the system’s co-activation state. That is, module cooperativity can enhance the co-activation of multiple modules in synthetic gene circuits. It would also be interesting to investigate the potential usages of cooperativity in other synthetic gene circuit systems in future studies. While enhancing cooperativity while impairing the competition in a host-circuit system remains challenging, future quantitative studies will provide more insights. Ribosome allocation between synthetic and endogenous plays an important role in the host-circuit system [35]. Therefore, it would be important to study how resource competition and metabolic burden relate to each other. Identifying this relationship could help to understand cooperativity in competing genes even further.

Overall, while this research provides valuable insights into the complex dynamics of synthetic gene circuits, there are still limitations that could be addressed in future studies. Here, our analysis considers two types of gene circuits to demonstrate the modeling framework. Future works could consider the effects of other circuits and other factors in the system. For example, previous studies have shown a relationship between important circuit parameters such as transcription/translation rates and growth rate [37, 12, 38, 39]. Therefore, it would be valuable to study the cooperation between multiple exogenous circuits under growth feedback by considering these additional factors under various growth conditions.

The Highlights of our study are as follows:

• We developed and analyzed a mathematical modeling framework for synthetic gene circuits by considering both resource competition and growth Feedback.

• We found that two competing gene circuits could cooperate under growth feedback.

• The cooperation between two competing circuits is determined by a non-monotonically relation between resource availability and metabolic burden.

• Our analysis suggests that one self-activating circuit can be activated and deactivated by one resource-competing circuit.

• We demonstrated the emergent bistability in one constitutively expressing circuit induced by one bistable resource competitor.

• We found that cooperativity could be used to remediate winner-take-all resource competition behavior.

6. Data availability

No data was used for the research described in the article.