Passively addressed robotic morphing surface (PARMS) based on machine learning

Abstract

Reconfigurable morphing surfaces provide new opportunities for advanced human-machine interfaces and bio-inspired robotics. Morphing into arbitrary surfaces on demand requires a device with a sufficiently large number of actuators and an inverse control strategy. Developing compact, efficient control interfaces and algorithms is vital for broader adoption. In this work, we describe a passively addressed robotic morphing surface (PARMS) composed of matrix-arranged ionic actuators. To reduce the complexity of the physical control interface, we introduce passive matrix addressing. Matrix addressing allows the control of N² independent actuators using only 2N control inputs, which is substantially lower than traditional direct addressing (N² control inputs). Using machine learning with finite element simulations for training, our control algorithm enables real-time, high-precision forward and inverse control, allowing PARMS to dynamically morph into arbitrary achievable predefined surfaces on demand. These innovations may enable the future implementation of PARMS in wearables, haptics, and augmented reality/virtual reality.

Passive matrix addressing and machine learning control enable under-actuated and highly programmable dynamic shape morphing.

INTRODUCTION

Soft actuating systems offer the potential to interface with humans and mimic the behaviors and efficiencies of biological organisms (1–3). While traditional rigid actuating assemblies have finite degrees of freedom (DoFs), soft actuating systems have infinite DoFs, inspiring new strategies to design and control their deformation (4). Innovation in soft materials, fabrication techniques, and computational algorithms has led to rapid improvement in the capabilities of soft robots. The emerging rich diversity of shape-morphing strategies has demonstrated value in applications such as implantable medical devices and wearable systems (5, 6). However, the coordinated movement of large numbers of actuators, which is necessary for applications such as human tactile interfaces and biomimetic robotics, is a nascent field that requires innovations in control strategies and control algorithms.

Robots that morph from one initial shape to one target shape have been developed on the basis of the spatial patterning of materials that deform in response to a global external stimulus (temperature, humidity, etc.), such as liquid crystal elastomers (LCEs) (7, 8), shape memory alloys (9), hydrogels (10, 11), and shape memory polymers (12, 13). For these stimulus-responsive materials, the complexity of the shape morphing is determined in the fabrication process. For example, the morphing of a two-dimensional (2D) sheet into a 3D shape can be pre-described by depositing stiff 2D structures or multilayers (14–16). Similarly, controlling the crease and cut marks of origami (17, 18) and kirigami (19, 20) structures can define 2D to 3D shape transformations. Meanwhile, the soft pneumatic actuators could achieve similar functionality by designing the internal channel structure (21) and the vertical fiber array structure for reinforcement (22). The design of patterned matter for shape morphing is facilitated by emerging fabrication approaches that include 3D/4D printing (23–25), ultraviolet lithography for magnetic particles (26), alignment technologies for LCE (27, 28), and laser or wafer-jet cutting (20, 29). For these shape-morphing strategies that are prescribed during the fabrication process, the control system can be considered as the modeling that predicts the deformation (30). The limitation of this predefined shape-morphing approach is that only one shape can be formed.

Dynamically programmable robots can morph from their initial shape into many different shapes on demand. This can be accomplished by spatially controlling the stimulus, such as light (31), magnetic field (18), or temperature (32). However, this approach requires an external system to create the spatially varied stimulus, such as an external laser to locally heat the device. Morphing surfaces that do not require external devices have been created using vertical arrays of linear actuators, including linear motors (33), pneumatic actuators (34), hydraulic actuators (35), and dielectric elastomer actuators (DEAs) (3). Independent control of the height of each actuator allows a discrete description of the surface. However, these arrays of linear actuators are typically very bulky because a large proportion of the actuator is located underneath the array.

A low-profile actuator array can be created using a surface of bending actuators. Morphing into a target structure can be achieved by adjusting the curvature of each ribbon/beam (36, 37). Since the pixels of bending actuators are coupled to each other, the height of each pixel is influenced by the surrounding pixels. This complex coupling leads to a system with infinite DoFs. Consequently, controlling an infinite DoF with a finite number of control inputs is a key challenge. Control involves two steps: the physical control interface that provides power to each pixel in the array and the control algorithm that determines how much power to provide to each pixel. To improve low-profile actuator arrays, innovations are required in both the physical control and the algorithms.

Actuator arrays most commonly use direct addressing (3, 33–35), which consists of powering each actuator independently using two wires. Controlling an N × N array of actuators with direct addressing requires N² independent inputs and 2N² wires. As the array size increases, the exponential increase of independent inputs can result in bulky control systems and challenges such as capacitive coupling between the wires. Passive matrix addressing activates individual pixels at overlapping regions of a crossbar array of electrodes (Fig. 1A), which only requires 2N control signals to address an N² matrix. Passive matrix addressing provides intermittent power to each pixel and has consequently previously been applied to static devices such as sensors and displays (38–41). Similarly, a passive matrix robotic system must include pixels that can operate with intermittent power.

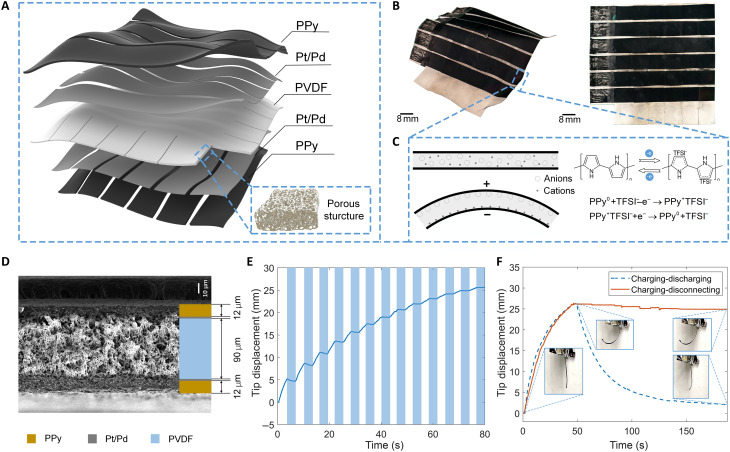
Fig. 1. The design and principle of the mechanism.

(A) Schematic of a passive matrix crossbar array consisting of polypyrrole (PPy) as an active electrode and porous polyvinylidene difluoride (PVDF) as an ionic conductor. (B) Image of the passively addressed robotic morphing surface (PARMS) in the actuated state and the original flat state. (C) The actuation principle of an ionic electro-active polymer actuator. The PPy at the anode is oxidized and binds the anion TFSI^‐ [bis(trifluoromethanesulfonyl)imide], while the PPy at the cathode is reduced, losing the anionTFSI^‐. This causes differential swelling in the PPy electrodes. (D) The cross section of the ionic actuator under an electron microscope. The thickness of the substrate and PPy layers are 90 and 12 μm, respectively. The thickness of Pt/Pd layers is less than 1 μm. (E) The intermittent application of voltage to an ionic actuator strip. The white areas represent the charging status (0.8 V), and the light blue areas represent the floating status. (F) Comparison between the “charging-discharging” and “charging-disconnecting” processes of an ionic actuator strip.

While passive matrix addressing provides an intriguing potential physical control interface, control algorithms based on traditional analog control concepts are challenging to implement due to complex mechanical coupling between pixels. The burgeoning machine learning (ML) methods empirically approximate complicated unknown models of systems, and have been widely implemented in sensors (42–44), analytical models (45, 46), and controllers (47, 48) of soft robots. An important step in implementing ML is to obtain a sufficiently large and reliable dataset. Finite element modeling (FEM) provides a very reproducible method to generate a large dataset of actuation conditions that are free from nonidealities of real devices, such as hysteresis and manufacturing defects. We have previously introduced the theory behind this combination of FEM and ML to predict the deformation of actuator arrays (49).

In this work, we described a passively addressed robotic morphing surface (PARMS) controlled using ML (Fig. 1, A and B). Ionic electro-active polymer actuators are used because their capacitive actuation mechanism allows them to retain their actuation state with intermittent power; the ionic actuator can only be actuated when the circuit is a closed loop and maintains its actuation state when the circuit is floating. Given the data from FEM simulations, a trained ML model based on multilayer perceptron (MLP) is implemented to attain model-free control. The ML model can predict the deformation given the voltage applied to each pixel (forward control) with high precision in real time (at least 50 Hz). The ML model also allows the determination of the voltage on each pixel necessary to achieve a target surface (inverse control). Using this ML algorithm for inverse control, PARMS can reproduce arbitrary achievable predefined surfaces statically and dynamically, which suggests possible applications in tactile displays and human-machine interactive devices.

RESULTS

Characterization of actuator mechanism and fabrication of array

In a passive matrix, a specific pixel is addressed by activating the corresponding row and column electrodes. Each pixel has a unique combination of row and column, but only several pixels can simultaneously be addressed independently (50). Consequently, setting the voltage on all pixels in the array requires sequentially addressing the pixels. During the time that a pixel is not being addressed, it is desirable to maintain the actuated state of the pixels. Otherwise, the array will not reach its target quasi-static deformation. Ionic electro-active polymer actuators (hereinafter referred to as ionic actuators) operate as ionic capacitors, which are well suited for energy storage. In this work, the ionic actuator has a laminated structure with five layers (Fig. 1A). The five-layered architecture exhibits top-to-bottom symmetry, comprising a central porous polyvinylidene difluoride (PVDF) layer, flanked by conductive polypyrrole (PPy) electrodes at the topmost and bottommost layers (51). The middle separator (porous PVDF) is infiltrated with an electrolyte solution composed of lithium bis(trifluoromethanesulfonyl)imide (Li⁺TFSI⁻) in propylene carbonate (PC). In response to an applied voltage, ions migrate to the electrodes. The ion migration causes asymmetric swelling in the two electrodes due to differences in the size of ions and their solvation properties (Fig. 1C) (52, 53). An intermediate layer of platinum/palladium (Pt/Pd) metal is coated on the middle separator by sputter coating. The role of the Pt/Pd layer is to enhance electrode conductivity and enable the deposition of PPy onto the surface of PVDF. We used electrochemical deposition to fabricate PPy onto the Pt/Pd-coated regions of PVDF. Compared to the mechanical coating methods for conjugated polymers [e.g., spinning coating (54) and inkjet printing (55)], the electrochemical deposition allows for both chemical and mechanical bonds between the layers, which exhibits better adhesion characteristics (56).

The PARMS array shown in Fig. 1A is fabricated by customizing the shape of the PPy and Pt/Pd layer to be six strips arranged perpendicularly which could provide the PARMS with 6 × 6 pixels, which are the primary independent control units. The total size of the actuation area is 54 mm by 54 mm where the actuation pixel is 7.5 mm by 7.5 mm and there is a 1.5 mm gap between each strip (Fig. 1B). While actuating the array, ions migrate across the thickness of the PVDF separator to activate the pixel. Ion migration laterally between pixels contributes to cross-talk which reduces the accuracy of the targeted shape morphing. To limit this horizontal migration of ions, we added polymer blockers in the gaps between electrodes (see fig. S1 for the fabrication schematic), which fills the pores in the PVDF membrane.

Figure 1D shows the cross section of the device structure. The commercial PVDF membrane is 90 μm, while the deposited PPy is about 12 μm. The thickness of the PPy layer could be controlled by the current input and the depositing time of the electrochemical deposition process. The mechanical properties of the overall system may be compromised by excessively thick PPy layers due to the difference in stiffness between PPy and PVDF, while insufficiently thickness PPy could result in reduced conductivity. The thickness of Pt/Pd layers is difficult to discern since it is less than 1 μm and it will not affect the mechanical property of the whole mechanism.

The actuation magnitude as a function of the applied voltage is quantified for a single strip of the ionic actuator using a new definition of tip displacement, the trajectory length of motion (see section S1, figs. S2 and S3, and movie S1). These data inform our finite element model of the actuation (described in the “Finite element modeling of PARMS array” section in Results). To characterize the ability of an individual ionic actuator to maintain its actuated state when the electrodes are in an open circuit (floating state), we apply 0.8 V to an ionic actuator strip intermittently (Fig. 1E). The actuator deforms when the voltage is connected and shows a small amount of spring back in the following floating status. When the actuator is connected to the ground after actuation, the actuator discharges in tens of seconds, and a residual actuation of only 2.4 mm remains (Fig. 1F). When the actuator is left floating after actuation, the device maintains its actuated state, relaxing by only 4% of the maximum deformation after 3 min (Fig. 1F). To illustrate how this feature enables independent electrical addressing of pixels in an array, we sequentially applied voltage to each pixel in a 1 × 6 array (see section S2, fig. S4, and movie S2). These pixels actuate when voltage is applied and maintain their actuated state during the actuation of other pixels.

Passive matrix addressing with progressive scan

We consider two different protocols for scanning a passive matrix array: direct passive addressing (DPA) and progressive scan (PS). DPA refers to applying a voltage to all rows and columns simultaneously, as shown in Fig. 2A. PS refers to setting the voltage on the pixels in the array by scanning the rows of electrodes sequentially. For example, in this step shown in Fig. 2B, the first electrode row is set to 0 V, while all other rows are left floating. The first row of pixels is actuated, while the rest of the pixels cannot be driven because they cannot draw a current. In the next step, shown in Fig. 2C, only the second-row input is connected to 0 V, and all other rows are left floating while the column inputs are set to be the target values of each pixel in the second row. The duty cycle of this PS approach is therefore 1/N, where N is the number of rows. After scanning over all rows, the process will start over again from the first row as a loop (Fig. 2D). In this way, the voltage on each pixel can be set independently but not simultaneously. To determine the refresh time of PS, we tested the current change over time for an actuator (see section S3 and fig. S5). The current decreases 85.3% in 3 s, which we adopt as the time that voltages are applied to each row during PS.

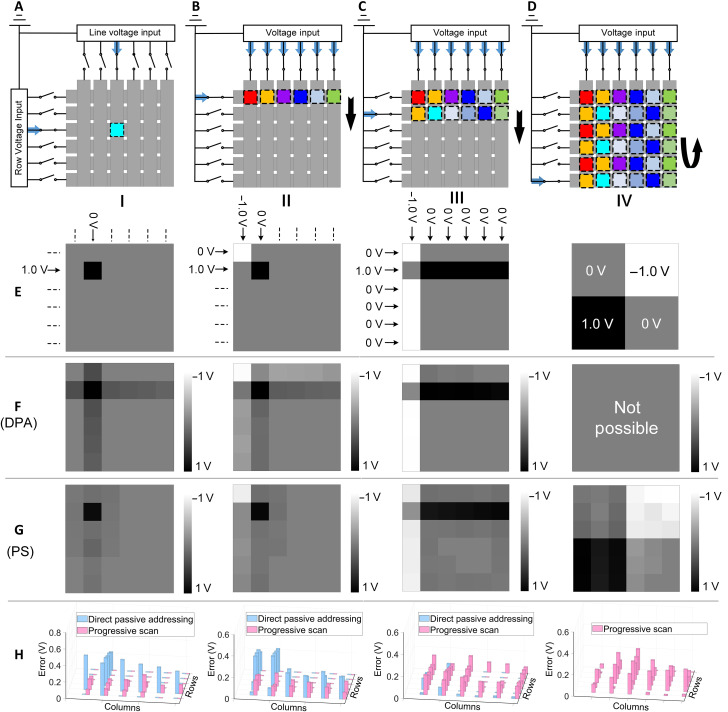
Fig. 2. Comparison of the passive matrix-addressing algorithms.

(A) The principle of the passive matrix addressing using direct passive addressing (DPA). (B to D) The principle of the passive matrix addressing using progressive scan (PS). (E) Four demos for illustrating example voltage distributions that may affect the average voltage error. (E-I) to (E-IV) indicate the ideal voltage distribution. (E-I) to (E-III) indicate the voltage inputs for DPA. (E-IV) indicates the voltage distribution for PS. (F) Measured voltage distribution after applying DPA addressing. (G) Measured voltage distribution after applying PS addressing. (H) The comparison of the error distribution. (H-I) to (H-III) compare the error distributions of DPA and PS using the PARMS with polymer blockers. (H-IV) only shows the error distributions of PS since the voltage distribution E-IV cannot be achieved by DPA.

To compare the performance of DPA and PS addressing in our actuator array, we test four demonstration voltage distributions (Fig. 2E). For each of these demos, we measure the voltage error (the error between measured and target voltage on each pixel) of each pixel in the 6 × 6 array. We use the average voltage error over all pixels to quantify the overall error on the voltage in the array, which is shown in Table 1 for all demos. The first demo (Fig. 2, E to I) consists of a single pixel at high voltage with all other pixels at zero voltage. The resulting voltage distribution highlights a classic challenge in passive matrix arrays: cross-talk between pixels, which manifests as unintended voltages on adjacent pixels (57, 58). This cross-talk can be caused by parasitic current paths through the electrodes and/or through the ionic separator. Using DPA, the maximum voltage error on an individual pixel is 37.2% (Fig. 2, H and I), while the average voltage error over all pixels is 13.4%. By using PS, this average voltage error is reduced to 3.8% (Fig. 2, G to I). The second demo (Fig. 2E-II) consists of two pixels with opposite polarity. Using DPA, this is achieved by applying voltage on the first two rows and columns. While the voltage on the two active pixels can be defined exactly, there is a significant error on the other pixels of the row and column. Again, the average voltage error is substantially reduced from 15.3% for DPA (Fig. 2F-II) to 4.1% for PS (Fig. 2G-II).

Table 1. The average voltage error of four demonstration voltage distributions under DPA and PS with and without polymer blockers.

	Demo 1		Demo 2		Demo 3		Demo 4
	DPA	PS	DPA	PS	DPA	PS	DPA	PS
Without blockers	16.4%	5.9%	22.8%	5.6%	11.7%	15.6%	N/A	33.1%
With blockers	13.4%	3.8%	15.3%	4.1%	2.0%	9.2%	N/A	11.1%

In demos I and II, the high average voltage error results from parasitic currents between the floating electrodes. For demo III, a voltage distribution is chosen that does not require any floating rows or columns. Consequently, DPA should be capable of determining the voltage distribution exactly. As expected, the average voltage error exhibits a low value of 2.0% (Fig. 2F-III). However, for PS, the average voltage error is 9.2% (Fig. 2G-III). This demonstrates that DPA can have high accuracy when there is no floating input, but this only applies to an extremely small subset of possible voltage distributions. Demo IV is chosen as a voltage distribution that is not possible to produce using DPA. The average voltage error for PS is 11.1% (Fig. 2G-IV).

On the basis of the observations of demos I to IV, PS can significantly reduce the voltage error when the voltage distribution requires a floating connection in DPA. DPA has the lowest voltage error for a very small subset of possible voltage distributions in which all pixels can be programmed simultaneously. PS can achieve arbitrary voltage distribution, which is a critical requirement for dynamic shape morphing. Consequently, all demonstrations of shape morphing in this work use PS.

Characterizing device nonidealities

Nonidealities in the array include the ionic coupling between pixels and resistive losses in the electrodes. Adding polymer blockers reduces the parasitic ionic currents, which decreases the average voltage errors (Table 1 and fig. S6). With the addition of blockers, the average voltage error using PS is reduced from 5.9 to 3.8% for demo I and from 5.6 to 4.1% for demo II. With more active pixels, the impact of polymer blockers becomes more pronounced. In demo III, the average voltage error decreases from 15.6 to 9.2%. In demo IV, adding polymer blockers reduces the average voltage error by ~2/3, from 33.1 to 11.1%. The introduction of polymer blockers reduces parasitic ionic coupling between pixels, realizing approximately a 30 to 50% reduction in voltage errors, and its impact increases with the number of active pixels.

Error in the voltage of the pixels can also originate from resistive losses in the electrodes. The voltage applied at the contacts is distributed on the PPy electrodes and across the PVDF dielectric (see fig. S7A). The low resistance through ionic dielectrics results in meaningful resistive losses in the electrodes. We applied 1 V to each pixel of a PARMS array to quantify the voltage drop caused by electrode resistance. The results (see fig. S7, B and C) are described in section S2. For the pixel furthest from the contacts (with the longest electrodes), 79.6% of the voltage dropped across the device and 20.4% in the electrodes. In the following demonstrations, we have compensated the input voltage based on this result.

Finite element modeling of PARMS array

FEM simulations provide a repeatable and low-labor method to collect training data on the actuation of PARMS arrays to train the model for ML control. However, when using a computationally generated dataset to predict the behavior of experimental devices, it is important to ensure that the simulated deformations closely match the experimental devices so that the training data are reflective of experimental conditions.

Abaqus is chosen because of its excellent capability to analyze problems with nonlinear large deformations. However, Abaqus does not include modules relevant to the ionic deformation of materials. Consequently, we adopt an approach proposed by Madden (59) to approximate ionic deformation using equations for thermal expansion. The strain of the ionic actuator created by ionic transport is proportional to the applied voltage in a particular range of deformation according to the diffusive elastic metal model: ɛ_V = βΔV, where ɛ_V is the strain indirectly caused by voltage change ΔV and β is the electrical expansion coefficient. The mathematical form of thermal expansion is the same as that of ion-induced strain: ɛ_T = αΔT, where ɛ_T is the strain generated by temperature change ΔT, and α is the thermal expansion coefficient. Consequently, the equations for thermal field deformation can be used to approximate the electrical fields. The thermal strain from the resulting simulations indicates the electrically induced strain in the devices.

As described in the previous section, the electrical resistance of PPy and PVDF can affect the voltage distribution among pixels. These nonidealities are taken into account in our FEM simulations by defining physically realistic values of the electrical/ionic conductivity; in the thermal formulation of the FEM simulations, the electrical conductivity is represented by the thermal conductivity.

To ensure that the simulations closely represent the real devices, the electrical expansion coefficient was calibrated by experimental data on a single actuator (see section S4 and figs. S8 to S10). The R² value and root mean squared error (MSE) of this fitting curve are 0.9977 and 0.0003519 (the unit is 1/V), respectively. Additional details of FEM simulation in Abaqus are shown in section S3. The parameters of the simulation are provided in table S1. After establishing the simulation parameters, simulations were performed on 6 × 6 arrays. The physical array is fixed by a pair of 2 mm–by–2 mm magnets at the center so that all four sides are free. Thus, simulations are performed with the same boundary condition (BC) (pinned at the center).

Machine learning–based model-free control

In some strain-driven shape-morphing mechanisms, the analytical model could be established because of their special structure. For example, in shape-morphing mechanisms based on structured heterogeneous lattices, pixel interconnections via point contacts simplify BC definitions (25). Neighboring pixel effects relate to force and torque at connection points, akin to mesh element interactions in FEM. In our work, it is straightforward to develop an analytical model for a single square pixel (section S2). However, since the connections between pixels are continuous edges, the resulting BCs are too complex partial differential equations. In a 6 × 6 system, the excessive quantity of BCs between pixels renders the PDEs intractable. Consequently, ML is the most suitable method to determine the deformation of this actuation mechanism. Hence, we previously proposed a model-free method based on ML to predict the deformation that results from a certain set of input voltages on each pixel (forward prediction) (49). The model could also determine the required input voltage on each pixel to achieve a desired surface (inverse design). This method is based on the ML algorithm, the MLP. The low repeatability of ionic actuators and potential errors in measurement tools could lead to inaccurate datasets that create inaccurate models. Generating the training datasets from the aforementioned accurate finite element simulations rather than physical device allows us to create a more accurate model.

To quantify the simulation results as training data for the ML model, we take n × n points uniformly on the surface of the simulation result and vectorize them into vectors of length n² in order, $\overrightarrow{x}=\{x_1,x_2,\dots ,x_{N^2}\}$. Then, we vectorize the 6 × 6 voltage BCs (BCs) in the simulation into a vector of length 36 in the same order, $\overrightarrow{y}=\{y_1,y_2,\dots ,y_{36}\}$. As shown in Fig. 3A, when predicting the deformation of the surface (forward control), the voltage BCs are used as the input layer, while the displacement vectors are the output layer. To determine the necessarily applied voltages to achieve a target surface (inverse control), the input and output are swapped. We build a fully connected neural network using the MLP model with the hidden layer sizes of (73, 300, 580, 880, and 1200) and (901, 700, 550, 300, and 180) for forward and inverse control, respectively. The parameters of the MLP model are provided in table S2.

Fig. 3. The diagram of the MLP model and its training properties.

(A) The diagram of the MLP model. (B) The R² score and MSE versus the size of training data for inverse control. (C) The R² score and MSE versus the size of training data for forward control.

Ionic actuators provide large bending actuation (almost bending to a circle) at only 0.8 V (fig. S8). Therefore, when generating the training datasets, the vectors of the applied voltage BCs are defined randomly from −1 to 1 V. Here, we predefined an array (−1.00, −0.95, −0.90, …, 0.90, 0.95, 1.00) in MATLAB and randomly picked a value for each pixel. After executing the FEM simulation, the displacement vectors extracted from Abaqus include the x, y, and z directions. However, the MLP model only allows the features to be a 1D vector, so we compared the use of z displacement and total displacement (derived from $\sqrt{x^2+y^2+z^2}$). Theoretically, an exhaustive search of all possible training datasets would require 36⁴¹ simulations. Performing all of these simulations is impractical due to the computational time required. Consequently, we examine the prediction accuracy as a function of the number of training datasets. One hundred datasets are used for testing. The R² score (the closer the R² score is to 1, the higher training accuracy the model has) and MSE are shown versus the number of trials in the training data in Fig. 3 (B and C). The training data must be greater than 1000 to achieve meaningful accuracy. Beyond 1000, the training accuracy continues increasing but begins to saturate. When the number of training simulations is 5000, the R² score of forward control trained by z displacement and total displacement is 0.8800 and 0.8728, respectively. For inverse control, these R² scores are 0.8223 and 0.8550 for the z displacement and total displacement, respectively. Here, the BC of fixing the central point in PARMS causes a significant z displacement at the edges with a noticeable x-y coordinate shift. Hence, only using z displacement to train the model cannot adequately capture all of the features of deformation. Nevertheless, incorporating the total displacement data partially considers the significant x-y coordinate shift at the edges (resulting in a higher value at the edges than z displacement), causing the training model to better represent the deformation features of PARMS. In a regression model, the input data is pivotal during the training process as the model’s objective is to predict the output based on the given input. Thus, the primary focus of the model training is to optimize the model parameters to minimize the discrepancy between the predicted and actual output. The accuracy and generalization ability of the model depend heavily on the quality and features of the input data. While in forward control, the voltage array serves as the input data, and the limitation of using only the z displacement is not evident. However, in inverse control, the input data shift to the displacement array, and the need for comprehensive features becomes critical. As a result, the total displacement data can yield higher training accuracy than the z displacement. The details of model training are shown in section S5.

Compared with FEM, which is the most direct way to predict the deformation, the computational burden of executing the ML method is much smaller. The total time for FEM to execute a deformation prediction is about 30 min, while our ML method only requires 0.010 s (see table S3), which means that online control loops can be executed at a rate of 100 Hz. Real-time FEM, up to 60 Hz, has been proposed (60, 61). However, it is based on simplifying assumptions such as using linear elasticity and a coarse mesh, which decreases the reliability of the prediction. For an actuator array with a large number of actuators, such a course mesh would not be able to accurately predict the deformation.

Forward control

Forward control predicts the deformation of the surface based on known input voltages. Figure 4 shows three examples of randomly generated input voltage arrays. During the PS control, the charging time for each row is 3 s based on fig. S5, and with six rows undergoing two cycles per round (one cycle for charging the pixels with a positive voltage and another for charging with a negative voltage), a single round of charging takes approximately 36 s. According to fig. S5, the 3 s changing process is estimated at around 85%. However, because of the ion diffusion process having a separate mass transport time constant, the observed deformation completion is approximately 70%. Assuming that a 10% rebound occurs during the waiting time, the deformation is approximately 93.6% completion after three rounds and about 97.4% completion after four rounds. The total deformation time of each case thus ranges from 108 to 144 s. In addition, for improved accuracy, the voltage difference between adjacent pixels was constrained to be less than 1 V. The deformation video of demo I is provided in movie S3.

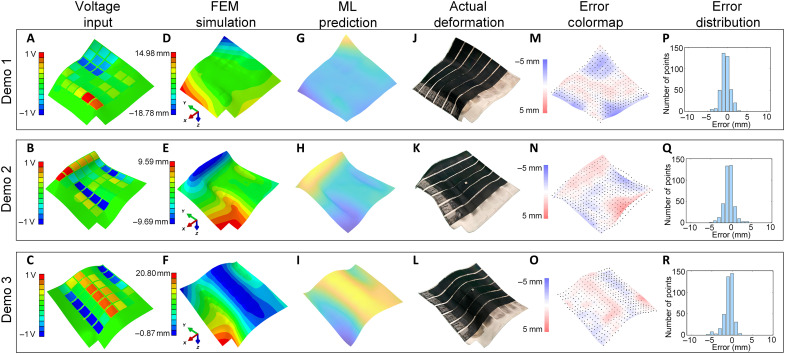
Fig. 4. Forward control of PARMS using ML.

(A, C, and E) The real deformation of the PARMS. (B, D, and F) The deformation predicted by the ML algorithm. (G to L) The deformation predicted by FEM, where (G), (I), and (K) show the distribution of the input voltage and (H), (J), and (L) show the magnitude of the z displacement. (M to R) The error distribution between the real deformation and the simulation result where (M), (O), and (Q) are the numerical distribution and (N), (P), and (R) are the spatial distribution.

The simulation results for the three demos are shown in Fig. 4 (A to F). The labels of the 20 × 20 nodes are first extracted uniformly from the first frame of the simulation data, which is undeformed. In the last frame, the x, y, and z coordinates of these nodes are extracted. Using the least squares method, these points are fitted to a plane and then the points are rotated to ensure the fitted plane is parallel to the x-y plane. At this point, the current z-displacement data of the simulation result is ready for further comparison. The ML results are derived from the forward model with the same voltage BC input. They are vectors of length 400 before decoding. Then, we decode them to 20 × 20 matrices and reproduce them in Fig. 4 (G to I). The data on the deformation of the physical PARMS device are collected from a depth camera and transformed into a point cloud (Fig. 4, J to L). Then, the same fitting and rotation operations are performed on this point cloud. After that, based on the x and y coordinates of the 20 × 20 simulation data, we search in the point cloud to find the closest points to these x and y coordinates (each x-y coordinate of the simulated data corresponds to a point in the point cloud). This way, we can obtain the 400 points in the point cloud with the exact x-y coordinates of the simulation data. Before comparison, we ensure that the x-y coordinates of each point in these three datasets are the same and they have the same fitted plane. Therefore, we can convincingly compare the z displacement of these three datasets. Figure 4 (M to O) depicts the spatial error distribution between the real dataset and the simulation dataset. The largest errors are close to the edges, and the errors are mainly in the range from −2 to 2 mm (Fig. 4, P to R). The MSE between real deformation and the FEM simulation results is 0.88, 0.86, and 0.86 mm, respectively. These errors represent 4.2, 6.3, and 6.0% of the maximum height difference in the respective shapes. When comparing the data between the real mechanism and the ML result, the MSE of these three demos is 0.87, 0.86, and 0.95 mm, respectively (fig. S12). The detailed error propagation analysis is provided in section S6 and fig. S13.

Inverse control

Inverse control generates the input voltage arrays necessary to achieve a target surface deformation. The target surfaces were created in Maya and were then exported as ‘*.stl’ documents. MeshLab software was used to transfer the ‘*.stl’ documents into the point cloud and save them as ‘*.xyz’ documents that include the x-y-z coordinates of each point. Next, MATLAB was used to extract the displacement vector from the point cloud as the input to our inverse model. The output voltage arrays were applied to our physical device.

To illustrate dynamic shape-morphing capability, we designed two sequences of surfaces as the inputs of the inverse control (Fig. 5). As shown in Fig. 5A, the PARMS started as an undeformed flat sheet, and then the voltage arrays for a sequence of target surfaces were applied. The approximate shape is identifiable, and the shape of PARMS is close to its simulation result. The discrepancies between the target surface and the shape produced through ML and the physical PARMS originate from the limited resolution of the current prototype (6 × 6 pixels). The fourth images from the left depict the spatial error distributions between the target and real shapes (T-R error). The average error (mean absolute error of each point on a surface) of each step is 0.88, 1.23, 1.30, 2.12, 2.46, and 1.12 mm, respectively. Figure 5B shows another sequence of shapes with mean errors 0.99, 1.68, 1.64, 1.41, 1.55, and 1.04 mm, respectively (movies S4 and S5). In fig. S12, the spatial error distributions between the simulated and real shapes (S-R error) are illustrated. In addition, table S4 presents the mean errors for both simulated-to-real and target-to-real shape comparisons.

Fig. 5. Inverse control of dynamic shape-morphing series.

(A) Demonstration series 1. (B) Demonstration series 2. At each step, the first image from the left indicates the input target surface, the second image from the left indicates the simulated deformation results, the third image from the left is an image of the deformation of the physical device, and the fourth image from the left shows the error distribution between the target and actuated shapes. The black dots are the processed point cloud data collected from a physical device, and the surface is derived from the simulation result.

As a third example of inverse control, the PARMS reproduced the acronym of Purdue University, “P” and “U.” The mean T-R and S-R errors for the letter P are 1.42 and 1.08, respectively. For the letter U, the mean T-R and S-R errors are 1.27 and 1.01 mm, correspondingly (fig. S11 and movie S6).

The error map shows that the largest errors are located at the edge. It is because our mechanism is fixed at its central point, so the total error is the accumulated error of each pixel moving away from this central BC. Generally, the S-R error is larger than the other errors, indicating that the best way to reduce the errors in our approach is to reduce discrepancies between the real and simulated devices, such as taking into account variable mechanical properties and using a dynamic FEM process rather than a quasi-static FEM process. The summary of the sources of error can be found in the Supplementary Materials (section S6 and fig. S13).

DISCUSSION

As applications of soft actuators extend to arrays of devices with coordinated movements, the physical control interfaces and controller complexity start to become a limitation. Discrete morphing surfaces have the advantage of good programmability, but their linear actuators and direct addressing system (N² control inputs for N² controllable pixels) result in bulky devices that are difficult to incorporate into microscale systems (3, 35). Morphing surfaces composed of bending actuators can be very thin, enabling low-profile device arrays. Recent morphing surfaces that use bending actuators have controlled the curvature of entire rows or columns rather than individual pixels. This limits the independently controllable parameters to 2N, which does not allow high programmability (37). The low-profile magnetic actuator array described by Bai et al. (62) used an addressing scheme that is unique to magnetic actuators and allows 4N independent inputs to control the deformation of N² DoFs. However, the current through each conductive segment must come from adjacent segments so that the pixels cannot be addressed fully independently. In contrast, the voltage on each pixel of our PARMS array can be determined fully independently, enabling a larger range of actuated shapes. Furthermore, the magnetic actuation mechanism in (62) requires a large externally applied magnetic field. In our PARMS array, the mechanism to actuate the device operates within the actuator array, without the need for external field sources. In addition, our implementation of passive matrix addressing allows the control of N² independent pixels using only 2N control signals. Figure 6 shows the scaling relationship between the control inputs and controllable DoF for different technology platforms. Compared to other approaches, matrix addressing demonstrates a compact control system, which could enable applications in portable and low-profile morphing surfaces. In section S7, we provide a more detailed benchmarking of PARMS against other works (33, 37, 62–66) from various perspectives. The comparison table is shown in table S5 and the radar chart is shown in fig. S17.

Fig. 6. Comparison of the independent control inputs versus the degree of freedom (number of actuators) for different actuator array systems.

The matrix linear actuator (InFORM) refers to (35). Matrix DEAs refer to (3). LCE bending actuators refer to (37). Bending EM actuators refer to (62).

While this iteration of our PARMS device uses ionic actuators, passive matrix control could enable dynamic shape morphing with any actuator that can store energy (4), such as DEAs and LCEs. In addition to the programmable surfaces described in this work, this matrix-addressing approach could be used in applications such as reflective displays (67) and microfluidic devices (68).

Our use of a control algorithm based on ML enables real-time inverse control, which suggests potential suitability for applications such as 3D tangible user interfaces and remote collaboration. For example, virtual surfaces could be valuable for AR/VR devices and remote human-computer interaction applications. A virtual surface created in an AR/VR device, such as 3D models, scanned faces, and topographical maps, could be displayed on a remote morphing surface in real time. Two people with the same morphing surfaces could physically interact through the real-time synchronization of two devices.

An important limitation of matrix addressing is the reduced duty cycle at which each pixel is addressed. Using PS, the array can be refreshed at a rate of 1/N of the time it takes to actuate each pixel. Consequently, matrix addressing is most suitable for applications in which it is acceptable for the shape change to occur at speeds lower than the maximum deformation rate of the actuation mechanism.

The ability to reproduce on-demand surfaces is limited by the 6 × 6 array size of the PARMS in this work. Consequently, future research will develop a higher resolution mechanism, which will benefit from innovations in the devices and the ML algorithms. As the array size becomes larger and the pixel size becomes smaller, the coupling between pixels will also become larger. This coupling could be reduced by adding a layer of nonlinear devices (e.g., diodes) into the array (69). In addition to improving the array size, it would be advantageous to improve the actuation rate of the array. This could be accomplished by optimizing the thicknesses of the Pt/Pd and PPy electrode layers (59) or using electrostatic actuators that operate at higher frequencies.

As the number of arrays increases, larger out-of-plane displacements could be possible, motivating the development of improved ML controllers. Data collected from simulations include 3D data of each node (x, y, and z displacement). However, MLP only allows 1D data input for each node (z displacement or total displacement). Consequently, the training accuracy could be improved by fully making use of the x, y, and z data. Therefore, some typical models for training point clouds such as 3D convolutional neural network and PointNet can be potentially applied to train the 3D deformation of the PARMS or other morphing devices.

In summary, we have demonstrated a PARMS that can morph into different 3D shapes on demand. Passive matrix addressing is implemented to control N² electrically independent outputs using 2N independent inputs, making the system highly under-actuated. Because of mechanical coupling between pixels, we implement ML-based model-free control. Forward control demonstrations indicate that the deformation of the PARMS can be predicted with high precision in real time. Inverse control demonstrations show that the PARMS can dynamically reproduce arbitrary achievable shapes on demand.

MATERIALS AND METHODS

Materials and devices

Porous PVDF membranes (Durapore, HVLP14250), lithium bis(trifluoromethane), PC (99%), pyrrole monomers, and SYLGARD 184 Kit were all purchased from Thermo Fisher Scientific Co, LLC and used as received.

The sputter coater was Cressington 208HR. The microcontroller was Arduino Mega 2560. The depth camera was Intel RealSense Depth Camera D435. The multi-material direct ink write (DIW) printer and electrochemical station were developed in-house.

Device fabrication

The details of fabrication are depicted in fig. S1. First, a hydrophilic PVDF membrane with 0.45 μm pores is cut into a 10 cm by 10 cm². Then, Pt/Pd is sputtered through a shadow mask to deposit six electrode strips on each side of the PVDF membrane to create a crossbar architecture. The sputter coater is operated at a current of 40 mA for 120 s on each side of the PVDF. When depositing the PPy, PPy is deposited on the Pt/Pd electrodes but not the membrane between the electrodes. This generates nonuniform stresses that can cause wrinkles on the membrane. Therefore, we designed a holder to prestress and fix the membrane with magnets while it is immersed in the electrochemical workstation. For the electropolymerization of PPy, we prepare a PC solution of 0.1 M pyrrole monomer with 0.1 M Li⁺TFSI⁻ as the electrolyte and add it to a self-made electrolytic bath. After wetting the membrane with the prepared solution, the membrane is prestressed and fixed on the holder by four pairs of magnets. The Pt/Pd strips on the membrane are connected to the positive electrode, while a steel wire mesh is connected to the negative electrode. A constant input current of 0.1 mA is used for electropolymerization. To ensure a uniform growth speed on different strips, each strip has an independent input, and it is disconnected from the electrode as soon as the coating process on this strip is finished. The coating is done one side at a time. After finishing the first side, the holder is removed from the electrolytic bath, the membrane is rotated by 90° and is prestressed and fixed on the holder again. The PPy deposition process is then repeated on the six electrode strips. The total time of the electrochemical reaction is approximately 4 to 5 hours. The membrane with PPy on all electrodes is then soaked in a solution of 0.5 M Li⁺TFSI⁻ in PC for another 30 min. Subsequently, the membrane is removed from the holder and washed with water. The membrane is placed between two glass sheets, and external force is applied for 24 hours to flatten the array.

Polymer blockers are printed in the gaps between two strips using a DIW printer. We chose SYLGARD 184 with a 10:1 ratio (base to a curing agent) as a hydrophobic material that limits ion migration. The composition is dispensed in the gaps between the electrodes using a 0.1 mm nozzle with 138 kPa pressure. Last, the sample is cut to 66 mm by 66 mm, and then mounted on the control system.

Control system

Figure S16 illustrates the overall control and measurement system for PARMS. Our mechanism requires a control system with a series of independent channels that generate both negative and positive voltage from −5 to 5 V. In addition, relays are needed to control the connection to each row and column. Thus, as shown in fig. S16B, the row inputs are active, generating the specific voltage. We use digital-to-analog converter chips (MCP4725), converting the digital signal from microcontroller unit (MCU) (Arduino Mega 2560) to the analog output from 0 to 5 V. The column inputs are passive and are connected directly to a general-purpose input/output of MCU that can only output 0 and 5 V. When the positive voltage is required, it outputs 0 V so that the row inputs minus the column inputs are positive. While the desired voltage is negative, it connects to 5 V so that the difference between the row and column inputs is negative. During the actuation process, positive and negative voltages are set sequentially. The whole process can be described as follows: first, turn on the relay of the first row and relays of line inputs with corresponding positive pixels [if (1,1) and (1,4) require positive voltage, only the relays on lines 1 and 4 turn on while the others remain off]; after 3 s, turn off the first row and turn on the second row; while only turn on the relays of line inputs that its corresponding second-row pixels are positive. The process is then repeated for all rows. The second round is for pixels with negative voltage, so the row inputs are sequentially connected to the 5 V. The 0.01 mm copper wire is used to connect the control electronics to the actuator array, which is secured to the mechanism with conductive carbon tape.

Measurement system

Measuring the deformation of the actuator array is done using a multiview stereo-imaging platform consisting of a depth camera (Intel RealSense Depth Camera D435) connected to a computer taking top-view images of the mechanism. The depth camera has two independent webcams inside and calculates depth from stereo vision. It can output point cloud with RGB information with 1280 × 720 resolution. Before use, ‘Self-Calibration’ codes are used in Intel RealSense SDK2.0 to improve accuracy. After running the on-chip self-calibration routine and storing the result in the flash memory, the depth accuracy improves from ±1.2 to ±0.2%. The output of the depth camera is in ‘*.ply’ format. The point cloud data are processed to isolate the surface data by transferring the format to ‘*.stl’ using MeshLab and then opening it in SolidWorks to manually delete irrelevant data. Then, the cleaned ‘*.stl’ documents are transferred to ‘*.xyz’ format, which is converted to ‘*.txt’ format that contains the 3D position and orientation information of each point cloud.

Finite element simulations and machine learning model

The FEM process is described in section S4 and table S1. The data preparation and ML algorithm are described in section S5 and tables S2 and S3.

Supplementary Materials

This PDF file includes:

Sections S1 to S7

Figs. S1 to S17

Tables S1 to S5

Legends for movies S1 to S6

References

Other Supplementary Material for this manuscript includes the following:

Movie S1 to S6