Intracellular environment can change protein conformational dynamics in cells through weak interactions

Abstract

Conformational dynamics is important for protein functions, many of which are performed in cells. How the intracellular environment may affect protein conformational dynamics is largely unknown. Here, loop conformational dynamics is studied for a model protein in Escherichia coli cells by using nuclear magnetic resonance (NMR) spectroscopy. The weak interactions between the protein and surrounding macromolecules in cells hinder the protein rotational diffusion, which extends the dynamic detection timescale up to microseconds by the NMR spin relaxation method. The loop picosecond to microsecond dynamics is confirmed by nanoparticle-assisted spin relaxation and residual dipolar coupling methods. The loop interactions with the intracellular environment are perturbed through point mutation of the loop sequence. For the sequence of the protein that interacts stronger with surrounding macromolecules, the loop becomes more rigid in cells. In contrast, the mutational effect on the loop dynamics in vitro is small. This study provides direct evidence that the intracellular environment can modify protein loop conformational dynamics through weak interactions.

Transient attractive interactions with surrounding macromolecules can suppress protein loop dynamics in E. Coli cells.

INTRODUCTION

The interior of a cell is crowded with ions, metabolites, and macromolecules. Through excluded volume effect (1) or direct weak interactions (such as electrostatics, H-bonding, and stacking), which drive proteins to form quinary structures (2–5), the cellular environment can change protein diffusion (6–9), protein folding (10–17), and protein ligand binding (18–24). For intrinsically disordered proteins (IDPs), the excluded volume effect limits their conformational space so that they tend to adopt more compact conformations (9, 25). For well folded proteins, the cellular environment may perturb local structures (26, 27), but the overall protein structures are unchanged (28, 29). The resolution of solved protein structures in cells (all by NMR) is not that high due to relatively short data acquisition time (limited by cell viability) and generally low signal-to-noise ratio (due to transient interactions with large molecules). More studies are needed to understand the exact cellular environmental effect on protein structures. On the other hand, proteins are not rigid structures. Protein dynamics through motions of loops, linkers, and hinges can generate distinctive conformations that are important for protein function (30, 31). However, whether the cellular environment can modify protein conformational dynamics is largely unknown. NMR is a particularly powerful technique in studying molecules in cells at the atomic level [see, e.g., (32–48)], but studies of protein conformational dynamics in cells are sparse. Previously, we used the ¹⁵N Carr-Purcell-Meiboom-Gill (CPMG) NMR relaxation dispersion method (49–53) to examine protein folding and unfolding exchange and found that folding of the studied protein is slowed down by the cellular environment (54). Here, we attempted to measure conformational dynamics of a protein in Escherichia coli cells and understand how weak interactions with the cellular environment may perturb protein dynamics.

¹⁵N longitudinal (R₁), transverse (R₂) relaxation rates, and heteronuclear nuclear Overhauser effect (¹⁵N-{¹H} NOE) measurements, coupled with the model-free analysis (55, 56), are commonly used to study picosecond to nanosecond timescale protein backbone conformational dynamics in solution (57). However, the relatively poor NMR signal-to-noise ratio for proteins in cells hinders the accurate measurement of ¹⁵N-{¹H} NOE, because the sensitivity of the NOE experiment is considerably lower than that of ¹⁵N R₁ and R₂ measurements. Recently, Bruschweiler and coworkers have proposed an elegant NMR relaxation method where only R₂ rate is required to determine protein dynamics in picosecond to microsecond timescale with the assistance of silica nanoparticles (SNPs) (58–61). SNPs create a fast exchange for the protein between the bound and free form, which extends the overall protein tumbling time. The dynamics slower than the tumbling time of the free protein, which is usually not observable in the relaxation measurement, can be observed due to the extended tumbling time. Inspired by their work, here we determined conformational dynamics for a model protein in buffer and in cells. Together with ¹⁵N CPMG NMR relaxation dispersion experiments (52, 53) and backbone N-H residual dipolar coupling (RDC) measurements, the timescale of dynamics is characterized. It is shown that the protein loop dynamics in E. coli cells is perturbed by cellular environment. Specifically, weak attractive interactions between the loop and macromolecules in cells tend to suppress the loop dynamics.

RESULTS

Backbone relaxation rates of a GB3 variant in buffer and in cells

GB3, the third immunoglobulin binding domain of protein G, is a small protein of 56 residues. Its dynamics has been studied by NMR ¹⁵N relaxation (62) and RDC methods (63, 64). The linkers G9-L12 and D40-G41 display elevated backbone dynamics. Here, the linker G9-L12 was converted to a longer loop by inserting a GNSGG sequence between K10 and T11. The amino acid sequence of the GB3 variant (named GB3L) is displayed in table S1, with the loop corresponding to residues G9-L17 (named loop 1). GB3L has an overall structure similar to the wild-type (WT) GB3, as indicated by the backbone ¹H-¹⁵N RDCs (see discussion below).

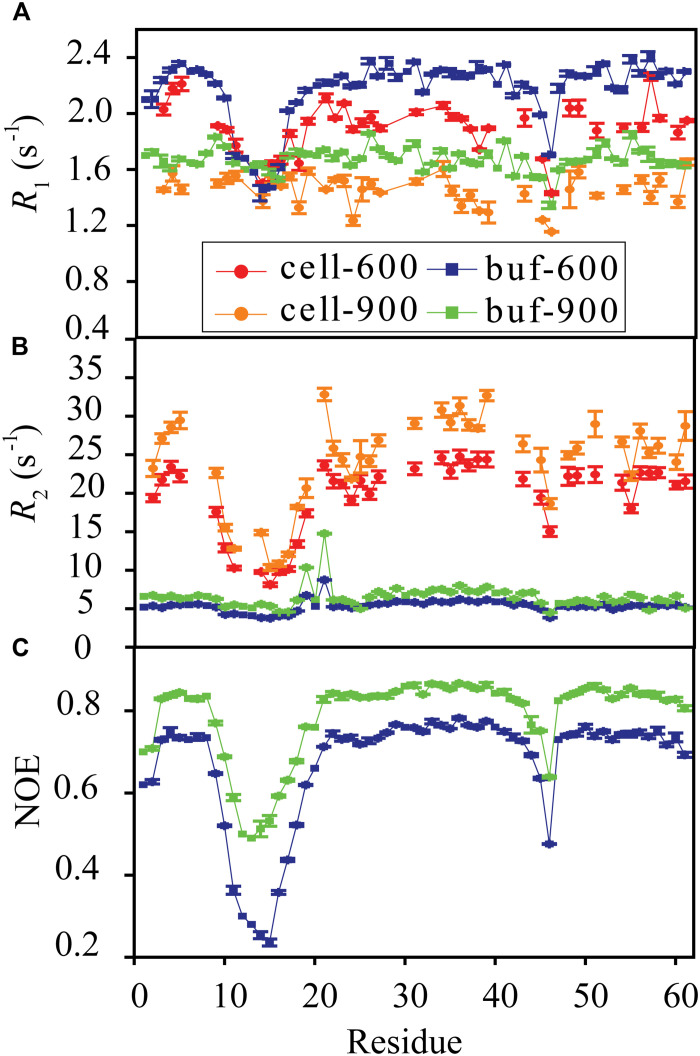
Backbone amide ¹⁵N R₁, R_1ρ, and ¹⁵N-{¹H} NOE data were collected for GB3L at both 600 and 900 MHz fields (65, 66) in the buffer of 40 mM bis-tris propane/40 mM Hepes (pH 6.8) (Fig. 1, A to C). From the NOE data, one can see that loop 1 and the linker D45-G46 (D40-G41 in GB3) show elevated conformational dynamics (see discussion below). The R₂ rates, derived from R₁ and R_1ρ (30), indicate that D19 and T21 display conformational exchanges.

Fig. 1. Protein backbone amide relaxation rates.

¹⁵N R₁ (A), R₂ (B), and ¹⁵N-{¹H} NOE (C) were measured for GB3L at both 600 and 900 MHz fields in the buffer and in E. coli cells at 303 K. The pH in cells, monitored by using ¹⁵N chemical shift of H33 (fig. S1), was adjusted to be the same as that in the buffer (40 mM bis-tris propane/40 mM Hepes, pH 6.8). Error bars are SEM (n = 3 independent experiments).

¹⁵N R₁ and R_1ρ data were also collected for GB3L in E. coli cells (Fig. 1, A and B). The pH in cells was monitored by using ¹⁵N chemical shift of H33 (the only histidine residue in the protein). This chemical shift is sensitive to pH changes from ~6 to 8 presumably caused by the ionization state change of H33, based on the GB3L pH titration experiment in buffer (fig. S1). The ¹⁵N chemical shift H33 in cells was matched to that in vitro [115.92 parts per million (ppm) at pH of 6.8] by adjusting the pH of the buffer (40 mM bis-tris propane/40 mM Hepes) used for cell suspension and in-cell NMR measurements (fig. S1). Therefore, the pH difference effect on dynamics and relaxation rates is eliminated. Compared to relaxation rates in the buffer, ¹⁵N R₁s in cells are slightly smaller, whereas ¹⁵N R₂s are considerably larger (Fig. 1B). To ensure that the relaxation rates were from GB3L in cells, a ¹H-¹⁵N heteronuclear single-quantum coherence (HSQC) spectrum was collected after R₁ and R_1ρ experiments (~3.5 hours). The protein concentration in the supernatant was very small (fig. S2), suggesting that the cell sample was stable during the relaxation measurements and signals were from GB3L in cells. The cells were viable after NMR experiments as proved previously (67).

Conformational dynamics (picosecond to nanosecond) of GB3L in the buffer

The model-free (55, 56) analysis was performed to extract the diffusion tensor (table S2), the order parameter (Fig. 2A), and the internal correlation time τ_e (fig. S3) from R₁, R₂, and NOE data at 600 and 900 MHz fields. Most residues are quite rigid, especially those from the α-helix and β-strand secondary structures. Loop 1 (G9-L17) displays elevated dynamics, with the inserted GNSGG (G11-G15) fragment being particularly flexible (Fig. 2A). The linker D45-G46 also shows some flexibility, consistent with that of the WT GB3 (62). The conformational exchange rate R_ex was also extracted for D19 and T21, yielding values of 2 and 3.78 s⁻¹, respectively, at 600 MHz field (table S3), indicating that these two residues have conformational exchanges.

Fig. 2. Conformational dynamics of GB3L.

(A) Order parameters in the buffer only, with anionic SNPs (aSNP), and in E. coli cells. The presence of anionic SNPs extends the dynamic observation time window so that picosecond to microsecond dynamics (S²_SNP) can be detected, which is undetectable in the conventional model-free analysis of ¹⁵N R₁, R₂, and NOE data measured in the buffer only (S²_buf). GB3L S² in E. coli cells (S²_cell) agrees better with S²_SNP, suggesting that the dynamics detected in cells is probably on picosecond to microsecond timescale. Picosecond to millisecond timescale S² fitted from backbone amide ¹H-¹⁵N RDCs (S²_RDC) was also included (only residues with at least two sets of experimental RDCs are shown). (B) Correlation of S² in E. coli cells (S²_cell) measured at 600 and 900 MHz fields. Two residues D19 and T21 show conformational exchanges (in red). Error bars (except for S²_RDC) are SEM (n = 3 independent experiments). Error bars for S²_RDC are SD from 10 independent ensemble fittings.

Conformational dynamics of GB3L in cells

The weak attractive interactions with larger molecules in cells are expected to increase ¹⁵N R₂ rates (68) of GB3L. Meanwhile, R₂ rates can also be increased by higher viscosity in cells than that of water (69, 70). For GB3L that binds transiently with surrounding molecules in cells, the ¹⁵N R₂ rate for its backbone amide can be written as

$$R_{2,\mathrm{cell}}=\sum p_i{R}_{2i,\mathrm{cell}}(i=0,1,2,\dots )$$ (1)

where i = 0 (i > 0) corresponds to the free (bound) state, R_2i,cell is the GB3L backbone amide ¹⁵N R₂ rate of state i (free GB3L or GB3L bound to different molecules in cells), and p_i is the state population (∑p_i = 1). The equation is valid provided that the binding/unbinding rate is slower than the tumbling of GB3L (~10⁹ s⁻¹), but much faster than the [¹H, ¹⁵N] chemical shift differences between different states. To extract the dynamic information, ΔR₂ was introduced (see more details in the Supplementary Materials),

$$\text{Δ}{R}_{2,\mathrm{cell}}=R_{2,\mathrm{cell}}-R_{2,\mathrm{buf}}\approx {cS}_{\mathrm{cell}}^2({\mathrm{\tau }}_{\mathrm{cell}}-{\mathrm{\tau }}_{\mathrm{buf}})$$ (2)

where R_2,buf is the GB3L backbone amide ¹⁵N R₂ rate in the buffer, c is a constant, τ_cell is the GB3L average tumbling time in cells (τ_cell = ∑p_iτ_i,cell,τ_i,cell is the tumbling time of state i), and τ_buf is the GB3L tumbling time in the buffer. S²_cell is a weighted average of S² from different state i

$$S_{\mathrm{cell}}^2=\frac{\sum p_i{S}_i^2({\mathrm{\tau }}_{i,\mathrm{cell}}-{\mathrm{\tau }}_{\mathrm{buf}})}{\sum p_i({\mathrm{\tau }}_{i,\mathrm{cell}}-{\mathrm{\tau }}_{\mathrm{buf}})}$$ (3)

Extracting order parameters from ΔR₂ was first proposed by Bruschweiler and coworkers where SNPs were used to broaden NMR dynamic detection timescale (58–60). In the in-cell system, the situation is a bit more complicated because the macromolecules are more diverse and the viscosity is different in cells. It is worth mentioning that S²_cell is not an arithmetic mean of S² of the free state and that of different bound states. It is a mean of S² weighted by the tumbling time difference between each state and that in the buffer. As the binding partner in cells becomes larger, its contribution to S²_cell is more prominent. It is also noteworthy that Eq. 2 is an approximation and can be substituted by a treatment using a numerical stochastic Liouville equation provided that the exchange rates between different states are known (71).

To evaluate the applicability of Eq. 2, we used a simple two-state model, a free state and a bound state in cells, to simulate the impact of GB3L binding partner size, binding population, and viscosity in cells on the predicted S². R_2,buf at 600 MHz was calculated using the GB3L dynamic parameters (Fig. 2A, fig. S3, and table S2), which were extracted from the experimental relaxation data in the buffer using the model-free analysis (55, 56). R_2,cell at 600 MHz was calculated using the same internal motion parameters but assuming that the viscosity in cells is 2.5 times that of water (69, 70). The binding partner has a molecular weight (MW) of 50 kDa, the average MW of proteins in cells. Equation 2 was used to predict S² from the synthetic ΔR₂ data. The S² error is ~6% when there is only the free state in cells, and decreases quickly when the bound state increases (fig. S4A). The relatively large S² error of the free state is mainly caused by the axially symmetric diffusion tensor of free GB3L in buffer and in cells. If an isotropic diffusion tensor is assumed with the same tumbling time, the error is much smaller (fig. S4B). The S² error is not very sensitive to the MW of binding partner or viscosity in cells (fig. S4C). The data simulation suggests that Eq. 2 can be used to extract S² with good accuracy.

GB3L backbone amide R₂ rates in cells were determined at both 600 and 900 MHz fields (Fig. 1). S² in cells (S²_cell) were extracted from ΔR₂ rates using Eq. 2 (Fig. 2A). The experimental ΔR₂ of ~18 s⁻¹ (Fig. 1) at the 600 MHz field corresponds to a bound population of ~15% in the model, or S² error of ~2% (fig. S4A). The quality of S²_cell is quite good, as suggested by the correlation between the values extracted independently from the two fields (Fig. 2B). Similar to S² in the buffer, order parameters in cells indicate that loop 1 and the linker D45-G46 display elevated dynamics. S²_cell values of 0.75 and 0.58 for D45 and G46 are almost the same as those in the buffer (Fig. 2A). In comparison, loop 1 becomes more flexible in cells. Moreover, the residues next to loop 1 (including K18 and D19) are also more flexible, as if the dynamics of loop 1 and neighboring residues is boosted in cells. However, one needs to be careful that only order parameters of the internal dynamics faster than the tumbling time (3.5 ns) of GB3L can be extracted from ¹⁵N R₁, R₂, and ¹⁵N-{¹H} NOE data in the buffer. If loop 1 has dynamics slower than 3.5 ns, it might only be detectable in cells where binding to large molecules in cytosol increases GB3L tumbling time.

Conformational dynamics (picosecond to microsecond) of GB3L in the buffer with the assistance of SNPs

To capture the dynamics slower than nanoseconds in the buffer, colloidal anionic SNPs with a mean diameter of 20 nm were added to the buffer where backbone amide ¹⁵N R₁ and R₂ rates were collected and S² were extracted (fig. S5 and Fig. 2A) (59). The presence of SNPs increases the (bound) protein tumbling time to a few microseconds (58), thus broadening the detection limit of conformational dynamics. S² values of D45 and G46 are similar to those in the buffer without SNPs, suggesting that these two flexible residues have no nanosecond to microsecond dynamics. But the smaller S² values of loop 1 than those in the buffer in the absence of SNPs indicate that this loop has dynamics on nanosecond to microsecond timescale (59). The comparable dynamic amplitude for loop 1 in cells and in the buffer with SNPs suggests that the dynamics observed in cells is probably on the same timescale.

Conformational dynamics (picosecond to millisecond) of GB3L in the buffer from RDCs

To independently determine the conformational dynamics of GB3L in the buffer, backbone ¹H-¹⁵N RDCs, which are sensitive to dynamics on picosecond to millisecond timescale, were measured from multiple alignments at 900 MHz field. Previously, we showed that five independent alignments could be obtained for GB3 by attaching a DO3MA-6MePy tag chelated with Tm³⁺ to K19C, V21C, K28C, Q32C, and D36C, respectively (64). For GB3L, attaching the tag to K24C and V26C was successful (corresponding to K19C and V21C in GB3). Attempts to attach the tag to the other three residues failed because these GB3L mutants were very unstable. Instead, we were able to attach the tag to A53C (of GB3L). Together with RDCs in the external alignment medium Pf1 (72), there are a total of four sets of ¹H-¹⁵N RDCs for the protein (tables S4 and S5). Singular value decomposition analysis shows that the ratio between the largest singular value and the smallest one is 4:1, suggesting that four independent RDC datasets are present (Fig. 3A). All the mutation sites are away from loop 1 (Fig. 3B) so that these cysteine mutations should have a very small impact on its dynamics.

Fig. 3. Ensemble fitting of GB3L backbone ¹H-¹⁵N RDCs.

A total of four sets of RDCs were measured at 900 MHz, with three from DO3MA-6MePy-Tm³⁺ attached to K24C, V26C, or A53C, and one from the external alignment medium Pf1. The x-ray structure of GB3 [pdb code: 2OED (87)] with the inserted loop was used as the starting structure for molecular dynamic simulation to generate an ensemble of eight structures for the experimental RDC fitting. (A) Correlation between experimental and back-calculated RDCs from the ensemble, and singular value decomposition of experimental RDCs, which was used to yield singular values (panel insert) and check the independence of RDCs (see more details in the main text). (B) Ensemble averaged structure displayed with the pointed DO3MA-6MePy-Tm³⁺ attaching sites. The order parameter S²_RDC is displayed in Fig. 2A for comparison with S² from the other methods.

A protein ensemble fitting was performed using GB3L backbone ¹H-¹⁵N RDCs. The average structure and order parameters S²_RDC were calculated (Figs. 2 and 3B). The overall structure is very similar to that of GB3, except with an elongated loop 1 (Fig. 3B). S²_RDC has a pattern similar to S²_SNP (S² in the presence of SNPs; Fig. 2A). The elevated dynamics of loop 1 extracted from RDCs (compared to that from model-free analysis) independently validates the information extracted from ΔR₂ in SNPs that this loop has conformational dynamics slower than the protein tumbling time. The somewhat smaller S²_RDC than S²_SNP also indicates that this loop has a bit of microsecond to millisecond timescale dynamics (Fig. 2A), since the protein dynamics detected from the RDCs is on the picosecond to millisecond timescale, broader than that from ΔR₂ in SNPs. Furthermore, residue G46 has a S²_RDC smaller than S²_SNP, suggesting that this residue has dynamics on microsecond to millisecond timescale as well.

Millisecond dynamics of GB3L in buffer from CPMG measurements

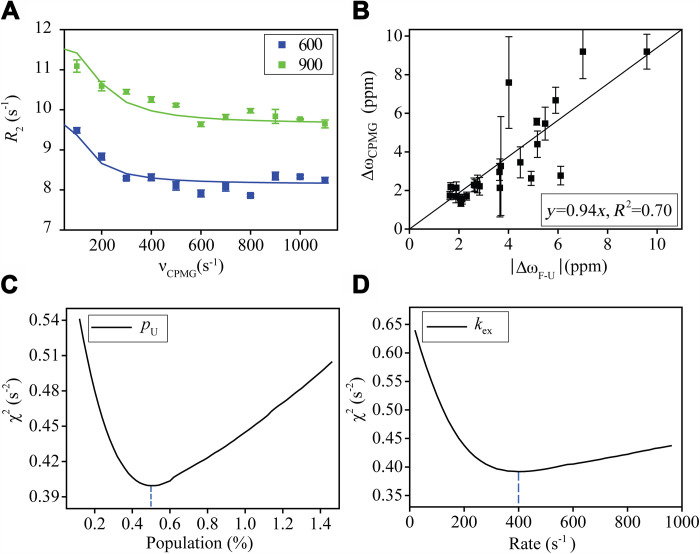
As stated above, two residues D19 and T21 show conformational exchanges (R_ex > 0). ¹⁵N CPMG NMR relaxation dispersion experiments (52, 53) were performed for GB3L at both 600 and 900 MHz fields to see whether the conformational exchange persists for the protein on the millisecond timescale. Dozens of residues (including D19 but not T21) display some (albeit small) exchanges as suggested by the apparent ¹⁵N R₂ relaxation rate differences at different 180° ¹⁵N CPMG pulsing frequencies (Fig. 4A). A two-site model was assumed where a global fitting was performed for 25 exchanging residues to extract the exchange rates (k₁ and k₋₁) and the chemical shift difference (Δω_CPMG). Δω_CPMG is correlated with the chemical shift difference between the unfolded and folded GB3L (Fig. 4B and fig. S6), suggesting that the exchange process corresponds to GB3L folding and unfolding. The relatively slow exchange rate (k₁ + k₋₁ = 400 s⁻¹) and the low population of the unfolded state (0.5%) indicate that the contribution of the folding-unfolding exchange to ¹⁵N R_1ρ rates is very small (Fig. 4, C and D). Thus, its impact on the model-free and ΔR₂ analyses is expected to be small as well. This exchange process is not pursued any further.

Fig. 4. ¹⁵N CPMG NMR relaxation dispersion data analysis for GB3L.

The data were measured in the buffer of 40 mM bis-tris propane/40 mM Hepes, pH 6.8, at 303 K. A two-site exchange model was used to fit the CPMG data for 25 residues that show chemical exchanges. (A) CPMG profile of A39 and its fitting curves. (B) Correlation between Δω_CPMG, the chemical shift difference from the fitting, and Δω_F-U, the chemical shift difference (absolute value) between the folded and unfolded GB3L. (C) Reduced χ² error versus the fitted unfolded state population. (D) χ² error versus the fitted exchange rate. The positive correlation between Δω_CPMG and Δω_F-U (absolute value) indicates that the conformational exchange corresponds to the protein folding and unfolding process. Error bars are SEM (n = 3 independent experiments).

Mutational effect on GB3L dynamics in buffer and in cells

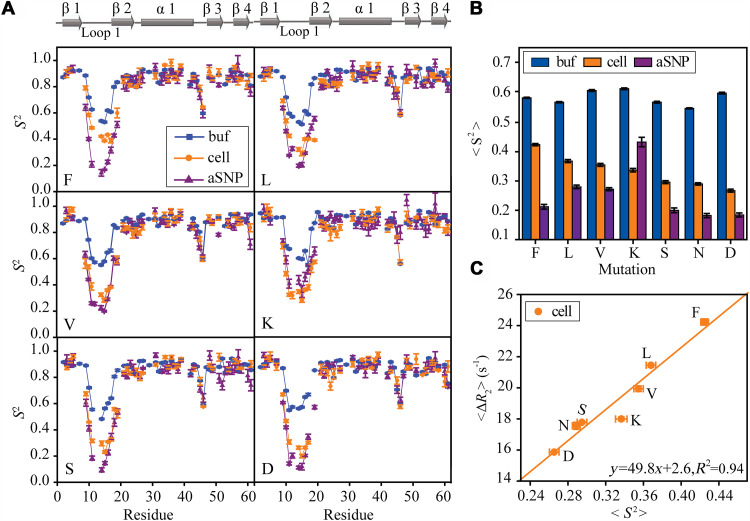
Weak interactions with large molecules increase the detection time window of R₂ relaxation experiments in cells. One important question is whether the weak interactions affect loop dynamics in cells. To address this question, several mutations were prepared by changing X in the inserted GXSGG sequence to F, L, V, K, S, and D (N in GB3L). The order parameters for all the mutants in the buffer and in cells were extracted from relaxation rates (Fig. 5A and figs. S7 and S8). The loop 1 order parameters S² of different mutants are compared to see how the loop sequence modulates its dynamics. The average loop order parameter (averaged over G11-L17, excluding residues X12 and S13, which have S² missing due to signal overlapping in certain mutants) variation in the buffer from model-free analyses is relatively small (Fig. 5B). In contrast, the results in cells show that <S²_cell> varies quite a bit, depending on the X amino acid type, generally in the order of hydrophobic > positively charged > polar and negatively charged amino acid (Fig. 5). The most rigid loop (F mutant) has an <S²_cell> ~60% higher than the most flexible one (D mutant) in cells. Furthermore, a positive correlation can be seen between the average order parameter and the average ΔR₂ of rigid GB3L residues (Fig. 5C). Increase of the average ΔR₂ can be caused by the population increase of the bound states due to the loop stronger interactions with surrounding macromolecules in cells (see Eq. 1). The positive correlation indicates that the loop becomes more rigid as the interactions become stronger. In other words, the loop attractive interactions with intracellular macromolecules tend to suppress GB3L loop dynamics in cells. It is worth mentioning that increasing the bound population alone (which increases ΔR₂) does not affect loop S² if the free and bound forms have identical S² values (Eq. 3). On the basis of the GXSGG mutational effect on <ΔR₂>, hydrophobic interactions contribute the most to the loop surrounding interactions, followed by electrostatic attraction between the positively charged loop (as in GKSGG) and generally negatively charged proteins in E. coli. These two types of interactions have the largest effect on S² (Fig. 5C). On the other hand, the electrostatic repulsion with the negatively charged loop (GDSGG) affects the loop dynamics the least. This may also explain that the dynamics of the loop D45-G46 in cells is very similar to that in the buffer (Fig. 5A). As for the whole protein that has both charged and hydrophobic residues on the surface, it is hard to tell whether hydrophobic or electrostatic interactions with cellular environment are more important.

Fig. 5. GB3L conformational dynamics and its sequence dependence.

The loop 1 sequence was varied by changing X in GXSGG to different amino acids. (A) S² order parameters for different mutants, F, L, V, K, S, and D. (B) Averages of loop S² (including G11, G14, G15, T16, and L17, which have S² values in all GB3L variants) of different mutants in the buffer only, in the presence of anionic SNP, and in cells. The loop S² average in cells (C) is correlated with <ΔR₂> [ΔR₂ = R₂(cell) − R₂(buffer)] averaged over rigid GB3L residues. Error bars are SEM (n = 3 independent experiments).

The order parameters S²_SNP of different mutants were also determined in the presence of SNPs (Fig. 5A and fig. S9). The loop 1 S²_SNP of F, S, and D mutants is ~0.2, comparable with GB3L (N; Fig. 5B), but that of L and V mutants is ~50% larger and the K mutant has the largest loop 1 S²_SNP (~140% larger than GB3L). It is noteworthy that weak interactions between the protein and anionic SNPs also exist (especially electrostatics), which can also perturb loop dynamics, as suggested by the positive correlation between ΔR₂ in anionic SNPs and S²_SNP of loop 1 (fig. S10). In particular, the K mutant has the most rigid loop 1 and highest ΔR₂. The particularly large ΔR₂ may arise from the cooperative binding between K10 and K12 to SNPs (73). To understand the role of electrostatics, S² of the K mutant was determined from ΔR₂ in the buffer with neutral SNPs (Fig. 6A and figs. S11 and S12), which should diminish the SNPs’ electrostatic attraction with the positively charged loop lysine residue. As can be seen, the average order parameter S² of loop 1 drops to 0.28, a 35% decrease compared to that from the anionic SNPs (Fig. 6B). Similarly, adding 200 mM (final concentration) lysine amino acid to the K mutant sample in the presence of anionic SNPs also decreases the order parameter of loop 1 roughly by the same percentage (the pH was adjusted to be the same as that without lysine). Meanwhile, <ΔR₂> of the rigid residues decreases by ~11%, suggesting that the interaction between the K mutant and anionic SNPs is weakened by free lysine amino acid. The abundant free lysine amino acid likely competes with the loop for the anionic SNPs. These results provide direct evidence that the electrostatic attraction between the K mutant loop and anionic SNPs rigidifies loop 1.

Fig. 6. Impact of SNPs on the conformational dynamics.

(A) Order parameters S² of the GB3L K mutant measured in 40 mM bis-tris propane/40 mM Hepes, at pH 6.8 and 303 K. (B) The average S² of loop 1 is smaller with additional 200 mM lysine in the anionic SNPs (aSNP) at the same pH and temperature. A similar decrease was seen in the same buffer but with neutral SNPs (nSNP). It is apparent that the electrostatic attraction between the GKSGG loop and anionic SNPs suppresses the loop dynamics. Error bars are SEM (n = 3 independent experiments).

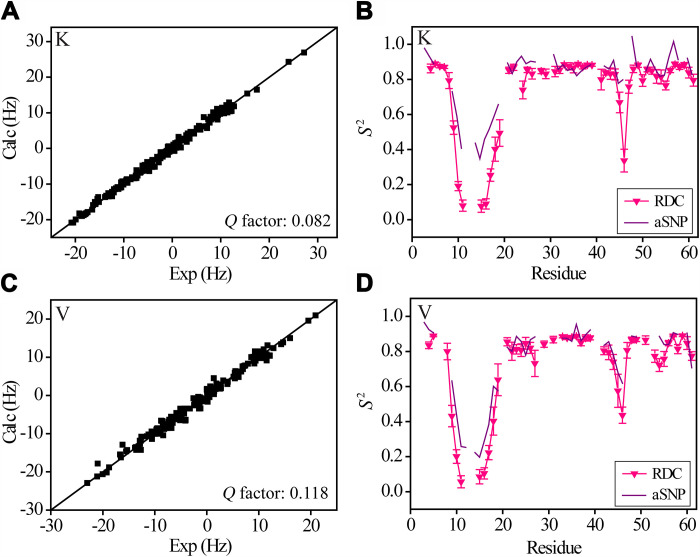
Although the model-free analysis shows that the mutational effect on loop 1 dynamics on picosecond to nanosecond timescale is rather small in the buffer, it is important to see how the mutations may affect dynamics on a slower timescale. In neutral SNPs, the K mutant still shows an average loop 1 S² (close to that of L and V mutants) ~50% higher than GB3L and the other mutants (Fig. 5B). But this dynamics difference may arise from the weak interactions with SNPs. To see how the K mutation may affect loop dynamics without SNPs, four sets of ¹H-¹⁵N RDCs (same as those for GB3L) were measured for the mutant and the order parameters were determined through ensemble fitting (Fig. 7A). For loop 1, S²_RDC of the K mutant is much smaller than S²_SNP (Fig. 7B), but comparable with S²_RDC of GB3L (Fig. 2A). The order parameter of the V mutant was also determined from RDCs (Fig. 7C), and a similar loop S²_RDC to that of GB3L was obtained. Again, for this mutant, the loop S²_RDC is smaller than S²_SNP (Fig. 7D). Together, these results indicate that the larger loop S²_SNP for the K and V mutants (Fig. 5B) is most likely caused by protein weak interactions with SNPs, whereas the mutational effect on loop dynamics is small, consistent with that from the model-free analysis.

Fig. 7. Order parameters derived from ensemble fitting of backbone ¹H-¹⁵N RDCs.

A total of four sets of RDCs were measured and fitted in the same way for GB3L. (A and C) Correlation between experimental and back-calculated RDCs (for K and V mutants) from the ensemble. (B and D) Dynamics (S²_RDC) calculated from the structure ensemble for the two mutants (only residues with at least two sets of RDCs are shown). S²_SNP is also displayed for comparison. Error bars are SD from 10 independent ensemble fittings.

DISCUSSION

Here, we studied the conformational dynamics of an inserted loop (loop 1) of GB3L in the buffer and in E. coli cells. The model-free analysis of ¹⁵N R₁, R₂, and NOE in the buffer suggests that loop 1 and a few neighboring residues have elevated dynamics on picosecond to nanosecond timescale (Fig. 2A). As demonstrated by Leeb and colleagues (68), the average protein amide ¹⁵N R₁, R₂ relaxation rates in cells, measured using 1D ¹⁵N-filtered HSQC-based pulse sequences, can be interpreted by a chemical exchange model, between the free and the bound forms to some large molecules. Because of complexity of cellular environment, there are likely many different bound forms. The simplest case is that only one free form and one bound form exist, as in the buffer with SNPs. Binding to large molecules slows down protein tumbling and thus broadens the conformational dynamic detection time window of the R₂ relaxation measurements. By taking this advantage, picosecond to microsecond timescale dynamics can be captured from ΔR₂. With the assistance of SNPs, conformational dynamics on picosecond to microsecond timescale was observed for loop 1. S²_SNP extracted from ΔR₂ using SNPs agrees reasonably well with that from RDCs, which are sensitive to dynamics up to milliseconds (Figs. 2A and 3). S²_cell of GB3L (GNSGG) has a profile similar to that in the buffer S²_SNP (Fig. 2A). In other words, the loop picosecond to microsecond dynamics in cells is consistent with that detected in the buffer by nanoparticle-assisted spin relaxation measurements and RDCs, which, in our opinion, validates the method used in this work. A folding-unfolding conformational exchange has been shown for the overall protein, with the population of the unfolded protein ~0.5% and the exchange rate ~400 s⁻¹ (Fig. 4). The impact of the exchange on loop dynamics is very small.

To extract S²_cell from ΔR₂, one assumption is made that the exchange contribution to R₂ in the buffer and in E. coli cells needs to cancel out each other. Taking residues D19 and T21 as an example, both residues have obvious conformational exchanges (positive R_ex) in the buffer (Fig. 1). R_ex can be altered if the molecules in cells interact differently with the ground state and the excited state. For the fast conformational exchange with R_ex proportional to the square of the field strength, as observed for D19 and T21 of GB3L, the change of R_ex would affect ΔR₂ and thus S²_cell at the 900 MHz field differently from that at the 600 MHz field (eqs. S2 and S3). If R_ex(cell) > R_ex(buffer), S²_cell at 900 MHz will be overestimated more than that at 600 MHz. Otherwise, if R_ex(cell) < R_ex(buffer), S²_cell at 900 MHz will be underestimated more than that at 600 MHz. For T21, S²_cell at both fields matches well (Fig. 2B). For D19, S²_cell at 900 MHz is a bit smaller than that at 600 MHz. But the deviation is only about two times the measurement error. Thus, we think that the impact of cellular environment on R_ex is relatively small for both residues. It is important to have S²_cell from the two fields to validate the assumption.

Mutations on loop 1 have a big impact on <S²_cell>, but their effect on <S²_buf> is small (Figs. 5 and 7). A positive correlation is shown between <S²_cell> and <ΔR₂>. A similar correlation is shown between <S²_SNP> and <ΔR₂>. The correlation is interpreted as that the loop becomes more rigid by interacting stronger with SNPs (Fig. 6) or macromolecules in cells. This is not that surprising because binding of the protein to macromolecular surfaces can hinder the motion of the loop and thus decrease its flexibility. However, the cellular environment is rather complex, composed of various proteins, RNAs, and DNAs. The size and concentration distribution of the in-cell proteins are unknown. If the timescale range detected by NMR in cells is different for different mutants due to their binding to macromolecules with different sizes, the situation becomes more complicated. Therefore, it is assumed that the NMR detected motion timescale range is insensitive to mutations. One scenario is that, compared to GB3L, the mutants may bind to larger macromolecules stronger in cells, which will increase <ΔR₂> of the rigid residues as well (eq. S5). The binding helps NMR to detect a slower timescale motion. On the basis of the fact that loop 1 has dynamics on the microsecond to millisecond timescale, this will further decrease loop S², meaning that <S²> and <ΔR₂> should be negatively correlated, opposite to the experimental observation. Another scenario is that hydrophobic or positively charged mutants bind stronger to smaller macromolecules but similarly to larger macromolecules compared to the WT. The stronger binding gives larger ΔR₂ and larger S²_cell as well (due to the narrower NMR detection timescale range), which would yield the same correlation as in Fig. 5C. One would expect that the attractive interactions with surrounding macromolecules are determined by their surface property, not their sizes. However, further studies are needed to investigate this scenario.

¹⁵N R₁, R₂, and ¹⁵N-{¹H} NOE rates have been measured before in E. coli cells at 700 MHz field and 298 K for phenylalanyl-glycyl-repeat–rich nucleoporins (FG Nups), which are IDPs (74). It has been suggested that “The cellular milieu maintains FG Nups as highly dynamic IDPs” (74). It is worth noting that the dynamic interpretation of the relaxation data of IDPs is far more complex than that of folded proteins. Relaxation rates measured at multiple fields are required to accurately quantify dynamics of IDPs (75). It is likely that weak interactions with cellular environment may suppress IDP dynamics as well. But a more thorough study is needed to address this issue.

The biomolecules in the interior of E. coli cells can reach 400 g/liter (76), which provides rich binding partners for proteins through weak attractive interactions. The weak interactions with intracellular environment can hinder protein loop dynamics. As the interactions increase, the impact on loop conformational dynamics becomes more prominent. This work highlights the role of intracellular environment on conformational dynamics and underlines the importance of direct dynamics study in cells. All biological functions are driven by interactions. The protein interactions with cellular environment have been shown to affect protein conformation (9, 23, 27–29), folding and stability (11, 12, 14, 16, 40), and protein-protein binding (18, 20–22) in cells. Here, we showed that the interactions also affect protein loop dynamics. Many loop dynamics important for protein functions (e.g., enzyme catalysis and signal transduction) have been elucidated (30, 31). We expect that the change on loop dynamics by cellular environment can affect protein functions in cells as well.

MATERIALS AND METHODS

Sample preparation for in vitro NMR experiments

The GB3L and its mutants were cultured and purified according to our previously described method (77). NMR samples were obtained by dissolving ~1.2 mM ¹⁵N-labeled GB3 mutants in 600 μl of buffer, which is 40 mM bis-tris propane/40 mM Hepes at pH 6.8 [80%/20% (v/v) H₂O/D₂O]. Colloidal anionic and neutral SNPs, with an average diameter of 20 and 34 nm, respectively (product names Levasil CS40-120 and CC503), were purchased from AkzoNobel. The SNPs were dialyzed against 20 mM Hepes buffer (pH 6.8) using concentrator tubes with a MW cutoff of 10 kDa. The dialyzed anionic (neutral) SNPs were 20 (5) times diluted and mixed with GB3L and various mutants to prepare the NMR experiment samples with the same conditions as before (58). The samples of DO3MA-6MePy-Tm³⁺ attached GB3L mutants were prepared as described previously (64). Because of instability of GB3L and different mutants, the protein DO3MA-6MePy-Tm³⁺ tag chelating condition was modified by decreasing the temperature to 30°C.

Sample preparation for in-cell NMR experiments

The in-cell experiments were prepared as previously described with some modifications (54). E. coli BL21 (DE3) cells containing plasmids encoding different mutants of GB3L were cultured in 250 ml of LB medium at 37°C until OD₆₀₀ ≈ 0.6. The viable cells were centrifuged at 1000g, 4°C for 20 min. The obtained pellet was gently resuspended to 250 ml of ¹⁵N-labeled M9 medium to cultured (37°C, 200 rpm, 30 min). Then, the E. coli cells were induced by additions of isopropyl-β-d-thiogalactopyranoside (with a final concentration of 0.2 mM) and cultivated for 1.5 hours. Finally, the viable cells were collected by centrifugation (1000g, 4°C, 20 min) and pipetted into the NMR tubes for NMR analysis {40 mM bis-tris propane/40 mM Hepes, pH 7.8 [80%/20% (v/v) H₂O/D₂O], in 600 μl volume}. Viability of E. coli cells was also verified by plating a sample in NMR tube before the measurement and 4 hours later (the total NMR measurement time is 3.5 hours). The colony numbers in two plates were comparable after 15 hours of incubation (fig. S13), suggesting that the cells were still viable after the NMR experiment.

NMR experiments and data analysis

All experimental data were collected at 303 K. A set of three-dimensional HNCACB and CBCA(CO)NH experiments was collected for ¹⁵N/¹³C-labeled GB3L (GNSGG) to confirm the ¹H-¹⁵N HSQC assignment (78). ¹⁵N spin relaxation (R₁ and R_1ρ) experiments were performed for GB3L in cells and in the buffer at 600 and 900 MHz (79). The R₁ and R_1ρ rates for GB3L in the buffer with SNPs were measured at 600 MHz using the same method. The R_1ρ relaxation delay intervals were [0.004, 0.01, 0.015, 0.02, 0.03 s] for GB3L in cells and for proteins in the buffer with SNPs. The R_1ρ relaxation delay intervals were [0.004, 0.02, 0.04, 0.08, 0.12 s] at 600 MHz and [0.004, 0.01, 0.02, 0.04, 0.06 s] at 900 MHz for proteins in the buffer without SNPs. The spin-lock field strength is 2765 Hz at 600 MHz field and 1584 Hz at 900 MHz field. For all the R₁ measurements, the relaxation delays were [0.1, 0.2, 0.3, 0.4, 0.5, 0.6 s]. NOE experiments were performed in the buffer with the water flip-back scheme (65) and a recycling delay of 5.0 s. All the relaxation measurements were performed in triplicates. For measurements in the buffer without SNPs, the same sample was used. For measurements in the buffer with SNPs and in cells, three samples were prepared independently. The intracellular pH was maintained at pH 6.8, indicated by the chemical shift of H33 (fig. S1). The ¹H-¹⁵N RDCs were measured using ¹H-¹⁵N IPAP (In-phase Antiphase)-HSQC experiments (80), for GB3L with the residue K24C, V26C, or A53C mutation attached to DO3MA-6MePy-Tm³⁺ tag, or aligned in Pf1 (~10 g/liter) (72). Same measurements were performed for the K and V mutants. The data of CPMG were collected in the same way as previously described (77).

The transverse spin relaxation rate (R₂) was extracted according to

$$R_2=R_{1\mathrm{\rho }}/{\sin }^2\mathrm{\theta }-R_1/{\tan }^2\mathrm{\theta }$$ (4)

where θ = arctan(Ω/ω), Ω is the chemical shift of each amino acid from the center position, and ω is the spin-lock field strength.

S² of each GB3L mutant in the buffer was obtained by model-free (55, 56) fitting using a total of six sets of R₁, R₂, and NOE data at 600 and 900 MHz fields. The extended model with S²_fast, S²_slow (S² = S²_fastS²_slow), and an internal correlation time τ_e were used (81). For D19 and T21 that have conformational exchanges, an additional parameter R_ex, which is assumed proportional to the square of magnetic field strength, was included in the model-free fitting. An effective N-H bond length of 1.04 Å was used for the dipole-dipole spectra density calculation. ¹⁵N Chemical Shift Anisotropy (CSA) tensor with (σ_XX, σ_YY, σ_ZZ) values of (71, 44, −115) ppm for α-helix residues, (70, 38, −108) ppm for β-strand residues, and (69, 42, −111) ppm for all other residues, were used in the fitting (82). The errors for S², τ_e, and R_ex were obtained from Monte-Carlo simulation by adding random noise to R₁, R₂, and NOE data. The SD of the R₁, R₂, and NOE random noise corresponds to the measured SEM of R₁, R₂, and NOE from triplicate measurements, respectively. The order parameters in cells were extracted from ΔR₂ as follows. The average model-free S² was calculated for protein rigid residues in the buffer. Then, the scaling factor k was calculated from eq. S7. A small correction was applied to k, because slightly different ¹⁵N CSA tensors were used for different secondary structure residues, which slightly changed the constant c. The order parameters in cells were obtained from ΔR₂ and k, with S²_cell = ΔR₂/k. S²_cell in cells at the two fields were averaged. The order parameters in the buffer with SNPs were obtained in the same way. All the dynamic analyses were performed using in-house programs.

Ensemble fitting of ¹H-¹⁵N RDCs

The ensemble fitting of ¹H-¹⁵N RDCs was performed using the GROMACS software (83), similar to the procedure in our previous work (64) and in the literature (84). The starting coordinates were generated from the RDC refined x-ray structure (2OED), by inserting the GXSGG loop between K10 and T16 using the Rosetta remodel application (85). The system was solvated in cubic boxes with 12.5 Å TIP3P waters. One-nanosecond molecular dynamic (MD) simulation was carried out at 350 K to equilibrate the system, after 5000 steps of energy minimization and 200 ps restrained (protein backbone heavy atoms only) NVT simulation using a force constant of 1000 kJ/ mol⋅nm². The MD snapshots were saved every 10 ps. The last 800 ps (a total of 80) MD snapshots were divided into 10 groups and used as the starting ensemble structures for RDC fitting. Ten ensemble refinements were carried out with a force constant of 0.4 kJ/mol⋅Hz² with a simulated annealing process from 350 K to 0 K (84). The order parameters S² and average structure were calculated for each ensemble (86) and averaged over 10 ensembles.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S13

Tables S1 to S5

References

View/request a protocol for this paper from Bio-protocol.