DISTRIBUTIONAL EFFECTS OF EDUCATION ON HEALTH

Abstract

This paper studies distributional effects of education on health. In 1972, England, Scotland, and Wales raised their minimum school-leaving age from 15 to 16 for students born after 9/1/1957. Using a regression discontinuity design and objective health measures for 129,000 individuals, we find that education reduced body size and increased blood pressure in middle age. The reduction in body size was concentrated at the upper tail of the distribution with an 8 percentage point reduction in obesity. The increase in blood pressure was concentrated at the lower tail of the distribution with no effect on stage 2 hypertension.

There is broad disagreement about whether education has a causal effect on health (Grossman 2015). Some studies find that more education causes better health (e.g. Lleras-Muney 2005) while others find little to no effect (e.g. Clark and Royer 2013). Galama, Lleras-Muney, and Kippersluis (2018) argue that heterogeneity in these effects may underlie these conflicting results. Their model lays out conditions for such heterogeneity to exist, and evidence indicates that such conditions are met: (i) heterogeneity in the labor market returns to education (Card 2001); (ii) heterogeneity in the non-market returns to education (Barcellos, Carvalho, and Turley 2018); and (iii) heterogeneity in skill formation as a result of education (Grenet 2013).

This paper investigates whether the effects of education on health are heterogeneous by studying how education affects the distribution of health. If education affects some parts of the health distribution but not others, then the effect of education on health must vary across individuals. In particular, the effect may be larger for individuals with poorer health. In a Grossman-type model, education will cause the unhealthy to invest more in their health than the healthy because of the diminishing marginal utility of health (Kippersluis and Galama 2014).¹

Since little is known ex-ante about the dimensions along which the effect of education on health may vary, a distributional approach is a suitable way to investigate heterogeneity. It avoids multiple hypotheses testing concerns and considerations about the lack of good measures of relevant dimensions. Moreover, if the effects are concentrated at particular parts of the health distribution, a distributional test may be better powered than a test of difference in means—see Online Appendix A.

We exploit a well-known schooling reform in the United Kingdom using a regression discontinuity design. In 1972, England, Scotland, and Wales raised their minimum school-leaving age from 15 to 16 for students born on or after September 1, 1957 (students born before this date could drop out at age 15), generating a discontinuity in the relationship between education and date of birth at the September 1, 1957 “cutoff.” The reform had the primary effect of inducing students who would have dropped out at age 15 to obtain exactly one additional year of education. We estimate the distributional effects of education on health from discontinuities in the cumulative distribution function (CDF) of health at the birthdate cutoff.

We use data from the UK Biobank, a study that collected multiple objective and continuous measures of health between 2006 and 2010; 34–38 years after the policy change. Using standardized protocols, healthcare technicians and nurses measured the height, weight, body fat percentage, waist and hip circumferences, lung function, and blood pressure of more than a quarter million people born in England, Scotland, and Wales between September 1, 1947 and August 31, 1967. The unprecedented availability of objective health measures for such a large sample permits well-powered estimation of distributional treatment effects. To ease concerns about multiple hypotheses testing, we focus our analysis on three health indices constructed from the multiple measures available: body size², lung function, and blood pressure.

There are three main takeaways from the distributional analysis. First, staying in school until age 16 improves one dimension of health—there is a reduction in body size—and worsens another: there is an increase in blood pressure.³ Second, it reveals that these effects vary considerably along the health distribution. To give a sense of how effects are concentrated, staying in school until age 16 reduces the 90th percentile of the body size distribution by 0.43 of a standard deviation—that is equal to 2.5 times the effect on average body size. Third, the effects on body size and on blood pressure occur in different parts of their respective distributions: while the effect on body size is concentrated at the upper tail (i.e., among the least healthy), the effect on blood pressure is concentrated at the lower tail (i.e., among the most healthy).⁴

We conduct a distributional test based on Shen and Zhang (2016) to formally investigate whether these changes are statistically significant, testing differences in the bottom and top halves of the CDFs of our three health indices. The test rejects at the 5% significance level the null of equality for the top half of the body size distribution (p-value of 0.013) and for the bottom half of the blood pressure distribution (p-value of 0.028). We only find suggestive evidence of a positive effect on lung function.

The results from our distributional analyses suggest that the effects of education on health are heterogeneous. Our estimates recover the distributional effects on compliers, that is, students who stayed in school an additional year because of the schooling reform. If the effects were homogeneous, we would see effects across the whole support of the complier distribution, with the largest effect at the mode (see Online Appendix B). This is because, if education affects each complier equally, the distributional effect at a given point should roughly correspond to the mass at this point in the pre-reform complier distribution. As described above, this is not what we find: effects are concentrated at the top of the body size distribution, with the largest effect at the 83^rd percentile. Therefore, our findings are not consistent with homogeneous treatment effects. Importantly, our method recovers differences in the health distribution of compliers only and does not rely on rank preservation assumptions.

We also conduct an exploratory analysis to investigate possible channels through which education may affect health. While improvements in SES and diet may explain the reduction in body size, the channels for the increase in blood pressure are less clear. We do show, however, that education allowed individuals to earn higher income in middle age, in part because they hold better jobs (Barcellos, Carvalho and Turley 2021). One possibility is that, by changing the types of occupations and careers individuals have, education might have had an effect on job responsibilities, expectations, and work-related stress. This would be consistent with evidence that academically successful African Americans in the U.S. have higher biomarkers related to cardiometabolic risk (i.e. blood pressure and stress hormones) than other groups (Brody et al. 2013, Miller et al. 2015, Chen et al. 2015) and with findings that, despite improving SES outcomes, the 1972 reform had detrimental effects on mental health (Avendano et al. 2020).⁵

For the sake of comparison, we also estimate the effects of education on average health. A number of studies have exploited changes in compulsory schooling laws to study such effects (e.g., Lleras-Muney 2005; Albouy and Lequien 2009; Silles 2009; Powdthavee 2010; Kemptner et al. 2011; Clark & Royer 2013; Jürges et al. 2013; Davies et al. 2018; Janke et al. 2020; Meghir et al. forthcoming). We find that staying in school until age 16 reduces body size by 0.17 of a standard deviation and increases blood pressure by 0.15 of a standard deviation, but these estimates are only significant at the 10% level.⁶

In an apparent contrast to the results of this paper, Clark and Royer (2013) estimate a precise null effect of the 1972 ROSLA reform on mortality. They also find no statistically significant effect on the averages of non-mortality health outcomes.⁷ Our estimates of the effects on average health are, however, broadly consistent with their corresponding estimates. While Clark and Royer had very large samples to estimate the effect of education on mortality, their estimates of the effects on non-mortality health outcomes are less precise because they had more limited samples for such outcomes. For this reason, our estimates lie within the 95% confidence intervals of Clark and Royer (2010, 2013)’s corresponding estimates.

In addition, our work is closely related to Davies et al. (2018) which also use the 1972 ROSLA and UK Biobank data to study the effects of education on health, albeit with a focus on the effects on average health. They find that the 1972 ROSLA reduced the risk of diabetes and mortality, which is consistent with our finding that the policy reduced body size and obesity. Their sample is almost 10 years older than Clark and Royer (2013)’s which could explain why they find effects on mortality when Clark and Royer (2013) do not.⁸

While the main take-away from Clark and Royer (2013) is that education does not affect health, our results suggest a more nuanced story. The distributional analysis shows that education can affect the health of some subpopulations. The heterogeneity of the effects of education on health may explain the conflicting findings in the literature (Galama et al. 2018). First, education affects different parts of the health distribution differently, implying that the effects vary across individuals. Second, the effects also vary across outcomes: the additional schooling caused a reduction in body size and an increase in blood pressure.

Despite this, the question remains as to how education could affect some health outcomes while having no downstream effects on mortality. There are several hypotheses for such a result. First, as noted above, those affected by the 1972 ROSLA would have been less than 50 years old at the time of the Clark and Royer study. It is possible that not enough time had passed to observe meaningful differences in mortality.⁹ Second, health is a multi-dimensional construct, and, as we see in this study, education may improve some dimensions of health while worsening others. As a result, the ultimate effect of education on mortality may be attenuated by these opposing factors.¹⁰ In short, Clark and Royer’s finding of no effect on mortality are plausibly consistent with Davies et al. (2018)’s and our results.

We note that, while the UK Biobank data are rich and the sample size is large, the sample is not nationally representative – its participants have higher SES than the target population (Fry et al. 2017). We compare objective health outcomes of compliers of the schooling reform we study (i.e. those born before the reform who dropped out of school before age 16) in the UK Biobank to compliers in the Health Survey for England – a nationally representative sample. We do not find unequivocal evidence that the UK Biobank sample is healthier than the average population (among compliers) and the health differences among the two samples, while statistically significant, are small. Still, such differences could threaten the external validity of our results.

The paper is structured as follows. Section I discusses the 1972 raising of the school leaving-age reform and the data. In Section II we present the effects of the reform on education and the effects on average health. Section III discusses the methods used to estimate the distributional effects with results shown in Section IV. Section V presents suggestive evidence on mechanisms and Section VI concludes.

I. Background and Data

A. The 1972 Raising of the School Leaving Age

The British compulsory schooling laws specify the maximum age by which children must start school and the minimum age at which they can leave school. In this paper, we exploit the 1972 Raising of School Leaving Age (ROSLA) legislation, which increased the minimum school-leaving age from 15 to 16 years of age in England, Scotland, and Wales. These laws and their implementation have been extensively documented in other studies (see Clark and Royer 2010, 2013) so we only include a brief summary of its main features here.

The UK’s 1944 Education Act raised the minimum school-leaving age from 14 to 15 years of age in England, Wales, and Scotland and gave the Minister of Education the power to further raise it to 16 years when conditions allowed. The Minister did so in January 1972 for Scotland (Statutory Instrument No. 59)¹¹ and in March 1972 for England and Wales (Statutory Instrument No. 444)¹². Both changes took effect in September 1, 1972, implying that those who were 15 or younger before that date (born on September 1, 1957 or later) had to stay in school until at least age 16 in the three countries (hereafter, we use the term “stayed in school until age 16” to refer to those who stayed in school until at least age 16). Infrastructure investments, such as school building to absorb the additional students, preceded the 1972 ROSLA but key elements of the school system did not change with the policy.

Figure 1, which displays the fraction of study participants who stayed in school until age 16 (y-axis) by quarter of birth (x-axis), shows that the policy generated a discontinuous relationship between these two variables. There is a large jump at the September 1, 1957 cutoff marked by the vertical dashed line. Those born during the summer months could in practice drop out at age 15 even after the 1972 ROSLA, since the law required students to be 16 by the start of the next school year. We estimate that the policy increased the fraction of UK Biobank participants who stayed in school until age 16 by 14 percentage points – see Table 1.¹³

Figure 1. Fraction Staying in School until Age 16 by Quarter of Birth.

Notes: The figure shows the fraction of study participants who stayed in school until age 16 by quarter of birth. The dashed vertical line marks the first birth cohort affected by the 1972 school-leaving age reform. Cohorts born to the right of the line had to stay in school until age 16 while cohorts born before could leave at age 15. The curves show linear trends in quarter of birth that capture birth cohort trends. The circumference of each circle reflects the number of participants born in that quarter. N = 129,370.

Table 1.

Effects on Education

	Left school at age ≥ 16		No Qualifications		CSE
Post	0.136 [0.004]***	0.136 [0.004]***	−0.046 [0.003]***	−0.046 [0.003]***	0.069 [0.005]***	0.069 [0.005]***
Additional Controls?	No	Yes	No	Yes	No	Yes
Mean of Y	0.826		0.113		0.206
	O-level		A-level		College Degree
Post	0.032 [0.006]***	0.033 [0.006]***	0.009 [0.006]	0.009 [0.006]	−0.011 [0.006]*	−0.011 [0.006]*
Additional Controls?	No	Yes	No	Yes	No	Yes
Mean of Y	0.513		0.325		0.368

Notes: The table shows the effects of the school reform on education. Each cell corresponds to a separate regression. We report the coefficient on the indicator variable for being born on or after September 1, 1957 (i.e., “Post”). The dependent variable mean in the bottom row is the weighted mean among those born in the 12 months before September 1, 1957. All regressions control for calendar month of birth. Additional controls include male, age in days and age squared dummies for ethnicity, and dummies for country of birth. Robust standard errors. N = 129,370 for “Stayed in school until 16” and N = 128,169 for all other outcomes.

*, **, and *** denote significance at the 10, 5 and 1 percent level.

Notice there is a cyclical drop in the fraction of students staying in school until age 16, corresponding to those born between June and August. This phenomenon is not specific to our data and has been noted by others. According to Clark and Royer (2013), “when the minimum leaving age became age 16, students had to stay until part way through grade 10. Grade 10 finishes with the “O level” exam period and, technically, students finish when they complete their last exam. Since the exam period starts in late May and finishes in mid-June, starting in 1972, students born in late June, July, and August could leave at 15, technically younger than the minimum leaving age (16)” (see page 2 of their online appendix). We include calendar month of birth dummies in our regressions to control for this seasonality.

B. Data

We use data from the UK Biobank, a large, population-based prospective study initiated by the UK National Health Service (NHS) (Sudlow et al. 2015). Between 2006 and 2010, invitations were mailed to 9.2 million people between the ages of 40 and 69 who were registered with the NHS and lived up to about 25 miles from one of 22 study assessment centers distributed throughout the UK (Allen et al. 2012) – see Online Appendix Figure D1.¹⁴ The sample is formed by 502,643 individuals who agreed to participate (i.e. a response rate of 5.46%). Although the sample is not nationally representative, our estimates have internal validity because there is no differential selection on the two sides of the September 1, 1957 cutoff – see Online Appendix C.¹⁵

Physical measures, such as anthropometrics, spirometry, and blood pressure, were collected of survey participants. The collection was standardized across centers and was conducted by trained nurses or healthcare practitioners. Every participant was genotyped.

In this paper, we focus on objective and continuous measures of health. Continuous measures because we are interested in studying how education affects the distribution of health. Objective measures because research shows that discrepancies between subjective (e.g. self-reported hypertension) and objective measures of health (e.g. objectively measured hypertension) vary with socioeconomic status (e.g. Johnston et al. 2009).

We restrict ourselves to three dimensions of health (that satisfy the two criteria above and) that can be arguably affected by education: body size, lung function, and blood pressure.¹⁶ Weight and body size can be affected by education through diet and physical exercise. Lung function can be affected by education through smoking and pollution. Blood pressure may be affected by education through diet, physical exercise, medication, and stress. Moreover, these health dimensions are risk factors for high-prevalence diseases such as diabetes (Chan et al. 1994), lung cancer (Tockman et al. 1987) and cardiovascular disease (Kannel 1996). The UK Biobank has multiple measures of each of these health dimensions.

Next, we describe how each of these health dimensions is measured in the data.

1. Body Size

We use three measures of body size: BMI, body fat percentage, and waist-hip ratio.¹⁷ A bioimpedance analyzer was used to calculate body fat percentage. This device passes a low electrical current through the body. Water conducts electricity. While fat contains very little water, muscle contains 70% water. The bioimpedance analyzer calculates body fat from the speed of the current: The slower the signal travels, the greater the fat content.

2. Lung Function

A spirometry test was conducted to measure participants’ lung function. The spirometer is a small machine attached to a mouthpiece by a cable that measures the volume and speed of air after a forced exhale. Participants were asked to fill their lungs as much as possible and to blow air out as hard and as fast as possible in the mouthpiece.¹⁸ Three parameters were measured: 1) forced expiratory volume in the first second is the amount of air exhaled during the first second; 2) forced vital capacity is the total amount of air exhaled during the forced breath; and 3) peak expiratory flow is the fastest rate of exhalation. These parameters are used to assess pulmonary conditions, such as chronic obstructive pulmonary disease and asthma. We follow DeMatteis et al. (2016)’s criteria to identify acceptable expiratory maneuvers in the UK Biobank data. Valid spirometry measures are available for 80% of our sample.¹⁹

3. Blood Pressure

Two measurements were taken of the diastolic and systolic blood pressures of each study participant. We use the average of these two measurements.

4. Summary Indices

For each health dimension, we construct a summary index that is a weighted average of the different outcomes measuring that dimension:

1. Body size: body mass index, waist-to-hip ratio, and body fat percentage;

2. Lung function: forced expiratory volume in the first second, forced vital capacity, and peak expiratory flow;

3. Blood pressure: diastolic and systolic blood pressures.

First, each measure is standardized separately by gender, using as a reference those born in the 12 months before September 1, 1957. We then follow the procedure proposed by Anderson (2008), weighting the measures by their variance-covariance matrix. The weights are calculated to maximize the amount of information captured in the index. Finally, we construct a fourth “summary index” that is a summary of the body size, the lung function, and the blood pressure indices, using the same weighting procedure. We construct all four indices so that a higher number corresponds to worse health.

These indices have two main advantages relative to traditional biomarker measures of health such as BMI and blood pressure. First, they reduce the number of outcomes and mitigate multiple hypotheses testing concerns. Second, they decrease noise by averaging out measurement error across the outcomes measuring the same health dimension, increasing the statistical power of our estimates. In addition, since only a very small fraction of our sample has low blood pressure (0.73%) or are underweight (0.6%), we can treat the relationships between our constructed indices and health as approximately monotonic over the range of the data. The main limitation is that these indices may not be as readily interpretable as more traditional measures such as BMI because they do not have clinical meanings.

The correlation between the body size and lung function indices is 0.18. The correlation between the body size and the blood pressure indices is 0.30. The correlation between the lung function and the blood pressure indices is 0.08. The correlations between the summary index and the body size, lung function, and blood pressure indices are respectively 0.68, 0.67, and 0.68.

II. Mean Effects

A. Effects of the Compulsory Schooling Change on Education

We use a regression discontinuity design (RDD) to estimate the “first stage”, i.e., the effect of the 1972 ROSLA on education. In particular, we estimate the following regression:

$${Educ}_i=a_0+a_1{Post}_i+f\left({DoB}_i\right)+{\mathit{x}}_i^{\text{'}}{\mathit{a}}_2+{\epsilon }_i,$$ (1)

where Educ_i is a measure of the educational attainment of individual i; Post_i is 1 if individual i was born on or after September 1, 1957 (and 0 otherwise); DoB_i is individual i’s date of birth; and the vector x_i contains predetermined characteristics. Date of birth is measured in days relative to the cutoff, such that DoB=0 for someone born on September 1, 1957. The function f(⋅) captures birth cohort trends in educational attainment, which are allowed to differ on either side of the September 1, 1957 cutoff. The coefficient a₁ gives the effect of the 1972 ROSLA on educational attainment.²⁰

We restrict the data to 129,730 study participants born in England, Scotland, or Wales within five years of September 1957 – that is, born between September 1, 1952 and August 31, 1962 – and use a linear trend in date of birth to capture cohort trends (i.e., function f(⋅) in equation (1)).^21,22 In Online Appendix E we show our main results are robust to the choice of bandwidth and to the use of quadratic trends.²³ We use triangular kernel weights that give greater weight to study participants born closer to the cutoff. All regressions include dummies for calendar month of birth to control for seasonality. We also present results adding other set of predetermined characteristics as controls including gender, age in days (at the time of the baseline assessment) and age squared, dummies for ethnicity, dummies for country of birth.²⁴

Notice that even though previous work studying the 1972 ROSLA clustered standard errors by month-year of birth (e.g., Clark and Royer 2013; Davies et al. 2018), we do not need to cluster our standard errors because our data include exact date of birth. As Card and Lee (2008) discuss, in applications where the running variable is only reported in coarse intervals (e.g., month-year of birth), researchers have to choose a particular functional form for the model relating the outcomes of interest to the running variable. The deviation between the expected value of the outcome and the predicted value from a given functional form is modeled as a random specification error, which is incorporated in inference by clustering the standard errors for different values of the running variable. This specification error is negligible in our context because our data include exact date (day-month-year) of birth.

Table 1 shows estimates of effects of the 1972 ROSLA on education. Each cell reports results from a separate ordinary least squares estimation of (1), where we vary the dependent variable (listed in the column) and whether the predetermined characteristics are included as controls (in addition to calendar month of birth dummies). The table shows the coefficient on the indicator variable for being born on or after September 1, 1957, a₁, and the mean of the dependent variable among those born in the 12 months before September 1, 1957. Robust standard errors are reported between brackets.

We estimate that the 1972 ROSLA increased the fraction of study participants staying in school until age 16 by 14 percentage points, an estimate significant at the 1% significance level.²⁵ Studies using nationally representative data, such as Clark and Royer (2013), estimate this figure to be closer to 25 percentage points. This difference is likely due to the composition of the UK Biobank sample, which is more educated than the overall population (despite the selectivity of the UK Biobank sample, our estimates have internal validity because there is no differential selection on the two sides of the September 1, 1957 cutoff – see Online Appendix C). One consequence is that the standard errors of our two stages least squares (2SLS) estimates will be ceteris paribus larger than of studies with nationally representative data, something that is compensated by the larger sample size of the UK Biobank.

One may worry that these students forced to stay in school an extra year did not learn much if they did not put effort into it. The evidence does not support this hypothesis. By the 70’s high schools offered a series of two-year courses that ran through grades 10 and 11 and required students to take exams at the end of grade 11 (the grade they are typically in by age 16): Certificate of Secondary Education (CSE) or a General Certificate of Education (GCE) Ordinary Level (also known as an O-level). By compelling students to stay in school until grade ten, the 1972 ROSLA gave students an incentive to complete these courses and get these qualifications, which are valued in the labor market (Dickson and Smith 2011).

Figure 2 shows that the policy generated a discontinuous increase in the fraction of study participants with these qualifications. In Table 1 we estimate that the policy increased the fraction of study participants with a CSE by 7 percentage points and the fraction with an O-level by 3 percentage points. The fraction without any formal qualification dropped by 5 percentage points. All of these reduced-form estimates are statistically significant at 1%. We find no effect of the policy on having an A-level or a college degree.²⁶ Consistent with these results, we document that the policy increased household income²⁷, especially at lower income levels – see Online Appendix Table F1.

Figure 2. Fraction with a CSE of O-level by Quarter of Birth.

Notes: The figure shows the fraction of study participants with a CSE or O-level qualification by quarter of birth. The dashed vertical line marks the introduction of the policy. Cohorts born to the right of the line had to stay in school until age 16 while cohorts born before could leave at age 15. The curves show quadratic polynomials in quarter of birth that capture birth cohort trends. The circumference of each circle reflects the number of participants born in that quarter. N = 128,169.

B. Effects on Average Health

We now turn to the effects of the 1972 ROSLA on average health. We are interested in the relationship between health and education:

$${Health}_i={\beta }_0+{\beta }_1{Educ16}_i+g\left({DoB}_i\right)+{\mathit{x}}_i^{\mathrm{\text{'}}}{\mathit{\beta }}_2+u_i,$$ (2)

where Health_i is a health measure for individual i. Educ16_i, an indicator for whether individual i stayed in school until age 16, is our endogenous measure of education. The function g(⋅) captures birth cohort trends in health and is allowed to differ on either side of the September 1, 1957 cutoff. We substitute (1) into (2) to get the “reduced-form” effect of the 1972 ROSLA on average health:

$${Health}_i={\gamma }_0+{\gamma }_1{Post}_i+j\left({DoB}_i\right)+{\mathit{x}}_i^{\mathrm{\text{'}}}{\mathit{\gamma }}_2+v_i.$$ (3)

The coefficient γ₁ gives the effect of the school leaving-age reform on average health. The RDD identifying assumption is that, in the absence of the reform, our outcomes of interest would have been smooth across the September 1, 1957 threshold. This assumption is violated if determinants of health are discontinuous at the cutoff (Lee 2008). In Online Appendix C we partially test for such violations by investigating whether the average (or the cumulative distribution function) of predetermined characteristics, such as gender and place of birth, are discontinuous around September 1, 1957. Since the UK Biobank genotyped the full sample, we also test for the smoothness of a pair of genetic variables, which are determined at conception and are objectively measured.²⁸ Our analyses indicate that these characteristics are smooth across the September 1 1957 threshold, which strengthens our confidence that the RDD results provide unbiased estimates of the causal effects of education on the health of UK Biobank participants.

We estimate the causal effect of staying in school until age 16 on average health, β₁, through two stages least squares (2SLS), using the indicator for being born on or after September 1, 1957 (i.e., Post_i) to instrument for staying in school until age 16 (i.e., Educ1616_i) in equation (2). We adopt the same specifications used to estimate the effects on education (see section II.A), namely: 5-year bandwidths, linear trends to capture birth cohort trends, triangular kernel weights, and the same set of controls. Online Appendix E shows our results are robust to quadratic cohort trends and other bandwidths.

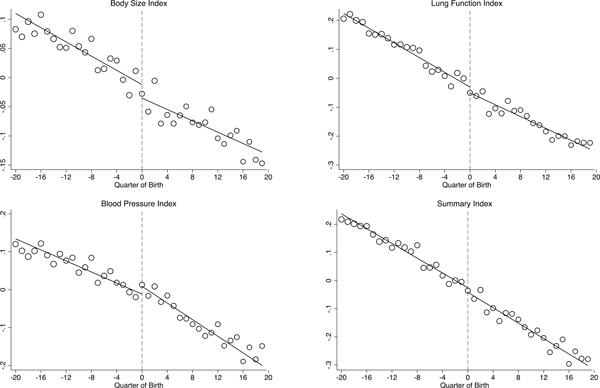
Figure 3 examines the effects of the 1972 compulsory schooling change on average health. The graphs show average health (y-axis) by quarter of birth (x-axis), where health is measured by the four health indices: the body size index (top left); the lung function index (top right); the blood pressure index (bottom left); and the summary index (bottom right).

Figure 3. – Effects on Average Health.

Notes: These figures show average health by quarter of birth. See Table 2 for number of observations.

Table 2 shows regression estimates of the effects of the 1972 compulsory schooling change on average health.²⁹ The first rows show the coefficients on the indicator variable for being born on or after September 1, 1957, γ₁ in equation (3), from reduced-form estimates. The third row shows the coefficients on staying in school until age 16 from 2SLS estimates, β₁ in equation (2), where the indicator variable for being born on or after September 1, 1957 is used to instrument for staying in school until age 16. Again, the health indices were constructed such that higher values correspond to worse health.

Table 2.

Effects on Average Health

	Body Size		Lung Function		Blood Pressure		Summary
Reduced-form
Post	−0.023 [0.012]*	−0.023 [0.012]*	−0.019 [0.014]	−0.020 [0.014]	0.020 [0.012]	0.020 [0.012]*	−0.014 [0.014]	−0.015 [0.014]
Two stages least squares
Stayed in school until 16	−0.170 [0.090]*	−0.170 [0.090]*	−0.155 [0.112]	−0.164 [0.112]	0.148 [0.091]	0.150 [0.091]*	−0.112 [0.112]	−0.118 [0.112]
Additional Controls?	No	Yes	No	Yes	No	Yes	No	Yes
N Observations	127,366	127,366	103,682	103,682	129,165	129,165	102,378	102,378

Notes: The table shows the effects on average health. The first two rows show reduced-form effects of the 1972 Raising of the School Leaving Age. The last two rows show two stages least squares estimates of the effect of staying in school until age 16 obtained by using an indicator for being born on or after September 1, 1957 to instrument for staying in school until age 16. Robust standard errors. All regressions control for calendar month of birth. Additional controls include male, age in days and age squared, dummies for ethnicity, and dummies for country of birth.

*, **, and *** denote significance at the 10, 5 and 1 percent level.

Overall Figure 3 suggests education may lead to small average improvements in health, with minor discontinuous decreases in the body size, lung function, and summary indices at the cutoff. One noteworthy exception is blood pressure. There is a discontinuous increase in the blood pressure index at the cutoff, suggesting that education may worsen this particular dimension of health. Online Appendix Figures E1–E4 assess the sensitivity of Figure 3 to changes in the bandwidth and to using quadratic trends.

Table 2 shows that the effects on body size and blood pressure are statistically significant at the 10% significance level. The 2SLS point estimates imply that staying in school until age 16 decreases the body size, the lung function, and the summary indices respectively by 0.23, 0.19–0.20, and 0.14–0.15 of a standard deviation. At the same time, staying in school until age 16 increases the blood pressure index by 0.20 of a standard deviation.

The p-value of a test of the difference between the effects on the body size and the blood pressure indices is 0.003. The difference between the effects on the lung function and the blood pressure indices has a p-value of 0.089. The difference between the effects on the body size and the lung function indices has a p-value of 0.901. These results, notably the difference between blood pressure and body size, point to the importance of treating health as multi-dimensional and considering the effects of education on different dimensions separately. Focusing on the analysis of summary measures of health can lead to misleading conclusions of no health impact if effects going on opposite directions cancel out, as is the case in Table 2.

Our estimates lie within the 95% confidence intervals of Clark and Royer (2010) – see Online Appendix Table D1.³⁰ Clark and Royer (2010) do not estimate the effects on systolic blood pressure or on lung function. As discussed above, even though we have a larger sample than Clark and Royer (2010), we have a smaller first stage, which explains why our standard errors are not substantially smaller than theirs.

When making this comparison, one should keep in mind that the UK Biobank is not a nationally representative sample. It recruited only individuals living within 25 miles of one of the 22 assessment centers, all of which were located in urban areas. Fry et al. (2017) also document that younger, males living in socioeconomically deprived areas and in particular regions of the UK were less likely to accept the invitation to join the study.

In Online Appendix G, we compare compliers in the UK Biobank to compliers in the Health Survey for England – a nationally representative sample – in terms of objectively-measured health outcomes, namely BMI, waist-hip ratio, and diastolic and systolic blood pressures.³¹ We find that compliers in the UK Biobank have lower BMIs and waist-hip ratios, but that they also have higher diastolic and systolic blood pressures.³² Thus, we do not find unequivocal evidence that the UK Biobank sample is healthier than the average population (among compliers). Moreover, while these differences in health are statistically significant, their magnitudes are small. Finally, for each health outcome, there is substantial overlap between the distribution in the UK Biobank sample and in the Health Survey for England sample.

We also used genetic data and a nationally representative sample, the English Longitudinal Survey of Ageing (ELSA), to investigate the selectivity of the UK Biobank sample. Genetic data may be useful in this regard because it is fixed at conception. We calculated the distribution of the polygenic score for educational attainment—an index created from millions of genetic markers—in the ELSA and the UK Biobank samples. Online Appendix figure G5 shows that, while there are differences, there is substantial overlap in the support of the two distributions. Moreover, despite concerns about sample selection, our results retain their internal validity—see Online Appendix C.

III. Methods for Distributional Effects Estimates

Even though the effects on average health are informative, they may conceal larger effects on particular parts of the health distribution with important policy implications. Moreover, the average effects documented here are suggestive at best, being only significant at the 10% level. As illustrated in Online Appendix A, if the effects of education on health are concentrated at particular parts of the health distribution, a distributional test may be better powered than a test of difference in means. In this section, we describe the methods we use to estimate how education affects the distribution of health.

In Section II.B, we estimated the effect of education on average health (of compliers) by investigating if there was a discontinuity in the relationship between average health and date of birth at the September 1, 1957 cutoff. Here we estimate the effect of education on the health distribution (of compliers) by investigating if, at the September 1, 1957 cutoff, there is a discontinuity in the relationship between the cumulative distribution function (CDF) of health and date of birth.³³

The assumptions of our proposed method are similar to those of a traditional RDD (Imbens and Lemieux 2008). The key difference is that, while a traditional RDD requires that the expected values of the potential outcomes are continuous in the running variable at the threshold, our method requires that the distributions of potential outcomes are continuous in the running variable at that point (Shen and Zheng 2015). While we cannot test this assumption formally, we find no significant discontinuity in the distributions of several predetermined variables, strengthening our confidence that this assumption holds—see Online Appendix C.

The rest of this section is structured as follows. In Section III.A, we define the reduced-form distributional effects of the 1972 ROSLA. The local distributional treatment effect is defined in Section III.B. Section III.C explains the approach we use to graphically display the estimates of the local distributional treatment effects. In these sections, we present analyses for BMI to illustrate our methods. Section III.D presents the hypothesis tests used for inference. Finally, Section III.E discusses some particularities of our approach.

A. The Reduced-Form Distributional Effect of the Compulsory Schooling Change

We begin by defining Pr(Health≤h|DoB as the CDF of health for individuals born on a specific date DoB. The CDF is a function of h, giving the fraction of those born on DoB with a health outcome smaller or equal to h. For example, if the health outcome is BMI, then some h values of particular interest are 18.5, 25, 30, and 40 because these correspond to standard clinical thresholds. To illustrate, in our data the fraction of individuals born on August 31, 1957 (i.e., DoB=−1) with a BMI below these clinical values are respectively 3%, 53%, 78%, and 100%. The CDF may differ for different dates of birth. For example, the fractions of those born on September 1, 1952 (i.e., DoB=−1826) with a BMI below 18.5, 25, 30, and 40 are respectively 0%, 22%, 69%, and 96%.

We want to investigate whether Pr(Health≤h|DoB changes discontinuously at September 1, 1957. For this purpose, it is useful to define the pre-reform and post-reform CDFs. Let the pre-reform CDF be the CDF in the limit when date of birth is converging to September 1, 1957 from the left (i.e., for those born right before September 1, 1957):

$$F_{pre}\left(h\right)=\underset{\mathit{DoB}\to 0^{-}}{\lim }\mathrm{P}\text{r}(Health\le h|DoB).$$

Similarly, the post-reform CDF is the CDF in the limit when date of birth is converging to September 1, 1957 from the right (i.e., for those born right after September 1, 1957):

$$F_{post}\left(h\right)=\underset{\mathit{DoB}\to 0^{+}}{\lim }\mathrm{P}\text{r}(Health\le h|DoB).$$

The reduced-form distributional effect of the 1972 compulsory schooling change ϕ(⋅) is the difference between the post-reform CDF F_postx(⋅) and the pre-reform CDF F_pre(⋅):

$$\varphi \left(h\right)=F_{post}\left(h\right)-F_{pre}\left(h\right)$$ (4)

which corresponds to the discontinuous change at September 1, 1957 in the fraction of the population with a health outcome less than or equal to h. To make it concrete, if the health outcome is BMI and we are interested in the effect of the ROSLA at h=30 (which is the clinically defined threshold for obesity), ϕ(30) is the effect of the compulsory schooling change on obesity rates.

We estimated the reduced-form average effect of the policy by estimating equation (3), which is reproduced here for convenience:

$${Health}_i={\gamma }_0+{\gamma }_1{Post}_i+j\left({DoB}_i\right)+{\mathit{x}}_i^{\mathrm{\text{'}}}{\mathit{\gamma }}_2+v_i.$$

Similarly, the reduced-form distributional effect ϕ(⋅) is estimated by running:

$${\text{I}(Health}_i\le h)={\gamma }_0(h)+{\gamma }_1(h){Post}_i+j\left({DoB}_i;h\right)+{\mathit{x}}_i^{\mathrm{\text{'}}}{\mathit{\gamma }}_2(h)+v_i(h)$$ (5)

where I(Health_i≤h) is 1 if individual i’s health outcome is smaller or equal to h.

There are two key differences between (3) and (5). The first one concerns the dependent variable. In (3), the dependent variable may be for example BMI while in (5) it is an indicator for whether individual i’s BMI is smaller or equal to h. The second difference is that, while (3) is one equation, (5) is a continuum of equations for each value of h.

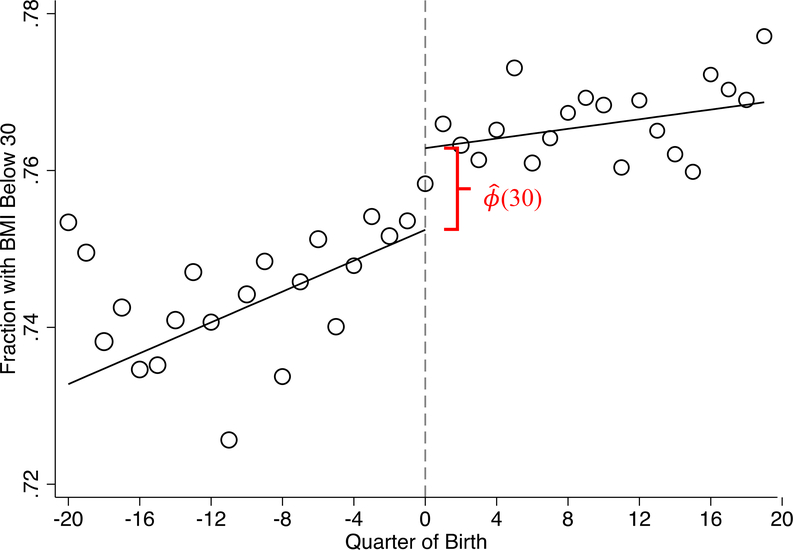
The coefficient γ₁(h) estimates the discontinuity in Pr(Health_i≤h) at DoB_i and thus provides an estimate of the reduced-form distributional effect ϕ(h). To illustrate, Figure 4 shows the usual RD graph for the fraction with a BMI below 30.³⁴ The jump at 0 is the estimate of ϕ(30). The observed increase in the fraction of individuals with a BMI less than 30 corresponds to a reduction in obesity rates of about 1 percentage point.

Figure 4. Fraction with a BMI Below 30.

Notes: The figure shows the fraction of study participants with a BMI below 30 by quarter of birth. The dashed vertical line marks the introduction of the policy. Cohorts born to the right of the line had to stay in school until age 16 while cohorts born before could leave at age 15. The curves show linear trends in quarter of birth that capture birth cohort trends. The circumference of each circle reflects the number of participants born in that quarter. N = 128,856.

We discuss in Section III.D how we use the estimates of ϕ(⋅) to construct our hypothesis tests.

B. The Local Distributional Treatment Effect

We are interested in how staying in school until age 16 affected the CDF of those affected by the policy, that is, the CDF of “compliers” who stayed in school until age 16 because of the compulsory schooling change but who would otherwise have dropped out at 15. This local distributional treatment effect (LDTE) is given by:

$$\begin{gathered} \mu \left(h\right)=F_{post}\left(h|C\right)-F_{pre}\left(h\right|C)= \\ =\underset{\mathit{DoB}\to 0^{+}}{\lim }\mathrm{Pr}\left(Health\le h|DoB,C\right)-\underset{\mathit{DoB}\to 0^{-}}{\lim }\mathrm{Pr}\left(Health\le h|DoB,C\right)= \\ =\frac{\underset{\mathit{DoB}\to 0^{+}}{\lim }\mathrm{Pr}\left(Health\le h|DoB\right)-\underset{\mathit{DoB}\to 0^{-}}{\lim }\mathrm{Pr}\left(Health\le h|DoB\right)}{\underset{\mathit{DoB}\to 0^{+}}{\lim }\mathrm{E}\left(Edu16|DoB\right)-\underset{\mathit{DoB}\to 0^{-}}{\lim }\mathrm{E}\left(Edu16|DoB\right)} \end{gathered}$$ (6)

where F_Post(⋅|C) and F_Pre(⋅|C) are the post-reform and the pre-reform CDFs for compliers (which are denoted by C). Edu16 is an indicator for staying in school until age 16. Note that the numerator of eq. 6 is equal to the reduced-form distributional effect ϕ(h).

The reader will notice the similarity between equation (6) and a local average treatment effect (LATE) estimator. As with LATE, we can estimate the LDTE through two-stage least squares (2SLS):

$${\mathrm{I}(Health}_i\le h)={\theta }_0(h)+{\theta }_1(h){Edu16}_i+l\left({DoB}_i;h\right)+{\mathit{x}}_i^{\mathrm{\text{'}}}{\mathit{\theta }}_2(h)+{\epsilon }_i(h).$$ (7)

using the indicator for being born on or after September 1, 1957 (i.e., Post_i) to instrument for staying in school until age 16 (i.e., Educ16_i). The coefficient θ₁(h) is an estimate of the LDTE μ(h). It estimates the effect of staying in school until age 16 on the probability of having a health outcome smaller or equal to h.

If we estimate (7) for a BMI below 30, for example, we get that staying in school until age 16 reduced obesity rates by 8 percentage points (i.e., $\widehat{\mu }$(30) = 0.08). We can do the same for other values of h. For example, staying in school reduces the probability of having a BMI smaller than 25 by approximately 0.3 percentage points.

C. Visualizing the Local Distributional Treatment Effect

We illustrate the LDTE in a single graph by plotting the pre- and the post-reform CDFs F_Post(⋅|C) and F_Pre(⋅|C) for compliers. To construct the post-reform CDF, we rewrite equation (6):

$$F_{post}\left(h|C\right)=F_{pre}\left(h\right|C)+\mu \left(h\right).$$

That is, for any given h, the vertical distance between the pre- and post-reform CDFs is μ(h).

The pre-reform CDF F_Post(h|C) and F_Pre(⋅|C) is defined as $\underset{\mathit{DoB}\to 0^{-}}{\lim }\mathrm{Pr}\left(Health\le h|DoB,C\right)$. To estimate it, we restrict the sample to respondents born before September 1, 1957 and who left school at age 15 or younger and estimate equation (8) via ordinary least squares (OLS):

$${\mathrm{I}(Health}_i\le h)={\delta }_0(h)+k\left({DoB}_i;h\right)+{\xi }_i(h),$$ (8)

where the function k(⋅;h) captures pre-reform birth cohort trends in health.³⁵ The sample used in this regression is a good approximation of the set of compliers because there are very few never-takers in our sample (i.e., individuals who drop out at age 15 irrespective of the policy). The coefficient on the constant, δ₀(h), estimates F_pre(h|C). It is an estimate of the fraction of compliers born on September 1, 1957 who would have had a health outcome smaller or equal to h in the absence of the policy. We estimate, for example, that ${\widehat{F}}_{pre}\left(30\right|C)=$0.68, such that ${\widehat{F}}_{post}\left(30|C\right)={\widehat{F}}_{pre}\left(30\right|C)+\widehat{\mu }\left(30\right)={\widehat{\delta }}_0(30)+\widehat{\mu }\left(30\right)=$ 0.68 $+$ 0.08 $=$ 0.76.

To illustrate, Figure 5 shows the distributional treatment effect of staying in school until age 16 on BMI. The dashed black line is the pre-reform CDF. The solid red line is the post-reform CDF. The vertical distance between the post- and pre-reform CDFS for h= 30 is $\widehat{\mu }\left(30\right)=$ 0.08. Theoretically, we could estimate F_Pre(⋅|C) and F_Post(⋅|C) for all values of $h\in \mathbb{R}$. In practice, we approximate this by discretizing the support of the distribution of the health outcome and plotting ${\widehat{F}}_{pre}\left(h\right)$ and ${\widehat{F}}_{post}\left(h\right)$ for each grid point.³⁶

Figure 5. Distributional Effects on Body Mass Index.

Notes: The figure shows the pre- and post-reform CDFs of body mass index for compliers. See section III.C for an explanation of how the figure is constructed. N = 128,856

We emphasize that the approach described in this section is used only to graphically display our results. The hypothesis tests, which are discussed next and represent the main results of this paper, depend only on the reduced-form distributional effects discussed in Section III.A.

D. Inference

Inference based on the standard errors generated by 2SLS estimates of (7) or by OLS estimates of (5) is problematic because it leads to an infinite number of highly correlated statistical tests, raising concerns about multiple hypothesis testing. We, therefore, use a single distributional test based on Shen and Zhang (2016) to formally investigate whether education changes the distribution of health. Our test compares the pre- and post-reform CDFs F_Pre(⋅) and F_Post(⋅) of the whole population. It is based on the reduced-form specification (5).

The basis of our test is that—under the null hypothesis of no effect on the health distribution—the function of estimates ${\widehat{\kappa }}_1\left[h\left(\tau \right)\right],$ where h(τ) is the value corresponding to the $\tau$^th quantile of Health_i, is a Brownian bridge (Shen and Zhang 2016).³⁷ We perform an Anderson-Darling test (Anderson and Darling 1952) using the following weighted integral as our test statistic:

$$T={\int }_0^1\frac{{\widehat{\kappa }}_1{\left[h\left(\tau \right)\right]}^2}{\tau \left(1-\tau \right)}d\tau .$$ (9)

This integral is approximated numerically using rectangular integration by evaluating the integrand at each percentile.³⁸ We chose the Anderson-Darling test because it is uniformly powered for the whole range τ∈[0,1] (Stephens 1974). In contrast, the Kolmogorov-Smirnov test used by Shen and Zhang (2016) is better powered to detect deviations of the distribution near the median. To test for differences in the bottom half of the health distribution, we use a modified version of (9), integrating only from zero to 0.5. Similarly, we test differences in the top half by integrating from 0.5 to 1.

The p-values for the test are calculated by simulation. Specifically, we generate an independent, standard normally distributed outcome for each individual (such that there is no discontinuous change in distribution at the discontinuity), and evaluate T (or the upper and lower distribution analogue) for this simulated variable. By Shen and Zhang (2016), this is equivalent to drawing from the test statistic distribution under the null. This is repeated 10,000 times. As the p-value, we report the fraction of times our simulated values of T are greater than our estimated value of T.

E. Discussion

The CDF approach described above is closely related to a quantile IV approach. The CDF approach is based on the vertical distance between the pre- and post-reform CDFs whereas a quantile approach is based on the horizontal distance between these two CDFs. Therefore, either approach would lead us to the same substantive conclusions. We opted to present the CDF approach because it is the framework used by Shen and Zhang (2016), whose results we use in our distributional tests. Nevertheless, when we present our results, we also discuss the effects on some particular quantiles of interest.

It is important to note that our method only recovers differences in the health distribution of compliers and it does not rely on rank preservation assumptions. Stronger assumptions would be needed to recover the distribution of treatment effects, but this is beyond the scope of our paper. Although we do not estimate the distribution of treatment effects, we can examine whether our estimates of the effect on the health distribution are consistent with homogeneous treatment effects. We show in Online Appendix B that, if treatment effects were homogeneous, our estimates of distributional effects would behave predictably. Namely, we would see the largest distributional effects where the largest mass of compliers is: around the mode of the distribution of compliers. Therefore, any other pattern of results is indirect evidence of heterogeneous treatment effects.

Importantly, our two-stage least squares estimates of distributional effects are not likely to be biased by heterogeneity in the first stage. There are two potential forms of first-stage heterogeneity for distributional effects: extensive- and intensive-margin heterogeneity. Extensive-margin heterogeneity means that the fraction of individuals staying in school for longer as a result of the 1972 ROSLA may vary depending on where in the health distribution these individuals would have been absent the reform. For example, unhealthy individuals may be more likely to be drop out of school at age 15 before the reform relative to their healthy peers and therefore may be more likely to be “compliers” in this setting. Intensive-margin heterogeneity means that, among compliers, one’s additional schooling associated with the ROSLA may vary depending on where in the health distribution s/he would have been in the absence of the reform. For example, healthy compliers may be more likely to stay in school for greater than one year due to the ROSLA despite only being compelled to stay for one.

Under the assumptions of the regression discontinuity design, extensive-margin heterogeneity does not affect on our two-stage least squares estimates (see Online Appendix H). The main intuition behind the proof is that two-stage least squares estimates of distributional effects recover differences in the health distribution of only compliers, who, by definition, were all affected by the policy. However, if there is heterogeneity on the intensive margin, the estimates of the distributional effects will overweigh the treatment effects of those who stayed in school longer. As a result, the largest distributional effects would not be observed at the mode of the distribution of compliers; instead, the estimates would be biased toward the mode of distribution of those who increased their schooling the most as a result of the ROSLA.

In practice, it is unlikely that heterogeneity on the intensive margin could explain our results. The main effect of the ROSLA was to keep in school until age 16 students who would have dropped out by age 15 otherwise; the increase in the fraction of students staying in school until at least age 17 as a result of the ROSLA is small and not statistically significant: about 0.5 percentage points (compared to 14 percentage points at age 16, see Online Appendix I). Clark and Royer (2013) reach a similar conclusion (see pg. 2102). These suggest little scope for first-stage, intensive-margin heterogeneity in our context.

IV. Distributional Effects of Education on Health

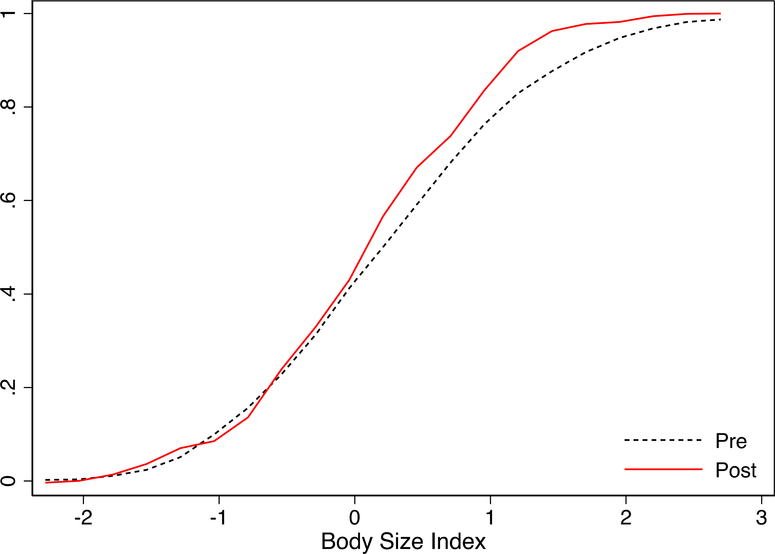
Figure 6 shows the distributional treatment effects of education on body size. It shows the pre- and post-reform CDFs of the body size index for compliers. As explained in Section III, the pre-reform CDF is obtained by estimating (8) for each grid point h and then plotting ${\widehat{\delta }}_0(h)$ against h.³⁹ The discontinuity in the CDF, μ(h), is obtained by estimating (7) through 2SLS for each grid point h. The post-reform CDF at a given grid point h is obtained by adding $\widehat{\mu }\left(h\right)$ “vertically” to ${\widehat{\delta }}_0(h)$.

Figure 6. Distributional Effects on Body Size Index.

Notes: The figure shows the pre- and post-reform CDFs of the body size index for compliers. See section III.C for an explanation of how the figure is constructed. N = 127,366.

Figure 6 shows that education reduces body size: The post-reform CDF is shifted to the left relative to the pre-reform CDF. Importantly, the shift is not parallel; the gains are concentrated at the top of the distribution, among the least healthy. This result is consistent with a Grossman-type model with diminishing marginal utility of health (Kippersluis and Galama 2014). Staying in school until age 16 increases the fraction of study participants with a body size index smaller than 1 standard deviation above the mean from 77.8% to 85.3%. Similarly, the 90^th percentile of the body size distribution decreases from 1.56 to 1.13 standard deviations. This effect is 2.5 times the average treatment effect (on the treated) of −0.17 standard deviations estimated in Table 2.

While Figure 6 has the advantage of graphically displaying the distributional treatment effects in just one figure, it lacks the transparency of traditional RDD graphs. In Online Appendix Figure J1, we present traditional RDD graphs for the 10th, 25th, 50th, 75th, 90th, and 95th percentiles of the distribution of the body size index (of those born between September 1, 1956 and August 31, 1957). Online Appendix Figures J2 and J3 present corresponding graphs for the lung function and blood pressure indices.

Figure 7 shows that education also improves lung function: The post-reform CDF is shifted to the left relative to the pre-reform CDF. Staying in school until age 16 increases the fraction of study participants with a lung function index smaller than 1 standard deviation above the mean from 78.1% to 85.5%. Similarly, the 90^th percentile of the lung function distribution decreases from 1.47 to 1.21 standard deviations. This effect is 1.6 times the average treatment effect (on the treated) of −0.16 standard deviations estimated in Table 2.

Figure 7. Distributional Effects on Lung Function Index.

Notes: The figure shows the pre- and post-reform CDFs of the lung function index for compliers. See section III.C for an explanation of how the figure is constructed. N = 103,682.

While Figures 6 and 7 show that education improves body size and lung function, Figure 8 shows that education worsens one dimension of health: it increases blood pressure.⁴⁰ The post-reform CDF lies to the right of the pre-reform CDF. Staying in school until age 16 decreases the fraction of study participants with a blood pressure index smaller than 0 from 49% to 40.1%. Similarly, the 30^th percentile of the blood pressure index distribution increases from −0.49 to −0.16 standard deviations. This effect is 2.2 times the average treatment effect (on the treated) of 0.15 standard deviations estimated in Table 2. This result is particularly striking because blood pressure can be controlled through medication, diet, and exercise (Chobanian et al. 2003), and there is a positive association between education and these healthy behaviors (Park and Kang 2008; Conti, Heckman, and Urzua 2010; Cutler and Lleras-Muney 2010).

Figure 8. Distributional Effects on Blood Pressure Index.

Notes: The figure shows the pre- and post-reform CDFs of the blood pressure index for compliers. See section III.C for an explanation of how the figure is constructed. N = 129,165.

A comparison of Figures 6 and 8 shows that not only the effect on the body size and blood pressure indices have different signs, but the effects also happen in different parts of the respective distributions. While the effects on body size occur in the upper part of the body size distribution, the effects on blood pressure occur in the lower part of the blood pressure distribution among the healthiest. Online Appendix Figures E5–E10 assess the sensitivity of Figures 6–8 to changing the bandwidth, using linear trends, and the inclusion of controls.

To test whether these shifts in our health indices CDFs are significant and where they are concentrated, we use distributional tests as described in Section III above. The first row in Table 3 shows p-values of tests of the equality of the pre- and post-reform CDFs. The middle and bottom rows show p-values of tests of the equality of the bottom half (i.e., the healthiest) and the top half (i.e., the least healthy) of pre- and post-reform CDFs.

Table 3.

P-values of Distributional Tests

	Body Size	Lung Function	Blood Pressure
Full Distribution	0.0674	0.2972	0.0592
Bottom Half	0.8985	0.4815	0.0282
Top Half	0.0132	0.1880	0.2244

Notes: The table shows the p-values of tests of the equality of the full distribution, the bottom and top halves of the pre- and post-reform CDFs.

We can reject the null for the top half of the body size distribution and for the bottom half of the blood pressure distribution (at the 5% significance level). Online Appendix Tables E1–E3 assess the sensitivity of these results to changing the bandwidth, using quadratic trends, and including controls. While the p-values change across specifications, the main patterns remain: in most cases, we can reject the null of equality for the top half of the body size distribution and for the bottom half of the blood pressure distribution.

Figures 5 and 9 shed light on these findings by plotting results for measures with clinical thresholds. Figure 5 shows the pre- and post-reform CDFs of body mass index (for compliers). Figure 9 shows the pre- and post-reform CDFs of diastolic blood pressure (for compliers).⁴¹

Figure 9. Distributional Effects on Diastolic Blood Pressure.

Notes: The figure shows the pre- and post-reform CDFs of diastolic blood pressure for compliers. See section III.C for an explanation of how the figure is constructed. N = 129,165.

Figure 5 shows that the reductions in BMI caused by more education occur where they matter the most: Staying in school until age 16 reduces obesity rates (i.e., the fraction of study participants with a BMI below 30) by 8 percentage points.⁴² These effects are especially important because the participants were in their 50s and being obese in middle-age is associated with a number of adverse health conditions and with lower quality of life in old age (Daviglus et al. 2003). In contrast, Figure 9 shows that the increase in blood pressure does not affect the prevalence of stage 2 hypertension (classified as having a diastolic blood pressure above 90 mmHg). Staying in school until age 16 may have increased the probability of stage 1 hypertension (defined as having diastolic blood pressure between 80 mmHg and 90 mmHg; known as “prehypertension” before the 2017 redefinition) but this change is not statistically significant.⁴³

These results illustrate the importance of studying distributional effects. While the average treatment effects show improvements in body size and deterioration in blood pressure, the distributional effects reveal in which part of the distributions these changes occur. The deterioration of blood pressure occurs with no observed consequences for the prevalence of stage 2 hypertension. In contrast, the improvements in body size are concentrated at the right tail, with a large reduction in obesity rates. These effects offer important information about trade-offs policy makers may wish to make when considering the health consequences of educational policies: while education may improve some dimensions of health while hurting others, it is important to consider where in the distribution these effects are occurring.

Our findings are not consistent with homogeneous treatment effects of education on health. The main effect of the schooling reform was to induce students who would have dropped out at age 15 (i.e., the compliers) to stay in school an additional year. Homogeneous treatment effects do not imply a constant ${\theta }_1\left(h\right)$ for all h in equation (7), or equivalently, a parallel vertical shift in Figures 5–9. Rather, if this additional year of schooling affected the health of all compliers equally, we would see effects across the whole support of the complier distribution, with the largest effect at the mode of the pre-reform distribution. This is because, when more people are near some threshold h₀ absent the reform, more people will cross the h₀ threshold after the reform is in place. Online Appendix B provides a formal proof.

The results show a different pattern. Figures 5–9 indicate that our effects are limited to some parts of the distributions of health of compliers. Indeed, the statistical tests in Table 3 cannot reject a null effect for the bottom half of the body size and lung function distributions and the top half of the blood pressure distribution. Importantly, the effects we do find are not concentrated around the modes of these distributions. For body size, they are concentrated around the 83^rd percentile of the complier distribution (69^th percentile for lung function and 37^th for blood pressure). These patterns imply heterogeneous effects of education on health.

V. Channels

One of the channels through which education may affect health is health behaviors. Correlational evidence shows that the more educated are more likely to use preventive care, that they manage chronic conditions more effectively, and that they are less likely to smoke and drink heavily (Cutler and Lleras-Muney 2008; Goldman and Smith 2002).⁴⁴

Taking advantage of the richness of the UK Biobank data, we investigate whether education has a causal effect on three types of health behaviors: diet, smoking, and physical activity. Diet was measured using a 24-h dietary assessment tool self-completed through the Internet (Galante et al. 2016).⁴⁵ Accelerometers worn for 7 days were used to measure physical activity.⁴⁶ Smoking was self-reported.

Online Appendix Table F3 shows the effects on diet. Staying in school until age 16 reduces the intake of fat and saturated fat (as a fraction of total energy intake). There are, however, no effects on total caloric intake, sugars, or carbohydrates. Online Appendix Table F4 shows no effects on the measures of smoking and physical activity we have available.⁴⁷

This analysis suggests that improved diet is an important channel through which education reduces body size. Those who stayed in school until age 16 had better diets in middle age – about 10% lower in fat and 15% lower in saturated fat. Even if the energy content of one’s diet is held constant, changes in diet composition can affect body weight (Hall et al. 2012).

The pathways are less clear for the harmful effect of education on blood pressure. We find no effects on a (self-reported) measure of hypertension diagnosis⁴⁸ and on (current) blood pressure medication (Online Appendix Table F4). One alternative hypothesis is that, by changing the types of occupations and careers individuals have, education might have an effect on job responsibilities, expectations, and work-related stress with negative implications for blood pressure.⁴⁹ In the U.S. context, for example, academically successful African Americans have higher biomarkers related to cardiometabolic risk (i.e. blood pressure and stress hormones) than other groups (Brody et al. 2013, Miller et al. 2015, Chen et al. 2015). This is potentially driven by stressors related to upward mobility, which could also be playing a role in the U.K context. We have no credible data to test this hypothesis in the UK Biobank so we leave it for future work.

VI. Conclusions

In this paper, we investigate how education affects the distribution of health along three dimensions: body size, lung function, and blood pressure. The distributional analysis shows that education affects the health of some subpopulations. We find, for example, that the school-leaving age reform shifted part of the body size distribution to the left—i.e., it caused reductions in body size. Importantly, our results do not rely on rank preservation assumptions and or on extensive-margin homogeneity in the effects of the ROSLA on education (i.e., the first stage).

Because the effects of the reform are concentrated at the upper tail of the distribution rather than at the mode, this is evidence that the effect of education on body size is heterogeneous. Indeed, in related work we show that the effect varies with one’s genetic predisposition to obesity: the reductions in body size were larger for individuals at greater genetic risk of obesity (Barcellos, Carvalho, and Turley 2018). These findings support Galama et al. (2018)’s hypothesis that heterogeneity in the effects of education on health explain why some studies find that more education causes better health while others find no effect.

We conduct a back-of-envelope calculation to illustrate the importance of accounting for the heterogeneity in the effects of education when evaluating its estimated impacts (Heckman et al. 2018). Take, for example, the relationship between BMI and mortality. It is U-shaped (Fogel 1994; Aune et al. 2016), suggesting that the reduction in mortality caused by a given reduction in BMI is larger for someone obese than for someone with normal weight. A reduction in average BMI of 0.4 caused by staying in school until age 16 (i.e., the average treatment effect on the treated) implies a reduction in the relative risk of death of 0.87%—see Online Appendix K for details. In contrast, the local distributional treatment effects yield a much larger reduction of 3.28%. That is because of the U-shaped relationship between BMI and mortality and because the effects on BMI were concentrated at the upper tail of the BMI distribution.

The effects of education on health may vary not only across people but also across different health dimensions. Besides reducing body size, the school-leaving age reform increased blood pressure. Education seems to have reduced body size through improvements in SES and diet, but it is not clear the channels through which education increased blood pressure. Interestingly, the improvement in body size was concentrated at the top half of the body size distribution (among the least healthy) while the worsening in blood pressure was concentrated at the bottom half of the blood pressure distribution (among the most healthy).

These results underscore the policy relevance of studying distributional effects. Even though the average treatment effects show a reduction in body size and an increase in blood pressure of similar magnitudes (0.15–0.17 of a standard deviation), a policy maker may wish to trade-off these effects based on which parts of the respective distributions are affected. Because the reductions in BMI occurred at the upper tail of the BMI distribution, staying in school until age 16 reduced obesity rates (i.e., BMI above 30) by 8 percentage points. In contrast, the increase in blood pressure was concentrated below the clinical threshold for stage 2 hypertension (i.e., diastolic blood pressure above 90 mmHg or systolic blood pressure above 140) with no statistically significant consequences for prevalence.

Our results offer evidence on the causal distributional health effects of one extra year of compulsory schooling at age 15 in a specific context. Therefore, it will be important to investigate whether our findings generalize to other contexts and levels of education. For example, it is not clear that increases in schooling due to other types of educational policies, such as policies that lower the cost of college attendance, would have similar effects. Moreover, our paper uses a sample which is not nationally-representative, which might threaten the external validity of our findings. Future research investigating distributional effects of education on health in other national, historic and policy contexts, preferably using nationally-representative samples, would increase our understanding of the role that education plays in population health.