Analysis of queue management in theme parks introducing the fast pass system

Abstract

Prolonged waits reduce tourist satisfaction and have become a major factor in the theme park experience. How to improve tourist satisfaction is one of the main challenges for theme parks, and the key is to develop an appropriate queue management strategy. We develop a theme park queueing model considering the Fast Pass system, derive the optimal pricing strategy under profit maximization, and analyze the Shanghai Disney theme park as an example. The contribution of this paper is to establish a mathematical model of the queuing of theme parks with heterogeneous tourists and incorporate tourist satisfaction into the objective function. The results show that the equilibrium result of the Fast Pass system under profit maximization can optimize both tourist satisfaction (travel utility) and theme park profit, which is more acceptable to theme park operators.

1. Introduction

In recent years, tourism has become an important part of people's lives, and theme parks are the main attention of the present and future. In 2021, the top 25 theme parks worldwide had more than 140 million tourists, a 70% increase over 2020 and a recovery of 56% from the 2019 tourism numbers [1]. The main challenge in the development of theme parks is the prolonged waiting time caused by numerous tourists. In a large theme park with more than 40 attractions, the prolonged waiting time results in an average of only time for each customer to visit 10 attractions [2,3]. “Endless waiting” has become the biggest dissatisfaction among tourists with theme parks. Therefore, it is essential to analyze queue management in theme parks in an effort to reduce long waiting times and enhance tourist contentment.

Many studies have discussed the factors influencing theme park tourist satisfaction, including experience value, capacity and queue waiting time [4]. Keliiholokai et al. [5] analyzed the reasons for declining theme park satisfaction, noting that long wait times are an important factor influencing tourists to reduce the number of trips. Zhang et al. [6] concluded that theme park tourist choices are influenced by experience value, facility capacity, and transportation network. Ali et al. [1] showed that the physical environment, attraction interest and interactivity of theme parks have a significant impact on tourist satisfaction. Niu et al. [7] analyzed theme park tourists' perceived experiences using social media big data, and the study showed that tourists' perceived experiences consisted of positive experiences (scenic features, food, and services) and negative experiences (waiting time, cost, and price). Milman et al. [8] analyzed survey data from theme parks and showed that perceived crowding significantly affects the word-of-mouth effect of theme parks, thereby reducing tourist satisfaction, willingness to spend, and willingness to revisit. Previous studies on theme park satisfaction have focused on queue waiting times and less on the influence of price factors. Wang et al. [9] explored the perceived value of theme park price differences among tourists and showed that price adjustments for different populations are one of the most effective ways to improve tourist satisfaction. In addition, previous studies tend to assume that the perceived value of theme parks is homogeneous for all tourists, and fewer studies have discussed the perceived value of heterogeneous tourists. The theme park industry has adopted an appropriate fee structure to help maximize profits, for example, tourists are charged differently for adult and child tickets, with child tickets being about 45% cheaper than adult tickets [10].

Long wait times are one of the main causes of theme park complaints, with tourists typically spending 20% of their time experiencing the attraction, but more than half of their time waiting [11]. Adopting effective queue management strategies to improve guest satisfaction has become one of the common challenges faced by theme parks. Theme park queuing management is a system optimization problem. From the perspective of operations research, we can consider the strategy of dividing the flow of tourists in time and space. Kawamura et al. [12] developed an algorithm for dynamic coordination of agents with the goal of increasing social welfare without decreasing individual tourist satisfaction. Lawson et al. [13] analyzed the transportation system services of a theme park to optimize the quality of the tourist experience. Tsai et al. [14] developed a route recommendation system for theme parks to provide tourists with recommendations on the order of visits to improve tourist satisfaction. Cheng et al. [15] used an agent-based simulation system to model the impact of management strategies on the theme park tourist experience. Yu et al. [16] designed a theme park tourist service system based on a personalized recommendation algorithm to provide route recommendations for tourists based on their location, queue length, and attraction duration to enhance the tourist experience. It is noted that previous research on queue management in theme parks is mainly based on route recommendation systems based on heuristic algorithms, which cannot provide accurate theoretical analysis for queue management in theme parks due to the lack of mathematical analysis models. The route recommendation system involves issues such as travel privacy and security, which are difficult to implement in practical management. In addition, the convergence results of existing heuristic algorithms are often not guaranteed and can cause frequent fluctuations, such as genetic algorithms.

Another solution to the problem of waiting in line is the Fast Pass system, which aims to incentivize tourists to visit popular attractions at specified times and reduce waiting times by allowing tourists to pay to use a priority virtual queue. Chang et al. [17] investigated tourists' willingness to pay for various attributes of theme parks, and the results indicated that consumers most valued the value of the park experience, followed by the Fast Pass system. In fact, the Fast Pass system based on priority queuing has been widely used in theme parks, such as Disneyland and Universal Studios parks. The Fast Pass system reduces waiting time in line by providing fast lanes and allowing tourists to pay for access to priority queues. Hernandez-Maskivker et al. [18] showed that there are differences in tourists' sensitivity to congestion, with some tourists being highly sensitive to wait times and willing to pay to avoid or reduce queues, while others are highly price sensitive and prefer to wait rather than pay extra money. Zhang et al. [19] showed that tourists with higher income and better socioeconomic status are more sensitive to congestion. The Fast Pass system not only relieves congestion, but also increases revenue for theme parks. Hernandez-Maskivker and Ryan [20] examined the theme park and tourist perspective, and the investigation showed that priority queues can reduce waiting times and create new revenue streams. Sakayori [21] developed a mathematical model considering the optimal route for fast-track theme parks, but did not give a solution algorithm. Ko and Park [22] developed a mathematical model of a theme park priority queuing system with the objective of maximizing revenue and solved it using a genetic algorithm. Note that one of the main criticisms of the Fast Pass system stems from unfairness, as it undermines the first-come, first-served (FCFS) principle [23]. Tourists in the priority queue gain time by paying, while those in the general queue are not compensated. In addition, current research on the Fast Pass system has focused on tourist satisfaction and profit maximization, and fewer studies have analyzed the model from the perspective of social welfare maximization.

We construct a mathematical model of theme park queueing considering the Fast Pass system and analyze the equilibrium results of the theme park under the objective of profit maximization. Finally, a simulation analysis and discussion are conducted with Shanghai Disney theme park as an example, and recommendations are made for queue management strategies in theme parks. The contributions of this study are as follows (see Table 1): (1) The perceived value of congestion for heterogeneous tourists is considered; (2) A mathematical model-based theoretical analysis is provided for queue management in theme parks; (3) The equilibrium of different objective functions (tourist satisfaction and profit maximization) is compared results; (4) The mechanism of the Fast Pass system is improved to compensate tourists in the general queue to improve the satisfaction of tourists.

Table 1.

Characteristics of some primary references.

References	Tourists		Research Methods		Objective function		Fast Pass system
	Homogeneous	Heterogeneous	Algorithm	Mathematic	Tourist satisfaction	Profit
[12]	◎		◎		◎
[13]	◎		◎		◎
[14]	◎		◎		◎
[15]	◎		◎		◎
[16]	◎		◎		◎
[21]	◎			◎	◎		◎
[22]	◎			◎		◎	◎
This study		◎		◎	◎	◎	◎

The remainder of the paper is structured as follows: Section 2 describes the problem, introduces the Fast Pass system; Section 3 establishes the theme park queuing model with Fast Pass system; Section 4 gives the equilibrium result of theme park with profit maximization; Section 5 uses the Shanghai Disney theme park as an example analysis; Section 6 concludes the paper.

2. Model description

Suppose $N$ tourists arrive at the theme park every day and there are $x$ attractions to choose from. There are two queues with queuing rules for tourists to choose in the theme park, the general queue for first-come-first-served and the priority queue for paying through the fast channel. The number of tourists who choose the general queue is $\left(1-\theta \left(x\right)\right)f\left(x\right)$ and the number of tourists who choose the priority queue is $\theta \left(x\right)f\left(x\right)$, $\theta \left(x\right)$ is the market penetration of the priority queue, $f\left(x\right)$ is the tourist flow of the theme park scenic spots and $x$ is the theme parks attraction sequence. For theme parks, excessively long waiting time is the norm, and the traditional queuing theory model cannot describe the waiting time of tourists when the service intensity is greater than 1. At present, the widely adopted roadblock function is BPR function [24], which is used to describe the queuing time of tourists

$$t\left(x\right)=\frac{f\left(x\right)}{s}.$$ (1)

In Eq. (1), $s$ is the capacity of the theme park scenic spots.

Tourists need to make a trade-off between the value of the attraction experience and the waiting time in the queue to maximize their own utility. Then the travel utility of tourists for general queue and priority queue are

$$u_{\text{MR}}\left(x\right)=v\left(x\right)-\left(1-\theta \left(x\right)\right)\frac{{\alpha }_{\mathrm{R}}f\left(x\right)}{s}-{\mu }_{\mathrm{R}}{p}_{\mathrm{R}},$$ (2)

$$u_{\text{MP}}\left(x\right)=v\left(x\right)-\theta \left(x\right)\frac{{\alpha }_{\mathrm{P}}f\left(x\right)}{s}-{\mu }_{\mathrm{P}}{p}_{\mathrm{R}},$$ (3)

where $u_{\text{MR}}\left(x\right)$ is the travel utility of tourists for general queue, $u_{\text{MP}}\left(x\right)$ is the travel utility of tourists for priority queue, $v\left(x\right)$ is the experience value of the theme park, ${\alpha }_{\mathrm{R}}$ is the unit time value of general queue tourists, ${\alpha }_{\mathrm{P}}$ is the unit time value of priority queue tourists, ${\mu }_{\mathrm{R}}{p}_{\mathrm{R}}$ is the ticket price for the general queue, ${\mu }_{\mathrm{P}}{p}_{\mathrm{R}}$ is the ticket price for the priority queue, $p_{\mathrm{R}}$ is the base ticket price, ${\mu }_{\mathrm{R}}\left(<1\right)$ is the discount constant of general queue and ${\mu }_{\mathrm{P}}\left(>1\right)$ is the premium constant of priority queue.

In Eq. (2) and Eq. (3), item 1 is the experience value of the theme park; item 2 is the waiting time in line for the general queue and the priority queue, respectively. Item 3 is the admission price for the general queue and the priority queue.

3. Theme park queuing model with fast pass system

In this section, we focus on the changes in tourist satisfaction (travel utility) after the introduction of the Fast Pass system in theme parks.

3.1. Theme park queuing model without fast pass system

First, we consider the simple scenario without the Fast Pass system, $\theta =0$ and ${\mu }_{\mathrm{R}}=0$. Then the tourist travel utility of the general queue is

$$u_{\mathrm{R}}\left(x\right)=v\left(x\right)-\frac{{\alpha }_{\mathrm{R}}f\left(x\right)}{s}-p_{\mathrm{R}},$$ (4)

where $u_{\mathrm{R}}\left(x\right)$ is the tourist travel utility of the general queue that does not include the Fast Pass system.

Assuming that the distribution of theme park attraction experience value is related to the attraction ranking $v\left(x\right)$ and follows a negative exponential distribution, it can be expressed as follows

$$v\left(x\right)=v_{\max }\exp \left(-\lambda x\right),$$ (5)

where $v_{\max }$ is the experience value of the most popular attraction, $\lambda$ is the negative exponential distribution constant.

Combining Eq. (4) and Eq. (5), we get

$$u_{\mathrm{R}}\left(x\right)=v_{\max }\exp \left(-\lambda x\right)-\frac{{\alpha }_{\mathrm{R}}f\left(x\right)}{s}-p_{\mathrm{R}}.$$ (6)

According to the Wardrop equilibrium principle [25], when the theme park reaches user equilibrium, the tourist travel utility of each attraction is equal. Let $\frac{\partial u_{\mathrm{R}}\left(x\right)}{\partial x}=0$, calculate the tourist flow distribution of each attraction in equilibrium as

$${\bar{f}}_{\mathrm{R}}\left(x\right)=\frac{s{v}_{\max }}{{\alpha }_{\mathrm{R}}}\exp \left(-\lambda x\right)+C,$$ (7)

where $C$ is the constant.

According to the constraint, the sum of tourist flow of each attraction is $N$.

$${\int }_0^m{\bar{f}}_{\mathrm{R}}\left(x\right)dx=N.$$ (8)

Combining Eq. (7) and Eq. (8), the tourist flow distribution of each attraction in the equilibrium state is calculated as

$${\bar{f}}_{\mathrm{R}}\left(x\right)=\frac{s{v}_{\max }}{{\alpha }_{\mathrm{R}}}\exp \left(-\lambda x\right)+\frac{N}{m}-\left(1-\exp \left(-\lambda m\right)\right)\frac{s{v}_{\max }}{{\alpha }_{\mathrm{R}}\lambda m},$$ (9)

Substituting Eq. (9) into Eq. (6), the tourist travel utility for each attraction in equilibrium as Eq. (10)

$${\bar{u}}_{\mathrm{R}}=\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\lambda m}-\frac{{\alpha }_{\mathrm{R}}N}{sm}-p_{\mathrm{R}.}$$ (10)

3.2. Theme park queuing model with fast pass system

Next, we consider the complex scenario of introducing a Fast Pass system. To reduce waiting times, theme park operators have introduced a Fast Pass system that incentivises tourists to visit popular attractions at designated times by allowing them to pay for the right to use a priority queue to save time. Each tourist can get real-time updates of the waiting time for each scenic spot through the App provided by the theme park, and take individual preferences into consideration to maximize the travel utility.

Substituting Eq. (5) into Eq. (2) and Eq. (3), the tourist travel utilities for the general and priority queues are

$$u_{\text{MR}}\left(x\right)=v_{\max }\exp \left(-\lambda x\right)-\left(1-\theta \left(x\right)\right)\frac{{\alpha }_{\mathrm{R}}f\left(x\right)}{s}-{\mu }_{\mathrm{R}}{p}_{\mathrm{R}},$$ (11)

$$u_{\text{MP}}\left(x\right)=v_{\max }\exp \left(-\lambda x\right)-\theta \left(x\right)\frac{{\alpha }_{\mathrm{P}}f\left(x\right)}{s}-{\mu }_{\mathrm{P}}{p}_{\mathrm{R}}.$$ (12)

Before solving for the equilibrium of the theme park attractions, we first calculate the equilibrium between the general queue and the priority queue. Let $u_{\text{MR}}\left(x\right)=u_{\text{MP}}\left(x\right)$, the market penetration of the priority queue in equilibrium can be calculated as

$${\bar{\theta }}_{\mathrm{M}}\left(x\right)=\frac{{\alpha }_{\mathrm{R}}f\left(x\right)+\left({\mu }_{\mathrm{R}}-{\mu }_{\mathrm{P}}\right)s{p}_{\mathrm{R}}}{\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right)f\left(x\right)}.$$ (13)

Substituting Eq. (13) into Eq. (11) or Eq. (12), the tourist travel utility in the equilibrium state of the general and priority queues can be obtained as

$${\bar{u}}_{\mathrm{M}}\left(x\right)=v_{\max }\exp \left(-\lambda x\right)-\frac{{\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}\frac{f\left(x\right)}{s}-\frac{{\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}{p}_{\mathrm{R}}.$$ (14)

Then, we solve for the equilibrium of each attraction in the theme park. Let $\frac{\partial {\bar{u}}_{\mathrm{M}}\left(x\right)}{\partial x}=0$, combined with the constraint Eq. (8), calculate the tourist flow distribution of each attraction in equilibrium as

$${\bar{f}}_{\mathrm{M}}\left(x\right)=\frac{\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right)s{v}_{\max }}{{\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}}\exp \left(-\lambda x\right)+C_{\mathrm{M}},$$ (15)

where $C_{\mathrm{M}}=\frac{N}{m}-\left(1-\exp \left(-\lambda m\right)\right)\frac{\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right)s{v}_{\max }}{{\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}\lambda m}$.

Substituting Eq. (15) into Eq. (13), the market penetration of the priority queue in equilibrium is obtained as Eq. (16)

$${\bar{\theta }}_{\mathrm{M}}\left(x\right)=-\frac{\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right){\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}s{p}_{\mathrm{R}}}{{\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right)}^{2}s{v}_{\max }\exp \left(-\lambda x\right)+\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right){\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}{C}_{\mathrm{M}}}+\frac{{\alpha }_{\mathrm{R}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}.$$ (16)

Substituting Eq. (15) into Eq. (14), the tourist travel utility for each attraction in equilibrium as Eq. (17)

$${\bar{u}}_{\mathrm{M}}=\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\lambda m}-\frac{{\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}\frac{N}{sm}-\frac{{\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}{p}_{\mathrm{R}}.$$ (17)

3.3. Analysis of model properties

In this section, we analyze the impact of introducing a Fast Pass system in a theme park. In order to analyze the impact of tourist VOT heterogeneity and theme park discriminatory pricing on tourist satisfaction (travel utility)

$${\alpha }_{\mathrm{P}}=k_1{\alpha }_{\mathrm{R}},{\mu }_{\mathrm{P}}=k_2{\mu }_{\mathrm{R}},$$ (18)

where $k_1\left(>1\right)$ represents the heterogeneity of different tourists regarding the value of time, called VOT heterogeneity constant, and $k_2\left(>1\right)$ represents the discriminatory pricing constant of theme parks.

Substituting Eq. (18) into Eq. (17), the tourist travel utility for each attraction in equilibrium Eq. (19) can be expressed as follows

$${\bar{u}}_{\mathrm{M}}=\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\lambda m}-\frac{k_1}{1+k_1}\frac{{\alpha }_{\mathrm{R}}N}{sm}-\frac{k_1+k_2}{1+k_1}{\mu }_{\mathrm{R}}{p}_{\mathrm{R}}.$$ (19)

4. Profit maximization of theme park

In this section, we analyze the changes in theme parks after the introduction of Fast Pass system under profit maximization, including theme park profit and tourist satisfaction (travel utility).

4.1. Profit maximization of theme park

The theme park maximizes profit by adjusting the ticket pricing strategy for each attraction. Then the profit of the theme park is

$$\pi \left(x\right)=\left(1-\theta \left(x\right)\right)f\left(x\right){\mu }_{\mathrm{R}}{p}_{\mathrm{R}}\left(x\right)+\theta \left(x\right)f\left(x\right){\mu }_{\mathrm{P}}{p}_{\mathrm{R}}\left(x\right).$$ (20)

Substituting Eq. (13) into Eq. (20), the objective function is calculated as Eq. (21)

$$\pi \left(x\right)=-\frac{{\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}^2}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}s{p}_{\mathrm{R}}^2\left(x\right)+\frac{{\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}f\left(x\right)p_{\mathrm{R}}\left(x\right).$$ (21)

Let the objective function be derived with respect to $P_{\mathrm{R}}$ as Eq. (22)

$$\frac{\partial \pi \left(x\right)}{\partial p_{\mathrm{R}}\left(x\right)}=-\frac{2{\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}^2}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}s{p}_{\mathrm{R}}\left(x\right)+\frac{{\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}\frac{\partial f\left(x\right)}{\partial p_{\mathrm{R}}\left(x\right)}{p}_{\mathrm{R}}\left(x\right)+\frac{{\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}f\left(x\right).$$ (22)

Let $\frac{\partial \pi \left(x\right)}{\partial p_{\mathrm{R}}\left(x\right)}=0$, calculate the optimal ticket pricing strategy as

$${\hat{p}}_{\mathrm{R}}\left(x\right)=\frac{{\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}}{2{\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}^{2}s}f\left(x\right).$$ (23)

Substituting Eq. (23) into Eq. (14), let the superscript “PM” denote the result with profit maximization equilibrium, then the tourist travel utility in the equilibrium state is

$${\bar{u}}_{\mathrm{M}}^{\text{PM}}\left(x\right)=v_{\max }\exp \left(-\lambda x\right)-\psi f\left(x\right),$$ (24)

where $\psi =\frac{2{\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}{\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}^2+{\left({\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}\right)}^2}{2\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right){\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}^{2}s}$.

Next, we solve for the equilibrium of each attraction in the theme park. Let $\frac{\partial {\bar{u}}_{\mathrm{M}}^{\text{PM}}\left(x\right)}{\partial x}=0$, combined with the constraint Eq. (8), calculate the tourist flow distribution of each attraction in equilibrium as

$${\bar{f}}_{\mathrm{M}}^{\text{PM}}\left(x\right)=\frac{v_{\max }}{\psi }\exp \left(-\lambda x\right)+\frac{N}{m}-\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\psi \lambda m}.$$ (25)

Substituting Eq. (23) and Eq. (25) into Eq. (13), the market penetration of the priority queue in equilibrium is obtained as Eq. (26)

$${\bar{\theta }}_{\mathrm{M}}^{\text{PM}}=\frac{{\alpha }_{\mathrm{R}}}{{\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}}-\frac{{\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}}{2\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right)\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}.$$ (26)

Substituting Eq. (25) into Eq. (24), the tourist travel utility for each attraction in equilibrium is

$${\bar{u}}_{\mathrm{M}}^{\text{PM}}=\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\lambda m}-\frac{{\alpha }_{\mathrm{R}}{\alpha }_{\mathrm{P}}N}{\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right)sm}-\frac{{\left({\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}\right)}^{2}N}{2\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right){\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}^{2}sm}.$$ (27)

Substituting Eq. (23) and Eq. (25) into Eq. (20), the maximum profit of the theme park in equilibrium is

$${\bar{\pi }}_{\mathrm{M}}^{\text{PM}}=\frac{{\left({\alpha }_{\mathrm{P}}{\mu }_{\mathrm{R}}+{\alpha }_{\mathrm{R}}{\mu }_{\mathrm{P}}\right)}^2}{4\left({\alpha }_{\mathrm{P}}+{\alpha }_{\mathrm{R}}\right){\left({\mu }_{\mathrm{P}}-{\mu }_{\mathrm{R}}\right)}^{2}s}{\left(\frac{v_{\max }}{\psi }\exp \left(-\lambda x\right)+\frac{N}{m}-\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\psi \lambda m}\right)}^2.$$ (28)

4.2. Analysis of model properties

Next, we analyze the impact of introducing a Fast Pass system in a theme park under profit maximization, both in terms of tourist satisfaction (travel utility) and theme park profit.

To analyze the effect of VOT heterogeneity and discriminatory pricing on tourist satisfaction (travel utility), substituting Eq. (18) into Eq. (27), we can get the tourist travel utility for each attraction in equilibrium as Eq. (29)

$${\bar{u}}_{\mathrm{M}}^{\text{PM}}=\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\lambda m}-\frac{2{\left(1-k_2\right)}^2{k}_1+{\left(k_1+k_2\right)}^2}{2\left(1+k_1\right){\left(1-k_2\right)}^2}\frac{{\alpha }_{\mathrm{R}}N}{sm}.$$ (29)

Then, we give the theme park profits without the introduction of the Fast Pass system as Eq. (30)

$${\bar{\pi }}_{\mathrm{R}}=p_{\mathrm{R}}N.$$ (30)

To analyze the effect of VOT heterogeneity and discriminatory pricing on theme park profits, substitute Eq. (18) into Eq. (28), we can get the maximum profit of the theme park in equilibrium as Eq. (31)

$${\bar{\pi }}_{\mathrm{M}}^{\text{PM}}=\frac{{\left(k_1+k_2\right)}^2{\alpha }_{\mathrm{R}}}{4\left(1+k_1\right){\left(1-k_2\right)}^{2}s}{\left(\frac{v_{\max }}{\psi }\exp \left(-\lambda x\right)+\frac{N}{m}-\left(1-\exp \left(-\lambda m\right)\right)\frac{v_{\max }}{\psi \lambda m}\right)}^2,$$ (31)

where $\psi =\left(\frac{k_1}{\left(1+k_1\right)s}+\frac{{\left(k_1+k_2\right)}^2}{2\left(1+k_1\right){\left(1-k_2\right)}^{2}s}\right){\alpha }_{\mathrm{R}}$.

5. Example analysis

5.1. Basic data and parameter setting

This research selects Shanghai Disney theme park to collect data of the 8 most popular scenic spots. The queuing time of each scenic spot was obtained according to the Shanghai Disney App, and the experience value distribution of theme park attractions can be calculated (see Table 2).

Table 2.

The attractions experience value of Shanghai Disney theme park.

No.	Theme park attraction names	Experience value
1	Soaring over the Horizon	387.88
2	Pirates of the Caribbean Battle for the Sunken Treasure	263.43
3	Roaring Rapids	257.25
4	Seven Dwarfs Mine Train	235.13
5	TRON Lightcycle Power Run-Presented by Chevrolet	202.00
6	Peter Pan's Flight	147.08
7	The Many Adventures of Winnie the Pooh	134.58
8	Woody's Roundup	68.25

Next, we use the negative exponential distribution to fit the experience value distribution of theme park attractions, and the fitting formula is as follows

$$v\left(x\right)=480\times \exp \left(-0.2\times x\right).$$ (32)

In Eq. (32), we can obtain $v_{\max }=480$ and $\lambda =0.2$.

As shown in Fig. 1, the fitted formula basically predicts the experience value distribution of theme park attractions, and the significance result is $R=0.92$, which indicates a good prediction result. The parameters are set as shown in Table 3.

Fig. 1.

Experience value distribution of theme park attractions.

Table 3.

Parameter setting.

Parameter	Definition	Value
$N$	Total tourists	80,000 (person)
$m$	Number of theme park attractions	8
$v_{\max }$	The maximum experience value of attractions	480
$\lambda$	Experience value distribution constant	0.2
$s$	Capacity of theme park attractions	3600 (person/d)
${\alpha }_{\mathrm{R}}$	The unit time value of general queue tourists	200 (CNY/d)
${\alpha }_{\mathrm{P}}$	The unit time value of priority queue tourists	1000 (CNY/d)
${\mu }_{\mathrm{R}}$	The discount factor of general queue	0.1
${\mu }_{\mathrm{P}}$	The premium constant of priority queue	1.0
$k_1$	VOT heterogeneity constant	5
$k_2$	Discriminatory pricing constant	10
$p_{\mathrm{R}}$	The base ticket price	50 (CNY)

5.2. Equilibrium results

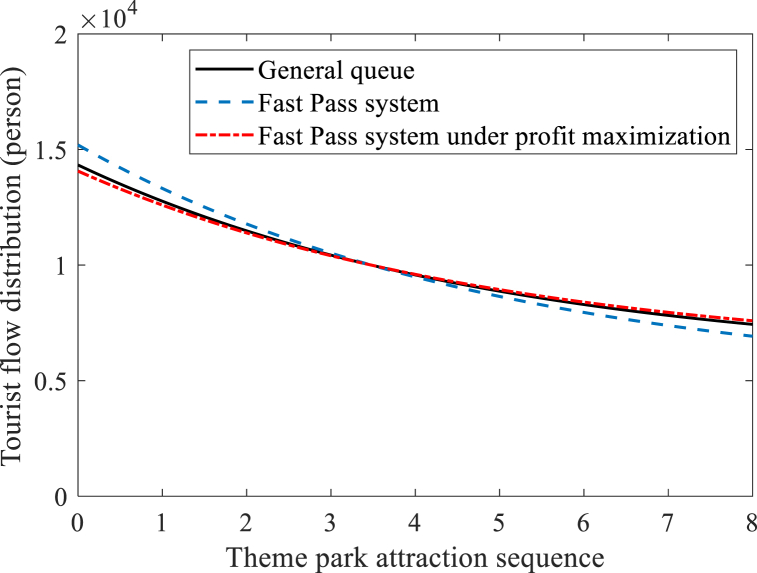
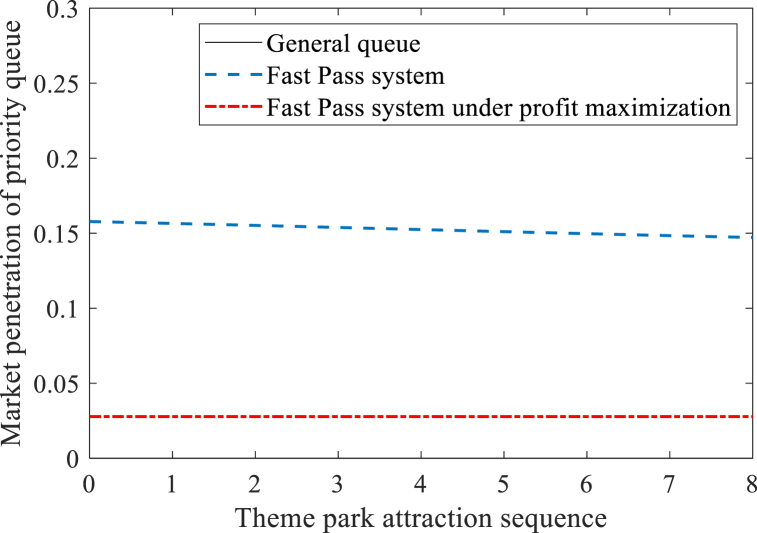
We simulated and compared the equilibrium results for three scenarios, including the general queue, the Fast Pass system, and the Fast Pass system under profit maximization. From Fig. 2, the tourist flow distribution in all three scenarios decreases monotonically with the theme park attraction sequence number. Compared to the equalization results of a general queue, the tourist flow distribution considering the introduction of a Fast Pass system will be more uneven, and the tourists will flow to the popular attractions with high experience value leading to overload. Considering the tourist flow distribution of the Fast Pass system under profit maximization can improve the problem of uneven attraction load and protect the theme park ecology. From Fig. 3, it can be obtained that the market penetration of the priority queue considering the introduction of the Fast Pass system decreases monotonically with the sequence of theme park attractions. Compared with the equilibrium result considering the introduction of Fast Pass system, the priority queue market penetration of Fast Pass system under profit maximization is lower, which can better ensure the benefits of priority queue tourists.

Fig. 2.

Simulation results with Tourist flows distribution.

Fig. 3.

Simulation results with Market penetration of priority queue.

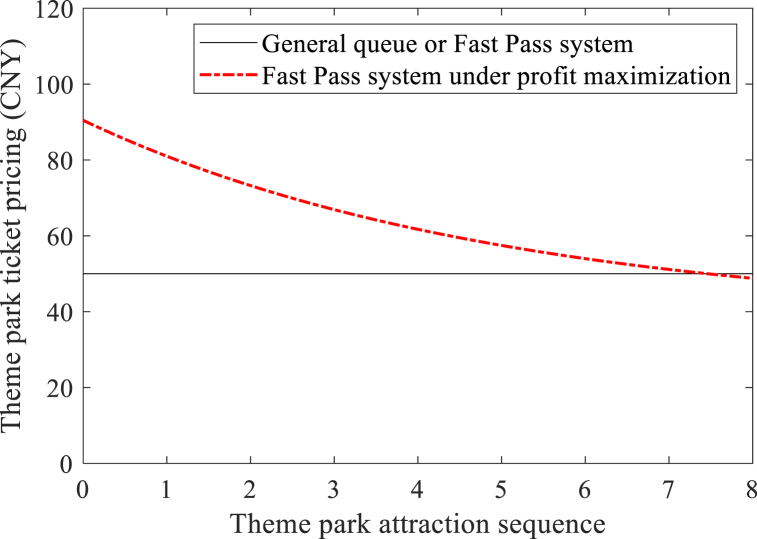
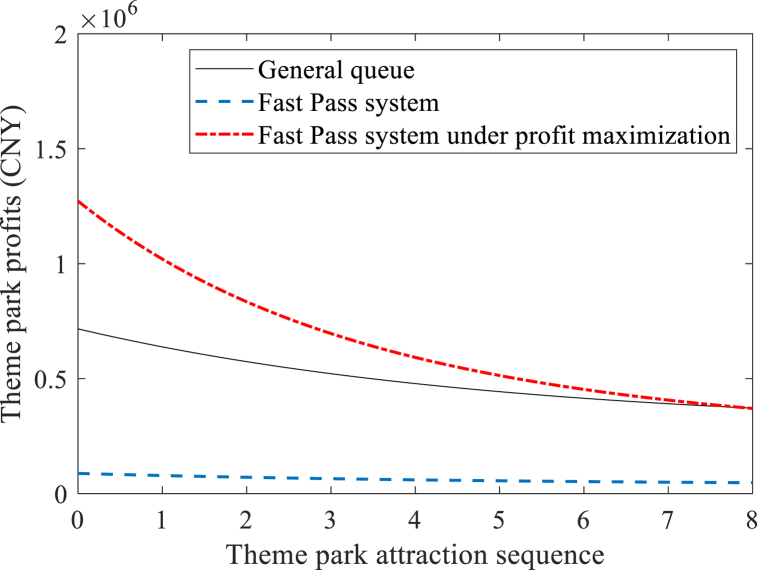
In Fig. 4, compared with the equilibrium results of the general queue and considering the Fast Pass system, the theme park ticket pricing for the Fast Pass system under profit maximization decreases monotonically with the attraction sequence, indicating that the pricing strategy of the theme park should vary according to the value of the attraction experience. In Fig. 5, compared with the equilibrium results of the general queue, the theme park profit decreases for the theme park considering the Fast Pass system, while the theme park profit is larger for the Fast Pass system under profit maximization, which proves the advantage.

Fig. 4.

Simulation results with Theme park ticket pricing.

Fig. 5.

Simulation results with Theme park profits.

Next, we compared the equilibrium results for three scenarios, including tourist satisfaction (travel utility) and the average profit of each attraction in the theme park. In Table 4, compared to the equilibrium results of the general queue, the tourist travel utility of the Fast Pass system is significantly improved by considering the Fast Pass system, but at the expense of the theme park's profits. However, both tourist travel utility and profits are improved for the Fast Pass system under profit maximization, which is more acceptable to the theme park operators.

Table 4.

The equilibrium results for three scenarios.

Scenarios	Tourist travel utility (CNY)	Theme park profits (CNY)
General queue	−366.12	478,620
Fast Pass system	−236.03	59,990
Fast Pass system under profit maximization	−352.13	592,400

5.3. Sensitivity analysis

Next, we performed a sensitivity analysis of key parameters on the equilibrium results, including the VOT heterogeneity constant for tourists and the discriminatory pricing constant for theme parks.

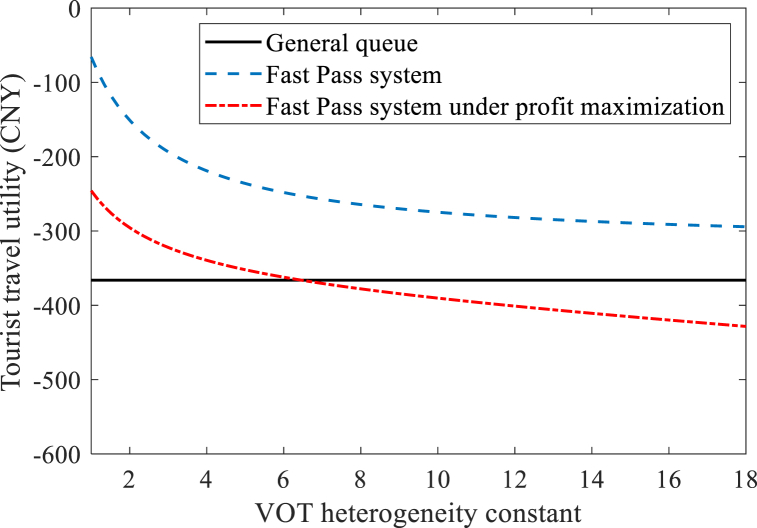
In Fig. 6, the tourist travel utility considering both the Fast Pass system and the Fast Pass system under profit maximization decreases monotonically with the VOT heterogeneity constant. In addition, the VOT heterogeneity constant needs to be controlled within 6.5 to ensure that the equilibrium results of the Fast Pass system under profit maximization are advantageous. In Fig. 7, the theme park profits of the Fast Pass system are considered to be monotonically decreasing with the VOT heterogeneity constant, while the theme park profits of the Fast Pass system under profit maximization first decrease and then increase with the VOT heterogeneity constant.

Fig. 6.

The influence of VOT heterogeneity constant on Tourist travel utility.

Fig. 7.

The influence of VOT heterogeneity constant on Theme park profits.

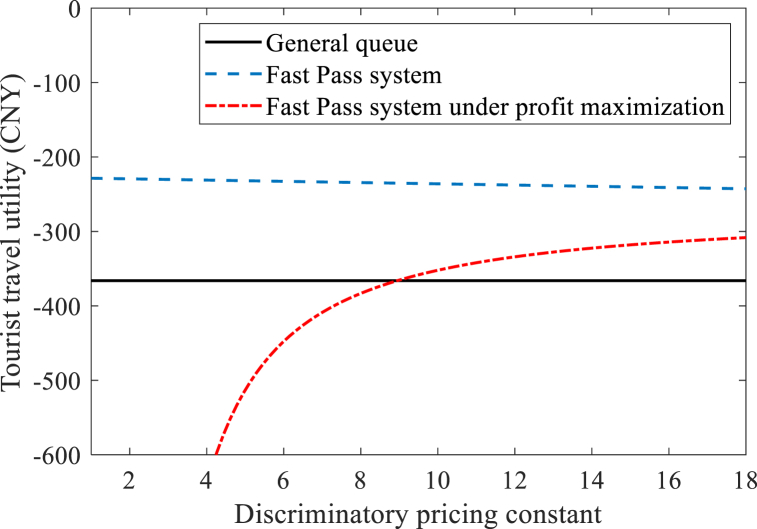
In Fig. 8, the tourist travel utility of the Fast Pass system is considered to be monotonically decreasing with the discriminatory pricing constant, while the tourist travel utility of the Fast Pass system under profit maximization are monotonically increasing with the VOT heterogeneity constant. In addition, a discriminatory pricing constant greater than 9 ensures that the equilibrium outcome of the profit-maximizing Fast Pass system is advantageous. In Fig. 9, the theme park profits of the Fast Pass system are considered to be monotonically increasing with the VOT heterogeneity constant, while the theme park profits of the Fast Pass system under profit maximization are monotonically decreasing with the VOT heterogeneity constant. In addition, a discriminatory pricing constant of less than 13 is required to ensure a favorable equilibrium outcome for the Fast Pass system under profit maximization.

Fig. 8.

The influence of discriminatory pricing constant on Tourist travel utility.

Fig. 9.

The influence of discriminatory pricing constant onTheme park profits.

6. Conclusion

We construct a mathematical model of theme park queuing considering the Fast Pass system and analyze the equilibrium results of the theme park under the profit maximization objective. Finally, a simulation analysis and discussion are conducted with Shanghai Disney theme park as an example, and suggestions are made for theme park queuing management strategies.

The simulation results show that considering only the Fast Pass system significantly improves tourism satisfaction (travel utility), but theme park profits are significantly reduced. In contrast, both tourist satisfaction (travel utility) and theme park profits are improved by implementing the Fast Pass system under profit maximization. The scenario analysis shows that VOT heterogeneity and discriminatory pricing do have an impact on visitor satisfaction (travel utility) and theme park profits, and gives conditions for optimizing VOT heterogeneity constant and discriminatory pricing constant.

It should be noted that, based on the model constructed under ideal assumptions, this study provides some suggestions on the operation strategy of theme parks, and many factors have not been considered. The future research directions are as follows: (1) Discussion of the impact of the spatial structure of theme parks on the spatial distribution of tourist flows; (2) This study only calculates the analytical model of theme park queues in equilibrium, however, the actual tourist flows are generally non-equilibrium, and effective algorithms can be designed to dynamically distribute tourist flows to achieve equilibrium in the future.

Author contribution statement

Jiaxin Li: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Qian Li: Contributed reagents, materials, analysis tools or data.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.