Influence of implants number on the biomechanical behavior of implant-supported complete prosthesis: A 3D finite element analysis

Abstract

The aim of this study was to define the relation between load distribution and the number of implants supporting mandibular implant-supported screw-retained complete prostheses (ISCP).

It is a three-dimensional (3-D) finite element study. Three models were simulated. The first one represents a 4-implant supported prosthesis (4ISP), the second one is a 3-implant supported prosthesis (3ISP) and the third one is a 6-implant supported prosthesis (6ISP).

The 6ISP model showed the best bone stress distribution among all models. Its maximum stress value was 63.3 MPa. The 4ISP (98.9 MPa) showed a better bone stress distribution than the 3ISP (122.9 MPa). A flexion of the prosthesis was more important for the 4ISP than 3ISP and then 6ISP model at 10 MPa. In the 4 ISP and the 3ISP models, the anterior implants were more solicited. However, the stress was evenly distributed on the 6 implants, in the 6ISP model. Concerning, the stress distribution in bone, the uppermost stress was found in the 3ISP, then the 4ISP and then the 6ISP model.

The increase of implants number reduces the stress on the bone and prosthesis and implants. The use of 6 implants to support screw-retained complete prostheses showed a better biomechanical behavior.

1. Introduction

The mandibular implant-supported screw-retained complete prosthesis (ISCP) is a common treatment used for edentulism. It has shown a good success rate, due to the amelioration of retention, stability and patient's quality of life [1,2].

When a fixed prosthesis is required for an edentulous mandible, 6 to 8 implants are typically inserted to support the superstructure, with good outcomes. This treatment leads to high costs and may require complex surgical procedures. In recent years, according to the All-on-four Concept, only 4 implants are inserted between the mental foramina, to support a full-arch fixed prosthesis. This alternative has offered a less invasive treatment option, as it requires fewer implants; it has also shown a high clinical success rate and a lower cost [3].

The longevity of these treatments is directly affected by the distribution of stress that is transferred to the implant and surrounding bone. Many factors affect load transfer by the implants such as the loading type, material properties, surrounding bone quality and implant shape and number [4,5].

Various experimental studies [[6], [7], [8]] have examined biomechanical behavior of the mandibular ISCP to investigate the influence of several parameters on stress distribution on implants, prosthesis and peri-implant bone to reduce the risk of prostheses and implants fracture, the bone resorbing and to improve the long-term outcome of such treatment.

The aim of this work was to use finite element analysis (FEA) in order to define the relation between load distribution and the number of implants supporting mandibular ISCP.

2. Materials and methods

2.1. Study presentation

It is a 3-D FEA. It analyses the mechanical behavior of the different components of the mandibular ISCP.

The FEA software package ABAQUS was used to perform the numerical simulation of the studied system. It is a powerful tool that allows the analysis of stress transmission in complex structure and the study of structure damage such as fracture and failure.

The measure of the force intensity is described as stress. The ‘Von Mises stress’ is going to be evaluated in this study. Indeed, it is an overall indicator of stress distribution and stress concentration location. It summarizes principal stresses in three dimensions.

Several steps were followed to achieve this numerical simulation.

• 1.
  Pre-processing and Modeling:

  • a.
    Model construction:

In this study, 3 models were used: The first one represents a 4-implant supported prosthesis (4ISP) (Fig. 1a). The second one is a 3-implant supported prosthesis (3ISP) (Fig. 1b). And the third one is a 6-implant supported prosthesis (6ISP) (Fig. 1c).

Fig. 1.

Geometric models: a: 3 implants model (3ISP); b: 4 implants model (4ISP); c: 6 implants model (6ISP).

The 3-D models represent the whole system.

• ⁃Bone: only anterior mandibular arch between mental foramina was modeled. It is the region concerned by the bone-implants interaction. A geometrical model, of 12 mm height (2 mm for cortical layer thickness and 10 mm of cancellous bone), 7.5 mm buccolingual width, and a dental arch diameter of 50 mm [9].
• ⁃Implants: In the three models, all implants were inserted vertically between the mental foramina. Cylindrical smooth implants were used. Their diameter was 5 mm and their length was 10 mm. These implants were connected to the prosthesis with middle pillar. In the 4ISP, the distance between anterior and posterior implants was 13 mm and the distance between the two anterior implants was 37 mm. In the 3ISP model the distance between implants was 31 mm and in the 6ISP model it was 13 mm.
• ⁃Prosthesis: Acrylic resin prosthesis was simulated. A geometrical model, of 7.5 mm height and 7.5 mm buccolingual width with a dental arch diameter of 50 mm

The mucosal thickness was not modeled during the analysis because the prosthesis was entirely implant-supported.

• b.Assigning material properties:

Homogenous and isotropic elastic properties are assumed for the implant, prosthesis, cortical and cancellous bone. The selected material for the dental implant was titanium. A superstructure made of acrylic resin,representing the prosthesis, was modeled.

The mechanical properties assigned to structural elements of the model such as Young's modulus, Poisson ratio and density were listed in Table 1 [10].

• c.Defining interface conditions:

Table 1.

Mechanical properties assigned to the different components of the Finite Element Analysis (FEA) model [5].

Materials	Young's modulus (MPa)	Poisson ratio	Density
Cortical bone	21,402	0.3	1990
Cancellous bone	1370	0.3	1874
Implant (Titanium)	104,500	0.37	4400
Prosthesis (resin)	2700	0.3	1190

In order to simulate a completely Osseo integrated situation, a perfect-fit situation was assumed among the implants, the bone, and the prosthesis showing fixed bonds at all material interfaces [11].

The conditions of contact between the parts were defined by an interface of the surface-to-surface contact type, with a friction coefficient of 0.3.

• d.Mesh of the 3-dimensional models:

In the 4 implants model, the number of elements forming the investigated model was 15,465 elements. In the 3 implants model, it was 14,706. In the 6 implants model, it was 16,445 (Table 2).

• e.Applying load and boundary conditions:

Table 2.

Mesh characteristics.

Model components	Meshing type			Elements number
	4 implants	3 implants	6 implants	4 implants	3 implants	6 implants
bone	Tetra	Tetra	Tetra	6543	6282	6807
implant	Tetra	Tetra	Tetra	3079	3079	3079
prosthesis	Tetra	Tetra	Tetra	5843	5345	6559

*Tetra: Tetrahedral mesh.

An occlusal pressure of 10 Mega Pascal (MPa) was applied vertically to the model. The load was 225 N (N) [12]. The force was evenly distributed over the prosthesis surface.

All the components were assumed to exhibit bonded contact (Fig. 2).

Fig. 2.

Loading and boundary conditions.

The implant is embedded in the bone tissue; the bone's inferior part is fixed.

• 2.Processing and solution:

The data set defined by the pre-processor is used as input to the finite element code, which constructs and solves a system of algebraic equations. Graphical displays could be then visualized with different stress levels in the model.

3. Results

The stress analysis was performed using Von Mises Stress values, which summarizes the effect of all stress components with a unique value.

Stress distribution in the FE model comes in numerical values that were converted into visual results represented by degrees of color. Maximum value of Von Mises stress is symbolized by red color, and minimum value of Von Mises stress is denoted by blue color. The in-between values are illustrated by bluish green, green, greenish yellow, yellow and yellowish red in the ascending order of stress distribution [4].

This study is going to investigate the Influence of the implants number on stress distribution in different parts of the model.

3.1. Stress distribution in the whole model

A flexion of the prosthesis was more important for the 4ISP than 3ISP and then 6ISP model at 10 MPa. This flexion was 2 mm in the 4ISP model bringing the prosthesis in contact with the bone. The stress in the prosthesis parts was spread between the two anterior implants in the 4ISP (Fig. 3a). While in the 3ISP (Fig. 3b) and 6ISP (Fig. 3c) models it was localized in front of implants.

Fig. 3.

Stress distribution in different parts of the three models during loading a: the 4-implant model (4ISP); b: the 3-implant model (3ISP); c: the 6-implant model (6ISP).

The highest Von Mises stress value was found in the 4ISP model (545.6 MPa). The 3ISP model showed a very close maximum stress value (527.9 MPa), while the 6ISP model exhibited a significantly lower maximum stress value (160.3 MPa).

In all models, the highest stress concentration was observed in the dental implants, precisely in the most anterior ones.

3.2. Stress distribution in the prosthesis

In the 4ISP model, the uppermost stress value was located around the two anterior implants, precisely in the mesial edge of the interface connecting the middle pillar and the prosthesis. This stress value was 246.6 MPa. Low stress value (123.8 MPa) was observed in contact with the posterior implants (distal edge). The anterior middle part of the prosthesis was also under stress with a value of 62.35 MPa (Fig. 4a). In the 3ISP model, high stress was located around all implants, precisely, in contact with the anterior implant and in mesial edge of the posterior implants. This maximum stress value was 257.4 MPa. A low stress was noted in the two flexion zones (64,56 MPa) (Fig. 4b). In the 6ISP model, the stress was distributed around all implants. The highest stress value was 136.9 MPa. The maximum stress concentration was observed around the two anterior implants. It was less extensive around the 2 most posterior implants (Fig. 4c).

Fig. 4.

Stress distribution in the prostheses models during the occlusal loading evaluated in Von Mises stress: a: the 4-implant model (4ISP); b: the 3-implant model (3ISP); c: the 6-implant model (6ISP).

3.3. Stress distribution in implants

In the 4ISP model, implants showed the uppermost Von Mises stress value, it was equal to 545.6 MPa. The maximum stress concentration was located in the mesial side of the anterior implants (Fig. 5 a).

Fig. 5.

Stress Distribution in body of dental implant during loading: a: the 4-implant model (4ISP); b: the 3-implant model (3ISP); c: the 6-implant model (6ISP).

In the 3ISP model, the highest stress value was 527.9 MPa. It was mostly located around the anterior implant, and also in the mesial sides of the two posterior implants (Fig. 5b).

In the 6ISP model, implants showed the lowest maximum stress value (160.3 MPa). The stress was evenly distributed on the 6 implants (Fig. 5c).

In the three models, higher stresses were found in the cervical part of the implant compared to the apical part, in which the stress was mostly low to moderate.

3.4. Stress distribution in mandibular bone

The uppermost stress was found in the 3ISP (122.9 MPa), then the 4ISP model (98.9 MPa) and then the 6ISP model (63.37 MPa).

In the 3ISP model, stress was concentrated in the cortical bone around the anterior implant. Moderate stress values were observed around the two posterior implants (Fig. 6b).

Fig. 6.

Stress distribution in the peri-implant bone during loading: a: the 4-implant model (4ISP); b: the 3-implant model (3ISP); c: the 6-implant model (6ISP).

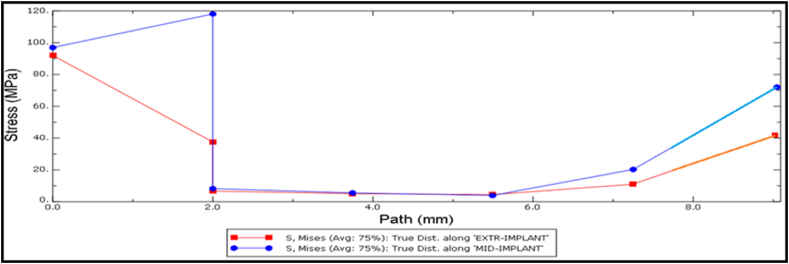
The graphs below show the stress distribution along the implant path in the mesial (anterior) and distal (posterior) implant holes in the mandibular bone.

For the mesial implant, it showed stress intensification in the 2 upper millimeters of the path; the stress decreases rapidly. Starting from a depth of 5.5 mm, an increase of the stress is noted.

For distal implants, in the 2 upper millimeters of the implant hole, the stress decreases gradually (Fig. 7).

Fig. 7.

Stress distribution along the anterior implant path (blue) and posterior implant path (red) in the 3-implant model (3ISP) model

In the 4ISP model, the maximum stress value recorded in peri-implant cortical bone was 98.9 MPa. The highest stress concentration was found around the 2 posterior implants, surrounding the implants’ neck, in the mesial side. High stress values were also detected in the cortical bone distally to the anterior implants (Fig. 6a).

According to the graphs below, showing the stress distribution along the implant path in the mesial and distal implants holes in the bone, the stress decreases linearly in the 2 upper mm, then, the curve flattens out. In the deepest 3 mm the stress increases linearly (Fig. 8).

Fig. 8.

Stress distribution along the anterior implant path (blue) and posterior implant path (red) in the 4-implant model (4ISP) model

The 6ISP model showed the lowest maximum stress value (63.3 MPa). Stress was observed to be concentrated in the cortical bone surrounding the neck of the 4 anterior implants. Moderate stress was detected around the posterior implants (Fig. 6c).

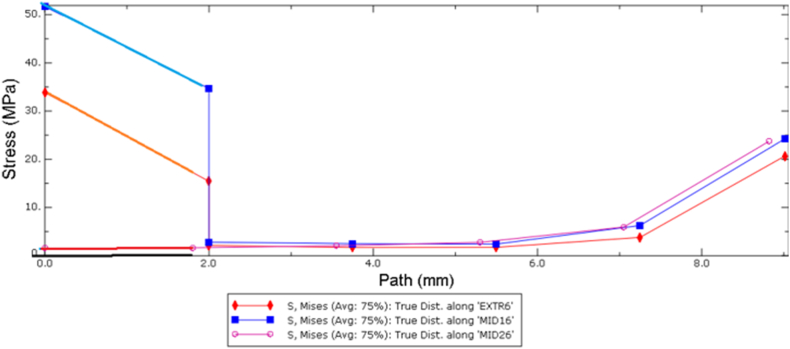
The graphs below show the stress distribution along the implant path in the anterior, medial and posterior implant holes in the mandibular bone (Fig. 9).

Fig. 9.

Stress distribution along the anterior implant path (blue), medial implant path (red) and posterior implant path (pink) in the 6-implant model (6ISP) model

According to the graphs, in the upper 2 mm; the stress is mostly concentrated around the 4 anterior implants, while the posterior implant hole showed a very low stress value. The stress decreases in the 6 implant holes from 2 to 6 mm depth. Then an increase of stress is noticed.

4. Discussion

In the present study, the 6ISP model showed the best bone stress distribution among all models. Its maximum stress value was 63.3 MPa. The 4ISP (98.9 MPa) showed a better bone stress distribution than the 3ISP (122.9 MPa). This result suggests the implants number influences the stress transmission on bone, implants and prosthesis. Indeed, when the number is higher, the stress distribution on implants will be larger and the stress transmission to the bone will be lower. Many studies [3,13,14] in the literature were in agreement with the present finding. Takahashi et al. [3] investigated the influence of implants number on stress distribution with the all-on-4 concept compared with a 6-implant supported prosthesis. They found that stress with 4 parallel implants was 9% higher than in the 6-implant model due to the presence of fewer implants. In their ex vivo study, Kokat et al. [15] analyzed human bone stress around immediately-loaded implants supporting mandibular fixed prostheses, using strain gauge in cadaver material. They found an increasing stress value from three, four to five implants supported prosthesis.

According to the present study, in the 4ISP model, the 2 anterior implants were concerned by the stress concentration, while in the two others models (3ISP, 6ISP) the stress was distributed on all implants. This can be explained by the presence of an anterior cantilevered prosthesis part which increased the stress in the mesial implants. In the 3 and 6ISP model the anterior part was well supported. This finding suggests that when the anterior implants are placed more mesially, the stress distribution will be better. Thus, if a 4ISP is to be used, the distance between the two mesial implants should be reduced. Therefore the risk of implants fracture seemed to be important in the 4 ISP model. Thus, if a 4ISP is to be used, the distance between the two mesial implants should be reduced to minimize the stress transmitted to the anterior implants and then, avoid the risk of the fracture.

Otherwise, some authors [10,16] found a concentration of the stress in the posterior implant. El Sayyed et al. [10] realized a 3-D FEA to study the biomechanics of 3-implant supported and 4-implant supported screw-retained prostheses, and found that for all applied loads, the highest stress values were detected at the mesiocoronal or distocoronal bone-implant interface of the most distal implant for the 2 models.

Concerning the stress pattern in the peri implant bone, the 4ISP showed a stress concentration around posteriors implants. It was lower in the 6ISP. This result suggest that bone resoption may appear around posterior if 4 implants were placed.

Examining the prosthesis stress distribution pattern in all models, a moderate concentration of the stress in the middle area was noted in the 4ISP model (62.35 MPa). In the 3ISP model, stress was observed in the two lateral regions (64.56 MPa). In the 6ISP model, the stress appeared only in the peri-implant zones. These results predict the risk of prosthesis fracture in the 4ISP and 3ISP and suggest that the increase of implants number decreases the stress on prosthesis and reduces the fracture risk.

The choice of the implant number in the mandibular implant-supported screw-retained complete prosthesis remains a compromise between the patient financial conditions, the clinical situation and the biomechanical requirements.

4.1. Study limits

This study used the finite element analysis which is virtual method. It have to be interpreted in relation with the data entered when modeling the system. Moreover, clinical conditions may not be completely replicated. The results may only be acknowledged qualitatively.

5. Conclusions

Within the limitation of this study, some conclusions can be retained: the placement of six implants to support a complete fixed screw retained prosthesis testifies to a better biomechanical behavior then 4 and 2 implants. When 4 implants are used, bone resoption around the posterior implants and prosthesis fracture in the anterior part, could occur in loading conditions.

Author contribution statement

Hamdi Aguir: Conceived and designed the experiments; Performed the experiments.

Yosra Mabrouk: Contributed reagents, materials, analysis tools or data.

Rayene Chamekh: Analyzed and interpreted the data; Wrote the paper.

Ines Saadellaoui: Contributed reagents, materials, analysis tools or data; Wrote the paper.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that there are no conflicts of interest.