Highlights
-
•
The load−velocity relationship variables (L0, v0, and Aline) are obtained with an acceptable reliability during the countermovement jump exercise regardless of the method (multiple-point vs. 2-point), load combination (heavy-squat vs. heavy countermovement jump), and velocity variable (mean velocity vs. mean propulsive velocity vs. peak velocity).
-
•
The concurrent validity of the 2-point method with respect to the multiple-point method was only acceptable for mean velocities.
-
•
The 2-point method obtained from a heavy squat load and mean velocities is a quick, safe, and reliable procedure to evaluate the maximal neuromuscular capacities of lower-body muscles through the assessment of the load−velocity relationship variables.
Keywords: Force−velocity relationship, Mean velocity, Multiple-point method, Peak velocity, Velocity-based training
Abstract
Purpose
This study aimed to examine the reliability and validity of load−velocity (L–V) relationship variables obtained through the 2-point method using different load combinations and velocity variables.
Methods
Twenty men performed 2 identical sessions consisting of 2 countermovement jumps against 4 external loads (20 kg, 40 kg, 60 kg, and 80 kg) and a heavy squat against a load linked to a mean velocity (MV) of 0.55 m/s (load0.55). The L–V relationship variables (load-axis intercept (L0), velocity-axis intercept (v0), and area under the L–V relationship line (Aline)) were obtained using 3 velocity variables (MV, mean propulsive velocity (MPV), and peak velocity) by the multiple-point method including (20–40–60–80–load0.55) and excluding (20–40–60–80) the heavy squat, as well as from their respective 2-point methods (20–load0.55 and 20–80).
Results
The L–V relationship variables were obtained with an acceptable reliability (coefficient of variation (CV) ≤ 7.30%; intra-class correlation coefficient ≥ 0.63). The reliability of L0 and v0 was comparable for both methods (CVratio (calculated as higher value/lower value): 1.11–1.12), but the multiple-point method provided Aline with a greater reliability (CVratio = 1.26). The use of a heavy squat provided the L–V relationship variables with a comparable or higher reliability than the use of a heavy countermovement jump load (CVratio: 1.06–1.19). The peak velocity provided the load–velocity relationship variables with the greatest reliability (CVratio: 1.15–1.86) followed by the MV (CVratio: 1.07–1.18), and finally the MPV. The 2-point methods only revealed an acceptable validity for the MV and MPV (effect size ≤ 0.19; Pearson's product-moment correlation coefficient ≥ 0.96; Lin's concordance correlation coefficient ≥ 0.94).
Conclusion
The 2-point method obtained from a heavy squat load and MV or MPV is a quick, safe, and reliable procedure to evaluate the lower-body maximal neuromuscular capacities through the L–V relationship.
Graphical Abstract
1. Introduction
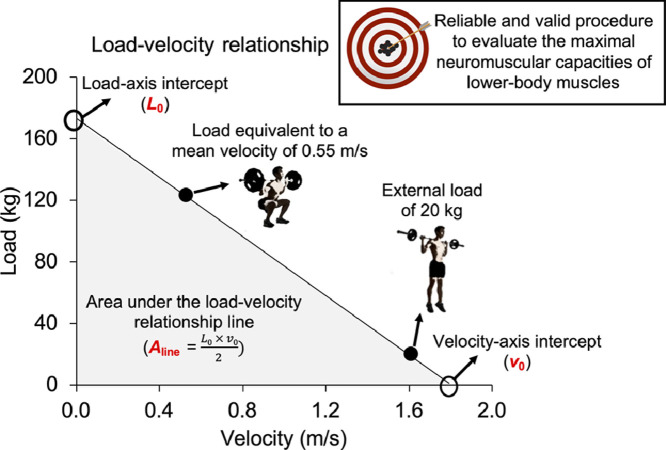
Velocity-based training has been popularized among strength and conditioning professionals due to its relevant and abundant practical applications1 and to the increasing affordability of velocity monitoring devices.2 For example, individualized load−velocity (L−V) relationships are used to regulate the training intensity,3,4 quantify training-induced fatigue,5,6 and assess changes in neuromuscular performance after training interventions.7,8 Note also that individualized L−V relationships have been recommended over the generalized L−V relationship equations because the velocity associated with each relative load is subject-specific.2 Furthermore, a novel application of the L−V relationship consists of determining the L−V relationship variables (load-axis intercept (L0), velocity-axis intercept (v0), and the area under the L−V relationship line (Aline = L0 × v0/2)), which may be accurate indicators of the maximal capacities of producing force, velocity, and power, respectively.9 In comparison to the force–velocity (F−V) relationship parameters (see Jaric10 for further details), the assessment of the L−V relationship variables may be simpler and more reproducible because (a) the force output does not need to be computed for the modeling, and (b) the extrapolation needed from the experimental points to v0 is reduced because only the external load lifted is considered for the analysis. However, little information is available in the literature concerning the reliability and concurrent validity of the L−V relationship variables.9
The countermovement jump (CMJ) is commonly used to evaluate neuromuscular function of lower-body muscles.11, 12, 13 The CMJ testing procedures have typically consisted of the assessment of mechanical variables (force, velocity, and power) against individual loads.14,15 More recently, the F−V relationship has been modeled through simple linear regressions by collecting force and velocity outputs against multiple loads (i.e., multiple-point method).11,12,16,17 However, since the F−V relationship in multi-joint tasks is highly linear,10 it is generally accepted that the same F–V relationship parameters could be obtained more efficiently (i.e., less time and fatigue) from the modeling of the force and velocity outputs against only 2 distant loads (i.e., 2-point method).18, 19, 20 Specifically, in order to maximize the accuracy of the F−V relationship parameters in the CMJ exercise, the 2-point method should be based on the minimum possible loading condition and a CMJ against a load that allows reaching a jump height of about 10 cm.19 Previous studies have sought to identify the optimal combination of experimental points (i.e., loads) to determine the F−V relationship in exercises such as vertical jumping,19 bench press throw,21 or cycling.22 However, no study has examined whether the 2-point method could also provide L−V relationship variables with an acceptable reproducibility and concurrent validity. For example, it could be of interest to examine the feasibility of 2-point methods differing in the magnitude of the heavy load (heavy squat vs. heavy CMJ) to determine the variables derived from the L−V relationship.
The determination of the F−V and L−V relationships require the assessment of lifting velocity under 2 or more loading conditions.23 Therefore, another important factor that could affect the reliability of the outcomes of the F−V and L−V relationships is the velocity variable used.11,12 For example, previous studies have shown that the F−V relationship parameters can be obtained with an acceptable reliability during the CMJ and squat jump (SJ) exercises using both the mean velocity (MV) and peak velocity (PV).11,12 Although in the study of Cuk et al.,11 the MV was shown to be more reliable than the PV, the study of García-Ramos et al.12 reported contrasting results (i.e., that PV was more reliable than MV). Moreover, a recent study by Kotani et al.24 has discouraged the use of the F−V and L−V profiles to make training decisions because their outcomes obtained using both MV and PV were generally unreliable during the SJ exercise. These suggestions were made despite the fact that both velocity variables were obtained with a high reliability at each load and that the outcomes of the F−V and L−V profiles did not differ significantly between sessions. Indeed, all the aforementioned studies have used force platforms to determine these profiles. It should be noted that, compared to linear position/velocity transducers, the lower reliability of outputs obtained by force platforms could be due to the greater manipulation of raw data needed to obtain the variable of interest.25 Therefore, further research is required to determine the between-session reliability of L–V relationship variables when velocity outputs are recorded with other devices such as linear position/velocity transducers, which are the technology most often used when implementing velocity-based training.1 Since previous studies have shown a greater reliability for PV compared to MV and mean propulsive velocity (MPV) during the loaded CMJ and SJ exercises when recorded by linear position/velocity transducers across a range of loads,26,27 it is also plausible that PV provides the variables derived from the L−V relationship with a higher reliability during jumping tasks. However, the lack of agreement in the literature highlights the need for further research on this topic.
To address the existing gaps in the literature, we assessed, on 2 separate occasions, the variables derived from the L−V relationship during the CMJ exercise using different load combinations and velocity variables. The main aim was to examine the between-session reliability and concurrent validity of the L−V relationship variables (L0, v0, and Aline) obtained by different 2-point methods compared to their respective multiple-point methods. The secondary aims were to determine the effect of the magnitude of the heaviest load (heavy squat vs. heavy CMJ) and velocity variable (MV vs. MPV vs. PV) used for modeling the L−V relationships on the reliability of the L−V relationship variables. We hypothesized that the 2-point methods would provide the L−V relationship variables with high and comparable reliability to that of the multiple-point methods, and that their outcomes would be highly valid.18,19 We also hypothesized a greater reliability (a) when using the heavy squat load compared to the heavier CMJ load due to a greater distance between the experimental points and increased proximity of the heavier experimental point to L0,19,21 and (b) for PV compared to MV and MPV because PV can be obtained with a greater reliability during loaded vertical jumps.26,27
2. Methods
2.1. Subjects
Twenty resistance-trained men (age = 22.2 ± 1.8 years (mean ± SD), range: 20−26 years; stature = 1.75 ± 0.06 m; body mass = 73.7 ± 8.2 kg) volunteered to participate in this study. Prior to data collection, all subjects participated in a 4-week training program (8 sessions) in which they performed the CMJ exercise at maximal intended velocity. No physical limitations, health problems, or musculoskeletal injuries that could compromise testing were reported. Subjects were required to avoid any strenuous exercise over the course of the study, and they were informed of the procedures and signed a written informed consent form before initiating the study. The study protocol adhered to the tenets of the Declaration of Helsinki and was approved by the institutional review board (687/CEIH/2018).
2.2. Study design
A repeated-measures design was used to examine the between-session reliability and concurrent validity of the L−V relationship variables obtained by different 2-point methods with respect to their multiple-point methods during the CMJ exercise. Subjects were tested on 2 sessions separated by 7 days. Each session consisted of 2 CMJs against 4 external loads (20 kg, 40 kg, 60 kg, and 80 kg) and a squat against an estimated load equivalent to a MV of 0.55 m/s (load0.55).28 Data from both sessions were used for reliability analyses, but only the data from the second session was used for validity analyses. Testing sessions were conducted at the University's research laboratory at the same time of day for each subject (±1 h) and under similar environmental conditions (∼ 22°C and ∼ 60% humidity).
2.3. Procedures
Each testing session began with a standardized warm-up consisting of 5 min of jogging at a self-selected moderate pace, dynamic stretching, joint mobilization exercises, and one set of 5 repetitions of the CMJ exercise performed with increasing effort against an external load of 20 kg (mass of the unloaded Smith machine barbell (Multipower Fitness Line; Peroga, Murcia, Spain)). After warming-up, subjects performed 2 CMJs against 4 external loads (20 kg, 40 kg, 60 kg, and 80 kg) and a squat against the load0.55 (124.1 ± 17.5 kg (range: 90–160 kg)). The MV collected under the 4 external loads was used to model the individualized L−V relationships by a linear regression model, and the load0.55 was calculated in each session from these relationships as the load associated with an MV of 0.55 m/s (0.54 ± 0.05 m/s (0.40–0.59 m/s)). An MV of 0.55 m/s was set to obtain an experimental point close to L0 without exposing the subjects to the unnecessary risk of injury associated with maximal lifts.28 The 5 loads were applied in an incremental order, and the rest period between the repetitions performed with the same and different loads was set to 1 min and 3 min, respectively. Subjects received velocity performance feedback immediately after completing each repetition to encourage maximal effort.29
The CMJ technique involved subjects standing with the knees and hips fully extended, feet approximately shoulder-width apart, and the barbell held across the top of the shoulders and upper back. Thereafter, subjects initiated a downward movement until reaching 90° knee flexion, followed immediately by a jump for maximum height. The execution technique for the load0.55 was identical to the CMJ, involving upward movement at maximal intended velocity, although without lifting the toes off the ground. To ensure the 90° knee angle, subjects descended until touching an adjustable rod of a tripod with their glutei.30 The 90° knee angle was individually measured with a manual goniometer (Pharmedic, Temuco, Chile), and the height of the tripod was recorded and maintained for both testing sessions.
2.4. Measurement equipment and data analysis
Stature (Seca 202 Stadiometer; Seca GmbH, Hamburg, Germany) and body mass (TBF-300A; Tanita Corp of America Inc., Arlington Heights, IL, USA) were measured at the beginning of the first session. A Smith machine (Multipower Fitness Line; Peroga, Murcia, Spain) was used in all sessions coupled with a linear velocity transducer (T-Force System; Ergotech, Murcia, Spain) that directly sampled the velocity-time data at a frequency of 1000 Hz. Validity and reliability of the T-Force system have been reported elsewhere.31 The T-Force software automatically calculated the 3 velocity variables: MV (i.e., average velocity from the first positive velocity until the velocity is 0 m/s), MPV (i.e., average velocity from the first positive velocity until the acceleration is lower than gravity (−9.81 m/s2)), and PV (i.e., the maximum instantaneous velocity value reached during the upward movement).
The L−V relationships were calculated considering the 3 velocity variables (MV, MPV, and PV) using 4 load combinations: (a) multiple-point with heavy squat (i.e., 20–40–60–80–load0.55), (b) multiple-point with heavy CMJ (i.e., 20–40–60–80), (c) 2-point with heavy squat (i.e., 20–load0.55), and (d) 2-point with heavy CMJ (i.e., 20–80). A least-square linear regression model (L(V) = L0 – s × V) was used to determine the individualized L−V relationships, where L0 represents the load at 0 velocity and s is the slope of the L−V relationship.8 The v0 and Aline were then calculated as follows: v0 = L0/s and Aline = L0 × v0/2.9 Only the repetition with the highest velocity value at each load was used for modeling the L−V relationships. Therefore, 12 L−V relationships (2 methods (multiple-point and 2-point) × 2 load combinations (heavy squat and heavy CMJ) × 3 velocity variables (MV, MPV, and PV)) were obtained (Fig. 1).
Fig. 1.
L–V relationships obtained from the data averaged across the subjects modeled by the different 2-point methods and their respective multiple-point methods using (A) the mean velocity, (B) mean propulsive velocity, and (C) peak velocity during the CMJ exercise. Mean values are shown for the 4 external loads (20 kg, 40 kg, 60 kg, and 80 kg) and load0.55, while the error bars represent the SD. Regression equations obtained from each individual method are also indicated (r, Pearson's correlation coefficient). Aline = area under the L−V relationship line; CMJ = countermovement jump; L0 = load-axis intercept; load0.55 = estimated load equivalent to 0.55 m/s; L−V relationship = load−velocity relationship; v0 = velocity-axis intercept.
2.5. Statistical analyses
Descriptive data are presented as mean ± SD and range. The normal distribution of the data was confirmed using the Shapiro-Wilk test (p > 0.05). The strength of the L−V relationships modeled by the multiple-point methods was examined through the Pearson's product-moment correlation coefficient (r). Paired samples t tests were used to compare the magnitude of the L−V relationship variables between both testing sessions. Between-sessions reliability was assessed by the coefficient of variation (CV = standard error of measurement/ subjects’ mean score × 100) and intra-class correlation coefficient (ICC; Model 3.1) with their corresponding 95% confidence intervals (95%CIs). Acceptable reliability was determined as a CV < 10% and ICC > 0.70.19 The ratio between 2 CVs was used to compare the reliability between the 2 methods (multiple-point and 2-point), 2 load combinations (heavy squat and heavy CMJ), and 3 velocity variables (MV, MPV, and PV). The smallest important ratio between 2 CVs was considered to be higher than 1.15.27 Paired samples t tests, Cohen's d effect size (ES), r coefficients, and Lin's concordance correlation coefficient (CCC) were used to assess the concurrent validity of the 2-point methods compared to their respective multiple-point methods. The criteria to interpret the magnitude of the ES was: trivial (<0.20), small (0.20–0.59), moderate (>0.59–1.19), large (>1.19–2.00), or very large (>2.00).32 The strength of the r coefficients was interpreted as: trivial (0.00–0.09), small (>0.09–0.29), moderate (>0.29–0.49), high (>0.49–0.69), very high (>0.69–0.89), or practically perfect (>0.89).33 The criteria to interpret the CCC were as follows: very poor (<0.70), poor (0.70–0.90), moderate (>0.90–0.95), good (>0.95–0.99), or very good (>0.99).34 The 2-point methods were deemed to have an acceptable validity if the following criteria were met: from trivial to small ES (<0.20), from very high to practically perfect correlations (r > 0.90), and from moderate to very good concordances (CCC > 0.90). The agreement between the multiple- and 2-point methods was also quantified using the Bland–Altman 95% limits of agreement (LoA) technique (bias ± 1.96 × SD). The r coefficients were also used to explore the association of the same L–V relationship variables obtained using different velocity variables. All reliability assessments were performed by means of a custom Excel spreadsheet,33 while other statistical analyses were performed using the software package SPSS (Version 22.0; IBM Corp., Armonk, NY, USA). Alpha was set at 0.05. Post hoc statistical power was conducted using G*Power (Version 3.1.9.6; https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower) with an ES of 0.5 and α of 0.05, and it revealed a 0.80 statistical power.
3. Results
All velocity variables reported an acceptable reliability for the 4 external loads (MV: CV = 2.48% (95%CI: 1.50%–2.99%), ICC = 0.89 (95%CI: 0.80–0.96); MPV: CV = 3.00% (95%CI: 2.31%–3.62%), ICC = 0.86 (95%CI: 0.73–0.94); PV: CV = 1.76% (95%CI: 1.41%–2.02%), ICC = 0.95 (95%CI: 0.91–0.97)). The strength of the individualized L−V relationships recorded from both multiple-point methods was practically perfect for the 3 velocity variables (MV: r = 1.00 (95%CI: 0.98–1.00); MPV: r = 1.00 (95%CI: 0.97–1.00); PV: r = 1.00 (95%CI: 0.98–1.00)).
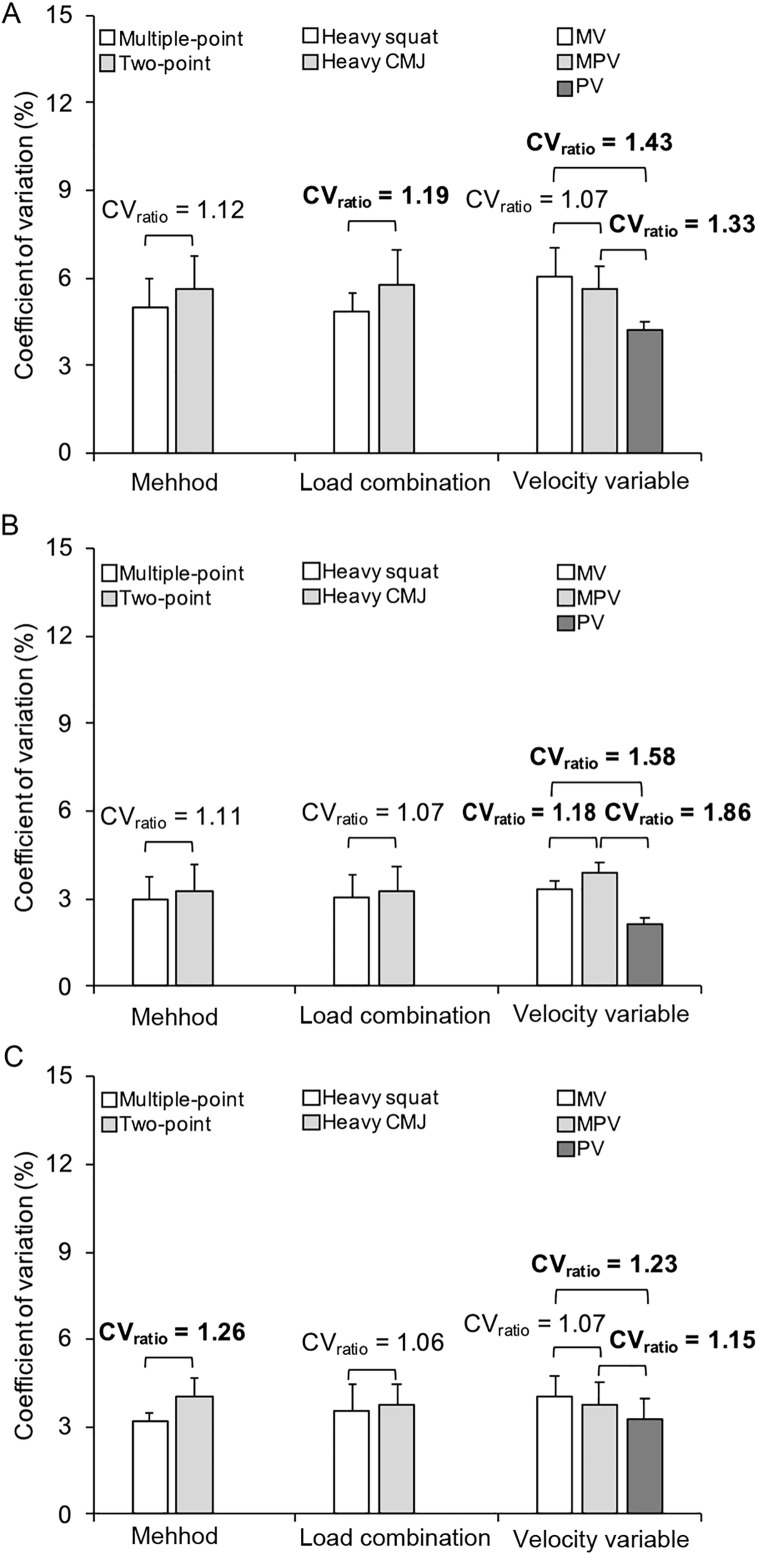
The between-session reliability was generally acceptable for L0 (CV = 5.31% (95%CI: 3.84%–7.30%), ICC = 0.80 (95%CI: 0.66–0.91)); v0 (CV = 3.12% (95%CI: 1.76%–4.27%), ICC = 0.75 (95%CI: 0.63–0.91)); and Aline (CV = 3.68% (95%CI: 2.79%–4.86%), ICC = 0.93 (95%CI: 0.86−0.96)) (Table 1). The reliability comparisons revealed that (a) the multiple-point method provided a comparable reliability for L0 (CVratio (caculated as higher value/lower value) = 1.12) and v0 (CVratio = 1.11) and a greater reliability for Aline (CVratio = 1.26) compared to the 2-point method, (b) the heavy squat load provided a comparable reliability for v0 (CVratio = 1.07) and Aline (CVratio = 1.06) and a greater reliability for L0 (CVratio = 1.19) compared to the heavy CMJ load, and (c) the PV provided all L–V relationship variables with greater reliability than the MV and MPV (CVratio ≥ 1.15), while the MV provided comparable reliability for L0 and Aline (CVratio = 1.07) and a greater reliability for v0 (CVratio = 1.18) compared to the MPV (Fig. 2).
Table 1.
Between-session reliability of the L−V relationship variables obtained from different methods, load combinations, and velocity variables during the CMJ exercise.
| Method | Load combination | Velocity variable | L−V variable | Session 1 (mean ± SD) | Session 2 (mean ± SD) | p | CV (95%CI)(%) | ICC (95%CI) |
|---|---|---|---|---|---|---|---|---|
| Multiple-point | Heavy squat (20–40–60–80–load0.55) | MV | L0 (kg) | 191.0 ± 23.5 | 184.2 ± 22.5 | 0.036 | 5.08 (3.87−7.42) | 0.84 (0.65−0.93) |
| v0 (m/s) | 1.61 ± 0.08 | 1.60 ± 0.09 | 0.413 | 3.05 (2.32−4.45) | 0.68 (0.35−0.86) | |||
| Aline (kg × m/s) | 153.9 ± 21.3 | 147.0 ± 19.3 | <0.001 | 3.07 (2.34−4.48) | 0.95 (0.89−0.98) | |||
| MPV | L0 (kg) | 176.6 ± 22.3 | 172.8 ± 21.1 | 0.167 | 4.79 (3.64−6.99) | 0.87 (0.69−0.94) | ||
| v0 (m/s) | 1.84 ± 0.09 | 1.80 ± 0.11 | 0.055 | 3.56 (2.71−5.20) | 0.63 (0.27−0.84) | |||
| Aline (kg × m/s) | 162.8 ± 22.9 | 155.6 ± 20.8 | <0.001 | 3.03 (2.30−4.42) | 0.96 (0.89−0.98) | |||
| PV | L0 (kg) | 195.2 ± 24.0 | 193.0 ± 22.2 | 0.367 | 3.84 (2.92−5.61) | 0.91 (0.78−0.96) | ||
| v0 (m/s) | 3.07 ± 0.17 | 3.03 ± 0.16 | 0.031 | 1.76 (1.34−2.57) | 0.91 (0.78−0.96) | |||
| Aline (kg × m/s) | 300.0 ± 44.1 | 292.5 ± 38.4 | 0.016 | 3.02 (2.29−4.41) | 0.96 (0.90−0.98) | |||
| Heavy CMJ (20–40–60–80) | MV | L0 (kg) | 193.5 ± 20.2 | 184.9 ± 25.1 | 0.031 | 6.21 (4.72−9.07) | 0.75 (0.48−0.89) | |
| v0 (m/s) | 1.60 ± 0.09 | 1.60 ± 0.11 | 0.731 | 3.23 (2.45−4.71) | 0.75 (0.47−0.89) | |||
| Aline (kg × m/s) | 155.0 ± 17.3 | 147.2 ± 18.8 | <0.001 | 3.77 (2.87−5.51) | 0.91 (0.79−0.96) | |||
| MPV | L0 (kg) | 170.0 ± 17.5 | 166.8 ± 20.4 | 0.331 | 5.96 (4.53−8.71) | 0.74 (0.45−0.89) | ||
| v0 (m/s) | 1.86 ± 0.12 | 1.82 ± 0.13 | 0.088 | 3.95 (3.00−5.77) | 0.67 (0.34−0.86) | |||
| Aline (kg × m/s) | 158.3 ± 17.6 | 151.7 ± 18.9 | <0.001 | 3.35 (2.54−4.89) | 0.93 (0.83−0.97) | |||
| PV | L0 (kg) | 184.1 ± 13.8 | 182.4 ± 18.3 | 0.490 | 4.22 (3.21−6.17) | 0.79 (0.54−0.91) | ||
| v0 (m/s) | 3.12 ± 0.20 | 3.08 ± 0.18 | 0.095 | 2.19 (1.67−3.20) | 0.89 (0.74−0.95) | |||
| Aline (kg × m/s) | 287.0 ± 30.2 | 280.6 ± 31.6 | 0.020 | 2.79 (2.12−4.08) | 0.94 (0.86−0.98) | |||
| Two-point | Heavy squat (20–load0.55) | MV | L0 (kg) | 190.7 ± 25.6 | 184.5 ± 23.7 | 0.079 | 5.61 (4.27−8.20) | 0.83 (0.63−0.93) |
| v0 (m/s) | 1.60 ± 0.09 | 1.60 ± 0.10 | 0.783 | 3.37 (2.56−4.92) | 0.72 (0.41−0.88) | |||
| Aline (kg × m/s) | 152.9 ± 23.8 | 147.3 ± 21.5 | 0.018 | 4.47 (3.40−6.54) | 0.92 (0.81−0.97) | |||
| MPV | L0 (kg) | 177.7 ± 24.5 | 174.4 ± 22.6 | 0.279 | 5.34 (4.06−7.80) | 0.86 (0.67−0.94) | ||
| v0 (m/s) | 1.87 ± 0.11 | 1.82 ± 0.12 | 0.084 | 3.94 (3.00−5.76) | 0.64 (0.28−0.84) | |||
| Aline (kg × m/s) | 165.9 ± 26.6 | 159.0 ± 23.8 | 0.013 | 4.86 (3.70−7.11) | 0.91 (0.79−0.96) | |||
| PV | L0 (kg) | 187.8 ± 13.9 | 185.5 ± 18.2 | 0.370 | 4.40 (3.35−6.43) | 0.76 (0.49−0.90) | ||
| v0 (m/s) | 3.14 ± 0.20 | 3.10 ± 0.18 | 0.140 | 2.41 (1.84−3.53) | 0.86 (0.68−0.94) | |||
| Aline (kg × m/s) | 294.8 ± 30.1 | 287.5 ± 32.1 | 0.014 | 2.96 (2.25−4.32) | 0.93 (0.83−0.97) | |||
| Heavy CMJ (20–80) | MV | L0 (kg) | 196.7 ± 19.5 | 185.8 ± 26.6 | 0.023 | 7.30 (5.55−10.67) | 0.66 (0.32−0.85) | |
| v0 (m/s) | 1.59 ± 0.09 | 1.60 ± 0.11 | 0.912 | 3.65 (2.77−5.33) | 0.71 (0.40−0.88) | |||
| Aline (kg × m/s) | 156.7 ± 17.4 | 147.8 ± 19.8 | 0.001 | 4.73 (3.59−6.90) | 0.86 (0.69−0.94) | |||
| MPV | L0 (kg) | 173.7 ± 16.8 | 168.7 ± 21.8 | 0.170 | 6.50 (4.95−9.50) | 0.69 (0.37−0.87) | ||
| v0 (m/s) | 1.87 ± 0.12 | 1.83 ± 0.13 | 0.157 | 4.27 (3.25−6.24) | 0.64 (0.28−0.84) | |||
| Aline (kg × m/s) | 162.1 ± 17.0 | 154.1 ± 19.7 | <0.001 | 3.77 (2.87−5.50) | 0.91 (0.78−0.96) | |||
| PV | L0 (kg) | 196.2 ± 26.9 | 194.9 ± 23.6 | 0.646 | 4.49 (3.41−6.56) | 0.89 (0.75−0.96) | ||
| v0 (m/s) | 3.13 ± 0.18 | 3.08 ± 0.17 | 0.056 | 2.09 (1.59−3.05) | 0.88 (0.72−0.95) | |||
| Aline (kg × m/s) | 307.5 ± 51.5 | 300.9 ± 43.0 | 0.127 | 4.28 (3.25−6.25) | 0.93 (0.84−0.97) |
Notes: p obtained through a paired samples t test. Bold numbers indicate an unacceptable reliability (CV > 10% and ICC < 0.70).
Abbreviations: 95%CI = 95% confidence interval; Aline = area under the L−V relationship line; CMJ = countermovement jump; CV = coefficient of variation; ICC = intra-class correlation coefficient; L−V relationship = load−velocity relationship; L0 = load-axis intercept; load0.55 = estimated load equivalent to 0.55 m/s; MPV = mean propulsive velocity; MV = mean velocity; PV = peak velocity; v0 = velocity-axis intercept.
Fig. 2.
Reliability comparisons between the different methods (multiple-point and 2-point), load combinations (heavy squat and heavy CMJ), and velocity variables (MV, MPV, and PV) for the (A) L0, (B) v0, and (C) Aline obtained during the CMJ exercise. Bars represent the average CV and their respective SD obtained combining the 2 load combinations and 3 velocity variables for the method, the 2 methods and 3 velocity variables for the load combination, and the 2 methods and load combinations for the velocity variable. Numbers depict the ratio between 2 CVs (CVratio= higher value/lower value), while meaningful differences in reliability (CVratio > 1.15) are indicated in bold. Aline = area under the L−V relationship line; CMJ = countermovement jump; CV = coefficient variation; L0 = load-axis intercept; L−V relationship = load−velocity relationship; MPV = mean propulsive velocity; MV = mean velocity; PV = peak velocity; v0 = velocity-axis intercept.
The 2-point methods revealed an acceptable validity when compared to their respective multiple-point methods for MV and MPV (ES ranged −0.19 to 0.07; r ranged 0.96–1.00; CCC ranged 0.94–0.99), but not for PV (ES ranged −0.54 to 0.60; r ranged 0.67–0.99; CCC ranged 0.55–0.98) (Table 2). Finally, regardless of the method and load combination, the 3 L–V relationship variables revealed nearly perfect correlations between MV and MPV (r = 0.98 (95%CI: 0.95–1.00)), and very high correlations between PV and MV (r = 0.81 (95%CI: 0.61–0.94)) and between PV and MPV (r = 0.79 (95%CI: 0.58–0.92)).
Table 2.
Comparison of the L−V relationship variables obtained by different 2-point methods compared to their respective multiple-point methods for each velocity variable during the countermovement jump exercise.
| Load combination | Velocity variable | L−V variable | p | ES | r (95%CI) | CCC (95%CI) | Bias (95%LoA) |
|---|---|---|---|---|---|---|---|
| Heavy squat (20–load0.55) | MV | L0 (kg) | 0.675 | −0.01 | 0.99 (0.98−1.00) | 0.99 (0.98−1.00) | −0.1 (−3.9 to 3.7) |
| v0 (m/s) | 0.911 | 0.01 | 0.96 (0.90−0.98) | 0.95 (0.89−0.98) | 0.00 (−0.04 to 0.04) | ||
| Aline (kg × m/s) | 0.792 | −0.01 | 0.98 (0.94−0.99) | 0.97 (0.93–0.99) | −0.1 (−5.7 to 5.5) | ||
| MPV | L0 (kg) | 0.105 | −0.07 | 0.99 (0.96−0.99) | 0.98 (0.95−0.99) | −0.5 (−5.3 to 4.3) | |
| v0 (m/s) | 0.008 | −0.19 | 0.96 (0.91−0.99) | 0.94 (0.86−0.98) | −0.01 (−0.05 to 0.04) | ||
| Aline (kg × m/s) | 0.029 | −0.16 | 0.97 (0.91−0.99) | 0.94 (0.87−0.98) | −1.2 (−9.3 to 6.9) | ||
| PV | L0 (kg) | 0.026 | 0.37 | 0.78 (0.51−0.91) | 0.71 (0.42−0.87) | 2.6 (−14.8 to 20.0) | |
| v0 (m/s) | <0.001 | −0.41 | 0.93 (0.82−0.97) | 0.85 (0.65−0.94) | −0.02 (−0.13 to 0.08) | ||
| Aline (kg × m/s) | 0.169 | 0.14 | 0.91 (0.79−0.97) | 0.89 (0.76−0.95) | 1.8 (−16.8 to 20.3) | ||
| Heavy CMJ (20–80) | MV | L0 (kg) | 0.168 | −0.04 | 1.00 (0.99−1.00) | 0.99 (0.99−1.00) | −0.3 (−3.6 to 3.0) |
| v0 (m/s) | 0.834 | 0.01 | 0.99 (0.97−1.00) | 0.99 (0.97−0.99) | 0.00 (−0.02 to 0.02) | ||
| Aline (kg × m/s) | 0.274 | 0.03 | 0.99 (0.99−1.00) | 0.99 (0.98−1.00) | 0.2 (−2.5 to 2.9) | ||
| MPV | L0 (kg) | 0.005 | −0.09 | 0.99 (0.99−1.00) | 0.99 (0.97−1.00) | −0.6 (−4.0 to 2.8) | |
| v0 (m/s) | 0.012 | 0.07 | 0.99 (0.99, 1.00) | 0.99 (0.98−1.00) | 0.00 (−0.02 to 0.02) | ||
| Aline (kg × m/s) | <0.001 | −0.12 | 0.99 (0.98−1.00) | 0.99 (0.96−0.99) | −0.8 (−4.2 to 2.6) | ||
| PV | L0 (kg) | 0.005 | 0.60 | 0.67 (0.33−0.86) | 0.55 (0.20−0.70) | 4.3 (−18.9 to 27.6) | |
| v0 (m/s) | 0.382 | 0.03 | 0.99 (0.96−0.99) | 0.98 (0.96−0.99) | 0.00 (−0.03 to 0.04) | ||
| Aline (kg × m/s) | 0.002 | −0.54 | 0.81 (0.57−0.92) | 0.67 (0.38−0.84) | −7.0 (−41.5 to 27.5) |
Abbreviations: 95%CI = 95% confidence interval; 95%LoA = 95% limits of agreement (± 1.96 × SD); Aline = area under the L−V relationship line; CCC = Lin's concordance correlation coefficient; ES = Cohen's d effect size; L−V relationship = load−velocity relationship; L0 = load-axis intercept; load0.55 = estimated load equivalent to 0.55 m/s; MPV = mean propulsive velocity; MV = mean velocity; PV = peak velocity; v0 = velocity-axis intercept.
4. Discussion
This study was designed to examine the between-session reliability and concurrent validity of L−V relationship variables obtained from the 2-point method with respect to the multiple-point method during the CMJ exercise using different load combinations and velocity variables. The main findings of this study revealed that (a) the 3 L−V relationship variables were obtained with an acceptable reliability regardless of the method, load combination, and velocity variable; (b) both methods provided L0 and v0 with comparable reliability, but the multiple-point method provided Aline with a greater reliability; (c) the use of a heavy squat provided the L−V relationship variables with a comparable or higher reliability than the use of a heavy CMJ load; (d) the velocity variables could be ranked from the most to the least reliable as follows: PV > MV > MPV; and (e) both 2-point methods only revealed an acceptable concurrent validity when compared to their respective multiple-point methods for MV and MPV. These results suggest that the 2-point method obtained from a heavy squat load and MV or MPV is a quick, safe, and reliable procedure to evaluate the maximal neuromuscular capacities of lower-body muscles through the assessment of the L−V relationship variables.
It has been recently shown that the L−V relationship variables could be a simpler and more reproducible alternative than the F−V relationship parameters to estimate the upper-body maximal neuromuscular capacities.9 However, further research is still needed to explore the reliability of this novel approach in other multi-joint tasks. Regardless of the method, load combination, and velocity variable, the results of the present study revealed that the 3 variables derived from the L−V relationship (L0, v0, and Aline) offered an acceptable between-session reliability during the CMJ exercise. These results are in agreement with previous studies showing that the 3 F−V relationship parameters (force-axis intercept (F0), v0, and maximal power (Pmax)) can generally be obtained with acceptable reliability (CV ranged 2.4%–13.0%; ICC ranged 0.69–0.98) during CMJ and SJ exercises.11,12 However, our results are in contrast to recent work that questioned the practical usefulness of the F−V and L−V profiles because their outcomes were not reliable (CV ranged 8.9%–39.4%, ICC ranged 0.03–0.92) during the SJ exercise. The discrepancy between the results of the present study and the Kotani et al.24 is probably due to (a) the lack of familiarity of the subjects with the loaded SJ testing protocol (only 1 familiarization session), (b) the fatigue developed throughout the testing protocol (11 loading conditions), and (c) the device used to measure the velocity output (system center-of-mass velocity calculated from the force-time signal recorded by a force platform). Therefore, our study is the first to show that not only L0 and v0, but also the Aline can be obtained with acceptable reliability from the barbell's velocity recorded by a linear velocity transducer during the loaded CMJ exercise.
One important aspect when determining the F−V and L−V relationships is to find a testing protocol that allows researchers to accurately determine their outcomes with minimum effort and time.23 In partial support of our main hypothesis, the 2-point method generally revealed the L−V relationship variables to have a comparable between-session reliability and an acceptable concurrent validity in comparison to the multiple-point method when using mean velocities. These findings are in line with previous studies showing that the L−V relationship modeled through the 2-point methods can be used to estimate the one repetition maximum with high precision in various upper-body resistance training exercises.35,36 More importantly, our results are in agreement with previous studies showing that the 2-point method is a reliable and valid procedure for the assessment of muscle mechanical capacities through the F−V relationship parameters obtained during the CMJ and SJ exercises.18, 19, 20 Due to the high linearity of the L−V relationship (r ≥ 0.97), it is evident that the addition of intermediate loads should not meaningfully improve the precision of the relationship modeling compared to using only the 2 most distant experimental points.23 However, it is worth noting that the reliability of the Aline was greater for the multiple-point method than for the 2-point method, likely because the error in determining Aline is affected by the errors of both L0 and v0. Nonetheless, our study provides additional evidence that the 2-point method is not only a reliable and valid alternative to the multiple-point method when using mean velocities, but also a procedure for evaluating the lower-body maximal neuromuscular capacities through the L−V relationship obtained during the loaded CMJ exercise that is quicker and less prone to fatigue.
The distance between the 2 most distant experimental points and the proximity of the experimental points to the axis intercepts are 2 of the most important methodological factors for obtaining accurate F−V relationship parameters.23 However, there is little information regarding the effect of the magnitude of the heaviest load in the modeling of the L−V relationship. Supporting our secondary hypothesis, the reliability of the L−V relationship variables was generally greater for the heavy squat load compared to the heavy CMJ load, likely due to the greater distance between the experimental points and increased proximity of the heavier experimental point to L0. These results are in agreement with Rivière et al.,37 who found that the goodness of fit of the F−V relationship obtained during the loaded SJ exercise did not differ with or without inclusion of the squat one repetition maximum point. Similarly, these data agree with those of García-Ramos et al.19 and Šarabon et al.,18 who observed that the 2-point method based on the heavy CMJ load provided a high between-session reliability and concurrent validity with respect to the multiple-point method to determine the F−V relationship parameters during the SJ and CMJ exercises. In contrast, Šarabon et al.18 found a poor-to-fair validity for the 2-point method based on an isometric maximal voluntary contraction task (squat exercise performed at 30°, 60°, and 90° knee angles). Such discrepancies may be attributed partially to the different force production modalities that represent a dynamic (full range of knee extension) and isometric task (fixed knee angle).37 In fact, it has been shown there is a weak association between F0 and the maximal isometric voluntary contraction during the squat exercise.38 Collectively, our results highlight that the 2-point method based on the heavy squat load is more reliable, equally valid, and potentially safer than the widely used 2-point method based on a heavy CMJ load.
A recent systematic review has shown that linear position/velocity transducers are the most used and accurate devices for measuring barbell velocity during resistance training.1 Note that although both systems consist of a sensor with a cable attached directly to the collar of the barbell, the linear velocity transducer measures barbell velocity by recording electrical signals proportional to the cable extension velocity, while the linear position transducer measures barbell velocity from the differentiation of the cable displacement with respect to time.39 The 3 velocity variables examined in this study (MV, MPV and PV) are commonly recorded through linear position/velocity transducers for modeling the F−V and L−V relationships.2,40 However, no study has examined which velocity variable provides the outcomes of the L−V relationship with the highest reliability. Since previous studies have shown a higher reliability for PV compared to MV and MPV across a range of relative loads during CMJ and SJ exercises,26,27 we hypothesized that PV would be the most reliable variable to determine the L−V relationship variables. Supporting our hypothesis, we found PV to be the most reliable variable, followed by MV and finally MPV. These results are in consensus with those of a previous study that examined the reliability of the velocity variables across the whole L−V relationship spectrum during the bench press throw exercise.40 However, regardless of the load combination, the concurrent validity of the 2-point method with respect to multiple-point method was only found to be acceptable for MV and MPV variables. The lower concurrent validity observed for PV may be attributed to a lower linearity of the L−V relationship.40 It is important to note that the L−V relationship variables obtained using the 3 velocity variables were strongly correlated (especially between MV and MPV). Therefore, since the 3 variables provide similar information, the MV could be recommended to obtain the L−V relationship variables during the CMJ exercise due to its greater reliability and concurrent validity.
There are several limitations that need to be acknowledged. First, the use of a relatively small sample size of resistance-trained men, all of whom were highly familiarized with the loaded CMJ performed at maximal intended velocity, makes the extrapolation of the present findings to less-skilled populations (e.g., untrained subjects) challenging. Second, the generalizability of the current results may also be limited to the use of a Smith machine, which restricts the movement of the barbell to the vertical direction, as well as to the use of a linear velocity transducer. This is because the mechanical variables recorded by a linear velocity transducer during the CMJ exercise can be obtained with a somewhat higher reliability using a Smith machine compared to free-weights.25 In addition, although the velocity measurements are highly related between force platforms and linear position/velocity transducers,41 their outcomes should not be used interchangeably due to systematic differences.25 Third, the minimum load was set to 20 kg (mass of the unloaded Smith machine barbell) to keep the same execution technique for all tested loads. It is possible that by including a jump against a very light load (e.g., 0.5 kg) and the reliability of v0 could be increased by reducing the extrapolation to the velocity intercept. Finally, the 2-point method was derived from a testing protocol based on multiple loads. Therefore, although a high reliability and validity of the F−V relationship parameters has been observed when the 2-point method was applied in field conditions (only 2 loads applied) in the leg cycle ergometer exercise,42 further research is warranted to explore the feasibility of the L−V relationship variables when only 2 loads are applied in the testing protocol.
5. Conclusion
The 2-point method provided the L−V relationship variables with an acceptable reliability regardless of the load combination and velocity variable. However, the concurrent validity of the 2-point method with respect to the multiple-point method was only acceptable for mean velocities. We recommend that practitioners use a heavy squat load and MV or MPV to model the L−V relationship through the 2-point method during the CMJ. Moreover, although L−V relationship variables (L0, v0, and Aline) do not present clear physiological meaning, unlike the parameters derived from the F−V relationship (F0, v0, and Pmax), this novel approach can provide practitioners with a simpler and more precise alternative due to the lower number of mechanical variables included in the modeling (force output is not considered) and the lower extrapolation from the experimental points to v0 (only the external load lifted is considered in the analysis).
Acknowledgment
We would like to thank all the participants who selflessly participated in the study.
Authors’ contributions
APC contributed to the conception and design of the study, organized the database, performed the statistical analysis, and wrote the first draft of the manuscript; RRC and JFTF interpreted the data and drafted the manuscript; AGR contributed to the conception and design of the study, supervised the study, and drafted the manuscript. All authors have read and approved the final version of the manuscript, and agree with the order of presentation of the authors.
Competing interests
The authors declare that they have no competing interests.
Footnotes
Peer review under responsibility of Shanghai University of Sport.
Supplementary materials
References
- 1.Weakley J, Mann B, Banyard H, McLaren S, Scott T, Garcia-Ramos A. Velocity-based training: From theory to application. Strength Cond J. 2021;43:31–49. [Google Scholar]
- 2.Weakley J, Morrison M, García-Ramos A, Johnston R, James L, Cole MH. The Validity and reliability of commercially available resistance training monitoring devices: A systematic review. Sports Med. 2021;51:443–502. doi: 10.1007/s40279-020-01382-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Orange ST, Metcalfe JW, Robinson A, Applegarth MJ, Liefeith A. Effects of in-season velocity- vs. percentage-based training in academy rugby league players. Int J Sports Physiol Perform. 2020;15:554–561. doi: 10.1123/ijspp.2019-0058. [DOI] [PubMed] [Google Scholar]
- 4.Banyard HG, Tufano JJ, Weakley JJS, Wu S, Jukic I, Nosaka K. Superior changes in jump, sprint, and change-of-direction performance but not maximal strength following 6 weeks of velocity-based training compared with 1-repetition-maximum percentage-based training. Int J Sports Physiol Perform. 2021;16:232–242. doi: 10.1123/ijspp.2019-0999. [DOI] [PubMed] [Google Scholar]
- 5.Vernon A, Joyce C, Banyard HG. Readiness to train: Return to baseline strength and velocity following strength or power training. Int J Sports Sci Coach. 2020;15:204–211. [Google Scholar]
- 6.Hughes LJ, Banyard HG, Dempsey AR, Peiffer JJ, Scott BR. Using load−velocity relationships to quantify training-induced fatigue. J Strength Cond Res. 2019;33:762–773. doi: 10.1519/JSC.0000000000003007. [DOI] [PubMed] [Google Scholar]
- 7.Pérez-Castilla A, García-Ramos A. Changes in the load–velocity profile following power- and strength-oriented resistance-training programs. Int J Sports Physiol Perform. 2020;15:1460–1466. doi: 10.1123/ijspp.2019-0840. [DOI] [PubMed] [Google Scholar]
- 8.Iglesias-Soler E, Rial-Vázquez J, Boullosa D, et al. Load−velocity profiles change after training programs with different set configurations. Int J Sports Med. 2021;42:794–802. doi: 10.1055/a-1323-3456. [DOI] [PubMed] [Google Scholar]
- 9.Pérez-Castilla A, Jukic I, García-Ramos A. Validation of a novel method to assess maximal neuromuscular capacities through the load–velocity relationship. J Biomech. 2021;127 doi: 10.1016/j.jbiomech.2021.110684. [DOI] [PubMed] [Google Scholar]
- 10.Jaric S. Force−velocity relationship of muscles performing multi-joint maximum performance tasks. Int J Sports Med. 2015;36:699–704. doi: 10.1055/s-0035-1547283. [DOI] [PubMed] [Google Scholar]
- 11.Cuk I, Markovic M, Nedeljkovic A, Ugarkovic D, Kukolj M, Jaric S. Force−velocity relationship of leg extensors obtained from loaded and unloaded vertical jumps. Eur J Appl Physiol. 2014;114:1703–1704. doi: 10.1007/s00421-014-2901-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.García-Ramos A, Feriche B, Pérez-Castilla A, Padial P, Jaric S. Assessment of leg muscles mechanical capacities: Which jump, loading, and variable type provide the most reliable outcomes? Eur J Sport Sci. 2017;17:690–698. doi: 10.1080/17461391.2017.1304999. [DOI] [PubMed] [Google Scholar]
- 13.Fernandes JFT, Lamb KL, Twist C. Low body fat does not influence recovery after muscle-damaging lower-limb plyometrics in young male team sport athletes. J Funct Morphol Kinesiol. 2020;5:79. doi: 10.3390/jfmk5040079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cormie P, McBride JM, McCaulley GO. Power-time, force-time, and velocity-time curve analysis during the jump squat: Impact of load. J Appl Biomech. 2008;24:112–120. doi: 10.1123/jab.24.2.112. [DOI] [PubMed] [Google Scholar]
- 15.McBride JM, Haines TL, Kirby TJ. Effect of loading on peak power of the bar, body, and system during power cleans, squats, and jump squats. J Sports Sci. 2011;29:1215–1221. doi: 10.1080/02640414.2011.587444. [DOI] [PubMed] [Google Scholar]
- 16.Jiménez-Reyes P, Samozino P, Pareja-Blanco F, et al. Validity of a simple method for measuring force−velocity−power profile in countermovement jump. Int J Sports Physiol Perform. 2017;12:36–43. doi: 10.1123/ijspp.2015-0484. [DOI] [PubMed] [Google Scholar]
- 17.Feeney D, Stanhope SJ, Kaminski TW, Machi A, Jaric S. Loaded vertical jumping: Force−velocity relationship, work, and power. J Appl Biomech. 2016;32:120–127. doi: 10.1123/jab.2015-0136. [DOI] [PubMed] [Google Scholar]
- 18.Šarabon N, Kozinc Ž, Marković G. Force–velocity profile during vertical jump cannot be assessed using only bodyweight jump and isometric maximal voluntary contraction tasks. Sci Rep. 2020;10:19127. doi: 10.1038/s41598-020-76262-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.García-Ramos A, Pérez-Castilla A, Jaric S. Optimisation of applied loads when using the two-point method for assessing the force−velocity relationship during vertical jumps. Sports Biomech. 2021;20:274–289. doi: 10.1080/14763141.2018.1545044. [DOI] [PubMed] [Google Scholar]
- 20.Zivkovic MZ, Djuric S, Cuk I, Suzovic D, Jaric S. A simple method for assessment of muscle force, velocity, and power producing capacities from functional movement tasks. J Sports Sci. 2017;35:1287–1293. doi: 10.1080/02640414.2016.1221521. [DOI] [PubMed] [Google Scholar]
- 21.Pérez-Castilla A, Jaric S, Feriche B, Padial P, García-Ramos A. Evaluation of muscle mechanical capacities through the two-load method: Optimization of the load selection. J Strength Cond Res. 2018;32:1245–1253. doi: 10.1519/JSC.0000000000001969. [DOI] [PubMed] [Google Scholar]
- 22.García-Ramos A, Torrejón A, Morales-Artacho AJ, Pérez-Castilla A, Jaric S. Optimal resistive forces for maximizing the reliability of leg muscles’ capacities tested on a cycle ergometer. J Appl Biomech. 2018;34:47–52. doi: 10.1123/jab.2017-0056. [DOI] [PubMed] [Google Scholar]
- 23.Garcia-Ramos A, Jaric S. Two-point method: A quick and fatigue-free procedure for assessment of muscle mechanical capacities and the one-repetition maximum. Strength Cond J. 2018;40:54–66. [Google Scholar]
- 24.Kotani Y, Lake J, Guppy SN, et al. Reliability of the squat jump force-velocity and load-velocity profiles. J Strength Cond Res. 2022;36:3000–3007. doi: 10.1519/JSC.0000000000004057. [DOI] [PubMed] [Google Scholar]
- 25.García-Ramos A, Jaric S, Pérez-Castilla A, Padial P, Feriche B. Reliability and magnitude of mechanical variables assessed from unconstrained and constrained loaded countermovement jumps. Sports Biomech. 2017;16:514–526. doi: 10.1080/14763141.2016.1246598. [DOI] [PubMed] [Google Scholar]
- 26.García-Ramos A, Stirn I, Strojnik V, et al. Comparison of the force−, velocity−, and power−time curves recorded with a force plate and a linear velocity transducer. Sports Biomech. 2016;15:329–341. doi: 10.1080/14763141.2016.1161821. [DOI] [PubMed] [Google Scholar]
- 27.Pérez-Castilla A, Jiménez-Reyes P, Haff GG, García-Ramos A. Assessment of the loaded squat jump and countermovement jump exercises with a linear velocity transducer: Which velocity variable provides the highest reliability? Sports Biomech. 2021;20:247–260. doi: 10.1080/14763141.2018.1540651. [DOI] [PubMed] [Google Scholar]
- 28.Pérez-Castilla A, García-Ramos A., Padial P, Morales-Artacho AJ, Feriche B. Load–velocity relationship in variations of the half-squat exercise. J Strength Cond Res. 2020;34:1024–1031. doi: 10.1519/JSC.0000000000002072. [DOI] [PubMed] [Google Scholar]
- 29.Jiménez-Alonso A, García-Ramos A, Cepero M, Miras-Moreno S, Rojas FJ. Pérez-Castilla A. Effect of augmented feedback on velocity performance during strength-oriented and power-oriented resistance training sessions. J Strength Cond Res. 2022;36:1511–1517. doi: 10.1519/JSC.0000000000003705. [DOI] [PubMed] [Google Scholar]
- 30.Morales-Artacho AJ, Padial P, García-Ramos A, Pérez-Castilla A, Feriche B. Influence of a cluster set configuration on the adaptations to short-term power training. J Strength Cond Res. 2018;32:930–937. doi: 10.1519/JSC.0000000000001925. [DOI] [PubMed] [Google Scholar]
- 31.Pérez-Castilla A, Piepoli A, Delgado-García G, Garrido-Blanca G, García-Ramos A. Reliability and concurrent validity of seven commercially available devices for the assessment of movement velocity at different intensities during the bench press. J Strength Cond Res. 2019;33:1258–1265. doi: 10.1519/JSC.0000000000003118. [DOI] [PubMed] [Google Scholar]
- 32.Hopkins WG, Marshall SW, Batterham AM, Hanin J. Progressive statistics for studies in sports medicine and exercise science. Med Sci Sports Exerc. 2009;41:3–13. doi: 10.1249/MSS.0b013e31818cb278. [DOI] [PubMed] [Google Scholar]
- 33.Hopkins WG. Spreadsheets for analysis of validity and reliability. Sportscience. 2015;19:36–42. [Google Scholar]
- 34.Martins WP, Nastri CO. Interpreting reproducibility results for ultrasound measurements. Ultrasound Obstet Gynecol. 2014;43:479–480. doi: 10.1002/uog.13320. [DOI] [PubMed] [Google Scholar]
- 35.Pérez-Castilla A, Suzovic D, Domanovic A, Fernandes JFT, García-Ramos A. Validity of different velocity-based methods and repetitions-to-failure equations for predicting the 1 repetition maximum during 2 upper-body pulling exercises. J Strength Cond Res. 2021;35:1800–1808. doi: 10.1519/JSC.0000000000003076. [DOI] [PubMed] [Google Scholar]
- 36.Pérez-Castilla A, Jerez-Mayorga D, Martínez-García D, Rodríguez-Perea Á, Chirosa-Ríos LJ, García-Ramos A. Comparison of the bench press one-repetition maximum obtained by different procedures: Direct assessment vs. lifts-to-failure equations vs. two-point method. Int J Sports Sci Coach. 2020;15:337–346. [Google Scholar]
- 37.Rivière J, Rossi J, Jimenez-Reyes P, Morin J-B, Samozino P. Where does the one-repetition maximum exist on the force−velocity relationship in squat? Int J Sports Med. 2017;38:1035–1043. doi: 10.1055/s-0043-116670. [DOI] [PubMed] [Google Scholar]
- 38.Rahmani A, Viale F, Dalleau G, Lacour JR. Force/velocity and power/velocity relationships in squat exercise. Eur J Appl Physiol. 2001;84:227–232. doi: 10.1007/PL00007956. [DOI] [PubMed] [Google Scholar]
- 39.Harris NK, Cronin J, Taylor KL, Boris J, Sheppard J. Understanding position transducer technology for strength and conditioning practitioners. Strength Cond J. 2010;32:66–79. [Google Scholar]
- 40.García-Ramos A, Pestaña-Melero FL, Pérez-Castilla A, Rojas FJ, Gregory Haff G. Mean velocity vs. mean propulsive velocity vs. peak velocity: Which variable determines bench press relative load with higher reliability? J Strength Cond Res. 2018;32:1273–1279. doi: 10.1519/JSC.0000000000001998. [DOI] [PubMed] [Google Scholar]
- 41.Pérez-Castilla A, Feriche B, Jaric S, Padial P, García-Ramos A. Validity of a linear velocity transducer for testing maximum vertical jumps. J Appl Biomech. 2017;33:388–392. doi: 10.1123/jab.2016-0142. [DOI] [PubMed] [Google Scholar]
- 42.García-Ramos A, Zivkovic M, Djuric S, Majstorovic N, Manovski K, Jaric S. Assessment of the two-point method applied in field conditions for routine testing of muscle mechanical capacities in a leg cycle ergometer. Eur J Appl Physiol. 2018;118:1877–1884. doi: 10.1007/s00421-018-3925-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.