Evaluating the robustness of targeted maximum likelihood estimators via realistic simulations in nutrition intervention trials

Abstract

Several recently developed methods have the potential to harness machine learning in the pursuit of target quantities inspired by causal inference, including inverse weighting, doubly robust estimating equations and substitution estimators like targeted maximum likelihood estimation. There are even more recent augmentations of these procedures that can increase robustness, by adding a layer of cross-validation (cross-validated targeted maximum likelihood estimation and double machine learning, as applied to substitution and estimating equation approaches, respectively). While these methods have been evaluated individually on simulated and experimental data sets, a comprehensive analysis of their performance across real data based simulations have yet to be conducted. In this work, we benchmark multiple widely used methods for estimation of the average treatment effect using ten different nutrition intervention studies data. A nonparametric regression method, undersmoothed highly adaptive lasso, is used to generate the simulated distribution which preserves important features from the observed data and reproduces a set of true target parameters. For each simulated data, we apply the methods above to estimate the average treatment effects as well as their standard errors and resulting confidence intervals. Based on the analytic results, a general recommendation is put forth for use of the cross-validated variants of both substitution and estimating equation estimators. We conclude that the additional layer of cross-validation helps in avoiding unintentional over-fitting of nuisance parameter functionals and leads to more robust inferences.

1 ∣. INTRODUCTION

Epidemiological studies, particularly based on randomized trials, often aim to estimate the average treatment effect (ATE), or another causal parameter of interest, to understand the effect of a health intervention or exposure on an outcome of interest. Most commonly, in observational studies, inverse probability of treatment weighted (IPTW) estimation and its variants have been used for this purpose.^1-3 Alternative estimators for causal inference include substitution (or direct) estimators based on G-computation,^4-7 those based on the approach of estimating equations (EE),^8,9 including IPTW and its augmented variant (A-IPTW), and substitution estimators developed within the framework of targeted learning (TL) (we also refer to targeted maximum likelihood estimator, TMLE, a product of this framework¹⁰). The latter of these has seen increasing use in recent years, both in biostatistical methodological research and applied public health and medical research.^11-15 In Table 1, we provide a list of studies that have examined the relative performance of TL-based and competing estimators (mainly against EE-based methods), including a summary of whether the results suggested superior, neutral, or poorer relative performance of TL-based estimators in comparison to other estimators (the “Pro/Con” column). Thus, while this work is contextualized within dozens of previous studies, few such studies performed “realistic” simulations, and even fewer compared several variants of TL estimators alongside corresponding EE approaches. For example, in Zivich and Breskin’s paper,¹⁶ the authors compared G-computation, IPTW, A-IPTW, TMLE, and double cross-fit estimators with data generated from predefined parametric models. Exceptions are efforts that used the proposed realistic bootstrap¹⁷ to evaluate the performance for data-generating distributions modeled semiparametrically (using ensemble machine learning) from an existing data set. These include a study of estimating variable importance under positivity violations using collaborative targeted maximum likelihood estimation (C-TMLE).¹⁸ In this article, we use an augmentation of this proposed methodology to examine the relative performance of several versions of both TL and EE estimators in ten realistic data simulations, each based on data collected as part of the Knowledge Integration (KI) database from the Bill & Melinda Gates Foundation.¹⁹ In so doing, we provide a realistic survey, across both different data-generating distributions and different study designs, of the relative performance of estimators of causal parameters.

TABLE 1.

Overview of literature on comparison of TMLE and other estimators

Authors	Title	Year	Description of results	Pro/Con
Chatton, et al20	G-computation, propensity score-based methods, and targeted maximum likelihood estimator for causal inference with different covariates sets: a comparative simulation study	2020	Article compares different semiparametic approaches, including TMLE and matching, but finds G-computation performs relatively best. Given their simulation, this was predictable because they simulated from a parametric model and used the same model for estimating the regression, thus showing the superiority of maximum likelihood estimation in parametric models. This is not a realistic setting.	Con
Talbot and Beaudoin21	A generalized double robust Bayesian model averaging approach to causal effect estimation with application to the study of osteoporotic fractures	2020	Proposed a generalized Bayesian causal effect estimation (GBCEE), which outperformed double robust alternatives(including C-TMLE). Also showed “target” A-IPTW is superior than C-TMLE in a nonrealistic setting(only using true confounders).	Con
Zivich and Breskin16	Machine learning for causal inference: on the use of cross-fit estimators	2020	A simulation study assessing the performance of G-computation, IPW, AIPW, TMLE, doubly robust cross-fit (DC) AIPW and DC-TMLE. With correctly specified parametric models, all of the estimators performed well. When used with machine learning, the DC estimators outperformed other estimators.	Neutral
Ju, et al22	Scalable collaborative targeted learning for high-dimensional data	2019	Results from simulations suggested superior performance of C-TMLE relative to both A-IPTW and noncollaborative (“standard”) TMLE estimators.	Pro
Ju, et al23	On adaptive propensity score truncation in causal inference	2019	By adaptively truncating the estimated propensity score with a more targeted objective function, the Positivity-C-TMLE estimator achieves the best performance for both point estimation and confidence interval coverage among all estimators considered.	Pro
Bahamyirou, et al24	Understanding and diagnosing the potential for bias when using machine learning methods with doubly robust causal estimators	2019	Simulation results showed superior performance of C-TMLE and TMLE relative to IPTW.	Pro
Wei, et al25	A data-adaptive targeted learning approach of evaluating viscoelastic assay driven trauma treatment protocols	2019	C-TMLE outperformed the other doubly robust estimators (IPTW, A-IPTW, stabilized IPTW, TMLE) in the simulation study.	Pro
Rudolph, et al.26	Complier stochastic direct effects: identification and Robust Estimation	2019	Showed that the EE and TMLE estimators have advantages over the IPTW estimator in terms of efficiency and reduced reliance on correct parametric model specification.	Pro
Pirracchio, et al.18	Collaborative targeted maximum likelihood estimation for variable importance measure: illustration for functional outcome prediction in mild traumatic brain injuries	2018	Showed much more robust performance of C-TMLE relative to TMLE using the same type of realistic parametric bootstrap as used in this paper. This was under severe near-positivity violations.	Pro
Luque-Fernandez, et al.27	Targeted maximum likelihood estimation for a binary treatment: A tutorial	2018	Showed relatively superior performance of TMLE when compared with A-IPTW estimator in terms of bias.	Pro
Levy, et al28	A fundamental measure of treatment effect heterogeneity	2018	Showed the advantage of CV-TMLE over TMLE in that TMLE was affected by overfitting while CV-TMLE appeared unaffected.	Pro
Schuler and Rose29	Targeted maximum likelihood estimation for causal inference in observational studies	2017	Showed superior performance of TMLE relative to misspecified parametric models.	Pro
Pang, et al30	Effect estimation in point-exposure studies with binary outcomes and high-dimensional covariate data—a comparison of targeted maximum likelihood estimation and inverse probability of treatment weighting	2016	Showed relatively superior performance for the TMLE to IPTW, which showed greater instability when positivity violations occurred.	Pro
Schnitzer, et al31	Variable selection for confounder control, flexible modeling and collaborative targeted minimum loss-based estimation in causal inference	2016	Using IPTW with flexible prediction for the propensity score can result in inferior estimation, while TMLE and C-TMLE may benefit from flexible prediction and remain robust to the presence of variables that are highly correlated with treatment.	Pro
Zheng, et al32	Doubly robust and efficient estimation of marginal structural models for the hazard function	2016	Showed that the TMLE for marginal structual model (MSM) for a hazard function has relatively superior performance. The bias reduction over a misspecified IPTW or Gcomp estimator is clear in the simulation studies even for a moderate sample size.	Pro
Schnitzer, et al33	Double robust and efficient estimation of a prognostic model for events in the presence of dependent censoring	2016	This study demonstrated that even when the analyst is ignorant of the true data generating form, TMLE with super learner can perform about as well as IPTW or TMLE with correct parametric model specification.	Pro
Kreif, et al34	Evaluating treatment effectiveness under model misspecification: A comparison of targeted maximum likelihood estimation with bias-corrected matching	2014	Examined the relative performance of TMLE, EE, and matching estimators showing superior performance of TMLE when the outcome regression is misspecified.	Pro
Schnitzer, et al35	Effect of breastfeeding on gastrointestinal infection in infants: A targeted maximum likelihood approach for clustered longitudinal data	2014	Compared TMLE with IPTW and G-computation, under the plausible scenario of being given transformed versions of the confounders. Only TMLE with super learner was able to unbiasedly estimate the parameter of interest.	Pro
Gruber and van der Laan36	An application of targeted maximum likelihood estimation to the meta-analysis of safety data	2013	Reported superiority of both TMLE and A-IPTW to misspecified parametric models, but the data-generating distributions used resulted in little difference between the semiparametric approaches.	Neutral
Lendle, et al37	Targeted maximum likelihood estimation in safety analysis	2013	Showed superior performance of TMLE and C-TMLE relative to A-IPTW estimators in the context of positivity violations.	Pro
Díaz and van der Laan38	Targeted data adaptive estimation of the causal dose response curve	2013	Showed relatively superior performance of CV-TMLE relative to CV-A-IPTW estimators, especially in the presence of empirical violations of the positivity assumption.	Pro
Schnitzer, et al39	Targeted maximum likelihood estimation for marginal time-dependent treatment effects under density misspecification	2013	In the simulation study, TMLE did not produce a reduction in finite-sample bias or variance for correctly specified densities compared with the G-computation estimator, but it had much better performance than G-computation when the outcome model was misspecified.	Neutral
Petersen, et al17	Diagnosing and responding to violations in the positivity assumption	2012	Showed superior performance of TMLE relative to misspecified parametric models, in comparison with A-IPTW, IPTW and G-computation.	Pro
van der Laan and Gruber40	Targeted minimum loss based estimation of causal effects of multiple time point interventions	2012	In the setting of multiple time point interventions, showed TMLE outperformed IPTW and MLE estimators.	Pro
Porter, et al.41	The relative performance of targeted maximum likelihood estimators	2011	Showed relatively superior performance of C-TMLE relative to A-IPTW estimators particularly when there are covariates that are strongly associated with the missingness, while being weakly or not at all associated with the outcome.	Pro
Wang, et al42	Finding quantitative trait loci genes with collaborative targeted maximum likelihood learning	2011	Based on actual genetic data, results suggested greater robustness of findings using C-TMLE relative to parametric approaches for high throughput genetic data.	Pro
Díaz and van der Laan43	Population intervention causal effects based on stochastic interventions	2011	Paper focused on new estimators for stochastic (eg, shift) interventions relevant to estimating causal effects of continuous interventions. In their simulation, they did not observe significant differences between the TMLE and the A-IPTW.	Neutral
Gruber and van der Laan44	An application of collaborative targeted maximum likelihood estimation in causal inference and genomics	2010	Showed more robust performance in high-dimensional simulations comparing TMLE to estimating equation approaches (A-IPTW).	Pro
Stitelman and van der Laan45	Collaborative Targeted Maximum Likelihood for Time to Event Data	2010	The results show that, compared with TMLE, IPTW, and A-IPTW, the C-TMLE method does at least as well as the best estimator under every scenario and, in many of the more realistic scenarios, behaves much better than the next best estimator in terms of both bias and variance.	Pro
Moore and van der Laan46	Covariate adjustment in randomized trials with binary outcomes: targeted maximum likelihood estimation	2009	Demonstrated how the use of covariate information in randomized clinical trials could use the TMLE framework, which results in improved performance, without bias, relative to standard methods.	Pro
Rose and van der Laan47	Simple optimal weighting of cases and controls in case-control studies	2008	IPTW method for causal parameter estimation was outperformed in conditions similar to a practical setting by the new case-control weighted TMLE methodology.	Pro

Note: The Pro/Con column refers to a simple binary classification of the relative performance of the TMLE estimators reported in the paper, “Pro” indicating that the TMLE performed superior to other competing estimators.

2 ∣. BACKGROUND

As large and complex data sets have become increasingly more commonplace, traditional parametric approaches can suffer from a large bias when the assumed functional form is different from the truth. This has led to machine learning (ML) taking a more central role in deriving estimators of causal impacts in very big statistical models (semi-parametric). The theory for the use of ML in the estimators discussed herein has been continuously refined, from developing double robust estimators (both A-IPTW and TMLE substitution estimators) to augmentations of these estimators that are more robust to the overfitting potentially introduced by flexible ML fits. The latter modifications to the original estimators are the cross-validated TMLE (or CV-TMLE, chapter 27 in van der Laan¹⁰ and Zheng⁴⁸), and subsequently the proposal for an analogous modification to estimating equation approaches (double machine learning or cross-fitting⁴⁹).

While simulation studies have investigated all of these estimators, they have yet to be analyzed together in a single series of realistic simulation studies. Here, we seek to determine how well these estimators perform in realistic settings, under which conditions they perform best, which augmentations provide the most robustness, and whether or not the results support more general recommendations. In addition, there exist other choices of target parameter when the one being analyzed fails to have adequate performance for any of the competing estimators, such as realistic rules.⁵⁰ A recently developed machine learning algorithm (the highly adaptive lasso; HAL⁵¹), is potentially an important improvement in constructing realistic data-generating distributions (DGD) for simulation studies such as ours. It can be optimally undersmoothed to dependably generate efficient estimates of the actual data generating distributions. HAL is particularly well suited to these types of simulations, as it uses a very large nonparametric model and can be tuned to be as flexible as the data support. In this article, we explore the use of undersmoothed HAL as a basis in conducting realistic data-inspired simulations. The results suggest the proposed use of HAL for realistic data-generating simulations could provide a general method for choosing between machine-learning-based estimators for a particular parameter and data set.

We first introduce the data sets that were selected to motivate our realistic simulations, describe the steps taken for simulating data, including a short description of the estimators tested, and discuss the results. The simulations suggest a general recommendation for the use of an additional layer of cross-validation (CV-TMLE and CV-A-IPTW) to ensure robust inference in finite samples.

3 ∣. METHODS

3.1 ∣. Study selection

We utilized data from ten nutrition intervention trials conducted in Africa and South Asia. In all studies, the measured outcome was a height-to-age Z-score for children from birth to 24 months, which was calculated using World Health Organization (WHO) 2006 child growth standards.⁵² Details about the resulting composite data, study design and data processing, can be found in companion technical reports.^19,53,54 All interventions were nutrition-based, and for the purposes of this analysis, multilevel interventions were simplified to a binary treatment variable (eg, nutrition intervention—yes/no). Although different baseline covariates were measured among these studies, there was significant overlap. The sample size of each study is shown in Table 2. We anonymized the study IDs and removed the location information due to confidentiality concerns. Details on each study can be found in the shuffled list in Appendix B.

TABLE 2.

Dimensions of datasets of nutrition intervention trials, with $n$ representing the number of children in sample and $p$ being the number of covariates

Study ID	$\mathit{n}$	$\mathit{p}$
1	418	20
2	4863	26
3	7399	22
4	1204	36
5	2396	42
6	3265	18
7	1931	38
8	840	30
9	27 275	42
10	5443	35

3.2 ∣. Data processing

Data from each study was cleaned and processed for this analysis. Our goal for defining the analysis data used to simulate is different from the goals of the original studies and thus our data processing might differ from that used in the resulting publications of the study results. We note that the data are used to motivate the simulations, but, since we define the true DGD to be one that we estimate for each study, and at that point differences with the original study become irrelevant to our comparisons of estimators. Data was filtered down to the last height-to-age Z-score measurement taken at the end of each study for each subject. Subjects were dropped if either their treatment assignment $(A)$ or outcome measurement $(Y)$ were missing. For covariates $(W)$ that were missing, those that were continuous and discrete were imputed using the median and mode, respectively. In both cases, missingness indicator variables were added to the data set for each covariate with missing rows. As mentioned above, the treatment assignment variable $(A)$ was binarized if it consisted of more than two treatment arms. The control and treatment groups were originally assigned in each study as described in Appendix B.

3.3 ∣. Simulation with undersmoothed highly adaptive lasso

To make the simulation more realistic, we want to simulate data from a distribution which is “close” to the true distribution that generates the observed data. Here, “close” means a rich set of target parameters of the simulated distribution are efficient estimators of the true target parameters. To that end, we estimate the true data distribution with the undersmoothed highly adaptive lasso, which is known to efficiently estimate smooth features of the true data distribution and also approximates the true data density at a rate $n^{-1∕3}$ up to $log(n)$ factors.⁵⁵ Another reason for using undersmoothed highly adaptive lasso instead of other popular methods is that we want to keep the simulation independent of the estimation by avoiding using same algorithms for both.

It is also worth pointing out that the simulation method proposed in this analysis is not the only option. Since the simulation process should serve as a black box that generates data for estimation later, one can use any other valid methods to implement real data based simulation and evaluate the estimators with that. Below we introduce our method in Section 3.3.1, the data simulating process in Section 3.3.2, and the true effect calculation in Section 3.3.3.

3.3.1 ∣. Undersmoothed highly adaptive lasso

Highly adaptive lasso (HAL) is a nonparametric regression estimator, which is capable of estimating complex functional parameters with mild assumptions that the true functional parameter is right-hand continuous with left-hand limits and has variation norm smaller than a constant, but neither relies upon local smoothness assumptions nor is constructed using local smoothing techniques.⁵¹ HAL has been shown to have competitive finite-sample performance relative to many other popular machine learning algorithms.⁵¹ The HAL estimator can be represented in the following form (the zeroth-order formulation^51,55):

$${\psi }_{\beta }={\beta }_0+\sum _{s\subset \{1,2,\dots ,p\}}\sum _{i=1}^n{\beta }_{s,i}{\varphi }_{s,i}\text{with}{\beta }_0+\sum _{s\subset \{1,2,\dots ,p\}}\sum _{i=1}^n\mid {\beta }_{s,i}\mid <C,$$

where $n$ is the sample size, $p$ is the number of covariates, $s$ denotes any subset of $\{1,2,\dots ,p\}$, and ${\varphi }_{s,i}:x_s\mapsto I({\tilde{x}}_{s,i}\le x_s)$ are the indicator basis functions defined by the support points ${\tilde{x}}_{s,i}$ from the observations. In other words, the HAL estimator constructs a linear combination of indicator basis functions to minimize the loss-specific empirical risk under the constraint that the $L_1$-norm of the vector of coefficients is bounded by a finite constant matching the sectional variation norm of the target functional.⁵⁶

Depending on the dimension of the data, the HAL estimator might start with a very large number (the size of the double sum in the equation above is at most $n\ast (2^p-1)$) of basis functions. In practice, when some covariates are categorical or binary, the number of unique basis functions will be much fewer. Moreover, the dimension of basis functions can be restricted in practice. For example, one can consider only main-term indicators for each of the original predictors as well as all second order tensor products (interaction terms involving the main effect terms). As for selecting the $L_1$-norm, one can use cross-validation to optimize the fit of the model to future observations from the DGD.

In addition to the standard implementation of HAL, in which the $L_1$-norm is selected with cross-validation, we undersmooth the HAL fit by updating the $L_1$-norm adaptively based on a criterion that guarantees that it will be efficient for a class of smooth features of the data density (see next paragraph and the Algorithm 1 below for more details). We call this whole process the undersmoothed HAL. It has been recently shown that undersmoothed HAL can yield asymptotically efficient estimators for functionals of the relevant portions of the DGD while preserving the same rate of convergence, and also solving the efficient score equation for any desired path-wise differentiable target feature of the data distribution.⁵⁵ This nice property is achieved by the fact that undersmoothed HAL is capable of solving lots of score equations in the form of the product of the basis functions and the residual, and thereby solving the linear combination of these score equations. This motivates the use of undersmoothed HAL in our settings; that is, to estimate the DGD by undersmoothed HAL in a way that optimally preserves the relevant functionals. More intuitively, HAL, with the properly chosen $C$, will result in a DGD for simulations that is as close as one can get nonparametrically to the true DGD, in the sense that a set of target parameters of the simulated distribution are efficient estimators of the true parameters Therefore, the key difference between using undersmoothed HAL and other methods (parametric models, sampling from the empirical, ML) for simulation is that the former captures the features of interest instead of mimicking the distributions of variables. More technical details can be found in van der Laan, Benkeser and Cai.⁵⁵ Thus, we argue that it can serve as the basis of a realistic simulation where one wishes to compare estimators for the data in hand.

In our study, the stopping criterion for this undersmoothing process is to iteratively increase the initial $L_1$-norm bound $C_{cv}$ (or equivalently decrease the penalty parameter $\lambda$) and refit the HAL model until the score equations formed by the product of basis functions and residuals are solved at the rate of $\frac{{\sigma }_n}{\sqrt{n}\log (n)}$.⁵⁷ Namely, for all basis functions ${\varphi }_{s,i}$ from the initial HAL fit, we want:

$$\mid P_n\left({\varphi }_{s,i}(Y-{\overline{Q}}_{n,C})\right)\mid \le \frac{{\sigma }_n}{\sqrt{n}\log (n)},$$ (1)

where $P_n$ is the empirical average function and ${\sigma }_n^2=Var\left({\varphi }_{s,i}(Y-{\overline{Q}}_{n,C_{cv}})\right)$. We provide more detailed justification for choosing this criterion in Appendix C.

Algorithm 1. Undersmoothing procedure

$$\begin{array}{cc}\hfill & \mathrm{Require}:\hfill \\ \hfill & \text{Observed outcome}{y}_k\text{from data},k=1,2,\dots ,n.\hfill \\ \hfill & \text{Penalty parameter}{\lambda }_{cv},\text{basis functions}{\varphi }_{s,l},\text{and predictions}{\widehat{y}}_{{\lambda }_{cv}}\text{from the initial HAL fit}.\hfill \\ \hfill & \text{Let}S\text{denote the set of basis functions}{\varphi }_{s,l}\text{with nonzero coefficients from the initial HAL fit}.\hfill \\ \hfill & \text{Let}ϵ\text{be a small positive number}.\hfill \\ \hfill & {\sigma }_n=\sqrt{\frac{1}{n}\sum \begin{array}{c}n\hfill \\ k=1\hfill \end{array}[(y_k-{\widehat{y}}_{{\lambda }_{cv}}){\varphi }_{s,l}-\frac{1}{n}\sum \begin{array}{c}n\hfill \\ k=1\hfill \end{array}(y_k-{\widehat{y}}_{{\lambda }_{cv}}){\varphi }_{s,l}{]}^2}\forall {\varphi }_{s,l}\in S\hfill \\ \hfill & \lambda ={\lambda }_{cv}\hfill \\ \hfill & \mathbf{while}{\max }_S\mid \frac{1}{n}\sum \begin{array}{c}n\hfill \\ k=1\hfill \end{array}[(y_k-{\widehat{y}}_{\lambda }){\varphi }_{s,l}]\mid ∕{\sigma }_n>\frac{1}{\sqrt{n}\log (n)}\mathbf{do}\hfill \\ \hfill & \lambda =\lambda -ϵ\hfill \\ \hfill & \text{Refit HAL with}\lambda \hfill \\ \hfill & \text{Obtain new predictions}{\widehat{y}}_{\lambda }\text{frome the update HAL fit}\hfill \\ \hfill & \mathbf{end}\mathbf{while}\hfill \end{array}$$

In practice, we speed up the algorithm by controlling the number of basis functions in the initial HAL fits. First, we set the maximum interaction degree to $\mathbb{I}(p\ge 20)\ast 2+\mathbb{I}(p<20)\ast 3$, where $p$ is the number of covariates. Second, we use binning method to restrict the maximum number of knots to $\sqrt{n}∕(2^{d-1})$ for the d^th degree basis functions. These hyperparameters can be set through the hal9001 package.^58,59 We make the decisions on hyperparameters based on two factors: they can help form a rich model with complex interaction terms and the computing time is acceptable. To make it more rigorous, a cross-validation-based tuning procedure can be considered in future practice.

In Appendix A, we provide a list showing the variables included in the $Q$ models after undersmoothing (Table A1).

3.3.2 ∣. Data generating process

The DGD for each study was based upon the following structural causal model (SCM):

$$\begin{gathered} W=f_W(U_W), \\ A=f_A(W,U_A), \\ Y=f_Y(W,A,U_Y), \end{gathered}$$

where $W$, $A$, and $Y$ are, in time ordering, the confounders, the binary intervention of interest and the outcome, respectively, with the $U$ exogenous independent errors and deterministic functions, $f.$. Specifically, the following steps were taken:

1. Covariates $W$ were sampled with replacement from the study data sets with sample size $n$, where $n$ is the size of the original data set.

2. Apply the undersmoothed HAL procedure twice to the observed data: first fit the model with $A$ as the outcome and $W$ as covariates, then fit the model with $Y$ as the outcome and $A$ and $W$ as covariates.

3. The first undersmoothed HAL fit was then used to predict $\mathbb{P}(A=1\mid W)$. The simulated $A$ was then sampled using a binomial distribution with the predicted $\mathbb{P}(A=1\mid W)$.

4. The second undersmoothed HAL fit was then used to predict $Y$ given the sampled $W$ and simulated $A$. Then we simulate $Y$ by adding random errors drawing from $𝒩(0,{\tilde{\sigma }}^2)$ to the predictions, where ${\tilde{\sigma }}^2$ is the residual variance of this undersmoothed HAL fit.

Note, we could have used other ways of estimating the error distribution in step 4, including density estimation using HAL,⁶⁰ but we left this for future studies.

Steps 1 through 4 were repeated 500 times to generate the data sets for each simulation. For each of the study data (Table 2), we repeated these steps and analyzed the performance of the competing estimators separately by study.

3.3.3 ∣. Target parameter

Our treatment variable $A$ is binary, and our outcome $Y$ is continuous, indicating a height-to-age Z-score. $W$ represents the measured covariates in each study. The data structure is defined as: $O=(W,A,Y)\sim {\mathbb{P}}_0\in ℳ$ with $n$ independent and identically distributed (i.i.d.) observations $O_1,\dots ,O_n$, where $ℳ$ denotes the set of possible probability distributions of ${\mathbb{P}}_0$. The target parameter is a feature of ${\mathbb{P}}_0$ that is our quantity of interest.²⁹ We selected as our target parameter the average treatment effect (ATE), or ${\Psi }^F({\mathbb{P}}_{U,X})={\mathbb{E}}_{U,X}(Y(1)-Y(0))$, ${\mathbb{P}}_{U,X}\in {ℳ}^F$; where ${ℳ}^F$ denotes the collection of possible distributions of $(U,X)$ as described by the SCM, and $Y(a)$ is the outcome for a subject if, possibly contrary to fact, they received nutrition intervention $A=a$. Given we simulated the data based upon on our causal model, under randomization assumption and positivity assumption we can show that this causal parameter is identified by the following statistical estimand:⁶¹

$$\Psi ({\mathbb{P}}_0)={\mathbb{E}}_{W,0}[{\mathbb{E}}_0(Y\mid A=1,W)-{\mathbb{E}}_0(Y\mid A=0,W)].$$

We calculate the true ATE value for each study by first randomly drawing a large number of observations (N = 50 000) from the empirical of $W$ and using:

$${\psi }_0=\frac{1}{N}\sum _{i=1}^N[{\mathbb{E}}_0(Y\mid A=1,W)-{\mathbb{E}}_0(Y\mid A=0,W)],$$

where we define the ${\mathbb{E}}_0(Y\mid A=1,W)$ and ${\mathbb{E}}_0(Y\mid A=0,W)$ term using the fitted undersmooth HAL model. Note that our simulation process insures the randomization assumption is true and there is no asymptotic violation of the positivity assumption. However, there can be practical violations of positivity (close to 0 or 1 estimated probabilities of getting treatment for some observations given the $W$) which can deferentially impact estimator performance.

3.4 ∣. The estimation problem

The target parameter depends on the true DGD, ${\mathbb{P}}_0$, through the conditional mean ${\overline{Q}}_0(A,W)={\mathbb{E}}_0(Y\mid A,W)$ and the marginal distribution $Q_{W,0}={\mathbb{P}}_0(W)$ of $W$, so we can write $\Psi (Q_0)$, where $Q_0=({\overline{Q}}_0,Q_{W,0})$. Our targeted learning estimation procedure begins with estimating the relevant part $Q_0$ of the data-generating distribution ${\mathbb{P}}_0$ needed for evaluating the target parameter.⁶²

The two general methods we compare are substitution and estimating equation estimators. Depending on the specific estimator, they can depend on estimators of the propensity score, $g_0(W)=\mathbb{P}(A=1,W)$, the outcome model, $Q_0(A,W)$, and sometimes both. We use consistent settings when modeling the outcome and the propensity score via super learner (see Section 3.8 below for details).

The estimators we compare are not exhaustive and new methods will be developed, so such studies will continue to be important sources of information for deciding what to do in practice. We quickly describe the particular estimators compared in our study below.

3.5 ∣. Inverse probability of treatment weighting estimator

The inverse probability of treatment weighting (IPTW) is a method that relies on estimates of the conditional probability of treatment given covariates $g(W)=\mathbb{P}(A=1\mid W)$, referred to as the propensity score.⁶³ After it is estimated, the propensity score is used to weight observations such that a simple weighted average is a consistent estimate of the particular causal parameter if the propensity score model is consistent.²⁹ For the ATE (if $g$ were known) the weight is $\frac{A}{g(W)}+\frac{1-A}{1-g(W)}$.

The average treatment effect is then estimated by:⁶⁴

$${\psi }_{IPTW,n}=\frac{1}{n}\sum _{i=1}^n\left(\frac{A_i}{g_n(W_i)}\ast Y_i\right)-\frac{1}{n}\sum _{i=1}^n\left(\frac{1-A_i}{(1-g_n(W_i))}\ast Y_i\right),$$

where $g_n(W)$ is the estimate of the true propensity score $(g_0(W))$. IPTW is not a double robust estimator, in that its consistency depends on consistent estimation of the propensity score.⁹ As it is not a substitution estimator, it is not as robust to sparsity.²⁹ However, it is a commonly used estimator of the ATE, and its form and relationship to well-known inverse probability methods in the analysis of survey data make it relatively popular.

We derived statistical inference using a conservative standard error which assumes that $g$ is known (there is an extensive literature on IPTW estimators, but⁹ is a good reference for technical details). Specifically, the standard error for this estimator was constructed by multiplying $1∕\sqrt{n}$ by the standard deviation of the plug-in resulting influence curve:

$$Y\left[\frac{A}{g_n(W)}-\frac{1-A}{1-g_n(W)}\right]-{\psi }_{IPTW,n}.$$

Since IPTW estimator has many problems such as not invariant to location transformation of the outcome and suffering from the extreme predictions of $g(W)$ (close to 0 or 1), we use the Hajek/stabilized IPTW² by normalizing the weights of $Y$ as follows:

$${\psi }_{IPTW-Hajek,n}=\frac{\sum _{i=1}^n\left(\frac{A_i}{g_n(W_i)}\ast Y_i\right)}{\sum _{i=1}^n\left(\frac{A_i}{g_n(W_i)}\right)}-\frac{\sum _{i=1}^n\left(\frac{1-A_i}{1-g_n(W_i)}\ast Y_i\right)}{\sum _{i=1}^n\left(\frac{1-A_i}{1-g_n(W_i)}\right)}.$$

3.5.1 ∣. Cross-validated inverse probability of treatment weighting (CV-IPTW) estimator

To avoid problems that arise when $g(W)$ is overfit, we also implemented the CV-IPTW estimator by adding another layer of cross-validation when estimating the propensity score.⁴⁹ Specifically, the same SL fitting procedure was implemented on training sets. Then, we use this estimate of $g$ on the corresponding validation sets; as such, we employ a nested cross-validation. In practice, we used the “Split Sequential SL” method, an approximation to the nested cross-validation proposed by Coyle,⁶⁵ to speed up the estimation while obtaining similar results to standard nested cross-validation. More details on the implementation can be found in Section 3.8 below.

3.6 ∣. Augmented inverse probability of treatment weighted (A-IPTW) estimator

The other estimating equation method included in our study is an augmented version of the IPTW estimator, aptly named the augmented inverse probability of treatment weighted (A-IPTW) estimator.⁶⁶ It is a double robust estimator that is consistent for the ATE as long as either the propensity score model $(g_0(W))$ or the outcome regression $(Q_0(A,W))$ is correctly specified. When compared with the IPTW estimator in a Monte Carlo simulation, A-IPTW typically outperformed IPTW with a lower mean squared error when either the propensity score or outcome model was misspecified.⁶⁶

Intuitively, the A-IPTW improves upon IPTW by fully utilizing the information in the conditioning set of covariates $W$, which contains both information about the probability of treatment and information about the outcome variable.⁶⁶ More formal justification comes from the fact that the A-IPTW estimator arises as the solution to the efficient influence curve (a key quantity in semiparametric theory), and thus is locally efficient if both $Q$ and $g$ are correctly specified.

For the ATE, A-IPTW estimator solves the mean of the empirical efficient influence curve and can be expressed explicitly for the average treatment effect as follows:

$${\psi }_{A-IPTW}=\frac{1}{n}\sum _{i=1}^n\left(\left[\frac{A_i{Y}_i}{g(W_i)}-\frac{(1-A_i)Y_i}{1-g(W_i)}\right]-\frac{(A_i-g(W_i))}{g(W_i)(1-g(W_i))}\left[(1-g(W_i))\mathbb{E}(Y_i\mid A_i=1,W_i)+g(W_i)\mathbb{E}(Y_i\mid A_i=0,W_i)\right]\right).$$

The standard error for this estimator was constructed by multiplying $1∕\sqrt{n}$ by the standard deviation of the plug-in efficient influence curve:

$$(Y-{\overline{Q}}_n(A,W))\left[\frac{A}{g_n(W)}-\frac{1-A}{1-g_n(W)}\right]+({\overline{Q}}_n(1,W)-{\overline{Q}}_n(0,W))-{\psi }_{A-IPTW,n}.$$

where ${\overline{Q}}_n(\cdot ,W)$ is the estimate of the true conditional mean ${\overline{Q}}_0(\cdot ,W)$.

3.6.1 ∣. Cross-validated augmented inverse probability of treatment weighted (CV-A-IPTW) estimator

Similar to CV-IPTW, to avoid overfitting of the outcome model $(Q)$ or propensity score model $(g)$, we implemented the CV-A-IPTW estimator by adding another layer of cross-validation when estimating the $Q$ and $g$. In practice, as discussed above for the IPTW estimator, we used the “Split Sequential SL” method proposed by Coyle⁶⁵ to speed up the estimation (for more details, see Section 3.8 below).

3.7 ∣. Targeted maximum likelihood estimator (TMLE)

The targeted maximum likelihood estimator (TMLE) is an augmented substitution estimator that, in context of the ATE, adds a targeting step to the original outcome model fit to optimize the bias-variance trade-off for the parameter of interest.⁶² Similar to A-IPTW, TMLE is doubly robust, producing consistent estimates if either ${\overline{Q}}_n(A,W)$ is consistent for ${\overline{Q}}_0(A,W)$ (ie, ${\mathbb{E}}_0(Y\mid A,W)$) or $g_n(W)$ is consistent for $g_0(W)$ (ie, ${\mathbb{P}}_0(A=1\mid W)$). It is asymptotically efficient when both quantities are consistently estimated and $\Vert {\overline{Q}}_n-{\overline{Q}}_0{\Vert }_2\Vert {\overline{g}}_n-{\overline{g}}_0{\Vert }_2$ converges to zero at faster rate than $1∕\sqrt{n}$ (chapter 5 in van der Laan¹⁰). As it is a substitution estimator, it is typically more robust to outliers and sparsity than EE estimators.²⁹ A finite sample advantage over estimating equation methods comes from the fact that the estimator respects constraints on the parameter bound, such as ensuring that an estimated probability in the [0, 1] range.⁶²

The TMLE, like the A-IPTW estimator, requires preliminary estimates of both $g$ and $Q$. The first step in TMLE is finding an initial estimate of the relevant part $Q_0$ of data-generating distribution ${\mathbb{P}}_0$. For all estimators, we use an ensemble machine learning algorithm, the Super Learner (SL) algorithm. This avoids arbitrarily using a single algorithm and ensures that the corresponding fit will be optimal (with respect to the true risk) relative to the candidate algorithms used in the estimation. Once this initial estimate has been found, TMLE updates the initial fit to make an optimal bias-variance trade-off for the target parameter.⁶²

For the ATE, the TMLE first requires ${\overline{Q}}_n(A,W)$, the estimate of the conditional expectation of the outcome given the treatment and covariates ${\overline{Q}}_0(A,W)$.²⁹ Next is the targeting step for optimizing the bias-variance trade-off for the parameter of interest. The propensity score $(g_0)$ can also be estimated with a flexible algorithm like the super learner,⁶⁷ and these fits are used to predict the conditional probability of treatment and no treatment for each subject $(g_n(W),1-g_n(W))$. These probabilities are used for updating the initial estimate of the outcome model. This updated estimate is then used to generate potential outcomes for when $A=1$ and $A=0$. Like the G-computation estimator, the TMLE estimate of the ATE is calculated as the mean difference between these pairs.²⁹

With the ATE as our target parameter, the Super Learner substitution estimator is:¹⁰

$${\psi }_{MLE,n}=\Psi (Q_n)=\frac{1}{n}\sum _{i=1}^n[{\overline{Q}}_n^0(1,W_i)-{\overline{Q}}_n^0(0,W_i)],$$

where $Q_n$ is the estimate of $Q_0$ and ${\overline{Q}}_n^0(\cdot ,W)$ the initial estimate of ${\overline{Q}}_0(\cdot ,W)$.

The next step is to update the estimator above toward the parameter of interest. The targeting process uses $g_n$ in a so-called clever covariate to define a one-dimensional model for fluctuating the initial estimator. The clever covariate is defined as:

$$H_n^{\ast }(A,W)=\left(\frac{I(A=1)}{g_n(W)}-\frac{I(A=0)}{1-g_n(W)}\right).$$

A simple, one-variable logistic regression is then run for the outcome $Y$ on the clever covariate, using $logit{\overline{Q}}_n^0(A,W)$ as the offset to estimate the fluctuation parameter $ϵ$. This is used for updating the initial estimate ${\overline{Q}}_n^0$ into a new estimate ${\overline{Q}}_n^1$ as follows:

$$logit{\overline{Q}}_n^1(A,W)=logit{\overline{Q}}_n^0(A,W)+{ϵ}_n{H}_n^{\ast }(A,W),$$

where ${ϵ}_n$ is the estimate of $ϵ$.

The updated fit is used to calculate the expected outcome under $A=1({\overline{Q}}_n^1(1,W))$ and $A=0({\overline{Q}}_n^1(0,W))$ for all subjects. These estimates are then plugged into the following equation for the final TMLE estimate of the ATE:

$${\psi }_{TMLE,n}=\Psi (Q_n^{\ast })=\frac{1}{n}\sum _{i=1}^n[{\overline{Q}}_n^1(1,W_i)-{\overline{Q}}_n^1(0,W_i)].$$

The fitting of both the $Q$ and $g$ models to the entire data set for the substitution estimator requires entropy assumptions on the fits and underlying true models. It is possible to violate this assumption by an overfit of the models of the DGD, and this can occur even when cross-validation is used to choose the resulting fits (though, this helps tremendously). One can generalize both the estimating equation approach and TMLE to estimators that do not need these entropy assumptions by inclusion of an additional layer of cross-validation (similar idea on sample splitting was mentioned in Bickel, Klaassen, and Robins^68-70). This has also been described as double-machine learning in the context of estimating equations,⁴⁹ though it had previously been proposed as a way of robustifying the TMLE.^10,48

The standard error estimate for TMLE can be constructed by multiplying $1∕\sqrt{n}$ by the standard deviation of the plug-in efficient influence curve:

$$(Y-{\overline{Q}}_n(A,W))\left[\frac{A}{g_n(W)}-\frac{1-A}{1-g_n(W)}\right]+({\overline{Q}}_n(1,W)-{\overline{Q}}_n(0,W))-{\psi }_{TMLE,n}.$$

3.7.1 ∣. Cross-validated targeted maximum likelihood estimation (CV-TMLE)

Though TMLE is a doubly robust and efficient estimator, its performance suffers when the initial estimator is too adaptive.¹⁰ Intuitively, if the initial estimator of $Q$ is overfit, there is not realistic residual variation left for the targeting step and the update is unable to reduce residual bias.

To address these shortcomings of TMLE, cross-validated targeted maximum likelihood estimation (CV-TMLE) was developed.⁴⁸ This modified implementation of TMLE utilizes 10-fold cross-validation for the initial estimator to make TMLE more robust in its bias reduction step. The result is that one has greater leeway to use adaptive methods to estimate components of the DGD while keeping realistic residual variation in the validation sample.

Whereas CV-TMLE can add robustness by making the estimator consistent in a larger statistical model, there is still another way for finite sample performance issues to enter estimation. Specifically, if the data suffers from a lack of experimentation such that $g_n(W)$ gets too close to 0 or 1, then the estimator can begin to suffer from the unstable inverse weighting in the targeting step, a violation “positivity”. There are simple methods to avoid this, by choosing a fixed truncation point, such as truncating the estimate of $g:g_n^{\ast }=\max (\text{min}(1-\delta ,g_n),\delta )$, for some small $\delta$ (typical value is $\delta =0.025$). However, there exists a more sophisticated method that does a type of model selection in estimating the $g$ model which prevents the update from hurting the fit of the $Q$ model. This is an area of active research and several collaborative-TMLE (C-TMLE) estimators have been proposed, including adaptive selection of the truncation level $\delta$.^23,62

3.7.2 ∣. Collaborative targeted maximum likelihood estimation (C-TMLE)

Collaborative targeted maximum likelihood estimation (C-TMLE) is an extension of TMLE. In the version used for estimation in this study, it applies variable/model selection for nuisance parameter (eg, the propensity score) estimation in a “collaborative” way, by directly optimizing the empirical metric on the causal estimator.⁷¹ In this case, we used the original C-TMLE proposed by van der Laan and Gruber,⁷¹ which is also called “the greedy C-TMLE algorithm”. It consists of two major steps: first, a sequence of candidate estimators of the nuisance parameter is constructed from a greedy forward stepwise selection procedure; second, cross-validation is used to select the candidate from this sequence which minimizes a criterion that incorporates a measure of bias and variance with respect to the targeted parameter.⁷¹ More recent development on C-TMLE includes scalable variable-selection C-TMLE²² and glmnet-C-TMLE algorithm,⁷² which might have improved computational efficiency in high-dimensional setting.

3.8 ∣. Computation

Our simulation study was coded in the statistical programming language R.⁷³ We used hal9001^58,59 and glmnet⁷⁴ packages to generate the data via undersmoothed HAL. We used sl3,⁷⁵ tmle3⁷⁶ and ctmle⁷⁷ packages to implement each of the estimators described above. To estimate the propensity score and the conditional expectation of the outcome, linear models, mean, GAMv (general additive models),⁷⁸ ranger (random forest),⁷⁹ glmnet (lasso), and XGBoost⁸⁰ with different tuning parameters were used to form the SL library. For “Study 9”, we dropped GAM and ranger from the learner library to improve the computational efficiency. Ten-fold cross-validation was chosen by default of sl3 package for every SL fit. We used logistic regression meta-learner for propensity scores, and non-negative least squares meta-learner for estimating conditional expectation of the outcome. We truncated the propensity score estimates $g_n(W)$ between [0.025,0.975] for all estimators.

Theoretically, when constructing CV-TMLE, CV-IPTW, and CV-A-IPTW estimators, we need to implement nested SL by adding one more layer of cross-validation. Namely, we first split the data, then fit the SL model (which itself uses a cross-validation) on the training set and make predictions on the validation set. Then we rotate the roles of the validation set and finally obtain a vector of cross-validated predictions of propensity scores and conditional expectations. As discussed above, in practice we used the “Split Sequential SL” approximation method proposed by Coyle.⁶⁵

After we estimated the relevant parts of the DGD separately for each of the data study data using undersmoothed HAL, the resulting fits were used to simulate data 500 times for each of the 10 studies. Details of the implementation, including the code, can be found in the GitHub repository: https://github.com/HaodongL/realistic_simu.git

4 ∣. RESULTS

4.1 ∣. Undersmoothed HAL models and the true average treatment effect

We implemented undersmoothed HAL on the real data and used the fitted model to generate sample for each simulation. Details of each model and the resulting true ATE values are presented in Table 3.

TABLE 3.

Statistics of the undersmoothed HAL fits to the individual studies, including the sample size, dimension, and number of basis functions used for the treatment model $(g)$ and the corresponding outcome model $(Q)$, the corresponding lambda penalty and the resulting $L_1$ norm

Study ID	$\mathit{n}$	$\mathit{p}$	TrueATE	Model	Undersmoothed	Num. coef.	Lambda_cv	Lambda	${\mathit{L}}_1$-norm_cv	${\mathit{L}}_1$-norm
				Q	T	167	2.6e+02	2.4e+01	5.0e−04	5.6e−03
1	418	20	−0.0109	g	T	180	7.7e+00	7.2e−01	1.6e−02	6.2e−02
				Q	T	1747	4.4e−01	3.1e−02	2.9e−02	4.5e−01
2	4863	26	0.0507	g	T	124	4.8e+00	3.9e−01	2.8e−04	1.4e−02
				Q	T	1496	2.3e−01	3.0e−02	3.5e−02	1.9e−01
3	7399	22	0.0007	g	T	6	5.2e+01	2.6e+01	7.0e−07	1.6e−03
				Q	T	503	4.9e+01	2.3e+00	5.0e−04	2.1e−02
4	1204	36	−0.0468	g	T	5	1.8e+03	3.8e+02	6.0e−07	2.2e−06
				Q	T	448	1.2e+02	4.5e+00	1.0e−04	6.9e−03
5	2396	42	−0.0136	g	T	15	8.5e+02	1.8e+02	7.0e−07	9.0e−06
				Q	T	2724	5.9e+00	3.9e−01	4.8e−03	7.6e−02
6	3265	18	0.2523	g	T	497	8.6e+00	1.1e+00	1.9e−03	2.4e−02
				Q	T	2274	5.7e−01	2.3e−02	7.6e−02	1.7e+00
7	1931	38	−0.0310	g	F	0	9.7e+01	9.7e+01	0.0e+00	0.0e+00
				Q	T	138	1.2e+01	1.4e+00	2.0e−03	2.1e−02
8	840	30	−0.0442	g	F	0	1.1e+02	1.1e+02	0.0e+00	0.0e+00
				Q	T	3700	5.4e+00	1.8e−01	2.2e−03	3.1e−02
9	27275	42	0.0089	g	T	102	1.9e+02	2.7e+01	2.2e−06	7.9e−06
				Q	T	503	1.0e+01	1.2e+00	9.0e−04	7.3e−03
10	5443	35	0.0203	g	F	0	3.5e+03	3.5e+03	0.0e+00	0.0e+00

Note: Lambda_cv and $L_1$-norm_cv from the initial HAL fit are also listed for comparison.

For Study 7, 8, and 10, the initial HAL fits of $g$ models contain no variables, so one $A$ is randomized as in a clinical trial. Thereby, the undersoomthing process for g model was omitted for these three studies, and the initial HAL models were used instead. This is not surprising since all ten studies were randomized controlled trials (RCT). Grouping categorical intervention variables into binary variables at data cleaning step might preserve or change the randomization. The remainder of the studies included basis functions in $W$ and so are more akin to observational studies. However, most of the HAL fits of $g$ are lower dimensional than the HAL fit of $Q$, thereby making these simulations not representative of studies in which the treatment mechanism is associated with measured confounders in complex ways. For Study 7, 8, and 10, we also compare the performance of the estimators above with the standard difference-in-means estimates, which is also provides consistent estimators for the ATE for these three data-generating distributions. On the other hand, the counts of nonzero coefficients (“Num.coef.” in Table 3) in the undersmoothed $Q$ models are large for the remaining studies, and so, regardless of the original treatment mechanism that underlied these studies, these ones do not come from a simple treatment randomization model. The details on the variables included after undersmoothing can be found in Table A1.

4.2 ∣. Estimators’ performance

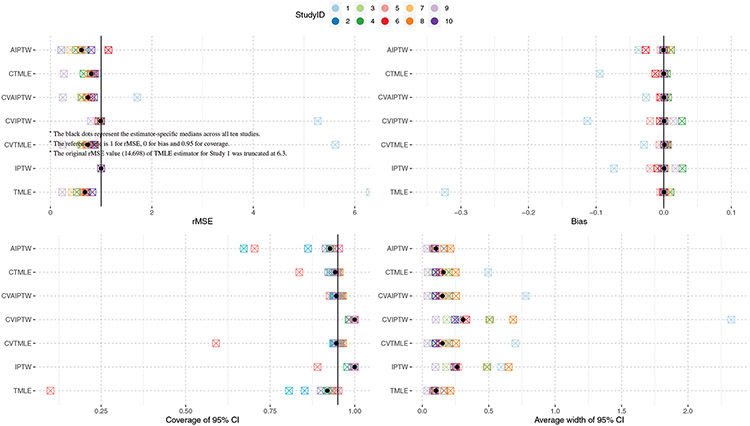
The results are shown in Figure 1 and Table 4. Variance dominates bias for all estimators and so contributes overwhelmingly to the mean squared error (MSE) and the relative MSE (rMSE), where rMSE was relative to the IPTW estimator’s MSE. Putting aside Study 1 for now, the MSE/rMSE results suggest that the A-IPTW generally is more efficient than the other estimators, the TMLE, CV-TMLE, CV-A-IPTW, and C-TMLE with similar MSE to each other, and the IPTW and CV-IPTW having more erratic performance. The bar plots of the main performance metrics in Table 4 can be found in the Appendix A (see Figures A1-A5)

FIGURE 1.

Dot plot of the main metrics of performance

TABLE 4.

Performance of targeted learning and estimating equation estimators by study within the HAL-based simulations

Method	Study ID	TrueATE	Variance	Bias	MSE	rMSE	Coverage	Coverage2	CIwidth
A-IPTW	1	−0.0109	0.0056	−0.0373	0.0070		0.704	0.912	0.1658
	2	0.0507	0.0005	−0.0012	0.0005		0.934	0.958	0.0849
	3	0.0007	0.0003	0.0007	0.0003		0.954	0.948	0.0737
	4	−0.0468	0.0019	0.0109	0.0020		0.928	0.950	0.1612
	5	−0.0136	0.0020	−0.0046	0.0020		0.926	0.952	0.1640
	6	0.2523	0.0010	−0.0266	0.0017		0.672	0.868	0.0829
	7	−0.0310	0.0012	0.0093	0.0013		0.862	0.938	0.1098
	8	−0.0442	0.0037	0.0037	0.0037		0.914	0.952	0.2112
	9	0.0089	0.0001	−0.0005	0.0001		0.940	0.948	0.0362
	10	0.0203	0.0006	−0.0001	0.0006		0.954	0.954	0.0961
C-TMLE	1	−0.0109	0.0219	−0.0947	0.0309		0.836	0.890	0.4956
	2	0.0507	0.0006	0.0016	0.0006		0.956	0.954	0.0993
	3	0.0007	0.0004	0.0018	0.0004		0.948	0.948	0.0782
	4	−0.0468	0.0026	0.0046	0.0026		0.948	0.950	0.2005
	5	−0.0136	0.0027	−0.0087	0.0027		0.928	0.950	0.1882
	6	0.2523	0.0011	−0.0124	0.0012		0.942	0.944	0.1295
	7	−0.0310	0.0025	0.0012	0.0025		0.936	0.948	0.1875
	8	−0.0442	0.0049	−0.0014	0.0049		0.922	0.960	0.2524
	9	0.0089	0.0001	−0.0008	0.0001		0.942	0.950	0.0409
	10	0.0203	0.0006	0.0007	0.0006		0.952	0.940	0.1037
CV-A-IPTW	1	−0.0109	0.0565	−0.0262	0.0572		0.926	0.954	0.7789
	2	0.0507	0.0006	0.0031	0.0006		0.960	0.954	0.0985
	3	0.0007	0.0004	0.0009	0.0004		0.966	0.950	0.0793
	4	−0.0468	0.0025	0.0063	0.0025		0.956	0.948	0.2008
	5	−0.0136	0.0024	−0.0062	0.0024		0.940	0.946	0.1881
	6	0.2523	0.0012	−0.0045	0.0012		0.938	0.944	0.1301
	7	−0.0310	0.0020	0.0030	0.0020		0.936	0.940	0.1737
	8	−0.0442	0.0045	0.0000	0.0045		0.950	0.952	0.2553
	9	0.0089	0.0001	−0.0002	0.0001		0.942	0.948	0.0394
	10	0.0203	0.0006	0.0011	0.0006		0.962	0.944	0.1026
CV-IPTW	1	−0.0109	0.1632	−0.1129	0.1759		0.984	0.944	2.3263
	2	0.0507	0.0008	−0.0012	0.0008		1.000	0.948	0.2686
	3	0.0007	0.0005	0.0020	0.0005		1.000	0.954	0.1831
	4	−0.0468	0.0032	0.0270	0.0040		1.000	0.936	0.5065
	5	−0.0136	0.0028	−0.0202	0.0032		0.982	0.936	0.2817
	6	0.2523	0.0014	−0.0057	0.0014		1.000	0.954	0.3305
	7	−0.0310	0.0033	0.0017	0.0033		1.000	0.948	0.5111
	8	−0.0442	0.0062	0.0006	0.0062		1.000	0.948	0.6842
	9	0.0089	0.0001	0.0143	0.0003		0.998	0.756	0.1016
	10	0.0203	0.0007	0.0006	0.0007		1.000	0.956	0.2451
CV-TMLE	1	−0.0109	0.1868	−0.0291	0.1876		0.590	0.938	0.7006
	2	0.0507	0.0006	0.0031	0.0006		0.958	0.966	0.0985
	3	0.0007	0.0004	0.0009	0.0004		0.966	0.958	0.0793
	4	−0.0468	0.0025	0.0064	0.0025		0.956	0.954	0.2008
	5	−0.0136	0.0024	−0.0063	0.0024		0.940	0.958	0.1881
	6	0.2523	0.0013	0.0046	0.0013		0.936	0.958	0.1301
	7	−0.0310	0.0020	0.0030	0.0020		0.938	0.946	0.1737
	8	−0.0442	0.0044	0.0000	0.0044		0.950	0.964	0.2551
	9	0.0089	0.0001	−0.0002	0.0001		0.942	0.952	0.0394
	10	0.0203	0.0006	0.0011	0.0006		0.962	0.956	0.1026
IPTW	1	−0.0109	0.0280	−0.0736	0.0334		0.890	0.932	0.5945
	2	0.0507	0.0008	−0.0028	0.0008		1.000	0.948	0.2544
	3	0.0007	0.0005	0.0022	0.0005		1.000	0.954	0.1789
	4	−0.0468	0.0033	0.0276	0.0040		1.000	0.926	0.4889
	5	−0.0136	0.0028	−0.0201	0.0032		0.978	0.940	0.2712
	6	0.2523	0.0014	−0.0091	0.0015		0.998	0.942	0.2536
	7	−0.0310	0.0033	0.0023	0.0033		1.000	0.946	0.4838
	8	−0.0442	0.0062	0.0003	0.0062		1.000	0.950	0.6504
	9	0.0089	0.0001	0.0172	0.0004		0.992	0.684	0.0990
	10	0.0203	0.0007	0.0007	0.0007		1.000	0.958	0.2410
TMLE	1	−0.0109	0.3860	−0.3235	0.4906		0.100	0.920	0.1681
	2	0.0507	0.0006	0.0005	0.0006		0.932	0.960	0.0849
	3	0.0007	0.0004	0.0007	0.0004		0.946	0.948	0.0737
	4	−0.0468	0.0020	0.0099	0.0021		0.916	0.950	0.1611
	5	−0.0136	0.0022	−0.0052	0.0022		0.922	0.948	0.1640
	6	0.2523	0.0010	−0.0015	0.0010		0.806	0.942	0.0828
	7	−0.0310	0.0013	0.0079	0.0014		0.852	0.932	0.1098
	8	−0.0442	0.0040	0.0020	0.0040		0.900	0.952	0.2111
	9	0.0089	0.0001	−0.0003	0.0001		0.936	0.948	0.0362
	10	0.0203	0.0006	0.0001	0.0006		0.952	0.954	0.0961

Abbreviations: Coverage, coverage using 95% Wald-type confidence intervals (CI) based upon standard error estimates, where “Coverage2” uses the true sample variance; CI width, average width of the “Coverage” CI’s; Variance, true sample variance; MSE, mean-squared error; rMSE, relative (to the IPTW estimator in denominator) mean-squared error.

The 95% confidence interval (CI) coverage, however, shows different relative performance (Figure 1 and Table 4). The CV-A-IPTW had roughly 95% coverage for all studies. The CV-TMLE and C-TMLE had had roughly 95% coverage for all studies except Study 1. The TMLE and A-IPTW had coverage ranging from 90% to 95% for most studies. IPTW and CV-IPTW estimates of CI had very conservative coverage (close to 100%) for most studies.

To examine more closely issues of CI coverage, we removed the bias introduced by the estimation procedure for the standard error by using the true sample variance of each estimator (ie, the sample variance of the estimator across 500 simulations) to derive the standard error (“Coverage2” in Table 4). The coverage of this CI is the oracle coverage one would obtain if one is given the true variance. For this measurement, both CV-TMLE and CV-A-IPTW achieved 95% coverage in all studies, followed by TMLE, C-TMLE, IPTW and CV-IPTW with 95% coverage for nine studies. A-IPTW had 95% coverage for eight studies.

The simulations suggest, across 10 realistic data-generating distributions, that CV-A-IPTW, CV-TMLE, and C-TMLE has overall relatively good performance in terms of MSE and reliable 95% coverage. The A-IPTW estimator had superior MSE-based performance, though the confidence interval coverage was sometimes between 90% and 95%. However, plugging in the true standard deviation of the A-IPTW estimator instead of the plug-in influence-curve based one typically used resulted in good coverage. This suggests more robust SE estimators could make it a more compelling choice than the empirical performance in these simulations. In addition, CV-A-IPTW can improve the coverage of A-IPTW in most cases, but, due to the estimator being consistent in a bigger model, will have bigger MSE. Overall, the results at least show that both the CV-A-IPTW and the CV-TMLE as implemented in the tmle3 package⁷⁶ can provide robust inferences, suggesting using them “off the shelf” provides reliable results. In next section, we will discuss situations where even the CV-TMLE under-performed, potentially because of small sample size and related empirical positivity violations.¹⁷

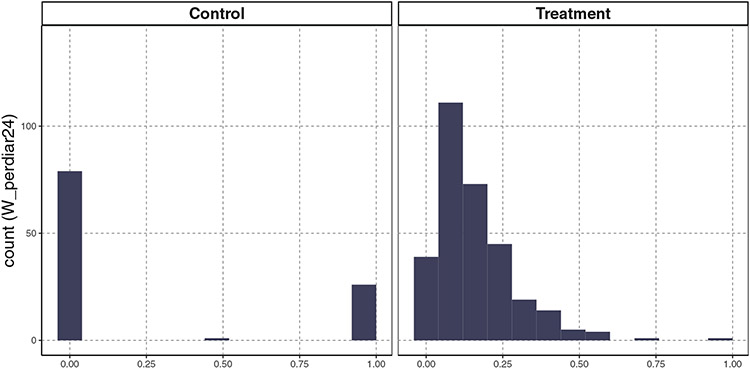
4.3 ∣. Exploration on positivity violation

We now consider Study 1, where the TMLE and CV-TMLE had significantly anticonservative coverage. In this case, certainly one cause appears to insufficient experimentation of treatment within some covariate groups. Specifically, consider Figure 2, which shows the distributions of the adjustment variable, W_perdiar24 in Study 1. This variable represents the percent of days monitored under 24 months with pediatric diarrhea. As one can see, there are large differences in the marginal distribution of this covariate; in fact, a fit $g_n$ without smoothing would result in a perfect positivity violation. However, given the variance-bias trade-off resulting in the estimators, it is possible that these empirical violations are smoothed over. A potential consequence of this positivity violation is that the resulting estimator, for the parameter which requires support in the data, will be unstable and biased. Table 5 shows the performance of estimators before and after dropping the variable W_perdiar24 in Study 1. We can observe that all estimators can benefit from removing the problematic variable in terms of higher coverage or lower MSE.

FIGURE 2.

Distributions of W_perdiar24 in Study 1 by intervention group

TABLE 5.

Estimators’ performance with/without W_perdiar24 in Study 1 to show the impact of one covariate on performance due to positivity violations

Method	Dropperdiar	TrueATE	Variance	Bias	MSE	Coverage	Coverage2	CIwidth
A-IPTW	No	−0.0109	0.0056	−0.0373	0.0070	0.704	0.912	0.1658
	Yes	0.0104	0.0084	−0.0010	0.0084	0.908	0.944	0.3117
C-TMLE	No	−0.0109	0.0219	−0.0947	0.0309	0.836	0.890	0.4956
	Yes	0.0104	0.0171	0.0020	0.0171	0.930	0.952	0.4829
CV-A-IPTW	No	−0.0109	0.0565	−0.0262	0.0572	0.926	0.954	0.7789
	Yes	0.0104	0.0131	0.0027	0.0131	0.950	0.940	0.4604
CV-IPTW	No	−0.0109	0.1632	−0.1129	0.1759	0.984	0.944	2.3263
	Yes	0.0104	0.0198	0.0097	0.0199	1.000	0.948	1.3311
CV-TMLE	No	−0.0109	0.1868	−0.0291	0.1876	0.590	0.938	0.7006
	Yes	0.0104	0.0132	0.0030	0.0132	0.950	0.946	0.4600
IPTW	No	−0.0109	0.0280	−0.0736	0.0334	0.890	0.932	0.5945
	Yes	0.0104	0.0202	0.0113	0.0203	1.000	0.948	1.2379
TMLE	No	−0.0109	0.3860	−0.3235	0.4906	0.100	0.920	0.1681
	Yes	0.0104	0.0096	−0.0006	0.0096	0.878	0.942	0.3116

Note: Columns are defined as in Table 4.

4.4 ∣. Estimators’ efficiency in randomized experiment setting

As mentioned in earlier section, the initial HAL models for propensity score include no variables for Study 7, 8, and 10, which leads to randomized experiments in the corresponding simulations. In these cases, we add the “difference-in-means” estimator (ie, $\frac{1}{n_1}{\sum }_{i=1}^n{A}_i{Y}_i-\frac{1}{n_0}{\sum }_{i=1}^n(1-A_i)Y_i$) with its variance estimator proposed by Neyman in 1923.⁸¹ Table 6 shows that the CV-TMLE and CV-A-IPTW estimators still gain efficiency in the randomized experiments setting. This is consistent with proposals for using doubly robust estimators of the ATE in randomized trials if there are informative covariates that can increase efficiency over simple, unadjusted estimates.^46,82

TABLE 6.

Relative performance of the two CV-estimators with a simple difference in means in the context of the three studies for which treatment was unrelated to covariates (thus equivalent to randomized clinical trial)

Study ID	Method	TrueATE	Variance	Bias	MSE	Coverage	Coverage2	CIwidth
7	CV-A-IPTW	−0.0310	0.0020	0.0030	0.0020	0.936	0.940	0.1737
	CV-TMLE	−0.0310	0.0020	0.0030	0.0020	0.938	0.946	0.1737
	Diff-in-Mean	−0.0310	0.0036	0.0021	0.0036	0.944	0.942	0.2435
8	CV-A-IPTW	−0.0442	0.0045	0.0000	0.0045	0.950	0.952	0.2553
	CV-TMLE	−0.0442	0.0044	0.0000	0.0044	0.950	0.964	0.2551
	Diff-in-Mean	−0.0442	0.0068	−0.0001	0.0068	0.942	0.952	0.3115
10	CV-A-IPTW	0.0203	0.0006	0.0011	0.0006	0.962	0.944	0.1026
	CV-TMLE	0.0203	0.0006	0.0011	0.0006	0.962	0.956	0.1026
	Diff-in-Mean	0.0203	0.0008	0.0007	0.0008	0.964	0.948	0.1167

Note: Columns are defined as in Table 4.

5 ∣. CONCLUSION

The ultimate goal of studies, such as ours, is to move incrementally toward algorithms that can take information on the design, causal model and known constrains in order to produce a data-adaptively optimized estimator without relying on arbitrary model assumptions. Asymptotic theory can provide guidance on some of the choices, but asymptotic efficiency is not a guarantee for superior performance in finite samples. Thus, simulation studies that are based on realistic DGD’s are invaluable for both evaluating estimators and modifying them to increase finite-sample robustness. We provided results supporting the use of a strategically undersmoothed HAL for estimating the relevant components of the DGD in data-driven simulations. Though much remains unresolved, such an approach could be an approach for generating synthetic data.⁸³

Our results suggest that if accurate inferences are the highest priority, then the CV-A-IPTW, CV-TMLE, and C-TMLE are good choices for providing robust inferences. Specifically, the results suggest that CV-A-IPTW and CV-TMLE might serve as “off the shelf” algorithms given that (1) they are asymptotically linear estimators; (2) they are consistent in a large class of statistical models; (3) they allow for the use of aggressive ensemble learning, while protecting the final performance of the estimator with an outer layer of cross-validation; (4) their influence-curve-based standard error combined with the well-behaved (normal) distribution of the estimator results in near perfect coverage In addition, the cross-validated estimators appear to be more robust for small sample with positivity violation. This implies the importance of using cross-validation in the longitudinal setting, where much more positivity violations can be expected. Our results also suggest that modifications to the algorithms for other estimators (such as improving the SE estimator for the A-IPTW) would result in an estimator with acceptable CI coverage and relatively low MSE. We also suggest one basis for deciding which estimator to use for particular data is to perform a similar simulation study for the data based upon fitting the undersmoothed HAL to derive the DGD. Then, one could choose to report the results from the estimator that provided the most reliable performance in such a simulation study. Of course, this is itself a form of over-fitting, since it uses the data both for estimator selection and for reporting the results of that estimator applied to the original data. However, it seems better than applying an arbitrary estimator and hoping that the advertised asymptotic performance matches the performance on the data of interest. Finally, our results support the observations that careful use of covariate information can be used to gain efficiency in the randomized experiment setting.

DATA AVAILABILITY STATEMENT

The data used in this analysis was held by Bill & Melinda Gates Foundation in a repository. The sensitive information contained in the data was still considered theoretically identifiable and can not be released to the public at this point, with the exception of the WASH Benefits trials. We provide the data from “WASH Benefits Bangladesh”⁸⁴ (Study 2) and “WASH Benefits Kenya”⁸⁵ (Study 3) as example data sets in the GitHub repository: https://github.com/HaodongL/realistic_simu.git