Abstract
Per- and polyfluoroalkyl substances (PFASs) are synthetic contaminants found in drinking groundwater sources and a wide variety of consumer products. Because of their adverse environmental and human health effects, remediation of these persistent compounds has attracted significant recent attention. To gain mechanistic insight into their remediation, we present the first ab initio study of PFAS degradation via hydrated electrons—a configuration that has not been correctly considered in previous computational studies up to this point. To capture these complex dynamical effects, we harness ab initio molecular dynamics (AIMD) simulations to probe the reactivities of perfluorooctanoic (PFOA) and perfluorooctane sulfonic acid (PFOS) with hydrated electrons in explicit water. We complement our AIMD calculations with advanced metadynamics sampling techniques to compute free energy profiles and detailed statistical analyses of PFOA/PFOS dynamics. Although our calculations show that the activation barrier for C–F bond dissociation in PFOS is three times larger than that in PFOA, all the computed free energy barriers are still relatively low, resulting in a diffusion-limited process. We discuss our results in the context of recent studies on PFAS degradation with hydrated electrons to give insight into the most efficient remediation strategies for these contaminants. Most importantly, we show that the degradation of PFASs with hydrated electrons is markedly different from that with excess electrons/charges, a common (but largely incomplete) approach used in several earlier computational studies.
Keywords: PFASs, hydrated electron, ab initio molecular dynamics, density functional theory, defluorination
Short abstract
In contrast to previous studies using simple excess electrons/charges, we show that PFAS degradation dynamics with explicit hydrated electrons are more complex and qualitatively different. The detailed mechanisms provided by our ab initio molecular dynamics calculations provide insight into experimental conditions that can be used to efficiently remediate these contaminants in aqueous systems.
Introduction
Per- and polyfluoroalkyl substances (PFASs) are hazardous, carcinogenic, and bioaccumulative contaminants found in groundwater, surface water, and a wide variety of consumer products. The strong carbon–fluorine (C–F) bonds in these artificially made compounds endow them with exceptional chemical stability and prevent most organisms from decomposing these persistent contaminants,1 which further exacerbates their bio-accumulation and toxicity. To mitigate and remove these persistent pollutants, many experimental efforts have been focused on chemical oxidation approaches to accelerate their degradation.2,3 In particular, oxidative conditions have been applied to both perfluorooctanoic acid (PFOA; see Figure 1) and perfluorooctane sulfonic acid (PFOS) contaminants. However, PFOS is more chemically resistant and challenging to treat by conventional methods, such as chemical oxidation/reduction, and thermal decomposition.4,5 Among the various reducing agents, hydrated electrons have recently garnered significant attention for PFAS degradation because of their extremely negative reduction potential of −2.9 V.6,7 As such, experiments have shown that these short-lived, aqueous species react with a multitude of quenchers in microseconds8,9 via a one-electron transfer mechanism.10
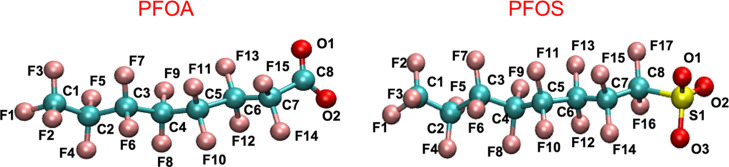
Figure 1.
Chemical structure and atom numbering scheme of the PFOA and PFOS anions examined in this study.
Over the past several years, a variety of approaches have harnessed hydrated electrons to chemically dissociate perfluorinated compounds. For example, previous studies have used UV photolysis to generate hydrated electrons via energetic photons for defluorinating PFOS.11−13 However, UV photolysis inherently has a low quantum yield, resulting in a myriad of other side reactions and a slow defluorination rate.14,15 UV photoirradiation of sulfite, iodide, dithionite, and ferrocyanide has been used to decompose PFASs in aqueous media,2,12,14,16−19 and the success of these reduction techniques has been ascribed to hydrated electron generation based on scavenging experiments.16 Previous studies have also shown that some of the hydrated electrons produced from the photoirradiation of sulfite/iodide can be scavenged using oxidizing agents, which reduces the overall efficiency of the degradation process. Several researchers have addressed this problem by using nitrilotriacetic acid,16 indole derivatives,20,21 or organomodified montmorillonite18,19 to more efficiently generate hydrated electrons to destroy PFAS. Regardless of the specific experimental approach, the use of hydrated electrons has been shown to effectively reduce both PFOA and PFOS when used in sufficiently large quantities and in a conducive environment (i.e., correct pH, solute concentration, and temperature).16,18,19,22−30 Despite their effectiveness, a detailed mechanistic and atomistic understanding of how these hydrated electrons accelerate PFAS degradation remains unclear.
Of the numerous experimental studies on PFAS degradation with hydrated electrons, most have either lacked the spectroscopic resolution to resolve these ultrafast dynamics or used fairly crude theoretical approximations. For example, several experimental studies30−32 have examined PFAS degradation products with hydrated electrons generated by ultraviolet light or electrodes; however, these approaches were not able to provide time-resolved details of the degradation mechanism itself due to the short timescales of these processes. However, there have been a few studies in the scientific literature that have explored time-resolved PFAS degradation kinetics with either hydroxyl radicals33 or hydrated electrons.12,29 In particular, pulse radiolysis experiments by Szajdzinska-Pietek have shown that PFOA is largely unreactive with hydroxyl radicals,33 resulting in biomolecular rate constants far lower than ∼107 M–1 s–1. Huang and co-workers explored photochemical reductive degradation (which produces hydrated electrons) of short- and long-chain PFASs12 and showed that the rate constant increases with chain length. Recently, the rate constants and activation energy associated with the initial reduction of PFASs were measured using temperature-dependent transient absorption spectroscopy,29 which showed no significant differences in the activation energy and rate constants associated with PFOA or PFOS degradation.
To date, all previous theoretical studies on PFAS degradation have used either static vertical/adiabatic density functional theory (DFT) calculations34,35 or dynamics calculations with an excess electron/charge to approximate a true hydrated electron.36,37 It is important to emphasize that simply introducing an excess electron/charge in a simulation does not accurately mimic a hydrated electron because this additional electron is not polarized by the surrounding water molecules. More importantly, this excess charge (which has been commonly used in theoretical calculations up to this point) does not directly capture the realistic configuration of a hydrated electron used in experimental studies. For example, excess electrons can be experimentally produced in neutral water via radiolysis or instantaneous ionization/detachment of other solutes;38,39 however, these processes do not yield hydrated electrons that are polarized by the surrounding water molecules. It is only when these electrons have lost sufficient energy to become metastable localized species bound with water that they can be designated as hydrated electrons.38,40 It is the latter configuration that we examine with advanced ab initio molecular dynamics (AIMD) to understand these important PFAS degradation mechanisms for the first time.
Materials and Methods
System Setup
Since its discovery, a general consensus has emerged that the hydrated electron occupies a quasi-spherical cavity in liquid water.41−44 To simulate this desired cavity, we first equilibrated a 24 × 24 × 24 Å3 periodic box containing 81 water molecules, a PFOA or PFOS molecule, and a chloride ion in an NVT (constant number N, volume V, and temperature T) canonical ensemble for over 10 ps with a 1 fs time step. A large simulation box was used to prevent chemical species from interacting artificially with its periodic image. The approximate dimensions of the PFOA and PFOS molecules are provided in the Supporting Information. After the equilibration step, we created five independent trajectories whose initial conditions were obtained from the last 5 ps of the PFOA/PFOS simulation (i.e., five independent trajectories were generated for each PFOA and PFOS configuration). Finally, for each of these five PFOA/PFOS trajectories, the chloride ion was removed and the system was then initialized with an extra negative charge to generate the desired hydrated electron. We then carried out an additional 6 ps of AIMD production runs with these pre-created cavities with a 0.5 fs time step (additional details are given in the Supporting Information). It is important to mention that the chloride ion was added to the system merely to create a cavity. During these simulations, the chloride ion was not reactive toward PFOA/PFOS (whereas the hydrated electron was reactive). To compare the degradation dynamics of hydrated electrons with crude configurations using an excess electron, we carried out 25 additional trajectories (13 and 12 trajectories for PFOA and PFOS, respectively) by simply initializing the system with an overall negative charge without preparing a cavity. Additional cavity preparation details are given in the Supporting Information.
Computational Details
All of our AIMD simulations utilized the QUICKSTEP45 module in the CP2K software package46 with the unrestricted Kohn–Sham formalism to capture the dynamics of the hydrated electron. All of our NVT simulations used a Nose-Hoover47,48 chain thermostat at 300 K, and the AIMD equations of motions were propagated with a 0.5 fs time step. GTH pseudopotentials49 and the TZV2P basis set50 were employed to describe the atomic core and valence electrons, respectively. All of our simulations (both hydrated and excess electron calculations) utilized a self-interaction-corrected PBE51−53 exchange–correlation functional with Grimme’s D354 dispersion corrections. Specifically, we incorporated a self-interaction correction (SIC) for all orbitals in our AIMD simulations using the average-density SIC, as implemented in the CP2K package. Following earlier studies,36 we set a = 0.2 and b = 0.25 for the scaling parameters in the SIC exchange–correlation functional, which was previously shown to give accurate electronic properties of PFOA/PFOS in water.36,55 For the auxiliary plane-wave (PW) basis used in the Gaussian and PW (GPW)56 scheme in CP2K, 600 and 60 Ry was used for the PW energy and reference grid cutoffs, respectively.
Results and Discussion
To confirm the accurate creation of a hydrated electron in our simulations, we calculated its radius of gyration (rg), which is a rigorous metric that can be experimentally measured or calculated with AIMD simulations.41−44 In short, the radius of gyration is a tensor describing the second moment of positions of a collection of particles. In our study, the radius of gyration was calculated from the spin density of the hydrated electrons, and further details of our calculations are given in the Supporting Information. Our calculated average rg values for a hydrated electron in explicitly solvated PFOA and PFOS are 2.46 and 2.45 Å, respectively, which are in close agreement with previous experimental (2.50 Å)57,58 and theoretical (2.16–2.65 Å)41,44 studies.
Figure 2 depicts the time evolution of rg for a hydrated electron in solvated PFOA and PFOS for the five independent trajectories described previously. Clearly, the rg profiles in Figure 2 are unique for each trajectory due to differences in their initial conditions. For trajectories 01–04 in the solvated PFOA system, rg decreases from its initial size to roughly 1.50 Å between 200 fs and 1.20 ps. This abrupt decay in rg for these trajectories corresponds to an irreversible reaction of the hydrated electron and the PFOA molecule. We obtained qualitatively similar results for solvated PFOS (see Figure 2b), where rg decreases to 1.50 Å for trajectories 01, 02, 03, and 05; however, the degradation process occurs later within the 400 fs to 4 ps time range. This longer time scale supports previous experimental findings showing that PFOS is more resistant to degradation than PFOA and is more challenging to treat with remediation approaches. Figure 2 also suggests that the hydrated electron transits from a localized state to a delocalized state several times before reacting with PFAS, which accounts for the large fluctuations in rg at early times (<1 ps). In other words, rg fluctuates when the hydrated electron has not yet reacted as it starts to delocalize over the PFAS molecule. It is also interesting to note that certain trajectories (trajectories 05 and 04 for PFOA and PFOS, respectively) show that the hydrated electron cavity is stable, with rg fluctuating around 2.50 Å throughout the simulation. The cavity of the hydrated electron in these two trajectories remains predominantly on the outer surface of the cluster, giving it stability.
Figure 2.
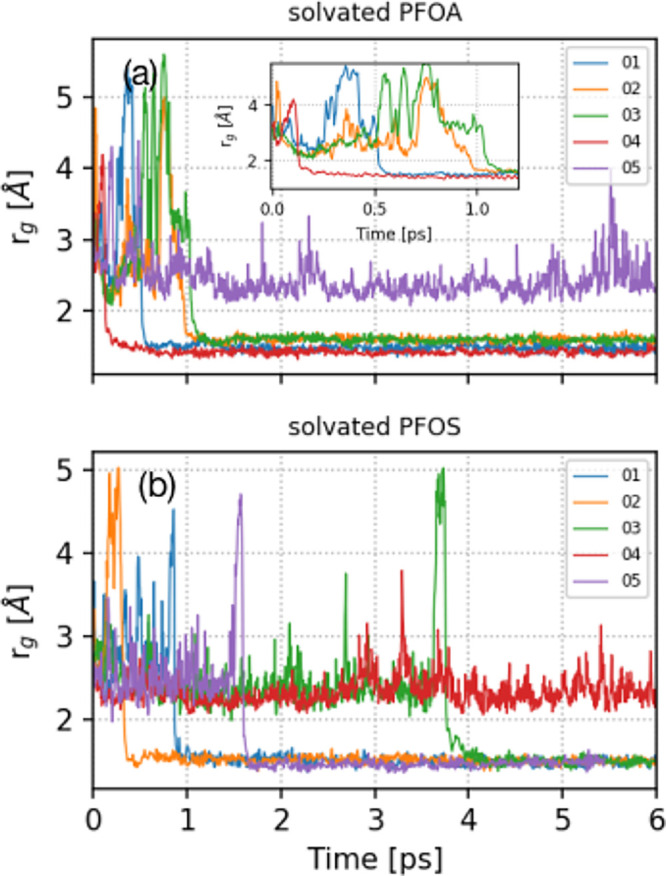
(a) Time evolution of the radius of gyration (rg) for a hydrated electron in explicitly solvated PFOA. The inset shows a magnified view of rg from 0 to 1.20 ps. (b) Time evolution of rg for a hydrated electron in explicitly solvated PFOS.
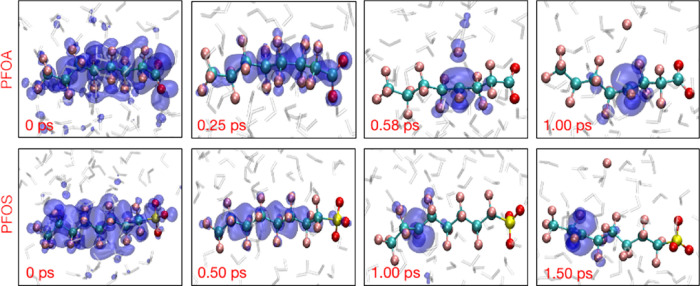
The upper panel in Figure 3 shows snapshots from a representative trajectory (03) for PFOA. At 0.25 ps, the hydrated electron is primarily localized in the pre-created cavity and is stabilized by approximately four water molecules, with O–H bonds pointing toward the center of the cavity as proposed by earlier studies.41,59 As the simulation proceeds, at 0.75 ps, the spin density is transferred from the cavity to the PFOA molecule and primarily delocalizes over the −COO functional group and the α-carbon (nearest C atom from the −COO group). Finally, as the spin density accumulates at the α-carbon dissociation site, rg shrinks and defluorination occurs at 1.25 ps. The lower panel in Figure 3 depicts three snapshots from trajectory 03 for solvated PFOS at 2.50, 3.75, and 5.00 ps. Initially, the hydrated electron cavity is confined by four water molecules on the outer surface of the cluster, with a radius of gyration of about 2.45 Å. However, at 3.75 ps, the hydrated electron starts to delocalize over the C3 and C4 atoms of a PFOS molecule with a radius of gyration of about 5 Å. After 3.75 ps, the spin density localizes at the dissociation site (the C3 center) and the C–F bond is cleaved. Figure S1 in the Supporting Information shows the time evolution of the average distance of the hydrated electron from the center of mass of the solvated PFOA and PFOS clusters. These distances decrease from their initial value of 5.2 Å to approximately 2.0 to 3.0 Å in which the hydrated electron interacts with the PFAS molecule. Nevertheless, in trajectories 05 and 04 for PFOA and PFOS, respectively, the cavity remains predominantly on the surface of the cluster, in accordance with previous studies of solvated electrons in similar systems.60,61
Figure 3.
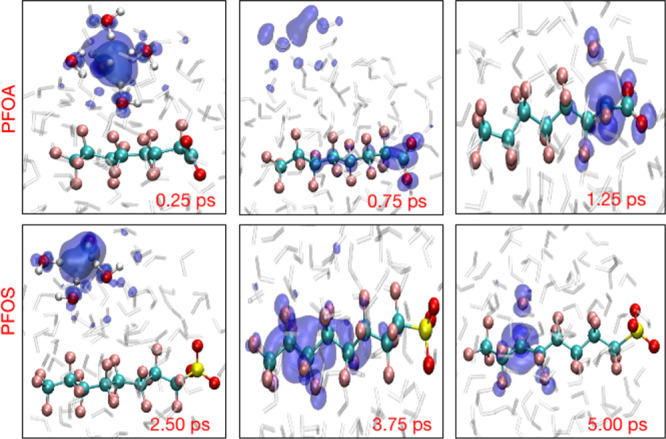
Time-resolved evolution of the spin density of the hydrated electron for representative trajectories of PFOA (top panels) and PFOS (bottom panels).
We also calculated several statistical properties of the hydrated electron to provide insight into its reactivity with PFOA and PFOS. Figure 4 shows the radial distribution functions (RDFs), g(r), and corresponding number integrals (NIs) for oxygen (Ow) and hydrogen (Hw) atoms of water molecules near the hydrated electron (eaq–). Values of g(r) that are nearly zero (i.e., near r < 0.25 and r < 0.42 for PFOA and PFOS, respectively) indicate the existence of an inner cavity. The radial distribution functions for both eaq–Ow and eaq––Hw show well-defined first maximum and minimum, indicating a first solvation shell structure. In the solvated PFOA system, we observe more distinct second and third solvation shells compared to PFOS, which signifies that the spin density of the hydrated electron is more diffuse in PFOA. The existence of an inner cavity is also vital for understanding the reactivity of the hydrated electron toward PFOA/PFOS; that is, larger r values in g(r) for eaq–Ow in PFOS indicate a more rigid/compact solvation shell structure. The higher peaks, deeper minima, and narrower shapes of g(r) for eaq––Ow and eaq–Hw indicate that water molecules are more strongly bound to the cavity in the solvated PFOS system compared to PFOA. As such, these strong interactions between the hydrated electron and the water molecules result in a reduced reactivity with PFOS.
Figure 4.
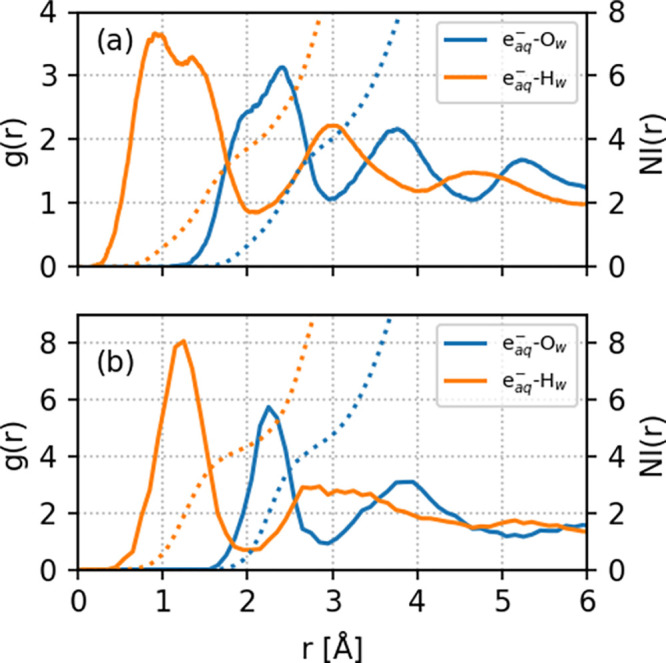
Radial distribution functions (g(r), solid lines, left axis) and number integrals (NIs, dotted lines, right axis) for oxygen (Ow) and hydrogen (Hw) atoms of water molecules near the hydrated electron (eaq–). Panels (a) and (b) represent solvated PFOA and PFOS, respectively.
It should be noted that the shape of the spin density of the hydrated electron at each instant is distorted from its spherical shape. Although spherically averaged g(r) values provide a simplified picture, one can obtain a more rigorous metric by integrating the first peak to get a mean number of water molecules. Our AIMD simulations give coordination numbers of 3.97 and 3.76 for the eaq––Ow and eaq–Hw radial distribution functions in solvated PFOA and 4.62 and 4.30 for the corresponding radial distribution functions in PFOS. The higher coordination number for eaq– in the solvated PFOS system indicates a more compact solvation shell structure, which supports our previous discussion on water being more strongly bound to the eaq cavity in PFOS.
The radius of gyration for an excess electron in solvated PFOA and PFOS (a total of 13 and 12 trajectories, respectively) is shown as a function of time in Figure S2 in the Supporting Information. In particular, Figure S2b shows that an excess electron in solvated PFOA exhibits qualitatively different dynamics from a true hydrated electron. Specifically, the excess electron trajectories are characterized with rg values decreasing rapidly to 1.25 Å in less than 100 fs (except for one trajectory, which decays to the same value after ∼0.60 ps). We also observed four trajectories with the same behavior in solvated PFOS in which rg initially fluctuates around 2.65 Å and decreases to its final value of 1.25 Å from ∼0.20 to ∼0.90 ps. Figure 5 shows four snapshots of the spin density from a representative trajectory of an excess electron in PFOA and PFOS. When the system is initialized with an instantaneous negative charge to create an excess electron, the charge artificially delocalizes over the entire PFAS molecule (this differs considerably from the hydrated electron dynamics shown in Figure 3). The excess electron then begins to shrink, further polarizing the PFAS molecule, until the spin density slowly accumulates at the dissociation site.
Figure 5.
Time-resolved evolution of the spin density of the excess electron for representative trajectories of PFOA (top panels) and PFOS (bottom panels).
To compare these different PFAS decomposition mechanisms, we calculated C–F bond distances for our pre-created cavity simulations for the hydrated electron (Figure 6). Four (out of five) trajectories resulted in C–F bond dissociation in the solvated PFOA and PFOS systems (Figure 6a,b). For all the trajectories, the C–F bond distances initially fluctuated around 1.35 Å. At the end of these simulations, the C–F bond distance stretched to 3 Å, showing a complete dissociation in the presence of the hydrated electron (C–F bond dissociation starts within 1.00 ps in solvated PFOA). Among the various CF2 groups along the PFOA backbone, we observe defluorination at the α position for trajectories 02 and 03. Previous studies have suggested two major reaction pathways for PFOA degradation with hydrated electrons, including H/F exchange and chain shortening. Among the different chemical functional groups present in PFOA, the −CF2– group at the α position has a high reactivity due to the inductive effect of the head group, resulting in reactions in this preferred region.30,62 Indeed, DFT calculations have shown that the simple addition of an excess charge to the PFOA molecule results in spontaneous stretching of C–F bonds at the α position, facilitating their cleavage.30 However, the same studies also proposed that C–F bonds in the middle of the carbon chain can also be cleaved.30 Therefore, although the α C–F bond is thermodynamically more reactive, all of the other C–F bonds also have a high probability (whose statistics are explored by our first-principles MD simulations) to dissociate. Accordingly, our AIMD simulations for the hydrated electron also showed defluorination at the C3 (trajectory 01) and C4 (trajectory 04) centers, in agreement with previous studies.30 It is also interesting to note the faster defluorination timescales at the C3 and C4 centers in PFOA (Figure 6a), which indicate regions of preferred reactivity for long-chain PFAS.
Figure 6.
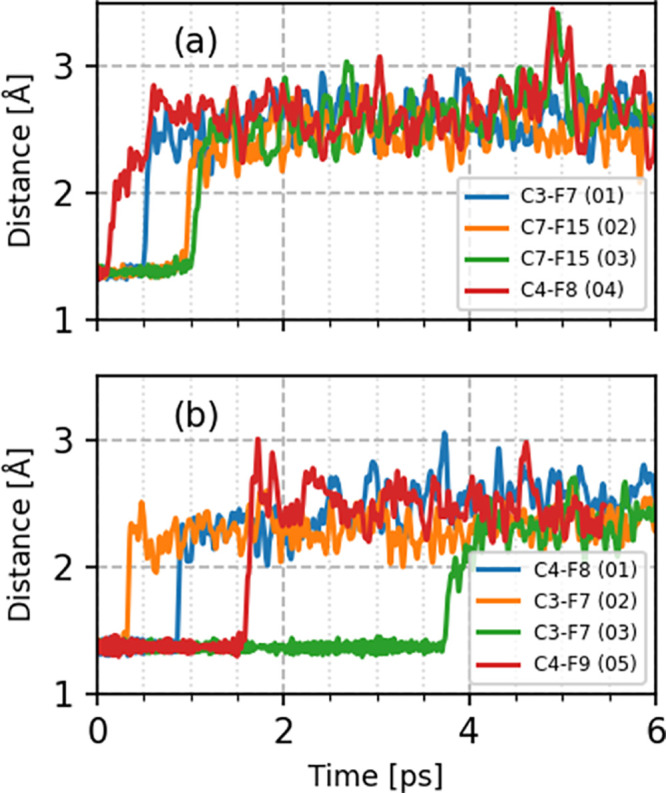
Time-resolved evolution of C–F bond distances depicting the defluorination of PFASs from pre-created cavity simulations for the hydrated electron. Panels (a,b) represent explicitly solvated PFOA and PFOS systems, respectively. The atom numbering scheme corresponds to the atom labels shown in Figure 1.
For solvated PFOS, we observe different C–F bond dissociation timescales ranging from femtoseconds to a few picoseconds. These observations indicate that the dissociation dynamics of each trajectory is unique and differs significantly from the solvated PFOA system. In solvated PFOS, the cavity of the hydrated electron is more compact and is strongly bound with water molecules (see g(r) and number integrals in Figure 4), making it less reactive toward the PFOS molecule. For these cases, the hydrated electron preferentially attacks either the C3 (trajectories 02 and 03) or C4 (trajectories 01 and 05) sites at the center of the molecule. Recent static DFT calculations have shown that the sulfonic functional group in PFOS causes the C3 and C4 centers to have the lowest bond dissociation energy among all the C–F bonds, resulting in a markedly different degradation process compared to PFOA degradation.30
We also compared C–F bond dissociation dynamics between our hydrated versus excess electron simulations. In the Supporting Information, Figure S3 depicts the dissociation dynamics as a function of time for an excess electron in solvated PFOA (Figure S3a) and PFOS (Figure S3b). For solvated PFOA with an excess electron, 12 out of 13 trajectories show C–F bond dissociation timescales less than 100 fs. In contrast, only one trajectory shows a C–F bond dissociation on a longer timescale (around 500 fs). For solvated PFOS, 8 out of 12 trajectories dissociate within a few femtoseconds, whereas four trajectories dissociate on a picosecond timescale. As such, our AIMD simulations suggest that the reaction dynamics of PFASs with hydrated electrons significantly differs from that of an excess electron.36 The faster C–F bond dissociation in the latter occurs because the spin density is artificially delocalized over the PFAS molecule at the beginning of the simulation. In contrast, for the hydrated electron, the spin density first polarizes the surrounding water molecules.
In previous studies on PFAS degradation with excess electrons, it was noted that the initial site of the C–F bond dissociation was random.36,63 Our studies with excess electrons also support these findings; however, we observe different dynamics for the hydrated electron. For example, in solvated PFOA, two out of four trajectories show dissociation at the C7 center, with two trajectories showing the C3/C4 center as an initial dissociation site. In solvated PFOS, two trajectories at each of the C3 and C4 centers are locations where a C–F bond dissociation occurs. Because the excess electron initially delocalizes over the entire PFAS molecule, all the C–F bonds are weakened with a nearly equal dissociation probability. Moreover, we find that the C2, C3, C4, and C5 centers act as an initial dissociation site when excess electrons are added to the solvated PFOA system. In contrast, we find that the C3, C4, C5, and C6 centers are C–F bond dissociation sites in solvated PFOS. As such, our AIMD simulations strongly indicate that the C–F bond dissociation site is largely dependent on the detailed nature of the charged species in the system, with excess electrons showing a qualitatively different behavior from a hydrated electron. Overall, our simulations indicate that the hydrated electron shows a somewhat directional nature toward the initial dissociation site. To probe this phenomenon further, Figures S4 and S5 in the Supporting Information show radial distribution functions between the defluorinated F atom and the H atoms of the surrounding water molecules from our hydrated and excess electron simulations. In Figure S4, the F–Hw radial distribution functions have sharp peaks near 1.58 Å, which is larger than the conventional H–F covalent bond distance of 0.91 Å and indicates a strongly hydrogen-bonded fluoride anion with water molecules. However, for an excess electron, the F–Hw radial distribution function has peaks near 1.00 Å and 1.58 Å. The F–Hw peak near 1.00 Å indicates formation of an H–F molecule as a byproduct,36,63 which is not found in the hydrated electron simulations.
Finally, to probe the energetics of these various degradation mechanisms, we carried out well-tempered metadynamics simulations to calculate free energy activation barriers for C–F bond cleavage initiated by the hydrated electron. Furthermore, details of the well-tempered metadynamics calculations are provided in the Supporting Information. The well-tempered metadynamics simulations are initialized by defining a single collective variable, which we choose to be the coordination number from C to F, as shown in Figure S6. Free energy profiles from our pre-created cavity simulations for the hydrated electron in solvated PFOA and PFOS are shown Figures S7 and S8, respectively. These free energy profiles indicate that the degradation process proceeds via a single transition state, and Figure 7a,b summarizes the C–F bond dissociation activation barriers in solvated PFOA and PFOS, respectively. To evaluate the convergence of our metadynamics simulations, we calculated the free energy difference between the transition state and reactant as a function of time (Figures S9 and S10 in the Supporting Information), which indicates that our metadynamics simulations are fully converged. Overall, the average free energy activation barrier for C–F bond dissociation is three times larger for solvated PFOS than for PFOA, resulting in a slower defluorination of PFOS. However, the free energy activation barrier for both PFOS and PFOA falls below the diffusion-controlled limit,12,29 and, therefore, the degradation process essentially becomes independent of the overall chemical rate constant.64,65 The relatively low free energy activation barriers obtained from our AIMD calculations provide atomistic details of this process to rationalize these previous experimental observations. Moreover, the trends in our computed activation barriers also support previous experiments that found PFOS to be more resistant to degradation than PFOA (although both degradations are still diffusion-controlled).
Figure 7.
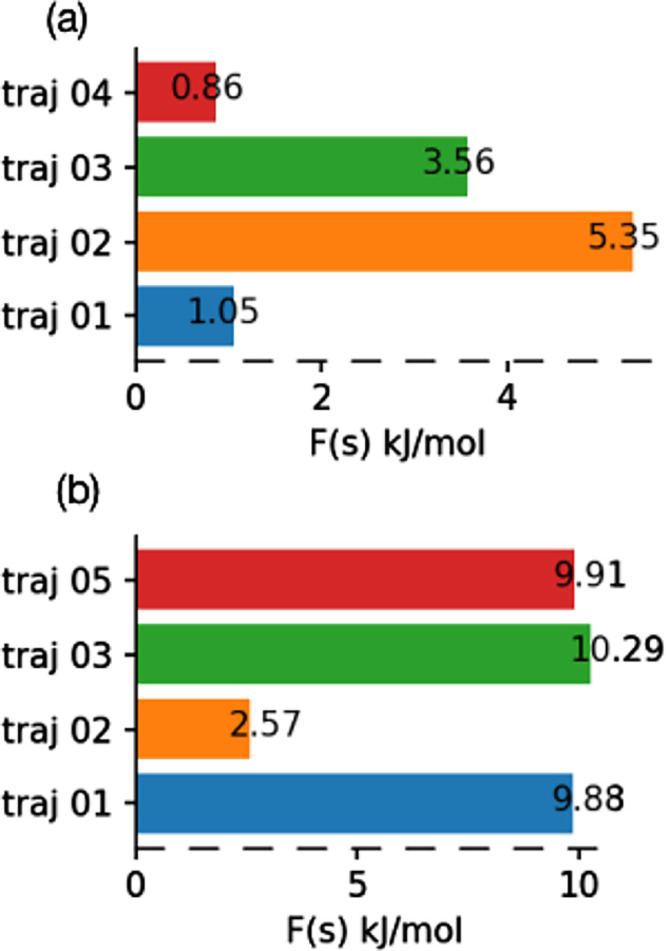
Free energy activation barrier values for C–F bond dissociation by a hydrated electron in explicitly solvated (a) PFOA and (b) PFOS.
Environmental Implications
The results of our extensive study have several important implications for environmental remediation efforts of PFAS contaminants with hydrated electrons. Because our AIMD calculations clearly show that PFAS degradation via hydrated electrons is diffusion-limited, one way to improve the efficiency of this process is to ensure that the source of hydrated electrons is as close to the PFAS contaminant as possible. For example, having PFAS molecules directly adsorbed on an electrified surface or electron-rich material would effectively minimize the diffusion distance that the generated hydrated electron would have to traverse to dissociate PFAS. Similarly, the efficiency of PFAS degradation via hydrated electrons could be enhanced by ensuring that the surrounding aqueous environment does not contain additional oxidizing scavengers because this can deplete the hydrated electrons as they diffuse/migrate through the solvent. Another important ramification of our study can be gleaned from the intrinsic kinetic/statistical nature of the PFAS degradation process itself. In particular, our AIMD calculations and metadynamics sampling techniques indicate that all of the C–F bonds in PFASs have a likely probability to dissociate (even though specific C–F bonds might be more thermodynamically reactive). As such, some of the efforts by other researchers to target specific C–F bonds in PFAS could be counterproductive because this process is inherently kinetically controlled. In other words, more research efforts should be directed toward minimizing the diffusion distance of hydrated electrons rather than targeting the weakest C–F bonds because the degradation process is ultimately dominated by statistical/kinetic effects.
In summary, we have provided the first detailed atomistic study of PFAS degradation dynamics using a correct treatment of hydrated electrons, which we probe with a suite of advanced AIMD and sampling techniques. Our calculations show that PFAS degradation with hydrated electrons is markedly different from that of excess electrons/charges, a common (but crude) approximation used in all previous studies up to this point. More specifically, we find that C–F bond dissociation with excess electrons occurs faster because the spin density is artificially delocalized over the PFAS molecule at the beginning of the simulation. In contrast, the spin density in a true hydrated electron first polarizes the surrounding water molecules before reacting with a PFAS molecule to initiate C–F bond dissociation, resulting in a diffusion-limited process. Finally, we calculate free energy activation barriers and radial distribution functions for these degradation processes to provide mechanistic insight into the different reactivities of PFOA and PFOS. The average free energy activation values for C–F bond dissociation from these independent trajectories are 2.70 and 8.16 kJ/mol for PFOA and PFOS, respectively. Our new metadynamics calculations show that the average activation barrier for C–F bond dissociation in PFOS is three times larger than that for PFOA, and our statistical analyses indicate that PFOS has a more rigid/compact solvation shell that also results in a slower defluorination. Collectively, our AIMD simulations (1) shed new light on PFAS degradation pathways using hydrated and excess electrons and (2) provide additional, critical mechanistic insight into the degradation of PFASs and other aqueous pollutants.
Acknowledgments
S.B. and B.M.W. acknowledge support from the National Science Foundation under grant no. CHE-1808242. S.S.R.K.C.Y. acknowledges support from IIT Madras through its new faculty support grants: NFSG (IP2021/0972CY/NFSC008973) and NFIG (RF2021/0577CY/NFIG008973).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.est.2c01469.
Additional details on computational methods, metadynamics simulations, volumetric data analysis, distance calculations, radius of gyration, radial distribution functions, and free energy profiles (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Liou J. S.-C.; Szostek B.; DeRito C. M.; Madsen E. L. Investigating the Biodegradability of Perfluorooctanoic Acid. Chemosphere 2010, 80, 176–183. 10.1016/j.chemosphere.2010.03.009. [DOI] [PubMed] [Google Scholar]
- Vellanki B. P.; Batchelor B.; Abdel-Wahab A. Advanced Reduction Processes: A New Class of Treatment Processes. Environ. Eng. Sci. 2013, 30, 264–271. 10.1089/ees.2012.0273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shiying Y.; Zhang Y.; Zheng Y. Advanced Reduction Processes: A Novel Technology for Water Treatment. Prog. Chem. 2016, 28, 934–941. [Google Scholar]
- Schröder H. F.; Meesters R. J. W. Stability of Fluorinated Surfactants in Advanced Oxidation Processes—A Follow up of Degradation Products Using Flow Injection–Mass Spectrometry, Liquid Chromatography–Mass Spectrometry and Liquid Chromatography–Multiple Stage Mass Spectrometry. J. Chromatogr. A 2005, 1082, 110–119. 10.1016/j.chroma.2005.02.070. [DOI] [PubMed] [Google Scholar]
- Shahsavari E.; Rouch D.; Khudur L. S.; Thomas D.; Aburto-Medina A.; Ball A. S. Challenges and Current Status of the Biological Treatment of PFAS-Contaminated Soils. Front. Bioeng. Biotechnol. 2021, 8, 1493. 10.3389/fbioe.2020.602040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swallow A. J.Radiation Chemistry. An Introduction; Longman: London, 1973. [Google Scholar]
- Schwarz H. A. Free Radicals Generated by Radiolysis of Aqueous Solutions. J. Chem. Educ. 1981, 58, 101. 10.1021/ed058p101. [DOI] [Google Scholar]
- Hare P. M.; Price E. A.; Stanisky C. M.; Janik I.; Bartels D. M. Solvated Electron Extinction Coefficient and Oscillator Strength in High Temperature Water. J. Phys. Chem. A 2010, 114, 1766–1775. 10.1021/jp909789b. [DOI] [PubMed] [Google Scholar]
- Garrett B. C.; Dixon D. A.; Camaioni D. M.; Chipman D. M.; Johnson M. A.; Jonah C. D.; Kimmel G. A.; Miller J. H.; Rescigno T. N.; Rossky P. J.; Xantheas S. S.; Colson S. D.; Laufer A. H.; Ray D.; Barbara P. F.; Bartels D. M.; Becker K. H.; Bowen K. H.; Bradforth S. E.; Carmichael I.; Coe J. V.; Corrales L. R.; Cowin J. P.; Dupuis M.; Eisenthal K. B.; Franz J. A.; Gutowski M. S.; Jordan K. D.; Kay B. D.; LaVerne J. A.; Lymar S. V.; Madey T. E.; McCurdy C. W.; Meisel D.; Mukamel S.; Nilsson A. R.; Orlando T. M.; Petrik N. G.; Pimblott S. M.; Rustad J. R.; Schenter G. K.; Singer S. J.; Tokmakoff A.; Wang L.-S.; Zwier T. S. Role of Water in Electron-Initiated Processes and Radical Chemistry: Issues and Scientific Advances. Chem. Rev. 2005, 105, 355–390. 10.1021/cr030453x. [DOI] [PubMed] [Google Scholar]
- Hart E. J.; Anbar M.. The Hydrated Electron; Wiley-Inter-Science: New York, 1970. [Google Scholar]
- Yamamoto T.; Noma Y.; Sakai S.-i.; Shibata Y. Photodegradation of Perfluorooctane Sulfonate by UV Irradiation in Water and Alkaline 2-Propanol. Environ. Sci. Technol. 2007, 41, 5660–5665. 10.1021/es0706504. [DOI] [PubMed] [Google Scholar]
- Huang L.; Dong W.; Hou H. Investigation of the Reactivity of Hydrated Electron Toward Perfluorinated Carboxylates by Laser Flash Photolysis. Chem. Phys. Lett. 2007, 436, 124–128. 10.1016/j.cplett.2007.01.037. [DOI] [Google Scholar]
- Sauer M. C.; Crowell R. A.; Shkrob I. A. Electron Photodetachment from Aqueous Anions. 1. Quantum Yields for Generation of Hydrated Electron by 193 and 248 nm Laser Photoexcitation of Miscellaneous Inorganic Anions. J. Phys. Chem. A 2004, 108, 5490–5502. 10.1021/jp049722t. [DOI] [Google Scholar]
- Buxton G. V.; Greenstock C. L.; Helman W. P.; Ross A. B. Critical Review of Rate Constants for Reactions of Hydrated Electrons, Hydrogen Atoms and Hydroxyl Radicals (H/O in Aqueous Solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. 10.1063/1.555805. [DOI] [Google Scholar]
- Vecitis C. D.; Park H.; Cheng J.; Mader B. T.; Hoffmann M. R. Treatment Technologies for Aqueous Perfluorooctanesulfonate (PFOS) and Perfluorooctanoate (PFOA). Front. Environ. Sci. Eng. 2009, 3, 129. 10.1007/s11783-009-0022-7. [DOI] [Google Scholar]
- Sun Z.; Zhang C.; Xing L.; Zhou Q.; Dong W.; Hoffmann M. R. UV/Nitrilotriacetic Acid Process as a Novel Strategy for Efficient Photoreductive Degradation of Perfluorooctanesulfonate. Environ. Sci. Technol. 2018, 52, 2953–2962. 10.1021/acs.est.7b05912. [DOI] [PubMed] [Google Scholar]
- Trojanowicz M.; Bojanowska-Czajka A.; Bartosiewicz I.; Kulisa K. Advanced Oxidation/Reduction Processes Treatment for Aqueous Perfluorooctanoate (PFOA) and Perfluorooctanesulfonate (PFOS) – A Review of Recent Advances. Chem. Eng. J. 2018, 336, 170–199. 10.1016/j.cej.2017.10.153. [DOI] [Google Scholar]
- Tian H.; Gao J.; Li H.; Boyd S. A.; Gu C. Complete Defluorination of Perfluorinated Compounds by Hydrated Electrons Generated from 3-Indole-acetic-acid in Organomodified Montmorillonite. Sci. Rep. 2016, 6, 32949. 10.1038/srep32949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian H.; Gu C. Effects of Different Factors on Photodefluorination of Perfluorinated Compounds by Hydrated Electrons in Organo-Montmorillonite System. Chemosphere 2018, 191, 280–287. 10.1016/j.chemosphere.2017.10.074. [DOI] [PubMed] [Google Scholar]
- Mialocq J. C.; Amouyal E.; Bernas A.; Grand D. Picosecond Laser Photolysis of Aqueous Indole and Tryptophan. J. Phys. Chem. 1982, 86, 3173–3177. 10.1021/j100213a022. [DOI] [Google Scholar]
- Tian H.; Guo Y.; Pan B.; Gu C.; Li H.; Boyd S. A. Enhanced Photoreduction of Nitro-aromatic Compounds by Hydrated Electrons Derived from Indole on Natural Montmorillonite. Environ. Sci. Technol. 2015, 49, 7784–7792. 10.1021/acs.est.5b01026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qu Y.; Zhang C.; Li F.; Chen J.; Zhou Q. Photo-Reductive Defluorination of Perfluorooctanoic Acid in Water. Water Res. 2010, 44, 2939–2947. 10.1016/j.watres.2010.02.019. [DOI] [PubMed] [Google Scholar]
- Song Z.; Tang H.; Wang N.; Zhu L. Reductive Defluorination of Perfluorooctanoic Acid by Hydrated Electrons in a Sulfite-Mediated UV Photochemical System. J. Hazard. Mater. 2013, 262, 332–338. 10.1016/j.jhazmat.2013.08.059. [DOI] [PubMed] [Google Scholar]
- Qu Y.; Zhang C.-J.; Chen P.; Zhou Q.; Zhang W.-X. Effect of Initial Solution pH on Photo-Induced Reductive Decomposition of Perfluorooctanoic Acid. Chemosphere 2014, 107, 218–223. 10.1016/j.chemosphere.2013.12.046. [DOI] [PubMed] [Google Scholar]
- Gu Y.; Dong W.; Luo C.; Liu T. Efficient Reductive Decomposition of Perfluorooctanesulfonate in a High Photon Flux UV/Sulfite System. Environ. Sci. Technol. 2016, 50, 10554–10561. 10.1021/acs.est.6b03261. [DOI] [PubMed] [Google Scholar]
- Sun Z.; Zhang C.; Chen P.; Zhou Q.; Hoffmann M. R. Impact of Humic Acid on the Photoreductive Degradation of Perfluorooctane Sulfonate (PFOS) by UV/Iodide Process. Water Res. 2017, 127, 50–58. 10.1016/j.watres.2017.10.010. [DOI] [PubMed] [Google Scholar]
- Sun M.; Zhou H.; Xu B.; Bao J. Distribution of Perfluorinated Compounds in Drinking Water Treatment Plant and Reductive Degradation by UV/SO32– Process. Environ. Sci. Pollut. Res. 2018, 25, 7443–7453. 10.1007/s11356-017-1024-9. [DOI] [PubMed] [Google Scholar]
- Cui J.; Gao P.; Deng Y. Destruction of Per- and Polyfluoroalkyl Substances (PFAS) with Advanced Reduction Processes (ARPs): A Critical Review. Environ. Sci. Technol. 2020, 54, 3752–3766. 10.1021/acs.est.9b05565. [DOI] [PubMed] [Google Scholar]
- Maza W. A.; Breslin V. M.; Owrutsky J. C.; Pate B. B.; Epshteyn A. Nanosecond Transient Absorption of Hydrated Electrons and Reduction of Linear Perfluoroalkyl Acids and Sulfonates. Environ. Sci. Technol. Lett. 2021, 8, 525–530. 10.1021/acs.estlett.1c00383. [DOI] [Google Scholar]
- Bentel M. J.; Yu Y.; Xu L.; Li Z.; Wong B. M.; Men Y.; Liu J. Defluorination of Per- and Polyfluoroalkyl Substances (PFASs) with Hydrated Electrons: Structural Dependence and Implications to PFAS Remediation and Management. Environ. Sci. Technol. 2019, 53, 3718–3728. 10.1021/acs.est.8b06648. [DOI] [PubMed] [Google Scholar]
- Su Y.; Rao U.; Khor C. M.; Jensen M. G.; Teesch L. M.; Wong B. M.; Cwiertny D. M.; Jassby D. Potential-Driven Electron Transfer Lowers the Dissociation Energy of the C–F Bond and Facilitates Reductive Defluorination of Perfluorooctane Sulfonate (PFOS). ACS Appl. Mater. Interfaces 2019, 11, 33913–33922. 10.1021/acsami.9b10449. [DOI] [PubMed] [Google Scholar]
- Rao U.; Su Y.; Khor C. M.; Jung B.; Ma S.; Cwiertny D. M.; Wong B. M.; Jassby D. Structural Dependence of Reductive Defluorination of Linear PFAS Compounds in a UV/Electrochemical System. Environ. Sci. Technol. 2020, 54, 10668–10677. 10.1021/acs.est.0c02773. [DOI] [PubMed] [Google Scholar]
- Szajdzinska-Pietek E.; Gebicki J. L. Pulse Radiolytic Investigation of Perfluorinated Surfactants in Aqueous Solutions. Res. Chem. Intermed. 2000, 26, 897–912. 10.1163/156856700x00381. [DOI] [Google Scholar]
- Raza A.; Bardhan S.; Xu L.; Yamijala S. S. R. K. C.; Lian C.; Kwon H.; Wong B. M. A Machine Learning Approach for Predicting Defluorination of Per- and Polyfluoroalkyl Substances (PFAS) for Their Efficient Treatment and Removal. Environ. Sci. Technol. Lett. 2019, 6, 624–629. 10.1021/acs.estlett.9b00476. [DOI] [Google Scholar]
- Van Hoomissen D. J.; Vyas S. Early Events in the Reductive Dehalogenation of Linear Perfluoroalkyl Substances. Environ. Sci. Technol. Lett. 2019, 6, 365–371. 10.1021/acs.estlett.9b00116. [DOI] [Google Scholar]
- Yamijala S. S. R. K. C.; Shinde R.; Wong B. M. Real-Time Degradation Dynamics of Hydrated Per- and Polyfluoroalkyl Substances (PFASs) in the Presence of Excess Electrons. Phys. Chem. Chem. Phys. 2020, 22, 6804–6808. 10.1039/c9cp06797c. [DOI] [PubMed] [Google Scholar]
- Yamijala S. S. R. K. C.; Shinde R.; Hanasaki K.; Ali Z. A.; Wong B. M. Photo-Induced Degradation of PFASs: Excited-State Mechanisms from Real-Time Time-Dependent Density Functional Theory. J. Hazard. Mater. 2022, 423, 127026. 10.1016/j.jhazmat.2021.127026. [DOI] [PubMed] [Google Scholar]
- Larsen R. E.; Glover W. J.; Schwartz B. J. Does the Hydrated Electron Occupy a Cavity?. Science 2010, 329, 65–69. 10.1126/science.1189588. [DOI] [PubMed] [Google Scholar]
- Devonshire R.; Weiss J. J. Nature of the Transient Species in the Photochemistry of Negative Ions in Aqueous Solution. J. Phys. Chem. 1968, 72, 3815–3820. 10.1021/j100857a020. [DOI] [Google Scholar]
- Hart E. J. The Hydrated Electron. Science 1964, 146, 1664. 10.1126/science.146.3640.19. [DOI] [PubMed] [Google Scholar]
- Wilhelm J.; VandeVondele J.; Rybkin V. V. Dynamics of the Bulk Hydrated Electron from Many-Body Wave-Function Theory. Angew. Chem., Int. Ed. 2019, 58, 3890–3893. 10.1002/anie.201814053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsalek O.; Uhlig F.; Frigato T.; Schmidt B.; Jungwirth P. Dynamics of Electron Localization in Warm versus Cold Water Clusters. Phys. Rev. Lett. 2010, 105, 043002. 10.1103/PhysRevLett.105.043002. [DOI] [PubMed] [Google Scholar]
- Marsalek O.; Uhlig F.; VandeVondele J.; Jungwirth P. Structure, Dynamics, and Reactivity of Hydrated Electrons by Ab Initio Molecular Dynamics. Acc. Chem. Res. 2012, 45, 23–32. 10.1021/ar200062m. [DOI] [PubMed] [Google Scholar]
- Uhlig F.; Marsalek O.; Jungwirth P. Unraveling the Complex Nature of the Hydrated Electron. J. Phys. Chem. Lett. 2012, 3, 3071–3075. 10.1021/jz301449f. [DOI] [PubMed] [Google Scholar]
- VandeVondele J.; Krack M.; Mohamed F.; Parrinello M.; Chassaing T.; Hutter J. Quickstep: Fast and Accurate Density Functional Calculations Using a Mixed Gaussian and Plane Waves Approach. Comput. Phys. Commun. 2005, 167, 103–128. 10.1016/j.cpc.2004.12.014. [DOI] [Google Scholar]
- Hutter J.; Iannuzzi M.; Schiffmann F.; VandeVondele J. CP2K: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
- Nosé S. A Unified Formulation of the Constant Temperature Molecular Dynamics Methods. J. Chem. Phys. 1984, 81, 511–519. 10.1063/1.447334. [DOI] [Google Scholar]
- Hoover W. G. Canonical Dynamics: Equilibrium Phase-Space Distributions. Phys. Rev. A 1985, 31, 1695–1697. 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- Goedecker S.; Teter M.; Hutter J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. 10.1103/physrevb.54.1703. [DOI] [PubMed] [Google Scholar]
- Schäfer A.; Huber C.; Ahlrichs R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. 10.1063/1.467146. [DOI] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
- Aquino F. W.; Shinde R.; Wong B. M. Fractional Occupation Numbers and Self-Interaction Correction-Scaling Methods with the Fermi-Löwdin Orbital Self-Interaction Correction Approach. J. Comput. Chem. 2020, 41, 1200–1208. 10.1002/jcc.26168. [DOI] [PubMed] [Google Scholar]
- Shinde R.; Yamijala S. S. R. K. C.; Wong B. M. Improved Band gaps and Structural Properties from Wannier–Fermi–Löwdin Self-Interaction Corrections for Periodic Systems. J. Phys.: Condens. Matter 2020, 33, 115501. 10.1088/1361-648x/abc407. [DOI] [PubMed] [Google Scholar]
- Grimme S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- Luo J.; Wang X.; Li S.; Liu J.; Guo Y.; Niu G.; Yao L.; Fu Y.; Gao L.; Dong Q.; Zhao C.; Leng M.; Ma F.; Liang W.; Wang L.; Jin S.; Han J.; Zhang L.; Etheridge J.; Wang J.; Yan Y.; Sargent E. H.; Tang J. Efficient and Stable Emission of Warm-White Light from Lead-Free Halide Double Perovskites. Nature 2018, 563, 541–545. 10.1038/s41586-018-0691-0. [DOI] [PubMed] [Google Scholar]
- Lippert G.; Hutter J.; Parrinello M. A Hybrid Gaussian and Plane Wave Density Functional Scheme. Mol. Phys. 1997, 92, 477–487. 10.1080/00268979709482119. [DOI] [Google Scholar]
- Bartels D. M. Moment Analysis of Hydrated Electron Cluster Spectra: Surface or Internal States?. J. Chem. Phys. 2001, 115, 4404–4405. 10.1063/1.1391476. [DOI] [Google Scholar]
- Bartels D. M.; Takahashi K.; Cline J. A.; Marin T. W.; Jonah C. D. Pulse Radiolysis of Supercritical Water. 3. Spectrum and Thermodynamics of the Hydrated Electron. J. Phys. Chem. A 2005, 109, 1299–1307. 10.1021/jp0457141. [DOI] [PubMed] [Google Scholar]
- Kumar A.; Walker J. A.; Bartels D. M.; Sevilla M. D. A Simple Ab Initio Model for the Hydrated Electron That Matches Experiment. J. Phys. Chem. A 2015, 119, 9148–9159. 10.1021/acs.jpca.5b04721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turi L.; Sheu W.-S.; Rossky P. J. Characterization of Excess Electrons in Water-Cluster Anions by Quantum Simulations. Science 2005, 309, 914–917. 10.1126/science.1115808. [DOI] [PubMed] [Google Scholar]
- Frigato T.; VandeVondele J.; Schmidt B.; Schütte C.; Jungwirth P. Ab Initio Molecular Dynamics Simulation of a Medium-Sized Water Cluster Anion: From an Interior to a Surface-Located Excess Electron via a Delocalized State. J. Phys. Chem. A 2008, 112, 6125–6133. 10.1021/jp711545s. [DOI] [PubMed] [Google Scholar]
- Qu Y.; Zhang C.; Li F.; Chen J.; Zhou Q. Photo-Reductive Defluorination of Perfluorooctanoic Acid in Water. Water Res. 2010, 44, 2939–2947. 10.1016/j.watres.2010.02.019. [DOI] [PubMed] [Google Scholar]
- Su Y.; Rao U.; Khor C. M.; Jensen M. G.; Teesch L. M.; Wong B. M.; Cwiertny D. M.; Jassby D. Potential-Driven Electron Transfer Lowers the Dissociation Energy of the C–F Bond and Facilitates Reductive Defluorination of Perfluorooctane Sulfonate (PFOS). ACS Appl. Mater. Interfaces 2019, 11, 33913–33922. 10.1021/acsami.9b10449. [DOI] [PubMed] [Google Scholar]
- Cercek B. Activation Energies for Reactions of the Hydrated Electron. Nature 1969, 223, 491–492. 10.1038/223491a0. [DOI] [Google Scholar]
- Cercek B.; Ebert M. Activation Energies for Reactions of the Hydrated Electron. J. Phys. Chem. 1968, 72, 766. 10.1021/j100848a076. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.