Abstract
Alzheimer’s Disease (AZD) is a neurodegenerative disease for which there is now no known effective treatment. Mild cognitive impairment (MCI) is considered a precursor to AZD and affects cognitive abilities. Patients with MCI have the potential to recover cognitive health, can remain mildly cognitively impaired indefinitely or eventually progress to AZD. Identifying imaging-based predictive biomarkers for disease progression in patients presenting with evidence of very mild/questionable MCI (qMCI) can play an important role in triggering early dementia intervention. Dynamic functional network connectivity (dFNC) estimated from resting-state functional magnetic resonance imaging (rs-fMRI) has been increasingly studied in brain disorder diseases. In this work, employing a recent developed a time-attention long short-term memory (TA-LSTM) network to classify multivariate time series data. A gradient-based interpretation framework, transiently-realized event classifier activation map (TEAM) is introduced to localize the group-defining “activated” time intervals over the full time series and generate the class difference map. To test the trustworthiness of TEAM, we did a simulation study to validate the model interpretative power of TEAM. We then applied this simulation-validated framework to a well-trained TA-LSTM model which predicts the progression or recovery from questionable/mild cognitive impairment (qMCI) subjects after three years from windowless wavelet-based dFNC (WWdFNC). The FNC class difference map points to potentially important predictive dynamic biomarkers. Moreover, the more highly time-solved dFNC (WWdFNC) achieves better performance in both TA-LSTM and a multivariate CNN model than dFNC based on windowed correlations between timeseries, suggesting that better temporally resolved measures can enhance the model’s performance.
Keywords: rs-fMRI, dynamic functional network connectivity, LSTM, explainable AI, mild cognitive impairment
1. Introduction
Alzheimer’s Disease (AZD) is an age-related leading cause of dementia and is listed as the fifth cause of death in elderly Americans [1]. People with AZD experience different levels of difficulties in cognitive skills, including memory, language, and problem-solving. To date, there is no effective treatment for curing or stopping the progression of dementia due to AZD. Mild cognitive impairment (MCI) is a precursor stage of AZD. An individual with MCI has experienced a faster cognitive decline than normal aging. Unlike AZD, MCI is reversible, and people with MCI have a chance to recover their normal cognitive ability [2]. Therefore, predicting how MCI progresses and investigating the biomarkers related to cognitive decline are strongly needed for early dementia intervention, such as lifestyle changes [3] and cognitive training [4] to prevent progression in patients with strong risk indicators.
Blood oxygenation level-dependent (BOLD) functional magnetic resonance imaging (fMRI) continuously measures the changes of blood flow as a proxy for localized neuronal brain activation. Resting-state fMRI (rs-fMRI) measures the activity under the task-free paradigm, representing the default brain signal. Resting state fMRI has been widely used for studying the evolving brain configuration related to mental disorders, such as MCI [5, 6], AZD [7], and schizophrenia [8]. The high-dimensionality and complexity of rs-fMRI has created a rich environment of transformations to study in connection with function and disease. One multi-stage transformation of the fMRI signal that has been of increasing interest to fMRI researchers is dynamic functional network connectivity (dFNC) [9], which represents the dynamic coupling between functional brain networks by computing the Pearson correlation on successive sliding windows through the scan (SWCdFNC) [10]. Windowless wavelet-based dFNC (WWdFNC) [11] computes the connectivity at each scan timepoint using time-varying frequency domain information from the continuous wavelet transform. The coupling measured in this way has higher temporal and spectral resolution than sliding window correlations, which functions as a low-pass filter on the dynamics and blurs the base of information [11].
Deep learning has made significant advances using neuroimaging data for classification [12, 13] and prediction [14] tasks. A number of previous studies have applied machine learning, e.g. support vector machines (SVMs) [14] or deep learning methods to identify MCI patients who will develop AZD based on neuroimaging data, including rs-fMRI. In one previous study, a deep learning network with random forest feature selection was built to perform a four-class classification: healthy control (HC), MCI patients who remain diagnosed with MCI (MCI-stable), MCI patients who develop AZD (MCI-converters) and patients who start the study with AZD and remain with that diagnosis (AZD) [15]. Multimodal fusion deep learning models have also used to predict the MCI conversion to AZD using magnetic resonance imaging (MRI) and positron emission tomography (PET) data [16, 17]. However, there is much less research attention on the group of patients exhibiting milder cognitive deficits falling into the questionable/ mild MCI category (qMCI) who recover healthy cognitive function (qMCI-R). That MCI patients can recover is confirmed in several research studies; the recovery rate is 8% in clinical studies and 25% in population studies [18]. The existing research investigates the qMCI-R predictors mainly in lifestyle activity [3], and other diseases’ affect [19, 20], but is very limited in neuroimaging. To fill the research gap, it is worth more attention to develop classification/ prediction methods involving qMCI-R group.
The problem of understanding “why deep learning models predict what they predict” has been attracting more attention recently, with an increased emphasis being placed on building interpretable and reliable models [21]. Explainable AI (XAI) allows us to explain the model’s result by highlighting the most contributed input features. We can evaluate the XAI’s interpretive power by comparing with prior knowledge. In turn, the reliable XAI method can help us to uncover unknown class-defining features. In the neuroimaging domain, deploying a comprehensive meta-analysis regarding the biomarkers related to brain disorders, such as functional or structural biomarkers, is not easy and sometimes not consistent because of the individual differentiation in complex brain systems, the limited size of the analyzed dataset, and the diversified analytical approaches. Reliable XAI is particularly important in domains of such as this, where the science is still poorly understood, and can broaden our understanding of class-relevant features. Numerous interpretability methods have been developed, including gradient-based [22, 23], perturbation-based [24, 25] and SHAP [26]. The saliency map approach [22] is a gradient-based black-box decoding approach that allows visualization of each input’s contribution. The perturbation-based method recursively eliminates or substitutes the input to generate feature importance maps based on the change in the predicted score. Perturbation can produce out-of-distribution samples and also requires substantial computational power. These and other XAI approaches help provide explanations of prediction scores based on input features and can be visualized as intensity maps on the input space. However, model interpretation for multivariate time series data remains challenging because of the conflation between time and features [27]. Temporal Saliency Rescaling (TSR) [27], a similar approach to our work, calculates the time and feature relevance scores separately. But TSR is evaluated each at each timepoint via perturbation, which does not consider the time-dependency of time series data.
Another critical concern impacting the practical utility of interpretation methods centers on the trustworthiness and human interpretability of the resulting model explanations. We argue that the model’s interpretive trustworthiness is built on the ability to identify at least a subset [28] of ground-truth class-defining predictors. Deep learning architectures are often underspecified [28, 29] and can achieve equivalent performance focusing on different features under random reinitialization. Understandable mappings of predictor importance allows humans using these models to learn critical relationships between predictors and predictive targets that can inform subsequent domain modeling, and also makes it easier for human domain experts to gauge model trustworthiness. A good interpretation should provide a qualitative representation of the relationship between the input and the model prediction [29] and be displayed in low-level dimensionality. For example, while image classification models use a tensor representation per pixel in each color channel to make the final prediction, a good interpretation result may be one channel map showing each pixel’s contribution. Likewise, for time series classification, the interpretation needs to translate the tensor representation of time-dependency and cell status used by the model into a qualitative representation with each time point.
Our contributions
To tackle the challenges outlined above, we introduce a gradient-based interpretation framework, Transiently-realized Event Classifier Activation Map (TEAM). This framework is capable of interpreting transiently-realized class-defining features of multivariate time series from time-attention LSTM (TA-LSTM) classifier. We systematically evaluated TEAM’s interpretation power in simulation studies to test the trustworthiness, which is a rare practice in other XAI studies. The results demonstrated that the TA-LSTM with TEAM efficiently learned from the multivariate time series data and was able to interpret the class-defining pattern occurrences (TPO) and class difference features with at least moderate correlation when compared to the ground truth, and it achieved 100% sensitivity and 98.13% mean specificity in interpreting the class difference features. The interpretive power-validated TEAM was then applied to a real neuroimaging dataset, the latest release in the Open Access Series of Imaging Studies (OASIS-3). Our objective was to train and interpret the classifier to predict the deterioration or recovery of the qMCI subjects. Furthermore, we studied the recovery qMCI groups, which has not been extensively explored in neuroimaging studies. The TEAM CDM interpretation results expanded our knowledge of potential biomarkers for predicting qMCI progression. Moreover, we find that our models are more accurate when trained on higher temporal resolution WWdFNCs vs. the more slowly varying SWCdFNCs: accuracy was 79.3% with TA-LSTM and 72.6% with multivariate CNN (refer to M-CNN below) trained with WWdFNCs in contrast with accuracies of 72.9% with TA-LSTM and 70.2% with M-CNN trained on SWCdFNCs suggests that better temporally resolved measures of dynamic brain connectivity can enhance the model’s performance. Furthermore, the TA-LSTM model outperformed the baseline model M-CNN on training with two types of dFNCs.
2. Materials and Methods
2.1. Overall procedure
In the initial phase of this study, six simulation studies were conducted to evaluate the interpretive capabilities of the TEAM framework. Multivariate time series data with predetermined class-defining features for each group were generated and evaluated using a train-test split approach. The TEAM interpretation framework was utilized to analyze the temporal pattern occurrences (TPO) and class difference map (CDM) of the class-defining features, which were then compared to the synthetic data’s ground truth to assess the TEAM’s trustworthiness. Upon validating the TEAM’s efficacy, the same methodology was applied to a neuroimaging study to predict the qMCI group’s progression or recovery in the next three-year timeframe after fMRI scanning. The rs-fMRI data underwent preprocessing and GICA decomposition to generate fifty-three independent components’ time courses in seven domains, as detailed in section 2.2.3. The time courses were transformed into Windowless wavelet-based dFNC (WWdFNC), as depicted in Fig. 1, and conventional successive sliding windows through the scan (SWCdFNC) was also generated for comparison purposes. TA-LSTM was employed to train and evaluate the dFNCs in a ten-fold cross-validation manner, and the multivariate CNN (M-CNN) model was also trained and evaluated using the same procedure for comparison. Finally, the trained models were interpreted using the simulation-validated TEAM to generate CDM. The overall procedure is depicted in Fig. 1.
Fig. 1.
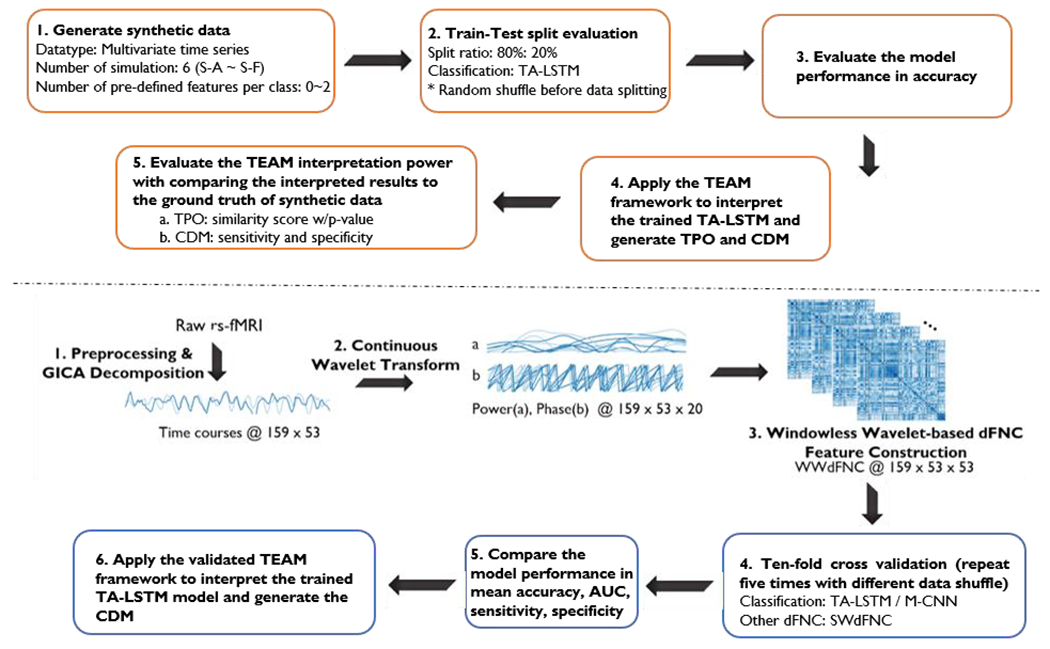
The figure illustrates the overall procedure used in this study that uses a rigorous methodology involving simulation and validation to develop and apply TA-LSTM model and TEAM interpretation work for predicting the conversion of qMCI using rs-fMRI data. The upper diagram illustrates the steps for conducting a simulation study, which involves generating synthetic data, training and evaluating the deep learning model, and validating the interpretation power of the TEAM model. The lower diagram outlines the steps for predicting the conversion of qMCI using rs-fMRI data, including generating WWdFNC data, evaluating deep learning models (TA-LSTM, M-CNN) on WWdFNC and SWCdFNC data, and interpreting the results using the TEAM model.
2.2. Materials and Data Processing
2.2.1. Synthetic data
To assess the trustworthiness of the interpretation results obtained from TEAM, we generated synthetic data, train it using a TA-LSTM model. We then interpreted the classifier using TEAM, and assessed the interpretation results. We simulated samples of multivariate time series data where each class is defined by transiently-realized feature patterns. Through TEAM, time points where these class-defining features occur should at least partially be identified as important, and those features are expected to be at least partially identified and displayed in the class difference map. We created six synthetic experiments. Each experiment consists of multivariate time series samples. Each sample is a -dimensional time series of length timepoints. In the synthetic experiments, every class contains class-defining features. Each class-defining pattern consists of two selected features occur in randomly selected five consecutive time points; and it follows the normal distribution with specified mean.
To be specific, we simulated the multivariate time series data following the base distribution, which is a Gaussian distribution with and except the class-defining feature patterns. Each class-defining feature pattern consists of two contiguous features that occur at non-repeating five consecutive time points following a distribution with a mean of . To avoid the repetition of time block selection, we chose the start time point for the “random” time block sequentially from the first time point to (or reversely). A simplified example is shown in Fig. 2, which contains five samples in the positive class of S-A. Two features (shown in red and green) act as class-defining features for the positive class of S-A, following a distribution with a mean of that is higher than the base distribution and lasts in random five consecutive time points. Once the TA-LSTM model finished training on the synthetic data, we expect that TEAM interprets the time blocks with class-defining feature patterns occurrences, which are the time points highlighted in the light grey blocks in Fig. 2, as well as the class-defining features represented by red and green lines. To investigate if TEAM is merely enhancing the global-wise attributes of class difference, in S-C, we balanced out the selected features by assigning value in non-selecting time points with a determined mean (as shown in the second black box in the Fig. 3 S-C). As a result, no feature demonstrates a class-level difference in the average statistics of full-time series between classes. More distinct feature patterns were simulated in S-D, S-E, and S-F in one or both classes. Table 1 displays all the parameters for the statistics of the synthetic data, while a comprehensive synthetic data set can be seen in Fig. 3. In each simulation within the figure, each block represents a multivariate data sample, with only one sample visualized for the null (negative) class, and the first four and the last sample visualized for the class with predefined class-sharing pattern(s). The color bar for each simulation is shown on the left side, and the predefined feature patterns for each non-null class are circled in small black boxes in the first displayed sample.
Fig. 2.
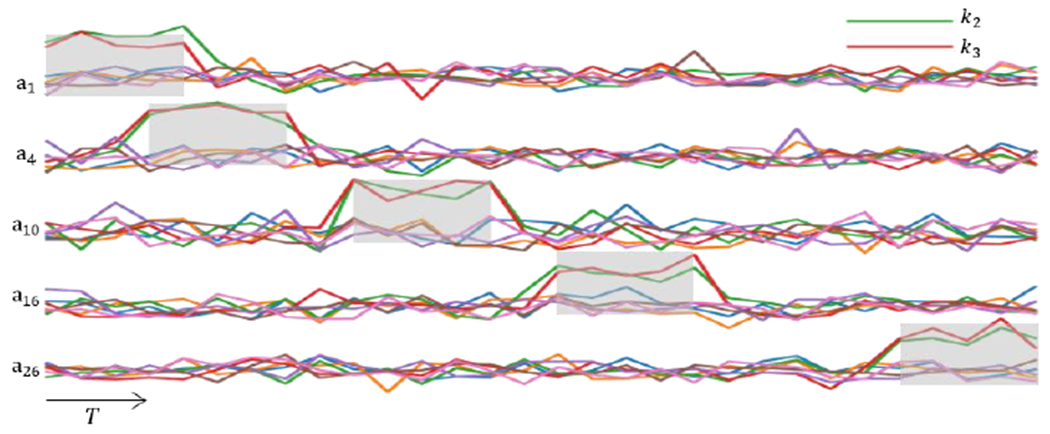
This figure visualizes a subset of simulated multivariate time series from one class (S-A positive class) that contains five samples . All samples in this class have assigned the same class-defining feature set (as shown in the green and red time series), and the statistics followed the normal distribution with a different mean and lasted for five consecutive time points. We referred to two selected class-defining features that follow a different statistic and last for five consecutive time points, as a class-defining pattern. The temporal occurrences of class-defining pattern for various samples begin at random time points, and the ground truth of temporal pattern occurrences are highlighted in light grey blocks.
Fig. 3.
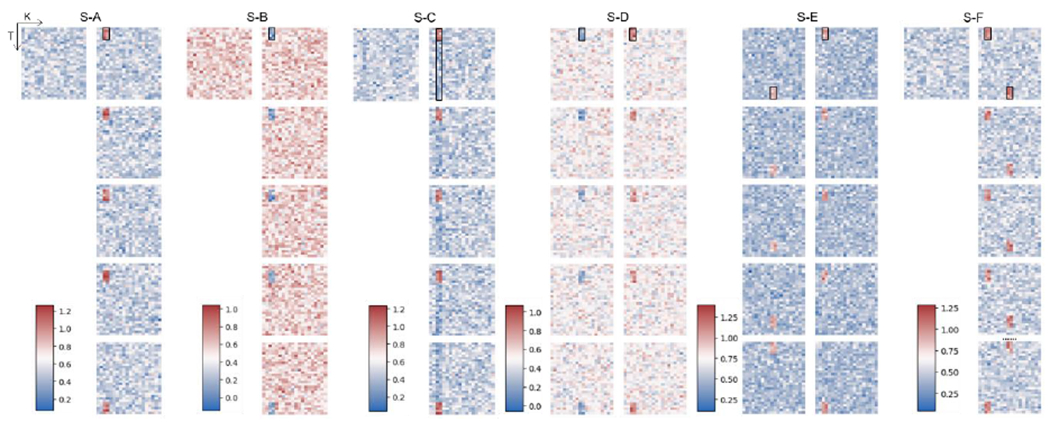
This visualization displays six groups of synthetic data, denoted as S-A to S-F. Each simulation is divided into two columns, with the left column representing the negative class and the right column representing the positive class. Each block within a simulation represents a multivariate data sample, with only one sample visualized for the null (negative) class. The x-axis in each block corresponds to the features, while the y-axis corresponds to time. The class-defining patterns for each class are highlighted in a small black box in the first displayed sample.
Table 1.
Table of statistical parameters defining classes in the synthetic data. The base multivariate time series follow a normal distribution where and ). Each pair of and s shown in the table represents one feature pattern. For example, the positive class in simulation A, the feature and and follows the normal distribution with and in selected five consecutive time points. All other features except and in entire T as well as and in time points except selected five consecutive time points follow the base distribution if no other parameters specified. For better visualized evaluation, the selected five consecutive time points (refer as time blocks below) starts at for for , and so on. Such pattern applied to all the simulations except the second pattern of positive class in simulation F, which the second pattern starts in reverse order (start at for for , and so on). All index used in the table is 0-indexing.
| Negative Class | Positive Class | |
|---|---|---|
| S-A | - | |
| S-B | - | |
| S-C | - | |
| S-D | ||
| S-E | ||
| S-F | - |
|
| Base Distribution: | ||
2.2.2. Resting-state fMRI Data
We used data from OASIS-3 [30] which is a longitudinal dataset of participants at various stages of cognitive decline related to Alzheimer’s Disease collected in Washington University Knight Alzheimer Disease Research Center with Institutional Review Board approval. The clinical dementia rating (CDR) scale score distinguish a questionable dementia/ mild cognitive impairment (CDR 0.5) with cognitively health (CDR 0) and dementia (). We use the CDR scale score at and three years after the MR imaging acquired session to identify the progression direction of qMCI patients. The qMCI recovery (qMCI-R) subjects had a CDR of 0.5 prior to the final scan, and returned to 0 within three years. The qMCI progression (qMCI-P) subjects had a CDR of 0.5 at the scan time and progressed to a CDR of greater than 0.5 in the three-year timeframe. We used one rs-fMRI session per participant in our final sample dataset, and the final dataset consists of 94 rs-fMRI scans (50 qMCI-R, 44 qMCI-P) with age and gender-balanced. The demographic information is summarized in Table 2.
Table 2.
Demographic and Clinical Information (Table reproduced from [31]) SD, Standard Deviation; qMCI, questionable Mild Cognitive Impairment; CDRYn, n-year after MR scan session;
| Mean ± SD | Recovery qMCI | Progressive qMCI | P value |
|---|---|---|---|
| Number | 50 | 44 | - |
| Age | 73.81 ± 6.77 | 75.23 ± 7.15 | 0.33a |
| Gender (M/F) | 27/23 | 27/17 | 0.47a |
| CDRY0 | 0.5 | 0.5 | - |
| CDRY3 | 0 ± 0 | 1.13 ± 0.38 | - |
Two sampled T-test
We excluded the qMCI subjects with a CDR of 0.5 at and three years after the MR session. Based on the available longitudinal clinical demographic records, the stable qMCI participants have the potential to recover or to progress within the 3 year timeframe of the study. Subjects who neither recover nor progress within this timeframe, so-called “stable qMCI” subject, are on indeterminate future paths, with prospective intermediate-horizon futures ranging from recovery of normal to persistent qMCI to development of AZD. In this group will be a mix of features that relate to disparate unmeasured future outcomes, including possible recovery or progression, so the “stable qMCI” cohort cannot be treated as the disjoint third class.
2.2.3. Data Preprocessing and dFNC Feature Representation
We preprocessed the rs-fMRI using statistical parametric mapping (SPM12, http://www.fil.ion.ucl.ac.uk/spm/) by removing first five time points and performing the rigid body motion correction and slice timing correction. We used an echo-planar imaging (EPI) template to fit the rs-fMRI data into standard Montreal Neurological Institute (MNI) space and resampled to 3 × 3 × 3 mm3 voxels. The data were smoothed using a Gaussian kernel (FWHM = 5mm), and were normalized to finalize the preprocessing. Next, we decomposed the preprocessed rs-fMRI with group independent component analysis (GICA) to the independent components (ICs) and the corresponding timecourses (TCs) by adopting the NeuroMark pipeline [32]. Fifty-three pairs of ICs and TCs were selected and arranged into seven functional domains based on the spatial location, and seven domains include subcortical (SC), auditory (AU), sensorimotor (SM), visual (VI), cognitive control (CC), default mode (DM), and cerebellar (CB). The fifty-three independent component network labels and peak coordinates are shown in Table 3. In this work, we use z-scored TCs in the analysis.
Table 3.
Independent Component Network labels and peak coordinates
| ICNs | X | Y | Z |
|---|---|---|---|
| Subcortical (SC) | |||
| Caudate (69) | 6.5 | 10.5 | 5.5 |
| Subthalamus/hypothalamus (53) | −2.5 | −13.5 | −1.5 |
| Putamen (98) | −26.5 | 1.5 | −0.5 |
| Caudate (99) | 21.5 | 10.5 | −3.5 |
| Thalamus (45) | −12.5 | −18.5 | 11.5 |
| Auditory (AU) | |||
| Superior temporal gyrus ([STG], 21) | 62.5 | −22.5 | 7.5 |
| Middle temporal gyrus ([MTG], 56) | −42.5 | −6.5 | 10.5 |
| Sensorimotor (SM) | |||
| Postcentral gyrus ([PoCG], 3) | 56.5 | −4.5 | 28.5 |
| Left postcentral gyrus ([L PoCG], 9) | −38.5 | −22.5 | 56.5 |
| Paracentral lobule ([ParaCL], 2) | 0.5 | −22.5 | 65.5 |
| Right postcentral gyrus ([R PoCG], 11) | 38.5 | −19.5 | 55.5 |
| Superior parietal lobule ([SPL], 27) | −18.5 | −43.5 | 65.5 |
| Paracentral lobule ([ParaCL], 54) | −18.5 | −9.5 | 56.5 |
| Precentral gyrus ([PreCG], 66) | −42.5 | −7.5 | 46.5 |
| Superior parietal lobule ([SPL], 80) | 20.5 | −63.5 | 58.5 |
| Postcentral gyrus ([PoCG], 72) | −47.5 | −27.5 | 43.5 |
| Visual (VI) | |||
| Calcarine gyrus ([CalcarineG], 16) | −12.5 | −66.5 | 8.5 |
| Middle occipital gyrus ([MOG], 5) | −23.5 | −93.5 | −0.5 |
| Middle temporal gyrus ([MTG], 62) | 48.5 | −60.5 | 10.5 |
| Cuneus (15) | 15.5 | −91.5 | 22.5 |
| Right middle occipital gyrus ([R MOG], 12) | 38.5 | −73.5 | 6.5 |
| Fusiform gyrus (93) | 29.5 | −42.5 | −12.5 |
| Inferior occipital gyrus ([IOG], 20) | −36.5 | −76.5 | −4.5 |
| Lingual gyrus ([LingualG], 8) | −8.5 | −81.5 | −4.5 |
| Middle temporal gyrus ([MTG], 77) | −44.5 | −57.5 | −7.5 |
| Cognitive control (CC) | |||
| Inferior parietal lobule ([IPL], 68) | 45.5 | −61.5 | 43.5 |
| Insula (33) | −30.5 | 22.5 | −3.5 |
| Superior medial frontal gyrus ([SMFG], 43) | −0.5 | 50.5 | 29.5 |
| Inferior frontal gyrus ([IFG], 70) | −48.5 | 34.5 | −0.5 |
| Right inferior frontal gyrus ([R IFG], 61) | 53.5 | 22.5 | 13.5 |
| Middle frontal gyrus ([MiFG], 55) | −41.5 | 19.5 | 26.5 |
| Inferior parietal lobule ([IPL], 63) | −53.5 | −49.5 | 43.5 |
| Left inferior parietal lobue ([R IPL], 79) | 44.5 | −34.5 | 46.5 |
| Supplementary motor area ([SMA], 84) | −6.5 | 13.5 | 64.5 |
| Superior frontal gyrus ([SFG], 96) | −24.5 | 26.5 | 49.5 |
| Middle frontal gyrus ([MiFG], 88) | 30.5 | 41.5 | 28.5 |
| Hippocampus ([HiPP], 48) | 23.5 | −9.5 | −16.5 |
| Left inferior parietal lobue ([L IPL], 81) | 45.5 | −61.5 | 43.5 |
| Middle cingulate cortex ([MCC], 37) | −15.5 | 20.5 | 37.5 |
| Inferior frontal gyrus ([IFG], 67) | 39.5 | 44.5 | −0.5 |
| Middle frontal gyrus ([MiFG], 38) | −26.5 | 47.5 | 5.5 |
| Hippocampus ([HiPP], 83) | −24.5 | −36.5 | 1.5 |
| Default mode (DM) | |||
| Precuneus (32) | −8.5 | −66.5 | 35.5 |
| Precuneus (40) | −12.5 | −54.5 | 14.5 |
| Anterior cingulate cortex ([ACC], 23) | −2.5 | 35.5 | 2.5 |
| Posterior cingulate cortex ([PCC], 71) | −5.5 | −28.5 | 26.5 |
| Anterior cingulate cortex ([ACC], 17) | −9.5 | 46.5 | −10.5 |
| Precuneus (51) | −0.5 | −48.5 | 49.5 |
| Posterior cingulate cortex ([PCC], 94) | −2.5 | 54.5 | 31.5 |
| Cerebellar (CB) | |||
| Cerebellum ([CB], 13) | −30.5 | −54.5 | −42.5 |
| Cerebellum ([CB], 18) | −32.5 | −79.5 | −37.5 |
| Cerebellum ([CB], 4) | 20.5 | −48.5 | −40.5 |
| Cerebellum ([CB], 7) | 30.5 | −63.5 | −40.5 |
We used a windowless wavelet-based functional network connectivity measure as detailed in [11] to investigate time-varying connectivity between brain networks. The coupling status of networks at each timepoint is represented using WWdFNC, a wavelet-based measure. The WWdFNC starts by performing a continuous wavelet transform of each univariate network timeseries using the complex Morlet wavelet at evenly spaced frequencies. For each univariate network timeseries, this results in a complex-valued multivariate time-frequency domain timeseries (mTFTs), . Assuming we have N samples and k TCs for each sample as input , we decompose network’s time-courses into and let denote the wavelet coefficient that represents the power and phase at frequency j in network k at time t. The network connectivity was then calculated by taking both power and phase synchrony into account. Power-weighted phase synchrony is used to compute the WWdFNC between and at t:
| (1) |
where and are the power and phase coefficient for network k at time t, respectively. The pipeline of construction of WWdFNC is shown in Fig. 1.
Another dFNC representation used in this work for evaluation and comparison is computed as a set of network-pair correlations on the successive sliding windows through the scan (SWCdFNC) [10]. SWCdFNC was computed from the rs-fMRI and underwent the same data preprocessing and GICA decomposition NeuroMark pipeline. The preprocessed TCs were segmented by a tapered window generated by convolving a rectangle (window size = 20, TR = 44s) with a Gaussian . The window was slid in the step of 1TR resulting in 139 windows in total.
2.3. Methodology
2.3.1. Long Short-term Memory (LSTM)
In this work, we used the LSTM-based model, TA-LSTM, which features a model architecture starting with three LSTM layers. Long short-term memory was initially proposed in [33], and has proved its performance in multiple domains while dealing with sequential data. Compared to recurrent neural networks, the LSTM architecture can more effectively manage and preserve the long-term dependencies. The repeating module, known as unit or cell, is the fundamental building block of the LSTM layer. Each unit includes three computation gates, namely forget , input , and output . These gates work together to regulate the flow of information into, storage within, and output from each memory unit. The forget, input and output gate have a sigmoid layer to regulate the new information , previous hidden state and long-term memory , and the input and output gate have the elementwise multiplication followed after the sigmoid function to produce the cell state candidate and cell output . The new cell state, is updated by the previous cell status , and . The gates computation and the calculation of the corresponding state formula are shown in equation (2) - (7), in which W and b are model parameters optimized during the training process.
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
2.3.2. Time Attention Layer
The attention mechanism proposed in [34] represents a state-of-art approach that offers more accurate and efficient performance when compared to conventional convolutional and recurrent models. Furthermore, [35] highlights the attention mechanism’s capability to resolve the vanishing gradient issue while on the interpretation work with an additive attention mechanism, as demonstrated in [36]. In this work, we incorporated a scaled dot-product layer after LSTM layers, integrating the self-attention key, query, and value mechanisms. To map the output of the attention layer to the class probabilities for the classification task, a common approach involves applying global pooling. Global pooling reduces the dimensionality and summarizes the features in one-cut at each hidden neuron level when applied in the LSTM-based model. Considering the context of time series data where the “event” occur at unknown and random time, such as rs-fMRI data, we have designed the time summarization approach that better extracts the high-level feature and represent them in the time representation vector. The time attention layer comprises a scaled dot-product and time summarization mechanism. The attention-weighted output calculated from time attention layer is computed by:
| (8) |
where the query , key , and value is the feature representation learned from the last LSTM layer. It is to be noted that query is generated by half random dropout to avoid overfitting. The scaled dot-product allow each time position connect to all of the position to compute the attention score first, then the attention output is computed by attention score weighted sum of the value . The attention output further be reduced to the dimensionality of one element at one time through the time pooling layer. After the time attention layer, a fully connected layer is connected to produce the class probability output. The overview of TA-LSTM architecture is shown in Fig. 4.
Fig. 4.
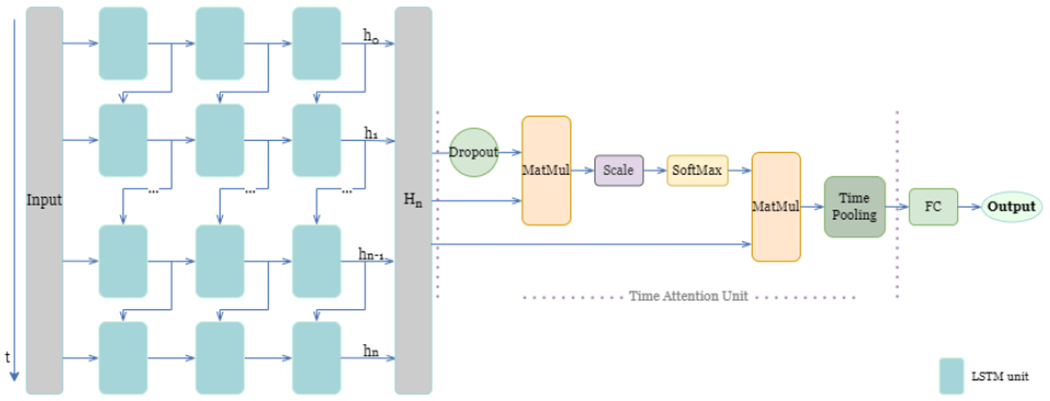
Time-Attention LSTM (TA-LSTM) model architecture includes LSTM layer(s) connected with time attention unit and fully connected layer. The hidden status of the n-th hidden units in the last layer of the model is represented by is a matrix that contains the hidden status of all the hidden units for each time point. The blue box on the left side of the diagram represents a single LSTM unit. The output of the LSTM layer(s), denoted as , is then utilized as the input of the time attention unit. The detailed formulation of the time attention unit is presented in Section 2.3.2. FC block in the right side stands for fully connected layer.
2.3.3. Transiently-realized Event Classifier Activation Map (TEAM)
XAI mechanisms have been proposed to provide an explanation for how the model arrives at its predictions [37], enhancing its trustworthiness and transparency. Additionally, when the interpretation mechanism is effective in explaining the data, it can be utilized to expand our understanding of data that is not yet fully understood. In this study, we first trained the TA-LSTM model, as described in previous sections, in this section, we introduced an interpretation framework called Transiently-realized Event classifier Activation Map (TEAM), to understand the reasoning, to be specific, the transiently-realized class-defining patterns, behind the predictions made by TA-LSTM model. TEAM framework is first tested on the simulation data, the interpretation power is evaluated by comparing the results to ground truth of synthetic data. Then we applied TEAM framework to understand the neuroimaging data, which in this study, was transformed rs-fMRI data used to predict the deterioration or recovery of qMCI subjects.
The proposed TEAM framework aims to capture transient time intervals that correspond to the occurrence of class-defining patterns, with the purpose of localizing short time intervals across the entire time period; and analyze the selected time intervals from input between classes to identify class difference features. To accomplish this, the saliency map approach [22] is employed to obtain the contribution of each input from the trained model. It computes the gradients of the predicted class score with respect to the input by finding the derivative via the backpropagation. The saliency map for input is . The values are averaged across all K features to obtain the temporal pattern occurrences (TPO), which shows the contribution of time points with class-defining patterns occurrences, as shown in Fig. 5A. Subsequently, we apply the statistical test to the original time series input corresponding to the positioning of highly contributing intervals acquired from TPO map. To select the highly contributing intervals, time points with value in TPO greater than 0.9 percentile threshold and lower than 0.1 percentile threshold in each class are extracted, as shown in Fig. 5B, as the red blocks and blue blocks represent the upper and lower salient time points, respectively. The and are separately mapped the corresponding position to the original input for each class, and four multivariate time series lists are acquired: , and . ( is a collection of multivariate time series that includes the positions of the positive class corresponding to represents the set where maps to the negative class, and so forth.) The statistics t-test with false discovery rate (FDR) correction is performed on each pair of salient time intervals and the class difference results are shown in Fig. 5D. The sign between two maps were unified by taking the sign of the maximum class-defining difference at each feature location to have the CDM, as shown in Fig. 5E.
Fig. 5.
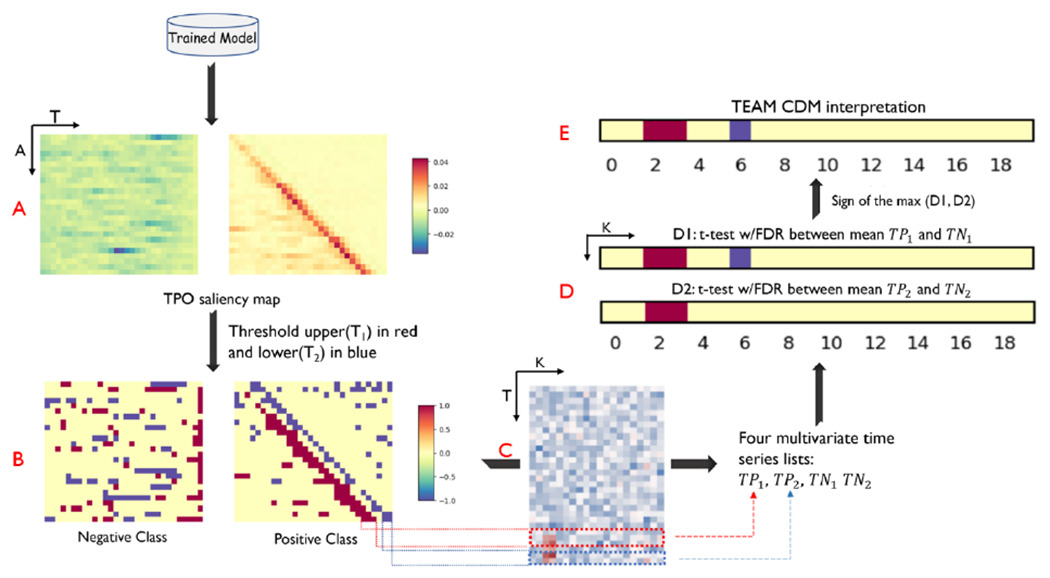
The pipeline of Transiently-realized Event classifier Activation Map (TEAM) interpretation framework. The temporal pattern occurrences (TPO) that define the class were analyzed in the time saliency map generated from the trained TA-LSTM model, as depicted in Figure 5A. Subsequently, the TPO saliency map was thresholded, and the time intervals that made a high contribution were extracted for calculating the class difference map (CDM). The negative and positive high-contributing time intervals were then separately evaluated using a t-test with false discovery rate (FDR) correction between the positive and negative classes, as shown in Figure 5D. The final interpretation result of the CDM was calculated by determining the sign of the maximum class difference between the two maps in Figure 5D. In the t-test with FDR correction plot, the red means the class average of positive class is significantly greater than the negative class ; the index is 0-index, consistent with the index in Table 1. The sample data results shown in the figure is from S-A result.
2.4. Evaluation
2.4.1. Model Training and Performance Evaluation
The simulation data is tested in the train-test split evaluation manner, in which 70% of the randomly selected simulation data is used for training and the remaining 30% hold-out dataset for testing. Considering the low dimensionality and small sample size in the simulation data, the TA-LSTM consists of one LSTM layer with 16 hidden units, the time attention layer, one fully connected layer, and one SoftMax output layer to produce the class probabilities. The optimizer is Adam.
As for the model used to predict the recovery vs. progression from qMCI, the TA-LSTM consists of three LSTM layers with 64 hidden units in each layer, followed by the time attention, fully connected, and output layers. The multivariate CNN model trained as the baseline consists of three convolutional layers with 32 filters in each layer (filter length = 3), one fully connected layer and one SoftMax output layer. Adam optimizer (lr = 1e-4) is used for training the models. We tested the model in a ten-fold cross-validation manner. The ninety-four data were divided into 90% for training and 10% for testing in each fold. The cross-validation evaluation was repeated five times with different random shuffles. A total of fifty trials were averaged and used to report the model performance, and the evaluation metrics include area under the curve (ROC), accuracy, sensitivity, and specificity.
2.4.2. TEAM Interpretation Power Evaluation
MIP of TEAM is evaluated by comparing the interpreted results acquired from TEAM with the ground truth described in Table1 for synthetic data. We evaluated MIP from two aspects: recognition of the Temporal Pattern Occurrence (MIP-TPO) and class difference map (MIP-CDM). We adapt Pearson correlation coefficient [38] to evaluate the MIP-TPO. The calculates the similarity between the mean saliency map and the pre-defined (ground truth) time stamp of the patterns. We believe that the hard threshold extracts the top relevant time points but has limitations since the ratio of the pattern occurrences’ stamp at each direction may not be 0.1. In this case, we measure the MIP-TPO to provide a global representation regardless of the duration of the event and the ratio of events over the entire time. The MIP-TPO includes Pearson correlation coefficient (equation (9)) with , in which is for testing whether the correlation is significant.
| (9) |
The MIP-CDM evaluation metrics include sensitivity and specificity. The sensitivity measures the correctly interpreted features (with the correct direction) over the pre-defined manipulated features, and the ground truth can refer in Table 1 (parameter s). The specificity measures the percentage of correctly interpreted non-manipulated features over all nonmeaningful features.
3. Results
3.1. TA-LSTM Model Performance on Synthetic data
The TA-LSTM model achieved 100% classification accuracy on evaluating the held-out dataset of Simulation A-F.
3.2. TEAM MIP on Synthetic data
From the observation of simulation results shown in Fig. 6, the mean saliency maps generated from the interpretation framework show consistent activation with the ground truth. The MIP-TPO evaluation r assess the similarity, and are shown in Table 4. The S-A, S-B, S-C, S-D (negative class), and S-E achieve the at least moderate correlation based on the rubrics of Dancey & Reidy interpretation [39]. The S-F shows a weak correlation ),but we can observe the mean saliency map interpret the transient intervals in first half time period clear. We also conclude that the signs of values in mean saliency map are consistent with the designed features’ sign with the relationship of null initialization. The designed pattern for positive class in simulation A has a higher value than the mean of the base distribution, and the corresponding interpretation shows the positive activation. The same relationship can be observed in other results. The positive class in S-D is the only one that shows a negative correlation. Remind its ground truths: two different patterns are designed and assigned for each class. The activation map correctly identified the negative class’s pattern but missed the pattern in the positive class. For all simulations, the p-value was also evaluated. All acquired p -value is less than 1e−3, which suggests the mean saliency maps have a statistically significant correlation with the ground truth.
Fig. 6.
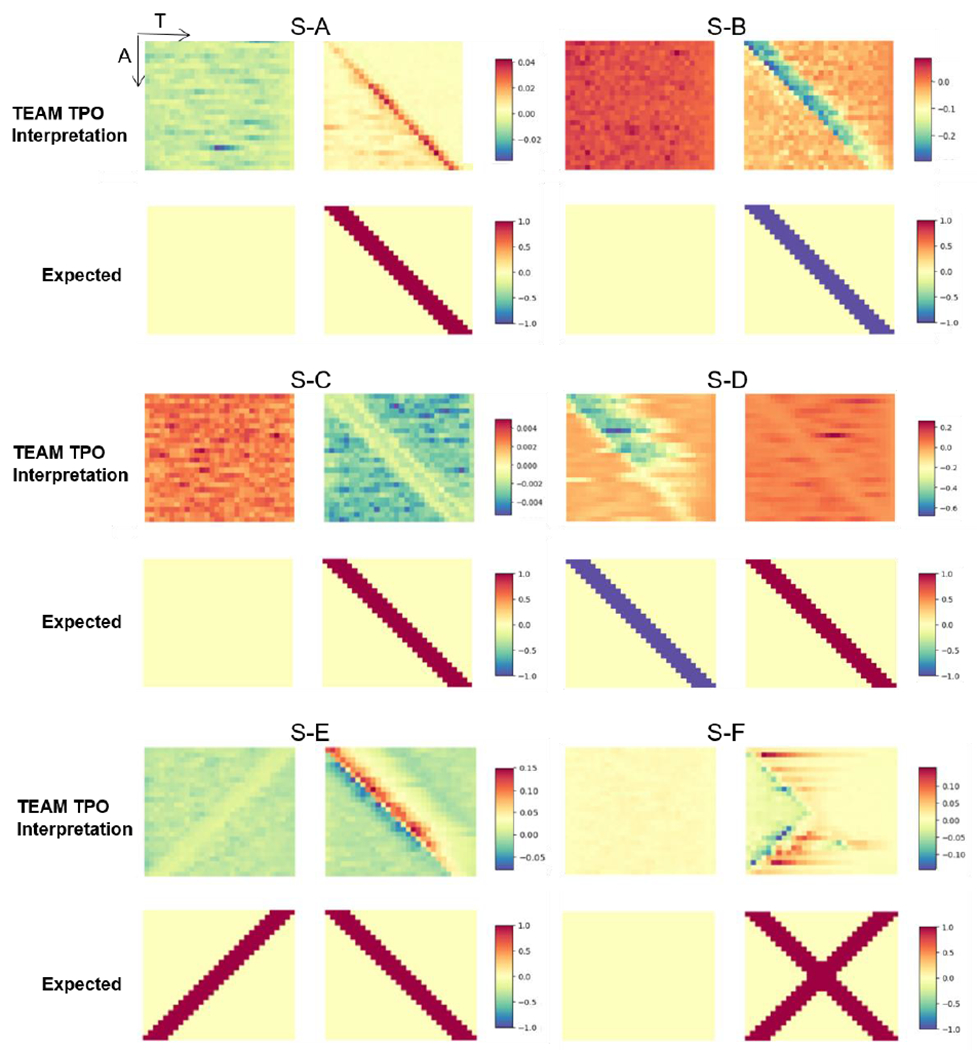
The figure shows the results of TEAM interpreting the temporal pattern occurrence (TPO) and their corresponding expected (ground truth) for simulation S-A through S-F. The left and right plots represent the negative and positive classes, respectively, for each representation. The upper plots show the heatmap are the mean gradient of the saliency map representing the interpreted TPO. The x-axis represents time, and the y-axis corresponds to each sample. The lower plots display the expected TPO, where each highlighted row in the y-axis represents five consecutive time points. For the null class, the expected TPO is null. It should be noted that the subject display sequence in y-axis is the sequence utilized for initializing simulation, and used for better visualization, the shuffled dataset is used for training, evaluation, and interpretation.
Table 4.
Interpretation evaluation for Simulation A-F. The correlation score and p-value for calculating the MIP-TPO is Pearson correlation coefficient, the p value for all simulation is lower than . MIP, model interpretation power; TPO, temporal pattern occurrences; CDM: class difference map.
| Simulation No. | MIP-TPO | MIP-CDM | ||
|---|---|---|---|---|
|
| ||||
| Negative Class | Positive Class | Sensitivity | Specificity | |
| S-A | - | 0.40* | 100% | 94.4% |
| S-B | - | 0.89* | 100% | 100% |
| S-C | - | 0.59* | 100% | 94.4% |
| S-D | 0.53* | −0.35* | 100% | 100% |
| S-E | 0.57* | 0.80* | 100% | 100% |
| S-F | - | 0.22* | 100% | 100% |
p – value
For the evaluation of MIP-CDM, the interpreted CDM obtained from t-test with FDR correction for S-A through S-F is shown in Fig. 7, and sensitivity and specificity metrics are shown in Table 4. The interpretation framework achieves 100% sensitivity in all simulation datasets, which means all designed features are correctly interpreted. At most one feature is incorrectly recognized across all non-relevant features. Two simulations achieved 94.4% specificity, and four simulations achieves 100% specificity.
Fig. 7.
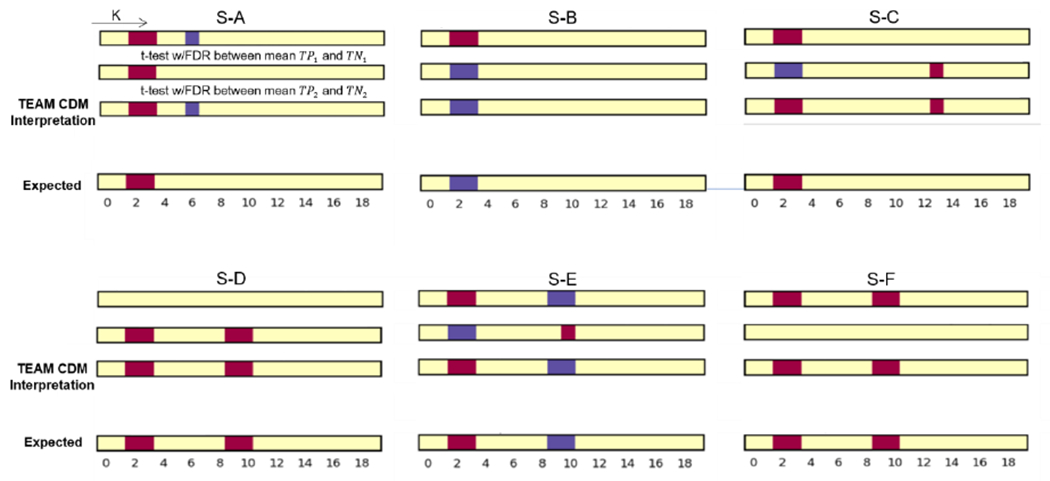
The figure shows the results of TEAM interpreting the class difference map (CDM) and their corresponding expected (ground truth) for simulation S-A through S-F. The top two plots are the statistical test result with FDR correction (p=0.05, and q=0.05) for - and - corresponded input, respectively. The sign of the maximum class difference was retained in the final CDM result. The bottom is the ground-truth feature difference plot. The red cell in feature k represent the average of positive class for k-th feature is significantly greater than negative class, blue cell represents the negative class is significantly greater than the positive class.
3.3. Model Performance on prediction of Recovery vs. Progression from qMCI
We evaluated WWdFNC and SWCdFNC feature representations by training with TA-LSTM model and multivariate CNN in the ten-fold cross-validation manner. For every ten-fold cross-validation, each scan was tested once. We repeated ten-fold cross-validation five times with different shuffle parameters, resulting in 50 trials. We used the mean of 50 trials’ AUC (Area Under the Curve), accuracy, sensitivity, and specificity as the evaluation metrics. The performance is shown in Table 5. The WWdFNC trained by the TA-LSTM achieved 0.789 of AUC and 79.3% accuracy, increasing an average of 0.06 on the AUC metric, and 3.1% on accuracy compared to SWCdFNC. The TA-LSTM outperforms an average of 0.1 in ROC metric than the multivariate CNN model in training both types of dFNC feature representations.
Table 5.
Model performance of prediction of Recovery vs. Progression from qMCI
| Accuracy | AUC | Sensitivity | Specificity | ||
|---|---|---|---|---|---|
| SWCdFNC | M-CNN | 0.702 | 0.659 | 0.528 | 0.852 |
|
|
|||||
| TA-LSTM | 0.729 | 0.762 | 0.706 | 0.808 | |
|
| |||||
| WWdFNC | M-CNN | 0.726 | 0.693 | 0.645 | 0.796 |
|
| |||||
| TA-LSTM | 0.793 | 0.789 | 0.748 | 0.836 | |
3.4. Analysis of class-defining connectivity patterns and discriminative FC biomarkers
We performed the statistical analysis on the cellwise properties on the “strongly-contributing” time intervals. Based on the observations reported in the preceding section, we selected all the and greater than or equal to 3 since we aim to dive into the intervals instead of the single or very short time. The independent samples t-test with multiple comparison correction results shown in two middle plots of Fig. 8. We also performed an additional statistical analysis for validation tests by applying no thresholding. The global (no thresholding) cellwise plot shows few levels of significant difference; and no significant cells after FDR correction. The validation tests elucidate that the model is not strengthening the global-wise attributes of class difference for feature learning and show the discriminative temporal patterns that extracted in the saliency maps. The final plot was constructed by unifying the middle two plots and shown in left most plot in Fig. 8.
Fig. 8.
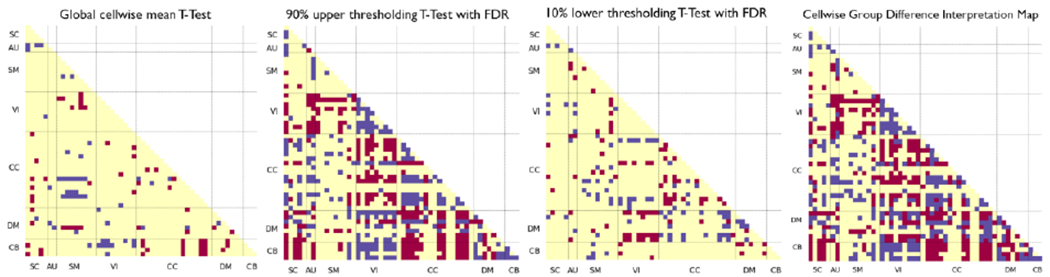
T-test for differences between qMCI-R and qMCI-P in mean cellwise WWdFNC connectivity: all samples (left-most); within intervals exceeding the 90% upper thresholding for saliency (second from the left); within intervals under the 10% lower saliency thresholding (second from the right). For the leftmost panel, we applied the no thresholding, for the second from the left plot, we used intervals of length at least 3 exceeding the 90% upper saliency threshold, and for the second from the right, we used intervals of length at least 3 with saliency under the 10% bottom saliency threshold computed from all WWdFNC. We averaged the connectivity features within time intervals and performed the 2-sample T-test with multiple comparison correction (False Discovery Rate Correction ). Red means the class-level average of qMCI-R is significantly greater than qMCI-P (), blue means the class-level average of qMCI-P is significantly greater than qMCI-R (FDR). The right most plot takes the sign of the maximum class level difference to unified the upper salient and lower salient class difference plot as the final interpretation result.
A number of previous studies have investigated the neuroimaging biomarkers for the HC, MCI (qMCI), AZD groups. However, to our best knowledge, very few studies have been conducted on the recovery qMCI group and the related biomarkers, and there is limited comprehensive meta-analysis of qMCI-P. To better consolidate our result and expand the comparison to the existing research work, we compared some of our final elementwise group FC biomarkers of qMCI-P to the existing AZD-related biomarkers. We believe qMCI-P should have a higher similarity to AZD than qMCI-R, and the same for qMCI-R, which should have a higher similarity to HC than qMCI-P. This kind of qMCI transition biomarkers between HC and AZD reflect activity brain networks also noted in [40].
In the left most plot in Fig. 8, we can observe that there is significant higher functional network connectivity (FNC) between the lingual gyrus and calcarine gyrus in the VI domain shown in qMCI-P compared with qMCI-R, which is consistent with the study that reported significant changes associated with AZD [41]. In addition, there are significant higher FNC between several occipital and temporal regions in the VI domain as well, which is consistent with the amplitude of low-frequency fluctuations (ALFF) study that reported the biomarkers related to the MCI group when compared with HC [42]. In the DMN, we found that qMCI-P group has significant lower FC between anterior cingulate cortex (ACC) and precuneus, as well as between anterior cingulate cortex and posterior cingulate cortex (PCC), which is consistent with findings in [40]. The PCC in qMCI-P group shows lower FNC with caudate and thalamus in the SC domain; frontal gyrus and frontal gyrus in the CC domain; and PCC shows an overall lower FNC with other networks. Our findings of PCC are consistent with [43] which states the decreased FNC is shown in MCI compared to HC as early cognition decline biomarkers, and [44] which concludes the lower FNC is shown in amnestic MCI and AD.
4. Discussion and Conclusion
In this work, we introduce TEAM to capture transiently-realized class-defining features by exploiting the TA-LSTM model. This framework is applicable in many domains involving time series data. The interpretation ability was evaluated on the aspects of a) performance of capturing the transient intervals and b) the performance of identification of class-defining feature in highly contributing intervals, and achieves high model interpretation power on the synthetic data. The simulation-validated interpretation framework was applied on the WWdFNC and captured the transiently-realized connectivity biomarkers expands our knowledge of dynamic biomarkers for the future recovery or progression from the qMCI. Furthermore, the additional accuracy achieved by using “instantaneous” WWdFNCs in this model suggests that greater temporal resolution of the input data can be productively exploited by LSTMs for improved performance relative to coarser-grained SWCdFNCs, highlighting the importance of continuing to refine our measures of time-varying connectivity. The accuracy achieved by training the two types of dFNC in TA-LSTM model outperformed the baseline mode multivariate CNN suggests the sequence learning helps the feature learning compared with convolutional-based model.
4.1. qMCI-R group
Prior research has centered on predicting qMCI conversion using machine learning techniques. The linked biomarkers connected to qMCI-P have been evaluated using sMRI, PET, rs-fMRI, age, and cognition scores, among other data types. The stable qMCI class representing the subject’s continued presence in the qMCI stage across the investigation is mostly studied as the contrast class in the prediction task. As we discussed before, stable qMCI subjects who neither recover nor progress are on indeterminate future paths. This group will be a mix of features that relate to disparate unmeasured future outcomes, and cannot be treated as a disjoint class. The qMCI-R group, which recovers to a healthier cognitive stage within three years, is on the opposite and definitive path as the qMCI-P group, but has received little attention in the neuroimaging data. We worked on tasks on the qMCI subject to predict the recovery or progress after the initial diagnosis of qMCI and investigated the potentially important predictors of the transition to fill the knowledge gap. Due to the limited studies on the qMCI-R group and considering the progression stage of AZD, we compared our findings with studies involving qMCI-P, cognitive health, and AZD groups. Our findings agreed with previous qMCI-P studies. Furthermore, our results agreed that the connectivity biomarkers interpreted for the qMCI-R group are more consistent with the cognitive health group reported in other studies, whereas the qMCI-P group is more consistent with the AZD group reported in previous works.
4.2. Trustworthiness and human interpretability of TEAM
Building the trustworthiness of both model and interpretation is vital for humans to take advantage of machine learning tools. When using model to assist with critical societal functions, such as medical diagnosis, the model’s predictions cannot be implemented as part of a decision process without assessing their trustworthiness. Furthermore, we can study the important features/ predictors from the trustworthy model when domain knowledge is still weak. As a result, assessing trustworthiness is critical to convincing humans who are experts to trust the model and in getting humans who are not experts in such domains to learn the domain and potential predictors. As discussed, trustworthiness is built on the ability to interpret a subset of ground truth predictors. The reason for not requiring the entire set of predictors is based on the underspecification model [28], which states that the model with random parameter initialization may focus on different predictors that are sufficient for the model to converge. We argued that if the interpretation can learn a set of predictors can build trustworthiness. However, many domains lack feature/predictor importance ground truth to validate trustworthiness. In this study, we designed six simulation studies with pre-defined predictors that served as ground truth to quantify the trustworthiness of the interpretation framework TEAM. Two metrics are evaluated for the model interpretation power for multivariate time series data input. We observed the underspecification model scenario in the simulation D and F. In simulation D, where the TA-LSTM learned the pattern for the negative class, which is indicated by the symbol in the TPO map. And in the simulation F, the TPO map mainly concentrated and correctly marked the “activated” time intervals in the first half time period. And in other simulations, TEAM interprets the almost entire set of ground truth predictors. Our simulation study results support that TEAM interprets at least a subset of ground truth predictors (and in more than half of the simulations, interprets the entire set of ground truth predictors) to confirm its trustworthiness. Considering the high dimensionality of multivariate time series data, the interpreted results must also be human interpretable. TEAM interprets the “activated” time intervals from the full-time axis first and class difference map in the selected time intervals. The interpretation result is shown in each dimension (time and feature); such low dimensional representation is human interpretable. Besides, two metrics, TPO and CDM, are proposed to quantify the model interpretation power on multivariate time series data input.
4.3. Why rs-fMRI and Recurrent-based model
To the best of our knowledge, no studies have compared qMCI-R and qMCI-P in a prediction task. We conducted a literature search on the most pertinent task, which is the prediction of progressive MCI from stable MCI. Some studies are use one or two types of neuroimaging data: sMRI and PET data with multimodal fusion and deep neural network models [16, 17], sMRI data with semi-supervised learning [45], and sMRI and rs-fMRI feature fusion with SVM [46]. Others combined the neuroimaging data with clinical ratings and age [45], age-adjusted [47], or cognitive function and longitudinal cerebrospinal fluid (CSF) [48] to make such prediction task. We found that characterization of the dynamics, which has been actively studied in other neurological diseases, attracted less attention in the existing qMCI studies. The average accuracy of mentioned studies’ predictions of progressive MCI against stable MCI is 0.836 with learning from images and 0.863 with learning from images, demographic data, and clinical scores combined. Despite our result of the average AUC 0.789 show slightly lower than the average of the mentioned previous studies 0.836 with only using the images, is not the most competitive. The TA-LSTM’s sequence learning and time attention unit both emphasizing the active intervals which are vital for the post-hoc TEAM interpretation. We believe that our study filled one of the small missing pieces of the qMCI study in both involving the recovery group as well as the brain dynamics perspective in rs-fMRI.
4.4. Limitation and Future works
We conducted studies on OASIS-3 to explore the prediction of qMCI progression and potential dynamic biomarkers related to patient deterioration or recovery from qMCI. Since at least three years of longitudinal information is required to recognize qMCI-R and qMCI-P subjects, we retrieved less than 100 subjects from OASIS-3. In addition to the present study, it is crucial to investigate the performance of the TA-LSTM and TEAM interpretation framework on larger and more diverse datasets in the future works. This would allow us to assess the scalability of the model and its adaptability to datasets that are more extensive and varied, such as ADNI or combinations of multiple public datasets. Additionally, it would be valuable to examine how the framework’s performance changes with variations in dataset size when presented a larger dataset. This would provide insights into the optimal dataset size required to achieve optimal results and identify any potential limitations that may arise when working with datasets of different sizes [49]. It is also essential to interpret the results on other datasets to identify reproducible biomarkers, including shared group dynamic biomarkers or biases in the interpretation process.
The existing studies regarding qMCI-R mainly focused on the lifestyle activity factors but lacked support from the neuroimaging domain. In this work, we employ a purely data-driven methodology on the two transition groups that the subject diagnosis with qMCI would convert after three years. Unlike other studies that compare the qMCI-P to Stable qMCI, we built the model for the qMCI-R and qMCI-P class since the stable qMCI will be a combination of attributes related to two conversion outcomes as we discussed in II.B. We believed it is important to bring attention on the recover group in triggering early dementia intervention. The future works could be to study neuroimaging data and other diverse factors, such as lifestyle, eating habits, and clinical treatment, which could influence such longitudinal study outcomes. All future works as well as this work, can extend our understanding of the potentially predictors relates to the conversion outcome of qMCI patients and provide important risk indicators.
Highlights.
Questionable mild cognitive impairment (qMCI) can be an early-stage of Alzheimer’s
LSTM-based model is trained to predict qMCI recovery vs. deterioration.
An interpretation framework is proposed to understand the model’s decision, and
Explore transient-realized dynamic biomarkers for qMCI prognostic future.
Interpretation framework’s trustworthiness is extensively validated in simulations.
Acknowledgments
Research supported by NSF 2112455 and NIH R01AG073949
Appendix A
| Abbreviation | Definition |
|---|---|
|
| |
| AZD | Alzheimer’s Disease |
| MCI/qMCI | (questionable) mild cognitive impairment |
| dFNC | dynamic functional network connectivity |
| TA-LSTM | time-attention long short-term memory |
| WWdFNC | windowless wavelet-based dFNC |
| SWCdFNC | sliding window dFNC |
| MIP | model interpretation power |
| TPO | temporal pattern occurrence |
| CDM | class difference map |
| M-CNN | multivariate convolutional neural network |
| CDR | clinical dementia rating |
| qMCI-R | recovery questionable mild cognitive impairment |
| qMCI-P | progressive questionable mild cognitive impairment |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
None declared.
References
- [1].A. s. Association, “2018 Alzheimer’s disease facts and figures,” Alzheimer’s & Dementia, vol. 14, no. 3, pp. 367–429, 2018. [Google Scholar]
- [2].Gauthier S. et al. “Mild cognitive impairment,” (in English), Lancet, vol. 367, no. 9518, pp. 1262–1270, Apr 15 2006, doi: Doi 10.1016/S0140-6736(06)68542-5. [DOI] [PubMed] [Google Scholar]
- [3].Shimada H, Lee S, and Makizako H, “Reversible predictors of reversion from mild cognitive impairment to normal cognition: a 4-year longitudinal study,” Alzheimer’s research & therapy, vol. 11, no. 1, pp. 1–9, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Ge S, Zhu Z, Wu B, and McConnell ES, “Technology-based cognitive training and rehabilitation interventions for individuals with mild cognitive impairment: a systematic review,” BMC geriatrics, vol. 18, no. 1, pp. 1–19, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Binnewijzend MA et al. “Resting-state fMRI changes in Alzheimer’s disease and mild cognitive impairment,” Neurobiology of aging, vol. 33, no. 9, pp. 2018–2028, 2012. [DOI] [PubMed] [Google Scholar]
- [6].Ibrahim B. et al. “Diagnostic power of resting-state fMRI for detection of network connectivity in Alzheimer’s disease and mild cognitive impairment: A systematic review,” Human brain mapping, vol. 42, no. 9, pp. 2941–2968, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Sendi MS, Zendehrouh E, Miller RL, Mormino EC, Salat DH, and Calhoun VD, “Brain state instability as a biomarker of Alzheimer’s disease progression: A dynamic functional network connectivity study,” Alzheimer’s & Dementia, vol. 17, p. e051468, 2021. [Google Scholar]
- [8].Miller RL, Vergara VM, Keator DB, and Calhoun VD, “A method for intertemporal functional-domain connectivity analysis: application to schizophrenia reveals distorted directional information flow,” IEEE Transactions on Biomedical Engineering, vol. 63, no. 12, pp. 2525–2539, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Calhoun VD, Miller R, Pearlson G, and Adalı T, “The chronnectome: time-varying connectivity networks as the next frontier in fMRI data discovery,” Neuron, vol. 84, no. 2, pp. 262–274, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Fu Z. et al. “Dynamic state with covarying brain activity-connectivity: on the pathophysiology of schizophrenia,” Neuroimage, vol. 224, p. 117385, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Miller RL and Calhoun VD, “Transient Spectral Peak Analysis Reveals Distinct Temporal Activation Profiles for Different Functional Brain Networks,” in 2020 IEEE Southwest Symposium on Image Analysis and Interpretation (SSIAI), 2020: IEEE, pp. 108–111. [Google Scholar]
- [12].Rashid B. et al. “Classification of schizophrenia and bipolar patients using static and dynamic resting-state fMRI brain connectivity,” Neuroimage, vol. 134, pp. 645–657, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Yan W, Zhao M, Fu Z, Pearlson GD, Sui J, and Calhoun VD, “Mapping relationships among schizophrenia, bipolar and schizoaffective disorders: A deep classification and clustering framework using fMRI time series,” Schizophrenia Research, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Hojjati SH, Ebrahimzadeh A, Khazaee A, Babajani-Feremi A, and A. s. D. N. Initiative, “Predicting conversion from MCI to AD using resting-state fMRI, graph theoretical approach and SVM,” Journal of neuroscience methods, vol. 282, pp. 69–80, 2017. [DOI] [PubMed] [Google Scholar]
- [15].Amoroso N. et al. “Deep learning reveals Alzheimer’s disease onset in MCI subjects: results from an international challenge,” Journal of neuroscience methods, vol. 302, pp. 3–9, 2018. [DOI] [PubMed] [Google Scholar]
- [16].Suk H-I, Lee S-W, Shen D, and A. s. D. N. Initiative, “Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis,” NeuroImage, vol. 101, pp. 569–582, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Cheng B, Liu M, Suk H-I, Shen D, and Zhang D, “Multimodal manifold-regularized transfer learning for MCI conversion prediction,” Brain imaging and behavior, vol. 9, no. 4, pp. 913–926, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Canevelli M. et al. “Spontaneous reversion of mild cognitive impairment to normal cognition: a systematic review of literature and meta-analysis,” Journal of the American Medical Directors Association, vol. 17, no. 10, pp. 943–948, 2016. [DOI] [PubMed] [Google Scholar]
- [19].Muangpaisan W, Petcharat C, and Srinonprasert V, “Prevalence of potentially reversible conditions in dementia and mild cognitive impairment in a geriatric clinic,” Geriatrics & gerontology international, vol. 12, no. 1, pp. 59–64, 2012. [DOI] [PubMed] [Google Scholar]
- [20].Rasquin S, Lodder J, and Verhey F, “Predictors of reversible mild cognitive impairment after stroke: a 2-year follow-up study,” Journal of the neurological sciences, vol. 229, pp. 21–25, 2005. [DOI] [PubMed] [Google Scholar]
- [21].Lipton ZC, “The Mythos of Model Interpretability: In machine learning, the concept of interpretability is both important and slippery,” Queue, vol. 16, no. 3, pp. 31–57, 2018. [Google Scholar]
- [22].Simonyan K, Vedaldi A, and Zisserman A, “Deep inside convolutional networks: Visualising image classification models and saliency maps,” in In Workshop at International Conference on Learning Representations, 2014: Citeseer. [Google Scholar]
- [23].Sundararajan M, Taly A, and Yan Q, “Axiomatic attribution for deep networks,” in International conference on machine learning, 2017: PMLR, pp. 3319–3328. [Google Scholar]
- [24].Zeiler MD and Fergus R, “Visualizing and understanding convolutional networks,” in European conference on computer vision, 2014: Springer, pp. 818–833. [Google Scholar]
- [25].Robnik-šikonja M and Bohanec M, “Perturbation-based explanations of prediction models,” Human and Machine Learning: Visible, Explainable, Trustworthy and Transparent, pp. 159–175, 2018. [Google Scholar]
- [26].Lundberg SM and Lee S-I, “A unified approach to interpreting model predictions,” Advances in neural information processing systems, vol. 30, 2017. [Google Scholar]
- [27].Ismail AA, Gunady M, Corrada Bravo H, and Feizi S, “Benchmarking deep learning interpretability in time series predictions,” Advances in neural information processing systems, vol. 33, pp. 6441–6452, 2020. [Google Scholar]
- [28].D’Amour A et al. “Underspecification presents challenges for credibility in modern machine learning,” Journal of Machine Learning Research, 2020. [Google Scholar]
- [29].Ribeiro MT, Singh S, and Guestrin C, ““ Why should i trust you?” Explaining the predictions of any classifier,” in Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining, 2016, pp. 1135–1144. [Google Scholar]
- [30].LaMontagne PJ et al. “OASIS-3: Longitudinal Neuroimaging, Clinical, and Cognitive Dataset for Normal Aging and Alzheimer Disease,” medRxiv, p. 2019.12.13.19014902, 2019, doi: 10.1101/2019.12.13.19014902. [DOI] [Google Scholar]
- [31].Gao Y, Calhoun VD, and Miller RL, “Transient Intervals of Significantly Different Whole Brain Connectivity Predict Recovery vs. Progression from Mild Cognitive Impairment: New Insights from Interpretable LSTM Classifiers,” in 2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), 2022: IEEE, pp. 4645–4648. [DOI] [PubMed] [Google Scholar]
- [32].Du Y. et al. “NeuroMark: An automated and adaptive ICA based pipeline to identify reproducible fMRI markers of brain disorders,” Neuroimage Clin, vol. 28, p. 102375, 2020, doi: 10.1016/j.nicl.2020.102375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Hochreiter S and Schmidhuber J, “Long short-term memory,” Neural computation, vol. 9, no. 8, pp. 1735–1780, 1997. [DOI] [PubMed] [Google Scholar]
- [34].Vaswani A. et al. “Attention is all you need,” Advances in neural information processing systems, vol. 30, 2017. [Google Scholar]
- [35].Lewis N. et al. “Can recurrent models know more than we do?,” in 2021 IEEE 9th International Conference on Healthcare Informatics (ICHI), 2021: IEEE, pp. 243–247. [Google Scholar]
- [36].Bahdanau D, Cho K, and Bengio Y, “Neural machine translation by jointly learning to align and translate,” arXiv preprint arXiv:1409.0473, 2014. [Google Scholar]
- [37].Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, and Batra D, “Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization,” (in English), Int J Comput Vision, vol. 128, no. 2, pp. 336–359, Feb 2020, doi: 10.1007/s11263-019-01228-7. [DOI] [Google Scholar]
- [38].Benesty J, Chen J, Huang Y, and Cohen I, “Pearson correlation coefficient,” in Noise reduction in speech processing: Springer, 2009, pp. 1–4. [Google Scholar]
- [39].Akoglu H, “User’s guide to correlation coefficients,” Turkish journal of emergency medicine, vol. 18, no. 3, pp. 91–93, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Rombouts SA, Barkhof F, Goekoop R, Stam CJ, and Scheltens P, “Altered resting state networks in mild cognitive impairment and mild Alzheimer’s disease: an fMRI study,” Human brain mapping, vol. 26, no. 4, pp. 231–239, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Khazaee A, Ebrahimzadeh A, and Babajani-Feremi A, “Identifying patients with Alzheimer’s disease using resting-state fMRI and graph theory,” Clinical Neurophysiology, vol. 126, no. 11, pp. 2132–2141, 2015. [DOI] [PubMed] [Google Scholar]
- [42].Han Y. et al. “Frequency-dependent changes in the amplitude of low-frequency fluctuations in amnestic mild cognitive impairment: a resting-state fMRI study,” Neuroimage, vol. 55, no. 1, pp. 287–295, 2011. [DOI] [PubMed] [Google Scholar]
- [43].Balthazar MLF, de Campos BM, Franco AR, Damasceno BP, and Cendes F, “Whole cortical and default mode network mean functional connectivity as potential biomarkers for mild Alzheimer’s disease,” Psychiatry Research: Neuroimaging, vol. 221, no. 1, pp. 37–42, 2014. [DOI] [PubMed] [Google Scholar]
- [44].Cha J. et al. “Functional alteration patterns of default mode networks: comparisons of normal aging, amnestic mild cognitive impairment and Alzheimer’s disease,” European Journal of Neuroscience, vol. 37, no. 12, pp. 1916–1924, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Moradi E, Pepe A, Gaser C, Huttunen H, Tohka J, and A. s. D. N. Initiative, “Machine learning framework for early MRI-based Alzheimer’s conversion prediction in MCI subjects,” Neuroimage, vol. 104, pp. 398–412, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Hojjati SH, Ebrahimzadeh A, Khazaee A, Babajani-Feremi A, and A. s. D. N. Initiative, “Predicting conversion from MCI to AD by integrating rs-fMRI and structural MRI,” Computers in biology and medicine, vol. 102, pp. 30–39, 2018. [DOI] [PubMed] [Google Scholar]
- [47].Gao F. et al. “AD-NET: Age-adjust neural network for improved MCI to AD conversion prediction,” NeuroImage: Clinical, vol. 27, p. 102290, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Lee G, Nho K, Kang B, Sohn K-A, and Kim D, “Predicting Alzheimer’s disease progression using multi-modal deep learning approach,” Scientific reports, vol. 9, no. 1, pp. 1–12, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Abrol A. et al. “Deep learning encodes robust discriminative neuroimaging representations to outperform standard machine learning,” Nature communications, vol. 12, no. 1, p. 353, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]


