Abstract
The brain is commonly understood as a complex network system with a particular organization and topology that can result in specific electrophysiological patterns. Among all the dynamic elements resulting from the circuits of the brain’s network, ephapticity is a cellular communication mechanism that has received little attention. To understand the network’s properties of ephaptic entrainment, we start investigating the ephaptic effect on a single neuron. In this study, we used numerical simulations to examine the relationship between alterations in ephaptic neuronal entrainment and impaired electrophysiological properties of the neuronal membrane, which can occur via spike field coherence (SFC). This change in frequency band amplitude is observed in some neurodegenerative diseases, such as Parkinson’s or Alzheimer’s. To further investigate these phenomena, we proposed a damaged model based on the impairment of both the resistance of the ion channels and the capacitance of the lipid membrane. Therefore, we simulated ephaptic entrainment with the hybrid neural model quadratic integrate-and-fire ephaptic (QIF-E), which mimics an ephaptic entrainment generated by an LFP (simulate a neuronal group). Our results indicate a link between peak entrainment (ephapticity) preference and a shift in frequency band when damage occurs mainly in ion channels. Finally, we discuss possible relationships between ephaptic entrainment and neurodegenerative diseases associated with aging factors.
Subject terms: Neurodegenerative diseases, Alzheimer's disease, Parkinson's disease, Mathematics and computing, Biological physics
Introduction
Neural oscillations are recognized as important mechanisms for understanding physiological and pathological phenomena1,2. Brain rhythms originate from cell communications3, by exchanging small molecules and ions, as gap junctions and synapses; or by electric fields4,5. Communication made by exclusively electric fields (short-range interactions)4,5 is called ephapticity3,4,6,7, and it is known for several decades6,8. However, its physiological function in the central nervous system is still poorly understood3,4,9. Despite the lack of information regarding the physiological function of ephapticity, some empirical studies have shown that ephaptic communication has an important role in synaptic plasticity3,10 or even in neural dysfunction5,11.
Clusters of neurons can exchange information by connecting with each other in particular rhythms, depending on the task involved2,12–14. Nevertheless, factors associated with aging in the nervous system can generate neural damage, and undermine dynamics of rhythms and consequently neuron communication15–17. In neurodegenerative diseases due to the aging process, such as Parkinson Disease (PD), Alzheimer Disease (AD) or Lewy body dementia (DLB), accumulations of peptide (oligomers) are observed18–21. As an example of dysfunctional proteins are the -synuclein (-syn in PD and DLB), that are associated with the formation of Lewy bodies, and -amyloid (in AD without Lewy body’s), which make up the senile plaques18–21. Oligomers have toxic cellular effects, compromising the structure of the plasmolemma, either by altering lipid and cholesteric composition18,22,23, or by inactivating ion channels15,23–26. Therefore, the brain rhythms from the damage regions are amended12,15,27, as observed in PD by the increase in the amplitude of the band28–30; or the lack of synchrony (low amplitude) in and bands and high synchronizations in and in AD27,31,32.
The idea that collective neuronal behavior is intrinsically related to individual neuron properties is a fundamental principle in understanding the dynamics of networks1,33. Although networks are composed of numerous interconnected neurons, every neuron has its own particular dynamics and behavior, which is associated with its inherent features, for instance, its intrinsic rhythms34,35. In this context and regarding the importance of applying mathematical models for neuronal studies36–40, the present work aims to investigate the hypothesis that given a level of impairment of the single neuronal membrane may produce a change in its ephaptic entrainment. To this purpose, we adopted the QIF-E hybrid model, which uses the electrophysiological properties of capacitance and electrical resistance of the membrane for the simulation39,41. Thus, two new parameters related to plasmolemma damage are thought for the modified QIF-E model: (1) The parameter h, associated with damage to the characteristics of the lipid bilayer; and (2) The b parameter, related to dysfunction of ion channel opening. As a result, for different degrees of damage in the electrophysiological parameters, a change in the frequency peak of the ephaptic entrainment is observed. Our results emphasize a relation between ephaptic communication in the process of frequency band preferences and neurodegenerative diseases.
The study begins with a description of the mathematical model used to simulate ephaptic entrainment. In the following, is shown the proposal for the mathematical development of the electrical damage parameters, and their applications in the hybrid model. The Spike Field Coherence (SFC) tool is explained as a way to quantify the entrainment. The results obtained are shown in section Results. Finally, a discussion and conclusion is made about the impacts of ephapticity on the emergence of frequency bands with the loss of neuronal membrane function in degenerative processes associated with senility diseases.
Firing neuron model with dysfunctional membrane
The quadratic integrate-and-fire model with ephapticity (QIF-E)41 is a simplified neuron model and a type of integrate-and-fire neuron that describes action potentials in neurons inserted in an electric field, given by the LFP, which here is referred as the ephaptic term. In contrast to physiologically accurate but computationally expensive neuronal models, the QIF-E model only seeks to produce action potential-like patterns and ignores subtleties such as control variables. According to Cunha et al.41, the ephaptic communication can be simulated with the QIF-E hybrid model, datum by the equation:
| 1 |
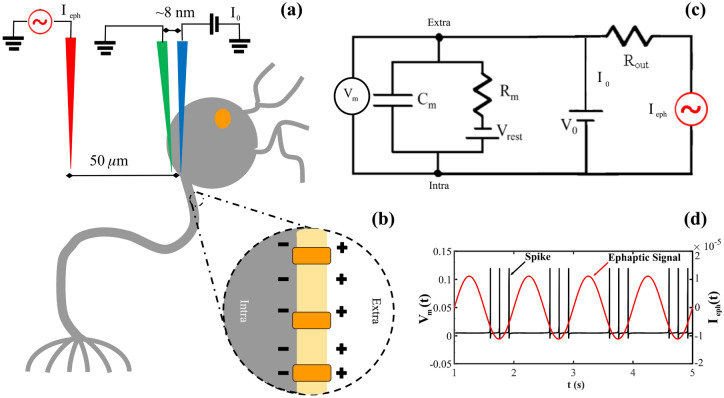
and, if . In Eq. (1), is the membrane capacitance, the membrane potential, the rest potential, the threshold of excitation value, the membrane resistance and the synaptic current across the membrane. The r parameter in the equation of the QIF-E model, is the distance between the external stimulus electrode (red in Fig.1a) and the electrode corresponding to (green in Fig.1(a)). Finally, is the ephaptic current that flow through of the membrane. The Table 1 shown the QIF-E model quantities use in the simulations. The ephaptic entrainment experiment are shown in the Fig.1, with the equivalents in the QIF-E model.
Figure 1.
Ephaptic Entrainment (a) Representative scheme of the experiment made by Anastassiou, et al.4 for ephaptic entrainment, and here simulated by the QIF-E41 model. (b) Magnification of the structure of the plasmatic membrane (yellow) with the ion channels (orange) and the ionic separation promoted between the extra-(positively charged - white) and intracellular (negatively charged - gray) milieu. (c) Simplified equivalent electrical circuit for the ephaptic entrainment experiment. (d) Temporal series from QIF-E simulation for (black) and (red).
Table 1.
Cell membrane biophysical parameters employed in the simulation of the quadratic integrate-and-fire model.
| Quantity | Value | Description | References |
|---|---|---|---|
| − 65 mV | Rest potential | 42,43 | |
| − 55 mV | Excitation thresholds | 42,43 | |
| Membrane capacitance | 44 | ||
| +55 mV | Peak Value | 42 | |
| c | − 70 mV | Hyperpolarization constant | 42 |
| 3.5 .m | Extracellular resistivity | 45,46 | |
| r | 50 m | Distance between stimulus electrode and the position of | 45 |
| Resistance of the neuronal membrane | 44 |
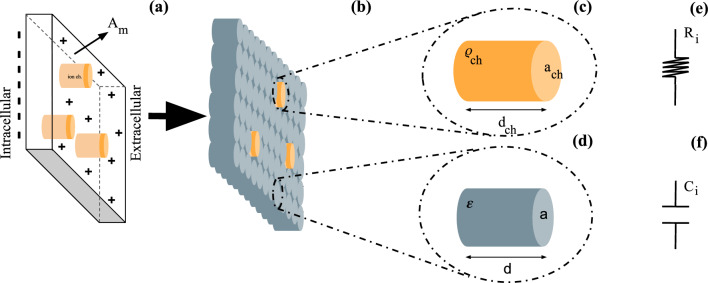
In this work, we have built the hypothesis that deficits in parameters associated to maintenance of synaptic homeostasis could dramatically impact ephaptic communication. Hence, we developed an adaptation in QIF-E model, such that the electrical properties of the model can be changed, in order to simulate the damage in the membrane. For this purpose, the neuronal membrane (Fig.2a) was conceived like an ensemble of unitary elements (Fig.2b), with each individual volume equivalent to or an ionic channel (Fig.2c) as electric resistance (Fig.2e); or a phospholipid structure patch (Fig.2d) as capacitance (Fig.2f).
Figure 2.
Representation of the unity volume element of the cell membrane. (a) Cell membrane (1) composed of various biological elements. (b) Membrane subdivided into equal volume elements. (c) Electrical properties of the ionic channel. (d) Electrical properties associated to unit capacitance of the membrane. (e) Equivalent resistor to an ionic channel present in the membrane. (f) Equivalent capacitance to a unit volume of the neuronal membrane.
Change in electric functionality of the generic ionic channels.
In accordance with the electrophysiological approach, the values of resistance were associated to the average values of the ionic channels. Therefore, the resistance of the membrane is provided by: . The parameter is the channel resistivity and reports the capacity of the channels to resist to ionic flows. The d distance is the length of the ionic channel. Finally, A is the total area (transversal sections sum) of available channels (open channels) to ionic flow through the neuronal membrane. For a damage analysis of neuronal membrane, we changed the and the and assign equal values of geometric and electrical properties to each unit of volume (See Fig.2b,c). The total area associated to the ionic channels can be described by ; with n equal to the maximum ion channels number, and is the single channel cross-section.
Total resistance of the membrane is provided by an association of unitary resistances, shown in Fig.3c. Thus:
| 2 |
Then the resistance is described by:
| 3 |
We idealized the dysfunctional scenario, for our model, as an inactivation of ion channels, leading to an increase in membrane resistance (See Fig.3f). The decrease of functional channels number will be analyzed by the difference between the total number of membrane channel, n, and the damage ionic channel parameter, m, i.e., . Known that and , the general expression to the resistance of neuronal membrane to provide the dysfunctional situation description () is:
| 4 |
insulating the term: (related to ionic channel), in the Eqs. (3) and (4), we obtain:
| 5 |
Normalizing the expression by the total number of ion channels (n):
| 6 |
being the new parameter that describe the ion channel inactivated proportion (damaged).
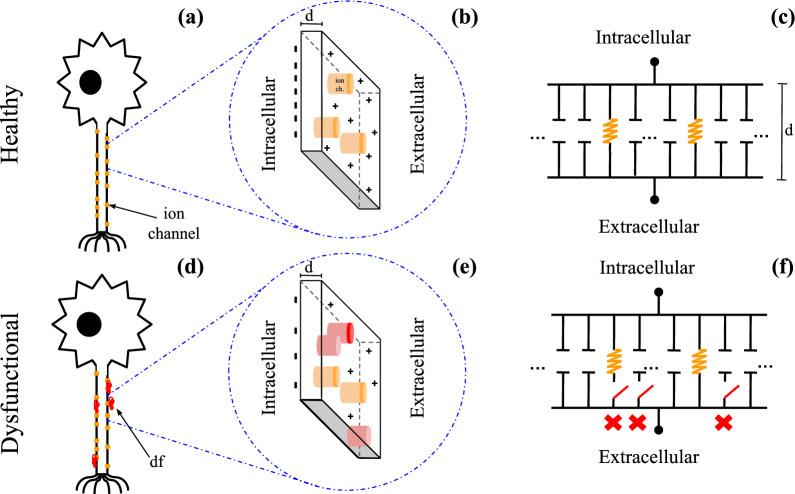
Figure 3.
Functional and Dysfunctional Scenarios. (a) Schematic representation of healthy neuron and the ionic channels (orange). (b) Healthy neuronal membrane amplified, with the ionic channel (orange) (c) The neuronal membrane representation on the basis of its electrophysiological properties. Resistances and capacitance provide, by classical electromagnetism, a description of the membrane average performance. (d) The neuron representation in a dysfunctional scenario, described by a damage (red) along of axon. (e) Cellular membrane applied with damage occurrence (red), leading to ion channel inactivation (improve of resistance), or a decrease of membrane capacitance. This damage can breach the neuronal membrane, as in the PD case23. (f) Damage in the membrane electrophysiological properties caused by degeneration. Shown partitions of the resistance and capacitance opened in the circuit.
With the progression of dysfunction, the proportion value increase of (healthy) to the condition (total damage), with values in . Thereby, the model can be expressed through the new parameter of ion channel damage.
Change in the membrane capacitive functionality
The neuronal membrane phospholipid structure can be thought as a capacitor (Fig.2f), with the total capacitance provided by the expression: . The parameter is associated to the membrane electrical permittivity (standard); the distance d, to the neuronal membrane thickness and the area to the total area available for the ion accumulation in the membrane. Similarly to the ionic channel’s resistance, the membrane average capacitance can be associated to a sequence of unitary capacitors (Fig. 3c). The total area is split in equal units area (similar to ionic channels area). Therefore, the membrane total capacitance is provided by each capacitor unit sum (): .
We consider that each capacitor unit are equivalents, this means that the element’s electric permittivity , the area a and the membrane thickness d, are equal to each other, then . Therefore:
| 7 |
where j is the total number of healthy capacitors C. The loss of the membrane function is modeled by the damage in unity capacitors, computed through of the inactivated capacitors (committed), defined by g (See Fig.3g). Known that and :
| 8 |
Normalizing the above expression via a proportion of committed capacitors by the total number of capacitors , we obtain:
| 9 |
with as the dysfunctional membrane capacitance.
In this way, it is possible to measure, via SFC, the changes in ephaptic communication with membrane damage progression: b and h (Fig.3f). Substituting the Eqs. (4) and (8) in the Eq. (1), the QIF-E is obtained, and is provided by the expression:
| 10 |
| 11 |
The QIF-E MatLab code is available in the Supplementary Material.
Spike field coherence - SFC
The SFC is a tool to measure the synchrony intensity, between a stimulus signal (Fig.1d in red) and a spike train (Fig. 1d in black), based on Spike Triggered Average (STA) analyses45,47. Thus, the SFC provides, given an external stimulus frequency (LFP), the entrainment preference to neuronal spikes. Through this procedure, empirical study45 and neuronal modeling41 estimated the ephaptic communication intensity.
The Spike Triggered Average (STA) is a tool to calculate the mean field profile to occur a spike in a neuron related to the preference input stimulus phase48. The STA associate two signals: an input signal and the membrane potential response. To obtain the STA one should take parts of the input stimulus interval, , around the spikes instants in the neuron signal49. This intervals, , are chosen with a time window defined by simulation conditions. In the present work, the temporal window assumed to obtain the STA is for f the stimuli frequency. Therefore, the STA describes the stimulus mean field where associated to a high spike occurrence probability.
Finally, the spike field coherence (SFC) is a tool that measures how strong is the synchronization between a stimuli signal phase and a spike train, based in the STA analysis45,47. The calculation to SFC is performed by the expression50 , where is the power spectrum, STA is the Spike Triggered Average. Therefore, the SFC it is defined between 0 (without signal synchrony) and 1 (totally synchronous signal) [see Fig. 4a and (d)]47. The Fig. 4a,d, exhibit the SFC for different frequencies of external stimulus, from 0 to 45Hz. In (a), we observe the preference frequency below 10 Hz (blue arrow in 5Hz corresponds to the time series observed in (b)). The yellow arrow at 17Hz indicated a 4% preference frequency for a damaged membrane. We depicted the time series for 5Hz in (b,c) and the time series for 17Hz in (e,f). We performed the SFC calculus in MatLab.
Figure 4.
SFC of QIF-E and temporal series. Panels (a–c) correspond to a healthy membrane (b = h = 0.00), while panels (d–f) correspond to a degenerate membrane (b = h = 0.04). Blue and orange arrows indicate frequencies (b), (e) - 5Hz and (c), (f) -17Hz. Two signals are indicated in these panels, the simulated QIF-E (spikes in black) and the input LFP (sine curve in red). In the healthy case, the spikes synchronize with the external LFP phase signal (red) at f=5Hz, but not at f=17Hz, resulting in a high SFC value for low frequencies (blue arrow) in figure (a). The opposite occurs in the damaged membrane case, here the spikes synchronize with the external LFP phase signal at f=17Hz, but not at f=5Hz, resulting in a high SFC value for higher frequencies (orange arrow) in figure (d).
Results
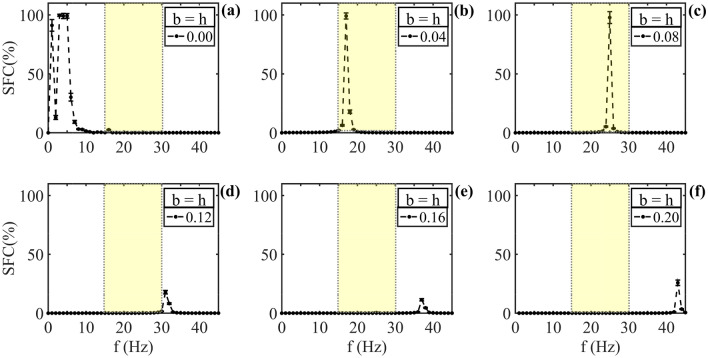
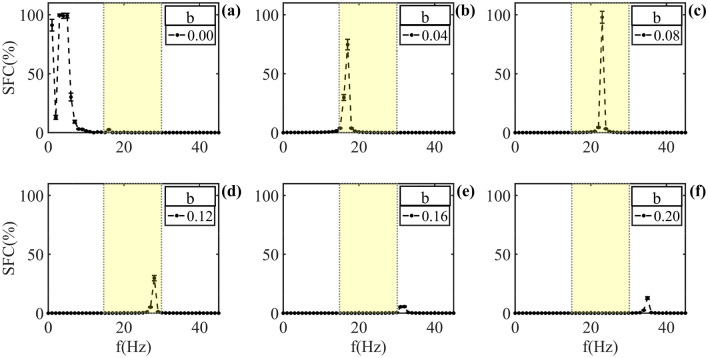
To show the results of the synchronization between the LFP-phase and the spikes (model response), we use the SFC tools for the cases without damage, seen in panels (a) of each figure, as well as the results with different levels of damage in the interval from 4% (0.04) in panels (b) to 20% (0.20), in panels (f), with a step of 4% (0.04). For simulations, we used the ephaptic model with damage QIF-E. For damage above 20% and accurate steps, see Supplementary Material.
The Fig. 5 shows the SFC for the equals damage values, i.e., . In 5a there is no damage in the simulation (electrophysiology standard, ) and consequently an entrainment preference in the frequency band stay below 10 Hz to the ephapticity. Note that in (b), for damage to 4% in the both parameters, the ephaptic entrainment shifted to an oscillation range in the band (yellow shaded region); in (c) the damage is 8% and observe an ephaptic entrainment in frequency band of 23–27 Hz, also in the band. In the (d) panel, the damage is 12% and the entrainment occurs in the band. It is interesting to note that the SFC intensity decrease with this damage intensity. In (e) the damage is 16% and the entrainment band occur around of 37Hz. Finally, in (f) the damage is 20% and the ephaptic entrainment is close to 42Hz.
Figure 5.
Ephaptic model response for an LFP with both: ionic channels and the membrane bilayer damages. (a) SFC for the QIF-E model without damage (b=h=0.00). Note an entrainment preference in the frequency bands below of 10Hz. (b) SFC results for damage membrane of 4% (0.04). A shift occurs in the ephapticty frequency preference between 15 Hz and 19 Hz. (c) SFC with 8% of damage and ephaptic preference in the frequency band between 23 and 27 Hz. (d) SFC with damage to 12% and entrainment preference shift to the frequency band of 30 to 34 Hz. (e) SFC for damage of 16% and ephaptic entrainment in the frequency band of 36–39 Hz. (f) SFC with damage of 20% and preference in frequency band between 42 and 45 Hz. The yellow shadow region is defined as the oscillation band.
For values of neuronal degeneration (damage) above 0.20, do not observed peak of entrainment in the study band frequency (0 to 45 Hz) (See Supplementary Material).
The Fig. 6 shows the SFC for damage values only in the resistance (b) lying between 0 and 20%. In Fig.6a the simulation present physiologic standard, and an ephaptic entrainment band preference below 10 Hz, as observed in Fig. 5a. Sequentially, with and , observed a migration behavior in the ephaptic entrainment again, to high frequency bands () when compared with . Thus, in (b) is shown damage to 4% and frequency band preference around 16 Hz. In (c) that damage is 8% and the oscillation preference is round about to 22Hz; in (d), with the damage to 12% and ephaptic entrainment preference between 26 and 29 Hz. (e) shows damage in 16%, and finally in (f) the damage is 20%. Note that from the damage to 16%, the coupling intensity decrease and lying out of frequency band ([13–30] Hz). In this figure, here is a similarity with Fig. 5 in terms of frequency preference changes. The similarity was observed include between the Figs. 5a and 6a in the frequency preference, just as between Figs. 5b and 6b.
Figure 6.
Ephaptic model response to LFP with neuronal damage in ionic channels only. b values between 0.00 and 0.20, step 0.02 chose between each simulation. In (a) the SFC shown without damage, equal to Fig.5(a). (b) SFC to . Here occur an ephaptic entrainment displacement for the band frequency in range of 15–19 Hz, similar result was shows in 5(b). (c) SFC of and a frequency preference in the band of 21 to 25Hz. In (d) the SFC for shows a frequency preference between 26 and 29 Hz. (e) SFC with and frequency preference for entrainment in 30 to 33 Hz band. (f) SFC for and band preference between 33 and 36 Hz. The yellow shadow region is defined as the oscillation band.
As from , is observed a decrease of intensity in the model ephaptic entrainment.
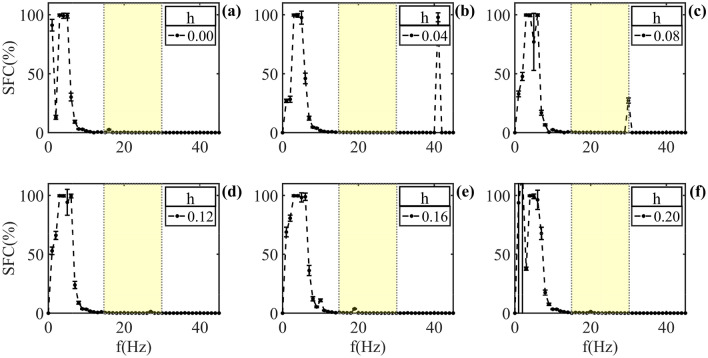
Figure 7 shown SFC values to changes in the capacitance degeneration, with fixed b. As noted in Figs. 5a and 6a, the Fig. 7a shows intense SFC in the low frequencies (). The difference in the Fig. 7b–f, compared to previous figures, is that the maximum value in the ephaptic entrainment not shift to the high frequencies. However, note that for and high frequencies peaks occurs together with the low frequencies maximum. Finally, in the Fig. 7f is possible to note that here significant dispersion in relation to the mean for a few values of low frequency band.
Figure 7.
Ephaptic model response for an LFP, with damage in membrane bilayer only. h values between 0.00 and 0.20, step by 0.02, and b fixed. (a) SFC for QIF-E no damaged. In (b) shown SFC for . Note entrainment preference retained in the low frequency (), and SFC presents a maximum in the band above 40Hz. (c) The SFC with shows a preference of ephapticity also in low frequencies. A new peak, smaller, is observed in the band of 29 to 31 Hz. In (d–f) the SFC with 12, 16 and of damage, respectively, the behavior is similar to the shown in panel (a).
Discussion
The present work shows the proposal of the membrane, (Fig.2a) as a set of unitary elements (Fig.2b), where each unit is equivalent either or to an ion channel (Fig.2c), or to a phospholipid structure (Fig.2d). The unitary elements that form the membrane are associated with electrical components: ion channels as electrical resistance (Fig.2e) and phospholipids as capacitors (Fig.2f). Thereby, we propose two damage parameters that mimic the resistance impairment (b), and the capacitor’s impairment (h). Sequentially, we estimated, using the QIF-E41 hybrid model, how ephaptic communication is affected by dysfunctions in neuronal membrane electrophysiology (Fig.3). As a result, for a simulated neuronal membrane damage levels, we obtained different preference frequency bands (via SFC—Fig. 4) for ephaptic entrainment. Furthermore, with the increase of the impairment in the generic ion channels and in the neuronal membrane, the maximum value of ephaptic entrainment is shifted to higher frequencies (f > 10Hz), as observed in Fig. 5.
Taking into account that the same pattern of deterioration happens in the phospholipidic bilayer (capacitance) and in ion channels (resistance), we adopted equal absolute values for both damages in the simulations, i.e., . In the Figs. 5, 6 and 7 (a)’s, for non-damage membrane, the SFC presents high intensities for low frequency values (Hz) due to the characteristics of ephaptic communication, since the neural tissue works as a low-pass filter, as indicated in empirically4,51,52 and theoretically41 studies. In Fig. 5b and (c), the intensity of the SFC preference (peak value) remains high and within the range band (13–30 Hz), with impairment between 2% and 10% (–0.1). As damage increases, there is a shift in the frequency preference of ephaptic communication and also a reduction in strength entrainment, see panels (d), (e) and (f). This decrease in SFC intensity is due to the above-mentioned low-pass filter characteristic of neural tissue, which reduces the amplitude of high-frequency signals4,51,52. For damage higher to 20%, ephaptic communication does not occur in analyzed frequency band. Fact observed by the absence of preference in the frequency band provide in the SFC (flat) (See Supplementary Material).
The ephaptic entrainment simulation demonstrates frequency preferences that are determined by the electrophysiological characteristics of the membrane. These characteristics can be modified by dysfunctional oligomers, such as -synuclein, which are found in the cellular environment, as outlined in other studies15,18,22–26. In this regard, our study unveils a potential relationship between electrophysiological impairment of the neuronal membrane and alteration in the ephaptic mechanism linked to degenerative disorders. For instance, in AD, there is a lack of synchronization in the (8 - 13 Hz) and (13 - 30 Hz) frequency bands, and a pronounced synchronization in the low frequency bands ( Hz)27,31,32. On the other hand, an escalation in the intensity of the band has been observed in patients with Parkinson’s Disease28–30. Once the frequencies observed in those disorders reach the upper threshold of 35 Hz, the model was executed utilizing LFP within the range of 0–45 Hz.
In order to evaluate the influence of altering neuronal membrane resistance (b) on frequency preference for ephaptic entrainment, we established the value of (indicating no phospholipid damage) and performed simulations of QIF-E with b ranging from 0 to 20%. Figure 6 illustrates the changing in the b parameter and a corresponding alteration pattern in frequency preference, akin to the depiction exhibited in Fig. 5. However, it is noteworthy that, at an equivalent level of damage, the frequency preference (in the LFP) is shifted into smaller values in comparison to those observed for the case when . In general, the alteration in frequency preference, at which the maximum ephaptic coupling takes place, is associated with the dynamics of ion channels, specifically their opening and closing mechanisms. This observation is reasonable, given that during the membrane potential variation, ion channels generate currents towards the extracellular medium and thereby produce ephaptic fields40,43.
Finally, the ephaptic response was examined by considering the reduction in capacitance of the neuronal membrane with no damage to the ion channels, as illustrated in Fig. 7. In this scenario, it is observed that the maximum value of ephaptic coupling persists at low frequencies ( Hz), as depicted in Fig. 7b–f. However, the standard-deviation values associated with each SFC value increases. This suggests that when considering alterations solely in the phospholipid layers, there is no notable modification in the preferred frequency range of maximum efficacy compared to the frequency preference observed in the healthy condition [see panel (a)]. This evaluation was conducted with damage levels of up to 20%. Modifications in both the phospholipid layers and cholesteric content within the neuronal membrane might be linked to heightened noise in ephaptic communication. This association has been previously indicated in a prior study41. The increase in background noise does not change the phase or the frequency of the ephaptic communication, but it can change the intensity of the ephaptic entrainment, which is linked to an increasing of the SFC error bars.
The outcomes of the current study intimate that the detriment to the electrophysiological attributes of the neuronal membrane exhibit a comprehensive influence on the ephaptic communication, engendering a discernible alteration in its interactive dynamics23,24,53–55. Hence, it can be posited that the ephaptic communication assumes a pivotal position in shaping the dynamic framework of the Central Nervous System, though the exact nature of this role continues to elude our understanding. Moreover, given its potential implications on neuronal efficacy, the intricate interplay of ephaptic mechanisms within the central neural networks warrants further investigation and exploration3,4,9. Indeed, the dysfunctionality that arises within neuronal membranes, particularly in the ionic channels, as a result of misfolded proteins, has been linked to an elevation in neuronal activity within specific oscillation bands. This phenomenon has been extensively documented in the scientific literature and is prominently observed in degenerative conditions such as Alzheimer’s disease12,15,27, Parkinson’s disease28,29,56, and Lewy body dementia27,31,32. Understanding the intricacies of ephaptic communication in the context of these degenerative disorders can assume paramount importance in advancing our knowledge of their pathophysiology and potentially uncovering novel therapeutic avenues.
Supplementary Information
Acknowledgements
GMC is recipient of the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq - Brazil) fellowship (#140895/2021-3). MMSL is recipient of the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq - Brazil) fellowship (#306432/2022-6). GZDL is recipient of the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq - Brazil) fellowship (#309440/2022-0).
Author contributions
G.M.C. conceived the code model and results, G.C. and G.Z.S.L analyzed the results. All authors wrote and reviewed the manuscript.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-023-38738-x.
References
- 1.Ahn S, Rubchinsky LL, Lapish CC. Dynamical reorganization of synchronous activity patterns in prefrontal cortex-hippocampus networks during behavioral sensitization. Cereb. Cortex. 2014;24:2553–2561. doi: 10.1093/cercor/bht110. [DOI] [PubMed] [Google Scholar]
- 2.Fell J, Axmacher N. The role of phase synchronization in memory processes. Nat. Rev. Neurosci. 2011;12:105–118. doi: 10.1038/nrn2979. [DOI] [PubMed] [Google Scholar]
- 3.Buzsáki G, Anastassiou CA, Koch C. The origin of extracellular fields and currents-eeg, ecog, lfp and spikes. Nat. Rev. Neurosci. 2012;13:407–420. doi: 10.1038/nrn3241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Anastassiou CA, Perin R, Markram H, Koch C. Ephaptic coupling of cortical neurons. Nat. Neurosci. 2011;14:217. doi: 10.1038/nn.2727. [DOI] [PubMed] [Google Scholar]
- 5.Jefferys J. Nonsynaptic modulation of neuronal activity in the brain: Electric currents and extracellular ions. Physiol. Rev. 1995;75:689–723. doi: 10.1152/physrev.1995.75.4.689. [DOI] [PubMed] [Google Scholar]
- 6.Arvanitaky A. Effects evoked in an axon by the activity of a contiguous one. J. Physiol. 1942;5:91–108. [Google Scholar]
- 7.Shifman AR, Lewis JE. ELfenn: A generalized platform for modeling ephaptic coupling in spiking neuron models. Front. Neuroinform. 2019;13:35. doi: 10.3389/fninf.2019.00035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Katz & Schmitt Eletric interaction between two adjacent nerve fibers. J. Physiol. 1940;97:471–488. doi: 10.1113/jphysiol.1940.sp003823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Goldwyn JH, Rinzel J. Neuronal coupling by endogenous electric fields: Cable theory and applications to coincidence detector neurons in the auditory brain stem. Journal of neurophysiology. 2016;115:2033–2051. doi: 10.1152/jn.00780.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Parastesh F, et al. Synchronizability of two neurons with switching in the coupling. Appl. Math. Comput. 2019;350:217–223. [Google Scholar]
- 11.Jefferys JG, et al. Mechanisms of physiological and epileptic hfo generation. Progress Neurobiol. 2012;98:250–264. doi: 10.1016/j.pneurobio.2012.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Berridge MJ. Calcium regulation of neural rhythms, memory and alzheimer’s disease. J. Physiol. 2014;592:281–293. doi: 10.1113/jphysiol.2013.257527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Palva S, Palva JM. Functional roles of alpha-band phase synchronization in local and large-scale cortical networks. Front. Psychol. 2011;2:204. doi: 10.3389/fpsyg.2011.00204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang X-J. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol. Rev. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nimmrich V, Gross G. P/q-type calcium channel modulators. Br. J. Pharmacol. 2012;167:741–759. doi: 10.1111/j.1476-5381.2012.02069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.dos Santos Lima GZ, et al. Hippocampal and cortical communication around micro-arousals in slow-wave sleep. Sci. Rep. 2019;9:5876. doi: 10.1038/s41598-019-42100-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.dos Santos Lima GZ, et al. Disruption of neocortical synchronisation during slow-wave sleep in the rotenone model of parkinson’s disease. J. Sleep Res. 2020;30:e13170. doi: 10.1111/jsr.13170. [DOI] [PubMed] [Google Scholar]
- 18.Ugalde CL, Lawson VA, Finkelstein DI, Hill AF. The role of lipids in -synuclein misfolding and neurotoxicity. J. Biol. Chem. 2019;294:9016–9028. doi: 10.1074/jbc.REV119.007500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nery AA, et al. Rescue of amyloid-beta-induced inhibition of nicotinic acetylcholine receptors by a peptide homologous to the nicotine binding domain of the alpha 7 subtype. PloS one. 2013;8:e67194. doi: 10.1371/journal.pone.0067194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baumann B, et al. Visualization of neuritic plaques in alzheimer’s disease by polarization-sensitive optical coherence microscopy. Sci. Rep. 2017;7:1–12. doi: 10.1038/srep43477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang Y-W, Thompson R, Zhang H, Xu H. App processing in alzheimer’s disease. Mol. Brain. 2011;4:1–13. doi: 10.1186/1756-6606-4-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Egawa J, Pearn ML, Lemkuil BP, Patel PM, Head BP. Membrane lipid rafts and neurobiology: Age-related changes in membrane lipids and loss of neuronal function. J. Physiol. 2016;594:4565–4579. doi: 10.1113/JP270590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fusco G, et al. Structural basis of membrane disruption and cellular toxicity by -synuclein oligomers. Science. 2017;358:1440–1443. doi: 10.1126/science.aan6160. [DOI] [PubMed] [Google Scholar]
- 24.Wie J, et al. A growth-factor-activated lysosomal k+ channel regulates parkinson’s pathology. Nature. 2021;591:431–437. doi: 10.1038/s41586-021-03185-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kim S, Rhim H. Effects of amyloid-β peptides on voltage-gated l-type cav1. 2 and cav1. 3 ca2+ channels. Mol. cells. 2011;32:289–294. doi: 10.1007/s10059-011-0075-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Neelands TR, King AP, Macdonald RL. Functional expression of l-, n-, p/q-, and r-type calcium channels in the human nt2-n cell line. J. Neurophysiol. 2000;84:2933–2944. doi: 10.1152/jn.2000.84.6.2933. [DOI] [PubMed] [Google Scholar]
- 27.van Dellen E, et al. Loss of eeg n etwork e fficiency i s r elated to c ognitive i mpairment in d ementia w ith l ewy b odies. Mov. Disord. 2015;30:1785–1793. doi: 10.1002/mds.26309. [DOI] [PubMed] [Google Scholar]
- 28.Hammond C, Bergman H, Brown P. Pathological synchronization in parkinson’s disease: Networks, models and treatments. Trends Neurosci. 2007;30:357–364. doi: 10.1016/j.tins.2007.05.004. [DOI] [PubMed] [Google Scholar]
- 29.Park C, Worth RM, Rubchinsky LL. Fine temporal structure of beta oscillations synchronization in subthalamic nucleus in parkinson’s disease. J. Neurophysiol. 2010;103:2707–2716. doi: 10.1152/jn.00724.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brown P. Abnormal oscillatory synchronisation in the motor system leads to impaired movement. Curr. Opin. Neurobiol. 2007;17:656–664. doi: 10.1016/j.conb.2007.12.001. [DOI] [PubMed] [Google Scholar]
- 31.Jelic V, et al. Quantitative electroencephalography in mild cognitive impairment: Longitudinal changes and possible prediction of alzheimer’s disease. Neurobiol. Aging. 2000;21:533–540. doi: 10.1016/S0197-4580(00)00153-6. [DOI] [PubMed] [Google Scholar]
- 32.Locatelli T, Cursi M, Liberati D, Franceschi M, Comi G. Eeg coherence in alzheimer’s disease. Electroencephal. Clin. Neurophysiol. 1998;106:229–237. doi: 10.1016/S0013-4694(97)00129-6. [DOI] [PubMed] [Google Scholar]
- 33.Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 2000;8:183–208. doi: 10.1023/A:1008925309027. [DOI] [PubMed] [Google Scholar]
- 34.Lima GZDS, et al. Mouse activity across time scales: Fractal scenarios. Plos one. 2014;9:e105092. doi: 10.1371/journal.pone.0105092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Galán RF, Ermentrout GB, Urban NN. Efficient estimation of phase-resetting curves in real neurons and its significance for neural-network modeling. Phys. Rev. lett. 2005;94:158101. doi: 10.1103/PhysRevLett.94.158101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952;117:500. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lapicque L. Quantitative investigations of electrical nerve excitation treated as polarization 1907. Biol. Cybern. 2007;97:341. doi: 10.1007/s00422-007-0189-6. [DOI] [PubMed] [Google Scholar]
- 38.Izhikevich EM. Hybrid spiking models. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010;368:5061–5070. doi: 10.1098/rsta.2010.0130. [DOI] [PubMed] [Google Scholar]
- 39.Ermentrout B. Type i membranes, phase resetting curves, and synchrony. Neural Comput. 1996;8:979–1001. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- 40.Holt GR, Koch C. Electrical interactions via the extracellular potential near cell bodies. J. Comput. Neurosci. 1999;6:169–184. doi: 10.1023/A:1008832702585. [DOI] [PubMed] [Google Scholar]
- 41.Cunha GM, Corso G, Miranda JGV, Dos Santos Lima GZ. Ephaptic entrainment in hybrid neuronal model. Sci. Rep. 2022;12:1–10. doi: 10.1038/s41598-022-05343-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kandel ER, et al. Principles of Neural Science. McGraw-hill; 2000. [Google Scholar]
- 43.Shneider MN, Pekker M. Correlation of action potentials in adjacent neurons. Phys. Biol. 2015;12:066009. doi: 10.1088/1478-3975/12/6/066009. [DOI] [PubMed] [Google Scholar]
- 44.Anastassiou CA, Montgomery SM, Barahona M, Buzsáki G, Koch C. The effect of spatially inhomogeneous extracellular electric fields on neurons. J. Neurosci. 2010;30:1925–1936. doi: 10.1523/JNEUROSCI.3635-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Anastassiou CA, Perin R, Markram H, Koch C. Ephaptic coupling of cortical neurons. Nat. Neurosci. 2011;14:217–223. doi: 10.1038/nn.2727. [DOI] [PubMed] [Google Scholar]
- 46.Tveito A, et al. An evaluation of the accuracy of classical models for computing the membrane potential and extracellular potential for neurons. Front. Comput. Neurosci. 2017;11:27. doi: 10.3389/fncom.2017.00027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fries P, Reynolds JH, Rorie AE, Desimone R. Modulation of oscillatory neuronal synchronization by selective visual attention. Science. 2001;291:1560–1563. doi: 10.1126/science.1055465. [DOI] [PubMed] [Google Scholar]
- 48.Paninski L. The spike-triggered average of the integrate-and-fire cell driven by gaussian white noise. Neural Comput. 2006;18:2592–2616. doi: 10.1162/neco.2006.18.11.2592. [DOI] [PubMed] [Google Scholar]
- 49.Zarei M, Jahed M, Daliri MR. Introducing a comprehensive framework to measure spike-lfp coupling. Front. Comput. Neurosci. 2018;12:78. doi: 10.3389/fncom.2018.00078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.García-Rosales F, et al. Low-frequency spike-field coherence is a fingerprint of periodicity coding in the auditory cortex. Iscience. 2018;9:47–62. doi: 10.1016/j.isci.2018.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Logothetis NK, Kayser C, Oeltermann A. In vivo measurement of cortical impedance spectrum in monkeys: Implications for signal propagation. Neuron. 2007;55:809–823. doi: 10.1016/j.neuron.2007.07.027. [DOI] [PubMed] [Google Scholar]
- 52.Milstein J, Mormann F, Fried I, Koch C. Neuronal shot noise and brownian 1/f2 behavior in the local field potential. PloS one. 2009;4:e4338. doi: 10.1371/journal.pone.0004338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Licker V, Kövari E, Hochstrasser DF, Burkhard PR. Proteomics in human parkinson’s disease research. J. Proteom. 2009;73:10–29. doi: 10.1016/j.jprot.2009.07.007. [DOI] [PubMed] [Google Scholar]
- 54.Ferrer I. Early involvement of the cerebral cortex in parkinson’s disease: Convergence of multiple metabolic defects. Progress Neurobiol. 2009;88:89–103. doi: 10.1016/j.pneurobio.2009.02.004. [DOI] [PubMed] [Google Scholar]
- 55.Moore DJ, West AB, Dawson VL, Dawson TM. Molecular pathophysiology of parkinson’s disease. Annu. Rev. Neurosci. 2005;28:57–87. doi: 10.1146/annurev.neuro.28.061604.135718. [DOI] [PubMed] [Google Scholar]
- 56.Brown P, et al. Dopamine dependency of oscillations between subthalamic nucleus and pallidum in parkinson’s disease. J. Neurosci. 2001;21:1033–1038. doi: 10.1523/JNEUROSCI.21-03-01033.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.