Finite element analysis of maxillary first molar with mesial-occlusal-distal-palatal defect restored with different post-and-core strategies

Abstract

Purpose

To explore which restoration strategy generates the most favorable stress distribution in an endodontically-treated maxillary first molar with mesial-occlusal-distal-palatal defect.

Methods

Models with one post in palatal canal (PP), each post in palatal and distobuccal canals (PDP), each post in palatal and mesiobuccal canals (PMP), and each post in all canals (PDMP) were established for an endodontically-treated maxillary first molar with mesial-occlusal-distal-palatal defect either with fiber-reinforced composite (FRC) post or gold alloy cast (GAC) post. A 400-N vertical force and a 225-N lateral force were respectively applied. The Mohr-Coulomb stress ratio (σ_{MC ratio}) in the residual tooth structure (RTS), the resin cement, and the crowns, the tensile stress (σ_t) and compressive stress (σ_c) in the FRC posts, the von-Mises stress ratio (σ_{vM ratio}) in the GAC post-and-cores, and the σ_t and shear stress (σ_s) at the adhesive interfaces were calculated using finite element analysis.

Results

FRC posts generated lower σ_{MC ratio} than GAC posts in the RTS (0.3274–0.3643 vs. 0.3399–0.4118). Among the FRC post groups, the PDMP group got the lowest σ_s at the dentin-post interface (14.92 MPa) and the abutment-crown interface (8.242 MPa) under vertical loading, as well as the lowest σ_{MC ratio} in the RTS (0.3381) and the lowest σ_s at the dentin-post interface (38.00 MPa) under lateral loading.

Conclusions

From the point of stress distribution, placing FRC posts in the palatal, distobuccal, and mesiobuccal canals is the optimal strategy in restoring a severely damaged maxillary first molar, provided that lateral occlusal force is reduced.

1. Introduction

Posts are often used in restoring severely damaged teeth to improve the retention of the restorations [1]. It is indicated that a post is vital for restoring a tooth with absence of one, two, or three coronal walls [2]. A post could be metallic or non-metallic. Metallic posts can be casted from nickel-chromium alloy, cobalt-chromium alloy, or gold alloy. Non-metallic posts are usually prefabricated and made of zirconia or fiber-reinforced composite (FRC) [1,3]. Gold alloy cast (GAC) posts have been used in clinic for decades and obtain a high ten-year success rate, ranging from 84 to 94% [1]. Gold alloy has elastic modulus close to enamel (80 GPa versus 84.1 GPa), high flexure strength (1542 MPa), and high resemblance to dentin owing to its yellow appearance [[4], [5], [6]]. However, the use of GAC posts requires additional removal of tooth structure and also introduces the risk of leakage before the definitive restoration is casted and cemented to the canals. FRC posts were introduced more than 30 years ago [7]. Due to their “dentin-like” elastic modulus (18.7–40 GPa), exceptional aesthetic properties and lower rate of catastrophic root fractures than metallic posts [3,8,9], FRC posts becomes more and more popular in clinic in recent years [10]. However, fracture at cervical portion of the residual tooth structure (RTS) is more common with FRC posts [11], thereby FRC posts have higher demand on the amount of RTS at this portion, such as coronal walls and ferrule, than GAC posts [9,12,13]. It is debatable whether GAC post (with high elastic modulus) or FRC post (with elastic modulus close to dentin) should be applied in post-and-core restoration. Some researchers recommend the use of posts with high elastic modulus as they reduce the stress in RTS and demonstrate higher fracture resistance [3,14,15]. Whereas others suggest the use of posts with elastic modulus close to dentin as the stress distribution is more uniform, as well as lower stresses were observed at middle and apical area of tooth structure and at the post-dentin interface [[16], [17], [18]].

A maxillary first molar usually has three roots and at least three root canals [19]. There are multiple choices of post-placing strategy for the restoration of a severely damaged and endodontically treated maxillary first molar, and which one is the most appropriate remains disputed. It has been accepted that the post should be inserted in the palatal canal of a maxillary first molar [20]. However, recent researches provide other points of view. Fu et al. reported that the stresses in the GAC post-and-core restored maxillary first molar with a two-post strategy (one post in the palatal canal and the other in the distobuccal or mesiobuccal canal) were lower than those with one-post strategy (one post in the palatal canal) or three-post strategy (posts in all the three canals) [21]. Zhao et al. reported a similar conclusion for both FRC and GAC post-and-core restorations and recommended inserting posts in the palatal and distobuccal canals to decrease the stress in the RTS, especially with GAC post-and-core restorations [16].

Mesial-occlusal-distal-palatal (MODP) defect is a common type of severe tooth defect on maxillary first molars in clinic. Due to the loss of three coronal walls, such a tooth is more likely to fracture upon mastication after endodontic treatment [2]. Thus, the optimal selection of material and application strategy for a post-and-core restoration of such a defect is critical to the prognosis of such a tooth. However, presently there is few researches which has systematically investigated stress distributions in the RTS, in the post(s), in the resin cement, in the crown, and at the adhesive interfaces of post-and-core restored maxillary first molars. Based on this background, the present work was carried out by using finite element analysis (FEA) to investigate the stress distribution over the RTS, the post-and-core system, the crown, the cement, as well as at the adhesive interfaces of a maxillary first molar with a MODP defect restored by FRC post-and-resin core or GAC post-and-core. The aim of the present work is to reveal the most appropriate post material and post-placing strategy for a post-and-core restored multirooted tooth with excessive loss of coronal structure. The null hypothesis was that FRC post-and-resin core is better than GAC post-and-core as to the stress distribution, and one FRC post in the palatal canal is the most appropriate strategy.

2. Materials and methods

2.1. Ethical committee approval

The acquisition of the extracted human molar in this study was reviewed and approved by the Ethics Committee of Shanghai Ninth People's Hospital, Shanghai Jiao Tong University School of Medicine (Approval Letter No. SH9H-2020-TK17-1), and the experimental protocols were carried out by following The Operational Guideline for The Ethic Review of Biomedical Research Involving Human Subjects. Consent letter has been signed by the donor.

2.2. Generation of FEA models

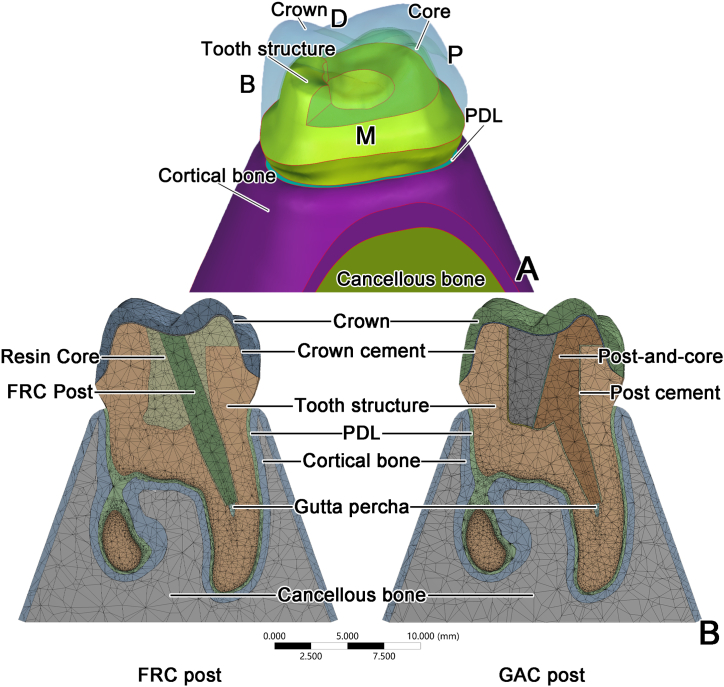
An extracted left maxillary first molar was scanned by micro-CT (GE Healthcare eXplore Locus SP Micro-CT，GE Company, U.S.A.) before and after endodontic treatment and subsequent tooth preparation for a crown. Images were saved in Digital Imaging and Communications in Medicine (DICOM) files and then imported into an image processing software program (Mimics Research 21.0; Materialise NV, Belgium) to convert the different parts into different Stereolithography (STL) files. The models of crown, core, tooth structure (with MODP defect and 1.5-mm-high ferrule, Fig. 1A), adhesive cement (with a thickness of 0.1 mm), gutta-percha, periodontal ligament (PDL, with a thickness of 0.25 mm), cortical bone (with a thickness of 0.5 mm) and cancellous bone were created in a reverse engineering software program (Geomagic Wrap 2015; 3D Systems Inc, U.S.A.) with Boolean operation [9]. The ferrule height was set as 1.5 mm as the presence of a 1.5-mm-high ferrule would increase the fracture resistance of endodontically treated teeth restored with a post [11]. The models of posts were created by a 3-dimensional computer-aided design software program (SolidWorks 2016; Dassault Systemes S.A, France) and saved in STL files.

Fig. 1.

Schematics of models (A: Three-dimensional schematic of the maxillary first molar with a MODP defect; B: Schematics of finite element models for different restoration groups).

B = buccal; D = distal; M = mesial; MODP = mesial-occlusal-distal-palatal; P = palatal; PDL = periodontal ligament.

The posts were selected with the limitation that the post diameter is no more than one third of the root diameter, namely #1.6 post (Φ0.86 mm at post end) for the palatal canal, #1.4 post (Φ0.77 mm at post end) for the distobuccal canal and #1.2 post (Φ0.68 mm at post end) for the mesiobuccal canal, and inserted into the canals with a 0.1-mm-thick cement layer around by Boolean operation [9]. The apical part of the canal had 5.0 mm of remaining gutta percha after post placement to ensure good apical seal and enough post length [22]. It is indicated that the palatal canal should be post-placed for post-and-core restoration on a maxillary molar in previous research [23]. Hence, models of four different groups were created for each post material: palatal post (PP), palatal and distobuccal posts (PDP), palatal and mesiobuccal posts (PMP), and palatal, distobuccal, and mesiobuccal posts (PDMP). A monolithic zirconia crown was applied in all the groups. For the groups with FRC post(s), if two posts overlapped in the resin core, the thinner one was trimmed 1 mm below the intersection point, perpendicular to the long axis of the post. In the groups with GAC post(s), the post(s) and the core were then merged into post-and-core. In the PDP, PMP, and PDMP groups with GAC posts, the post-and-core was then split according to the number of posts to ensure passive emplacement of each part. All these parts were converted into non-uniform rational B-splines surfaces and saved in the Initial Graphics Exchange Specification (IGES) files. Those files were imported into Design Modeler, a part of a computer-aided engineering software program (ANSYS v.19.0; ANSYS Inc., U.S.A.) to assemble the FEA models.

2.2.1. Mesh

A static structural analysis system was created for each model in ANSYS. Automatic convergence test provided by the software was used. It detected high stress regions and refined mesh at these regions. Then the result was evaluated again and compared to the former one to decide whether the data was convergent or not. Based on the convergence analysis, all the models were meshed by 311,653–464,683 ten-node tetrahedron elements (SOLID187, Fig. 1B). Pairs of bonded contact elements, TARGE170 and CONTA174, were applied at all the interfaces.

2.3. Boundary and loading conditions

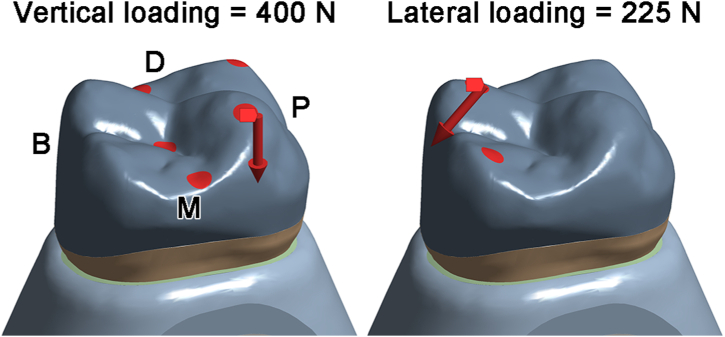
The mesial, distal, and bottom aspects of the alveolar bone were set as fixed support, while the buccal and palatal aspects were defined as freedom boundaries [24]. A total force of 400 N was applied to five 1 mm² areas on the occlusal surface parallelly to the long axis of the tooth, to simulate the vertical occlusal force [25]. Another total force of 225 N was applied to two 1 mm² areas on the palatal planes of the buccal cusps at a 45-degree inclination in a palatal-buccal direction to the long axis of the tooth, to simulate the lateral occlusal force (Fig. 2) [26].

Fig. 2.

Schematics of force loading.

B = buccal; D = distal; M = mesial; P = palatal.

2.4. Material properties

Zirconia ceramic was set as the material for the crown, and was bonded with the abutment using resin cement in all the groups. In the groups with FRC post, glass FRC post and resin core was applied. Each post was cemented to the corresponding canal with the same composite resin material as the core. In the groups with GAC post(s), post-and-core was made of type IV gold alloy. Tooth and post-and-core were bonded together with the same resin cement as crown cement. All materials except FRC post were assumed to be homogeneous, isotropic, and linear elastic; FRC post was considered as orthotropic (the long axis was defined as X axis) and linear elastic material. The material properties in the present work were listed in Table 1.

Table 1.

Mechanical properties of materials and tooth structure.

Material	Elastic modulus (E, MPa)	Poisson ratio (ν)	Tensile strength (Rt, MPa)	Compressive strength (Rc, MPa)	Reference
Cancellous bone	1370	0.30	–	–	[14]
Cortical bone	13,700	0.30	–	–	[14]
Dentin	18,600	0.31	105.5	297	[27]
Gutta Percha	141.9	0.45	–	–	[28]
Periodontal ligament	68.9	0.45	–	–	[29]
Resin cement	8300	0.35	45.1	178	[27]
Resin core build-up	14,100	.24	41	293	[29]
Gold alloy	80,000	0.30	355.45		[4,30]
Zirconia ceramic	210,000	0.30	745	2000	[30]
Glass FRC post	Ex = 37,000 Ey = 9500 Ez = 9500 Shear modulus(G): Gyz = 14,567 Gxy = 3544.8 Gxz = 3544.8	νyz = 0.34 νxy = 0.27 νxz = 0.27	Rtx = 1200 Rty = 73 Rtz = 73	Rcx = 1000 Rcy = 160 Rcz = 160	[6,27]

FRC = fiber-reinforced composite.

2.5. Stress analysis

Mohr-Coulomb failure criterion, which is typically used to predict fracture in brittle materials under quasi-static loading [31], was used to analyze the stress in the RTS, crown, and composite materials in the present work. It compares the maximal principal stress (σ_max), almost the tensile stress (σ_t), to the material's tensile strength (TS) and the minimal principal stress (σ_min), almost the compressive stress (σ_c), to the material's compressive strength (CS). The Mohr-Coulomb stress ratio (σ_{MC ratio}) is calculated according to the following formula. ${\sigma }_{MCratio}=\frac{{\sigma }_{\mathit{max}}}{TS}+\frac{{\sigma }_{\mathit{min}}}{CS}$ If the σ_{MC ratio} value exceeds 1, the material will fail [31].

A cylindrical coordinate system was created for the FRC post (Fig. 3). Due to the software limitation, the long axis was converted into Z axis. The Poisson ratios (ν) were also recalculated according to the following formula. $\frac{{\upsilon }_{12}}{{\upsilon }_{21}}=\frac{E_1}{E_2}$ where 1 and 2 represent the corresponding axis, ν₁₂ means the Poisson ratio from axis 1 to axis 2, and E is the elastic modulus along the axis. After the conversion, axial, circumferential, and radial stress in the FRC post could be evaluated through calculating the normal stresses along the three axes. The positive value referred to σ_t and negative value referred to σ_c.

Fig. 3.

Schematic of cylindrical coordinate system created for FRC post.

X = radial direction; Y = circumferential direction; Z = axial direction.

Unlike the other materials, gold alloy is a kind of ductile materials. Von-Mises failure criterion is used to predict fracture in ductile materials. It compares the von-Mises equivalent stress (σ_vM) to the TS of the material [27]. The von-Mises stress ratio (σ_{vM ratio}) is calculated according to the following formula. ${\sigma }_{vMratio}=\frac{{\sigma }_{vM}}{TS}$ If the σ_{vM ratio} value exceeds 1, the material will fail [27].

Pressure and frictional stress at the adhesive interfaces, namely dentin-post cement-post (D–PC–P) interface and abutment-crown cement-crown (A–CC–C) interface, were calculated to evaluate the possibility of adhesive failure. Negative value of pressure reflects the trend of separation normal to the interface, which is assumed as σ_t [31]. Frictional stress indicated the trend of sliding along the interface and was thereby considered as shear stress (σ_s) [32].

3. Results

3.1. Volume of residual tooth structure

Table 2 shows the volume of RTS. The volume of RTS was lower in the groups with GAC post(s) than in the groups with FRC post(s).

Table 2.

Volume of residual tooth structure (mm²).

Group	Volume
	FRC	GAC
PP	666.9	655.6
PDP	662.2	651.2
PMP	661.7	650.2
PDMP	656.9	645.7

FRC = fiber-reinforced composite; GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

3.2. Stress in the residual tooth structure

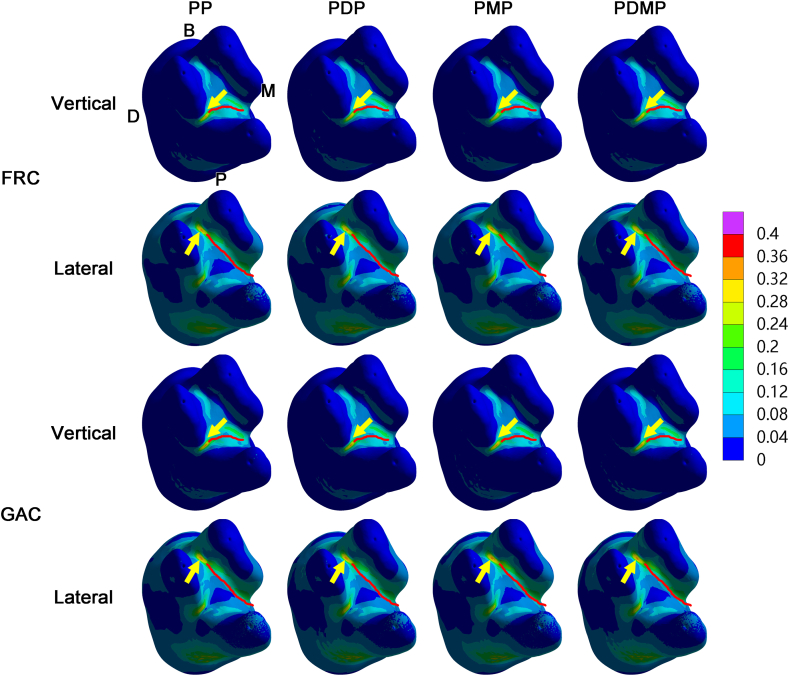
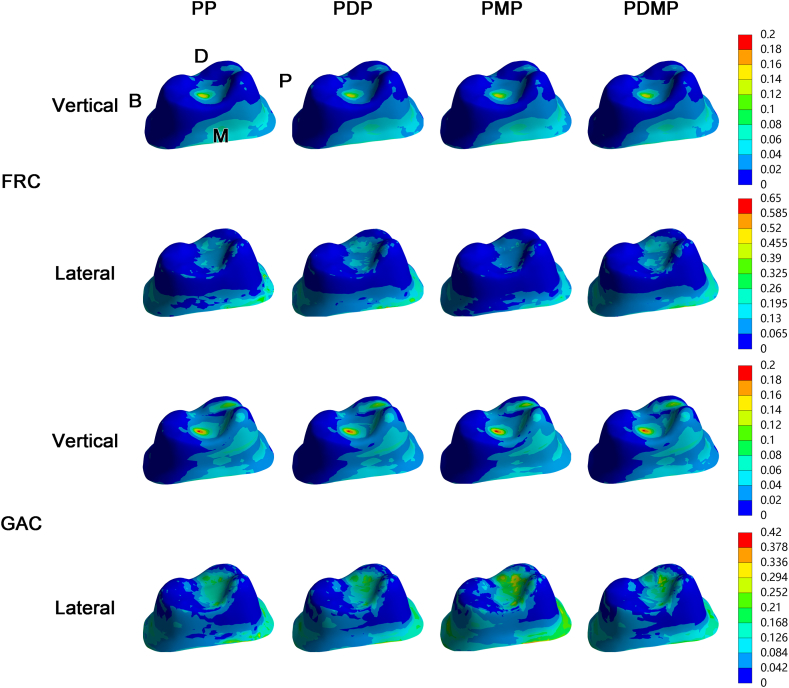
Fig. 4 shows the σ_{MC ratio} distribution and Table 3 demonstrates the maximal σ_{MC ratio} (Mσ_{MC ratio}) in the RTS in all the groups under both loadings. The Mσ_{MC ratio} was located at the mesial portion of the furcation area under vertical loading, and at the buccal portion under lateral loading (yellow arrows in Fig. 4). Under vertical loading, high σ_{MC ratio} region was around palatal root, and around mesiobuccal root under lateral loading (red curves in Fig. 4). The lowest Mσ_{MC ratio} was in the PMP group with FRC posts, and in the PDMP group with GAC posts under vertical loading. Under lateral loading, the lowest Mσ_{MC ratio} was in the PDMP group with either FRC posts or GAC posts. The Mσ_{MC ratio} in the RTS with GAC post(s) were higher than that with FRC post(s).

Fig. 4.

The Mohr-Coulomb stress ratio distributions in the residual tooth structure under vertical and lateral loading.

B = buccal; D = distal; FRC = fiber-reinforced composite; GAC = gold alloy cast; M = mesial; P = palatal; yellow arrow = maximal Mohr-Coulomb stress ratio; red curve = high Mohr-Coulomb stress ratio regions.

Table 3.

Maximal Mohr-Coulomb stress ratio in the residual tooth structure.

Group	Vertical loading		Lateral loading
	FRC	GAC	FRC	GAC
PP	0.3454	0.3486	0.3633	0.4118
PDP	0.3300	0.3471	0.3643	0.3708
PMP	0.3274	0.3495	0.3595	0.3712
PDMP	0.3341	0.3399	0.3381	0.3455

FRC = fiber-reinforced composite; GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

3.3. Stress in the post-and-core system

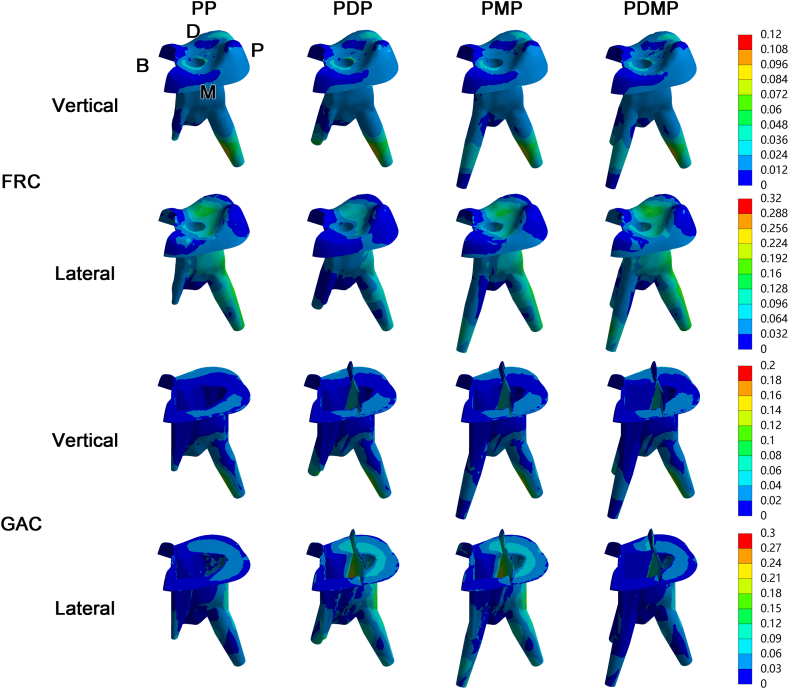
The σ_{MC ratio} distributions in the post cement and resin core under both loadings are exhibited in Fig. 5. The Mσ_{MC ratio} in the resin core in the groups with FRC post(s) under both loadings are listed in Table 4. Higher Mσ_{MC ratio} was detected under lateral loading than under vertical loading. Under vertical loading, the Mσ_{MC ratio} were close to each other. Under lateral loading, the lowest Mσ_{MC ratio} was in the PDP group.

Fig. 5.

The Mohr-Coulomb stress ratio distributions in the resin core and post cement under vertical and lateral loading.

B = buccal; D = distal; FRC = fiber-reinforced composite; GAC = gold alloy cast; M = mesial; P = palatal.

Table 4.

Maximal Mohr-Coulomb stress ratio in the post cement and resin core in the FRC post groups.

Group	Vertical loading	Lateral loading
PP	0.1114	0.3062
PDP	0.1110	0.1756
PMP	0.1094	0.2917
PDMP	0.1100	0.2852

FRC = fiber-reinforced composite; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

The maximal axial, circumferential, and radial stress in the FRC post under both loadings are shown in Table 5. Lateral loading generated higher axial and radial σ_t than vertical loading. Lower axial and radial σ_c were found in the groups without mesiobuccal post (the PP and PDP groups) under lateral loading, compared with those in other groups.

Table 5.

Maximal axial (A), circumferential (C), and radial (R) stress in the FRC post (MPa).

Group	Direction	Vertical loading		Lateral loading
		σt	σc	σt	σc
PP	A	1.622	19.91	13.65	6.723
	C	2.811	2.081	2.359	2.311
	R	2.491	4.895	4.164	2.922
PDP	A	2.299	20.00	13.76	15.91
	C	3.397	2.068	3.981	3.265
	R	3.593	4.874	4.160	3.699
PMP	A	1.602	20.00	13.65	27.19
	C	2.869	2.039	3.374	3.578
	R	2.552	4.943	4.184	4.484
PDMP	A	2.150	19.94	13.82	27.71
	C	3.341	2.060	3.825	3.601
	R	3.613	4.871	4.162	4.480

FRC = fiber-reinforced composite; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

As shown in Table 6, the Mσ_{MC ratio} in the post cement in the groups with GAC post(s) were higher under lateral loading than under vertical loading. Under vertical loading, Mσ_{MC ratio} in two-post groups (the PDP and PMP groups) were higher than the other groups. Under lateral loading, the groups with mesiobuccal post (the PMP and PDMP groups) had higher Mσ_{MC ratio} than the groups without it (the PP and PDP groups).

Table 6.

Maximal Mohr-Coulomb stress ratio in the post cement in GAC post groups.

Group	Vertical loading	Lateral loading
PP	0.1557	0.2578
PDP	0.1601	0.2654
PMP	0.1652	0.2838
PDMP	0.1552	0.2827

GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

Table 7 presents the maximal σ_{vM ratio} (Mσ_{vM ratio}) in the GAC post-and-core under both loadings. The Mσ_{vM ratio} was lower in the PDMP group than any other group under vertical loading. Under lateral loading, the Mσ_{vM ratio} was higher in the groups with mesiobuccal post (the PMP and PDMP groups) than the groups without it (the PP and PDP groups).

Table 7.

Maximal von-Mises stress ratio in the post-and-core in GAC post groups.

Group	Vertical loading	Lateral loading
PP	0.1071	0.1616
PDP	0.1096	0.1242
PMP	0.1153	0.2613
PDMP	8.789 × 10−2	0.2428

GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

3.4. Stress in the crown and crown cement

Similar Mσ_{MC ratio} in the crown were detected in all the groups with the same post under the same loading (Table 8).

Table 8.

Maximal Mohr-Coulomb stress ratio in the crown.

Group	Vertical loading		Lateral loading
	FRC	GAC	FRC	GAC
PP	0.2462	0.2296	0.1553	0.1523
PDP	0.2465	0.2280	0.1553	0.1524
PMP	0.2461	0.2283	0.1553	0.1550
PDMP	0.2462	0.2282	0.1553	0.1525

FRC = fiber-reinforced composite; GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

Fig. 6 illustrates the σ_{MC ratio} distributions in the crown cement in all the groups under both loadings, while the Mσ_{MC ratio} in the crown cement in all the groups under both loadings are listed in Table 9. Under vertical loading, similar Mσ_{MC ratio} were found in all the groups with the same post. Under lateral loading, the Mσ_{MC ratio} differed considerably. The lowest Mσ_{MC ratio} was in the PMP group with FRC posts, whereas in the PDMP group with GAC posts. Mσ_{MC ratio} was lower with FRC post(s) under vertical loading, but higher under lateral loading than with GAC post(s).

Fig. 6.

The Mohr-Coulomb stress ratio distributions in the crown cement under vertical and lateral loading.

B = buccal; D = distal; FRC = fiber-reinforced composite; GAC = gold alloy cast; M = mesial; P = palatal.

Table 9.

Maximal Mohr-Coulomb stress ratio in the crown cement.

Group	Vertical loading		Lateral loading
	FRC	GAC	FRC	GAC
PP	0.1574	0.1951	0.5611	0.4108
PDP	0.1533	0.1984	0.6359	0.3218
PMP	0.1576	0.1978	0.5123	0.3998
PDMP	0.1540	0.1926	0.5472	0.3172

FRC = fiber-reinforced composite; GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

3.5. Stress at the adhesive interfaces

Table 10 shows the maximal tensile stress (Mσ_t) and the maximal shear stress (Mσ_s) at the D-PC-P interface. GAC posts generated higher Mσ_t than FRC posts under both loading. Under vertical loading, Mσ_t were slightly lower in the two-post groups (the PDP and PMP groups) with FRC posts, whereas Mσ_t were lower in the PP and PDP groups than in the PMP and PDMP groups with GAC posts. Lateral loading generated far higher Mσ_t than vertical loading in all the groups, with the lowest in the PP group with either post. The lowest Mσ_s was in the PDMP group with FRC posts under both loadings, whereas in the PP group under vertical loading and in the PDP group under lateral loading with GAC post(s).

Table 10.

Maximal stress at the dentin-post cement-post interface.

Stress	Group	Vertical loading		Lateral loading
		FRC	GAC	FRC	GAC
Tensile	PP	2.716	4.842	8.152	10.46
	PDP	2.054	4.004	13.46	17.69
	PMP	2.142	7.207	9.625	27.06
	PDMP	2.984	7.712	9.275	27.49
Shear	PP	19.74	11.70	39.26	41.47
	PDP	16.34	19.02	39.09	32.22
	PMP	24.25	17.58	39.75	34.91
	PDMP	14.92	16.61	38.00	35.84

FRC = fiber-reinforced composite; GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

Table 11 shows the maximal tensile stress (Mσ_t) and the maximal shear stress (Mσ_s) at the A–CC–C interface. The PP group with FRC post had a bit lower Mσ_t than the PMP and PDMP groups, but obviously lower than the PDP group under vertical loading. On the other hand, similar Mσ_t were found in all the groups with GAC post(s) under vertical loading, which were higher than those in groups with FRC post(s). Under lateral loading, the PMP group with FRC posts and the PDP group with GAC posts got the lowest Mσ_t. The lowest Mσ_s was in the PMP group with GAC posts under vertical loading, and in the PP group with FRC post and in the PDMP group with GAC posts under lateral loading, whereas the Mσ_s were close to each other in groups with FRC post(s) under vertical loading.

Table 11.

Maximal stress at the abutment-crown cement-crown interface.

Stress	Group	Vertical loading		Lateral loading
		FRC	GAC	FRC	GAC
Tensile	PP	1.952	5.199	9.132	19.59
	PDP	3.293	5.180	19.19	8.311
	PMP	2.109	5.095	5.847	14.01
	PDMP	2.060	5.239	9.015	10.94
Shear	PP	8.256	10.90	27.40	33.14
	PDP	8.296	8.474	31.87	41.65
	PMP	8.279	7.725	33.61	26.80
	PDMP	8.242	7.792	28.62	23.40

FRC = fiber-reinforced composite; GAC = gold alloy cast; PDP = palatal and distobuccal posts; PDMP = palatal, distobuccal, and mesiobuccal posts; PMP = palatal and mesiobuccal post; PP = palatal post.

4. Discussion

The PDMP group with FRC posts demonstrated optimal stress in the RTS, in the post-and-core system, in the crown cement, in the crown, and at the D-PC-P and A–CC–C interfaces. The null hypothesis that FRC post-and-resin core is better than GAC post-and-core as to the stress distribution should be accepted, but that one FRC post in the palatal canal is the most appropriate strategy was rejected.

In the present study, it was revealed that high σ_{MC ratio} regions on RTS were around mesiobuccal root under lateral loading, and around palatal root under vertical loading. This finding indicated that mesiobuccal root and palatal root were of greater opportunity to fracture, which was consisted with a previous finding that the most common fracture sites on devitalized maxillary first molars are mesiobuccal root and palatal root [33].

It was found that lateral occlusal force generated apparently higher stress in RTS than vertical occlusal force did [24]. In the present work, lateral loading led to higher stress level in almost all the components except the crown and at almost all the adhesive interfaces. Additionally, lateral loading generated higher axial and redial σ_t in all the FRC posts. This finding pointed out that lateral occlusal force should be carefully controlled in restoring a maxillary first molar with MODP defect by using the post-and-core technique.

Due to the elimination of undercut in the pulp chamber, a larger amount of tooth tissue was removed in the groups with GAC post(s) than in the groups with FRC post(s). It is accepted that the more tooth structure was preserved, the more strength and fracture resistance would be provided [34]. Thus, from the point of preserving tooth structure and fracture resistance, FRC posts would be a better choice than GAC posts.

In the present work, σ_{MC ratio} was used to evaluate the fracture risk of brittle materials, including RTS, resin cement, FRC post, and zirconia crown. Since none of the groups had higher Mσ_{MC ratio} than one in any component, there was no evidence that restoration with either of the post materials would cause fracture in these brittle components. Yet, considering the fatigue effect which would weaken the material's resistance to stress, lower Mσ_{MC ratio} represents lower long-term fracture risk and is better for its long-term serving [31].

Similar σ_{MC ratio} distribution patterns were detected in the RTS among all the groups under the same loading. It is considered that the tooth's morphological feature and the loading protocol, rather than the post material and post-placing strategy, are the determining factors on the stress distribution in the RTS. In addition, stress was found concentrated at the furcation area. Tooth structure at these portions should thereby be preserved to prevent fracture.

Nokar et al. found that the increase of elastic modulus of the post led to decrease in stress values in the root dentin [3]. Durmuş et al. reported similar finding and claimed that increases in the elastic modulus of the post resulted in decreases in stress values in the root and increases in stress values in the post [35]. In the present work, the Mσ_{MC ratio} in the RTS were found lower with FRC posts than with GAC posts, which is inconsistent to their findings. Once loaded, components with higher elastic modulus tends to transfer the load to the adjacent structures [36]. Thus, GAC post led to higher Mσ_{MC ratio} in RTS and was not recommended. Despite the second highest Mσ_{MC ratio} under vertical loading, the PDMP group with FRC posts had far lower Mσ_{MC ratio} under lateral loading than any other group. This indicated that placing FRC posts in the palatal, distobuccal, and mesiobuccal canals helps RTS to resist lateral occlusal force. On the other hand, for groups with GAC post(s), regardless of the loading direction, the lowest Mσ_{MC ratio} was in the PDMP group, indicating that placing GAC posts in the palatal, distobuccal, and mesiobuccal canals might be the appropriate choice for GAC post-and-core restoration.

In the groups with FRC post(s), the Mσ_t and the Mσ_c in all the directions in the FRC posts were far lower than the post's TS and CS. In the groups with GAC post(s), the Mσ_{vM ratio} were all apparently lower than 1. Therefore, both the FRC posts and the GAC posts were unlikely to fracture under the occlusal force.

High stress in the post cement will cause cohesive adhesive failure [37]. Previous research indicated that stress would concentrate at the interface between two materials with high difference of elastic modulus [17]. Compared to a FRC post, a GAC post has higher elastic modulus than dentin. Thus, in the present work, higher Mσ_{MC ratio} in the post cement were observed in groups with GAC posts, compared with those in the groups with FRC posts under vertical loading. Under lateral loading, the Mσ_{MC ratio} in the post cement considerably increased in all the groups. On the other hand, the Mσ_t in the FRC post(s), and the Mσ_{vM ratio} in the GAC post-and-core(s) were also higher under lateral loading than under vertical loading, which confirmed that higher stress would be generated under lateral occlusal force. Lateral occlusal force should be controlled in clinical practice. In addition, the axial Mσ_c in the FRC posts and the Mσ_{MC ratio} in the FRC post cement and resin core in the groups with mesiobuccal post (the PMP and PDMP group) were higher than those in the other groups. It was supposed that the FRC post in mesiobuccal canal endured more lateral occlusal force than any other post, thereby underwent larger deformation and generated more stress in the post cement. On the other hand, under lateral loading, the groups with either post in the mesiobuccal canal (the PMP and PDMP groups) had lower Mσ_{MC ratio} in the crown cement, which confirmed the ability to transmit lateral occlusal force into root tooth tissue of the mesiobuccal post. Therefore, a mesiobuccal post plays a crucial role in post-and-core restoration on a maxillary first molar.

Retention could be evaluated with the stress at the adhesive interfaces [38]. Lower stress links to lower risk of debonding, thus better retention. Tensile bond strength (TBS) and shear bond strength (SBS) are often tested to evaluate the adhesive property of the agents [39]. Thus, both σ_t and σ_s were calculated in the present work. Since SBS is usually numerically larger than TBS with the same bonding agent and interface [39], whereas σ_s were found all numerically higher than σ_t in this work, σ_s is more meaningful to discuss than σ_t.

At the D-PC-P interface, the lowest σ_s was in the PDMP group with FRC posts, regardless of the loading direction. At the A–CC–C interface, the PDMP group with FRC posts had the lowest σ_s under vertical loading, and the second lowest σ_s under lateral loading, which was slightly higher than the lowest one. When it came to groups with GAC post(s), the PDMP group had the second lowest σ_s under vertical loading, and the second highest σ_s under lateral loading at the D–PC–P interface, but the second lowest σ_s under vertical loading, and the lowest σ_s under lateral loading at the A–CC–C interface. Therefore, placing posts in the palatal, distobuccal, and mesiobuccal canals thereby provides the greatest retention for post-and-core restoration on a maxillary first molar.

In conventional FRC post-and-resin core restoration as studied in this work, two adhesive interfaces are generated between post and tooth. Recently, CAD/CAM monolithic FRC post-and-core is commercially available. It can reduce the number of adhesive interfaces into one, and thereby reduce the probability of adhesive failure. Previous research indicated that CAD/CAM monolithic FRC post-and-core showed potential in restoring endodontically-treated teeth [40]. Further FEA studies on CAD/CAM monolithic FRC post-and-core should be carried out later.

In this research, all the tooth structure and periodontal tissues were considered as homogeneous, isotropic, and linear elastic materials when they are actually neither homogeneous nor isotropic. In addition, the modulus of FRC would decrease after water absorption [41]. The FEA could also not exactly simulate all clinical conditions owing to the simplifications and approximations of the models. In addition, only one type of tooth defect with a single ferrule height was investigated. Within the scope of these limitations, the interpretation of this research's results should be validated by in vitro and clinical studies, and followed by studies on other types of defects and ferrule heights. On the other hand, artificial thermomechanical aging does have long-term effect on the survivability of the restoration and the remaining tooth structure. It will decrease the marginal continuity of the restoration and bond strength of resin adhesive [42,43]. Further studies should be carried out on the effect of artificial thermomechanical aging.

5. Conclusion

Within the limitations of this FEA study, the following conclusions could been draw on the stress distribution in a post-and-core restored maxillary first molar with a MODP defect and the presence of a 1.5 mm-high ferrule:

• 1Lateral occlusal force must be controlled for post-and-core restoration.
• 2The restoration with FRC post-and-resin core led to lower amount of tooth tissue removal, lower stress in the RTS, in the crown cement, and at the adhesive interfaces, compared with the GAC posts. From this point, FRC posts are more appropriate than GAC posts in restoring such a maxillary first molar.
• 3On the premise of reducing lateral occlusal force, FRC posts should be placed in the palatal, distobuccal, and mesiobuccal canals to obtain optimal retention and resistance to fracture.
• 4If GAC posts were applied, they should be placed in the palatal, distobuccal, and mesiobuccal canals, along with more strict lateral occlusal force reduction.

Author contribution statement

QI ZHONG: Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Ximeng Cao: Performed the experiments; Analyzed and interpreted the data.

Yingyi Shen; Yingshuang Song; Yaqin Wu; Fang Qu: Analyzed and interpreted the data.

Shaohai Wang: Conceived and designed the experiments.

Chun Xu: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data.

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Chun Xu reports financial support was provided by National Natural Science Foundation of China. Shaohai Wang reports financial support was provided by National Natural Science Foundation of China. Chun Xu reports financial support was provided by Shanghai Municipal Health Commission. Shaohai Wang reports financial support was provided by Specialty Feature Construction Project of Shanghai Pudong New Area Health Commission.