锥束CT系统几何校正的偏差因素敏感性分析方法

Abstract

Objective

To propose a sensitivity test method for geometric correction position deviation of cone-beam CT systems.

Methods

We proposed the definition of center deviation and its derivation. We analyzed the influence of the variation of the three-dimensional spatial center of the steel ball point, the projection center and the size of the steel ball point on the deviation of geometric parameters and the reconstructed image results by calculating the geometric correction parameters based on the Noo analytical method using the FDK reconstruction algorithm for image reconstruction.

Results

The radius of the steel ball point was within 3 mm. The deviation of the center of the calibration parameter was within the order of magnitude and negligible. A 10% Gaussian perturbation of a single pixel in the 3D spatial coordinates of the steel ball point produced a deviation of about 3 pixel sizes, while the same Gaussian perturbation of the 2D projection coordinates of the steel ball point produced a deviation of about 2 pixel sizes.

Conclusion

The geometric correction is more sensitive to the deviation generated by the three-dimensional spatial coordinates of the steel ball point with limited sensitivity to the deviation generated by the two-dimensional projection coordinates of the steel ball point. The deviation sensitivity of a small diameter steel ball point can be ignored.

锥形束CT（CBCT）系统是一种先进的非接触无损检测技术，具有射线利用率高、辐射剂量低、重建图像质量高、可以选择任意角度扫描的优点，被广泛应用于医学诊疗领域^[1-4]。在几何校正中，系统的几何参数能否精确获取是影响CBCT图像重建质量的关键因素，精确的几何参数估计通常借助钢珠点空间中心及其在探测器上的投影中心建立几何映射关系进行确定^{[5, 6]}。钢珠点的CBCT投影图像为椭圆，在探测器上得到的投影最大强度值出现在由射线源发出射线穿过钢珠点中心（与钢珠点最长交线）打在探测器上的位置，我们将该位置标记为投影中心。理想情况下，利用投影中心可以获取精确的几何参数，继而得到高质量的重建图像，然而在实际情况中，通常利用质心或椭圆中心来估计投影中心^[7-12]，由此必然会产生位置偏差。有研究在数学上已经严格证明了质心、椭圆中心和投影中心按顺序依次位于通过原点的直线上^[13]。有文献利用椭圆的中心位置以及两个轴长计算出了精确的投影中心位置^[14]。有研究通过使用已校准的氮化硅陶瓷球组成的双球模体为研究对象，分析了系统误差等对测量结果不确定度的影响，指出系统误差主要来源于分割算法、放大比及系统空间分辨率^[15]，但是并没有进行定量分析。另有研究提出一种利用一个简单的校正模型获得少量的投影，计算出几何参数的方法, 分析结果对模型误差的敏感性^[16]，此方法对模型不同偏差设定较为单一。Crhistian等^[17]提出了一种用于确定锥束CT系统几何误差的基于图像的测量方法的性能评估，系统的几何误差受计算钢珠点中心坐标的算法受图像的清晰度及对比度的影响，还受系统部件的尺寸稳定性及定位重复性等影响。有研究提出一种基于四椭圆快速获取全参数的方法，从成像敏感几何参数剖析，获取系统几何参数^[18]；但该方法并没有指出具体参数误差区间，且在标定前需要调整模体使得两个钢珠投影重合，会人为增大误差及实验难度。张俊等^[19]提出了一种适用于旋转平移轨迹的几何参数标定方法。该方法受小球投影坐标求取精度以及噪声等因素的影响，采取均值代替真值，实际测量值自然会产生相应偏差，可以看出几何校正中对偏差因素的敏感性影响是不容忽视的。

因此，针对上述问题，本研究提出一种锥束CT系统几何校正的偏差因素敏感性分析方法，提出中心偏差的定义及其推导，并通过基于Noo解析方法^[10]得到几何校正参数，同时利用FDK重建算法进行图像重建，借助直线线性关系和探测器阵列大小，具体分析模拟钢珠点三维空间中心、投影中心以及钢珠点大小的变化对几何参数偏差及重建图像结果产生的影响。不同于现有研究中直接利用质心或椭圆中心进行投影点定位，本文利用投影中心计算几何参数更加精确并设定不同偏差进行敏感性分析，该分析方法易实现，对于进行锥束CT测量偏差因素的评定具有参考意义。

1. 材料和方法

1.1. CBCT成像几何及中心偏差公式推导

CBCT系统的硬件设备主要包括射线源、旋转平台和平板探测器^{[20, 21]}（图 1）。用S表示射线源, 在旋转平台上建立世界坐标系X_WY_WZ_W，该坐标系原点Q位于旋转平台的旋转中心，Y_W轴表示旋转轴，平行于探测器的纵轴u，Z_W轴为射线源S发出的中心射线方向，经过旋转轴并垂直打在探测器中心O(u₀, v₀)处，X_W轴在满足右手定则条件下平行于探测器的横轴v。同时在射线源S上建立x-y-z坐标系，以S为原点，z轴垂直指向探测器，直线SO与z轴重合，并确定x轴垂直z轴，根据右手定则确定y轴。探测器上的u轴平行于x轴，v轴平行于y轴，焦距SDD为射线源S垂直打在探测器上的距离，C(c, 0)为椭圆中心，从射线源S出发，与钢珠点中心连接的直线倾斜地打在探测器上，交点为M(m, 0)点，称为投影中心，并且使得从O到M的射线指向u轴正方向。

图 1.

锥形束CT系统的理想几何结构及钢珠点投影中心M点位置

Ideal geometry of the cone-beam CT system and the location of the projection center M point of the steel ball point.

在x-y-z坐标系中，设钢珠点中心坐标为(x₀, y0, z₀)，半径设为r₀，令y₀=0，即中心在x-z平面内，且要求x₀>0，为防止钢珠点CB投影被截断，总假设z₀>r₀。定义椭圆中心C(c, 0)与投影中心M(m, 0)的偏差ε c和质心G(g, 0)与投影中心M(m, 0)的偏差ε g为中心偏差。

探测器上的投影值用函数p(u, v)表示，若假设钢珠点具有单位密度，则函数p(u, v)是从射线源S到探测器(u, v)的直线与钢珠点相交的直线长度。这条直线到钢珠点中心的距离用r(u, v)来表示，具体表达式为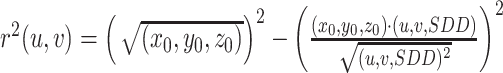。因为y0=0，所以上式可化简得到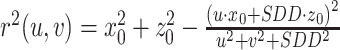：，由此即可得到探测器上的投影值p(u, v)，当r₀ > r(u, v) 时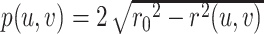，，当r₀ ≤ r(u, v) 时，p(u, v) =0。当r²(u, v) =0时，p(u, v) 可取得最大值，此时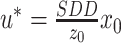，由于投影中心为M(m, 0)，因此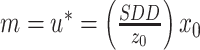。通过数学几何关系亦容易得出此结果，利用三角形相似即可得知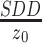为放大系数。椭圆中心为C(c, 0)，并且r(u, v) ≤ r₀在几何上是可视化的，所以r²(u, v) ≤ r₀²利用公式(6)可化简得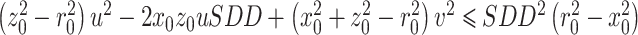，经过变形可以得到椭圆方程式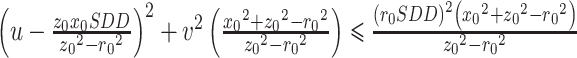，与椭圆标准形式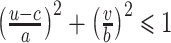进行对照，可直接得到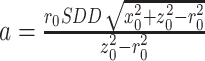、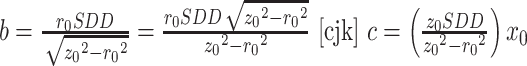，通过对比可知a>b，因此u轴是椭圆长轴，又因为m<c，则椭圆中心与投影中心的偏差ε c为ε_c =c-m，质心与投影中心的偏差ε g可表示为：ε_g =g-m。理想情况下，希望可以像公式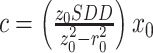一样，通过SDD，r₀，(x₀, y_0, z₀)表示出g的表达式，以便直接与关于m和c的公式进行比较，这样的表达式在文献中似乎不存在。Clackdoyle等证明了ε c与ε g的关系式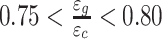，为了方便获得质心与投影中心的偏差ε_g，本文中假设ε_g=0.775× ε_c。

1.2. FDK重建算法

在CBCT系统中，图像重建最经典算法是FDK算法^[22]，FDK算法是FBP算法^{[23, 24]}的三维拓展，该算法因具有重建速度快且对数据储存空间要求较小等的优点，被广泛应用在CBCT成像系统中。本研究不再推导这两种算法，直接列出FDK重建算法的整体公式及其具体实现的步骤。FDK重建的表达式为f(x, y, z) 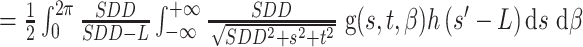, 其中，SDD表示射线源垂直打在探测器上的距离。s和t分别表示投影点到中心射线与探测器的交点在X轴方向和Y轴方向的距离，即投影点的坐标。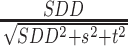表示射线的入射角大小。L表示待重建点到探测器上的距离（沿中心射线方向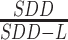）。表示投影点与待重建点之间的比例系数。

利用代码实现FDK重建可以分为以下3个步骤：第一步：对探测器2D投影数据进行余弦加权修正。对每一个投影角度β_i采集到的投影数据利用每条射线入射角度的余弦值修正投影数据中各个像素的值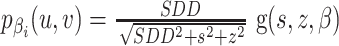：；第二步：进行卷积滤波。对第一步进行余弦加权修正后的投影数据，逐行做一维卷积滤波运算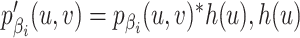：一般为Hanning窗滤波器；第三步：进行反投影运算。对第二步进行卷积滤波后所得到的投影数据，按照映射比例关系逐行进行加权反投影，其中(x, y, z)表示待重建的点，(u, v)表示点(x, y, z)经过投影映射之后打在探测器上的像素点。在重建时，待重建点(x, y, z)是人为指定的，再根据映射关系寻找投影图像上的点(u, v)，最后再将点(u, v)所对应的灰度值反投影到空间中的待重建点的。

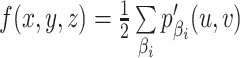标准的FDK算法要求系统几何结构同时满足以下两个条件才能得以实现：（1）由射线源S与探测器中心点的连线（即中心射线）经过旋转平台的旋转中心并垂直打在平板探测器的中心点(u0, v0)上；（2）旋转轴YW平行于探测器的u轴和v轴。

1.3. Noo解析算法

对于几何校正算法，最为经典的是基于两个钢珠点的校正算法，该方法设计的校正模体是将两个半径为4 mm的钢珠点固定在一个低衰减矩形板的对角线上，文中假设探测器与旋转平台的旋转轴平行且未发生几何失真，以等角度间隔进行采集两个钢珠点旋转1周的投影数据，再利用最小二乘法追踪两个钢珠点的椭圆投影轨迹，通过得到的椭圆参数与两个钢珠点位置信息建立映射关系，利用解析求解的方式确定几何参数。该方法的校正模体制作简单，解析求解方式易于实现，且鲁棒性强。

2. 结果

2.1. 影响几何校正精度的因素

2.1.1. 钢珠点大小对几何校正的影响

在射线源坐标系下，本节模拟了一个钢珠点坐标(x₀, y₀, z₀) =(50, 0, 1000) mm，SDD=1500 mm，为了探究钢珠点大小对中心偏差产生的影响，选取半径为r₀=i(i =1, 2, 3, …, 10)，分别在每一个半径下计算得出椭圆中心C(c, 0)、质心G (g, 0)及投影中心M(m, 0)，然后计算出中心偏差（图 2）。

图 2.

钢珠点的不同半径对中心偏差的影响

Influence of different radius of the steel ball point on the center deviation. A: Magnitudes of the transverse coordinates of the ellipse center C(c, 0), the center of mass G(g, 0) and the projection center M(m, 0) obtained from the steel ball point at different radius; B: Central deviation εc of the ellipse center C(c, 0) from the projection center M(m, 0) and the central deviation εg of the center of mass G(g, 0) from the projection center M(m, 0).

由图 2可知，在其他条件不变的情况下，随着钢珠点半径的增大，其椭圆中心c和质心g都会增大，但不会使钢珠点中心投影位置m发生改变，因为钢珠点未发生位移，即放大系数并未发生改变，因此椭圆中心与钢珠点投影中心的距离ε c和质心与钢珠点投影中心的距离ε g也会随着钢珠点半径的增大而增大，质心与钢珠点投影中心的距离ε g总是比椭圆中心与钢珠点投影中心的距离ε c小，并且会随着钢珠点半径的增加，两者差距会变明显。

2.1.2. 钢珠点三维空间中心位置变化影响

在世界坐标系下模拟两个关于原点对称的钢珠点A和B围绕旋转轴Z进行360°旋转（图 3）。钢珠点空间中心坐标相距178.89 mm，射线源到探测器的距离SDD设为1500 mm，射线源到旋转轴的距离SAD设为1000 mm，探测器阵列大小为512×384，像素尺寸为0.78 125 mm。

图 3.

钢珠点空间中心几何结构

Geometrical structure of spatial center of steel ball point.

利用Noo解析方法对空间中的钢珠点坐标加入均值为0，不同标准差的高斯扰动，图 4显示了该过程对钢珠点空间中心坐标精度的影响。横轴表示增加均值为0，标准差为探测器像素的σ/pixel（倍）的高斯扰动，纵轴表示几何参数偏差。当钢珠点产生均值为0，标准差为单个像素的10%的高斯扰动时，u₀、SDD和SAD的偏差已经达到了1.5~2.5 mm，v0的误差稍小。当钢珠点的空间坐标加入均值为0，标准差为单个像素的25%的高斯扰动时，u₀、SDD和SAD的偏差甚至达到了8 mm左右。

图 4.

钢珠点空间中心坐标受高斯扰动对几何参数影响

Effect of Gaussian perturbation on the geometric parameters of the spatial center coordinates of the steel ball point. A: Magnitude of the deviation of the projection position of the source (u₀, v₀), the vertical distance SDD from the source to the detector and the distance SAD from the source to the center of rotation with different Gaussian perturbations added to the 3D spatial coordinates of the steel ball point. B: Two rotation angles η and Φ of the detector with different Gaussian perturbations added to the 3D spatial coordinates of the steel ball point.

2.1.3. 钢珠点投影位置变化影响

对理想投影位置加入均值为0，不同标准差的高斯扰动，得到的几何参数结果（图 5）。同比钢珠点空间中心坐标受高斯扰动对几何参数影产生的影响，钢珠点二维投影中心受扰动后对几何参数影响较小，在加入均值为0，标准差为单个像素的10%的高斯扰动后，产生的偏差大约为两个像素尺寸，这也比较符合用阈值分割确定质心的方法产生的定位偏差^{[25, 26]}。

图 5.

钢珠点投影中心坐标受高斯扰动对几何参数影响

Effect of Gaussian perturbation on geometric parameters of the projection center coordinates of the steel ball point. A: Magnitude of the deviation from the projection position of the source (u₀, v₀), the vertical distance SDD from the source to the detector and the distance SAD from the source to the center of rotation with different Gaussian perturbations added to the 2D projection coordinates of the bead point. B: Two rotation angles η and Φ angle of the detector with different Gaussian perturbations added to the 2D projection coordinates of the bead point.

图 6为实验室配置的6轴机械臂CT系统，射线源和探测器分别挂载在两端的机械臂上，旋转平台放置于射线源与探测器之间，用于承载实验物体，可控制载物台的转动及高度的调节。

图 6.

基于自由轨迹的锥束CT实验系统

Cone-beam CT experimental system based on free trajectory.

为了分析偏移误差受钢珠点投影中心坐标定位精度的影响，在实验中对投影图像钢珠点坐标进行不同程度的扰动，每个扰动实验均进行多次取平均，使实验结果更加可信和稳定。同时，为了探究投影张数对结果的影响以及不同个数的钢珠点对误差的容忍程度，我们对每组数据使用不同的投影张数及不同钢珠点个数进行误差比对实验（图 7）。结果分析，平均每个钢珠点的优化误差会随着钢珠点定位坐标的扰动增大而增大，且在观测范围内大致呈线性增长，投影张数增加会使得平均每个钢珠点的误差下降，对于相同的投影张数来说，钢珠点个数越多，平均每个钢珠点的优化误差越小。

图 7.

钢珠点投影中心坐标定位精度对偏移误差分析

Analysis of offset error of coordinate positioning accuracy of steel ball point projection center. A: Results of 25 projection averages. B: Results of 50 projection averages.

2.2. 影响校正因素的敏感性研究

为探究影响校正因素的敏感性，设置不同大小的几何参数偏差仿真实验（表 1），并且与理想的重建结果进行比较。两组实验SAD均设为1000 mm，SDD设为1500 mm。成像模体大小为512×512×100，体素大小为0.24 mm×0.24 mm×0.24 mm。产生的投影大小为512× 384，尺寸为30 cm×40 cm。两组实验几何偏差的值设置如表 1所示。

表 1.

两组仿真实验几何参数误差设置

Geometric parameter error settings of two groups of simulation experiments

Group	∆u	∆v	∆SDD	∆SAD	∆η
Experiment1	1 mm	1 mm	100 mm	100 mm	1°
Experiment2	2 mm	2 mm	200 mm	200 mm	2°

图 8展示了不同大小的几何参数偏差对重建结果的影响，为了方便对比各参数偏差大小结果，将两组实验参数放在一起进行对比，所有图像均以相同的窗宽窗位显示。∆u对重建结果的影响较为敏感，1 mm的偏差产生的重建图像几何伪影较为轻微，但是偏差为2 mm时重建图像出现的几何伪影则十分明显（图 8A~E）。而∆v对重建图像产生的影响并不敏感。仅有∆SDD或∆SAD的存在只会对重建图像的缩放比例产生影响，一般在实际几何校正中，∆SDD和∆SAD会与其他参数偏差一起出现，此时∆SDD和∆SAD会对重建图像产生比较大的影响（图 8F~I），不能忽视两者的敏感性。分析探测器平面沿Z旋转角度偏差对重建图像产生的影响，当其值为2°时，重建图像几何伪影已经十分明显（图 8J、K）。图 8L、M展示了两组实验中所有几何参数偏差对重建图像的总体影响，从视觉上可直观地看出，两组实验均导致非常明显的几何伪影，严重影响了对成像物体的分析。

图 8.

两组不同大小的几何参数偏差对重建结果的影响

Reconstruction results of two groups of simulation experiments with different errors of geometric parameters. A: Ideal reconstruction image. B: Reconstruction result image with deviation ∆u=1 mm. C: Reconstruction result image with deviation ∆u=2 mm. D: Reconstruction result image with deviation ∆v=1 mm. E: Reconstruction result image with deviation ∆v=2 mm. F: Reconstruction result image with deviation ∆SDD=100 mm. G: Reconstruction result image with deviation ∆SDD=200 mm. H: Reconstruction result image with deviation ∆SAD=100 mm. I: Reconstruction result image with deviation ∆SAD=200 mm. J: Reconstruction result image with deviation ∆η=1°. K: Reconstruction result image with deviation ∆η =2°. L: Reconstruction result image with overall impact of Experiment 1. M: Reconstruction result image with overall impact of Experiment 2.

3. 讨论

针对已有的利用质心或椭圆中心定位投影点方法，如若不对钢珠点的自身条件加以限定，则会产生位置偏差。本文利用更精确的投影中心进行定位，提出中心偏差定量分析了投影中心与质心及椭圆中心的偏差大小，并设定不同偏差分析了钢珠点大小对几何校正的影响，通过结果发现，钢珠点半径在3 mm以内时，中心偏差在10^-4量级内，此时可以用椭圆中心或者质心来代替投影中心，可以简单理解为M(m, 0)≈C(c, 0)≈G(g, 0)，以得到较为精确的几何参数，进而得到较为高质量的重建图像。因此，在钢珠点较小的情况下，中心偏差可忽略不计，即可用椭圆中心或质心代替投影中心进行几何校正。该结论在工程上具有较高的实用价值。

基于投影中心获取精确的几何参数，可得到高质量的重建图像，利用Noo解析方法及FDK重建算法进行图像重建分析。我们利用投影中心测试锥束CT系统几何校正位置偏差的敏感性，分析了不同条件下的偏差对重建图像的不同影响。传统方法在分析系统结果对偏差的敏感性时，或设置条件略为单一，或忽略分割步骤对校正结果产生的影响等因素，相反，本文进行了锥束CT系统几何校正计算机仿真实验，探究钢珠点空间中心位置变化对几何参数产生的影响，设置不同于传统方法的单一条件，增强结果的比对，经过验证发现当钢珠点产生均值为0，标准差为单个像素的10%的高斯扰动时，u₀、SDD和SAD产生的偏差足以使得重建图像出现相当大的模糊伪影和结构扭曲。当钢珠点的空间坐标加入均值为0，标准差为单个像素的25%的高斯扰动时，u₀、SDD和SAD产生的偏差对于系统的几何结构已经没有校正的意义。其次，本研究利用直线线性关系和探测器阵列大小，确定两个钢珠点在探测器上的投影位置，该方法优点是可以检验钢珠点三维空间坐标的分割步骤对几何校正结果产生的影响，即钢珠点投影中心位置在分割过程中发生变化所产生的影响，本研究对钢珠点投影中心坐标加入高斯扰动，其结果表明若分割过程中出现偏差，打在探测器上的投影中心位置也会有相应的错位，但是同比钢珠点空间中心坐标受高斯扰动产生的影响对比来看，此偏差对几何参数的影响较小。

综上所述，本研究所提出的锥束CT系统几何校正位置偏差因素的敏感性测试方法，得出几何校正中对钢珠点三维空间坐标产生的偏差较为敏感，对钢珠点二维投影坐标产生的偏差敏感有限，使用直径较小的钢珠点其偏差对校正的敏感可忽略的结论。

Biography

王海龙，在读硕士研究生，E-mail: 952578798@qq.com

Funding Statement

国家重点研发课题（2022YFA1204203）；国家自然科学基金（61971463）；广东省基础与应用基础研究基金项目（2023A1515010537）广州市科技计划项目（202002030385）

Supported by National Natural Science Foundation of China (61971463)