Binaural masking level difference for pure tone signals

Abstract

The binaural masking level difference (BMLD) is a psychoacoustic method to determine binaural interaction and central auditory processes. The BMLD is the difference in hearing thresholds in homophasic and antiphasic conditions. The duration, phase and frequency of the stimuli can affect the BMLD. The main aim of the study is to evaluate the BMLD for stimuli of different durations and frequencies which could also be used in future electrophysiological studies. To this end we developed a GUI to present different frequency signals of variable duration and determine the BMLD. Three different durations and five different frequencies are explored. The results of the study confirm that the hearing threshold for the antiphasic condition is lower than the hearing threshold for the homophasic condition and that differences are significant for signals of 18ms and 48ms duration. Future objective binaural processing studies will be based on 18ms and 48ms stimuli with the same frequencies as used in the current study.

1. Introduction

The binaural masking level difference (BMLD) indicates humans' ability to detect signals masked in noise in different conditions. BMLD is relevant for clinical groups such as aging adults with and without hearing loss and cochlear implant users. Many possible stimuli can be used for the BMLD, involving the supply of different combinations of signals (S) and noise (N) maskers to the ears. The most common scenario is where threshold calculations were done by presenting the signal homophasic to both ears (S0N0), compared to presenting the signal in one ear in an antiphasic way with respect to the other ear (SπN0) (Blauert, 1996; Fastl and Zwicker, 2007). The noise (N) masker can also be presented in an antiphasic way. A BMLD can occur when the SπN0 or S0Nπ threshold is lower than the S0N0 threshold, demonstrating the benefit of binaural processing.

The BMLD generation in response to auditory signals occurs most likely in the superior olivary complex of the brain (Gilbert et al., 2015; Moore, 1991; Nakamoto et al., 2010). However, some electrophysiological studies of auditory evoked potentials indicate that the BMLD generation is at cortical level (Kevanishvili and Lagidze, 1987; Wallace et al., 2002; Xu et al., 2019). It is important to understand the effect of similar stimuli in both traditional psychophysical studies (BMLD tests), which are based mainly on subjective feedback from the subjects, and electrophysiological studies. There are several characteristics that affect the size of the BMLD, including stimulus type (e.g., spondaic words or pure tones) frequency, type of masking noise, masker level and masking bandwidth. Binaural hearing affects detection of stimuli in noise as well as recognition tasks. Literature indicates that BMLDs of normal-hearing subjects for pure tones are functions of frequency (Hirsh, 1948). The size of the BMLD is highly dependent on the stimulus frequency. BMLD thresholds can be 5–15 dB which tends to be maximal for low-frequency bands (Snik et al., 2015). With increasing frequencies, the BMLD tends to decline (Webster, 1951). Tones, clicks and speech can all elicit a BMLD (Moore, 2013). However, the present study is focused on pure tones which is an area that has been identified as relevant for future research. As there is a research gap in identifying neural correlates of BMLD generation, it is important to study the BMLD stimuli which are able to evoke potentials in physiological studies related to the brain-hearing activities. This may help future researchers to make use of suitable frequencies, signal lengths and other parameters for electrophysiological hearing studies. This study investigates the BMLD for the pure tone signals which can evoke auditory potentials in objective hearing research.

For this research a MATLAB based Graphical User Interface (GUI) is developed for the convenient conduction of BMLD experiments. This GUI makes it easier to select stimulus frequencies, types of masking noise, masker levels and masking bandwidths during the trials. This study also investigates what effect the duration of pure tone stimuli for frequencies ranging from 125 Hz to 1000 Hz has on BMLD values. The duration of signals was selected in a way that they can elicit auditory evoked potentials in the electrophysiological binaural hearing experiments, which will be described in our next paper. In the present study we make use of three stimuli durations 3 ms, 18 ms and 48 ms at five different frequencies to record the corresponding BMLD responses. During these initial studies we kept all the other tonal and noise parameters constant in order to get a good understanding of the effect of duration of pure tone of stimuli for different frequencies.

2. Methodology

2.1. Subjects

The study was approved by the Humans Ethics Committee of Charles Darwin University, Australia as explained in H18014 _ Detecting Binaural Processing in the Audiometric EEG (Ignatious et al., 2021; Miles et al., 2021). The willingness of volunteers to take part in the BMLD testing was documented through written consent and each subject completed a questionnaire regarding their otological history. The study group consisted of 35 participants (17 females and 18 males). The participants ranged in age from 20 to 35 years (mean age = 26.17 years; SD = 4.06 years).

2.2. Screening

All participants were screened to fulfil the inclusion criteria through a questionnaire and a pure tone audiometry hearing test. The hearing test was carried out to detect the hearing threshold levels of participants at different frequencies, in accordance with the relevant Australian Standards, and to determine whether these were acceptable. All the selected subjects had normal audiograms with a threshold value of 25 dB hearing level (HL) for the frequency range 125 Hz to 2 KHz.

2.3. Stimuli

A Blackmann windowed pure tone was used for testing. The tone was embedded in a 10 Hz bandwidth and of 500 ms duration Gaussian noise masker. We tested the frequencies 125 Hz, 250 Hz, 500 Hz, 750 Hz and 1000 Hz. The centre frequency of the masker and the frequency of the tone were set the same for each set of the trials. The tones for BMLD testing were given with a duration of 3 ms, 18 ms and 48 ms. The time durations were chosen to corresponds to the duration of signals that can be used for the generation of AEPs (Ignatious et al., 2021; Miles et al., 2021): 3 ms for the Auditory Brainstem Response (ABR), 18 ms for the Middle Latency Response (MLR) and 48 ms for the Late Latency Response (LLR). The initial dB level for the masker is set as 20 dB while it is set at 40 dB for the tone. A total of 50 trials are done for each frequency, out of which 25 had stimuli with both tone and noise in phase (S0N0) in both the ears while the remaining had stimuli with the tone out of phase and the noise in phase (SπN0). The selected condition of tone and noise is differently for each subject but 25 trials for each condition are carried out. The stimuli were delivered to the ER.2 insert earphones via an external sound card (Creative Sound Blaster Omni Surround 5.1). The ER.2 research earphones used for the audio stimulus delivery were calibrated at 60 dB Sound Pressure Level (SPL) before the start of every hearing test.

2.4. APP development

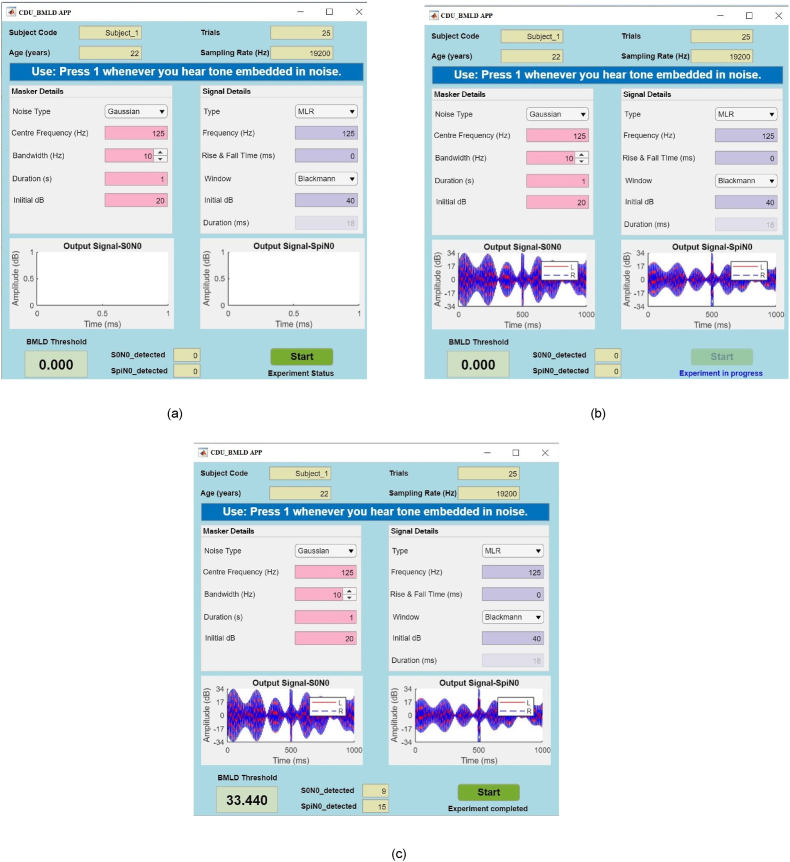
MATLAB was used in the study for developing a GUI to assist the data collection for BMLD. In our approach, an interactive MATLAB based CDU_BMLD APP was developed for stimulus generation and presentation. The APP enables easier and more efficient conduction of the BMLD tests for different conditions (including frequencies and time periods). Table 1 describes the details of the APP. Fig. 1. (a) shows the main window of the app. This is the first window that the data collector (user) sees upon running the app.

Table 1.

CDU_BMLD_APP details.

CDU_BMLD_APP Tiles	Options in list
General Details
Subject Code	User written
Age	User written
Trials	User written and it will be taken for S0N0 condition and SπN0 condition (ex: if 25- 25 S0N0 and SπN0 will be send to the subject)
Sampling Frequency (Hz)	User written - will be taken in Hz
Masker
Noise Type	Drop down options – Gaussian –White Noise
Centre Frequency (Hz)	User written - will be taken in Hz
Bandwidth (Hz)	User written - will be taken in Hz
Duration (s)	User written - will be taken in s
Initial dB	User written - will be taken in dB
Signal
Type	Drop down options – ABR -MLR -LLR -Others
Frequency (Hz)	User written - will be taken in Hz
Rise & Fall Time (ms)	User written - will be taken in ms
Window	Drop down options – Blackmann
Duration (ms)	While selecting “Type” for ABR, MLR and LLR it will be automatically 3, 18 and 48ms For other: User written - will be taken in ms
Initial dB	User written - will be taken in dB

Fig. 1.

(a) Starting window of APP (b) APP window during experiment progress (c) APP window during experiment progress.

Once the window appears, the user completes the initial basic fields subject code, age, number of trials and the sampling rate. The user can then select the masker and signal details that are required to generate the stimuli. After completing the details, the start button is pressed. The App will then generate signals according to specifications given by the user and shows these in the figure areas of the app window, refer to Fig. 1. (b). The experiment is then in progress. The participant presses the key “1” when they detect the signal (tone) embedded in the masker. The key presses are saved, and once the experiment is completed, a window as in Fig. 1. (c) is shown, from which the BMLD values can be obtained for further offline analysis.

2.5. Procedure

The participants were instructed to press the key “1” on keyboard, when they were able to detect the tone masked in the noise. Once the participant understood the test procedure, after a few practice trials, the test, designed with the GUI, was presented. The automated test process was carried out by presenting stimuli in a simple up-down adaptive procedure (Mackie and Dermody, 1986; Plant, 1990). The stimulus was initially presented at 40 dB in a 20 dB masker noise with a starting SNR of 20 dB. Depending on the subject's response, the level of the stimulus is either increased or decreased. If either an incorrect response or no response is given, the subsequent level of stimuli is increased by 2 dB. If a correct response is given, the stimulus level is decreased by 5 dB (Aithal et al., 2006). The order of the S0N0 and SπN0 conditions was randomized. After a total of 25 trials for each condition, the measurements were terminated. The measurements for each participant were completed in a single visit lasting for approximately 45–60 min, including rest intervals and breaks. All testing was conducted in a sound-proof room at the laboratory of Charles Darwin University. The BMLD was calculated by taking the difference between the corresponding S0N0 and SπN0 thresholds.

3. Analysis of results

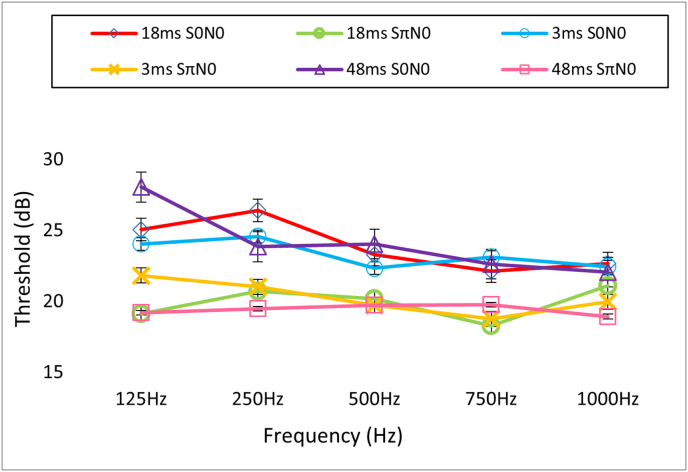
IBM SPSS Statistics V26 (IBM Corp., Armonk, NY, USA), Excel Office 2010 (Microsoft, Redmond, WA, USA) and MATLAB 2017 were used for the statistical analysis. The data are studied to understand the distribution among subjects and groups. The BMLD measurements obtained for the input stimuli 3 ms, 18 ms and 48 ms respectively at five different frequencies are plotted in Fig. 2. It can be seen that the variability among the three signals of different duration per frequency. The data points represent the average across the thirtyfive normal hearing subjects. Error bars represent ±1 standard error of the mean. However, they differ for different frequencies. For the signal durations 18 ms and 48 ms the frequency of 125 Hz produced significantly higher BMLD values compared to the other four frequencies (250 Hz, 500 Hz, 750 Hz and 1000 Hz). This agrees with previous literature. However, for 3ms, 125 Hz signal results in the lowest BMLD. The mean (M) and standard deviations (SD) for each condition were calculated and are shown in Table 2.

Fig. 2.

BMLD Vs Frequency.

Table 2.

Descriptive statistics of data set.

		N	3ms		18ms		48ms
			Mean	Standard Deviation (SD)	Mean	Standard Deviation (SD)	Mean	Standard Deviation (SD)
125 Hz	BMLD	35	2.22	8.27	5.93	9.85	8.87	8.89
	S0N0	35	24.04	9.23	25.06	10.9	28.05	11.69
	SπN0	35	21.82	8.79	19.13	8.59	19.19	8.25
250 Hz	BMLD	35	3.55	7.56	5.71	6.29	4.36	6.08
	S0N0	35	24.58	10.56	26.41	12.17	23.85	11.48
	SπN0	35	21.03	10.57	20.7	9.75	19.49	8.74
500 Hz	BMLD	35	2.63	5.78	3.1	6.24	4.3	7.76
	S0N0	35	22.34	8.58	23.28	10.74	24.03	11.94
	SπN0	35	19.71	8.36	20.18	8.85	19.73	8.32
750 Hz	BMLD	35	4.36	5.48	3.85	5.94	2.85	6.28
	S0N0	35	23.13	11.32	22.13	11.45	22.62	11.38
	SπN0	35	18.77	8.37	18.27	7.66	19.77	9.33
1000 Hz	BMLD	35	2.48	7.5	1.57	5.84	3.12	6.37
	S0N0	35	22.45	11.48	22.66	10.35	22.05	11.37
	SπN0	35	19.97	8.38	21.1	12.09	18.93	8.99

The plot in Fig. 3 provides an overview of the distribution of S0N0 and SπN0 thresholds for different frequencies and different durations. The datapoints represent the average thresholds for 35 normal hearing subjects. Error bars represent ±1 standard error of the mean. Both S0N0 and SπN0 thresholds vary with the frequency, although the S0N0 thresholds vary more drastically. For the lowest frequency (125 Hz), the BMLD value is less for the 3ms input signal than for the longer signals.

Fig. 3.

SoNo and SpiNo Vs Frequency for 3ms, 18ms and 48ms input signals.

To test the influence of phase reversal, a statistical test was conducted. To determine which inferential statistics could be performed, the normality of data and equality in variance were tested. Normality was checked using the Shapiro-Wilks test, with the null hypothesis assuming that the data were normally distributed. Results shown in Table 3 demonstrate that for most of the data this null hypothesis was rejected, indicating that the data were not normally distributed. To check the equivalence of variance between threshold recordings under phasic and antiphasic conditions, Levene's Test was performed. The results suggested that the variances were not equal.

Table 3.

Shapiro-wilks test result.

	Duration (ms)	Frequencies (Hz)	N	Statistic (W)	p-value	Decision at level (5%)
BMLD	3	125	35	0.94533	0.08144	Can't reject normality
		250	35	0.95037	0.11634	Can't reject normality
		500	35	0.88876	0.002	Reject normality
		750	35	0.9849	0.90157	Can't reject normality
		1000	35	0.93469	0.03864	Reject normality
	18	125	35	0.82539	6.6885E-5	Reject normality
		250	35	0.9403	0.05716	Can't reject normality
		500	35	0.94207	0.0647	Can't reject normality
		750	35	0.82819	7.6633E-5	Reject normality
		1000	35	0.90334	0.00487	Reject normality
	48	125	35	0.94204	0.06457	Can't reject normality
		250	35	0.82204	5.6901E-5	Reject normality
		500	35	0.9306	0.02915	Reject normality
		750	35	0.92563	0.02078	Reject normality
		1000	35	0.83849	1.2775E-4	Reject normality
S0N0	3	125	35	0.85524	3.0396E-4	Reject normality
		250	35	0.87617	9.6068E-4	Reject normality
		500	35	0.86515	5.1892E-4	Reject normality
		750	35	0.94607	0.08581	Can't reject normality
		1000	35	0.9412	0.06086	Can't reject normality
	18	125	35	0.86809	6.1028E-4	Reject normality
		250	35	0.92769	0.0239	Reject normality
		500	35	0.901	0.00421	Reject normality
		750	35	0.85257	2.6388E-4	Reject normality
		1000	35	0.96295	0.27989	Can't reject normality
	48	125	35	0.88288	0.00141	Reject normality
		250	35	0.87403	8.5062E-4	Reject normality
		500	35	0.94315	0.06983	Can't reject normality
		750	35	0.87687	9.9989E-4	Reject normality
		1000	35	0.84098	1.4494E-4	Reject normality
SπN0	3	125	35	0.83323	9.8194E-5	Reject normality
		250	35	0.84652	1.9249E-4	Reject normality
		500	35	0.8654	5.2599E-4	Reject normality
		750	35	0.93236	0.03291	Reject normality
		1000	35	0.83235	9.4022E-5	Reject normality
	18	125	35	0.84969	2.2690E-4	Reject normality
		250	35	0.92642	0.02192	Reject normality
		500	35	0.87951	0.00116	Reject normality
		750	35	0.89779	0.00345	Reject normality
		1000	35	0.87777	0.00105	Reject normality
	48	125	35	0.91346	0.00928	Reject normality
		250	35	0.80761	2.8873E-5	Reject normality
		500	35	0.84525	1.8025E-4	Reject normality
		750	35	0.86055	4.0379E-4	Reject normality
		1000	35	0.82903	7.9836E-5	Reject normality

Based on the normality test, the equivalence of variance, and a sample size of 35, non-parametric tests such as the Wilcoxon rank-sum test or Kruskal-Wallis test were considered more appropriate than parametric tests. It was important to consider whether the data were paired or non-paired. In this study, the same subjects were tested under different conditions, making the data paired. A Kruskal-Wallis test would assume independence between observations, whereas repeat observations on the same subjects can be related. Therefore, the non-parametric Wilcoxon signed rank test, which accounts for the pairing of observations by making pairwise comparisons, was applied to determine statistical significance.

The test statistic calculated by the Wilcoxon signed rank test is the sum of the signed ranks of the differences between the two samples, i.e., under inphase and antiphase conditions, with positive ranks given to the sample with the larger value. In this case, a large absolute value of the test statistic indicates strong evidence against the null hypothesis, and a small absolute value indicated weak evidence against the null hypothesis. The sign of the test statistic indicates the direction of the difference between the medians of the two samples. If the p-value returned by the Wilcoxon test is greater than the chosen significance level (p = 0.05), and the test statistic (sum of the positive signed ranks of the differences between the two samples) is relatively high, there is weak or no evidence against the null hypothesis, which in this case was that the mean of threshold recorded under inphase and antiphase conditions were not significantly different. Table 4 showed the result of the Wilcoxon test performed for the threshold of 35 subjects in inphase condition vs. antiphase for all three durations and all five frequencies. The differences between S0N0 and SπN0 conditions were statistically significant except for the duration was 3 ms s combined with a frequency of 1000 Hz.

Table 4.

Wilcoxon test results.

Duration (ms)	Frequency (Hz)	pvalue	Significance	STATS
3	125	0.0387335	Significant	189
	250	0.0074584	Significant	141
	500	0.0042495	Significant	120.5
	750	4.227E-05	Significant	58
	1000	0.0618649	Non Significant	176
18	125	0.000998	Significant	105
	250	1.532E-05	Significant	38.5
	500	0.000998	Significant	105
	750	0.0001936	Significant	79.5
	1000	0.0091218	Significant	145
48	125	2.692E-06	Significant	23
	250	3.922E-05	Significant	57
	500	0.0044193	Significant	131
	750	0.0062278	Significant	137.5
	1000	0.0075571	Significant	131

In this study, we utilized BMLD data to evaluate the impact of time duration and frequency. The BMLD represents the difference in minimum detectable levels between in-phase and anti-phase presentations and is measured in decibels (dB). We selected one duration and compared the BMLD for all 5 frequencies (125 Hz vs 250 Hz, 500 Hz vs 750 Hz vs 1000 Hz). We repeated this test for two additional durations. As the BMLD data failed the normality test, we opted for a non-parametric test, specifically the Friedman test. The Friedman test is useful for determining whether differences between the means of three or more related groups are significant, unlike the Wilcoxon signed-rank test, which compares two related groups. The F score generated by the Friedman test was used to evaluate the degree of difference between the groups being compared. A higher F score indicates a greater degree of difference, while a lower F score indicates less difference. The results of the Friedman test are shown in Table 5. It was found that the results for the 3ms duration were not significant, with a correspondingly low F score compared to the results for the 18ms, 48ms durations.

Table 5.

Friedman test results (125 Vs 250 Vs 500 Vs 750 Vs 1000).

Duration (ms)	Fscore	P_value	Significance
3	3.0117	0.55587	Non significant
18	11.079	0.02569	signifiacant
48	15.947	0.00309	signifiacant

The Nemenyi test, also referred to as the Nemenyi-Damico-Wolfe-Dunn (NDWD) test, is a post-hoc test commonly used to compare all possible pairs of frequencies subsequent to the null hypothesis being rejected in a Friedman test. This test compares all potential groups using a critical value that is based on the studentized range distribution. If the mean rank difference between a pair of groups is larger, then these two groups are significantly different from each other. The interpretation of the Mean Rank Differences for BMLD using Nemenyi test involves identifying significant differences in BMLD between the frequncies based on their mean ranks and the critical difference value (CD = 0.4910 for 35 subjects and 5 frequenies). If the mean rank difference between two groups is greater than the CD value, the two groups are considered significantly different from each other. CD is calculated as follows

$$CD=q\sqrt{\frac{K(K+1)}{6D}}$$

where K = 5 (number of frequencies), D = 35 (number of subjects) and the value of q is derived from the studentized range statistic. To calculate the value of q for alpha = 0.05 and K = 5 (number of frequencies), we need to refer to the Studentized range distribution table. The table provides critical values for the distribution at different levels of significance and degrees of freedom. Degrees of freedom (DF) is calculated as follows

$$DF=\frac{K(K-1)}{2}$$

For K = 5, the degrees of freedom would be equal to 10. Looking at the Studentized range distribution table, we can find the critical value q for DF = 10 and alpha = 0.05. The value of q for alpha = 0.05 and k = 5 is approximately 2.905. The resulting CD is 0.4910 and CD is the same for all durations because it depends on the number of frequencies and subjects.

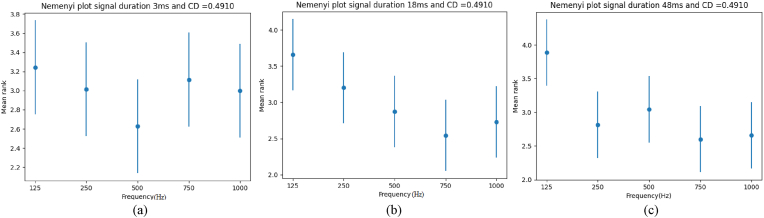
The Friedman Test is followed by the Nemenyi post hoc test to compare the frequencies based on their mean ranks. By utilizing the mean rank differences, the groups can be ranked, based on their BMLD differences, with the group possessing the highest mean rank being considered the best frequncey for stimuli and the group possessing the lowest mean rank being considered the worst frequency. The results of these tests are shown in Fig. 4, Fig. 5. Mean ranks for each frequency for corresponding durations are shown in Table 6.

Fig. 4.

Nemenyi-Damico-Wolfe-Dunn (NDWD) test result for (a) 3ms (b) 18ms (c) 48ms.

Fig. 5.

Mean Ranks of frequencies for (a) 3ms (b) 18ms (c) 48ms.

Table 6.

Mean ranks (125 Hz Vs 250 Hz Vs 500 Hz Vs 750 Hz Vs 1000 Hz).

Mean Ranks
	125 Hz	250 Hz	500 Hz	750 Hz	1000 Hz
3ms	3.2428	3.01428	2.6285	3.11428	3
18ms	3.6571	3.2	2.8714	2.5428	2.7285
48ms	3.8857	2.8142	3.04285	2.6	2.6571

We have a dataset with 35 subjects, and we run the Friedman test on BMLD values for 5 different frequencies (125, 250, 500, 750, and 1000 Hz). We find that the p-value of the test is less than 0.05, indicating that there is a significant difference between the frequencies. We then perform the Nemenyi post hoc test and compute the mean rank differences between all pairs of frequencies.

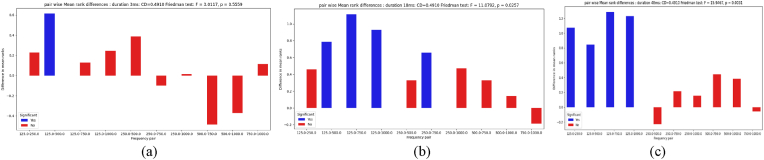
From Fig. 4(c), we can see that the mean rank difference between 750 Hz and 1000 Hz is −0.1857 for 48 ms and the mean rank difference between 125 Hz and 1000 Hz is 0.9286. Based on these results, we can say that 1000 Hz has a higher rank than 750 Hz (on average) and a lower rank than 125 Hz (on average). Similarly, we can compare the ranks of other pairs of frequencies. If the absolute mean rank difference of two frequencies is less than the critical difference value, the difference is significant. The critical difference value for all duration is 1.258. Pair wise mean rank differences for each duration i.e 3ms, 18ms and 48 ms are shown in Fig. 4 (a), (b) and (c) respectively and the mean differences in ranks of each frequency pair for each duration are provided in Table 7.

Table 7.

Mean rank difference for frequency pairs (3ms Vs 18ms Vs 48ms).

Frequency Pair		Difference in mean ranks
		3ms	18ms	48
125	250	0.2286	0.4571	1.0714
125	500	0.6143	0.7857	0.8429
125	750	0.1286	1.1143	1.2857
125	1000	0.2429	0.9286	1.2286
250	500	0.3857	0.3286	−0.229
250	750	−0.1	0.6571	0.2143
250	1000	0.0143	0.4714	0.1571
500	750	−0.486	0.3286	0.4429
500	1000	−0.371	0.1429	0.3857
750	1000	0.1143	−0.1857	−0.057

The blue round dots in Fig. 5 (a), (b) and (c) represent the mean rank for each frequency for 3ms, 18ms and 48ms respectively and the vertical blue lines show the CD. The frequencies for each duration can be compared, based on their mean ranks and sorted in descending order based on them. For example, from Fig. 5(c) we can see that 125 Hz has highest mean rank of 3.8857 for duration of 48 ms. We can say that 125 Hz has the highest rank and is therefore the most effective frequency, followed by 500 Hz and 250 Hz for 48 ms duration. From Fig. 4(a) we can see although Friedman test failed across all frequency groups, the difference between the 125 Hz and 500 Hz pair is significant according Nemenyi post hoc test. Similarly, from Fig. 4(b) and (c) we can see although the Friedman test indicated that there were significant differences between the frequencies, the pair wise difference is not significant for all individual pairs.

4. Discussion

In the initial analysis, the lower frequencies resulted in the highest BMLDs, except for the 3 ms duration stimuli. In our study, 125 Hz resulted in the highest BMLD values for the 18ms and 48 ms signals, which agrees with previous studies (Zwicker and Henning, 1984). However, it was not true for 3ms signal. The difference between the two signal conditions, in phase (S0N0) and out of phase (SπN0), seems to be relevant. When the phase of the stimuli is the same as that of the noise, the threshold is high because the stimuli and noise seem to be coming from the same source. In the antiphasic condition, the signal is reversed relative to that of the noise, and the threshold value is lower, as the signal and the noise seem to be coming from a different source (McCullagh and Bamiou, 2014). Hence SπN0 provides better auditory cues compared to that of the S0N0 condition. The lower threshold for the antiphasic condition indicates an increase in detectability of signals in noise (Brown and Musiek, 2013). The normality test for the data demonstrated that the samples are not normally distributed which supports findings of similar BMLD studies in literature (Koiek et al., 2022).

The higher F score obtained by the Friedman non-parametric test shows that for the 18 ms and 48 ms stimuli, the BMLD values were significantly different across frequencies different whereas the BMLD for the 3ms signal was not (Fowler, 2017). The origin of the response might be one of the reasons for non-significance of the 3ms data. The 3 ms signals may be processed in a different way. It is possible that the response to such a short stimulus does not involve the output from the neurons responsible for BMLD generation (Fowler and Mikami, 1996; Kevanishvili and Lagidze, 1987). The brain processes corresponding to auditory processing of longer signals may follow a different pathway (Fowler, 2017), resulting in the BMLD (Wong and Stapells, 2004). In addition, signals of low frequencies have a relatively long period and it can be questioned whether people can really detect the frequency of a tone in such a short signal. This may explain why low frequencies do not result in a large BMLDs for 3 ms stimuli. However, a significant BMLD can be observed for the 18ms and 48ms stimuli. The evoked potentials resulting from these stimuli are to be analysed in detail in future research. The alertness and attentiveness of the subjects during the test may also affect the BMLD values (Polonenko and Maddox, 2021).

The Nemenyi test post hoc statistical test is used to evaluate whether there are pairwise, statistically significant differences between the frequency pairs for each stimulus duration. From the pairwise mean rank differences in Fig. 4 (a), (b) and (c) we can see that for the 3ms stimuli, most of mean rank differences are less than the CD value. The Friedman test also failed to show significant differences for 3 ms. On the other hand, as can be seen from Fig. 4 (b) and (c), most of pairwise mean rank differences are greater than the CD for the 18 and 48 ms stimuli. The corresponding Friedman test for 48ms resulted in the highest F score. These differences will be further explored in EEG experiments.

The optimal frequencies for the BMLD are different for signals of different durations. Nemenyi plots are used to show the mean rank for all the frequencies and each duration, as shown in Table 7. In Table 7 we can see that the highest mean rank, is for 125 Hz; 3.2428, 3.6571 and 3.8857 for 3ms, 18ms and 48 ms respectively. We have failed to establish statistically significant difference between the frequencies for the duration of 3ms. It is important to analyze the effect of these frequencies in the electrophysiological studies as well.

5. Conclusion

The present study confirms that the hearing thresholds for the SπN0 condition are lower than the hearing threshold for the S0N0 condition. Signals of 18ms and 48ms duration result in significant differences between in phase and antiphasic conditions and will therefore be used for further studies on binaural interactions. The frequency dependence of the BMLD is not the same for signals of different duration, however.

6. Future research

The future scope of the current study is to analyze the underlying auditory processing for subcortical region with BMLD generating stimuli of different frequencies. Based on the present study, the electrophysiological studies related to binaural processing will be carried out with 18ms and 48ms stimuli for the same frequencies as described in this paper. This may allow a comparison of binaural processing result based on subjective and objective hearing tests.