Bidding to Commit

Abstract

Economists and biologists have both theorized that individuals can benefit from committing to courses of action because it forces others to concede a greater share of any surpluses, but little experimental work has tested the actual benefits of such a strategy and people’s willingness to so “tie their hands.” Participants played a Battle-of-the-Sexes (Experiment 1) or Hawk–Dove game (Experiment 2), where one member of each pair could not change his or her action once played (committed), whereas the other could change actions in response (uncommitted). Committed players were more likely to achieve their preferred outcomes. When bidding to select roles, most participants preferred to be committed rather than uncommitted, though they bid slightly less than the committed role was actually worth. These results provide empirical support for people’s willingness to use commitment to their advantage and show that commitment devices (e.g., “irrational” emotions) can bring long-term benefits.

The commitment problem is a classic in economics, game theory, and psychology (e.g., Nesse, 2001; Schelling, 1960, 2001). If one can make a credible commitment to a particular course of action, it can change others’ incentives in a way that is beneficial to self. For example, a person who has a reputation for retaliating against personal transgressions, even when doing so harms himself or herself, will tend to receive fewer future transgressions (Chagnon, 1997; Daly & Wilson, 1988; Nisbett & Cohen, 1999); past retaliations and/or the emotions that cause such retaliation make the commitment to retaliate credible. In this way, the “irrational” act of retaliating can bring actual long-term benefits (Frank, 1988): When one party “ties their hands” by demonstrating commitment to a particular course of action, self-interested partners who wish to avoid mutually detrimental outcomes have to change their behavior in a way that can benefit the committed party. Thus, when two parties interact, one with the ability to commit to a course of action will have an advantage over one who cannot do so because the former can make a demand and force the latter to adapt. ¹

Biologists have recently discovered a similar principle. Within highly antagonistic relationships such as parasite–host and predator–prey relationships, faster evolving species have an evolutionary advantage (the “Red Queen” effect, e.g., Ridley, 1993). However, within less antagonistic relationships such as mutualisms where there is some advantage to coordinating one’s response with one’s partner, slower evolving organisms can have an evolutionary advantage (the “Red King” effect; Bergstrom & Lachmann, 2003a, 2003b). The slower evolving species in a mutualism can “claim” a larger share of any surplus produced by the mutualistic relationship, and the faster evolving species will be forced to adapt by evolving to meet the slower evolving species’ optimum in order to prevent a failure to coordinate.

The advantages of commitment are well known in economics, and much theoretical work has been done on commitment, including first-mover advantages (e.g., Bagwell, 1995; Frank, 1988; Hoffman, Yoeli, & Nowak, 2015; Kambe, 1999; Morgan & Várdy, 2007; Schelling, 1960, 2001). However, despite the wealth of theoretical work, there has been a surprising dearth of experimental work on how humans actually behave. Do people actually take advantage of being committed (as predicted from theory), and do they benefit from doing so? How much do people value being able to tie their hands and commit to a course of action? The present study sought to test the following predictions: (1) committed individuals will claim more of a surplus from coordination than will uncommitted individuals, (2) individuals will benefit from the ability to commit to a course of action because players will coordinate more often on the committed players’ preferred outcomes and (3) when given the choice, people will prefer to tie their hands by committing to a course of action, in proportion to the actual value of commitment. I used two experimental games to test this: a Battle-of-the-Sexes (henceforth BoS; Experiment 1) and Hawk–Dove (HD) game (aka Chicken or Snowdrift game; Experiment 2). In both of these two-player games, each player has an incentive to avoid a mutually detrimental outcome, but there is an element of conflict because both players differ as to their preferred outcome. To simulate commitment, participants played these games for multiple rounds, where one player (the committed player) could commit to the same action for multiple rounds and the other (the uncommitted player) could change his or her action every round.

Experiment 1

Method

Participants and earnings

Twenty-three males and 25 females (mean ages: 23.7 and 20.6 years, ±SD 7.7 and 1.8 years, respectively) were recruited from the Cornell community via posters and a subject-recruitment website. Participants received US$1 for every 6 points earned in the experiment, rounded up to the nearest US$0.25 (median earnings: US$22.50, range US$16.50–25.50). Participants gave informed consent by signing consent forms. These methods were approved by the institutional review board at Cornell University.

BoS game

Participants were paired and assigned to be Player 1 or Player 2 within their pair. At each decision stage, participants could choose to play A or B. If both played A, then Player 1 earned 3 points while Player 2 earned 2 points. If instead both played B, then Player 1 earned 2 points while Player 2 earned 3 points. However, if one of them played A while the other played B, then both earned 1 point. Thus, participants benefited from coordinating their actions but differed as to their preferred action to coordinate on. Decisions were made simultaneously. The complete instructions are available upon request.

Commitment

Participants made five BoS decisions (a “round”) with the same partner. They were assigned one of the two roles within the pair: One member could change his or her decision within the round, whereas the other partner chose a decision to do for the entire round of five decisions (i.e., he or she was committed to a particular decision for the round). It is a Nash equilibrium for both players to play the committed player’s preferred action (A or B); neither player can increase their earnings by deviating from that choice. However, the opposite is not true even if the uncommitted player could signal intent to play his or her preferred action on the first decision in a round. Rather than conform to the uncommitted player’s optimum, the committed player could benefit from choosing his or her own preferred action and taking the failure to coordinate on the first outcome of that round, knowing that the uncommitted player’s best response would be to change his or her actions to the committed player’s optimum in order to avoid more failures to coordinate.

After a round of five BoS decisions with one partner, pairs were shuffled such that no person would be paired with the same partner for two consecutive rounds. Participants changed roles (able/unable to change decisions) with each new partner. There were two practice rounds followed by six paid rounds (each with five decisions per round). Practice rounds were identical to the paid rounds except that payoffs did not count toward participants’ earnings. Participants were not told the number of rounds, but otherwise had full knowledge of the structure of the game.

Choice

After the six paid rounds, participants did six more rounds of the BoS where they could bid to assign roles (i.e., able/unable to change decisions with a round). Within each pair, both partners indicated their preferred role and how many points (0–10) they would bid to implement their choice; the highest bidder paid his or her bid and was assigned his or her preferred role, while the lower bidder paid zero and was assigned the other role. Ties were decided randomly. If participants coordinate on the committed players’ preferred outcome as predicted, that committed player would receive 1 point more than the uncommitted player at every decision (totals for the round: 15 vs. 10, respectively). Since there was ideally a 5-point advantage to being committed, participants should be indifferent toward bidding five and bidding zero, such that bidding 4 points represents the optimal balance between maximizing one’s chance of winning the bid and paying so much as to eliminate the advantage of assigning roles. This assumes that partners automatically defer to committed players, but an a posteriori value of commitment can be created using the observed incidences of each outcome (see Results section).

Anonymity

Participants were seated in booths where they could not see others’ faces or computer screens, and all decisions were recorded via computer. The computer program was designed by the author using the software z-Tree (version 3.3.6) (Fischbacher, 2007). To ensure anonymity, participants received a code number which was used for payout purposes only. After the experiment, earnings were placed in envelopes with those code numbers, and participants took the envelope with their code number without the experimenters observing which envelope they took.

Results

Participants interacted with multiple partners within each session, so each session was treated as an N of 1 to control for nonindependence of decisions within the session. Overall, participants were more likely to coordinate on the preferred outcome of the committed player than on that of the uncommitted player or even all other outcomes combined (Fs_1,7 = 103.69 and 60.89, respectively, both ps < .001, Table 1, see Figure 1). These effects did not change with successive rounds or when the option to bid for role was introduced (all interactions Fs < 1.6, ps > .20). ² These patterns even occurred (albeit not as strongly) in the first decision of each round with new partners (F_1,7 = 49.02, p < .001 and F_1,7 = 14.74, p = .006, respectively) and that effect did not change with successive rounds or with the bidding for roles either (all interactions Fs < 3.4, all ps > .10). ³ The stability of this pattern suggests that many participants anticipated the advantage of committed players and acted accordingly right from the start of each new pairing; committed players selected their most desirable option more than 95% of the time in every round except Rounds 3 and 11 (Table 1 columns 1 and 3 combined). The second-most common outcome (especially on the first decision with each new partner) was each member of pair choosing his or her preferred outcome; some uncommitted participants attempted to get their preferred outcome at first but quickly switched when their partner was committed.

Table 1.

Average Rate of Occurrence (and Standard Errors) of Each Possible Outcome per Session in the Battle-of-the-Sexes.

Round	Coordinate on Committed Player’s Preferred Outcome	Coordinate on Uncommitted Player’s Preferred Outcome	Failure to Coordinate: Each Chooses Own Preferred Outcome	Failure to Coordinate: Each Chooses Other’s Preferred Outcome
1	(a) .84 (.08) (b) .63 (.12)	(a) .04 (.04) (b) .04 (.04	(a) .12 (.04) (b) .33 (.09)	(a) .00 (.00) (b) .00 (.00)
2	(a) .88 (.04) (b) .63 (.10)	(a) .00 (.00) (b) .00 (.00)	(a) .12 (.04) (b) .37 (.10)	(a) .00 (.00) (b) .00 (.00)
3	(a) .79 (.11) (b) .67 (.09)	(a) .11 (.07) (b) .04 (.04)	(a) .08 (.05) (b) .21 (.06)	(a) .02 (.02) (b) .08 (.08)
4	(a) .89 (.04) (b) .67 (.09)	(a) .00 (.00) (b) .00 (.00)	(a) .11 (.04) (b) .33 (.09)	(a) .00 (.00) (b) .00 (.00)
5	(a) .88 (.09) (b) .79 (.14)	(a) .03 (.03) (b) .00 (.00)	(a) .08 (.05) (b) .17 (.11)	(a) .01 (.01) (b) .04 (.04)
6	(a) .88 (.05) (b) .71 (.08)	(a) .03 (.03) (b) .00 (.00)	(a) .08 (.04) (b) .25 (.08)	(a) .01 (.01) (b) .04 (.04)
Average 1–6	(a) .86 (.05) (b) .68 (.07)	(a) .04 (.03) (b) .01 (.01)	(a) .10 (.03) (b) .28 (.02)	(a) .01 (.00) (b) .03 (.02)
7	(a) .86 (.07) (b) .58 (.10)	(a) .04 (.04) (b) .04 (.04)	(a) .10 (.03) (b) .38 (.10)	(a) .00 (.00) (b) .00 (.00)
8	(a) .87 (.07) (b) .71 (.12)	(a) .04 (.04) (b) .04 (.04)	(a) .09 (.05) (b) .25 (.10)	(a) .00 (.00) (b) .00 (.00)
9	(a) .90 (.05) (b) .75 (.10)	(a) .00 (.00) (b) .00 (.00)	(a) .10 (.05) (b) .25 (.10)	(a) .00 (.00) (b) .00 (.00)
10	(a) .89 (.05) (b) .75 (.10)	(a) .04 (.04) (b) .04 (.04)	(a) .07 (.03) (b) .21 (.09)	(a) .00 (.00) (b) .00 (.00)
11	(a) .82 (.10) (b) .71 (.12)	(a) .07 (.04) (b) .00 (.00)	(a) .10 (.05) (b) .21 (.09)	(a) .02 (.01) (b) .08 (.06)
12	(a) .85 (.09) (b) .67 (.14)	(a) .04 (.04) (b) .04 (.04)	(a) .11 (.05) (b) .29 (.12)	(a) .00 (.00) (b) .00 (.00)
Average 7–12	(a) .86 (.07) (b) .69 (.10)	(a) .04 (.03) (b) .03 (.02)	(a) .09 (.04) (b) .26 (.09)	(a) .00 (.00) (b) .01 (.01)
Grand mean	(a) .86 (.06) (b) .69 (.08)	(a) .04 (.03) (b) .02 (.02)	(a) .10 (.03) (b) .27 (.06)	(a) .00 (.00) (b) .02 (.01)

Note. (a) For all five decisions with the same partner in each round and (b) only the first decision within a given round. In Rounds 1–6, participants could not choose roles (committed/uncommitted). In Rounds 7–12, they could choose roles. Each six-person (three-pair) session was treated as an N of 1 due to nonindependence of data points. Totals might not be equal to 1 due to rounding.

Figure 1.

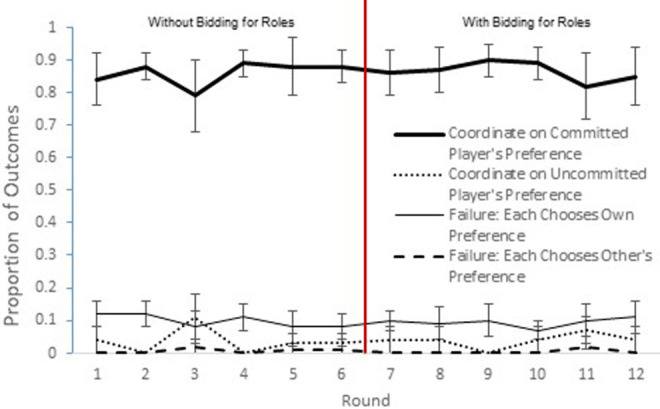
Average rate of occurrence (and standard error of the mean [SEM]) of each possible outcome in the Battle-of-the-Sexes in Experiment 1: coordination on committed player’s preference (thick solid line), coordination on uncommitted player’s preference (dotted line), failure to coordinate because each chooses own preferred outcome (thin solid line), and failure to coordinate each chooses other’s preferred outcome (dashed line). Results are based on five decisions with the same partner each round, with each six-person (three-pair) session treated as an N of 1 due to nonindependence of decisions. In Rounds 1–6, partners could not bid for roles (i.e., committed vs. uncommitted player), whereas in Rounds 7–12, they could bid for roles; the vertical red line separates these two kinds of rounds.

When given the option of choosing, participants preferred to be committed to a particular course of action by being unable to change decisions midround (one sample t₇ = 3.35, p = .012; Table 2). This preference changed across rounds (F_5,35 = 4.82, p = .002), showing linear, quadratic, and cubic trends (Fs_1,7 = 3.96, 7.31, and 6.50; ps = .087, .030, and .038, respectively). The average bid for these roles (2.6 points ± SE 0.3 points) was significantly greater than 0 but less than the ideal predicted bid of 4 points (one sample ts₇ = 7.55 and 3.99, respectively, both ps < .006), with four outliers (4/48) who always bid zero. Bids did not change across rounds, F_5,35 = 1.03, p = .42). To create an a posteriori value of commitment, one multiplies the overall frequency of the outcomes by the scores the committed player obtains in those outcomes and compares that to what a rational uncommitted player could get. The a posteriori value of commitment was thus 3.74 points, such that the a posteriori optimal bid is 3. The observed average bids of 2.6 were slightly but nonsignificantly lower than the a posteriori optimal bid, whether analyzed by session (one sample t₇ = 1.33, p = .22), by individual (one sample t₄₇ = 1.93, p = .06), or by individual with zeros removed (one sample t₄₄ = 1.13, p = .27), suggesting that bids were somewhat matched with their actual value in the experiment (albeit lower).

Table 2.

Average Bid (and Standard Errors) to Choose Uncommitted/Committed Roles and Percent of Time (and Standard Errors) that Participants Chose to Be Committed in the Battle-of-the-Sexes (BoS: Experiment 1) and Hawk–Dove (HD: Experiment 2) Games in the Rounds, Where Bidding and Role Choice Were Possible (7–12).

	Average Bid to Choose Roles		Percent of Time Choosing to Be Committed
Round	BoS	HD	BoS	HD
7	3.0 (0.2)	2.6 (05)	66.7 (10.0)	66.7 (8.6)
8	2.5 (0.3)	2.8 (0.6)	79.2 (8.2)	80.6 (10.0)
9	2.6 (0.4)	3.2 (0.7)	83.3 (8.0)	80.6 (8.0)
10	2.4 (0.5)	3.2 (0.9)	81.3 (8.6)	80.6 (8.0)
11	2.5 (0.4)	2.9 (1.0)	79.2 (8.8)	86.1 (8.0)
12	2.6 (0.5)	2.8 (0.7)	81.3 (8.6)	86.1 (5.1)
Average	2.6 (0.3)	2.9 (0.7)	78.5 (8.5)	80.1 (7.5)

Note. Because pairs within a session were not independent, each session of six participants was treated as an N of 1.

Experiment 2

Method

HD game

Participants were paired and assigned to be Player 1 or Player 2 within their pair. At each decision stage, participants could choose to play A or B. If both played A, then each earned 1 point. If both played B, then each earned 3 points. However, if one played A while the other played B, the former received 4 points while the latter received 2. In this game, one earns the most by playing A while one’s partner plays B. However, both receive the lowest payoff if both play A, such that one is better off playing B if one’s partner plays A. Partners have a confluence of interest in avoiding mutually playing A, but a conflict of interest in that each would do best by sticking with A and getting the other to switch to B.

Procedure and participants

Other than using an HD instead of a BoS, the procedure (commitment, rounds of five decisions, practice and paid rounds, and bidding for roles after six paid rounds) was the same as in Experiment 1. The participants were 19 males and 17 females (mean ages: 19.5 and 19.9 years; ±SD 1.3 and 1.0 years, respectively) recruited from the Cornell community via posters and a subject-recruitment website. Participants received US$1 for every 7 points earned in the experiment, rounded up to the nearest US$0.25 (median earnings: US$19.75; range: US$13.00–27.25). If participants coordinate on the committed player’s preferred outcome (4 points to committed player and 2 points to uncommitted player), there is a 2-point benefit to being committed at every decision, for a total benefit of 10 points across a round of five decisions. Thus, participants should be indifferent toward bidding 0 and bidding 10, such that bidding 9 represents the optimal bid.

Results

HD Game

Participants interacted with multiple partners within each session, so each session was treated as an N of 1 to control for nonindependence of decisions within the session. Overall, the committed player’s preferred outcome (4 points for committed player and 2 points for uncommitted player) was more likely to occur than the uncommitted player’s preferred outcome (F_1,5 = 42.26, p < .001, Table 3, see Figure 2), and these effects did not change with successive rounds, Fs < 1. This pattern even occurred in the first decision of each round with new partners (F_1,5 = 73.20, p < .001) and that effect did not change with successive rounds or with the bidding for roles either (all interactions Fs < 1.5, all ps > .25). The stability of this pattern suggests that participants anticipated the advantage of committed players and acted accordingly; committed players played Hawk more than 67% of the time in all early rounds and more than 89% of the time in all bidding rounds (Table 3, columns 1 and 3 combined).

Table 3.

Average Rate of Occurrence (and Standard Errors) of Each Possible Outcome per Session in the Hawk–Dove Game.

Round	Committed Player’s Optimum (Committed Plays Hawk and Uncommitted Player Dove)	Uncommitted Player’s Optimum (Committed Plays Dove and Uncommitted Plays Hawk)	Both Play Hawk (i.e., Mutual Antagonism)	Both Play Dove (i.e., Cooperation)
1	(a) .52 (.08) (b) .39 (.09)	(a) .24 (.06) (b) .00 (.00)	(a) .14 (.03) (b) .28 (.10)	(a) .09 (.03) (b) .33 (.09)
2	(a) .48 (.11) (b) .33 (.12)	(a) .24 (.12) (b) .17 (.11)	(a) .24 (.04) (b) .39 (.16)	(a) .03 (.02) (b) .11 (.11)
3	(a) .54 (.09) (b) .50 (.08)	(a) .14 (.10) (b) .06 (.06)	(a) .29 (.05) (b) .33 (.12)	(a) .02 (.01) (b) .11 (.07)
4	(a) .52 (.13) (b) .50 (.14)	(a) .21 (.07) (b) .11 (.07)	(a) .20 (.09) (b) .22 (.14)	(a) .07 (.04) (b) .17 (.08)
5	(a) .69 (.19) (b) .61 (.13)	(a) .10 (.07) (b) .00 (.00)	(a) .09 (.04) (b) .17 (.11)	(a) .12 (.06) (b) .22 (.11)
6	(a) .67 (.10) (b) .50 (.08)	(a) .19 (.09) (b) .11 (.07)	(a) .11 (.05) (b) .28 (.10)	(a) .03 (.03) (b) .11 (.11)
Average 1–6	(a) .57 (.07) (b) .47 (.05)	(a) .19 (.06) (b) .07 (.04)	(a) .18 (.02) (b) .28 (.05)	(a) .06 (.02) (b) .18 (.04)
7	(a) .78 (.09) (b) .67 (.12)	(a) .000 (.000) (b) .00 (.00)	(a) .22 (.09) (b) .33 (.12)	(a) .00 (.00) (b) .00 (.00)
8	(a) .61 (.10) (b) .50 (.17)	(a) .06 (.06) (b) .06 (.06)	(a) .33 (.07) (b) .44 (.14)	(a) .00 (.00) (b) .00 (.00)
9	(a) .59 (.05) (b) .50 (.09)	(a) .04 (.04) (b) .00 (.00)	(a) .36 (.04) (b) .44 (.07)	(a) .01 (.01) (b) .06 (.06)
10	(a) .60 (.05) (b) .67 (.09)	(a) .00 (.00) (b) .00 (.00)	(a) .40 (.05) (b) .33 (.09)	(a) .00 (.00) (b) .00 (.00)
11	(a) .59 (.07) (b) .56 (.07)	(a) .11 (.07) (b) .11 (.07)	(a) .30 (.07) (b) .33 (.09)	(a) .00 (.00) (b) .00 (.00)
12	(a) .54 (.08) (b) .33 (.12)	(a) .00 (.00) (b) .00 (.00)	(a) .46 (.08) (b) .67 (.12)	(a) .00 (.00) (b) .00 (.00)
Average 7–12	(a) .62 (.03) (b) .54 (.05)	(a) .04 (.02) (b) .03 (.02)	(a) .34 (.02) (b) .43 (.03)	(a) .00 (.00) (b) .01 (.01)
Grand mean	(a) .59 (.04) (b) .51 (.04)	(a) .11 (.03) (b) .05 (.02)	(a) .26 (.01) (b) .35 (.020	(a) .03 (.01) (b) .09 (.03)

Note. (a) For all five decisions with the same partner in each round and (b) only the first decision within a given round. In Rounds 1–6, participants could not choose roles (committed/uncommitted), and in Rounds 7–12, they could choose roles. Each six-person (three-pair) session was treated as an N of 1 due to nonindependence of decisions. Totals might not be equal to 1 due to rounding.

Figure 2.

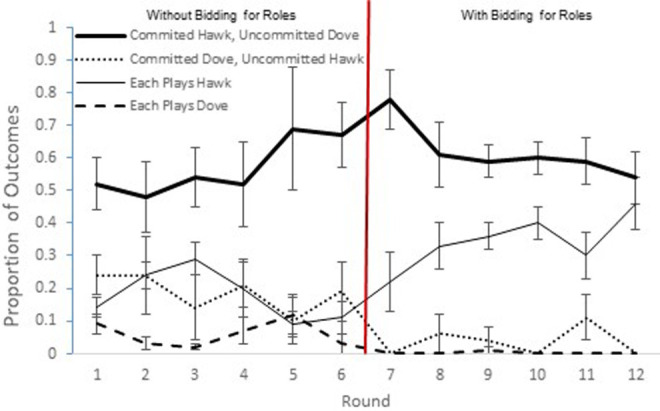
Average rate of occurrence (and standard error of the mean [SEM]) of each possible outcome in the Hawk–Dove game in Experiment 2: committed player plays Hawk while uncommitted player plays Dove (thick solid line), committed player plays Dove while uncommitted player plays Hawk (dotted line), both players play Hawk (thin solid line), and both players play Dove (dashed line). Results are based on five decisions with the same partner each round, with each six-person (three-pair) session treated as an N of 1 due to nonindependence of decisions. In Rounds 1–6, partners could not bid for roles (i.e., committed vs. uncommitted player), whereas in Rounds 7–12, they could bid for roles; the vertical red line separates these two kinds of rounds.

The committed player’s preferred outcome was also more likely to occur than the other three outcomes combined (F_1,5 = 8.50, p = .033), but this effect changed depending on the round number and whether participants could bid for roles (interaction F_5,25 = 4.23, p = .006). When participants could not bid for roles, the committed player’s preferred outcome occurred just as often as all three other possible outcomes combined (F_1,5 = 1.09, p = .35), and this difference did not change across rounds (F_5,25 = 1.10, p = .39). When participants could bid for roles, the committed player’s preferred outcome was more likely to occur (F_1,5 = 18.82, p = .007), and this difference did not change across rounds either (F_5,25 = 1.11, p = .38). Like the BoS, the second-most common outcome (especially on the first decision with each new partner) was each member of the pair choosing his or her preferred outcome, although the uncommitted player’s optimum occurred with moderate frequency when bidding was not possible (i.e., before too much learning had occurred)—apparently the result of committed players attempting for the cooperative outcome (Dove–Dove) but getting exploited by the uncommitted players.

When given the option, participants preferred to be committed to a particular course of action by being unable to change decisions midround (one sample t₅ = 4.01, p = .010, Table 2), and this preference changed with rounds (F_5,25 = 4.81, p = .003) in a linear increase (F_1,5 = 7.66, p = .039). The average bid (2.9 points ± SE 0.7 points) was significantly greater than 0 and less than the predicted bid of 9 (one sample ts₅ = 4.24 and 8.90, respectively, both ps < .01), with three outliers (3/36) who always bid zero. Bids did not change across rounds (F < 1). I calculated the a posteriori value of commitment of 4.1 points in the same way as in Experiment 1, such that the a posteriori optimal bid is 4. The observed average bid of 2.9 was lower than the a posteriori optimal bid of 4; this was not significant when analyzed by session (one sample t₅ = 1.57, p = .18) but was when analyzed by individual (one sample t₃₅ = 3.12, p = .004), even with zeros excluded (one sample t₃₂ = 2.39, p = .02).

Comparison of Outcomes Between the BoS and the HD Games

Relative to the BoS, participants in the HD game were less likely to coordinate on the committed player’s preferred outcome (F_1,12 = 12.39, p = .004), and this did not interact with round number or the option to bid for roles (all interactions involving game type F < 1.3, all ps > .30). All other outcomes were more common in the HD game than in the BoS: uncommitted player’s preferred outcome (F_1,12 = 3.53, p = .085), Hawk–Hawk outcomes and the BoS equivalent where each player tries for his or her preferred outcome (F_1,12 = 17.17, p = .001), and Dove–Dove outcomes and the BoS equivalent where each player defers to the other’s preferred outcome (F_1,12 = 14.45, p = .003). However, for each of these three other outcomes, the effect of game type varied with the availability of bidding for role (Fs_1,12 = 9.80, 17.17, and 19.39, respectively, all ps < .01; compare Tables 1 and 3): The uncommitted player’s preferred outcome was more likely in the HD game than in the BoS when bidding was absent but not when it was present; Hawk–Hawk outcomes (and BoS equivalent) were more common in the HD game than in the BoS and this effect was magnified when bidding for roles was present; and the rare Dove–Dove outcomes (and BoS equivalent) were more likely in the HD game than in the BoS when bidding for roles was absent but disappeared in both games once bidding was introduced. Average bids and the percent of choices for the committed role did not differ between the BoS and the HD game, nor did game interact with round number (all Fs < 1.1). It is not immediately clear why uncommitted players were more willing to experience a coordination failure (Hawk–Hawk outcome) in the HD game than in the BoS; perhaps, they were averse to the greater inequality in outcomes in the HD game, or they were punishing the committed player for a blatantly uncooperative Hawk move when a Dove–Dove outcome could have been good for both players.

General Discussion

In both a BoS and a Hawk–Dove game, players who were committed to a course of action were more likely to achieve their optimal outcomes than players who were not so committed, because the former could force the latter to cede to their demands and accommodate. This provides an incentive to tie one’s hands and commit to a particular action. Indeed, participants chose to do so approximately 80% of the time.

Furthermore, participants were willing to pay a significant amount to tie their own hands: In both games, the average bid was over half of the minimum earnings for a given round and one sixth of the maximum earnings for the round. In the BoS, the average bid was one half of the total theoretical benefit for being committed (2.6/5), and in the HD game, it was 30% of the total theoretical benefits of commitment (2.9/10). Given that noncoordination (BoS) and Hawk–Hawk outcomes (HD game) occurred, ⁴ a better estimate of the actual benefits of commitment is the a posteriori value calculated based on the frequencies and payoffs of the possible outcomes, and the observed average bids were closer to these values. In other words, participants’ willingness to pay to tie their own hands was somewhat matched with (albeit generally lower than) the expected value of doing so.

These results support theories on the advantages of commitment (Nesse, 2001; Schelling, 1960), in that public commitment to courses of action can be beneficial to the committer. These ideas have received much mathematical attention in economics and evolution, but surprisingly few empirical tests to see if humans actually behave as predicted by these theories. Of course, not all commitment is as strategic as it was for these participants. Many real-world commitments are emotional responses, such as anger or love, which commit us to certain courses of action and have cues that can be reliably detected by others (Frank, 1988). These emotional responses (and cues thereof) arguably evolved because of the tangible benefits for credibly signaling one’s commitment; the benefits within this experiment are a proof of concept that others do indeed defer to such commitment on average and that commitment can be beneficial. Within an individual lifetime, one could even learn to follow such irrational emotions more often, given that doing so can result in increased reinforcement by changing others’ responses. This being said, I am agnostic as to how much real-world commitment is strategic rational commitment, as in this experiment, versus irrational (but nonetheless adaptive) emotional commitment.

Of course, if everyone commits to courses of action, there will be far more failures to coordinate or Hawk–Hawk outcomes. Thus, in the absence of clearly defined roles like announcing a commitment first (e.g., Hirshleifer, 2001) and “Bourgeois”-like strategies that respect such roles (e.g., Maynard Smith, 1982), the evolution of commitment is somewhat like an overarching Hawk–Dove game itself that encompasses other Hawk–Dove or coordination situations. Committing to courses of action is like playing Hawk in that one can get better outcomes for oneself, but one runs the risk of meeting other committed players who are also trying to get better outcomes for themselves (Leventoğlu & Tarar, 2005). ⁵ If everyone else commits to the courses of action, then there is a niche for those who are more flexible because they will suffer fewer failures to coordinate. Thus, the payoff of commitment will depend on the frequency of committed types: Commitment is advantageous when flexibility is common and vice versa. In the regular Hawk–Dove game, one successful strategy for avoiding coordination failures is assessor who plays Hawk if it is stronger than its opponent and Dove otherwise (Maynard Smith, 1982). Similarly, in the meta-Hawk–Dove game of commitment, an ideal decision-making system could involve assessment of one’s partner’s potential commitment, possibly based on their past actions or population averages, before finalizing one’s own commitment; if one’s partner appears much more committed, then it pays to assess that and become more flexible and vice versa.

If people base their assessments of others’ commitment in part on those others’ reputation for past actions, then this creates an incentive to suffer some repeated failures to coordinate in order to signal one’s commitment or stubbornness, just as there is an incentive to signal other Hawk-like tendencies (e.g., McElreath, 2003) or fight harder when observed than you otherwise would (Johnstone & Bshary, 2004). For example, one would expect more commitment when observed than when anonymous. In fact, in situations with a conflict of interest, one must signal one’s individual commitment in order to benefit from it; otherwise, one will pay the costs of failures to coordinate yet get none of the benefits of others yielding to one’s firm stance. This principle is best depicted in the Kubrick film Dr. Strangelove, where the Soviets develop a “doomsday device” to deter nuclear attacks by automatically destroying all life on the planet in the event of an attack, but it does not fulfill its deterrent purpose because the Soviets do not announce its existence, resulting in the destruction of all life.

Signaling one’s commitment could be as simple as public statements of intention to carry through with a course of action (e.g., Leventoğlu & Tarar, 2005) because if one does not follow through, then one loses one’s reputation and the ability to force concessions in the future. This has probably been historically important, given humans tendency to use gossip to convey social information and reputation (Dunbar, 2004). Such public verbal statements can be used by unions by voting to commit their bargainers to obtaining certain outcomes, political leaders by using statements such as “we will not negotiate with terrorists” in attempts to reduce terrorist demands, those working toward conflict reduction by encouraging public statements of willingness to de-escalate conflicts, and so on. In such cases, the honesty of the signal of commitment is maintained by the possibility of future interactions; it would not pay to take the short-term benefits of not following through if it reduced one’s ability to commit to courses of action in the future.

Commitment is not advantageous in all situations (Bergstrom & Lachmann, 2003a); it depends on a moderate confluence of interests and some nonzero sum payoff (Hirshleifer, 2001). With zero conflict of interest, there is no need for commitment because neither party has an incentive to deviate from the mutually beneficial outcome. With a complete zero-sum interaction without any confluence of interests, there is no advantage to committing because parties don’t benefit from avoiding a failure to coordinate, and commitment can be detrimental if it allows others to change their response to their advantage and one’s own disadvantage (Hirshleifer, 2001). The present experiment provides empirical evidence that people will accept costs to commit to actions when there is a moderate degree of conflict and that they benefit from doing so; future studies should extend this work by testing people’s willingness to commit and benefits (or lack thereof) for doing so under situations of low conflict (e.g., pure coordination) and high conflict (zero-sum games).