Normative cerebral microvascular blood flow waveform morphology assessed with diffuse correlation spectroscopy

Abstract

Microvascular cerebral blood flow exhibits pulsatility at the cardiac frequency that carries valuable information about cerebrovascular health. This study used diffuse correlation spectroscopy to quantify normative features of these waveforms in a cohort of thirty healthy adults. We demonstrate they are sensitive to changes in vascular tone, as indicated by pronounced morphological changes with hypercapnia. Further, we observe significant sex-based differences in waveform morphology, with females exhibiting higher flow, greater area-under-the-curve, and lower pulsatility. Finally, we quantify normative values for cerebral critical closing pressure, i.e., the minimum pressure required to maintain flow in a given vascular region.

1. Introduction

Blood flow in the brain is driven by a continuous stream of compression waves that originate from the contractions of the heart. Thus, cerebral blood flow is inherently pulsatile (on the order of 1 Hz). As they propagate, flow waveforms are attenuated by the complex and dynamic structure of the cerebral circulation. Every branch point and change in vessel caliber within the cerebrovascular tree represents a site of resistance to forward flow, where a proportion of the incoming pulse waveform will be transmitted while some is reflected. The net constructive and destructive interference of forward- and back-propagating pulsatile flow encodes information about vascular tone. As a result, the pulsatile blood flow/blood pressure relationship carries information about cerebrovascular resistance, compliance, and intracranial pressure [1–4]. Leveraging this information through waveform analysis of pulsatile cerebral hemodynamics has played a key role in improving both clinical management and mechanistic understanding of numerous neurovascular pathologies [5–8].

The state-of-the-art approach for probing pulsatile hemodynamics in the brain is transcranial Doppler ultrasound (TCD). TCD is a high-speed (>100 Hz) technique that is sensitive to blood flow velocities in the large arteries that feed the brain. TCD measurements of flow velocity waveform morphology, alone or in combination with measurements of pulsatile arterial blood pressure (ABP), have been shown to provide clinically actionable biomarkers in numerous pathological conditions, including ischemic [9,10] and hemorrhagic stroke [11–13], traumatic brain injury (TBI) [14–16], elevated intracranial pressure (ICP) [17–23], age-related vascular degradation [24–27], and dementia [28–30]. However, TCD is fundamentally limited to measurements in large arteries, and as such, it cannot directly interrogate features of the flow waveform in the downstream microcirculation, i.e. the arterioles and capillary beds. This limitation is significant, because numerous circulatory pathologies originate at the microvascular level and erode macro-/micro-vascular coupling as they progress. In such cases, micro-level damage will remain undetected by TCD until overt clinical symptoms emerge, at which point the damage may be irreversible [31]. Microvascular waveform dynamics can provide a more complete assessment of cerebrovascular function, potentially facilitating earlier intervention and ultimately improved treatment outcomes.

Assessing microvascular pulsatility requires both sensitivity to small vessels and high temporal resolution (on the order of 10 Hz or higher). While neuroimaging modalities such as magnetic resonance imaging (MRI), positron emission tomography (PET), and computed tomography (CT) can measure microvascular perfusion, their temporal resolution is generally too slow to resolve pulsatility. Diffuse correlation spectroscopy (DCS) [32–35] is a relatively newer, non-invasive optical modality that can measure an index of regional microvascular blood flow (BFI) in the brain. Recent technological advances have allowed DCS to achieve acquisition speeds up to 100 Hz [36,37]. Initial investigations into the utility of BFI waveforms at the cardiac frequency [38–45] have predominantly targeted noninvasive estimation of critical closing pressure (CrCP), i.e., the minimum pressure required to maintain flow in a given vascular region [1]. At present, little is known about what constitutes “normal” BFI waveform morphology or CrCP ranges in healthy adults. Knowledge of the bounds of normality for these metrics will be required to define clinically actionable biomarkers of microvascular compromise.

This study uses DCS to quantify regional microvascular CBF waveforms at the cardiac frequency in a cohort of thirty healthy adults. We develop a data analysis pipeline to extract pulsatile flow waveforms with high signal-to-noise (SNR) from the inherently low SNR raw BFI time series. We use this pipeline to test the hypothesis that resting-state BFI waveform morphology differs by sex, given reports of sex-differences at both the macro- and microvascular level measured by other modalities [46–48]. Furthermore, we test the hypothesis that BFI waveform morphology changes with reductions in vascular tone induced by hypercapnia. Lastly, we use this dataset to quantify normative CrCP values at rest and during hypercapnia.

2. Methods

2.1. Experimental protocol

Healthy adult volunteers >18 y were recruited for this study. Exclusion criteria included history of major head injury within the past 2 years or prior diagnosis of cardiovascular, neurovascular, renal, respiratory, or hematological disorders. Subjects were instructed to abstain from stimulants or depressants, such as caffeine, alcohol, or nicotine, for at least 12 h prior to the study. Written informed consent was obtained for all participants. All protocols were approved by the Emory University Institutional Review Board.

During measurements, subjects were seated with their upper-arm resting at heart level, legs bent at 90-degrees, and feet flat on the floor. Brief measurements of resting-state tissue optical properties were first made with frequency domain near infrared spectroscopy (FDNIRS) by gently holding an optical sensor consecutively over the right and left forehead for 5 s/hemisphere and repeating 3-5 times on each side to account for local inhomogeneities under the tissue surface. Next, to assess regional blood flow waveforms over the prefrontal cortex, a non-invasive DCS sensor was secured to the forehead to continuously monitor BFI at 20 Hz. Concurrent monitoring of arterial blood pressure (ABP) was performed non-invasively with a CNAP system (NIBP100D-1, cnsystems) [49,50]. After a resting state monitoring period of 5-10 minutes, a 6-minute hypercapnic challenge was performed. Hypercapnia was induced by delivering medical grade 5% CO₂/balance room air (Nexair, Memphis TN) through a mask secured over the nose and mouth [51].

2.2. Frequency-domain near-infrared spectroscopy

FDNIRS measurements of resting-state optical properties, namely, the wavelength-dependent absorption and reduced scattering coefficients ( ${\mu }_a$ and ${{\mu }_s}^{\mathrm{\prime }}$ ), were performed with a customized system (Imagent, ISS Inc, Champaign IL) containing eight near-infrared laser diode sources (690, 730, 750, 775, 785, 800, 825, and 830 nm) modulated at 110 MHz and rapidly multiplexed, along with four photomultiplier tube detectors with gain modulation of 110 MHz + 5 kHz for heterodyne detection at 5 kHz. A 3D-printed rigid black sensor was used that contained five 2.5 mm fiber bundles (50 µm multimode fibers, NA = 0.66, FTTIIG23767, FiberOptics Technology, Pomfret, CT), one of which was used as the source, and the other four of which were used as detectors spaced 20, 25, 30, and 35 mm from the source. Amplitude $AC(r,\lambda )$ and phase shift $\theta (r,\lambda )$ of the detected signal were recorded at 20.8 Hz and then averaged over the 3-5s measurement duration for each source-detector separation, r, and wavelength, $\lambda$ , for analysis (see Section 2.4.1).

2.3. Diffuse correlation spectroscopy

DCS data was acquired using a custom-built system containing an 852 nm long coherence laser (iBEAM smart, TOPTICA Photonics) and 8 single photon-counting avalanche photodiodes (SPCM-AQ4C-IO, Perkin-Elmer). A counter/timer data acquisition board (PCIe-6612, National Instruments, Austin, TX) was used in conjunction with a software correlator for real-time, 20 Hz quantification of the intensity autocorrection function ( $g_2(\tau )$ , where $\tau$ is the correlation delay time) [36]. A flexible sensor with embedded optical fibers for light delivery and detection was secured to the subject’s forehead over the hemisphere that yielded the highest detected intensities using a cloth strap (Masimo Corporation, Irvine CA). The sensor consisted of a 1 mm fiber bundle source (FTIIG23767, Fiberoptics Technology, Pomfret, CT) spaced 25 mm from a bundle of seven 5 µm single-mode detection fibers (780 HP, Thorlabs, Newton NJ). Both source and detector fiber bundles were coupled to 5 mm right angle prism mirrors (MRA05-E03, Thorlabs) using custom-designed 3D printed housings (VeroBlack, Stratasys, Eden Prairie MN) molded within the flexible black rubber of the sensor (Vytaflex30, Smooth-on Inc., Macungie PA).

2.4. Data analysis

2.4.1. FDNIRS analysis

To quantify tissue optical properties, we employed the semi-infinite solution of the photon diffusion equation, which relates the slopes of $AC(r,\lambda )$ and $\theta (r,\lambda )$ versus r to the absorption $({\mu }_a(\lambda ))$ and reduced scattering coefficients $({\mu }_s^{\mathrm{\prime }}(\lambda ))$ [33]. First, average $AC(r,\lambda )$ and $\theta (r,\lambda )$ values were computed over each 3-5s measurement repetition. Individual repetitions were discarded if the standard deviation of $\theta (r,\lambda )$  >  $5^{\circ }$ or if the standard deviation/mean of $AC(r,\lambda )$ was $>0.05$ . After calibrating AC and $\theta$ with coefficients obtained from a phantom with known optical properties, linear regression was used to estimate the slopes of $ln(AC(r,\lambda )\times r^2)$ vs. r and $\theta (r,\lambda )$ vs. r. Wavelengths were discarded from further analysis if the linear model $R^2<0.97$ for either AC or $\theta$ . The linear slopes were then used to estimate ${\mu }_a(\lambda )$ and ${\mu }_s^{\mathrm{\prime }}(\lambda )$ . Finally, we extrapolated ${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ to 852 nm to find the relevant optical properties for incorporation into the DCS analysis (see Section 2.4.2). For this extrapolation, measured ${\mu }_s^{\mathrm{\prime }}(\lambda )$ were fit to a linear model, and measured ${\mu }_a(\lambda )$ were fit to the hemoglobin spectrum, as described in previous work [52].

2.4.2. DCS analysis

DCS data was acquired continuously at 20 Hz. Each data frame, acquired at time t, consisted of 7 normalized intensity autocorrelation curves $g_2(t,\tau ),$ one from each detector. Curves from detectors with photon count rates < 10 kHz were discarded; $g_2(t,\tau )$ was then averaged across the remaining detectors to improve signal-to-noise (SNR). The average $g_2(t,\tau )$ curves were thresholded to $g_2(t,\tau )$  > 1.2 to improve brain sensitivity [53]. If the 1.2 threshold resulted in < 10 remaining delay times, the threshold was removed, and the entire autocorrelation curve was used for fitting. The resulting averaged and thresholded $g_2(t,\tau )$ curves were fit to the semi-infinite solution of the correlation diffusion equation for the coherence factor, $\beta$ , and an index of cerebral blood flow (BFI, cm²/s) [33]. Subject-specific ${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ , measured at rest with FDNIRS and extrapolated to 852 nm (see Section 2.4.1) were incorporated into the fits when available (n = 26); if unavailable (n = 4, 3 male), sex-based cohort averages were used: ${\mu }_s^{\mathrm{\prime }}$  = 8.07 cm^-1 and ${\mu }_a$  = 0.14 cm^-1 for females and ${\mu }_s^{\mathrm{\prime }}$  = 7.95 cm^-1 and ${\mu }_a$  = 0.15 cm^-1 for males (Appendix 1). Index of refraction of tissue was assumed to be 1.4.

2.4.3. Blood flow waveform characterization

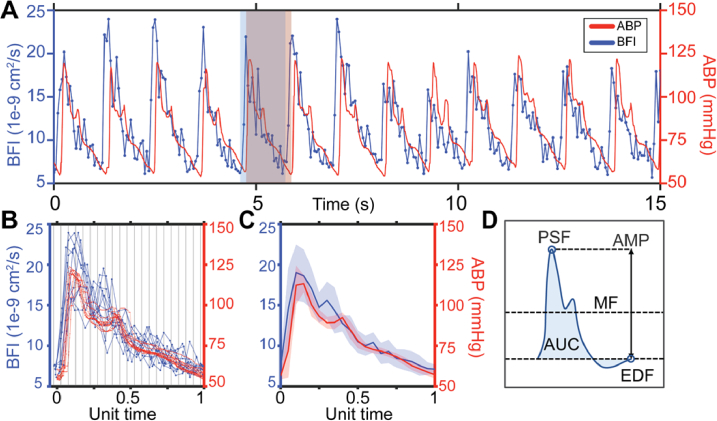
The light-starved nature of probing deep-tissue dynamics inherently limits the SNR of high-speed DCS measurements. Consequently, although cardiac pulsatility can generally be observed in BFI at 20 Hz, such as in the example in Fig. 1(A), noise renders both robust delineation of individual pulses and quantification of their features (e.g., amplitude, area under the curve) challenging. To address the challenge of delineating each pulse in the BFI time series, we leveraged the higher SNR ABP signal, which possesses easily distinguishable cardiac waveforms that can be used to identify the onset of each BFI pulse (shaded boxes in Fig. 1(A)). To address the subsequent challenge of identifying specific features of the extracted waveforms, pulses were averaged over 15 s windows. A 15 s window duration was experimentally seen to provide sufficient SNR improvements while preserving the temporal resolution needed to capture changes in waveform morphology (0.067 Hz).

Fig. 1.

Estimating microvascular blood flow waveforms. (A) Representative 15s window of pulsatile blood flow index (BFI, blue) and arterial blood pressure (ABP, red) signals. The flow waveform leads pressure. The red shaded box shows the boundaries of an ABP pulse, while the blue box denotes the boundaries of the corresponding BFI pulse. (B) Waveforms extracted from the 15s window are overlayed, preserving the sampling offset between ABP and BFI. Each pulse pair is normalized by the same factor such that ABP pulse length is set to a unit length of 1, then binned and averaged. (C) Final average blood flow and pressure waveforms over the 15s time window, shading shows standard deviation. (D) Schematic diagram of morphological features directly quantified from each pulse: mean flow (MF), peak systolic flow (PSF), end diastolic flow (EDF), amplitude (AMP) and area under the curve (AUC).

To quantify normative waveform features at rest and in response to vasomotor perturbation (hypercapnia), data from the 5-10 min resting-state and the final 3 minutes of hypercapnia were broken into non-overlapping 15 s windows. Within each window, we first linearly interpolated single missing BFI data points (interp MATLAB, MathWorks). If two or more consecutive BFI datapoints were missing, the entire window was discarded from analysis. Next, ABP and BFI timeseries were time-aligned to account for the characteristic lead time of flow relative to pressure [54]. The time shift was determined by maximizing the cross correlation of BFI and ABP (resampled to the 20 Hz BFI time axis) using xcorr (MATLAB). ABP waveforms were then processed at their native sampling frequency (125 Hz) with the MATLAB program delineator [55] to identify the onset and dicrotic notch of each pulse in the window. To mitigate the potential impact of changing heart rate on morphological quantification, each ABP pulse was normalized to unit length. The corresponding BFI pulse was scaled by the same factor to preserve the relationship between ABP and BFI pulse pairs. Next, all pulses were overlaid for averaging by setting the ABP onsets to start at t =  $0$ and by shifting BFI accordingly (Fig. 1(B)). An average ABP dicrotic notch position was computed from the individual length-normalized pulses. Finally, waveforms were aggregated in 20 bins of width 0.05 and averaged (Fig. 1(C)). The bin that contained the average ABP dicrotic notch was set as the dicrotic notch of the final window-averaged pulse.

The higher SNR of the window-averaged BFI/ABP pulses was leveraged for waveform feature quantification. First, the “systolic upstroke” and “diastolic runoff” regions, which are the sharp rise in pressure/flow prior to the first peak and the gradual decline after the dicrotic notch, respectively, were identified in each pulse. To do this, the findpeaks (MATLAB) function was used to identify the first peak in the i^th averaged BFI/ABP pulse as the systolic peak (PSF _i / PSP _i ). The first peak following the dicrotic notch of the ABP pulse was used as the onset of diastolic runoff for both ABP and BFI. The value of BFI/ABP at the last timepoint in the pulse were taken as the end diastolic flow/pressure (EDF _i / EDP _i ). Next, waveform features for the $i^{th}$ window-averaged pulse were quantified (Fig. 1(D)), including mean flow/pressure (MF _i / MAP _i ), pulse amplitude (flow amplitude $\text{AM}{\text{P}}_i\equiv PS{F}_i-ED{F}_i$ , pressure amplitude ( $\text{AM}{\text{P}}_{p_i}\equiv \text{PS}{\text{P}}_i-\text{ED}{\text{P}}_i$ ), and area under the curve (AUC _i $\equiv {\sum }_{j=1}^{20}0.05\times (BF{I}_i(j)-ED{F}_i))$ . Pulsatility and resistivity indices (PI and RI, respectively) were defined as $P{I}_i\equiv AM{P}_i/M{F}_i$ and $R{I}_i\equiv AM{P}_i/PS{F}_i$ .

For quality control, window-averaged BFI/ABP waveforms were excluded from further analysis if 1) maximum value of ABP or BFI occurred in the latter portion of the pulse, i.e., after bin 12; 2) either the pulse amplitude or the initial slope of the systolic upstroke (obtained from the first 3 points) was negative; 3) the end diastolic value >  $2\times$ the value at the pulse onset or > the mean value. These criteria were chosen conservatively to remove pulses overtly lacking features of the cardiac waveform. If either of the BFI/ABP pulse pair from the i^th window was rejected, the other was also removed from further analysis. Only datasets with > 5 windows passing quality control for both resting state and hypercapnia were included for analysis. Note, while ABP was recorded in all subjects and used for pulse segmentation, 6 out of 30 ABP timeseries exhibited artifacts introduced by automatic recalibration of the CNAP device. ABP pulse morphology was only quantified in the subset of 24/30 for whom the CNAP instrumentation was able to record a continuous time trace without recalibration.

2.4.4. Critical closing pressure

Critical closing pressure (mmHg) was computed for each 15 s window with both time-domain [6,56] and frequency-domain [20] models. In the time domain, TD-CrCP was defined as the ABP-axis intercept of the linear model of window-averaged ABP vs. BFI waveforms [5]. Linear regression was applied either to the entire pulse, thus maximizing the sampling of the instantaneous pressure/flow relationship, or to only the diastolic runoff portion. In the frequency domain, FD-CrCP was estimated using a resistive-only model of the cerebrovascular system [38]:

$$\begin{array}{c}\text{FD - CrCP}=⟨ABP⟩\left(1-\frac{\left|\mathit{A}\mathit{B}\mathit{P}\left(f_{hr}\right)\right|/⟨ABP⟩}{\left|\mathit{B}\mathit{F}\mathit{I}\left(f_{hr}\right)\right|/⟨BFI⟩}\right).\end{array}$$ (1)

Here $|\mathit{A}\mathit{B}\mathit{P}(f_{hr})|$ and $|\mathit{B}\mathit{F}\mathit{I}(f_{hr})|$ are power spectral amplitudes at the cardiac frequency $(f_{hr})$ of ABP and BFI within the $i^{th}$ 15s window (both sampled at the 20 Hz BFI time axis), and $⟨ABP⟩$ and $⟨BFI⟩$ are the temporal means over the window.

For both methods, CrCP, values < 0 mmHg were discarded. For the TD method, CrCP was only estimated from fits where a significant linear correlation between pressure and flow was observed (p < 0.05). Finally, because accurate ABP is needed for quantification of CrCP, ABP timeseries in which automatic recalibration of the CNAP device occurred at any point within the monitoring were excluded from CrCP analysis (n = 6).

2.5. Statistical analysis

Data are reported as median (interquartile range, IQR) unless otherwise stated to be mean (standard deviation, SD). To account for varied resting-state duration across subjects, time-weighted waveform feature averages were obtained using the twa() function from R package “SvenR” (version 4.1.2, R Foundation) [57]. All other statistical analyses were performed with MATLAB (MathWorks). Two-sided Wilcoxon rank-sum tests were used to assess sex-dependence of BFI waveform morphology at rest (room air inhalation) and during hypercapnia. Paired two-sided Wilcoxon signed-rank tests were used to compare BFI waveform morphology at rest vs. hypercapnia. Agreement between FD- and TD-CrCP was assessed by simple linear regression, Pearson’s correlation coefficient (R), and Lin’s concordance correlation coefficient (CCC). A Bland-Altman plot was used to visually assess agreement. For all analysis, significance was assessed at p < 0.05.

3. Results

Thirty-two healthy adults were recruited for this study. Of these, one subject was excluded due to early termination of monitoring, and one was excluded because < 5 window-averaged waveforms passed quality control criteria both at rest and in hypercapnia. Thus, 30 subjects were included in the final cohort. Subjects were mostly female (13 male/17 female) with a median age of 26 y, ranging from 23-37 y. No difference in age was observed between sexes (males: 26 (24, 29) vs. females: 26 (26, 29), p > 0.05).

3.1. BFI waveform morphology is sex-dependent

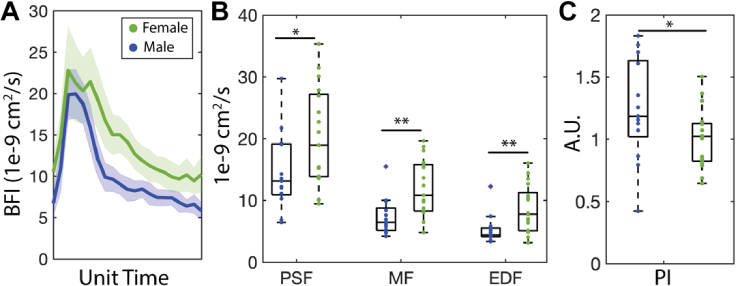
The median (IQR) resting-state values of each morphological feature of the BFI waveform stratified by sex are reported in Table 1; aggregated values can be found in Table 2. The sex-based morphological differences we observed in the BFI waveform are exemplified by the waveforms shown in Fig. 2(A). Females had significantly elevated EDF, MF, and PSF vs. males (p = 0.012, 0.036, and 0.004, Fig. 2(B)) as well as increased AUC (p = 0.009). Conversely, PI was significantly lower in females than males (p = 0.045, Fig. 2(C)).

Table 1. Blood flow waveform morphology by sex. Data are reported as median (interquartile range) over the 13 male and 17 female subjects at rest. Bold p-values denote significance assessed at the 0.05 level with a two-sided Wilcoxon rank sum test. (Abbreviations: EDF = end diastolic flow, MF = mean flow, PSF = peak systolic flow, AMP = pulse amplitude, AUC = pulse area under the curve, PI = pulsatility index, RI = resistivity index).

Parameter	Males (n = 13)	Females (n = 17)	p-value
EDF (1e-9 cm2/s)	4.41 (4.13, 5.51)	7.78 (5.11, 11.26)	0 . 012
MF (1e-9 cm2/s)	6.46 (5.16, 8.77)	10.82 (8.27, 15.78)	0.004
PSF (1e-9 cm2/s)	13.14 (10.91, 19.13)	18.96 (13.86, 27.17)	0.036
AMP (1e-9 cm2/s)	8.69 (6.11, 12.44)	10.06 (8.47, 14.45)	0.241
AUC (1e-9 cm2/s)	2.13 (1.59, 3.30)	3.63 (3.27, 4.72)	0.009
PI (unitless)	1.19 (1.02, 1.63)	1.02 (0.82, 1.13)	0.045
RI (unitless)	0.61 (0.57, 0.71)	0.57 (0.51, 0.63)	0.586

Table 2. Normative BFI waveform morphology at rest and during hypercapnia. Median (interquartile range) values for morphological features of the BFI waveform at rest (room air inhalation) and during hypercapnia, along with the percent change in each parameter from rest to hypercapnia. Bold p-values denote significance assessed at the 0.05 level with a two-sided Wilcoxon signed-rank test between rest and hypercapnic values. (Abbreviations: EDF = end diastolic flow, MF = mean flow, PSF = peak systolic flow, AMP = pulse amplitude, AUC = pulse area under the curve, PI = pulsatility index, RI = resistivity index).

	Comparison between resting and hypercapnia (n = 30)
Parameter	Resting state	Hypercapnia	p-value	% Change
EDF (1e-9 cm2/s)	5.61 (4.40, 10.13)	7.79 (6.03, 12.36)	< 0.001	29.61 (16.37, 57.84)
MF (1e-9 cm2/s)	8.57 (6.45, 13.67)	12.45 (8.01, 18.00)	< 0.001	31.01 (18.64, 53.32)
PSF (1e-9 cm2/s)	14.73 (12.18, 22.72)	19.51 (15.06, 29.12)	< 0.001	24.29 (9.75, 40.77)
AMP (1e-9 cm2/s)	9.44 (7.80, 14.12)	10.91 (8.98, 15.24)	0.001	18.25 (3.31, 33.76)
AUC (1e-9 cm2/s)	3.44 (2.08, 4.12)	4.30 (2.81, 5.89)	< 0.001	31.84 (14.22, 47.71)
PI (unitless)	1.07 (0.83, 1.31)	0.87 (0.78, 1.32)	0.014	-9.08 (-23.96, 3.02)
RI (unitless)	0.59 (0.51, 0.66)	0.54 (0.49, 0.67)	0.054	-4.53 (-16.71, 3.91)

Fig. 2.

Sex-dependence of blood flow waveform morphology (A) Example BFI waveforms from representative male and female subjects. (B) Females (n = 17) had significantly elevated peak systolic flow (PSF, p = 0.036), mean flow (MF, p = 0.004), and end diastolic flow (EDF, p = 0.012) vs. males (n = 13). (B) Pulsatility index (PI) was significantly elevated in males (p = 0.045). For each boxplot, the central line denotes the median and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers. Individual data points are shown in blue for males and green for females. Significance was assessed at the 0.05 level using a Wilcoxon rank-sum test.

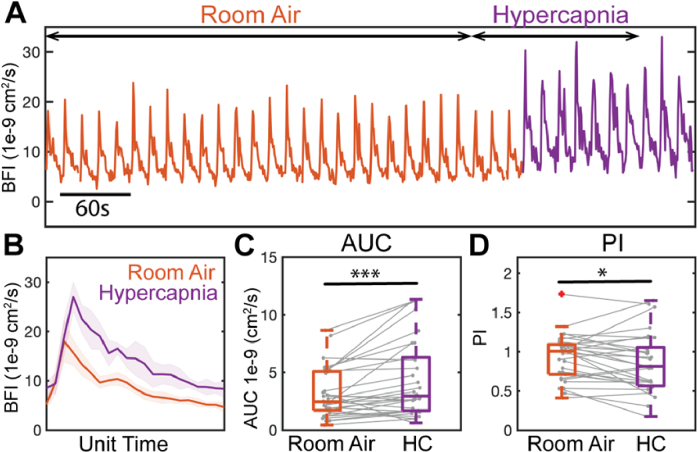
3.2. BFI waveform morphology changes with hypercapnia

Median (IQR) hypercapnic values for each morphological feature of the BFI waveform as well as the % change from rest are reported in Table 2. As can be seen in the representative data in Fig. 3(A)-(B), the shape of the BFI waveform changed markedly during hypercapnia. Waveforms became more rounded, AUC increased by a median of 32% (p = 0.009, Fig. 3(C)), and PI decreased by a median of 9% (p = 0.014, Fig. 3(D)). EDF, MF, PSF, and AMP all increased significantly (p ≤ 0.001, Table 2). ABP waveform morphology was also altered with hypercapnia, though to a lesser extent. EDP, PSP, and MAP all increased by approximately 5% (p < 0.001, Appendix 2).

Fig. 3.

Waveform response to hypercapnia in a representative subject and at the cohort-level (n = 30). (A) Representative window-averaged waveforms as a function of time during room air inhalation (orange) and hypercapnia (purple). Scale bar denotes 60 s of window-averaged data, i.e., 4 window-averaged pulses. (B) Average waveform across each state. Shaded region denotes standard deviation. (C) Area under the curve (AUC) increased significantly during hypercapnia (p = 0.009) while (D) pulsatility index (PI) decreased (p = 0.014). For each boxplot, gray lines represent individual subject trends. Significance was assessed at the 0.05 level using a Wilcoxon signed-rank test.

The sex-based differences in BFI waveform morphology observed during room air inhalation persisted during hypercapnia (Appendix 3, Table 6). MF (p = 0.002), PSF (p = 0.006), EDF (p = 0.004), and AUC (p = 0.007) all remained significantly elevated in females vs. males during hypercapnia. PI continued to trend higher in males vs. females (1.12 vs. 0.83), although the difference was no longer statistically significant (p = 0.19). AMP continued to trend higher in females (12.97 vs. 8.98e-9 cm²/s), with the difference now rising to the level of significance (p = 0.026).

3.4. Critical closing pressure

Median resting-state CrCP was 43 and 46 mmHg for the frequency- and time-domain methods, respectively (IQR TD: (28, 58) vs. FD: (35, 60) mmHg, Table 3). No significant change in CrCP was observed during hypercapnia with either method (p > 0.05). Values were trending higher in males by ∼15-25 mmHg at rest and during hypercapnia (Appendix 4, Table 7).

Table 3. Critical closing pressure (CrCP) estimated with frequency domain (FD) and time domain (TD) methods in 24 subjects. Results shown at rest and during hypercapnia as well as percent change from rest to hypercapnia. Data are reported as median (interquartile range). p-values were obtained from a Wilcoxon rank-sum test.

	Comparison between resting state and hypercapnia (n = 24)
Method	Resting state	Hypercapnia	p-value	% Change
FD-CrCP	43 (28, 58)	43 (27, 54)	0.63	1 (-17, 14)
TD-CrCP	46 (35, 60)	45 (29, 56)	0.51	1 (-13, 9)

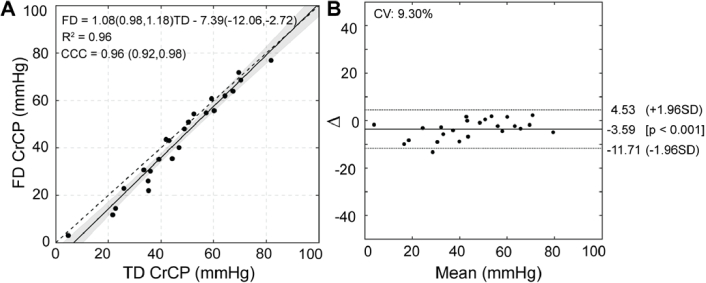
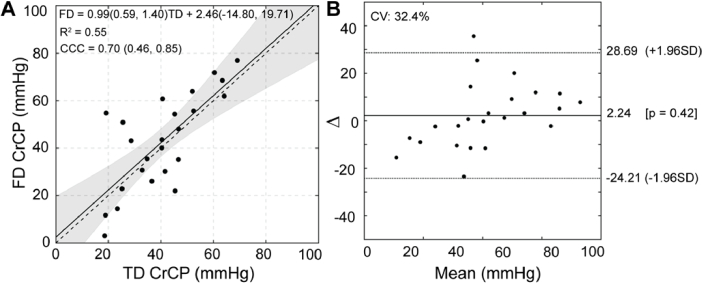
A simple linear model was used to investigate the correlation between the FD- and TD-CrCP calculation methods (Fig. 4(A)). The slope of the line of best fit was 1.08 with a 95% CI that encompasses the line of unity (95% CI: 0.98, 1.18). Strong agreement was observed between the methods, with Lin’s concordance correlation coefficient CCC = 0.96 (95% CI: 0.92, 0.98) and R² = 0.96 (p < 0.001). Bland Altman analysis revealed a median difference between estimates of -3.6 mmHg and coefficient of variation of 9.3% (Fig. 4(B)).

Fig. 4.

Relationship between frequency and time-domain estimates of critical closing pressure (CrCP) in 24 subjects. (A) A significant linear relationship between time domain (TD) vs. frequency domain (FD) CrCP (R²= 0.96, p < 0.001). Solid black line represents the model fit with 95% confidence intervals shaded. Dashed black line is the line of unity. Model slope and intercept coefficients are given with 95% confidence bounds. R² = coefficient of determination, CCC = Lin’s concordance correlation coefficient (95% CI). (B) Bland-Altman plot of the TD/FD CrCP agreement. Solid line represents mean difference, dotted lines show limits of agreement given as 1.96 $\times$ standard deviation (SD). CV = coefficient of variation = SD/mean.

TD-CrCP was also calculated using only the end diastolic runoff portion of the pulse (Appendix 5, Fig. 6). A significant linear relationship with FD-CrCP was still observed (slope = 0.99 (95% CI: 0.59, 1.40), p < 0.001), however, the agreement was reduced, as seen by lower values for R² = 0.55 and CCC = 0.70 (95% CI: 0.46, 0.85)

4. Discussion

In this study, we used diffuse correlation spectroscopy (DCS) to measure cardiac pulsatility in the microvascular cerebral blood flow index (BFI) of 30 healthy adults. We found that BFI waveform morphology exhibits significant sex-dependence, and it is sensitive to alterations in vasomotor tone induced via a hypercapnia challenge. Our results pave the way for further investigations into the use of BFI waveform morphology as a biomarker of cerebrovascular health.

Typical BFI waveform morphology in healthy young adults at rest

To the best of our knowledge, this work is the first to report normative values for morphological features of BFI waveforms in an appreciably sized cohort of healthy adults. Qualitatively, our values for MF, EDF, PSF, and AMP are in agreement with the handful of previous examples of healthy BFI waveforms from existing literature [36,42,58]. The unitless metrics of pulsatility and resistivity index (PI/RI), as well as CrCP (mmHg), can be directly compared with more established TCD benchmarks. Relative to TCD, our median PI and RI of 1.07 and 0.59 are higher than typical values of ∼0.85 and ∼0.55, respectively, seen in healthy young adults [24,25,59]. In TCD, PI and RI are broadly considered metrics of resistance to flow that originates from vasculature tone and intracranial pressure distal to the site of insonation [60–62]. Elevated DCS-derived RI and PI relative to TCD could potentially be due to microvascular structures that present high resistance to forward flow, such as precapillary sphincters [63,64]. Alternatively, local tissue pressure might have a larger influence on smaller vessels due to their high degree of collapsibility compared to large arteries, which are encased in vasoactive smooth muscle. Regardless of reason, the differences in DCS vs. TCD pulsatility metrics suggest that DCS may provide insight into intracranial dynamics that is unique from information accessible with TCD.

Influence of sex on BFI waveform morphology

At rest, we observed significant differences in waveform morphology between males and females. Females had significantly higher EDF (p = 0.012), MF (p = 0.004), PSF (p = 0.036) and AUC (p = 0.009) than males, while males had higher PI (p = 0.045). Sex-dependence of BFI waveform morphology was observed in the absence of ABP differences, suggesting a cerebrovascular rather than systemic origin. Previous PET and MRI studies have similarly reported higher steady-state microvascular perfusion in the prefrontal cortex of females vs. males, further corroborating the idea that DCS is sensitive to physiological sex-based differences in microvascular hemodynamics [46–48]. On the macrovascular level, TCD studies have likewise observed elevated mean, peak, and diastolic cerebral blood flow velocity in females vs. males [27,24]. Importantly, while our sex-based differences agree qualitatively with those derived from other modalities, the magnitude of the differences we saw are 4-5x higher than what is typically observed. For example, we observed ∼70% higher MF in females than males, versus the ∼15% elevation commonly observed in literature with other perfusion modalities [46–48]. One explanation for this exaggerated sex difference could be the confounding influence of hematocrit. Hematocrit is lower in females [65], which would lead to an overestimation of BFI if not accounted for [66]. This result highlights the need to measure hematocrit and to correct for its influence when assessing pulsatile BFI waveform morphology. It is also possible that sex-based anatomical differences (e.g., skull/scalp thickness, head curvature) could contribute to the exaggerated sex differences in BFI. This explanation is less likely, as females have been shown to have increased skull thickness [67,68] and reduced head circumference [69], both of which would likely lead to underestimations in BFI.

We also observed significant sex-based differences in CrCP with the time domain method, and the differences were trending with the frequency domain method. In contrast, a recent TCD study of older healthy adults (n = 194, 104 males), no sex based differences were observed [70]. Notably, the cohort in this study averaged ∼25y older than in the present study.

We note that age is likely to be important when considering sex-based effects. In general, TCD-measured sex differences in waveform morphology are most pronounced between ages 20-40 y, corresponding to the primary reproductive years of life [71]. If the same is true on the microvascular level, our cohort (ages 23-37 y) may represent the peak differentiation in microvascular waveform morphology between sexes.

Given the limited age range of our cohort (14 y range), we did not investigate the influence of age in this work. As risk of neurovascular injuries such as stroke increases with age and has a pronounced interaction with sex [72–74], expected age-related changes in BFI waveform morphology still remain to be characterized to develop the clinical utility of DCS for monitoring microvascular health.

Sensitivity of BFI waveforms to changes in vascular tone

Hypercapnia refers to a state of elevated concentration of CO2 in the blood. The cerebrovascular system compensates to this increase with a reduction in vascular tone, leading to an increase in cerebral blood flow and blood volume [7,75–77]. Accordingly, we observed significant changes in BFI waveform morphology during hypercapnia, with PSF increasing by 24% (p < 0.001), MF by 31% (p < 0.001), EDF by 30% (p < 0.001), AMP by 18% (p = 0.001), and AUC by 32% (p < 0.001). PI decreased significantly by 9% (p = 0.014). Overall, these pronounced changes in the BFI waveform with hypercapnia lend support to the idea that BFI waveform morphology is sensitive to changes in vascular tone.

Critical closing pressure

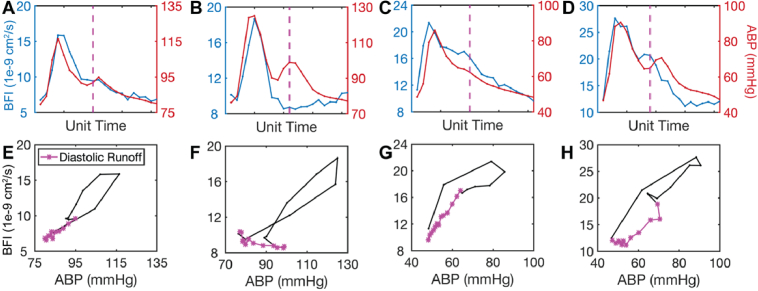
CrCP is a combined index of vascular tone and ICP [1]. As the applicability of DCS as a noninvasive CrCP monitor continues to be explored, researchers will have to choose from a plethora of proposed models for CrCP estimation. In this work, we employed time domain (TD) and frequency domain (FD) calculation methods, which have been widely used with TCD [17–23] and preliminarily applied to DCS [38–45]. We observed strong agreement between FD and TD methods (R²= 0.96, CCC = 0.96), as has been reported in other recent work [42,43]. Interestingly, agreement was strongest when the entire pulse was used for the TD approach, which is in contrast to findings from TCD that see stronger agreement when using the diastolic runoff portion only [78]. Isolating diastole for CrCP calculation is a relatively common practice in TCD based on the observation of a nonlinear “hysteresis loop” during systole followed by improved linearity in the diastolic runoff. We observed a high degree of variability in the shape of the pressure/flow relationship within and between subjects, with a substantial fraction not exhibiting the “classic” hysteresis loop seen in TCD (Appendix 5, (Fig. 7). Our results further highlight the differences between micro and macrovasculature pulsatility and emphasize the need for further exploration into the nuances of the pressure/flow relationship at the microvascular level.

Generally, TCD-measured CrCP ranges between 20-40 mmHg in healthy adults [79–81], which is lower than our DCS-derived values (median of 44 mmHg with both TD and FD methods). One possible explanation for the differences between TCD and DCS-measured CrCP is that ABP measured peripherally may not represent the true inlet pressure of the cerebral microcirculation [38]. To mitigate this possible source of error, Baker et al. applied a proportionality coefficient of $\gamma =0.6$ to their ABP waveform, chosen based on previous studies in rodent models [82]. As direct comparison with TCD was not a primary goal of this work, we did not apply a scaling factor.

Influence of respiration

Features of the arterial blood pressure waveform at the cardiac frequency are well-documented to change with respiration [83–85]. These changes in driving pressure would be expected to translate to changes in flow. We could not systematically quantify changes in BFI pulsatile morphology with respiration because breathing rate was not controlled in the current study. Anecdoctally, changes in BFI waveform morphology at the cardiac frequency could be observed over the respiratory cycle in many subjects. One subject exhibited markedly rhythmic breathing, and we used that dataset to quantify the effects of respiration on BFI morphological features at the cardiac frequency (Appendix 6). Peak, mean, pulse amplitude, and area under the curve of the BFI waveform increased gradually with inhalation and decreased during exhalation. In practice, the 15 s window-averaging pipeline we employ to enhance SNR averages over any respiratory changes in BFI waveform morphology at the cardiac frequency, which increases the standard deviation in the average waveform we measure. A paced-breathing approach could be used in future studies to control for the influence of respiration.

Sex-based differences in optical properties

To prevent variability in optical properties from confounding BFI comparisons between subjects, we used FDNIRS at the start of each measurement to capture reduced scattering and absorption coefficients, ${\mu }_s^{\mathrm{\prime }}$ and ${\mu }_a$ , respectively. While not a primary objective of this study, this effort led to the incidental finding of sex-dependent trends in optical properties. A significant difference in ${\mu }_a$ was observed in males vs. females (0.15 (0.02) vs. 0.14 (0.02) cm^-1, p = 0.02, Appendix 1). Sex differences in ${\mu }_s^{\mathrm{\prime }}$ were not observed (p > 0.05).

Limitations and Future Directions

Although subject-specific optical properties measured during baseline were incorporated into estimates of BFI, we did not account for changes in optical properties over the cardiac cycle or during hypercapnia. While we do not anticipate these changes to significantly alter the overall trends observed in this work, future work could benefit from incorporating continuous FDNIRS-measured optical properties into BFI estimation. Further, we note that the optical properties were not physically measured at 852 nm. Instead, they were interpolated based on measurements from 8 wavelengths ranging from 690-830 nm and are thus subject to potential error inherent to that process. Lastly, we did not account for extracerebral influence on the BFI waveform. To maximize the brain sensitivity of our DCS measurements, we used a threshold of $g(\tau )>1.2$ when fitting the data [53]. However, extracerebral contributions still likely impact BFI waveform morphology and contribute to inter-subject variability [86]. To mitigate these effects, future work will leverage exciting new hardware and analytical approaches that aim to mitigate this influence [87].

5. Conclusion

We report normative values of microvascular pulsatile cerebral blood flow waveforms measured with DCS. Morphology is sex dependent and sensitive to perturbations in vessel tone. These findings can provide a reference for future investigations into pulsatile CBF as a biomarker of vascular health.

Appendix

Appendix 1: Sex-dependence of optical properties measured with FDNIRS

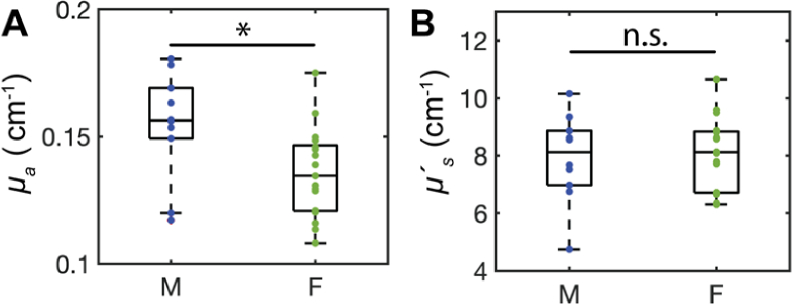
Aggregated and sex-specific mean (standard deviation) reduced scattering ( ${\mu }_s^{\mathrm{\prime }})$ and absorption ( ${\mu }_a$ ) coefficients measured with FDNIRS in 26 healthy adults (10 male) are recorded in Table 4. Mean optical properties across all subjects were ${\mu }_s^{\mathrm{\prime }}=$ 8.03 (1.34) cm^-1 and ${\mu }_a=$ 0.14 (0.021) cm^-1. The effect of sex on optical properties was assessed with a Wilcoxon rank-sum test. ${\mu }_a$ was seen to be significantly higher in males vs. females (0.15 (0.02) vs. 0.14 (0.02) cm^-1, p = 0.02, Fig. 5(A), Table 4). ${\mu }_s^{\mathrm{\prime }}$ did not exhibit significant sex-dependence (p > 0.05, Fig. 5(B), Table 4).

Fig. 5.

Sex-based differences in optical properties measured in 10 males and 16 females. (A) Absorption coefficient (µ_a) at 852 nm is significantly higher in males vs. females (p = 0.022). (B) Scattering coefficient (µ’_s) at 852 nm is not sex-dependent (p = 0.9).

Table 4. Optical properties stratified by sex. Mean (standard deviation) absorption (µ_a) and scattering (µ'_s) coefficients at 852 nm quantified with FDNIRS dichotomized by sex (left columns) and averaged over the entire cohort (right column). Males had significantly elevated µ_a vs. females (p = 0.022). No difference in µ'_s was observed between sexes (p = 0.9). Significance was assessed at the 0.05 level using a Wilcoxon rank-sum test.

	Males (n = 10)	Females (n = 16)	P-value	Aggregated
µa (cm-1)	0.154 (0.021)	0.136 (0.018)	0.022	0.143 (0.021)
µ's (cm-1)	7.920 (1.541)	8.070 (1.284)	0.900	8.033 (1.338)

Appendix 2: ABP waveform morphology at rest and during hypercapnia

In subjects where continuous ABP recordings free from recalibration artifacts were available (n = 24), pressure pulse morphology was quantified (Table 5). EDP, MP, and PSP, were observed to increase ∼5% during hypercapnia (p < 0.001), while AMP_p increased < 3% (p > 0.05). Heart rate (HR) was quantified across the entire cohort (n = 30) and was seen to increase significantly by ∼4% (p = 0.003).

Table 5. ABP waveform features at rest and during hypercapnia. Only datasets in which recalibration did not occur over the course of monitoring (n = 24) were used to compute end diastolic pressure (EDP), mean arterial pressure (MAP), peak systolic pressure (PSP), and amplitude (AMP). Heart rate was quantified over all subjects (n = 30). Data are reported as median (interquartile range). Significance was assessed with a cutoff of 0.05 using a two-tailed Wilcoxon signed-rank test.

	Comparison between resting and hypercapnia
Parameter	Resting state	Hypercapnia	p-value	% Change
EDP (mmHg)	69 (56, 79)	73 (58, 83)	< 0.001	4.5 (1.8, 9.2)
MAP (mmHg)	81 (66, 90)	87 (69, 96)	< 0.001	6.4 (2.9, 10.3)
PSP (mmHg)	115 (94, 122)	122 (97, 128)	< 0.001	3.4 (0.3, 8.5)
AMPp (mmHg)	41 (32, 48)	44 (32, 53)	0.20	2.6 (-2.4, 9.3)
HR (bpm)	73 (66, 81)	76 (68, 82)	0.003	4.39 (-0.21, 8.71)

Appendix 3: BFI waveform morphology during hypercapnia, stratified by sex

Table 6. Blood flow waveform features during hypercapnia by sex. Data are reported as median (interquartile range) 13 male and 17 female subjects at rest. Bold p-values denote significance assessed at the 0.05 level with a two-sided Wilcoxon rank sum test. ((Abbreviations: EDF = End diastolic flow, MF = mean flow, PSF = peak systolic flow, AMP = pulse amplitude, AUC = pulse area under the curve, PI = pulsatility index, RI = resistivity index)).

Parameter	Males (n = 13)	Females (n = 17)	p-value
EDF (1e-9 cm2/s)	6.07 (4.51, 7.61)	10.95 (7.38, 15.55)	0 . 004
MF (1e-9 cm2/s)	8 (6.77, 12.95)	16.2 (10.68, 21.43)	0.002
PSF (1e-9 cm2/s)	15.36 (13.07, 20.57)	25.21 (18.81, 32.95)	0.006
AMP (1e-9 cm2/s)	8.98 (7.8, 11.94)	12.97 (10.15, 18.92)	0.026
AUC (1e-9 cm2/s)	2.92 (2.11, 3.91)	4.81 (4.16, 6.66)	0.007
PI (unitless)	1.12 (0.79, 1.43)	0.83 (0.73, 1.06)	0.197
RI (unitless)	0.58 (0.48, 0.68)	0.51 (0.47, 0.65)	0.586

Appendix 4: CrCP at rest and in hypercapnia, stratified by sex

Table 7. TD- and FD-CrCP in males (n = 13) vs. females (n = 17) at rest and in hypercapnia. Values given as median (interquartile range) in mmHg. Significance was assessed with a cutoff of 0.05 using a Wilcoxon rank sum test.

	Resting state			Hypercapnia
Method	Males	Females	P value	Males	Females	P value
FD	54 (39, 61)	30 (22, 43)	0.06	49 (40, 58)	29 (20, 44)	0.07
TD	53 (46, 61)	36 (28, 43)	0.05	53 (45, 63)	32 (25, 43)	0.06

Appendix 5: Agreement between TD- and FD-CrCP using diastolic runoff fitting

Fig. 6.

Agreement of critical closing pressure (CrCP) between time-domain (TD) and frequency-domain (FD) methods (n = 24). (A) TD-CrCP calculated from only the diastolic runoff vs. FD-CrCP. Solid line represents the model fit; 95% confidence intervals shaded, dashed line is the line of unity. (B) Bland-Altman plot of the TD/FD CrCP agreement. Solid line represents mean difference, dotted lines show limits of agreement given as 1.96 $\times$ standard deviation (SD).

Fig. 7.

Sample pressure/flow relationships. (A-D) Window-averaged arterial blood pressure (ABP, red) and blood flow index (BFI, blue) pulses from four different subjects. Dotted vertical line represents the timepoint identified as the start of diastolic runoff. (E-H) ABP versus BFI for the corresponding pulses from A-D. The diastolic runoff is shown in purple.

Appendix 6: BFI waveform morphology changes over the respiratory cycle

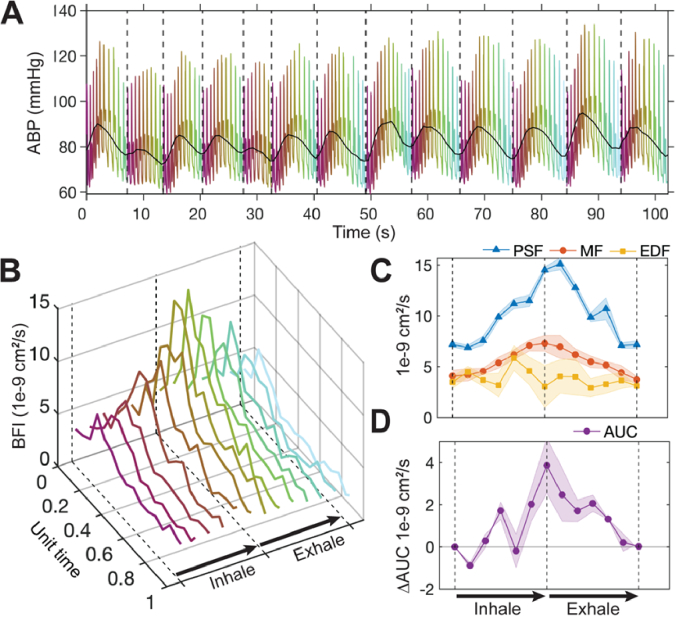
An investigation of the effects of respiration on BFI waveform morphology at the cardiac requency was performed for one subject who had markedly rhythmic breathing accompanied by strong oscillations in blood pressure. To quantify BFI waveform changes with respiration, a period of 13 breaths was included for analysis. First, the time shift between ABP and BFI was determined via cross correlation. BFI pulses were defined based on the bounds of the time-shifted ABP pulses [55]. The bounds of each breath were delineated by minima in the MAP trace (Fig. 8(A)) [85]. BFI pulses were extracted based on their position in the respiratory cycle and then length normalized, binned into 20 evenly spaced bins, and averaged as in Sec. 2.4.3. The first waveforms at the start of each inhalation were averaged, the second waveforms within each breath cycle were averaged, etc. The final sequence of average BFI pulses thus represented the average pulse morphology change during respiration (Fig. 8(B)).

Fig. 8.

Changes in BFI pulse waveform morphology with respiration. (A) Arterial blood pressure (ABP) versus time. Mean arterial pressure (MAP) is shown in black. Dotted vertical lines denote the onset of each of the 13 breaths included for analysis, identified as MAP minima. Cardiac pulses are colored based on their position in each respiratory cycle. (B) Average blood flow index (BFI) pulses over the respiratory cycle, colors correspond to position in the respiratory cycle in A. (C) Average changes in peak systolic, mean, and end diastolic flow (PSF, MF, and EDF, respectively) over the respiratory cycle. (D) Change in area under the curve (AUC) relative to the start of inhalation. Shading in B-C represents standard error. Dotted lines in B-D represent the beginning, peak, and end of the respiratory cycle, labeled accordingly in B and D. Video representation of this data available in Visualization 1 ^{(260.2KB, mp4)} .

During inhalation, BFI waveforms broadened and the PSF was right-shifted in time (Visualization 1 ^{(260.2KB, mp4)} ). These alterations gradually reversed on exhalation. Quantitatively speaking, PSF and MF increased during inspiration and decreased during exhalation, while EDF remained relatively stable throughout the respiratory cycle (Fig. 8(C)). AUC was elevated ∼3x at peak inhalation vs. end exhalation (Fig. 8(D)). Notably, our observation of varied response to respiration across waveform features suggests that respiratory effects could not be removed from the pulsatile BFI signal with high pass filtering. Although filtering would reduce oscillations in mean BFI, morphological changes in the cardiac waveform would remain. Instead, a paced breathing approach could be used in future studies to rigorously characterize the relationship between BFI waveform morphology and respiration.

Funding

National Science Foundation10.13039/100000001 (DGE-1650044); National Heart, Lung, and Blood Institute10.13039/100000050 (5R01HL152322-03); National Institute of Neurological Disorders and Stroke10.13039/100000065 (1R01NS130036-01).

Disclosures

The authors declare that there are no conflicts of interest in this article.

Data availability

Waveform analysis code used in this paper can be found on the Buckley Lab Github page [88]. Data underlying the results may be obtained from the authors upon reasonable request.