Likelihood-Based Tests of Species Tree Hypotheses

Abstract

Likelihood-based tests of phylogenetic trees are a foundation of modern systematics. Over the past decade, an enormous wealth and diversity of model-based approaches have been developed for phylogenetic inference of both gene trees and species trees. However, while many techniques exist for conducting formal likelihood-based tests of gene trees, such frameworks are comparatively underdeveloped and underutilized for testing species tree hypotheses. To date, widely used tests of tree topology are designed to assess the fit of classical models of molecular sequence data and individual gene trees and thus are not readily applicable to the problem of species tree inference. To address this issue, we derive several analogous likelihood-based approaches for testing topologies using modern species tree models and heuristic algorithms that use gene tree topologies as input for maximum likelihood estimation under the multispecies coalescent. For the purpose of comparing support for species trees, these tests leverage the statistical procedures of their original gene tree-based counterparts that have an extended history for testing phylogenetic hypotheses at a single locus. We discuss and demonstrate a number of applications, limitations, and important considerations of these tests using simulated and empirical phylogenomic data sets that include both bifurcating topologies and reticulate network models of species relationships. Finally, we introduce the open-source R package SpeciesTopoTestR (SpeciesTopology Tests in R) that includes a suite of functions for conducting formal likelihood-based tests of species topologies given a set of input gene tree topologies.

Introduction

Hypothesis testing is a fundamental concept of statistical inference that has been a cornerstone of contemporary systematics and evolutionary research in general for much of the past century (Pearson 1896; Felsenstein 1985; Brandon 1994; Ayala 2009; Kumar et al. 2012). Phylogenetic trees represent explicit hypotheses concerning the degree of evolutionary relatedness among organisms, and decades of research have produced many hypothesis-testing frameworks for evaluating features of phylogenies. Examples of these phylogenetic characteristics include topology (Goldman et al. 2000), specific branches (e.g., Lewis et al. 2005; Anisimova and Gascuel 2006), species delimitations (e.g., Carstens and Dewey 2010; Fujita et al. 2012), and phylogenetic congruency (e.g., Huelsenbeck and Bull 1996; Leigh et al. 2008). Testing phylogenetic hypotheses is therefore an essential component of evolutionary analysis that can be useful for many applications, such as assessing statistical confidence (e.g., Efron et al. 1996; Holmes 2005; Shi et al. 2005), performing model selection (e.g., Huelsenbeck and Crandall 1997; Posada and Crandall 2001; Sullivan and Joyce 2005), understanding model fit and adequacy (e.g., Goldman 1993; Ripplinger and Sullivan 2010), and illuminating model misspecification and tree reconstruction bias (e.g., Buckley 2002; Naser-Khdour et al. 2019; Jiang et al. 2020).

Given such widespread adoption of phylogenetic hypothesis-testing frameworks, it is somewhat surprising that they have been comparatively underdeveloped and underutilized for species tree inference (Liu et al. 2019). In practice, it is quite common for studies to simply measure node support (e.g., bootstrap or posterior probabilities) without any formal statistical evaluation of hypotheses in a more rigorous testing framework. Bayesian methods provide a natural assessment of statistical support by obtaining posterior probabilities of tree topologies, as well as Bayes factor support for hypotheses (e.g., *BEAST, *BEAST2, SNAPP, BPP, and BEST; Rannala and Yang 2003; Liu 2008; Heled and Drummond 2009; Bryant et al. 2012; Ogilvie et al. 2017). However, many Bayesian approaches tend to scale poorly with the size of modern phylogenomic data sets (Rannala and Yang 2003; but see recent improvements in Rannala and Yang 2017), such that genome-scale inference is typically conducted using more computationally efficient heuristic methods (e.g., STEM, MP-EST, STELLS, and ASTRAL; Kubatko et al. 2009; Liu et al. 2010; Wu 2012; Mirarab, Bayzid, et al. 2014; Mirarab, Reaz, et al. 2014). Importantly, many likelihood-based tests of phylogenetic hypotheses (i.e., Goldman et al. 2000) evaluate the fit of gene trees at individual loci and thus may best represent tests of genealogical relationships among alleles, rather than population or species relationships. Reconstructing evolutionary relationships among organisms is typically the primary objective of phylogenetic studies, and yet, the past few decades of research have amassed widespread evidence that gene trees and species trees are not necessarily the same (Nichols 2001; Degnan and Rosenberg 2009; Edwards et al. 2016). Incomplete lineage sorting (ILS) is a particularly notorious and pervasive source of conflict that can mislead even genome-scale analyses (Maddison 1997; Kubatko and Degnan 2007; Edwards 2009; Liu et al. 2015), which led to the development of coalescent-based species tree methods for modeling gene tree evolution as a function of species trees (e.g., Rannala and Yang 2003; Liu and Pearl 2007; Kubatko et al. 2009; Wu 2012; Edwards et al. 2016). The distinction between gene tree and species tree inference is critical because many classical phylogenetic methods explicitly assume gene tree homogeneity (i.e., all loci share a single tree; Felsenstein 1981) and may exhibit statistical biases in the presence of such conflict (Roch and Steel 2015). Long-established phylogenetic hypothesis-testing frameworks that apply these same principles (i.e., Goldman et al. 2000) may also be sensitive to gene tree heterogeneity.

Recently, Liu et al. (2019) highlighted the paucity of likelihood techniques for assessing and comparing support for species topologies under the multispecies coalescent (MSC) model and emphasized a need for research into approaches for testing species tree hypotheses. The authors also demonstrated one such version of a likelihood ratio test that uses gene tree estimates and a two-step species tree algorithm (MP-EST; Liu et al. 2010) that was applied to a data set of fairy wrens (Lee et al. 2012) to evaluate three alternative phylogenetic hypotheses (i.e., figure 5 in Liu et al. 2019); a similar test was used for assessing topological support of the mammalian tree of life (Du et al. 2019). Carstens and Knowles (2007) provided one of the first of only a few examples of formal testing of species topology hypotheses using a coalescent-based approach to species tree inference. They applied an efficient approximation to a likelihood ratio test (Anisimova and Gascuel 2006) to assess whether the maximum likelihood (ML) species topology given input gene trees was significantly better than all possible alternatives. Follow-up studies applied similar principles for testing species topologies given a set of gene trees (e.g., Hung et al. 2012), and some heuristics have been developed that use other statistics and characteristics of phylogenomic data in lieu of the likelihood ratio, such as quartet frequencies of input gene trees (e.g., Gaither and Kubatko 2016; Sayyari and Mirarab 2018) and splits based on nucleotide site pattern frequencies (e.g., Gaither and Kubatko 2016). A more common practice is to simply compare bootstrap support without conducting any formal hypothesis test. In addition to these approaches, a number of Bayesian methods have been implemented for testing phylogenetic hypotheses using Bayes factors (i.e., Xie et al. 2011; Oaks et al. 2019; Fourment et al. 2020), though these are less commonly applied to large-scale genomic data. Given these findings, a natural question is whether we can reformulate classical likelihood tests of phylogenies for the purpose of testing species tree hypotheses. That is, can we synergize MSC-based tree models with the hypothesis-testing frameworks that have been extensively applied for comparing support of gene topologies?

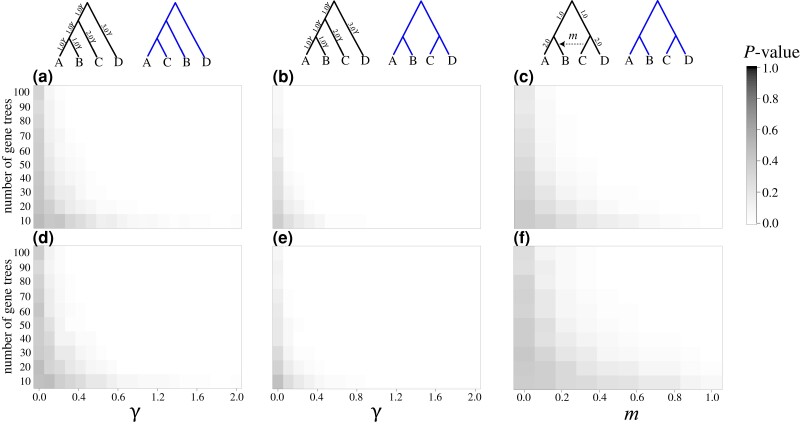
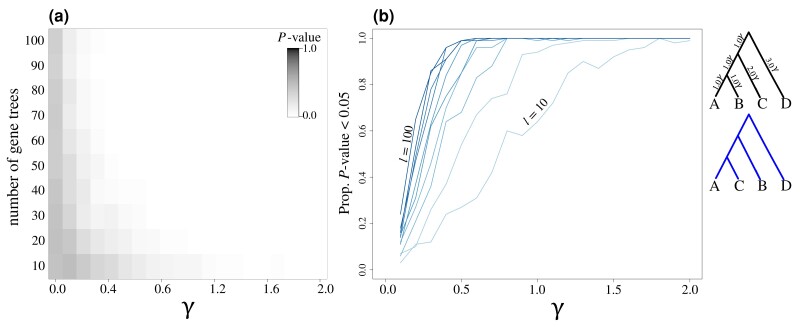
Fig. 5.

Demonstrating the KH* test across an array of simulation scenarios for evaluating bifurcating topologies (left and center panels) and a species network (right panels). Heatmaps depict the mean P value obtained across 100 replicate analyses for each combination of simulation conditions (darker to lighter colors represent higher to lower P values), and the two topologies that are tested are shown above each respective heatmap. The data set sizes (i.e., number of input gene trees l) are represented on the y-axes, whereas the x-axes depict the scaling of different evolutionary parameters used in the simulations. For each set of conditions, gene trees were simulated using the left, “true” (generating) species topology shown above each respective set of analyses, with the alternative topology shown to the right in blue, and either the divergence times scaled by multiplying branches by a scaling factor $\gamma \in [0.1,2]$ (all branches multiplied by the value of γ) for the left and center panels (a, b, d, and e) or by varying the migration fraction $m\in [0,1]$ for the network shown in the right panels (c and f). The top panels (a–c) were conducted using the true, simulated gene trees, while the results shown in the bottom panels (d–f) were analyzed using estimates of the gene trees.

Here, we propose several likelihood-based tests of species topologies that use a set of gene tree topologies as input by reformulating a number of classical phylogenetic hypothesis tests in light of the MSC. Specifically, we extend the Kishino–Hasegawa (KH; Hasegawa and Kishino 1989; Kishino and Hasegawa 1989), Shimodaira–Hasegawa (SH; Shimodaira and Hasegawa 1999), and Swofford–Olsen–Waddell–Hillis (SOWH; Hillis et al. 1996; Swofford et al. 1996) tests to evaluate bifurcating and reticulate species hypotheses. In addition, we introduce these species topology tests within the open-source R package SpeciesTopoTestR (SpeciesTopology Tests in R).

New Approaches

Background: Heuristic Species Tree Inference

Gene trees may disagree with the overall species tree relationships among a set of organisms for many reasons (Maddison 1997; Kubatko and Degnan 2007; Edwards 2009; Liu et al. 2015), and recent years have witnessed a wealth of new approaches for using multilocus data to infer species trees despite such conflict, including both Bayesian frameworks (e.g., *BEAST, *BEAST2, SNAPP, BPP, and BEST; Rannala and Yang 2003; Liu 2008; Heled and Drummond 2009; Bryant et al. 2012; Ogilvie et al. 2017) and heuristic methods (e.g., STEM, MP-EST, STELLS, and ASTRAL; Kubatko et al. 2009; Liu et al. 2010; Wu 2012; Mirarab, Bayzid, et al. 2014; Mirarab, Reaz, et al. 2014). Bayesian methods typically integrate over gene tree branch lengths, topologies, and other parameters when computing a posterior probability distribution over species trees using gene sequence data as input. This task typically requires substantial computational time and resources to integrate over the large parameter space that includes both gene (e.g., substitution models and gene tree topologies) and species tree (e.g., divergence times and species tree topologies) parameters conditional on input multilocus alignments.

To decrease computational burden and increase scalability, heuristic methods have been designed for larger-scale phylogenomic analyses by using estimated gene trees as input for reconstructing species trees under the MSC without computing posterior probabilities. Most likelihood-based heuristic methods use gene tree topologies as input for computing the likelihood of a species tree given a set of gene trees (e.g., MP-EST and STELLS). Similarly, some heuristic methods compute explicit MSC likelihoods (e.g., STELLS) or pseudo-likelihoods (MP-EST), while others use nonlikelihood criteria (e.g., ASTRAL). Bayesian methods provide a number of benefits (e.g., accounting for uncertainty in both gene and species tree inference), yet the need to integrate over many parameters reduces their efficiency, leading to a dominance of heuristic approaches for more computationally efficient analyses of genome-scale data.

To ensure that our species tree hypothesis tests scale with the size of multilocus data sets, we focus on the application of heuristic algorithms in this study. Debates over both the power and pitfalls of heuristic methods have persisted for decades now, and we do not attempt to solve these debates here; instead, we seek to understand whether these popular methods—though imperfect—can be leveraged for testing species topology hypotheses in a more computationally efficient manner, and we also evaluate their performances using estimated gene trees taken from gene sequence data. In particular, we apply the coalescent-based ML strategy implemented in STELLS2 (Pei and Wu 2017), which uses input gene tree topologies to optimize the species tree topology and coalescent branch lengths under the MSC model. For STELLS2, the likelihood of a species tree given a set of input gene tree topologies is computed under the MSC model, rather than directly from the sequence data. Additionally, we include the option to use the coalescent-based likelihood function provided in PhyloNet (Yu et al. 2013, 2014), which can also be used for evaluating bifurcating or network species topologies under the MSC model. Though we focus on these implementations, we note that other approaches may be implemented in a similar manner (and we discuss future implementations in the Discussion section).

Like similar heuristic strategies (e.g., ASTRAL and MP-EST), a key assumption of our new approaches is that input gene tree topologies are known with certainty. Of course, in practice, input gene tree topologies are typically estimated from sequence data using standard phylogenetic procedures, such as RAxML (Stamatakis 2014) or IQ-TREE (Nguyen et al. 2015), which adds a source of error that can influence downstream inference. Because poorly estimated gene trees can reduce species tree accuracy (Yang 2002; Burgess and Yang 2008; Xi et al. 2015; Xu and Yang 2016), we consider the performance of these tests using both the set of true (simulated) gene trees and the associated set of estimated gene trees inferred from molecular sequence data. As we will show, gene tree estimation error may reduce statistical power of our species tree hypothesis tests, but with only minimal impact on false positive rates. In the next subsection, we discuss the formulation of our species tree hypothesis tests in light of classical phylogenetic testing frameworks that have been historically used for single-gene tree inference.

Likelihood-Based Tests of Tree Topology Given Input Gene Tree Topologies

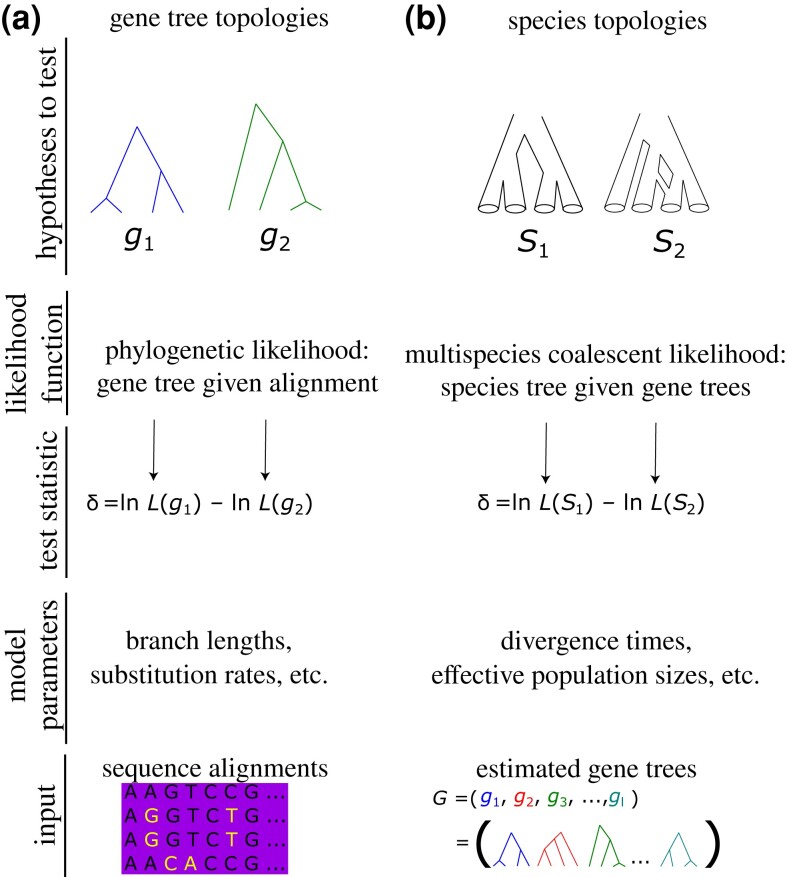
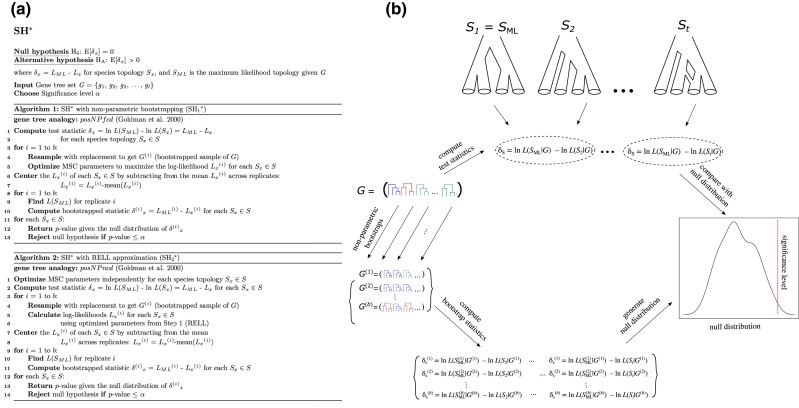
Phylogenetic trees present a number of unique challenges to statistical inference, and nearly three decades of systematic research have focused on the development of likelihood-based frameworks to account for these inherent peculiarities when conducting hypothesis tests (Huelsenbeck and Crandall 1997; Irisarri and Zardoya 2013). Goldman et al. (2000) provided an overview of popular likelihood-based tests of tree topology that were—and still are—widely used and relevant for comparing the fits of competing phylogenetic hypotheses. For continuity, we follow the terminology of Goldman et al. (2000) while introducing natural extensions of these principles for comparing species topologies. Importantly, Goldman et al. (2000) discussed several implementations and limitations of the popular KH (Hasegawa and Kishino 1989; Kishino and Hasegawa 1989) and SH (Shimodaira and Hasegawa 1999) tests and also described a third test (SOWH) that applies parametric bootstrapping. Given a sequence alignment, these tests perform an array of statistical procedures to generate null distributions that are used to evaluate differences in likelihoods measured between gene trees (fig. 1a). Our focus is to adapt these phylogenetic hypothesis-testing frameworks to the problem of species tree inference from input gene tree topologies (fig. 1b).

Fig. 1.

Comparing the components of classical likelihood-based tests of gene tree topologies (a) with the analogous tests of species topologies derived in this study (b). While topology is the primary focus of both tests (top row), a species tree hypothesis-testing framework (b) is concerned with the fit of species topologies (examples depicted by $S_1$ and $S_2$) to gene tree distributions (G shown in lower right) under the MSC model, rather than the fit of specific gene tree topologies (i.e., $g_1$ and $g_2$) to molecular sequence data (example alignment in lower left). The test statistics are computed by optimizing relevant model parameters according to either the standard phylogenetic likelihood function (a) or the MSC likelihood (b), respectively. Note that the example species topology $S_2$ represents a hybridization network.

Developing Analogous Tests of Species Topologies Given Input Gene Tree Topologies

To derive analogous tests of species topologies, we apply the MSC to compute species tree likelihoods given a set of input gene tree topologies (Rannala and Yang 2003). We therefore adopt the principles of two-step species tree methods (e.g., MP-EST, ASTRAL, and STELLS; Liu et al. 2010; Mirarab, Bayzid, et al. 2014; Mirarab, Reaz, et al. 2014; Pei and Wu 2017) commonly employed for phylogenomic inference to derive MSC-based topology tests that mirror the original tests (KH, SH, and SOWH) based on individual gene tree inference. Specifically, we test whether the MSC-based likelihoods of two or more species topologies differ significantly. As an analogy to Goldman et al. (2000) and the methods discussed within, we are primarily interested in testing the topologies of species trees, and we use ML to optimize the MSC parameters of topology hypotheses (e.g., using STELLS to optimize branch lengths conditional on a species topology) given input gene tree topologies, rather than Bayesian inference given multilocus sequence alignments (e.g., Rannala and Yang 2003; Liu 2008; Heled and Drummond 2009; Bryant et al. 2012; Ogilvie et al. 2017). That is, we test hypotheses about the overall species topology (similar to the original tests in Goldman et al. 2000), with branch lengths that are optimized to compare topologies at their peak MSC likelihoods.

Consider a set $G=\{g_1,g_2,\dots ,g_l\}$ of independent gene tree topologies computed on a phylogenomic data set, where $g_1$ is the gene tree topology estimated for the first locus, and so on, up to the lth locus for $g_l$. Each gene tree in G can be estimated using likelihood methods such as RAxML (Stamatakis 2014), IQ-TREE (Nguyen et al. 2015), or similar approaches. We wish to test hypotheses concerning the relationship among species that gave rise to G (fig. 1b). Borrowing from two-step species tree algorithms, we treat G as input data for estimating and testing species topologies (e.g., testing if the MSC likelihoods of two distinct topologies are statistically different given G). We can test such hypotheses using the log-likelihood ratio

$$\delta =\ln L(S_1)-\ln L(S_2),$$

where $\ln L(S_1)$ and $\ln L(S_2)$ indicate the respective log-transformed and maximized MSC-based likelihoods of species topologies $S_1$ and $S_2$ (fig. 1b), respectively. Maximizing the likelihoods of $S_1$ and $S_2$ can be accomplished by optimizing their coalescent branch lengths with an appropriate ML algorithm (e.g., STELLS or PhyloNet). Thus, we seek to test species tree hypotheses related to $\delta$, rather than individual gene tree hypotheses (i.e., fig. 1a and b), and can derive analogs to the KH, SH, and SOWH tests by replacing computations of classical phylogenetic likelihoods (i.e., sequence models) with the those of coalescent likelihoods relevant to $\delta$ (figs. 2–4).

Fig. 2.

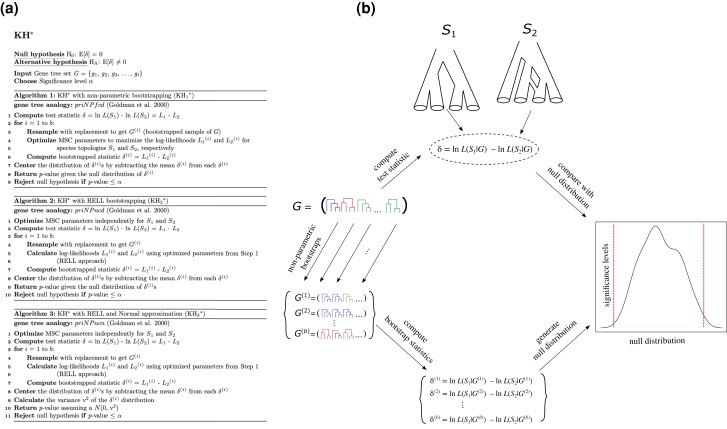
The KH* test for species tree hypotheses. Details for the three KH* algorithms (${\mathrm{KH}}_1^{*}$, ${\mathrm{KH}}_2^{*}$, and ${\mathrm{KH}}_3^{*}$) are provided in (a), and a general schematic overview of the KH* test is shown in (b). Briefly, the KH* test evaluates whether the difference in MSC likelihoods $\delta$ computed between two species topologies $S_1$ and $S_2$ (b, top) is a plausible draw from a null distribution obtained using nonparametric bootstrapping (b, right). Two example topologies are shown in (b): a classical bifurcating topology on the left ($S_1$) and a species network on the right ($S_2$). Nonparametric bootstrapping of the input gene tree set G is conducted to obtain b total replicate sets $G^{(1)}$, $G^{(2)}$, …, $G^{(b)}$ (b, left), which, in turn, yields a distribution of ${\delta }^{(1)}$, ${\delta }^{(2)}$, …, ${\delta }^{(b)}$ (b, bottom) under the null hypothesis. The primary difference between the three KH* algorithms is whether RELL bootstrapping is used (${\mathrm{KH}}_2^{*}$ and ${\mathrm{KH}}_3^{*}$) or not (${\mathrm{KH}}_1^{*}$), while ${\mathrm{KH}}_3^{*}$ also uses normal approximation to evaluate significance. See table 1 for a description of gene tree analog acronyms priNPfcd, priNPncd, and priNPncn.

Fig. 4.

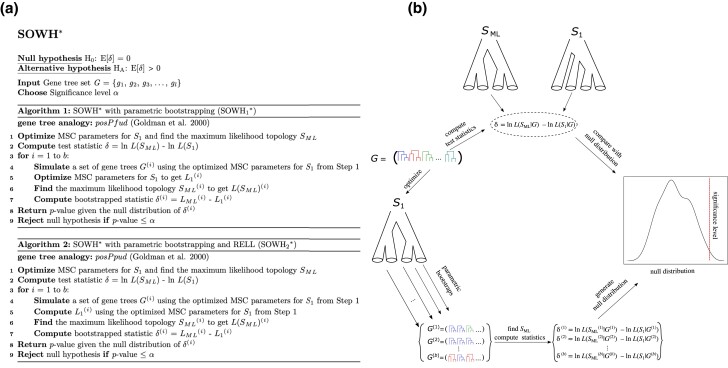
The SOWH* test for species tree hypotheses. Details for the two SOWH* algorithms (${\mathrm{SOWH}}_1^{*}$ and ${\mathrm{SOWH}}_2^{*}$) are provided in (a), and a general schematic overview of the SOWH* test is shown in panel (b). Briefly, the SOWH* test evaluates whether the difference in MSC likelihoods $\delta$ computed between a hypothesized target species topology ($S_1$; b, top) and the ML estimate ($S_{\mathrm{ML}}$; b, top) is a plausible draw from a null distribution obtained using parametric bootstrapping (b, right). Parametric bootstrapping is conducted using the optimized branch lengths of $S_1$ (b, left) to obtain b total replicates $G^{(1)}$, $G^{(2)}$, …, $G^{(b)}$ (b, bottom left) that are used to find a ML topology for each replicate which, in turn, yields a distribution of ${\delta }^{(1)}$, ${\delta }^{(2)}$, …, ${\delta }^{(b)}$ (b, bottom right) under the null hypothesis. Each round of parametric bootstrapping is followed by a search for a ML topology that is used to compare with the target topology $S_1$ at their optimized parameter values (branch lengths) to compute the values of ${\delta }^{(i)}$. As with KH* and SH*, the two SOWH* algorithms differ on whether RELL bootstrapping is used (${\mathrm{SOWH}}_2^{*}$) or not (${\mathrm{SOWH}}_1^{*}$) in the processes of generating the null distribution of ${\delta }_S$. See table 1 for a description of gene tree analog acronyms posPfud and posPpud.

Table 1.

Summary of Abbreviations Used to Describe the Gene Tree Analogs for the Species Topology Tests (inspired by table 1 of Goldman et al. 2000).

Tree Choice	Statistical Procedure	Optimization Algorithm	Test Statistic and Distribution	Test Statistic Comparison
pri: topologies selected a priori	NP: nonparametric bootstrap	f: all parameters are estimated (full)	c: centered distribution	d: test statistic is compared directly with its distribution
pos: topologies chosen from analysis of data (posteriori)	P: parametric	p: some parameters are fixed (partial) n: no optimization of any parameters	u: uncentered distribution	n: normal distribution assumed for statistic

As with two-step species tree algorithms (e.g., MP-EST, STELLS, and ASTRAL), these tests assume that input gene trees are known without error, which we expand upon in the Discussion section. For comparisons that include at least one network topology (e.g., one or both of $S_1$ and $S_2$ include at least one reticulating branch), we also include the option to use the coalescent-based likelihood function of PhyloNet (Yu et al. 2013, 2014). Importantly, though we focus on the STELLS or PhyloNet frameworks for computing species tree likelihoods, we note that other heuristic, likelihood-based functions could be applied in a similar manner. We refer to our new species tree hypothesis tests as the KH*, SH*, and SOWH* tests, which are each described in the three immediately following subsections.

The KH* Test

The KH test has been widely adopted for conducting likelihood tests of topology hypotheses for single genes by assessing fit of molecular sequence data to two distinct gene topologies at their branch length-optimized likelihood values (Goldman et al. 2000). Subsequent studies expanded this test, highlighting several of its properties and limitations (e.g., Kishino et al. 1990), such as requiring that gene tree hypotheses be defined beforehand (Swofford et al. 1996; Shimodaira and Hasegawa 1999), and its diminished performance under evolutionary model misspecification (i.e., Buckley 2002; Strimmer and Rambaut 2002); features that are also likely to be relevant to species tree implementations that are based on similar principles.

We refer to our KH test extension for conducting tests of species topologies under the MSC as KH*. The KH* test compares the likelihoods of two species topologies $S_1$ and $S_2$, while using variations of nonparametric bootstrapping to assess significance. Details of specific KH* algorithms are described in figure 2a, and a schematic of the general KH* procedure is depicted in figure 2b. Suppose we wish to test whether topologies $S_1$ and $S_2$ are equally supported by a given input set of gene trees G. For the KH* test, the null ($H_0$) and alternative ($H_{\mathrm{A}}$) hypotheses can be defined as

$$H_0:E[\delta ]=0$$

$$H_{\mathrm{A}}:E[\delta ]\ne 0,$$

where $\delta =\ln L(S_1)-\ln L(S_2)$ and the expectations $E[\cdot ]$ are functions of the model parameters and taken over data samples. Note that this is the identical terminology for both the null and alternative hypothesis as stated in Goldman et al. (2000) based on the original KH test. Using our input gene tree sets, we seek to test whether the difference in MSC log-likelihoods $\delta$ diverges significantly from this expectation under $H_0$. During the testing procedure, the model parameters are optimized using ML under the MSC. The KH* test thus evaluates whether two topologies $S_1$ and $S_2$ are equally likely to have generated gene tree topologies in G. The general protocol of the KH* test is defined in the following steps (fig. 2):

1. Two topologies $S_1$ and $S_2$ are defined a priori.

2. Coalescent branch lengths of both $S_1$ and $S_2$ are optimized independently using ML.

3. The observed statistic $\delta$ is computed using the two branch length optimized trees from Step (2).

4. A total of b nonparametric bootstrap samples are obtained by resampling (with replacement) from the original gene tree set G.

5. For each bootstrap replicate gene tree set, the branch lengths of topologies $S_1$ and $S_2$ are optimized again using ML to obtain a null distribution for $\delta$.

6. The bootstrap distribution is used to evaluate whether the observed test statistic $\delta$ is a plausible sample under the null hypothesis.

Mirroring their gene tree counterparts (Goldman et al. 2000), we implemented three versions of KH* (${\mathrm{KH}}_1^{*}$, ${\mathrm{KH}}_2^{*}$, and ${\mathrm{KH}}_3^{*}$; fig. 2a) by replacing computations of gene-tree likelihoods (Felsenstein 1981) with MSC-based likelihoods (Yang 2002; Rannala and Yang 2003). As with the KH tests, all three versions of KH* apply nonparametric bootstrapping of the set G to obtain a null distribution of $\delta$ for computing two-sided P values (fig. 2). The ${\mathrm{KH}}_1^{*}$ test shares many properties with the species topology tests implemented in Liu et al. (2019) and Du et al. (2019) that compare the pseudolikelihood of two different topologies using the framework of MP-EST. The ${\mathrm{KH}}_2^{*}$ and ${\mathrm{KH}}_3^{*}$ algorithms differ from ${\mathrm{KH}}_1^{*}$ in Step (5) by applying the resampling estimated log-likelihood (RELL; Kishino et al. 1990; Hasegawa and Kishino 1994) approach to speed up computation by avoiding branch length optimization for each bootstrap replicate. ${\mathrm{KH}}_3^{*}$ tests whether the observed $\delta$ statistic is a plausible sample from a normal distribution with mean 0 and variance computed across bootstrap replicates.

The SH* Test

The SH test was designed to improve upon KH by relaxing the requirement that two trees be selected in advance (Shimodaira and Hasegawa 1999; Goldman et al. 2000). While KH* is only valid when comparing two topologies selected before comparing their likelihoods, the SH* test is applied to all topologies included within a set $M=\{S_1,S_2,\dots ,S_t\}$ containing t different species topologies, correcting for multiple comparisons in the process. This set ideally encompasses all plausible topologies, including the ML estimate (Goldman et al. 2000). We can therefore formulate the SH* test for evaluating multiple species topologies by examining the null and alternative hypotheses, which we describe below. Details of specific SH* algorithms are described in figure 3a, and a schematic of the general SH* procedure is depicted in figure 3b. For topology $S_x$ in M, let $\ln L(S_x)$ represent the log-likelihood value of topology $S_x$ at maximized coalescent branch lengths given input gene tree set G. We can define the null and alternative hypotheses as

Fig. 3.

The SH* test for species tree hypotheses. Details for the two algorithms (${\mathrm{SH}}_1^{*}$ and ${\mathrm{SH}}_2^{*}$) are provided in (a), and a general schematic overview of the SH* test is shown in (b). Briefly, the SH* test evaluates whether the difference in MSC likelihoods $\delta$ computed between two or more species topologies $S_1,S_2,\dots ,S_t$ (b, top) included in a set of t topologies is a plausible draw from a null distribution obtained using nonparametric bootstrapping. Specifically, the difference in MSC likelihood is computed between the species topology in the set with ML ($S_{\mathrm{ML}}$) and each of the other $t-1$ topologies. Several example topologies include two classical bifurcating trees on the left ($S_1$ and $S_2$) and a species network on the right ($S_t$). In this schematic, the first topology $S_1$ also happens to be $S_{\mathrm{ML}}$. Nonparametric bootstrapping of the input gene tree set G is conducted to obtain b total replicates $G^{(1)}$, $G^{(2)}$, …, $G^{(b)}$ (b, left), yielding a distribution of ${\delta }^{(1)}$, ${\delta }^{(2)}$, …, ${\delta }^{(b)}$ (b, bottom) under the null hypothesis. As with KH*, the two SH* algorithms differ on whether RELL bootstrapping is used (${\mathrm{SH}}_2^{*}$) or not (${\mathrm{SH}}_1^{*}$). See table 1 for a description of gene tree analog acronyms posNPfcd and posNPncd.

$$H_0:E[{\delta }_x]=0$$

$$H_{\mathrm{A}}:E[{\delta }_x]>0,$$

where ${\delta }_x=\ln L(S_{\mathrm{ML}})-\ln L(S_x)$ and $S_{\mathrm{ML}}$ is the ML topology given the set of input gene trees G. Our terminology for the null and alternative hypotheses is identical to those stated in Goldman et al. (2000) and Shimodaira and Hasegawa (1999) based on the original SH test.

The SH* test is conceptually similar to KH* with the important distinction of correcting for the ML topology. Steps of the SH* test include the following (fig. 3):

1. A set $M=\{S_1,S_2,\dots ,S_t\}$ of t species topologies is defined to include all reasonable topologies, as well as the ML topology $S_{\mathrm{ML}}$.

2. For each topology $S_x$ in M, optimize the coalescent parameters and compute the observed test statistic ${\delta }_x=\ln L(S_{\mathrm{ML}})-\ln L(S_x)$ using the ML topology $S_{\mathrm{ML}}$.

3. Conduct nonparametric bootstrap resampling to obtain a set of b samples of the original gene tree set G.

4. For each bootstrap replicate i, find $S_{\mathrm{ML}}^{(i)}$ (i.e., ML topology specific to replicate i), and for each topology $S_x$ in M, compute the statistic ${\delta }_x^{(i)}$ to obtain a null distribution of ${\delta }_x$.

5. Test whether the null distribution of ${\delta }_x$ is a plausible outcome under the null hypothesis for each species topology $S_x$ in M.

6. If the observed statistic ${\delta }_x$ of any tree is outside the significance cutoff, then reject the null hypothesis, otherwise fail to reject.

We implemented two versions of SH* (${\mathrm{SH}}_1^{*}$ and ${\mathrm{SH}}_2^{*}$; figure 3a) in SpeciesTopoTestR that are analogs to the original algorithms (Goldman et al. 2000). As with the KH* test, SH* also uses nonparametric bootstrapping either with (${\mathrm{SH}}_2^{*}$) or without (${\mathrm{SH}}_1^{*}$) RELL to generate a null distribution for computing P values (fig. 3). During bootstrap resampling, the ML topology $S_{\mathrm{ML}}^{(i)}$ computed for bootstrap gene tree set $G^{(i)}$ must be considered in the set M of plausible species tree candidates for significance levels to be appropriate (Westfall et al. 1993; Goldman et al. 2000). An exhaustive consideration of all possible topologies may be infeasible for large trees with many species, but a potential solution could be to first generate bootstrap gene tree sets, compute the $S_{\mathrm{ML}}^{(i)}$ for each set, and include all distinct ML bootstrap tree topologies in the set of plausible topologies M.

The SOWH* Test

We expanded the SOWH test (Hillis et al. 1996; Swofford et al. 1996) to develop the SOWH* test defined by the null and alternative hypotheses

$$H_0:E[\delta ]=0$$

$$H_{\mathrm{A}}:E[\delta ]>0,$$

where $\delta =\ln L(S_{\mathrm{ML}})-\ln L(S_1)$, $S_{\mathrm{ML}}$ is the ML topology given the set of input gene trees G, and $S_1$ is a target topology of interest. Details of specific SOWH* algorithms are described in figure 4a, and a schematic of the general SOWH* procedure is depicted in figure 4b. As with the original SOWH, parametric bootstrapping (Goldman et al. 2000) is used to simulate replicate gene tree sets under the MSC according to optimized branch lengths of $S_1$, which provide a null distribution for assessing significance. This application of parametric bootstrapping (i.e., simulating data under a parametric model) rather than nonparametric bootstrapping is a key distinction between SOWH* and both KH* and SH*. Here, the difference in MSC likelihoods $\delta$ between a target topology $S_1$ and the ML topology $S_{\mathrm{ML}}$ is used to test the null, and each round of parametric bootstrapping is followed by a search for the ML topology to compute null test statistics.

The general steps of the SOWH* test include (fig. 4):

1. The target species topology $S_1$ is specified and its coalescent branch lengths are optimized using ML.

2. The ML topology $S_{\mathrm{ML}}$ is found using the entire original gene tree set G.

3. The observed test statistic $\delta =\ln L(S_{\mathrm{ML}})-\ln L(S_1)$ is computed using the optimized topology $S_1$ and the ML topology $S_{\mathrm{ML}}$.

4. A total of b parametric bootstrap replicates are obtained by simulating gene trees with the MSC under the optimized species topology $S_1$.

5. A new ML topology $S_{\mathrm{ML}}^{(i)}$ is estimated independently for each bootstrap replicate i, and the branch lengths of $S_1$ are optimized to compute the null distribution of $\delta$.

6. The observed statistic $\delta$ is tested whether it represents a plausible sample under the null hypothesis.

We implemented two versions of SOWH* (fig. 4a) that differ in whether RELL approximation is applied (${\mathrm{SOWH}}_2^{*}$) or not (${\mathrm{SOWH}}_1^{*}$).

Results

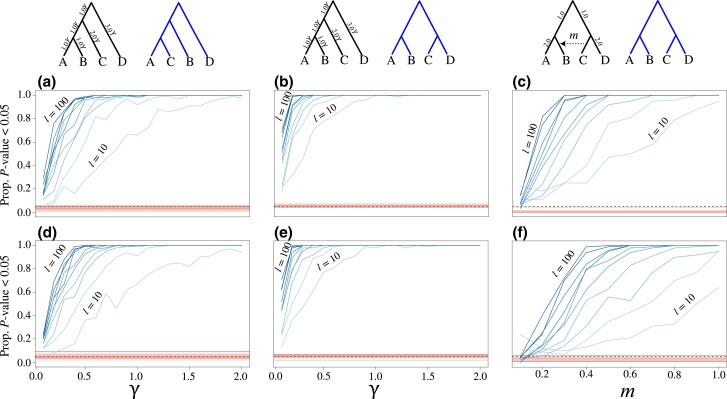
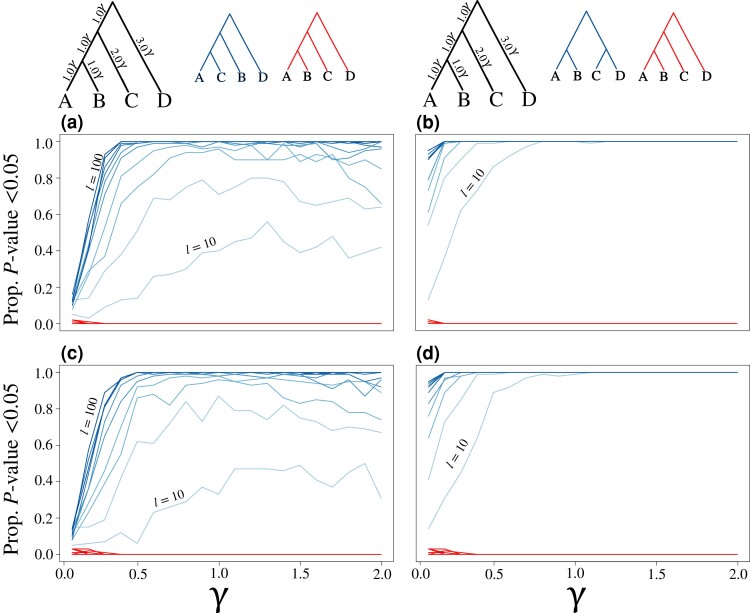
We explored the statistical properties of the KH*, SH*, and SOWH* tests across an array of simulation conditions that included both the true, known (simulated) gene trees as well as estimated gene trees. Specifically, we investigated the statistical power for rejecting the null hypotheses when a specific tree is used to generate the data, as well as the false positive rate for each test when gene trees are generated under a null hypothesis (details provided in Methods and Materials). Our simulations highlight the utility of KH* for testing hypotheses involving both bifurcating topologies and hybridization networks (figs. 5 and 6). As expected, the power of KH* is a function of evolutionary model parameters as well as the number of input gene trees. In particular, we find that the significance of KH* tends to increase (i.e., P values decrease) as the number of input gene tree topologies increases (bottom to top across the y-axes of fig. 5) and as species divergence times increase (left to right across the x-axes of fig. 5a and b). We also see that KH* can evaluate hypotheses concerning the presence or absence of hybridization edges (fig. 5c). In particular, the hybridization proportion m has a strong influence over KH* when applied to increasingly larger data sets (bottom to top along the y-axis of fig. 5c). Statistical significance increases with both the strength of migration and the number of input gene trees (i.e., left to right and bottom to top in fig. 5c, respectively), as the dominant phylogenetic signal induced by the network changes from one of a symmetric topology (matching the alternate) to an asymmetric one with increasing m. As expected, significance was slightly reduced when using estimated instead of the known (simulated) gene trees (fig. 5a–f).

Fig. 6.

Assessing the statistical performance of the KH* test across an array of simulation scenarios for evaluating true positives (blue trees and lines) and false positives (red lines) for bifurcating topologies (a, b, d, and e) and a species network (c and f). Results shown for tests of scenarios involving true positives (alternative topologies tested shown in dark blue) and false positive rates (red lines). For estimating power (blue lines), gene trees were simulated using the left, “true” (generating) species topology shown above each respective set of analyses, with the alternative topology shown to the right in blue above each set of analyses. False positive rates were estimated using randomly generated coalescent gene trees (red lines). Lines indicate the proportion of replicates with P ≤ 0.05, with colors ranging from light ($l=10$ gene trees) to dark ($l=100$ gene trees) in increments of 10 gene trees. Top panels (a–c) show results when using the true, simulated gene trees, whereas estimated gene trees were used in the test results shown in the bottom panels (d–f). See figure 5 caption for additional information regarding the parameters γ and m.

These results were consistent when evaluating the proportion of replicates with P ≤ 0.05 for scenarios of both true positive (blue lines, fig. 6) and false positive (red lines, fig. 6) settings. As the number of loci increases from $l=10$ to $l=100$ (i.e., increasingly darker blue lines in fig. 6), the test demonstrates higher power to reject the null hypothesis when gene trees were simulated under a specific generating topology (black topology at the top of fig. 6) that differed from an alternate tested topology (blue topology at the top of fig. 6). Furthermore, we observe lower statistical power to distinguish between trees when using estimated gene tree topologies (fig. 6d–f) compared with using true, known gene tree topologies (fig. 6a–c). For applications of the KH* test to species trees involving hybridization events (fig. 6c and f), power to reject the null under true positive scenarios was highest when using large data sets ($l=100$ gene trees) and moderate to high migration proportions ($m\ge 0.4$). Across our simulations, we find consistent evidence of low false positive rates to reject the null hypothesis of the KH* test regardless of data set size (darker red lines indicate more loci; fig. 6).

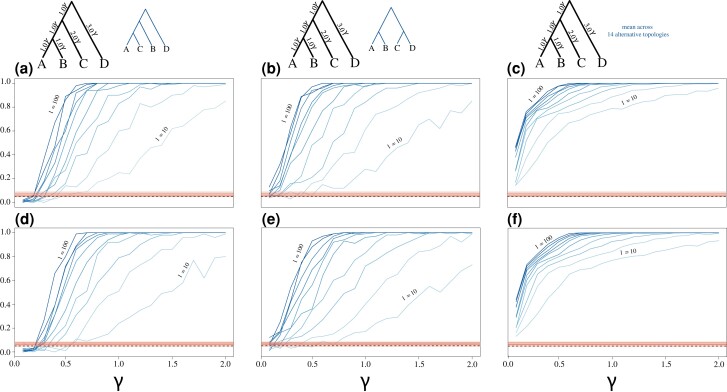
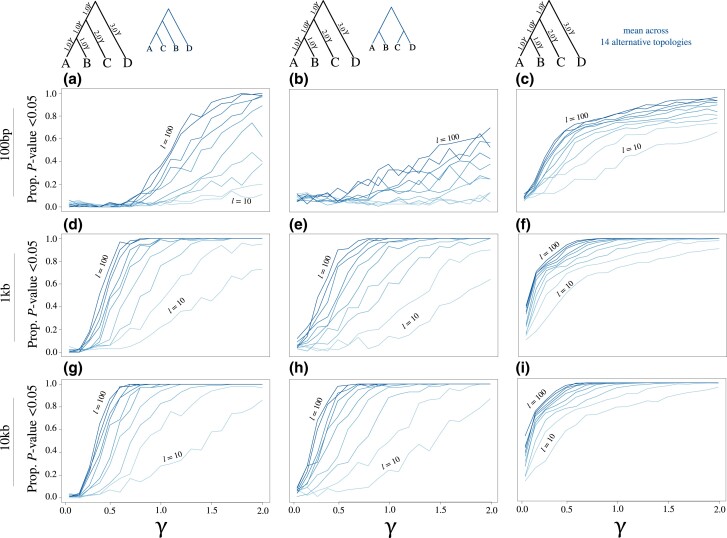
We also evaluated the statistical power for rejecting the null hypothesis using simulated and estimated gene trees for a scenario of bifurcating and reticulating species trees with the SH* test (fig. 7) using the ${\mathrm{SH}}_2^{*}$ algorithm. We tracked P values of the SH* test across simulations for the true species tree used to generate the input genealogies (black trees; fig. 7), two specific alternative topologies (blue trees; fig. 7), and the mean across all 14 alternative topologies (right column; fig. 7). We also conducted a separate series of analyses to investigate false positive rates under randomly generated genealogies (red lines; fig. 7), with false positive rates elevated slightly (∼0.05–0.07 across different numbers of input gene trees). Note that these elevated false positive rates are due to using the fast SH* algorithm (${\mathrm{SH}}_2^{*}$), and we later show that the false positive rates are better controlled when using the ${\mathrm{SH}}_1^{*}$ algorithm instead. Increasing the number of input genes from $l=10$ to $l=100$ (increasingly darker blue lines in fig. 7) improves the power of the SH* test for both known (fig. 7a–c) and estimated (fig. 7d–f) gene trees. Moreover, echoing the findings of the KH* test, we observe that statistical power is reduced when applying the SH* test to estimated gene trees (fig. 7d–f) compared with known gene trees (fig. 7a–c).

Fig. 7.

Assessing the statistical performance of the SH* test across an array of simulation scenarios for evaluating true positives (blue trees and lines) as well as estimated false positive rates (red lines). Lines indicate the proportion of replicates with P ≤ 0.05, with colors ranging from light ($l=10$ gene trees) to dark ($l=100$ gene trees) in increments of 10 gene trees. Top panels (a–c) show results when using the true, simulated gene trees, whereas estimated gene trees were used in the test results shown in the bottom panels (d–f). The third column shows the fraction of replicates with P ≤ 0.05 averaged across all 14 alternative rooted topologies for four-species trees. Generating species topology shown on the left, with the alternative topologies shown in blue. See figure 5 caption for additional information regarding the parameter γ.

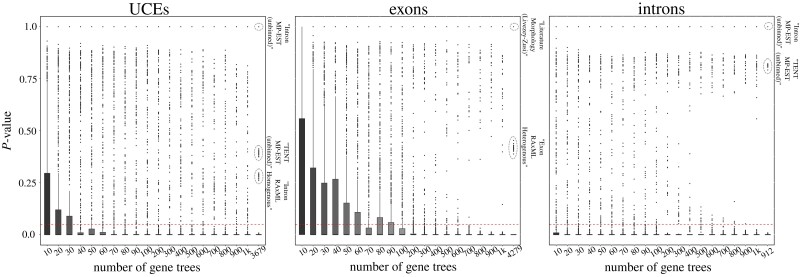
In addition to our simulation analyses, we also explored the application of the SH* test to an empirical data set comprising a total of 8,870 gene trees (4,279 exon, 912 intron, and 3,679 ultraconserved elements [UCEs]) obtained from Jarvis et al. (2014), including a set of t = 33 distinct proposed 20-taxon topologies for the avian phylogeny. Specifically, we applied the SH* test to evaluate these 33 species topologies when sampling increasing larger sets of input gene trees. In these empirical analyses, we find that increasing the number of gene trees analyzed resulted in strong statistical support for rejecting the null hypothesis across the 33 bird topologies in our applications of SH* (fig. 8). These analyses also highlight quantitative differences in results of the SH* test depending on locus type (UCEs vs. exons vs. introns) and data set size (number of genes). For example, SH* displays higher significance (i.e., lower P values) when analyzing intron-based gene trees. However, even with large data sets (i.e., $\ge 100$ gene trees), null hypotheses are not rejected for certain topologies. For example, the UCE and intron analyses that used all available gene trees fail to reject the “Intron_MP-EST_unbinned” (topology inferred with MP-EST using introns only) and “TENT_MP-EST_unbinnned” (topology inferred using all nucleotide data with MP-EST) topologies that were both inferred without locus-binning methods (i.e., “statistical” binning”; Mirarab, Bayzid, et al. 2014; Mirarab, Reaz, et al. 2014; Adams and Castoe 2019), while the “Literature_Morphology_LivezeyZusi” (morphology-based topology) and “Exon_RAxML_Heterogeneous” (concatenated RAxML tree inferred using exons only with heterogenous model partitions) topologies are identified in the exon-only applications of SH* (fig. 8; for more details on these trees, see Jarvis et al. 2014).

Fig. 8.

Applying $\mathrm{S}{\mathrm{H}}^{*}$ to the avian phylogenomic data set. Boxplots summarizing the distribution of P values across 100 replicate analyses for each data set size obtained for 33 avian species topologies computed for different data set sizes (number of genes) and for different locus types: UCEs (left), exons (center), and introns (right). Tree labels in the upper right of each panel indicate the names of particular trees defined in Jarvis et al. (2014).

As with both the KH* and SH* tests, we also estimated the statistical power and false positive rate of the SOWH* test under various evolutionary simulations. Our applications of SOWH* highlight both its statistical properties under simulated settings (fig. 9) and its utility for testing contentious species tree hypotheses in an empirical application (fig. 10). As with the KH* test, we find higher statistical power of the SOWH* test as both the branch lengths (increasing from left to right along the x-axes) and the number of input gene trees (increasingly darker blue lines) increase (fig. 9). That is, providing more input gene trees increases the power of the test for rejecting the null hypothesis. We also find evidence of low false positive rates across different data set sizes (increasingly darker red lines; fig. 9) with the SOWH* test for testing two scenarios that differ in the shape of the tested trees (i.e., unbalanced topology vs. balanced topology; fig. 9a–d), particularly when the branch lengths of the species tree are longer.

Fig. 9.

Investigating the statistical performance of the SOWH* test across an array of simulation scenarios for evaluating true positives (blue trees and lines) and false positives (red trees and lines). Lines indicate the proportion of replicates with P ≤ 0.05, with colors ranging from light blue ($l=10$ gene trees) to dark blue ($l=100$ gene trees) in increments of 10 gene trees. Results shown for the scenarios using the true, simulated gene trees (a and b), and the estimated gene trees (c and d). Generating species topologies shown in black to the left above each set of analyses, with the tested topologies shown in blue (i.e., true positives) or red (i.e., false positives). See figure 5 caption for additional information regarding the parameter γ.

Fig. 10.

Applying the $\mathrm{SOW}{\mathrm{H}}^{*}$ to three example test cases: Amphibians (left columns), Reptiles (center columns), and Neoaves (left columns). Violin plots depict the distribution of the test statistic ${\delta }^{(i)}$ across b = 10³ replicates for each pair of trees shown at the bottom. Stars indicate the value of the observed statistic, with colors of the stars indicating whether the result is statistically significant (red stars) or not (blue stars) given the null distribution (gray violin distributions). The top row of violin plots (a–c) indicates the results obtained using the ${\mathrm{SOWH}}_1^{*}$ algorithm, while the bottom row (d–f) shows the results of the ${\mathrm{SOWH}}_2^{*}$ algorithm.

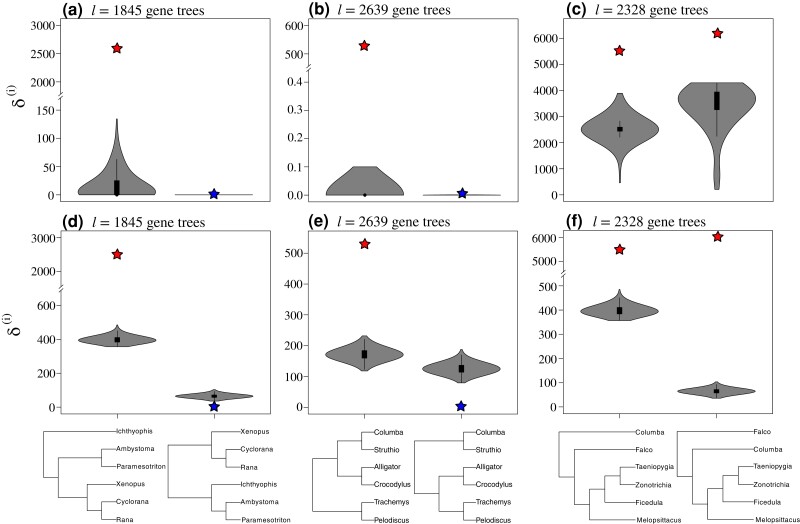
In addition to our simulation analyses, we applied the SOWH* test to three example case studies of contentious phylogenetic relationships in amphibians, reptiles, and birds (hypotheses shown in fig. 10). In each of the three empirical demonstrations (Amphibians, Reptiles, and Neoaves), SOWH* identifies evidence to reject the null hypothesis for at least one of the proposed topologies (fig. 10). In our analyses of the Amphibian trees, we find that SOWH* fails to reject the null hypothesis for one of the target trees using both algorithms (fig. 10a and d). For the Reptile analysis, SOWH* fails to reject the null hypothesis for the placement of birds as sister to turtles and crocodiles (fig. 10b and e), whereas both topologies reject the null in our Neoaves demonstration (fig. 10c and f). We find that the shape of the null distribution of the test statistic (gray violin plots in fig. 10) depends on whether RELL approximation is used (i.e., ${\mathrm{SOWH}}_1^{*}$ vs. ${\mathrm{SOWH}}_2^{*}$; top vs. bottom panels in fig. 10) but with matching outcomes for rejecting or failing to reject the null.

Discussion

These methods seek to synergize both the “old” and the “new” within a unified framework and represent a first step toward developing new approaches that incorporate more complex species models, hypotheses, algorithms, and statistical procedures. For example, we can envision hypothesis-testing frameworks for species models that include additional processes that influence gene tree distributions (e.g., Lanier and Knowles 2012; Adams et al. 2018; Koch and DeGiorgio 2020). Importantly, we view these tests as complementary with existing methods for evaluating species tree hypotheses and models, such as Bayesian approaches for phylogenetic model testing (e.g., *BEAST, SNAPP, and BPP; Rannala and Yang 2003; Heled and Drummond 2009; Bryant et al. 2012). Such Bayesian approaches make use of full sequence alignments and provide a natural measure of reliability with posterior probabilities and thus are a gold standard for species tree inference. Yet, because they employ Markov chain Monte Carlo algorithms in their estimation procedure, they are highly computationally expensive. Our approaches provide a model-based framework for testing species topology hypotheses while making computations on large genomic data sets more tractable via heuristic ML algorithms that operate on input gene tree topologies rather than sequence alignments. Additionally, our implementation of the ${\mathrm{KH}}_1^{*}$ test most closely resembles that of the species topology test implemented in Liu et al. (2019).

These species topology tests mirror their gene-based counterparts and share many of the same assumptions; we emphasize that most any consideration of the original tests is also likely relevant. For example, as with the original KH test, KH* is only valid when comparing species topologies that have been defined a priori, meaning that it is inappropriate to apply the test when one of the topologies has already been selected as the ML estimate because the null expectation of $\delta =0$ no longer holds. Similarly, the SH* and SOWH* tests are also subject to considerations and limitations of their respective gene tree counterparts. For example, SH is often more conservative than SOWH, and SOWH may be more prone to false positives, at least when models are misspecified (Buckley 2002). Another limitation of these tests in their current form is that only gene topologies are considered, similar to two-step species tree algorithms (e.g., STELLS and ASTRAL). Here, we focused our study on exploring the application of the MSC likelihood function as implemented in STELLS and PhyloNet frameworks; other similar approaches (e.g., STEM, MP-EST, and PRANC; Kubatko et al. 2009; Liu et al. 2010; Kim and Degnan 2020) may prove fruitful for future studies and work on phylogenetic hypothesis tests.

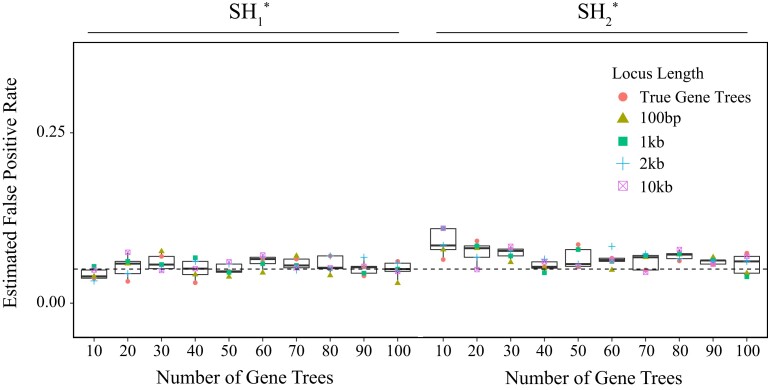
We also wish to underscore the important assumption of these tests, which is that input gene trees are error free. Though this assumption is shared with many heuristic approaches for species tree inference, it can inflate phylogenetic conflict when violated (Yang 2002; Burgess and Yang 2008; Seo 2008; Xu and Yang 2016; Forthman et al. 2022). Using the SH* test as an example, we observed reduced power when estimating gene tree topologies from shorter loci (fig. 11a–c) when compared with longer loci (fig. 11d–i) for which gene tree estimates would be more reliable. Nonetheless, we find evidence of low and consistent estimates of false positive rates (fig. 12), even for short loci, with slightly lower false positive rates with the ${\mathrm{SH}}_1^{*}$ algorithms compared with the ${\mathrm{SH}}_2^{*}$ (RELL bootstrap approximation) for the conditions explored here (left vs. right results in fig. 12, respectively). Though we probed the behavior of these tests when applied to both simulated and estimated gene trees (figs. 5–7, 9, 11, and 12), a broader exploration of evolutionary and experimental settings may reveal a parameter space for which these tests perform differently. As with other methods that assume error-free input, accuracy is likely to be heavily influenced by gene tree quality, and we believe that input quality should be carefully considered when using SpeciesTopoTestR. To address such concerns, a potential area of future improvement is to incorporate multiple levels of bootstrapping that resample both gene trees and sequence alignment columns. However, such a strategy is expected to require a significant computational burden as well as assumptions about the models of sequence evolution, while missing data from the original sequence alignments may also pose challenges.

Fig. 11.

Estimated gene trees and statistical power of the SH* test. Results are shown for estimates of true positive rates (blue lines and trees) across a range of branch scaling values $\gamma =[0.1,2]$ with gene trees estimated from simulated alignments comprising 100 bp (a–c), 1 kb (d–f), and 10 kb (g–i). Lines indicate the proportion of replicates with P ≤ 0.05, with colors ranging from light blue ($l=10$ gene trees) to dark blue ($l=100$ gene trees) in increments of 10 gene trees. The third column shows the fraction of replicates with P ≤ 0.05 averaged across all 14 alternative rooted topologies for four-species trees. See figure 5 caption for additional information regarding the parameter γ.

Fig. 12.

Evaluating the impact of gene tree estimation error on false positive rates of the SH* test. Results are shown for false positive rates estimated using randomly generated gene trees of uniform probability (i.e., no species tree was used) for both the ${\mathrm{SH}}_1^{*}$ (left) and ${\mathrm{SH}}_2^{*}$ (right) algorithms across increasing numbers of input gene trees (left to right; 10–100 gene trees) and different locus lengths (points; from 100 bp to 10 kb), with red circles indicating the use of the true, simulated gene trees.

Related to these concerns is the potential for recombination to influence species tree inference and therefore the hypothesis tests described in this study. Traditional approaches to gene tree inference using ML or Bayesian inference typically assume that all sites within a locus are genetically linked and therefore share the same genealogical history (i.e., no recombination within a sequence alignment). Likewise, most species tree methods assume free recombination between loci and a lack of recombination within a locus. The tests described in this study implement similar frameworks and therefore make the same assumptions. Recombination can be a challenge for gene tree estimation by influencing branch length and topology estimates under certain conditions (Schierup and Hein 2000; Posada and Crandall 2002). These challenges may be particularly relevant for analyses of large phylogenomic data sets sampled across many species with ample opportunity for recombination events across a tree (Adams and Castoe 2018). For species tree inference, recent studies have found evidence that commonly used species tree algorithms may be relatively robust to intralocus recombination for some methods (Lanier and Knowles 2012). However, the impacts of simultaneously violating both assumptions—free recombination among loci but no recombination within a locus—remain an open question (Wang and Liu 2016). Methods that seek to test for evidence of phylogenetic congruency may hold promise for evaluating evidence for intralocus recombination (Paraskevis et al. 2005; Martin et al. 2011; Adams et al. 2021). Importantly, we caution that users carefully consider this and all other assumptions when conducting the KH*, SH*, and SOWH* tests. Similar to previous studies (e.g., Lanier and Knowles 2012), we also found evidence that the KH* test may be relatively robust to certain conditions of recombination (fig. 13). Future work will help our understanding of recombination and other model violations on species tree tests and inference.

Fig. 13.

Exploring the impact of recombination on the statistical performance of the KH* test. Results are shown for the mean P value across replicates (a) and proportion of replicates with P ≤ 0.05 (b). For each set of conditions, gene trees within a recombining locus were simulated using the “true” (generating) species topology shown to the right in black, with the alternative topology shown in blue. Divergence times for the true topology were scaled by multiplying branches by a scaling factor $\gamma \in [0.1,2]$. See Materials and Methods for our simulation protocol.

Materials and Methods

Evaluating the KH* Test

To explore the behavior of the KH* test (fig. 2), we conducted simulations across varying evolutionary (e.g., topologies and divergence times) and experimental (e.g., number of input gene trees l) parameters. We first evaluated KH* for assessing support between two alternative bifurcating four-taxon species topologies (fig. 5a) by simulating data sets that varied in number of gene trees $l\in \{1,2,\dots ,10,20,\dots ,100\}$ and coalescent branch lengths on the species tree. We used these analyses to evaluate the statistical power of the test for rejecting the null hypotheses when the null hypotheses are indeed false because one specific topology was used to generate a set of gene trees, and a separate, alternative topology was included in the test. Specifically, gene trees were simulated using a “true” (generating) species tree (fig. 5a, left topology in black) with branches (in coalescent units) scaled by multiplying by a factor $\gamma =[0.1,2]$, and KH* was applied using an “incorrect” alternative topology with a swapped branch (fig. 5a, right topology in blue) and 10⁴ bootstrap replicates to compute P values under the null hypothesis. That is, we used these simulations to evaluate the power of the test for rejecting the null hypothesis, as we expect that the “correct” topology (fig. 5a, left topology in black) should be more supported than the “incorrect” topology (fig. 5a, right topology in blue) as the number of input gene trees increases, because the “correct” topology was used to directly simulate the input gene trees. For each combination of branch length scaling and gene tree counts, we performed 100 replicates to obtain a distribution of P values across the different simulation settings.

We also conducted similar analyses that assumed a different symmetric topology as the “incorrect” alternative topology (right topology in blue; fig. 5b) using these same simulation conditions to demonstrate power for rejecting the null hypothesis with different topologies. Input gene trees were simulated using the “correct” topology (fig. 5b, left topology in black), and we evaluated power for rejecting the null hypotheses using the “incorrect” alternative topology (right topology in blue; fig. 5b). Additionally, we explored the behavior of KH* for evaluating hybridization hypotheses. Gene trees were simulated under a network topology (fig. 5c, left network) using PHYLONET (Than et al. 2008) with a single directional pulse of migration with proportion $m\in [0,1]$, which were then used to assess support for this network and an “incorrect” alternative bifurcating topology with the migration edge removed (i.e., $m=0$). These simulations evaluated the power of the test for rejecting the null hypotheses because a hybridization network was used to simulate the input gene trees, while we tested an alternative “incorrect” bifurcating tree (blue topology; fig. 5c).

Across these simulations, heatmaps illustrate mean P values computed across the 100 replicates using the true species topology (left topologies in fig. 5a–c) and an alternative topology (right topologies in fig. 5a–c) with the ${\mathrm{KH}}_2^{*}$ algorithm for each set of simulation conditions. Additionally, we also used these simulation scenarios to quantify the proportion of replicates with P ≤ 0.05 to investigate true positives (blue trees and results shown in fig. 6). We evaluated the false positive rate of the KH* test (red curves displayed in fig. 6) by simulating random input gene trees under the coalescent process without any species trees using the rcoal function provided in the R package APE (Paradis et al. 2004).

Investigating the Impact of Input Gene Tree Error

To assess the performance of the KH* test under scenarios with gene tree estimation error, we repeated each simulation analysis using estimated gene trees (figs. 5d–f and 6d–f) instead of the known simulated gene trees. Using a uniform per-base, population-scaled mutation rate of $\theta =0.01$, we simulated 2-kb alignments for each simulated gene tree under the HKY model (Hasegawa et al. 1985) with parameter values inspired by Burgess and Yang (2008): a transition/transversion ratio of 4.6 and base equilibrium frequencies of 0.3 (A), 0.2 (C), 0.2 (G), and 0.3 (T). A single gene tree was estimated for each 2-kb alignment using IQ-TREE (Nguyen et al. 2015), and the estimated set of gene trees was then used as input to KH*. We evaluated both true positives (blue lines in fig. 6) and false positives (red lines in fig. 6) using these estimated gene trees instead of the true, simulated gene trees. In addition to the KH* test, we used this strategy to assess the performance of both the SH* and SOWH* tests with estimated gene trees as well as simulated gene trees (details provided in the following sections).

Our chosen branch lengths and their associated scaling by γ permit evaluation of species hypotheses that are difficult for inference. Specifically, in our simulations with short internal branch lengths in terms of coalescent time units (i.e., small γ), we expect extensive gene tree variation as well as discordance of gene trees with species trees (Degnan and Rosenberg 2009) due to ILS (Maddison 1997). For extreme settings in which the scaling parameter leads to particularly small internal branch lengths, the level of gene tree incongruence would be consistent with expectations from adaptive radiations, such as in the evolution of Aves and other Amniotes (Jarvis et al. 2014; Shen et al. 2017). However, under mutation, our tested scenarios are not completely concordant with Amniote evolution, as species branching tends to be deep in the past (e.g., Song et al. 2012) and we would therefore expect larger numbers of mutations along such branches, and in the extreme case of deep evolution of Aves, recurrent mutation may reduce phylogenetic signal and increase gene tree estimation error (Salichos and Rokas 2013; Xi et al. 2015; Xu and Yang 2016). However, our experiments still represent difficult cases, as the external branches of our experiments would have little bearing on gene tree topology estimation, with the exception that recurrent mutation is unlikely to be an additional factor for gene tree estimation error and hence inaccuracies of our species tree topology tests. Instead, we focus on how gene tree estimation error can hamper our tests, as it has been shown to enhance phylogenetic conflict (Seo 2008; Xu and Yang 2016; Forthman et al. 2022).

Evaluating the SH* Test

To evaluate the statistical properties of the SH* test, we conducted a series of simulations based on the same scenarios used for our KH* investigations (species tree models shown at top of fig. 7). Briefly, we simulated gene tree sets of varying size $l\in \{1,2,\dots ,10,20,\dots ,100\}$ and coalescent branch lengths scaled by $\gamma =[0.1,2]$. For each set of simulation conditions, we generated 100 replicate data sets and applied the ${\mathrm{SH}}_2^{*}$ algorithm to estimate true positive rates for “incorrect” alternative topologies (blue topologies; fig. 7). To evaluate false positive rates, as with our KH* experiments, we simulated genealogies using rcoal without any particular species tree because the null hypothesis $H_0:E[\delta ]=0$ is predicted to hold because we do not expect, on average, that any species tree should be favored over another for these gene trees. We evaluated the performance of the SH* test for both the true simulated gene trees and estimated gene trees using the same protocol as with our KH* test experiments, which involved simulating 2-kb alignments for each gene tree under the HKY model with a transition/transversion ratio of 4.6 and base equilibrium frequencies of 0.3 (A), 0.2 (C), 0.2 (G), and 0.3 (T). Gene tree estimates were then obtained for each alignment using IQ-TREE, and the estimated set of gene trees was then used as input to SH*.

Throughout our simulations, we evaluated the true positive rate of the SH* test by tracking the fraction of replicates with P ≤ 0.05 of two alternative topologies (i.e., blue trees shown at the tops of fig. 7a and b) as well as the fraction of replicates with P ≤ 0.05 averaged across all 14 possible alternative topologies for four species (fig. 7c). We conducted a separate array of analyses to investigate the impacts of different locus lengths when estimating gene trees to be used as input into the SH* test. We varied the number of base pairs across three orders of magnitude (100 bp, 1 kb, and 10 kb) and applied SH* using the gene tree estimates following the same protocol as with the KH* test simulations to estimate both the true positive rates (i.e., trees shown at top of fig. 11; application of ${\mathrm{SH}}_2^{*}$ algorithm) and false positive rates (results shown in fig. 12; applications of ${\mathrm{SH}}_1^{*}$ and ${\mathrm{SH}}_2^{*}$).

We also demonstrated SH* on an empirical phylogenomic example consisting of 8,870 gene trees (4,279 exon, 912 intron, and 3,679 UCEs) obtained from the Jarvis et al. (2014) bird study. We applied SH* on these trees for a set of t = 33 distinct proposed 20-taxon topologies for the avian phylogeny (Jarvis et al. 2014; fig. 8) using the ${\mathrm{SH}}_2^{*}$ algorithm with 10⁴ RELL replicates in distinct analyses of only exons, introns, or UCEs and explored the influence of data set size by varying the number of input gene trees on a logarithmic scale (i.e., 10, 20, …, 100, 200, …, 1000). For each of the three locus types (exons, introns, or UCEs) and data set sizes, we conducted 100 replicate analyses by sampling (with replacement) from their respective gene tree sets (i.e., only exons, introns, or UCEs) and applying SH* to each replicate. We also conducted separate analyses using either all 4,279 exons, all 912 introns, or all 3,679 UCEs.

Evaluating the SOWH* Test

We first investigated the statistical performance of the SOWH* test using two four-tip species trees scenarios (shown at top of fig. 9). Following the same protocol for the simulation-based investigation of the KH* and SH* tests, we evaluated the fraction of replicates that resulted in false positives (i.e., red trees at top of fig. 9) and true positives (i.e., blue trees at top of fig. 9) by repeatedly simulating gene tree sets for $l\in \{1,2,\dots ,10,20,\dots ,100\}$ loci according to the black species trees shown at the top of figure 9 with branch lengths scaled by a factor $\gamma =[0.1,2]$. We conducted 100 replicates for each set of simulation conditions and applied the ${\mathrm{SOWH}}_2^{*}$ algorithm with 10³ bootstrap replicates to compute P values under the null hypothesis. Additionally, we repeated these analyses to investigate the behavior of the SOWH* test using gene tree estimates obtained from IQ-TREE following the same protocol as applied for the KH* and SH* tests, with 2-kb alignments simulated according to the HKY model with a transition/transversion ratio of 4.6 and base equilibrium frequencies of 0.3 (A), 0.2 (C), 0.2 (G), and 0.3 (T).

We also conducted an empirical demonstration of the SOWH* using three example case studies (Amphibians, Reptiles, and Neoaves) that were previously investigated by Shen et al. (2017) to explore the causes and consequences of phylogenomic conflict. Thus, we sought to apply SOWH* to characterize statistical support for contentious species topology hypotheses in each of these examples (hypothesized topologies shown in fig. 10). We employed both ${\mathrm{SOWH}}_1^{*}$ and ${\mathrm{SOWH}}_2^{*}$ with 10³ bootstrap replicates on two plausible rooted Neoaves, Reptiles, or Amphibian topologies using the 2,328, 2,639, or 1,845 respective gene trees of Shen et al. (2017).

Simulations with Recombination

Lastly, we conducted a series of simulation analyses to explore potential impacts of intralocus recombination on the statistical performance of the KH* test. For these analyses, we used the software ms (Hudson 2002) to simulate gene trees with recombination under the bifurcating species tree shown in black on the right of figure 13. Mirroring our previous analyses for evaluating the KH* test (i.e., figs. 5 and 6), we conducted simulations across varying divergence times (scaling branches by $\gamma \in [0.1,2]$) and a number of input gene trees $l\in \{1,2,\dots ,10,20,\dots ,100\}$. In these simulations, we included a per-base, population-scaled recombination $\rho =0.0004$ for each locus was simulated for a total length of 2 kb. At the end of each simulated locus, we collected the gene trees and associated length of each recombination block (i.e., alignment blocks separated by recombination events). Next, we simulated sequences for each separate recombination block within a locus using the associated gene tree and the HKY model parameters used previously (e.g., figs. 5 and 6) and concatenated across all blocks within a locus to construct a single alignment of 2-kb total length. We then estimated a single gene tree from the entire 2-kb concatenated alignment; this procedure effectively violated the standard assumption of no recombination within a locus because recombination events and blocks were ignored. Finally, we used these sets of gene tree estimates as input for the ${\mathrm{KH}}_2^{*}$ test using the original topology (black tree in fig. 13) and an alternative topology (blue tree in fig. 13) to evaluate statistical properties.

Data Availability

All versions of our species tree hypothesis tests are implemented in the open-source R package SpeciesTopoTestR (github.com/radamsRHA/SpeciesTopoTestR), which requires the dependencies APE (Paradis et al. 2004), HYBRID-LAMBDA (Zhu et al. 2015), PHYLONET (Wen et al. 2018) and STELLS2 (Pei and Wu 2017).

Conflict of interest statement. The authors of this study (R.H.A and M.D.) do not report any conflicts of interest.