Abstract
Forecasting blood glucose (BG) levels with routinely collected data is useful for glycemic management. BG dynamics are nonlinear, complex, and nonstationary, which can be represented by nonlinear models. However, the sparsity of routinely collected data creates parameter identifiability issues when high-fidelity complex models are used, thereby resulting in inaccurate forecasts. One can use models with reduced physiological fidelity for robust and accurate parameter estimation and forecasting with sparse data. For this purpose, we approximate the nonlinear dynamics of BG regulation by a linear stochastic differential equation: we develop a linear stochastic model, which can be specialized to different settings: type 2 diabetes mellitus (T2DM) and intensive care unit (ICU), with different choices of appropriate model functions. The model includes deterministic terms quantifying glucose removal from the bloodstream through the glycemic regulation system and representing the effect of nutrition and externally delivered insulin. The stochastic term encapsulates the BG oscillations. The model output is in the form of an expected value accompanied by a band around this value. The model parameters are estimated patient-specifically, leading to personalized models. The forecasts consist of values for BG mean and variation, quantifying possible high and low BG levels. Such predictions have potential use for glycemic management as part of control systems. We present experimental results on parameter estimation and forecasting in T2DM and ICU settings. We compare the model’s predictive capability with two different nonlinear models built for T2DM and ICU contexts to have a sense of the level of prediction achieved by this model.
Our goal is to robustly model and forecast blood glucose (BG) levels of patients using sparse, routinely collected data. Human glycemic regulation is a nonlinear and coupled dynamical system whose main components (BG, plasma and interstitial insulin levels) form complex feedback loops complexified by time delays. Glycemic dynamics of diabetes and critically-ill patients are even more chaotic, nonstationary, and affected by several case-specific factors. Forecasting BG levels of patients is useful for glycemic management. However, routinely collected data in either setting are sparse and not sufficient for forecasting using high-fidelity, nonlinear models. Thus, we approximate these complex and nonlinear dynamics by a physiology-based, relatively simple, linear, and stochastic model representing BG dynamics. Because of the complexity of the BG regulation, unmeasured but important variables such as plasma and interstitial insulin, unmodeled variables such as exercise and drug interventions, and the sparsity of routinely collected data, robust BG trajectory forecasting can be difficult, especially without careful hand-tuning of parameters. We soften the trajectory forecasting using ordinary differential equation (ODE) models to forecasting the mean and variation of glycemic response to observable inputs (nutritional intake and exogenous insulin) using stochastic differential equations (SDEs) that can provide sufficient resolution for plausible glycemic management. Specifically, we develop a SDE model of BG that incorporates minimal but present physiological mechanics that can robustly forecast the mean and variance of BG based on past BG measurements, nutritional intake, and exogenous insulin data. The aim and constraints of our goal inform our modeling approach: we model the BG levels as a diffusion process with the mean BG behavior modeled by the drift term and the nonlinear oscillatory dynamics with the diffusion term. The resulting model has a small number of low-fidelity, physiologically interpretable parameters. These parameters do not represent any specific physiological processes, such as insulin sensitivity but rather bulk processes, such as the rate of return to BG homeostasis. This loss in physiological fidelity results in a substantial gain: one can estimate all unknown model parameters robustly with data, eliminating the need for parameter hand-tuning. This feature of the model yields the potential for the model’s use for patient and provider-based glycemic management. While results include the development of a new SDE model of the glucose system, a key finding from this work is that, given real-world data, the model can be analytically estimated resulting in low and robust mean squared error between the mean model output and BG measurements and accurate BG variability prediction.
I. INTRODUCTION
A. Background
A high-fidelity physiology-based mechanistic model coupled with data sampled at sufficient frequency provides accurate prediction. However, in real-world settings, human physiological data are often too sparse to accurately resolve high-fidelity physiological models. Moreover, such measurement sparsity can induce severe model unidentifiability, thereby resulting in non-robust predictive performance. To reduce this problem, there are two approaches. One approach is to constrain inference.1 The other approach, and the approach we take here, is to focus on applying model reduction and stochastic closure techniques. This comes with the cost of reduced physiological fidelity. However, we find that the trade-off between reduced model complexity vs model estimatability is effective, especially when data are sparse and noisy, the underlying system is highly complex, and not fully understood. The human glucose–insulin system provides an important example of this challenge. In many settings, insulin (plasma or interstitial insulin) is rarely measured outside of highly specialized research settings. Conceptually, this unobserved but important missing dynamical variable leads to our reduced model becoming a glucose model rather than a glucose–insulin model where we treat insulin impact as a bulk glucose removal process.
The dynamics of human glycemic regulation shows very complex nonlinear behavior, which could be represented accurately by a high-fidelity nonlinear deterministic model. However, because of constraints and limitations described above, we aim to explore another approach: to develop a mathematically simpler mechanistic model. This approach will reduce model unidentifiability with available sparse data at the cost of reduced fidelity to a level, which still achieves robust and accurate BG forecasting. Therefore, we approximate this nonlinear system using an Ornstein–Uhlenbeck process (a linear SDE with exponential mean-reversion), and introduce forcing terms that parameterize exogenous effects of nutrition and medication. The resulting model represents the mean BG behavior and a confidence region quantifying the amplitude of the BG oscillations. With appropriate adjustments, the model can be used to represent and forecast BG levels in two different settings: outpatient type 2 diabetes mellitus (T2DM) and inpatient intensive care unit (ICU). The BG levels of patients in these two settings exhibit characteristically different behavior.
B. Clinical settings
Glucose dynamics in T2DM setting are driven by a combination of diet, activity, time delay for the effect of insulin on glucose production, medication, and internal physiology. Here, we specifically focus on modeling the effect of carbohydrate intake on glycemic levels of people with T2DM. The BG levels of T2DM patients show non-stationary behavior over long time scales reflecting gradual changes in the health condition. The observable BG behavior change could occur over time scales on the order of months. Therefore, it is possible to capture system dynamics with a mechanistic model over shorter time intervals, i.e., weeks, and use that information to forecast BG levels over the following few weeks. This type of predictive tool would be beneficial for T2DM patients in managing their disease. Thus, in this setting, we design the predictive framework to provide decision aid to T2DM patients in self-management.
Patients in the ICU typically have much more volatile physiological dynamics for at least four reasons: glycemic dynamics under continuous feeding are oscillatory, time delay of insulin on glucose production, the patients are acutely ill and their health state changes quickly because of their disease state, and the patients often receive dextrose-containing fluids and medications that impact glycemia such as glucocorticoids. These patients’ BG levels change rapidly and are often non-stationary in complex ways and on different time scales. On slower time scales, patients eventually leave the ICU because their health either improves or declines. But there can be fast time scale changes too due to interventions and/or sudden health-related events, such as a stroke. These health changes will lead to changes in the best-fit parameters of the model. In other words, the patient-specific model itself may change abruptly, in contrast to the T2DM case. Also, on average, 8%–10% of the ICU patients are diabetic and only 5% of those are T1DM patients. However, more than 90% of ICU patients require glycemic management and 10%–20% of them experience a hypoglycemic event over the course of management. Consequently, regardless of being diabetic or non-diabetic, they are typically given IV insulin to control BG levels.
More detail about these clinical settings can be found in Appendix A.
C. Literature review
Researchers have developed various mathematical models ranging from extremely simple to highly complex, using ODEs and machine learning (ML) to predict and describe human glucose metabolism. We discuss these efforts organized according to model usage.
Some mechanistic models are developed to investigate a specific phenomenon of the glucose–insulin system such as to understand the different phases of insulin secretion with respect to different glucose stimulation patterns, to estimate insulin sensitivity in the intravenous glucose tolerance test (IVGTT) setting, and to elucidate the cause of the ultradian (long-period) oscillations of insulin and glucose.2–8 Others have developed models by clinically minded motivations to describe -cell mass, glucose, and insulin dynamics and to investigate T2DM pathophysiology.9–12 Some researchers developed models to describe the underlying system in more detailed way such as the events that occur during oral glucose ingestion,13,14 or relevant organ systems.15 Mari et al. provide a nice review of the models developed for clinical and physiological investigation of BG homeostasis and T2DM.16
Researchers have developed mechanistic models to address challenges including fast evolution of the underlying system (parameter variation in time), wide variation in clinical response within and between patients, sparse measurements, and concerns about safety issues with the goals of prediction and control of BG levels.17–27 Others developed stochastic (mechanistic) models with the same purpose.28–34
Glucose control based on mechanistic modeling is the focus of the artificial pancreas (AP) project in the type 1 diabetes mellitus (T1DM) setting. An artificial pancreas consists of a glucose sensor, an insulin pump, and a mathematical model-based algorithm to predict optimal amount of insulin delivery. These devices are currently used by T1DM patients to regulate their BG levels.35–37 Several nonlinear and complex models of glucose–insulin dynamics are developed to be used within AP systems.38–42 There are also nonlinear but relatively simple models43,44 and linear models45 developed to reduce parameter identifiability issues and computational cost. Accounting for the physiological effects of exercise on glucose–insulin regulation is important for accurate insulin delivery during exercise for T1DM patients. Others developed models to represent the system dynamics during exercise.44,46,47 On the other hand, some models are developed to provide a virtual testing environment for closed-loop glucose regulation algorithms.48,49 Chee et al. give a comprehensive range of BG control algorithms.50 Finally, other researchers conducted clinical trials to compare the efficacy between different closed-loop artificial pancreas systems and sensor-assisted pump therapy for T1DM patients.51–55
ML approaches have been proposed in pure prediction tasks such as predicting next glucose values or hypoglycemia. For these purposes, some researchers used classification methods and neural network models,56–62 while others used ARIMA (auto-regressive integrated moving average) and linear regression models.63–70
Finally, Miller et al. developed a hybrid model balancing a physiological and statistical model of glucose–insulin dynamics to forecast long-term BG levels of T1DM patients based on real-world data, showing the possibility of outperforming the forecasting of BG levels obtained by either pure physiological or pure statistical models alone.71
Patient-centered disease self-management is a crucial tool to improve health condition of patients focusing on their needs, life style, and preferences. Some researchers investigated techniques for effective self glycemic management and developed computational model-based decision support tools for T2DM patients.72–81
In all of the models discussed above, parameter estimation plays a vital role in the accuracy of predictions. Parameters are rarely directly measurable, and their values will vary from one patient to another. There are two overarching approaches to estimating parameters, optimization where a model-data mismatch is minimized to determine parameters,82 and the Bayesian approach83 where the distribution of the parameters, given the data and given the assumed (noisy) model-data framework, is computed. Researchers used various approaches for parameter estimation. The most common approaches are the standard least squares optimization,18,84 nonlinear least squares optimization,85 and Bayesian approach to estimate both time-invariant and time-varying model parameters.86
D. Our contribution
Our contribution in this paper is summarized below.
-
•
We develop a simple, interpretable, modeling framework limited to states and parameters that are directly observable or inferable from data for prediction within the human glucose–insulin system, based on a continuous time linear, Gaussian, stochastic differential equation (SDE) for glucose dynamics, in which the effect of insulin appears parametrically.
-
•
We completely describe the necessary inference machinery—in a data assimilation and inverse problem framework—to estimate a SDE model of glucose dynamics with real-world data.
-
•
The framework is sufficiently general to be usable within the ICU, T2DM, and potentially T1DM settings.
-
•
The model has analytical solutions, which means that it does not require numerical solver and the prediction could quickly be obtained in an online setting. Hence, the model could easily be used in any platform for prediction based on real-world data.
-
•
We demonstrate, in a train-test setup, that the models are able to fit individual patients with reasonable accuracy, both ICU and T2DM data are used. The test framework we use is a predictive one laying the foundations for future control methodologies.
-
•
Comparison of the data fitting for T2DM and ICU patients reveals interesting structural differences in their glucose regulation.
-
•
We compare the predictive power of our stochastic modeling framework with that of more sophisticated models developed for both T2DM and the ICU, demonstrating that the simple stochastic approach is at least as accurate as these models in both settings.
The intended audience of this paper is interdisciplinary. Approximating a nonlinear, complex, time delayed system with a stochastic model with parameters that can be estimated with real-world data is the core of this paper. Here, we use a linear stochastic model to approximate these dynamics, where the deterministic chaos is represented with a stochastic process. Understanding what is possible given data, and what is gained and lost with respect to the representation of a deterministic system by a stochastic model is focused at the dynamical systems community. However, we also develop a new model of BG dynamics, and this is important for endocrine modelers and the clinicians who may find such a model useful, especially in the context of ICU glycemic management and T2DM educators. Similarly, the model construction, and the formulation of the analytical solution of parameters given data may be of interest to engineers or dynamical systems researchers interested in applying control to the BG system.
In Sec. II, we introduce the general continuous-time mathematical model (Sec. II A) and its specific versions relevant in T2DM and ICU settings (Sec. II B). The two model classes all derive from a single general model and differ according to how nutrition uptake and glucose removal are represented. In Sec. III, we construct the framework for stating the parameter estimation problem and its solution. In Sec. IV, we describe the datasets, the experiments we design for parameter estimation and forecasting, and the methods we use for parameter estimation and forecasting for the T2DM and ICU settings. Section VI presents the experimental results on parameter estimation and forecasting along with some uncertainty quantification (UQ) results separately for T2DM and ICU settings. Finally, in Sec. VII, we make some concluding remarks and discuss future directions that we intend to pursue.
II. MODEL DEVELOPMENT
A. Continuous-time model
To begin construction of a simple, one-state model for glucose dynamics, we first consider the classical two-state Bergman equations3
| (1a) |
| (1b) |
Here, denotes the plasma glucose concentration and denotes the plasma insulin concentration. External inputs of nutrition and insulin are given by and , respectively. The insulin dynamics, beyond external forcing, are primarily governed by a glucose-dependent secretion rate , insulin-producing beta-cell mass , and linear degradation rate . The glucose dynamics, aside from external forcing (i.e., meals), are driven by a glucose-dependent (insulin independent) hepatic glucose production , an insulin-dependent glucose removal rate (with insulin sensitivity factor ), and a linear degradation rate .
In this work, we hypothesize that the pancreatic and hepatic regulation of glucose can instead be approximated by a simple function of glucose . We also account for the effect of external insulin to the blood glucose level and add a closure term, . This results in a new single-state equation
| (2) |
where the closure term accounts for additional glycemic dynamics not captured by the first three terms. To begin evaluating the utility of this perspective, we choose simple forms for these unknown functions.
Specifically, we assume that glucose regulation can be roughly approximated by an exponential decay to a fixed point at rate such that . We also assume that the effect of external insulin delivery has a simple relationship with proportionality constant and we denote (t) by for ease of exposition. Finally, we assume that the possibly large residual errors induced by these simplifying assumptions are given by a Brownian motion with variance quantified by , i.e., . Note that, the term, is included to actually have to represent the variance of the process and is a relaxation time scale. Although counter intuitive in this representation, the solution of the event time model, given in (4) below, shows the variance of the system dominantly represented by . These choices yield the following Ornstein–Uhlenbeck model for the evolution of blood glucose :
| (3) |
There are four parameters for the model in Eq. (3). (mg/dl) is the basal glucose (i.e., the mean of the unforced process), (1/min) is the decay rate for the exponential mean reversion, (mg/(dl*U)) is a proportionality constant for the linear effect of IV insulin-based glucose removal, and (mg/dl) governs the variance of the oscillations described by .
We use simple models for the meal function and the insulin delivery function (defined in Sec. II B) that enable explicit solution of the continuous time model between events, which refer to meal or insulin delivery or BG measurements.
The simple linear Gaussian structure of Ornstein–Uhlenbeck models, along with appropriately simple forcing terms (defined in Sec. II B), allows for tractable solutions to Eq. (3). Specifically, integration of the system leads to a solution that is normally distributed with analytically calculable mean and variance.
B. Event-time model
For computational purposes, and because data are typically available at discrete times, we develop a discrete-time version of the model (3). The time discretization is informed by the events as defined above. We define event times as times at which the meal or insulin delivery functions change discontinuously, or BG is measured. The ordered collection of all these recorded times is the discrete times. We first present the event-time model in generality, then develop it specifically for outpatient T2DM glucose modeling (see Sec. II B 1) and for inpatient ICU glucose modeling (see Sec. II B 2). Note that ICU and T2DM settings are also the focus for our data-driven studies.
The time discretization is defined completely by a dataset in the following sense. Let denote the times of relevant nutrition events, let denote the times of relevant insulin delivery events, and let denote the times of glucose measurements. We call the re-ordered union of these sets,
as event times, where the superscripts, , , and , are used to distinguish the relevant nutrition delivery, insulin delivery, and BG measurement times, respectively.
We can obtain the following event-time model by integrating (3) over the event-time intervals, for , via use of the Itô formula,87 which is equivalent to using integrating factors in this case:
| (4) |
where and independent random variables. We exhibit specific versions of this general event-time model for T2DM and ICU settings in more detail in the following sections.
1. T2DM model
Based on the conditions of T2DM setting detailed in Sec. I and Appendix A, we set , i.e., we ignore the exogenous insulin term in the T2DM event-time model. The meal function, , on the other hand, is essential for capturing the uptake of glucose into the bloodstream from consumed carbohydrates. Here, we define as the difference of two exponential functions (this choice was shown to be effective in the T2DM case88),
| (5) |
where is the time of the th meal, (mg/dl) is the total amount of glucose in the th meal divided by the approximate volume of blood, and is a dimensionless normalizing constant so that . Note that is the indicator function and defined as
Therefore, the model in (3) becomes
| (6) |
in the T2DM setting. In this model, the first term represents the body’s own effect to remove insulin from the bloodstream, the second term represents the effect of nutrition on the rate of change of BG, and the last term models the unmodeled dynamics by the first two terms as white noise. Integrating over , we can write the analytic solution of this equation as
| (7) |
Note that, in practice, we need to evaluate the BG level at specific time points and hence need the discrete-time model implied by the continuous time representation in (7). Now, by integrating (6) over and denoting , we obtain
| (8) |
as a special case of (4). Also, for any fixed , find the meal times such that and denote the index set of these meal times by . Then, in (8) becomes
| (9) |
In this case, we have five model parameters to be estimated: . Recall that in this setting, represents the basal glucose value that the BG level stays around starting some time after nutrition intake until the next nutrition intake. represents the decay rate of BG level to after the nutrition intake, and represents the amplitude of the BG level oscillations. The parameters and entering the meal function implicitly control the time needed for the glucose nutrition rate to reach its peak value, and the time needed for this rate to return back to the vicinity of . Because of these simple physiological meanings, the parameters entering the event-time model are important not only for accurately capturing and predicting glucose dynamics based on data, but also contain implicit information about the health condition of the patient. For example, the basal glucose value is measured during some tests to check if an individual is healthy pre-diabetic, or diabetic.
2. ICU model
The specifics of the ICU setting and the available data, as described in Sec. I B and Appendix A, defines the structure of our ICU model. In this case, we model both the carbohydrate intake, , and IV insulin delivery, .
We choose to model these external forcings as piecewise constants functions; this choice corresponds to clinical practice, in which constant infusions are periodically adjusted, and also allows for simple calculations.
Here, we define the nutritional forcing function as
| (10) |
where is the time at which a clinician changes the nutrition delivery rate, is the nutrition rate over the time interval ; these features are both directly available in our clinical dataset.
Similarly, we define the external insulin delivery rate as
| (11) |
where is the rate of insulin over the time interval , again obtained directly from the dataset.
Therefore, substituting (10) and (11) into the general equation (3), the ICU version of the model becomes
| (12) |
In this model, the first term models the glucose removal rate with the body’s own effort ( ), the second term shows the effect of nutrition on the BG level, the third term, , models the external insulin effect, and the last term models unmodeled dynamics by the first three terms as a white noise term.
We integrate (12) to get the analytical solution for any as follows:
| (13) |
As in the previous section, we can also integrate (12) over to obtain solutions at event-times, with ,
| (14) |
as another special case of (4). Here, we have four model parameters to estimate: . Remember once again, is the basal glucose value and is the decay rate of the BG level to its basal value, and is a measure for the magnitude of the BG oscillations. Finally, is a proportionality constant, which is used to scale the effect of IV insulin on the BG rate change appropriately. These four parameters represent physiologically valid quantities that could properly resolve the mean and variance of the BG level.
III. PARAMETER ESTIMATION
In this section, we formulate the parameter estimation problem. We construct an overarching Bayesian framework for our parameter estimation problems. We then describe two solution approaches for this problem: an optimization based approach which identifies the most likely solution, given the model we developed and data assumptions; and Markov Chain Monte Carlo (MCMC), which samples the distribution on parameters, given data, under the same model and data assumptions. These two solution approaches are detailed in Appendices D and E.
As shown in detail before, the model takes slightly different forms in the T2DM and ICU settings. In the former, the model parameters to be estimated are , whereas in the latter, the unknown parameters are . However, we adopt a single approach to parameter estimation. To describe this approach, we let the vector, represent the unknown model parameters to be determined from the data, noting that this is a different set of parameters in each case. Many problems in biomedicine, and the problems we study here, in particular, have both noisy models and noisy data, leading to a relationship between parameter and data of the form
| (15) |
where unknown is a realization of a mean zero random variable, but its value is not known to us. The objective is to recover from . We will show how the model of the glucose regulatory system developed here leads to such a model.
The Bayesian approach to parameter estimation is desirable for two primary reasons: first, it allows for seamless incorporation of imprecise prior information with uncertain mathematical model and noisy data, by adopting a formulation in which all variables have probabilities associated to them; second, it allows for the quantification of uncertainty in the parameter estimation. While extraction of information from the posterior probability distribution on parameters given data is challenging, stable and practical computational methodology based around the Bayesian formulation has emerged over the last few decades.89 In this work, we will follow two approaches: (a) obtaining the maximum a posteriori (MAP) estimator, which leads to an optimization problem for the most likely parameter given the data, and (b) obtaining samples from the posterior distribution on parameter given data, using MCMC techniques.
Now, let us formulate the parameter estimation problem. Within the event-time framework, let be the vector of BG levels at event times , and be the vector of measurements at the measurement times . By using the event-time version, and defining to be independent and identically distributed standard normal random variables, we see that given the parameters , has a multivariate normal distribution, i.e., . Equivalently,
| (16) |
Let be a matrix that maps to . That is, if a measurement is taken at the event time , , then the th row of has all 0’s except the st element, which is 1. Adding a measurement noise, we state the observation equation as follows:
| (17) |
where is a diagonal matrix representing the measurement noise. Thus, we obtain the likelihood of the data, given the glucose time-series and the parameters, namely,
However, when performing parameter estimation, we are not interested in the glucose time-series itself, but only in the parameters. Thus, we directly find the likelihood of the data given the parameters (implicitly integrating out ) by combining (16) and (17) to obtain
| (18) |
where . Since has a multivariate normal distribution, using the properties of this distribution, we find that given the parameters, , also has a multivariate normal distribution with mean and covariance matrix . This is the specific instance of Eq. (15) that arises for the models in this paper.
We have thus obtained , that is,
| (19) |
this is the likelihood of the data, , given the parameters, . Also, since we prefer to use rather than directly using for the sake of computation, we state it explicitly as follows:
| (20) |
Moreover, by using the Bayes theorem, we write
| (21) |
Note that the second statement of proportionality follows from the fact that the term, , on the denominator is constant with respect to the parameters, , and plays the role of a normalizing constant.
From another point of view, considering (16) and (18), we see that given , has a multivariate normal distribution with mean and covariance matrix that could be computed from the above equations since, given , everything is explicitly known. Then, integrating out, in other words, computing the marginal distribution, we obtain the distribution of , which corresponds to the one stated in (18).
Now, to define the prior distribution , we assume that the unknown parameters are distributed uniformly across a bounded set and define
| (22) |
where is the indicator function and is the volume of the region defined by . Thus, by substituting the likelihood, (19), and the prior distribution, (22), into (21), we formulate the posterior distribution as follows:
| (23) |
Then, we use this posterior distribution to state the parameter estimation problem, whose details can be found in Appendix D.
IV. EXPERIMENTAL DESIGN
In this section, we describe the datasets in more detail, the experiments that we design to present our results, and the methods that we follow to perform parameter estimation and forecasting. Depending on the specifics of each case and to reflect the real-life situation, we designed different experiments in the T2DM and ICU settings. However, the mathematical approaches for parameter estimation and forecasting stay the same for both settings because we use similar mechanistic models.
We theoretically define the observational noise covariance , given in (17), to be a diagonal matrix with the form , which represents that it is proportional to the mean BG level. However, we observed that the variation in glycemic response, which we will define later more formally, is the sum of the measurement noise and personal glycemic variation, accounted by the model parameter, . Because of this relationship, for more accurate estimation of , we set the measurement noise to 0. Note that this is only a practical choice and with this choice, we can still estimate the variation in glycemic response accurately.
A. T2DM
1. Model, parameters, and dataset
In this setting, we use the model (8) with the function defined as in (9). Hence, there are five parameters to be estimated: basal glucose value, , BG decay rate , the measure for the amplitude of BG oscillations, , and and , which are the parameters implicitly modeling the time needed for the rate of glucose in the nutrition entering the bloodstream to reach its maximum value and the total time needed for this rate to decrease back to 0. We assume that the prior distribution is non-informative and initially the parameters are independent, except for a constraint on the ordering of and . We determine realistic lower and upper bound values for each of them, define (in the order of ), and then define from by adding the constraint We thereby form the prior distribution as defined in (22). Recall that these bounds define the constraints employed when we define the parameter estimation problem in the optimization setting for the MAP point. The set is determined from clinical and physiological prior knowledge, and by simulating the model (6) and requiring realistic BG levels.
The self-monitoring T2DM dataset is from a previous prospective self-management trial. It contains the carbohydrate intake in the meals and one to two BG measurements collected before and after the meals with the corresponding timing of each event. The carbohydrate amounts are reviewed and confirmed by expert nutritionists. None of the T2DM patients in our dataset took exogenous insulin to control their BG level. This means that the carbohydrate intake is the only input to the model developed here. More information on the dataset can be found in Table I.
TABLE I.
Information about the dataset that is used in the T2DM setting, which is collected from three different T2DM patients. Note that there is a considerable variability between the data collection behavior of each patient, which is also reflected in the number of recorded measurements and meals. Also, recall that we intentionally used one week of data for training and the following three weeks of data for testing.
| Patient ID | Patient 1 | Patient 2 | Patient 3 |
|---|---|---|---|
| Total # glucose measurement | 304 | 211 | 91 |
| Total # meals recorded | 122 | 76 | 46 |
| Total # days measured | 26.6 | 27.67 | 28.12 |
| Mean measured glucose | 113±25 | 127±32 | 124±26 |
| Training set: # glucose measurement | 80 | 53 | 29 |
| Training set: # meals recorded | 26 | 18 | 15 |
| Training set: # days measured | 7.02 | 7 | 7.05 |
| Training set: mean measured glucose | 112±25 | 116±28 | 125±24 |
| Testing set: # glucose measurement | 224 | 158 | 62 |
| Testing set: # meals recorded | 96 | 58 | 46 |
| Testing set: # days measured | 19.58 | 20.67 | 21.07 |
| Testing set: mean measured glucose | 113±25 | 130±33 | 123±27 |
2. Parameter estimation and uncertainty quantification
We perform parameter estimation for three patients separately. First, we estimate parameters by using data over four consecutive, non-overlapping time intervals with optimization and MCMC approaches. Besides estimated values, we also provide UQ results. In the optimization setting, we use the Laplace approximation as detailed in Appendix D. The optimal parameters determine the mean of the Gaussian approximation, and the inverse of the Hessian matrix becomes the covariance matrix, providing the tools for UQ. In the MCMC approach, we use the resulting random samples for UQ.
3. Forecasting
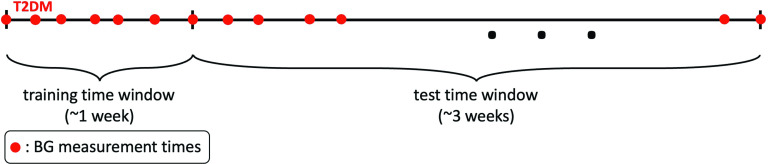
We adopt a train-test setup as follows. Since the health conditions of the T2DM patients are unlikely to change over time intervals that are on the order of days, we design an experiment in which we use one week of data for estimating the patient-specific parameters. Then, we use the estimated parameters to form a patient-specific model and use this model to forecast BG levels for the following three weeks, using the known glucose input through the meals; this leads to a three-week testing phase. We provide a visual representation of this process in Fig. 1. From a practical patient-centric point of view, this leads to a setting in which forecasting BG levels for the following three weeks require patients to collect BG data for only one week in every month, and then the patient-specific model will be able to capture their dynamics and provide forecasts based on nutrition intake data over the rest of the month.
FIG. 1.
This schema shows how we divided T2DM patients’ data into training and test time windows. For each patient, the first week of data is the training time window used to estimate the model. The estimated model represents each patient’s personalized BG behavior and is used to forecast BG values over the test time window, which is of length three weeks and follows the training time window.
B. ICU
1. Model, parameters, and dataset
In the ICU setting, we use the model (14), and there are now four parameters to be estimated: basal glucose value, , BG decay rate, , the parameter used to quantify the amplitude of the oscillations in the BG level, , and a proportionality constant, to scale the effect of insulin IV on the BG level. Similar to what we did in the T2DM setting, we find realistic lower and upper bounds for the unknown parameter values and set to obtain the prior distribution as defined in (22). In this case, we impose two further linear constraints, namely, and . These constraints are imposed to ensure that the model predictions remain biophysically plausible and are determined simply by forward simulation of the SDE model; the resulting inequality constraints do not overly constrain the parameters in that good fits can be found which satisfy these constraints, and yet they yield more realistic BG level behavior than solutions found without them. Thus as in the T2DM case, we choose the bounds and the constraints based on physiological knowledge and requiring simulated BG levels resulting from values within the region to be realistic.
The retrospective ICU dataset is extracted from the Columbia University Medical Center Clinical Data Warehouse. It contains carbohydrate rate through the enteral feeding tube, IV insulin rate, BG measurements, and the timing of all these events. It is important to emphasize that we do not have plasma insulin or interstitial insulin rate, as they are collected rarely. The carbohydrate and IV insulin rates are the inputs to the model. Considering the highly non-stationary behavior of the system, the BG measurements are sparse, at most 15 measurements per day. In this case, we aim this predictive framework to be used as a clinical decision support tool in the ICU setting. Summary statistics about our ICU dataset can be found in Table II. Note that in this case, we used all available data for each patient to perform parameter estimation and forecasting, and all three ICU patients are non-T2DM.
TABLE II.
Information about the dataset that is used in the ICU setting, collected from three ICU patients who are not T2DM. Because of the experiment we designed, the training sets are moving with by overlapping with each other. So, we provide average number of glucose measurements over these moving windows. Also, since we forecast until the next measurement time following the training time window, each testing set contains only one glucose measurement. Other information that is included in Table I, but not here, such as mean measured glucose over training set(s) is neither meaningful nor helpful in this setting.
| Patient ID | Patient 4 | Patient 5 | Patient 6 |
|---|---|---|---|
| Total # of glucose measurement | 177 | 204 | 271 |
| Total # of days measured | 13.99 | 16.8 | 24.48 |
| Mean measured glucose | 141±18 | 151±32 | 151±43 |
| Training set: average # of | |||
| glucose measurement | 14.13 | 13.5 | 14.07 |
| Testing set: average # of | |||
| glucose measurement | 1 | 1 | 1 |
2. Parameter estimation and uncertainty quantification
We use both the optimization and MCMC approaches for parameter estimation in a patient-specific manner, in this setting, too. However, for UQ, we use only MCMC to estimate the posterior mean and variance on the parameter; this is because there were cases where it was not appropriate to use the Laplace approximation, something that will be explained in more detail in Sec. VI B.
3. Forecasting
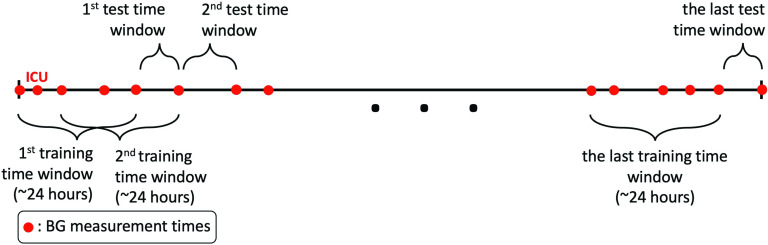
The characteristics of the health conditions of ICU patients are described in Sec. I B and Appendix A. The abrupt changes in their health conditions are reflected in the model parameters. To avoid compensating for different values of parameters over longer time intervals, and to make more accurate predictions, we use only one day of data for parameter estimation in the ICU. Moreover, to construct an experiment that reflects real-life scenarios, we need be able to estimate the model parameters with smaller size datasets than in the T2DM case, because of the imperative of regular intervention within the ICU setting, typically on a time scale of hours. As a consequence our train-test setup in this case differs quantitatively from the T2DM case. The training sets for each patient consist of approximately one day of data over a moving time intervals, with end points chosen to be BG measurement times. Thus, the time windows are obtained by moving the right end point to the next BG measurement time and choosing its left end point with the constraint that it contains approximately one day of data. In this case, there is a large overlap between the consecutive time windows of the training sets.
On the other hand, because of rapidly changing conditions, forecast of BG levels needs only to be accurate over shorter time scales. It is important to know glycemic dynamics on the order of hours (not days) to manage the glycemic response of ICU patients. Thus, the test time windows include only one BG measurement, which is the next BG measurement collected right after the BG measurement defining the right end point of the corresponding training time window. We follow the same procedure over the moving time intervals to the end of the whole dataset for each patient. We visually exhibit this procedure in Fig. 2. From a practical point of view, this experiment exhibits a real-life situation in which we use only one day of data for parameter estimation and then perform forecasting for the next few hours based on the estimated parameters. Such a setup would be desirable as a support to glycemic management of these patients.
FIG. 2.
This schema shows our experimental design for the ICU setting. Each training time window has a length of approximately 24 h, which is used for model estimation. Then, we forecast the first BG value measured after the training time window. We perform this prediction for the whole dataset by moving the time windows.
V. MODEL EVALUATION
In this section, we introduce the statistics that we will use to evaluate and compare the forecasting capability of the models. Let denote the true BG measurements over the predefined testing time window for an experiment. Let denote the forecast obtained by a model at the measurement time points. Note that for a stochastic model, represents the mean of the model output. When a stochastic model is used, it is natural to obtain a confidence interval as this may be obtained as a direct consequence of the fact that the model output is in the form of a random variable; such an output cannot be obtained for an ODE model when parameters are learned through optimization. However, by using appropriate parameter and state estimation techniques, it may again be possible to obtain a similar kind of confidence interval for the model output which is in the form of a point-estimate. When we have probabilistic forecasts, we let denote the corresponding standard deviation for each forecast at the true measurement points so that we can form 1- and 2-stdev bands as and , respectively. Then, for each model, we can compute the percentage of true measurements, , that are captured in their respective 1- and 2-stdev bands. These percentages will be the tools that we will use for evaluation. In addition, we will use standard measures such as root-mean-squared error (RMSE), mean percentage error (MPE), and Pearson’s correlation coefficient, (CORR) which are computed as follows:
In addition to these metrics, we compare the forecasting accuracy of this model with other physiology-based mechanistic models. In the T2DM setting, we use the longitudinal diabetes pathogenesis model (LDP),90 describing BG dynamics of T2DM patients. In the ICU setting, we use ICU Minimal Model (ICUMM),18,85 describing BG dynamics of ICU patients. Also, in both settings, we use the mean and variance computed from the respective training data for comparison. We call this model, mean-variance model. We provide more detail about these models in Secs. VI A 3 and VI 2 3.
Here, by comparing models, we mean comparing their forecasting ability given available data and the limitations of model estimation. Both the LDP model and ICUMM are nonlinear mechanistic models while the model developed here is a linear mechanistic model. To compare models, we must optimize the models or computationally solve for model parameters that minimize the distance between model output and data. Model estimation problems formulated based on a nonlinear model requires solving a nonlinear optimization problem. Solutions to nonlinear optimization problems often have multiple global minima, but it is not possible to know for sure how many global minima exist nor whether you have found one of them. In contrast, solutions to quadratic optimization problems have a unique minimum that produces the optimal solution to model the estimation problem. In the setting here, we are comparing a model whose global optimal parameters can be calculated and known vs models for which these the global optimal parameters cannot be known. Because of these characteristic differences, an absolute comparison between models that require nonlinear optimization methods to compute parameters and models for which quadratic optimization methods are used is not possible. Therefore, comparison of prediction accuracy between these different types of models should be carefully handled. For example, obtaining a smaller error with a linear model does not imply that this model is better than the nonlinear model, as it is unknown if the global minimum is reached by the nonlinear model. However, comparing the prediction accuracy is useful to have a sense of the level of prediction accuracy achieved by these models.
VI. RESULTS
In this section, we present results concerning the simple yet interpretable model introduced in this paper; we now refer to this as the minimal stochastic glucose (MSG) model. The two primary conclusions are that:
-
•
We obtain BG forecasting results at least as accurate as other established models in both the T2DM and ICU settings,85 and the uncertainty bands with which we equip our forecasts play an important role in this regard;
-
•
We learn a substantial amount about the interpretable parameters within the models, with possible clinical uses deriving from the parameter estimates, and from tracking them over time, again using the uncertainty measures that accompany them as measures of confidence.
The combination of simple predictive model and data acquisition accounts for the uncontrolled and complex nature of the data, including data sparsity, inaccuracy, noisiness, non-stationarity, and biases resulting from the health care process,91–98 while also being interpretable and leading to patient-specific parameter inference and prediction. Even though the MSG model is relatively simple it is not always identifiable, given data. For example, having two parameters, and , related to BG decay rate in the ICU context made it hard to identify these parameters accurately because of the complexities mentioned above. Despite lack of identifiability of some parameters, parameters as estimated lead to models which are able to forecast and represent the glucose dynamics. To answer whether the parameter estimates, forecasts, and uncertainty quantification are good enough to impact clinical understanding and decision-making or to construct physiologically-anchored phenotypes would require evaluation,76,99,100 e.g., manual chart review in conjunction with a qualitative trial of clinical decision-making or a phenotyping analysis, respectively. In the absence of these analyses, we will rely on face validity,101–103 to evaluate effectiveness of the model in representing the dynamics and in forecasting.
A. T2DM
In this setting, our results demonstrate the effectiveness of the MSG model in capturing the patients’ BG dynamics. Specifically, the effectiveness is reflected in the estimated parameter values and in forecasting future BG levels, using these parameters, over time periods of length up to three weeks.
1. Parameter estimation
Our results exhibit three substantive pieces of evidence that support the validity of the model and its potential effectiveness for understanding the physiologic state of an individual and forecasting. First, the estimated model parameter values and their evolution over time are physiologically valid. That is, the estimated values reflect the patient’s state as evaluated given available data. Moreover, the evolution of the estimated parameter values over time reflects changes in the patients’ states in a manner consistent with both the data and what is known about the non-stationary nature of T2DM. Second, the UQ intervals for the estimated parameters are physiologically plausible and have three features that make the model potentially useful: (i) relative to the value of the estimated parameter, the UQ intervals are wide enough to provide information on the reliability of the point estimates, (ii) the UQ intervals’ evolution over time, demonstrating sensitivity to time and the ability to adapt to non-stationary patients, and (iii) the UQ intervals are narrow enough to plausibly be used to differentiate behavior choices, such as carbohydrate consumption. And third, the UQ and parameter estimation appears to be robust; different estimation methods arrive at similar results. A comparison of the estimated parameter values and corresponding UQ intervals obtained using optimization and MCMC are very similar in almost all of the cases, supporting the robustness of the estimates and relative insensitivity to the estimation methodology. Together, these features imply that with a reasonable inference scheme, this model could provide useful information for decision-making and a robust clinical understanding of the patient.
To demonstrate that the estimated parameters are physiologically valid, consider Fig. 3 where we see the point estimates and UQ intervals for all parameters and all three patients obtained with optimization and MCMC methods. The estimated basal glucose, , values are in the ranges of – mg/dl, – mg/dl, and – mg/dl over the course of four weeks for patients 1, 2, and 3, respectively. These values are indeed in the expected ranges based on the BG measurements of these patients.
FIG. 3.
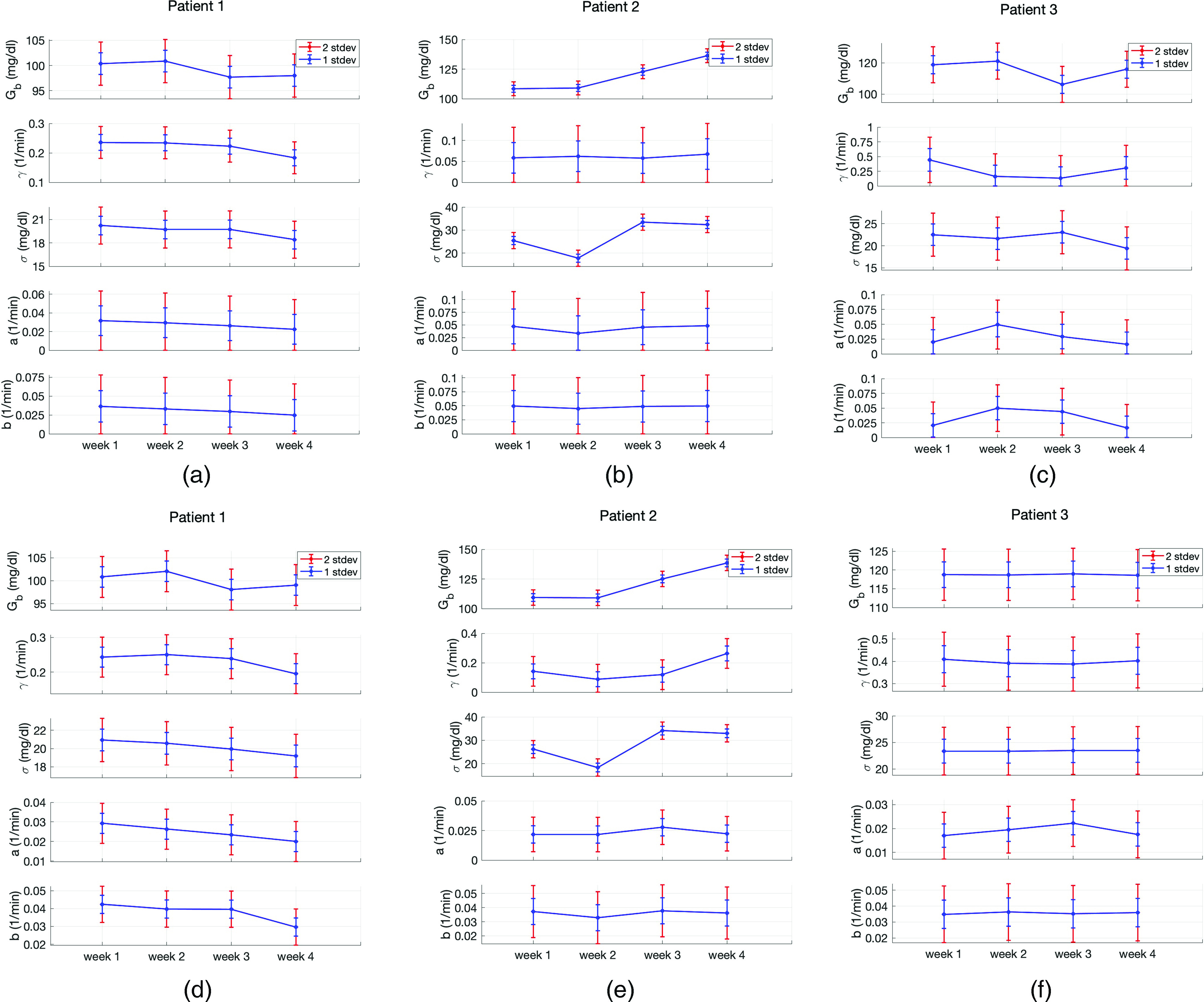
Parameter estimation and uncertainty quantification in the T2DM setting. Panels (a)–(c) show results obtained with optimization and panels (d)–(f) show results obtained with MCMC for patients 1, 2, and 3, respectively. Both approaches are used in a patient-specific manner. We see that the point estimates obtained with two approaches are very close to each other in most cases. Also the width of the 1- and 2-stdev intervals, which are obtained with Laplace approximation (optimization) and directly from the approximate posterior samples (MCMC), are also in agreement with each other. Here, these intervals quantify the uncertainty in the point-estimates of the parameters. The parameter estimates and agree with real physiological values and the non-stationary behavior of the glucose dynamics of T2DM patients is reflected in the time-evolving behavior of the estimated parameters. All these features enforce the reliability of the parameter estimation results.
To show that the UQ intervals are potentially useful in practice, once again consider Fig. 3. The range of UQ intervals for each estimated parameter in most cases contains physiologically plausible parameter values that are tight enough to enforce the reliability of the point estimates. To quantify this statement, we computed the coefficient of variation, defined as the standard deviation divided by the mean and can be interpreted as a measure of variability of the point estimator in this context. For and , which are the most influential parameters in characterizing the mean and variance of the model output, the coefficient of variation is in the – band and – band, respectively, for all three patients. These results support the reliability of the point estimates that are used to form patient-specific models to describe dynamics of each patient.
We can see the robustness of the estimated parameter values by comparing parameter estimates using two different methods, optimization, and MCMC. The results are shown in Fig. 3; the upper and lower panels show parameter estimates using optimization and MCMC, respectively. The point estimates as well as the corresponding UQ intervals for and obtained with optimization and MCMC are very close to each other in most cases. Some parameters have more variation between methods; specifically, , , and do show variation between the results obtained with optimization and MCMC methods. This variation does not seem to have substantial effect on the model’s ability to represent patient dynamics. The overall result is a model whose ability to represent the data is relatively insensitive to parameter estimation techniques.
2. Forecasting
We evaluate forecasting ability of the model in this setting along two pathways, a face validity pathway that is mostly motivated by potential clinical decision-making, and a more statistical-based pathway that is motivated by our desire to be quantitative. In a sense, both evaluations address whether the data could plausibly be generated by the model.
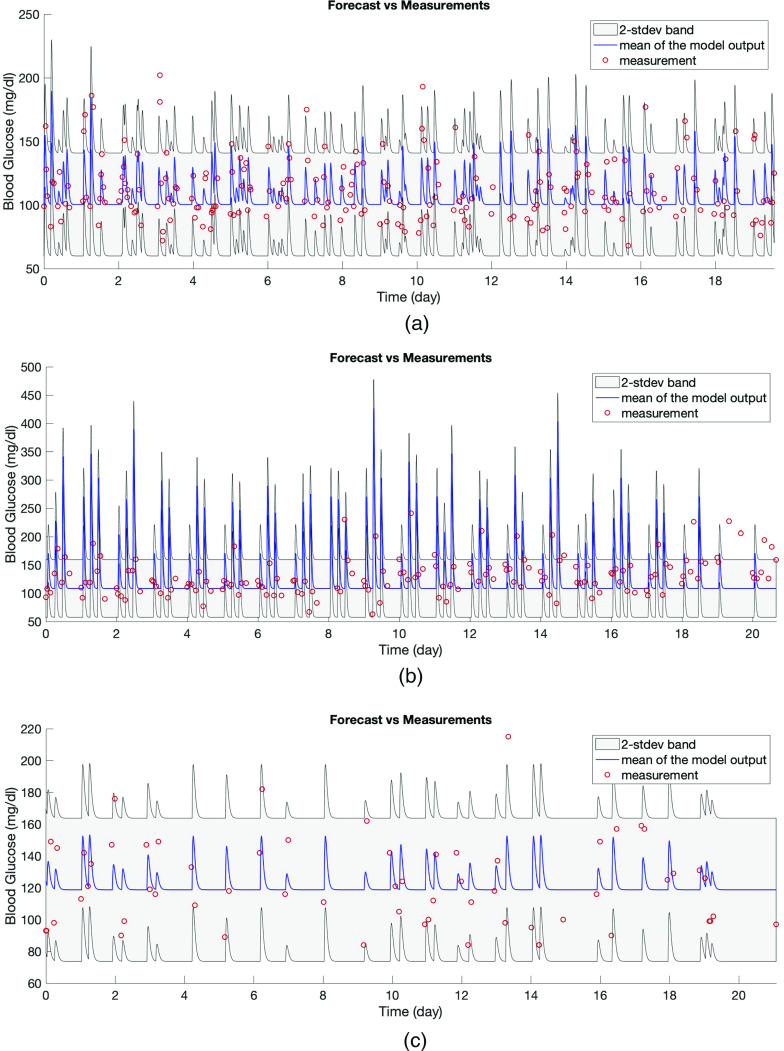
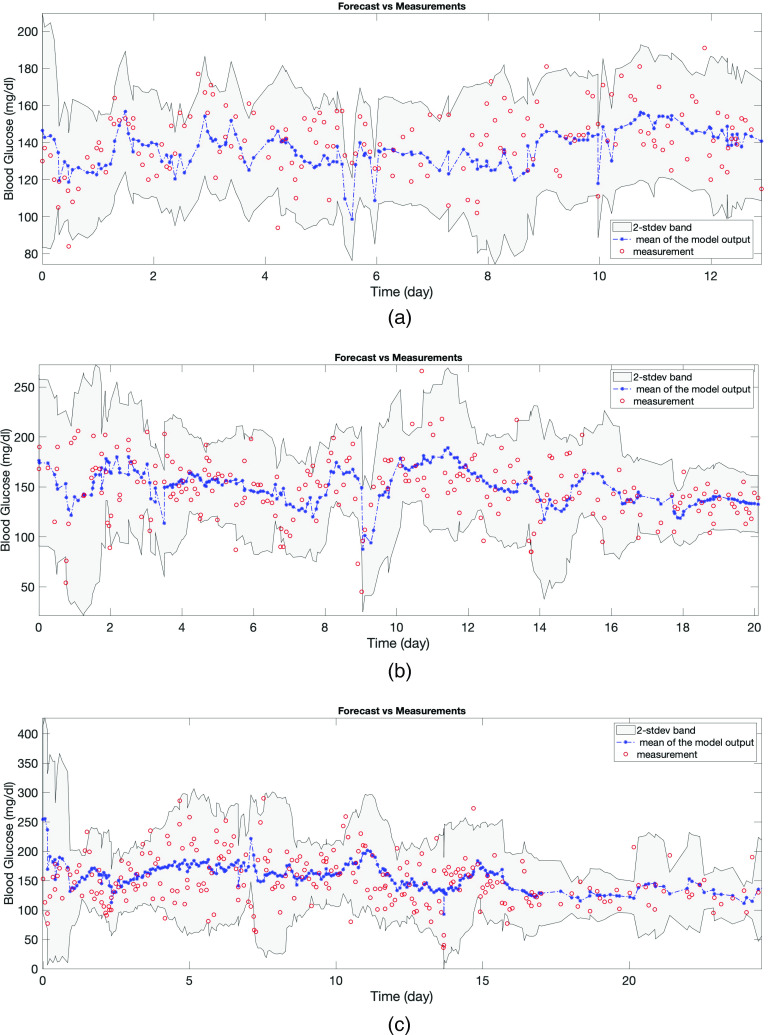
The first evaluation—face validity—is to consider whether the model can capture the dynamics qualitatively. Because the model’s forecast is in the form of a distribution, the forecast we have to evaluate is anchored to the mean and standard deviation. In Figs. 4(a) and 5, the red circles are the BG measurements and from our modeling perspective are also a realization of the stochastic process whose mean is shown by the blue curve and variance is represented by the gray region. Figure 4(a) shows the training time window for one of the patients and Figs. 5(a)–5(c) show the test time window for each patient. An initial inspection of these figures implies that the model output seems to represent the data well. Figure 5 demonstrates the model’s effectiveness in quantifying the oscillating BG measurements with two standard deviation (2-stdev) bands around the model mean; these bands capture most of the future BG measurement. These results are further quantified in Table III that shows summary statistics for how often the future measurements were captured by the 2-stdev bands. Being able to contain – of the true BG measurements in these confidence regions for all three patients is an indicator of this model’s predictive capability. Because of more dangerous consequences of hypoglycemia, we also check the percentage of measurements that are smaller than the lower 2-stdev band, i.e., missed by the 2-stdev band on the lower-end, over the test time window, which are 1.79% (four measurements out of 224 total BG measurements), 0%, and 0% for patient 1, 2, and 3, respectively. These four measurements for patient 1 are 88, 94, 102, and 118 mg/dl, and the lower bound of the 2-stdev band for these measurements are estimated to be 94, 99, 105, and 123 mg/dl. Also, this patient had total of 31 BG measurements in the range of 68–88 mg/dl, and the estimated 2-stdev band missed only one of BG measurements (88 mg/dl) in that range and estimated the possibility of occurrence of all the remaining ones. This result shows that model could provide decision support for the possible occurrence of hypoglycemia. Thus, this model is providing substantial forecasting information beyond what is available given the data alone.
FIG. 4.
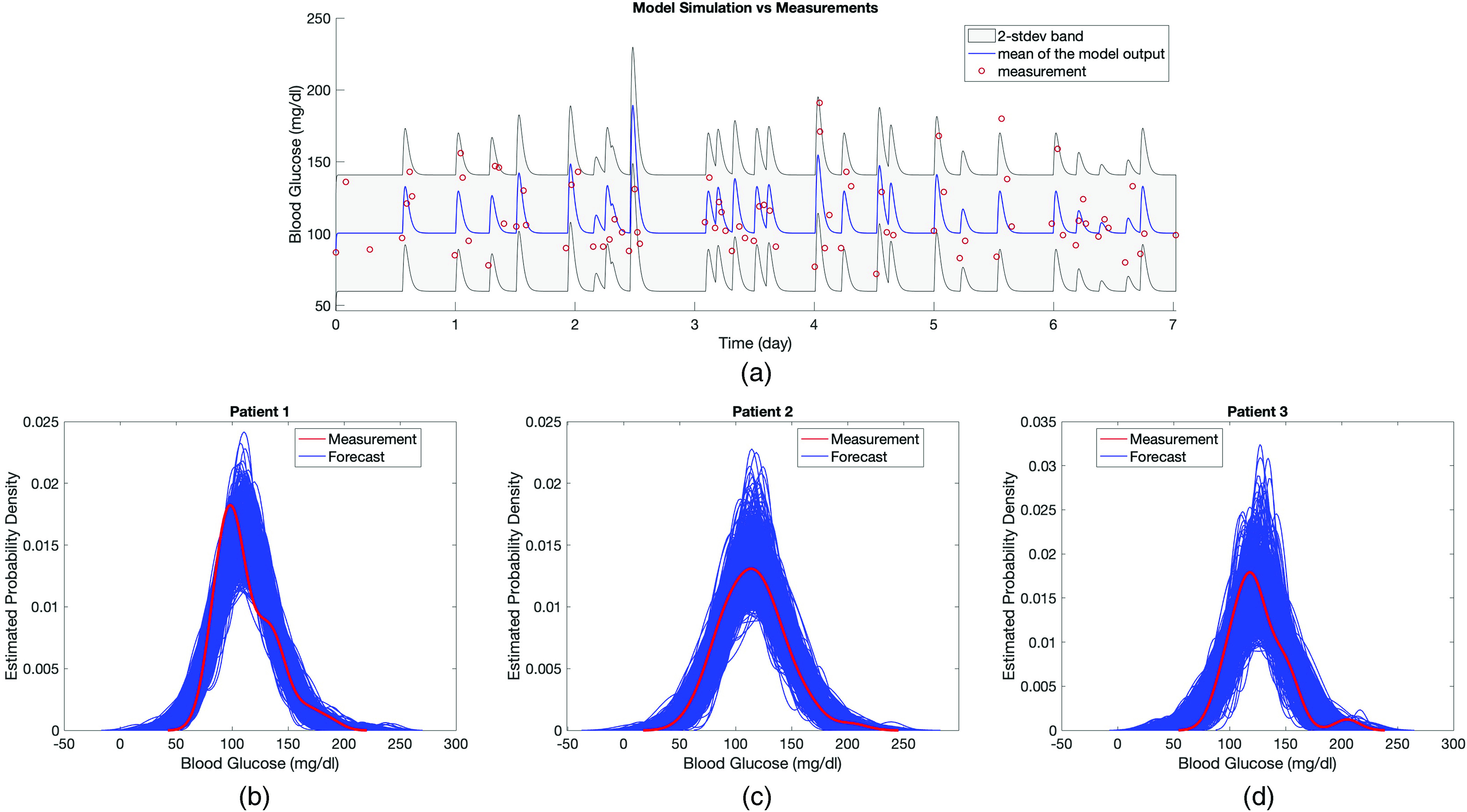
In panel (a), the model output of the estimated linear stochastic model is shown over the week of the training data along with the true BG measurements. Model output is a stochastic process and described by a mean and variance. The red circles show true BG measurements, the blue curve shows the mean of the model output, and the gray area represents the estimated 2-stdev band around the mean. Here 2-stdev band is used to quantify the oscillations of BG levels, which are not aimed to be tracked by the mean of the model output, but rather to be encapsulated by the gray region. The peaks in the model output show the BG response to the nutrition. Since the model aims to track the mean BG behavior (by blue curve) and capture the amplitude of BG oscillations (by the gray region), we plot the model output using a curve and a region. In panels (b)–(d), kernel density estimate (KDE) of 1000 different realizations of the estimated model output and BG measurements are shown for each patient. Comparison of the true BG measurements, which are assumed to be a realization of the model output, with the mean and 2-stdev band of the stochastic process—being the model output—along with the KDE plots in panels (b)–(d) implies that BG measurements could indeed be considered as a realizations of the random process.
FIG. 5.
Panels (a)–(c) show forecasting results in the T2DM setting obtained via models formed by using the estimated parameters with the optimization approach for patients 1, 2, and 3, respectively. In each plot, the red circles show the true BG measurements, the blue curve shows the mean of the model output, and the gray region is the estimated 2-stdev band around the mean of the model output, quantifying possible low and high values of the forecasted BG levels. These forecasting results show that the proposed model mean, when equipped with confidence bands found from standard deviations, estimate the BG levels accurately, and in a patient specific way. This reinforces the claim that the model parameters could be used to provide information about the health condition of individual patients.
TABLE III.
Comparison of the forecasting results with three different models. For each different case of the LDP model, the results in the corresponding row show which parameters are estimated during the whole forecasting experiment. We obtain better forecasting accuracy with the MSG model than with the LDP model and mean-variance model, in general. Furthermore, for the LDP model, the forecasting accuracy decreases as the number of parameters being estimated increases.
| Patient 1 | ||||||
| 1-std % | 2-std % | RMSE | MPE | CORR | ||
| MSG Model | 75.45 | 93.30 | 20.12 | 12.97 | 0.5680 | |
| 2-parameter | 36.16 | 62.50 | 21.66 | 13.65 | 0.4947 | |
| LDP Model | 3-parameter | 37.05 | 61.61 | 21.66 | 13.71 | 0.4826 |
| 4-parameter | 37.50 | 63.84 | 21.83 | 13.48 | 0.5028 | |
| 11-parameter | 36.61 | 61.16 | 21.31 | 14.03 | 0.4926 | |
| Mean-Variance Model | 73.66 | 95.98 | 24.48 | 16.97 | 0 | |
| Patient 2 | ||||||
| 1-std % | 2-std % | RMSE | MPE | CORR | ||
| MSG Model | 63.29 | 89.24 | 33.52 | 17.35 | 0.3674 | |
| 2-parameter | 26.58 | 44.30 | 32.75 | 17.21 | 0.4524 | |
| LDP Model | 3-parameter | 22.15 | 42.41 | 35.05 | 18.35 | 0.4364 |
| 4-parameter | 22.15 | 44.30 | 34.12 | 17.67 | 0.4428 | |
| 11-parameter | 23.42 | 45.57 | 33.23 | 17.30 | 0.4376 | |
| Mean-Variance Model | 68.99 | 90.51 | 35.54 | 18.17 | 0 | |
| Patient 3 | ||||||
| 1-std % | 2-std % | RMSE | MPE | CORR | ||
| MSG Model | 51.61 | 96.77 | 24.27 | 17.12 | 0.4759 | |
| 2-parameter | 26.49 | 49.01 | 25.97 | 16.50 | 0.3799 | |
| LDP Model | 3-parameter | 29.14 | 50.99 | 26.20 | 16.73 | 0.3642 |
| 4-parameter | 27.15 | 53.64 | 26.19 | 16.47 | 0.3761 | |
| 11-parameter | 28.48 | 50.99 | 26.42 | 6.89 | 0.3586 | |
| Mean-Variance Model | 58.07 | 95.16 | 26.96 | 18.74 | 0 | |
The second evaluation quantifies how plausible it is that the data we observe could have originated from the model. We quantify this plausibility using the two-sample Kolmogorov–Smirnov (KS) test. To start, Figs. 4(b)–4(d) show the kernel density estimates (KDEs) obtained from the BG measurements (red curve) and from 1,000 independent realizations of the estimated stochastic process (blue curves) over the training time window for each patient. The KDEs in Figs. 4(b)–4(d) support the idea that the BG measurements could be assumed to be drawn from the distribution given by the estimated model output. To perform the two-sample Kolmogorov–Smirnov (KS) test, we created datasets by resampling 10 000 independent realizations of the model output at the BG measurement times and performed the test using each generated sample against BG measurements with the kstest2 function in MATLAB with 1% significance level. We performed this procedure over one-week of training window and three-week of test window for each patient separately. Note that the null hypothesis states that the two samples are drawn from the same distribution and not rejecting the null hypothesis supports that the MSG model could accurately represent the distribution of the measurements. Moreover, the null hypothesis here is a distributional one so that re-ordering measurements or forecasts will have no effect on the KS test.
Out of 10 000 different samples in each case, the rejection rates were , , and over the training time window and they were , , and over the test time window, respectively, for patients 1, 2, and 3. First, observe that the rejection rates are much smaller over the training time window. This is expected as the random samples used against the BG measurements in the KS test are generated by the model output estimated using the same BG measurements. However, the model output used to generate samples over the test time window was obtained only using the patient-specific model, which is trained by the training data and nutrition intake data of those patients over the test time window. Therefore, even though we have a high rejection rate for patient 2 over the test time window, those much smaller numbers for patients 1 and 3 are still reassuring and show that our initial assumption, which is that our simplified stochastic model can describe the BG values, is a valid assumption in this setting.
While the KS test establishes the distributional similarity between the data and our fitted model, we also evaluate pointwise correlations to establish the validity of the model’s predicted dynamics; i.e., responses to meals. We report the Pearson correlation coefficients in Table III and show substantial positive correlation. This indicates that the MSG model is superior to a constant statistical model of the data distribution.
Finally, we see from Fig. 5(b) that the mean of the model output exhibits unusually high peak BG values after the meals. In addition, the Kolmogorov–Smirnov test has a high rejection rate for this patient. Investigation of parameter values shown in Figs. 3(a)–3(c) reveals that there is an order of magnitude difference between estimated gamma values for patient 2 and for patients 1 and 3. Since represents the decay rate to the patient’s basal glucose value, we hypothesized the reason for not estimating the gamma parameter accurately for this patient could be related to their BG measurement pattern. To investigate, we checked the time difference between the recorded meal times and the first BG measurement times after each meal. We found that patient 2 had 18 meals over their training time window and that time difference was exactly 2 hours for each meal. Patients 1 and 3 had variability among their measurement times. We believe such a regular measurement pattern without any variability is the reason for not being able to estimate the gamma parameter, representing the decay rate to the basal glucose value. In addition, we believe this is also the reason for the high rejection rate for the Kolmogorov–Smirnov test for patient 2. We provide more detail about the BG measurement pattern of these patients in Appendix F.
3. Comparison of forecasting accuracy with longitudinal diabetes pathogenesis model
In this section, we compare the forecasting accuracy of the T2DM version of the MSG model with a well-known model, the longitudinal diabetes pathogenesis (LDP) model90 developed by Ha and Sherman and a simple mean-variance model. The LDP model is developed to understand different pathways of T2DM pathogenesis. It represents the metabolic state of T2DM patients at any time during the disease progression over years. The model consists of four differential equations and 11 model parameters. We perform the same forecasting task by estimating the most commonly estimated sets of parameters, , setting the remaining parameters at known default values and estimating all 11 parameters.
The experiment in this setting will be the same as described above in Sec. VI A 2. For a fair comparison, the mean-variance model corresponds simply to computing the sample mean and variance from the training data and to using the mean as the point estimator over the test time window and the variance for quantifying the BG oscillations in the forecast. On the other hand, the LDP model consists of a set of coupled ODEs. To estimate the unknown model parameters and forecast BG levels with the LDP model, we used the constrained Ensemble Kalman Filter (EnKF) algorithm.1 We coded the algorithm on MATLAB for parameter estimation and BG forecasting using the constrained EnKF method based on the LDP model. We used MATLAB’s ODE solver ode23 to solve the LDP model numerically.
Note that we use the constrained EnKF algorithm because it is validated to provide accurate forecasting results with complex ODE models.1 Moreover, the ensembles of state estimates could be used for uncertainty quantification. However, using a filtering algorithm requires exploiting all the data collected up until the forecasting time point; unlike the optimization algorithm paired with MSG model, which could use data collected only over the training time window to train the model and then simulate over the test time window for forecasting. Note that with LDP model—EnKF algorithm pair, we used all the data contained in the training and test time windows. Then, we used the BG forecasting values over the test time window for comparison. The comparison results are shown in Table III, where the sets of estimated parameters are referred by the number of parameters in each set.
The results in Table III show that the MSG model provides at least the same level of accuracy in forecasting future BG levels in T2DM patients than all variants of the LDP model and mean-variance model when compared holistically.
First, the MSG model achieves slightly lower, or the same level of RMSE and MPE obtained with all different variations of the LDP model and mean-variance model for all three patients, demonstrating that mean of the MSG model output is also useful as a point estimator.
Second, we see the benefit of using a stochastic model, which inherently quantifies the level of certainty in the BG predictions. It is worth noting that the MSG model is based on learning parameters of a stochastic model, while the LDP quantifies uncertainties by learning an ensemble of parameters and states; this may contribute to the differences between them at the level of uncertainty prediction. The percentages in Table III show that the MSG model captures a significantly larger number of the BG measurements in the respective confidence bands compared to the LDP model. However, it is not as good as the mean-variance model for these percentages. Nevertheless, comparing the correlation values over the test time window shows a higher correlation between BG forecasts and measurements with the MSG model, except for patient 2 when estimated by the LDP model.
In summary, the MSG model provides BG prediction results that are as least as accurate with the results we obtained by the LDP and mean-variance model. Note that these forecasting results support the rationale behind our modeling approach, which is using the linear MSG model for BG forecasting: trading physiological resolution for the robustness of forecasts.
B. ICU
We now move to the more complex and difficult case of modeling and forecasting glycemic dynamics in the ICU, where non-stationarity is manifest on much shorter time scales. Parameter estimation and forecasting are, in general, harder in the ICU context because of the characteristics of ICU patients as explained in Sec. I B and Appendix A. A detailed explanation about how the MSG model represent the dynamics in ICU setting is provided in Appendix F.
1. Parameter estimation
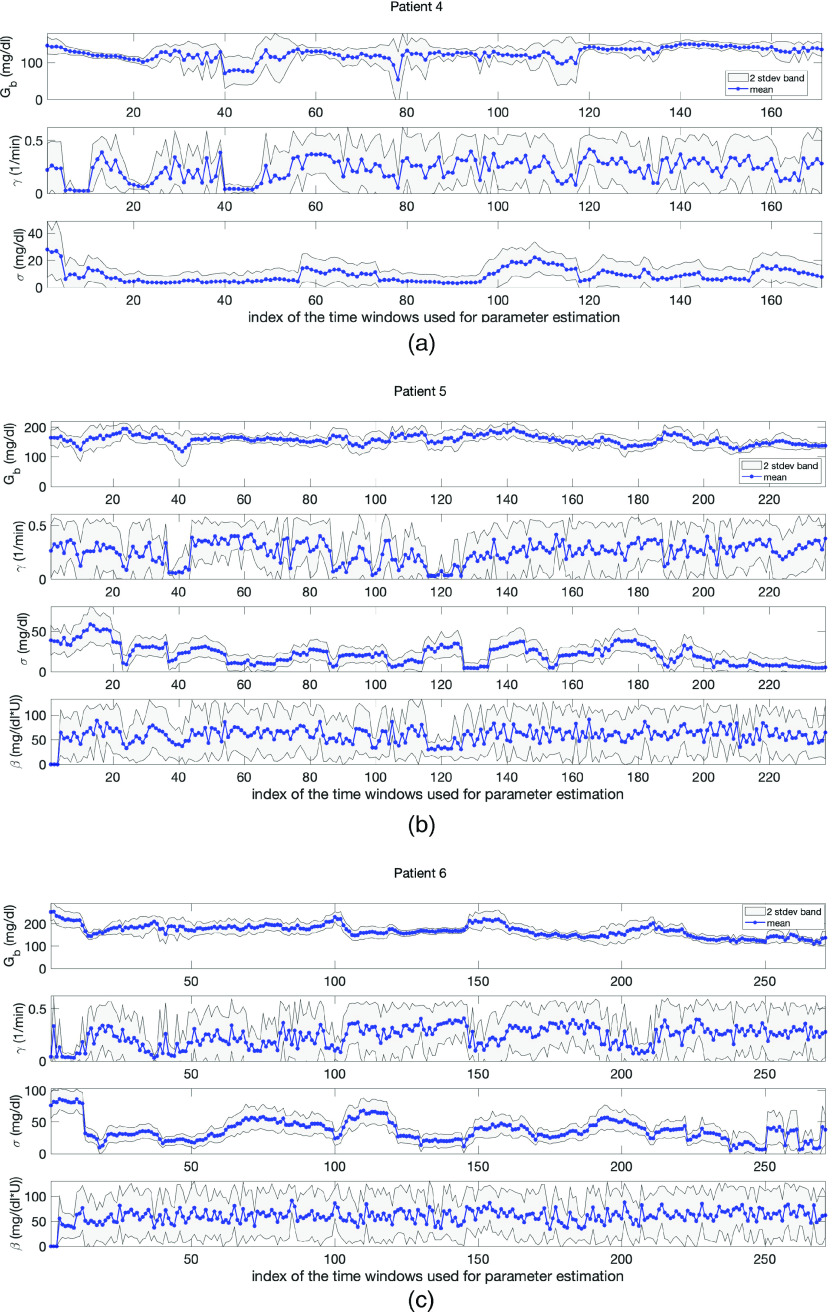
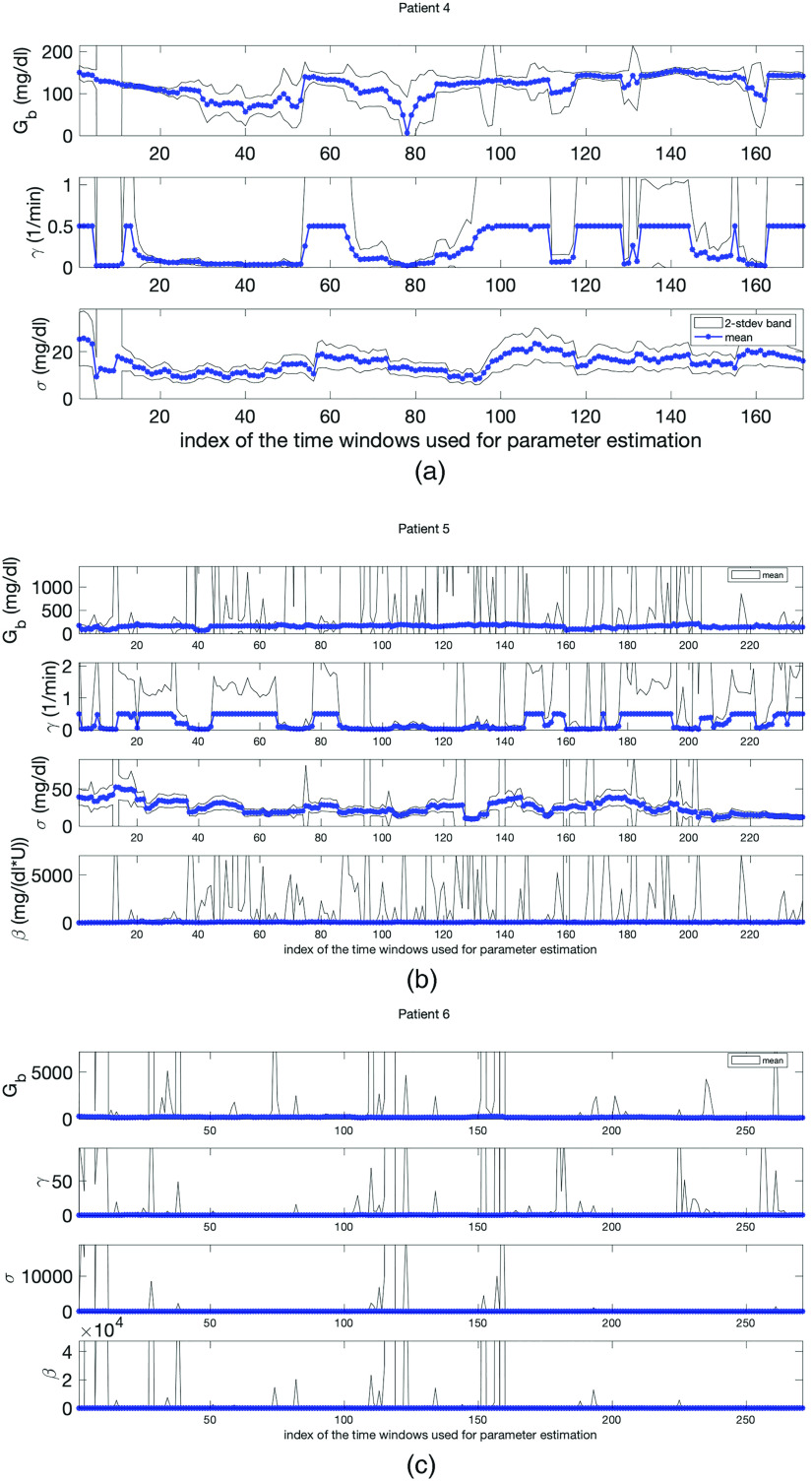
The difficulties presented in the ICU setting are reflected in our parameter estimation results. Despite these complexities, our results exhibit four substantive pieces of evidence which support the validity of the model and its potential effectiveness for understanding the physiological state of ICU patients and for forecasting. First, the model captures the dynamics reflected in the parameter estimates with sparse data. Second, the estimated model parameters, which have the most influence in resolving the mean and variance of the BG level, are physiologically valid in most of the cases. Third, the changes in the parameter estimation results over moving time windows are realistic and reflective of the expected non-stationary behavior of ICU patients. And fourth, the UQ results show that the parameters (basal glucose rate, and the model standard deviation, ), which have the most influence in resolving mean and variance of BG levels are estimated with more certainty. Having tighter bands around the point estimates for these parameters indicates the robustness of the estimation. We explain these claims in detail in the following paragraphs. Figure 6 contains evidence supporting all these results and Table II shows the sparsity of the BG measurements.
FIG. 6.
Panels (a)–(c) show parameter estimation and uncertainty quantification results in the ICU setting obtained with MCMC for patients 4, 5, and 6, respectively. In each plot, the blue stars are the point-estimate of each parameter and the gray area is the 2-stdev band around the point-estimates (both obtained from the resulting random samples). Here, the gray region represents the uncertainty in the point-estimates. The estimated model parameters exhibit biophysically realistic values. Also, 1- and 2-stdev bands enforces the reliability of the estimated parameters, especially, and , which are the most influential parameters in predicting the mean and variance of BG levels.
With the complexity of ICU data in mind, consider the parameter estimation results. Figure 6 shows the parameter estimates over moving time windows with length of 24 h for each ICU patient obtained with MCMC approach. The mean of each chain is shown using blue stars. These parameter estimates are physiologically plausible for all three patients except in a small number of cases. For example, estimates of the basal glucose rate, , were around – , – , – , for patients 4, 5, and 6, respectively, all plausible values given the patient’s data. As shown in Appendices F and G, it was not possible to compute good estimates for parameters and in some of the cases.
Figure 6 also shows that the time evolution of the estimated parameters is realistic within the ICU context. In ICU, the training time windows move in the positive (increasing time) direction of measurements—given a measurement, the model is estimated using the previous 24 h of data, data points to forecast the future measurement whenever it comes—so that the consecutive time windows have an overlap of 20–23 h. This means that the model varies relatively continuously between consecutive time windows. This relative continuity is reflected in Fig. 6 that shows the time evolution of estimated parameters for all three patients. Even though the health condition of the ICU patients can change rapidly, the estimated parameters do not change wildly (in most of the cases), reflecting the expectation under these settings. Nevertheless, the patients are clearly non-stationary and the observed evolution of the parameter estimates, shown in Fig. 6, reflects this non-stationarity.
And finally, as was the case in the T2DM setting, the model is relatively robust to the methods used to estimate it; however, as can be inferred from the discussion above about parameters and their face validity to physiology, the ICU formulation of the model can have more complex parameter estimation issues compared to the T2DM setting. In particular, in the ICU setting, there are some cases where the Laplace approximation does not work well because the parameter misfit solution surface is flat in some parameter directions—a reflection of identifiability issues. We provide more insight about this issue in Appendix E. Even though the point estimates for each patient and parameter pair by MCMC and optimization are close to each other, since UQ results are more meaningful by MCMC, we present the plots obtained by MCMC. In general, we observe that and , both allow for more robust estimation compared to the estimation of and . The robustness of the estimation of and is important for clinical applications because the mean and variance are what is used for glycemic management. As a demonstration of the robustness of and , consider Fig. 6. Here, we can see the 2-stdev band around the mean for and is tighter than the 2-stdev bands for and for all three patients. Remember that both and are related to the glucose removal rate from the blood. This is, perhaps, an indicator of an identifiability issue for these parameters. But it is also true that we are indeed less certain about this physiology; glucose can be removed at different rates by different physiological processes, e.g., liver vs adipose tissue, and we are not resolving these physiological subsystems. Moreover, due to the non-stationary and sparse nature of the data in the ICU setting, it is harder to estimate some of the model parameters accurately. Separating these inference issues is not possible given the data presently collected in these settings. Nevertheless, the parameters that play a key role in resolving the mean and variance of the BG dynamics can be estimated accurately up to the desired level.
2. Forecasting
Forecasting results in the ICU setting are indicative of two major features of this model: (i) we can capture the trend of BG measurements through the mean of the model and (ii) we can estimate the variance of the BG measurements accurately. Once again, since resolving mean and variance of BG dynamics is central to glycemic management, these results show potential usefulness of this model in the ICU context.
Figure 7 demonstrates that the forecasted mean of the model output encapsulates the essence of the behavior of BG measurements for all three patients. In each of the plots in Fig. 7, the red circles show the BG measurements, the blue stars are the mean of the model, and the gray region is the 2-stdev band around the mean, each one obtained separately with the corresponding patient-specific model.
FIG. 7.
Panels (a)–(c) show forecasting results obtained based on parameters estimated with MCMC in the ICU setting for patients 4, 5, and 6, respectively. In each plot, the red circles show the true BG measurements, the blue stars show the mean of the model output, and the gray region shows the 2-stdev band around this mean, obtained from the model output of the stochastic model, forecasting the magnitude of the BG oscillations. These results are, in general, very close to those obtained using the optimization approach, and the most relevant properties are shared by them both. Obtaining similar results with another numerical solution technique based on the same mechanistic model shows the reliability of the model and estimated model parameters.
To observe the effectiveness of this model in estimating the variance of the BG measurements accurately, consider Fig. 7 and Table IV. Figure 7 shows the ability of the model to estimate the variance in glycemic dynamics visually where a large number of true BG measurements are contained in the gray regions that represent the forecasted 2-stdev bands around the forecasted mean. These results are quantified in Table IV which contains summary statistics both for optimization and MCMC methods and demonstrate the forecasting accuracy of the MSG model and imply potential use in the ICU for glycemic management. Note that given the forecast, data, and the fundamental challenges of the ICU setting, we should expect forecast UQ bands to be quite large. But, this does not mean it is not valuable to clinicians but rather means that we can provide a realistic estimate of the possible BG oscillations in an extremely volatile and poorly measured system.
TABLE IV.
Comparison of the forecasting results obtained with the MSG, ICUMM, and mean-variance models. The percentages of 1- and 2-stdev bands that capture the true BG measurements with the MSG model is substantially higher than the ICUMM whereas they are smaller than mean-variance model. On the other hand, RMSE and MPE values are closer when comparing all three models, yet the MSG model still provides smaller values for these measures, as well. In addition, the forecasted BG levels by the MSG model give the highest correlation with the BG measurements for all three patients.
| Patient 4 | ||||||
| 1-std % | 2-std % | RMSE | MPE | CORR | ||
| MSG Model | Optimization | 56.14 | 89.47 | 17.27 | 10.29 | 0.3177 |
| MCMC | 60.82 | 91.81 | 18.60 | 11.07 | 0.2341 | |
| ICUMM | 45.61 | 80.12 | 17.35 | 9.87 | 0.3232 | |
| Mean-Variance Model | 59.06 | 94.15 | 18.07 | 10.96 | 0.1753 | |
| Patient 5 | ||||||
| 1-std % | 2-std % | RMSE | MPE | CORR | ||
| MSG Model | Optimization | 58.65 | 83.97 | 33.27 | 18.91 | 0.2751 |
| MCMC | 64.14 | 88.19 | 30.95 | 18.51 | 0.2773 | |
| ICUMM | 29.54 | 53.59 | 34.45 | 18.81 | 0.1427 | |
| Mean-Variance Model | 64.14 | 89.87 | 31.79 | 19.06 | 0.1737 | |
| Patient 6 | ||||||
| 1-std % | 2-std % | RMSE | MPE | CORR | ||
| MSG Model | Optimization | 59.04 | 87.45 | 43.16 | 25.22 | 0.2859 |
| MCMC | 63.84 | 91.14 | 44.78 | 27.12 | 0.1859 | |
| ICUMM | 18.45 | 38.01 | 44.77 | 26.18 | 0.1374 | |
| Mean-Variance Model | 63.84 | 91.14 | 46.66 | 28.04 | 0.1231 | |
3. Comparison of forecasting accuracy with the ICU minimal model
In this section, we use the ICUMM and mean-variance model in a similar manner as in T2DM context for the comparison of the forecasting results. The ICUMM is a nonlinear physiological model that represents the glucose–insulin dynamics of ICU patients and was developed to be used for glycemic management in ICU. The model consists of four coupled differential equations and has 12 model parameters. One of those model parameters is used for the purpose of having units equal on both sides of the equation and set to 1. Two of the model parameters represent the volume of glucose and insulin distribution space and are set to nominal values from the literature. This leaves us with nine unknown model parameters to be estimated. For parameter estimation and BG forecasting, we used the constrained EnKF method, which enables us to obtain confidence bands for the forecasting results using the ensembles. We implemented the BG forecasting algorithm using the EnKF method based on the ICUMM on MATLAB. We used MATLAB’s ODE solver ode45 to obtain the solution of ICUMM. The mean-variance model uses the mean and variance of BG measurements over the training time window for forecasting.
The comparison results are shown in Table IV. These results indicate the efficiency of the MSG model in forecasting mean and vaiance of BG measurements.
First, the point estimators in the MSG case exhibit comparable or improved, accuracy in comparison to the ICUMM and mean-variance model, as observed from the comparison of RMSE and MPE values. In addition, correlation values obtained with the MSG model are significantly larger than those with the ICUMM and the mean-variance model, except for patient 2 when estimated with the ICUMM. These results show that with a relatively simple model, we are able to reach at least the same level of accuracy in forecasting BG levels with the other two models, ICUMM and the mean-variance model.
Second, the confidence bands that we use to quantify possible high and low values of BG levels contain a larger number of BG measurements with the MSG model then the ICUMM. Compared to ICUMM, the improved accuracy of the MSG model in terms of forecasting the variance may be related, in part, to the fact that the model we use is inherently stochastic, and fits the stochastic fluctuations of data; in contrast, ICUMM provides bands quantifying the BG oscillations only through the ensemble of solutions which are a product of the algorithm used to fit the data, and not inherent to the model itself. These 2-stdev bands contain only a slightly larger number of BG measurements with mean-variance model compared to the MSG model. On the other hand, the MSG model’s mean model output shows a higher correlation with the BG measurements than both the ICUMM and mean-variance model except for the forecasting of patient 4 with ICUMM. Even though the mean-variance model provides a comparable level of prediction accuracy to the MSG model, it does not give any physiological understanding of the system.
In summary, a comprehensive comparison of the MSG model with a more complex physiology-based mechanistic model and a simpler data-driven model suggests that the MSG model, a linear mechanistic model with a small number of parameters work at least as good as these models in representing BG behavior and forecasting future BG levels in the ICU setting.
C. Limitations
These results have some limitations. For each of the T2DM and ICU settings, we only had three patients. The model should be evaluated with larger patient cohorts in both settings. Also, for each of these settings, we chose one nonlinear glucose–insulin model (the LDP model90 for T2DM and the ICUMM18,85 for ICU) representing respective BG dynamics to exhibit what we mean with resolving mean and variance of BG behavior for robust BG forecasting and show our stochastic model’s effectiveness in BG forecasting compared to existing mechanistic glucose–insulin models. However, we did not hand-tune these nonlinear models but left many parameters fixed at their nominal values and only estimated the commonly estimated parameters since it is not possible to estimate all of the unknown model parameters based on the available data as explained in Sec. I.
Approximating the distribution of glucose levels by Gaussian distribution is a limitation of our modeling approach because the distribution of Glucose levels resembles Gamma distribution rather than Gaussian distribution.97 However, the developed model producing a Gaussian process is appropriate because it is analytically solvable and provides sufficiently accurate and robust forecasting results.
VII. DISCUSSION AND CONCLUSION
A. Summary of the modeling framework
In this paper, we introduce a new mathematical model of the glucose regulatory system in humans. The model was created with five goals in mind: (i) the model should be robustly identifiable/estimable and verifiable with real-world human data104—data collected for health management—such that the model could potentially be useful for personalized parameter estimation and state forecasting;104 (ii) the model should be interpretable in the sense that patient specific parameters may be used to explain, and quantify basic physiological mechanisms; (iii) the model should be physiologically simple, even if it is functionally complex, to minimize parameter identifiability problems present in many existing physiological models; (iv) the modeling framework generalizable and adaptable to several contexts including T2DM and ICU; and (v) the model should be amenable to a model-based control environment. With these goals driving the model development, the MSG model follows different approach, as explained in Sec. II compared to many other glucose–insulin modeling efforts. The most important departure of the MSG model compared with others is the inclusion of insulin as a lumped parameter affecting the glucose state rather than as an independent state(s). We formulated the model this way because, in clinical settings, insulin is rarely measured, and therefore difficult to estimate.
B. Benefits of a linear SDE model
In accordance with our goal, which is to develop a highly simplified yet interpretable model, we work with a forced SDE of Ornstein–Uhlenbeck type to describe glucose evolution, together with a linear observation model, subject to additive Gaussian noise. The Gaussian structure allows for computational tractability in prediction since probability distributions on the glucose state are described by Gaussians and hence represented by simply a mean and variance. On the other hand, the protocols for managing glucose depend on intervals; e.g., a goal may be to keep glucose between 80–150 mg/dl and interval deviation from this goal, e.g., 151–180 mg/dl, induce changes in the insulin dosage. This means that decisions are made based on boundaries of glycemic trajectories. Nevertheless, because glucose oscillates under continuous feeding, clinicians typically aim to ensure that the glycemic mean does not fall below 60 mg/dl or above 180 mg/dl for any length of time. The intervals are then a proxy for this balance of managing the mean and protecting against trajectories diverging too high or low at any time, including between observations.105 Hence Gaussian approximation with accurate mean and variance prediction can potentially be sufficient for forecasting and glycemic management purposes.
C. Balancing physiological fidelity and forecasting accuracy with sparse data
With this modeling approach, we balance the trade-off between the physiological fidelity of the model and its effectiveness for robust forecasting. We gain robust model parameter estimation with sparse data. The developed stochastic model can accurately forecast the region where the oscillating nonstationary BG levels will lie, which is useful for glycemic management. The model has an analytical solution, which makes it potentially useful within clinical decision support tools for real-time BG forecasting. Also, as a linear model, it could be coupled with a wide range of control-theoretical algorithms for model-based glucose control systems. The cost of the gained robustness is that we cannot resolve the exact glycemic trajectory and fine physiological processes such as insulin secretion or resistance.
D. Generalizability of modeling approach
In our modeling framework, we replaced high-fidelity ODE model(s) with a lower fidelity SDE model to obtain useful BG forecasts with the available sparse data. The deterministic component of the model represents the mean behavior of the BG dynamics and the stochastic component encapsulates the BG oscillations. Similar approach could be used in many settings to give access to predictive power given sparse data.
E. Model development constrained by real-world data
Restricting model development to the constraints imposed by readily available real-world data is a severe, but important, restriction. To be directly useful in applications, models must be estimable using data that are collected within the context of the given application, and these data are almost always much more sparse than ideal laboratory experiments. To circumnavigate these problems, we are forced to use data collected to manage health and the models that can be applied with these data will likely be different than models built to be estimable with, e.g., laboratory data. Therefore, to help facilitate the circular process of allowing our knowledge of systems physiology to inform and impact how clinicians manage the health of people, we need a bridge between these worlds, and the bridge proposed here is through inference with data based on simple yet interpretable models.
F. Including insulin in a mechanistic modeling framework
There are, at a high level, two pathways for estimating and modeling blood glucose behavior. First, one can include dynamic equations for glucose and insulin, along with other related processes. Second, one can include a dynamic equation for glucose that includes a parameterized function capturing the impact of insulin on glucose that is not dynamic. The second option excludes a model equation for insulin and instead has a parameterized function that represents the impact of glucose on insulin that is hypothesized to exist. The most common tactic is the first approach. However, as we emphasized before, insulin measurements rarely exist in any practical setting and insulin levels are not interpretable or meaningful for patients or for most clinicians. This implies that modeling glucose together with insulin leaves one of two primary variables free to vary, causing the system to be ill-posed and not identifiable. In contrast, the second option does not have these pathologies, will be uniquely estimable under most circumstances, and will provide a more stable forecast.
G. Blood glucose variability and its effect on uncertainty quantification
Both in T2DM and ICU settings, we obtain the forecasted mean and 2-stdev bands around this mean as the model output. The characteristics of BG behavior, in particular, BG variability, affect the width of the 2-stdev bands in these two settings. It is natural to expect to have wider bands in the ICU setting because of the highly non-stationary BG behavior of ICU patients. However, there are other factors affecting the width of these bands. First, BG measurements are relatively dense in the ICU, compared to T2DM. The second factor is the difference between the experiments that were designed according to the specific needs of each setting, which is depicted in Figs. 1 and 2. Using the latest 24-hour data for model estimation and forecasting in the ICU setting could help reduce uncertainty in the forecasts and may result in occasional more narrow 2-stdev bands. In addition, the GM is performed by clinicians in ICU and by patients in the T2DM setting. A clinician’s management is likely to reduce the variability in BG behavior, which can be reflected in the width of the estimated 2-stdev bands.
H. Impact of the nutrition function choice in the ICU context:
We also considered a different form for the nutrition function in the ICU setting to test robustness of the MSG model to the simplistic piecewise constant meal function that we adopt in this case. Because ICU patients are tube-fed with nutrition quantities that are considerably less than a healthy individual would ingest, per unit time, it is reasonable to consider the use of a piecewise constant function. Nonetheless, we investigated if modifying the piecewise constant function as shown in Fig. 8 could improve the parameter estimation and/or forecasting results. Using this function introduces two more parameters to be estimated in the ICU setting, increasing the flexibility and the complexity at the same time. Hence the parameters to be estimated are . Using this function modeling the nutrition delivery did not improve the forecast accuracy which leads us to use the simpler version of the model.
FIG. 8.
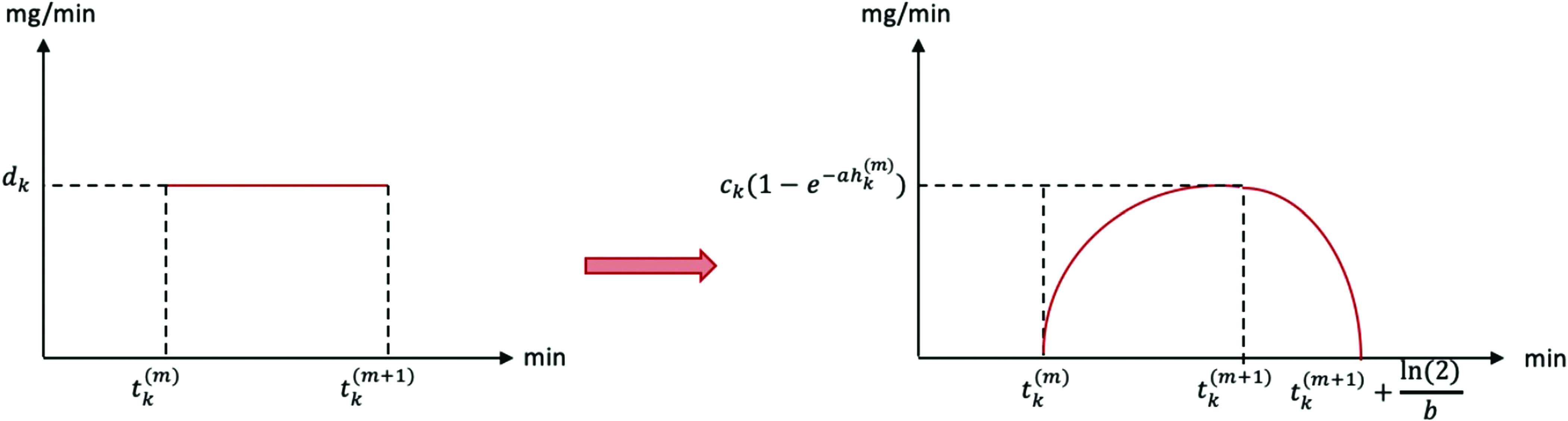
Smoothing piecewise constant nutrition function that is used for ICU patients.
The function shown on the right hand side of Fig. 8 is formulated as follows:
| (24) |
where and
is the normalizing constant for .
I. Outlook
The model we have developed has demonstrable predictive capability in a patient-specific manner. Yet it has some limitations, which give space for future development, and also suggests some natural next-step applications. We outline a number of possible future directions.
Glycemic control: Given the MSG model construction, an obvious next step is to formulate the work on the control problem where we determine estimates of the input ranges of nutrition and insulin, necessary to keep the output, here BG, in a desired target range.
Phenotyping: Because the parameters of the MSG model are interpretable, we could potentially use the model parameter estimates for phenotyping studies.76,99,100 Meaning, we could estimate parameter for individuals in a given health state, establishing an inferred phenotype for the patient, and then relate this phenotype to other external health features or cluster the patient phenotypes in an effort to find structure among the inferred physiology. We have deemed efforts such as this high-fidelity phenotyping96 and believe that this model could be used to these ends.
Gamma process: As we mentioned in Sec. VI C, approximating the underlying BG dynamics by a Gaussian process is a limitation of this work. BG levels resemble Gamma distribution. However, SDEs producing Gamma distribution require numerical solution techniques. We will investigate the use of such SDEs to model and forecast BG levels in future work.
Continuous Glucose Monitoring Data: Continuous glucose monitoring (CGM) data provides valuable information about the BG dynamics. However, these data are collected mostly for T1DM patients and are far from being collected routinely in ICU and T2DM settings. Because of this reason, we aimed to develop this model accounting for routinely collected sparse data rather than CGM data. In addition, availability of CGM data reduce data sparsity only for BG measurements and other important system components, such as interstitial or plasma insulin, will still be missing. Therefore, it is interesting to understand how this stochastic model performs with noisy but dense CGM data.
ACKNOWLEDGMENTS
We acknowledge financial support from NIH R01 LM012734 “Mechanistic Machine Learning.” D.J.A. acknowledges helpful discussions with Bruce Gluckman, Rammah Abohtyra, Cecilia Diniz Behn, and Arthur Stewart Sherman.
APPENDIX A: CLINICAL SETTINGS OF INTEREST
The model that we develop can be used in T2DM and ICU settings with appropriate adjustments, which is presented in Sec. II. Here, we describe the respective clinical settings in more detail.
1. Type 2 Diabetes Mellitus (T2DM)
T2DM is a highly heritable chronic disease characterized by insulin resistance and pancreatic beta-cell failure resulting in hyperglycemia. Comorbid conditions include overweight or obesity, hypertension, and dyslipidemia. Individuals with T2DM are at markedly increased risk of chronic vascular and other complications such as atherosclerotic cardiovascular disease, renal dysfunction, neuropathy, visual impairment, and need for limb amputation. Uncontrolled hyperglycemia causes acute symptoms and risk for infections. Individuals usually develop insulin resistance early in the disease course, and progress through impaired glucose tolerance and/or abnormal fasting glucose before serum glucose concentrations meet the criteria for diagnosis of diabetes mellitus. When compared with individuals having normal glucose tolerance, T2DM patients experience marked glycemic variability related to carbohydrate intake, activity, glucose-lowering medications, and individual pathophysiology. Training and testing the model developed here in patients with T2DM not requiring pharmacologic therapy allows us to isolate the effects of carbohydrate intake and individual pathophysiology without the additional variable of medication effects.
2. Intensive Care Unit (ICU)
Critically-ill patients often develop stress hyperglycemia from physiologic responses to medical or surgical stress, burns, and/or trauma, including upregulation of inflammatory cytokine pathways and activation of the hypothalamic–pituitary–adrenal axis with increased cortisol and epinephrine production leading to decreased glucose uptake, increased lipolysis, and increased hepatic glucose production. The resulting stress hyperglycemia can also exacerbate critical illness leading to impaired immunity, hypercoagulability, myocardial injury, oxidative stress, decreased endothelial function, impaired wound healing, and electrolyte loss, in an escalating cycle. Conversely, insulin therapy and conditions such as sepsis and critical illness can lead to increased risk for hypoglycemia, especially in the setting of acute kidney injury, hypovolemia, and impaired gastrointestinal function. Constantly and rapidly changing physiologic states and invasive interventions such as need for mechanical ventilation, invasive monitoring, and the need to be nil per os for most procedures can result in dramatic variance in blood glucose levels in ICU patients with stress hyperglycemia.
APPENDIX B: OPTIMIZATION
In solving the parameter estimation problem with the optimization approach, our goal here is to determine parameter values, , which maximize the posterior distribution, and is called to be the maximum a posteriori (MAP) estimator. Using the prior distribution as specified above, the parameter estimation problem becomes
| (D1) |
Remember that for the parameter estimation problem with the minimal stochastic glucose model, we have
| (D2) |
Then, substituting (B2) into (B1), the problem will take the form
| (D3) |
Hence, placing uniform prior distribution turns the problem of finding the MAP estimator into a constrained optimization problem. To solve this problem, we use built-in MATLAB functions, such as fmincon and multistart. fmincon is a gradient-based minimization algorithm for nonlinear functions. multistart starts the optimization procedure from the indicated number of starting points that are picked uniformly over the region defined by the constraints. It uses fmincon and other similar algorithms to perform each optimization process independently and provides the one that achieves the minimum value among the results of all separate runs. With this approach, we have the opportunity to compare different optimization procedures that start from different initial points. This provides some intuitive understanding of the solution surface and hence the estimated optimal parameters.
Once an optimal point has been found, we may also employ the Laplace approximation106,107 to obtain a Gaussian approximation to the posterior distribution. The Laplace approximation is a reasonable approximation in many data rich scenarios in which all parameters are identifiable from the data, because of the Bernstein Von Mises Theorem,108 which asserts that the posterior distribution will then be approximately Gaussian, centered near the truth and with variance which shrinks to zero as more and more data is acquired. However, data is not always abundant, and not all parameters are identifiable, even if it is; in this setting, sampling the posterior distribution is desirable, and for this purpose, we use Markov Chain Monte Carlo (MCMC) techniques.
APPENDIX C: MARKOV CHAIN MONTE CARLO
MCMC methods are a flexible set of techniques which may be used to sample from a target distribution, which is not necessarily analytically tractable.109,110 For example, the distribution is the conditional distribution of the random model parameters, given the data, . Even though we can explicitly formulate it using Bayes’ theorem, it is not always an easy task to extract useful quantities, such as posterior mean and variance, from that formula. In such cases, MCMC techniques are used to generate random samples from this target distribution and this random sample is used to obtain the desired information, which could be anything such as the mean, mode, covariance matrix, or higher moments of the parameters. Moreover, this technique is also very helpful to obtain uncertainty quantification (UQ) results for the estimated parameters.
In order to obtain more extensive knowledge than MAP estimator can provide about the posterior distribution of parameters given the data, , we use MCMC methods as a natural choice to sample from that distribution. Among different possible algorithms,111 we use the standard random walk Metropolis–Hastings algorithm. In order to make sure the resulting sample is indeed a good representer of the posterior distribution, we perform some diagnostics such as checking if chains for each parameter converged and if they are uncorrelated. Then, after removing the burn-in period, we compute the mean and the covariance matrix from the remaining part of the sample. We use the mean as a point estimator for simulation and forecasting, and the covariance matrix provides valuable information to quantify uncertainty for the estimated parameters.
In general, it is hard to obtain efficient results with MCMC methods even when sampling from the joint distribution of four or five parameters, due to the issues such as parameter identification. Moreover, obtaining accurate results with this approach requires careful choice of starting point and tuning some other parameters. In general, the performance of the algorithm will depend on the initial point. We tested the use of both random starting points and MAP estimators as starting point. The former enables us to detect when several modes are present in the posterior distribution. The latter helps to focus sampling near to the most likely parameter estimate and to quantify uncertainty in it. However, it is also important to note that using MAP estimator as a starting point is not helpful in all cases. More precisely, if the MAP estimator is not a global minimum but a local minimum, then the chain could get stuck around this point. Therefore, it requires careful analysis, comparison, and synthesis of the results obtained with these different approaches.
APPENDIX D: INSIGHT ABOUT THE MSG MODEL’S ABILITY TO CAPTURE ICU DYNAMICS
We explain here how the model captures the BG dynamics in the ICU setting. Consider Fig. 9, which demonstrates both the model’s relative robustness and its capability of capturing the dynamics and various complexities encountered in different conditions in the ICU setting. These figures show simulated BG values for patient 4 over different training time windows for which the parameters are estimated with the optimization approach. Here the the red curves represent the mean of the BG dynamics that are assumed to be oscillatory, the amplitude of oscillations are expected to lie in the gray region as it is the 2-stdev band around the mean. The red circles show the BG measurements the light blue curve shows the tube-nutrition input rate. For simplicity, we consider patient 4 who did not need any exogenous insulin, so the tube-feed nutrition is the only driver of the BG level. Each subfigure of Fig. 9 shows a different training time window that is representative of different circumstances relative to our ability to estimate , , and .
FIG. 9.
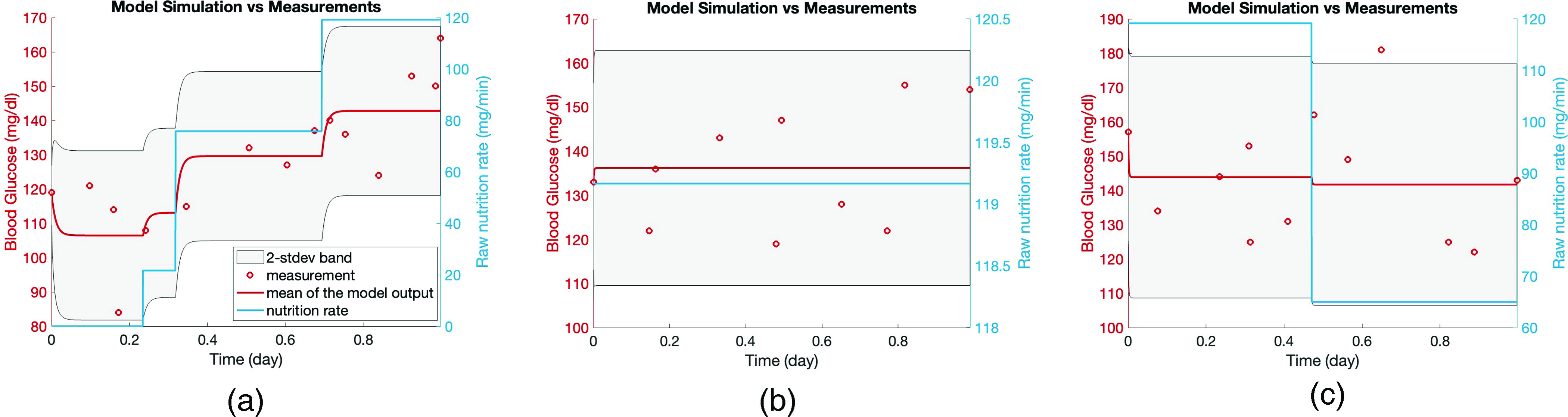
BG simulations are shown with respective to the estimated parameters over respective training time window. In each plot, the light blue curve is the glucose rate in the nutrition delivered to the patient (right y-axis), the red circles show the true BG measurements (left y-axis), the red curve is the mean of the model output (left y-axis), and the gray area is the 2-stdev band around the mean of the model output (left y-axis). These figures show two main cases that could arise as a result of parameter estimation in the ICU setting: Panel (a): the input (nutrition rate) is reflected in the output (BG measurements), panels (b) and (c): the input is not reflected in the output, which makes it impossible to estimate the decay rate accurately.
Figure 9(a) shows a situation where the BG measurements (the output of the system) reflect the nutrition rate (the input to the system) quite well. As the nutrition rate, the only driver of the system included in the model, the BG measurements increases, which is reflected in the mean of the model output.
In contrast, Figs. 9(b) and 9(c) demonstrate a situation where the BG measurements do not reflect the nutrition rate over the shown time window. In Fig. 9(b), we see that there is no change in the nutrition rate over the whole time window, which is clearly reflected by the mean of the model output. However, having no change in the nutrition rate means that there is no opportunity to “learn” the glycemic decay parameter, . Therefore, in the absence of any information, the optimization algorithm provides the possible largest value to reflect non-changing nutrition rate in the mean of the model output, which also around the mean of all the BG measurements in the respective training time window.
On the other hand, the situation in Fig. 9(c) occurs when the changes in the BG measurement are uncorrelated with the changes in the nutrition rate, potentially due to changes in health states or other interventions, e.g., other hormone drips. Hence, it is impossible for the model parameters to accurately reflect the physiology as they are accounting for dynamical glucose features that they were not designed to accommodate. Observe from Fig. 9(c) that, with a value as in Fig. 9(a), there should be a substantial decrease in the mean of the model output due to the decrease in the nutrition rate. Since this is not the case as seen by the BG measurements, the optimization algorithm provides a reasonable mean model output (characterized by ) and set the decay rate as high as possible (here the upper bound for this parameter) so that it could keep the mean model output constant over the whole interval accommodating for the two widely different nutrition rate regimes.
These issues do not mean that the model cannot represent and forecast the glycemic dynamics, it still is usually able to represent glycemic dynamics, but some of the parameters might lose their intended meaning. For example, in the two respective examples, despite parameter estimate issues, in both of these cases the estimated , and values are enough to capture the mean and variance of the BG measurements accurately. These examples are not the only cases where we observe parameter estimates that are not physiologically valid while at the same time the glucose forecast and modeling itself remains accurate. The other examples are all variations of the same theme: we either do not have the available data to estimate a parameter accurately, or the data are behaving in a more complex manner, and in both cases, the parameters make up for these data-driven and model-driven short-comings by deviating from their normal roles to render a robust glucose forecast. It is likely that problems such as these will not be eliminated by using more complex datasets and more complex models, because full representation of the relevant processes is out of reach in such non-stationary ICU settings.
APPENDIX E: PARAMETER IDENTIFIABILITY ISSUES IN THE ICU SETTING
We encountered some parameter identifiability issues while solving the optimization problem stated in (D3) in the ICU setting, which caused the solution surface, the function we minimize ( ), to be flat in some parameter directions. Because of this reason, the Hessian matrix becomes ill-conditioned. However, the Laplace approximation requires computing the inverse of the Hessian matrix, which gives the variance of the estimated unknown model parameters on the diagonal. When we compute the inverse of an ill-conditioned Hessian matrix, the resulting matrix has very large entries. Hence, the variance of the estimated model parameters is also unreasonably large, resulting in non-useful UQ results, which can be seen in Fig. 10.
FIG. 10.
Panels (a)–(c) show the UQ bands when we use the optimization approach for parameter estimation in the ICU setting for patients 4, 5, and 6, respectively. The blue stars are the point estimates for the respective parameters and the gray region quantifies the uncertainty in the estimation. Because of the parameter identifiability issues, the Hessian matrix is ill-conditioned. When we compute its inverse to obtain the variance in the estimated model parameters, we obtain unreasonably wide UQ bands.
APPENDIX F: THE EFFECT OF BLOOD GLUCOSE MEASUREMENT PATTERN TO PARAMETER ESTIMATION IN THE T2DM SETTING
We observed that the BG measurement pattern of T2DM patients significantly affects the values of estimated model parameters based on this patient-collected data. For each patient, we computed the time difference between the meal time and the first BG measurement after that meal time for each meal recorded during the training time window. We show the histogram of these time differences for each patient in Fig. 11. We see that patients 1 and 3 measured their BG levels at varying times after meal consumption. However, patient 2 measured precisely after two hours for each meal.
FIG. 11.
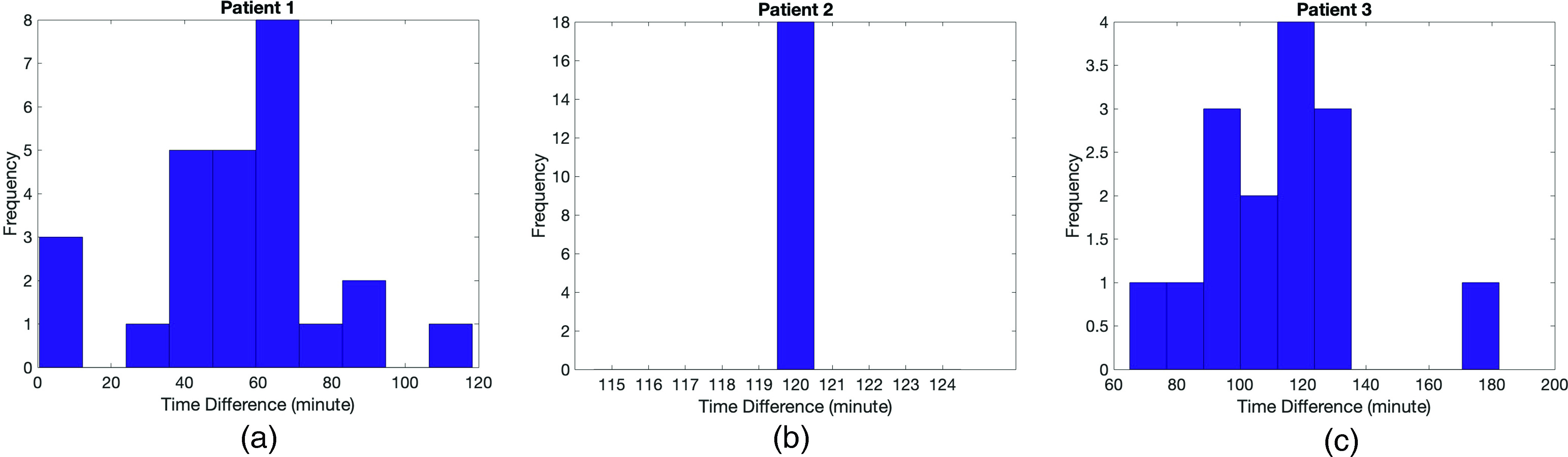
Panels (a)–(c) show histograms for the elapsed time after meal time until the first BG measurement for all recorded meal data in the training time window for patients 1, 2, and 3, respectively. Lack of variability in the data of patient 2 causes suboptimal parameter estimation and forecasting results for this patient.
AUTHOR DECLARATIONS
Conflict of Interest
The authors have no conflicts to disclose.
Ethics Approval
Ethics approval for experiments reported in the submitted manuscript on animal or human subjects was granted. The Columbia University IRB approved the collection of these T2DM data with the number AAAM0057. The ICU data were collected from the Columbia University Clinical Data Warehouse. The consent was waved because it was secondary use of EHR data.
Author Contributions
Melike Sirlanci: Formal analysis (lead); Methodology (lead); Software (lead); Visualization (lead); Writing – original draft (lead); Writing – review & editing (equal). Matthew E. Levine: Methodology (equal); Writing – review & editing (equal). Cecilia C. Low Wang: Writing – review & editing (equal). David J. Albers: Funding acquisition (equal); Supervision (equal); Writing – review & editing (equal). Andrew M. Stuart: Funding acquisition (equal); Supervision (equal); Writing – review & editing (equal).
DATA AVAILABILITY
The Columbia University IRB approved the collection of these T2DM data with the number AAAM0057. The ICU data were collected from the Columbia University Clinical Data Warehouse, are identified data, and can be made available upon request and approval of a data use agreement. We are currently working to make these data publicly available.
REFERENCES
- 1.Albers D. J., Blancquart P.-A., Levine M. E., Seylabi E. E., and Stuart A., “Ensemble Kalman methods with constraints,” Inverse Probl. 35, 095007 (2019). 10.1088/1361-6420/ab1c09 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Grodsky G. M., “A threshold distribution hypothesis for packet storage of insulin and its mathematical modeling,” J. Clin. Invest. 51, 2047–2059 (1972). 10.1172/JCI107011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bergman R. N., Ider Y. Z., Bowden C. R., and Cobelli C., “Quantitative estimation of insulin sensitivity,” Am. J. Physiol. Endocrinol. Metab. 236, E667 (1979). 10.1152/ajpendo.1979.236.6.E667 [DOI] [PubMed] [Google Scholar]
- 4.Sturis J., Polonsky K. S., Mosekilde E., and Van Cauter E., “Computer model for mechanisms underlying ultradian oscillations of insulin and glucose,” Am. J. Physiol.-Endocrinol. Metab. 260, E801–E809 (1991). 10.1152/ajpendo.1991.260.5.E801 [DOI] [PubMed] [Google Scholar]
- 5.Li J. and Kuang Y., “Analysis of a model of the glucose-insulin regulatory system with two delays,” SIAM J. Appl. Math. 67, 757–776 (2007). 10.1137/050634001 [DOI] [Google Scholar]
- 6.Liu W., Hsin C., and Tang F., “A molecular mathematical model of glucose mobilization and uptake,” Math. Biosci. 221, 121–129 (2009). 10.1016/j.mbs.2009.07.005 [DOI] [PubMed] [Google Scholar]
- 7.Li J., Wang M., De Gaetano A., Palumbo P., and Panunzi S., “The range of time delay and the global stability of the equilibrium for an IVGTT model,” Math. Biosci. 235, 128–137 (2012). 10.1016/j.mbs.2011.11.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shi X., Zheng Q., Yao J., Li J., and Zhou X., “Analysis of a stochastic IVGTT glucose-insulin model with time delay,” Math. Biosci. Eng. 17, 2310–2329 (2020). 10.3934/mbe.2020123 [DOI] [PubMed] [Google Scholar]
- 9.Topp B., Promislow K., Devries G., Miura R. M., and Finegood D. T., “A model of -cell mass, insulin, and glucose kinetics: Pathways to diabetes,” J. Theor. Biol. 206, 605–619 (2000). 10.1006/jtbi.2000.2150 [DOI] [PubMed] [Google Scholar]
- 10.Bertuzzi A., Salinari S., and Mingrone G., “Insulin granule trafficking in b-cells: Mathematical model of glucose-induced insulin secretion,” Am. J. Physiol. Endocrinol. Metab. 293, E396–409 (2007). 10.1152/ajpendo.00647.2006 [DOI] [PubMed] [Google Scholar]
- 11.Goel P., “Insulin resistance or hypersecretion? the ig picture revisited,” J. Theor. Biol. 384, 131–139 (2015). 10.1016/j.jtbi.2015.07.033 [DOI] [PubMed] [Google Scholar]
- 12.Ha J., Satin L. S., and Sherman A. S., “A mathematical model of the pathogenesis, prevention, and reversal of type 2 diabetes,” Endocrinology 157, 624–635 (2015). 10.1210/en.2015-1564 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lehmann E. and Deutsch T., “A physiological model of glucose-insulin interaction in type 1 diabetes mellitus,” J. Biomed. Eng. 14, 235–242 (1992). 10.1016/0141-5425(92)90058-S [DOI] [PubMed] [Google Scholar]
- 14.Dalla Man C., Rizza R. A., and Cobelli C., “Meal simulation model of the glucose-insulin system,” IEEE Trans. Biomed. Eng. 54, 1740–1749 (2007). 10.1109/TBME.2007.893506 [DOI] [PubMed] [Google Scholar]
- 15.Eddy D. M. and Schlessinger L., “Archimedes: A trial-validated model of diabetes,” Diabetes Care 26, 3093–3101 (2003). 10.2337/diacare.26.11.3093 [DOI] [PubMed] [Google Scholar]
- 16.Mari A., Tura A., Grespan E., and Bizzotto R., “Mathematical modeling for the physiological and clinical investigation of glucose homeostasis and diabetes,” Front. Physiol. 11, 1548 (2020). 10.3389/fphys.2020.575789 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lin J., Chase J., Shaw G., Doran C., Hann C., Robertson M., Browne P., Lotz T., Wake G., and Broughton B., “Adaptive bolus-based set-point regulation of hyperglycemia in critical care,” in The 26th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEEE, 2004), Vol. 2, pp. 3463–3466. [DOI] [PubMed]
- 18.Van Herpe T., Pluymers B., Espinoza M., Van den Berghe G., and De Moor B., “A minimal model for glycemia control in critically ill patients,” in 2006 International Conference of the IEEE Engineering in Medicine and Biology Society (IEEE, 2006), pp. 5432–5435. [DOI] [PubMed]
- 19.Haverbeke N., Van Herpe T., Diehl M., Van den Berghe G., and De Moor B., “Nonlinear model predictive control with moving horizon state and disturbance estimation-application to the normalization of blood glucose in the critically ill,” IFAC Proc. Vol. 41, 9069–9074 (2008). 10.3182/20080706-5-KR-1001.01531 [DOI] [Google Scholar]
- 20.Roy A. and Parker R. S., “A phenomenological model of plasma FFA, glucose, and insulin concentrations during rest and exercise,” in Proceedings of the 2010 American Control Conference (IEEE, 2010), pp. 5161–5166.
- 21.Lin J., Razak N. N., Pretty C. G., Le Compte A., Docherty P., Parente J. D., Shaw G. M., Hann C. E., and Chase J. G., “A physiological intensive control insulin-nutrition-glucose (icing) model validated in critically ill patients,” Comput. Methods Programs Biomed. 102, 192–205 (2011). 10.1016/j.cmpb.2010.12.008 [DOI] [PubMed] [Google Scholar]
- 22.Sedigh-Sarvestani M., Albers D. J., and Gluckman B. J., “Data assimilation of glucose dynamics for use in the intensive care unit,” in 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEEE, 2012), pp. 5437–5440. [DOI] [PMC free article] [PubMed]
- 23.Vilkhovoy M., Pritchard-Bell A., Clermont G., and Parker R. S., “A control-relevant model of subcutaneous insulin absorption,” IFAC Proc. Vol. 47, 10988–10993 (2014). 10.3182/20140824-6-ZA-1003.02360 [DOI] [Google Scholar]
- 24.Knab T. D., Clermont G., and Parker R. S., “Zone model predictive control and moving horizon estimation for the regulation of blood glucose in critical care patients,” IFAC-PapersOnLine 48, 1002–1007 (2015). 10.1016/j.ifacol.2015.09.099 [DOI] [Google Scholar]
- 25.Knab T. D., Clermont G., and Parker R. S., “A ‘virtual patient’ cohort and mathematical model of glucose dynamics in critical care,” IFAC-PapersOnLine 49, 1–7 (2016). 10.1016/j.ifacol.2016.12.094 [DOI] [Google Scholar]
- 26.Pritchard-Bell A., Clermont G., Knab T. D., Maalouf J., Vilkhovoy M., and Parker R. S., “Modeling glucose and subcutaneous insulin dynamics in critical care,” Control Eng. Pract. 58, 268–275 (2017). 10.1016/j.conengprac.2016.07.005 [DOI] [Google Scholar]
- 27.Parker R. S., Knab T. D., and Clermont G., “The impact of a responsive endogenous pancreas in critical care glucose control,” in 2018 Annual American Control Conference (ACC) (IEEE, 2018), pp. 3595–3601.
- 28.Lin J., Lee D., Chase J. G., Shaw G. M., Hann C. E., Lotz T., and Wong J., “Stochastic modelling of insulin sensitivity variability in critical care,” Biomed. Signal Process. Control 1, 229–242 (2006). 10.1016/j.bspc.2006.09.003 [DOI] [Google Scholar]
- 29.Lin J., Lee D., Chase J. G., Shaw G. M., Le Compte A., Lotz T., Wong J., Lonergan T., and Hann C. E., “Stochastic modelling of insulin sensitivity and adaptive glycemic control for critical care,” Comput. Methods Programs Biomed. 89, 141–152 (2008). 10.1016/j.cmpb.2007.04.006 [DOI] [PubMed] [Google Scholar]
- 30.Le Compte A. J., Lee D. S., Chase J. G., Lin J., Lynn A., and Shaw G. M., “Blood glucose prediction using stochastic modeling in neonatal intensive care,” IEEE Trans. Biomed. Eng. 57, 509–518 (2009). 10.1109/TBME.2009.2035517 [DOI] [PubMed] [Google Scholar]
- 31.Duun-Henriksen A. K., Schmidt S., Røge R. M., Møller J. B., Nørgaard K., Jørgensen J. B., and Madsen H., “Model identification using stochastic differential equation grey-box models in diabetes,” J. Diabetes Sci. Technol. 7, 431–440 (2013). 10.1177/193229681300700220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Zhang Y., Holt T. A., and Khovanova N., “A data driven nonlinear stochastic model for blood glucose dynamics,” Comput. Methods Programs Biomed. 125, 18–25 (2016). 10.1016/j.cmpb.2015.10.021 [DOI] [PubMed] [Google Scholar]
- 33.Davidson S., Pretty C., Uyttendaele V., Knopp J., Desaive T., and Chase J. G., “Multi-input stochastic prediction of insulin sensitivity for tight glycaemic control using insulin sensitivity and blood glucose data,” Comput. Methods Programs Biomed. 182, 105043 (2019). 10.1016/j.cmpb.2019.105043 [DOI] [PubMed] [Google Scholar]
- 34.Davidson S. M., Uyttendaele V., Pretty C. G., Knopp J. L., Desaive T., and Chase J. G., “Virtual patient trials of a multi-input stochastic model for tight glycaemic control using insulin sensitivity and blood glucose data,” Biomed. Signal Process. Control 59, 101896 (2020). 10.1016/j.bspc.2020.101896 [DOI] [PubMed] [Google Scholar]
- 35.Parker R. S., Doyle F. J., and Peppas N. A., “The intravenous route to blood glucose control,” IEEE Eng. Med. Biol. Mag. 20, 65–73 (2001). 10.1109/51.897829 [DOI] [PubMed] [Google Scholar]
- 36.Brunetti P., Federici M. O., and Benedetti M. M., “The artificial pancreas,” Artif. Cells, Blood Substitutes, Biotechnol. 31, 127–138 (2003). 10.1081/BIO-120020169 [DOI] [PubMed] [Google Scholar]
- 37.Haidar A., “The artificial pancreas: How closed-loop control is revolutionizing diabetes,” IEEE Control Syst. Mag. 36(5), 28–47 (2016). 10.1109/MCS.2016.2584318 [DOI] [Google Scholar]
- 38.Cobelli C. and Ruggeri A., “Evaluation of portal/peripheral route and of algorithms for insulin delivery in the closed-loop control of glucose in diabetes—A modeling study,” IEEE Trans. Biomed. Eng. 30, 93–103 (1983). 10.1109/TBME.1983.325203 [DOI] [PubMed] [Google Scholar]
- 39.Sorensen J. T., “A physiologic model of glucose metabolism in man and its use to design and assess improved insulin therapies for diabetes,” Ph.D. thesis (Massachusetts Institute of Technology, 1985). [Google Scholar]
- 40.Parker R. S., Doyle F. J., Ward J. H., and Peppas N. A., “Robust glucose control in diabetes using a physiological model,” AIChE J. 46, 2537–2549 (2000). 10.1002/aic.690461220 [DOI] [Google Scholar]
- 41.Fabietti P. G., Canonico V., Federici M. O., Benedetti M. M., and Sarti E., “Control oriented model of insulin and glucose dynamics in type 1 diabetics,” Med. Biol. Eng. Comput. 44, 69–78 (2006). 10.1007/s11517-005-0012-2 [DOI] [PubMed] [Google Scholar]
- 42.Man C. D., Micheletto F., Lv D., Breton M., Kovatchev B., and Cobelli C., “The UVA/PADOVA type 1 diabetes simulator: New features,” J. Diabetes Sci. Technol. 8, 26–34 (2014). 10.1177/1932296813514502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bock A., François G., and Gillet D., “A therapy parameter-based model for predicting blood glucose concentrations in patients with type 1 diabetes,” Comput. Methods Programs Biomed. 118, 107–123 (2015). 10.1016/j.cmpb.2014.12.002 [DOI] [PubMed] [Google Scholar]
- 44.Alkhateeb H., El Fathi A., Ghanbari M., and Haidar A., “Modelling glucose dynamics during moderate exercise in individuals with type 1 diabetes,” PLoS One 16, e0248280 (2021). 10.1371/journal.pone.0248280 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.El Fathi A., Kearney R. E., Palisaitis E., Boulet B., and Haidar A., “A model-based insulin dose optimization algorithm for people with type 1 diabetes on multiple daily injections therapy,” IEEE Trans. Biomed. Eng. 68, 1208–1219 (2021). 10.1109/TBME.2020.3023555 [DOI] [PubMed] [Google Scholar]
- 46.Balakrishnan N. P., Samavedham L., and Rangaiah G. P., “Personalized mechanistic models for exercise, meal and insulin interventions in children and adolescents with type 1 diabetes,” J. Theor. Biol. 357, 62–73 (2014). 10.1016/j.jtbi.2014.04.038 [DOI] [PubMed] [Google Scholar]
- 47.Deichmann J., Bachmann S., Burckhardt M.-A., Pfister M., Szinnai G., and Kaltenbach H.-M., “New model of glucose-insulin regulation characterizes effects of physical activity and facilitates personalized treatment evaluation in children and adults with type 1 diabetes,” PLoS Comput. Biol. 19, e1010289 (2023). 10.1371/journal.pcbi.1010289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wilinska M. E., Chassin L. J., Acerini C. L., Allen J. M., Dunger D. B., and Hovorka R., “Simulation environment to evaluate closed-loop insulin delivery systems in type 1 diabetes,” J. Diabetes Sci. Technol. 4, 132–144 (2010). 10.1177/193229681000400117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Haidar A., Wilinska M. E., Graveston J. A., and Hovorka R., “Stochastic virtual population of subjects with type 1 diabetes for the assessment of closed-loop glucose controllers,” IEEE Trans. Biomed. Eng. 60, 3524–3533 (2013). 10.1109/TBME.2013.2272736 [DOI] [PubMed] [Google Scholar]
- 50.Chee F. and Fernando T., Closed-Loop Control of Blood Glucose (Springer, 2007), Vol. 368. [DOI] [PubMed] [Google Scholar]
- 51.Thabit H., Tauschmann M., Allen J. M., Leelarathna L., Hartnell S., Wilinska M. E., Acerini C. L., Dellweg S., Benesch C., Heinemann L. et al., “Home use of an artificial beta cell in type 1 diabetes,” N. Engl. J. Med. 373, 2129–2140 (2015). 10.1056/NEJMoa1509351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tauschmann M., Thabit H., Bally L., Allen J. M., Hartnell S., Wilinska M. E., Ruan Y., Sibayan J., Kollman C., Cheng P. et al., “Closed-loop insulin delivery in suboptimally controlled type 1 diabetes: A multicentre, 12-week randomised trial,” Lancet 392, 1321–1329 (2018). 10.1016/S0140-6736(18)31947-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Benhamou P.-Y., Franc S., Reznik Y., Thivolet C., Schaepelynck P., Renard E., Guerci B., Chaillous L., Lukas-Croisier C., Jeandidier N. et al., “Closed-loop insulin delivery in adults with type 1 diabetes in real-life conditions: A 12-week multicentre, open-label randomised controlled crossover trial,” Lancet Digital Health 1, e17–e25 (2019). 10.1016/S2589-7500(19)30003-2 [DOI] [PubMed] [Google Scholar]
- 54.Brown S. A., Kovatchev B. P., Raghinaru D., Lum J. W., Buckingham B. A., Kudva Y. C., Laffel L. M., Levy C. J., Pinsker J. E., Wadwa R. P. et al., “Six-month randomized, multicenter trial of closed-loop control in type 1 diabetes,” N. Engl. J. Med. 381, 1707–1717 (2019). 10.1056/NEJMoa1907863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bruttomesso D., “Toward automated insulin delivery,” N. Engl. J. Med. 381, 1774–1775 (2019). 10.1056/NEJMe1912822 [DOI] [PubMed] [Google Scholar]
- 56.Murata G. H., Hoffman R. M., Shah J. H., Wendel C. S., and Duckworth W. C., “A probabilistic model for predicting hypoglycemia in type 2 diabetes mellitus: The diabetes outcomes in veterans study (doves),” Arch. Intern. Med. 164, 1445–1450 (2004). 10.1001/archinte.164.13.1445 [DOI] [PubMed] [Google Scholar]
- 57.Zitar R. A. and Al-Jabali A., “Towards neural network model for insulin/glucose in diabetics-II,” Informatica 29, 227–232 (2005). [Google Scholar]
- 58.Rollins D. K., Bhandari N., Kleinedler J., Kotz K., Strohbehn A., Boland L., Murphy M., Andre D., Vyas N., Welk G. et al., “Free-living inferential modeling of blood glucose level using only noninvasive inputs,” J. Process Control 20, 95–107 (2010). 10.1016/j.jprocont.2009.09.008 [DOI] [Google Scholar]
- 59.Beverlin L. P., Rollins D. K., Vyas N., and Andre D., “An algorithm for optimally fitting a Wiener model,” Math. Probl. Eng. 2011, 570509 (2011). 10.1155/2011/570509 [DOI] [Google Scholar]
- 60.Gibson B. S., Colberg S. R., Poirier P., Vancea D. M. M., Jones J., and Marcus R., “Development and validation of a predictive model of acute glucose response to exercise in individuals with type 2 diabetes,” Diabetol. Metab. Syndr. 5, 33 (2013). 10.1186/1758-5996-5-33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sudharsan B., Peeples M., and Shomali M., “Hypoglycemia prediction using machine learning models for patients with type 2 diabetes,” J. Diabetes Sci. Technol. 9, 86–90 (2014). 10.1177/1932296814554260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Zeevi D., Korem T., Zmora N., Israeli D., Rothschild D., Weinberger A., Ben-Yacov O., Lador D., Avnit-Sagi T., Lotan-Pompan M. et al., “Personalized nutrition by prediction of glycemic responses,” Cell 163, 1079–1094 (2015). 10.1016/j.cell.2015.11.001 [DOI] [PubMed] [Google Scholar]
- 63.Bremer T. and Gough D. A., “Is blood glucose predictable from previous values? A solicitation for data,” Diabetes 48, 445–451 (1999). 10.2337/diabetes.48.3.445 [DOI] [PubMed] [Google Scholar]
- 64.Reifman J., Rajaraman S., Gribok A., and Ward W. K., “Predictive monitoring for improved management of glucose levels,” J. Diabetes Sci. Technol. 1, 478–486 (2007). 10.1177/193229680700100405 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Sparacino G., Zanderigo F., Corazza S., Maran A., Facchinetti A., and Cobelli C., “Glucose concentration can be predicted ahead in time from continuous glucose monitoring sensor time-series,” IEEE Trans. Biomed. Eng. 54, 931–937 (2007). 10.1109/TBME.2006.889774 [DOI] [PubMed] [Google Scholar]
- 66.Gani A., Gribok A. V., Rajaraman S., Ward W. K., and Reifman J., “Predicting subcutaneous glucose concentration in humans: Data-driven glucose modeling,” IEEE Trans. Biomed. Eng. 56, 246–254 (2009). 10.1109/TBME.2008.2005937 [DOI] [PubMed] [Google Scholar]
- 67.Zhang Z., “A mathematical model for predicting glucose levels in critically-ill patients: The Pignoli model,” PeerJ 3, e1005 (2015). 10.7717/peerj.1005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Montaser E., Díez J.-L., and Bondia J., “Stochastic seasonal models for glucose prediction in the artificial pancreas,” J. Diabetes Sci. Technol. 11, 1124–1131 (2017). 10.1177/1932296817736074 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yang J., Li L., Shi Y., and Xie X., “An arima model with adaptive orders for predicting blood glucose concentrations and hypoglycemia,” IEEE J. Biomed. Health Inf. 23, 1251–1260 (2018). 10.1109/JBHI.2018.2840690 [DOI] [PubMed] [Google Scholar]
- 70.Abbas H. T., Alic L., Erraguntla M., Ji J. X., Abdul-Ghani M., Abbasi Q. H., and Qaraqe M. K., “Predicting long-term type 2 diabetes with support vector machine using oral glucose tolerance test,” PLoS One 14, e0219636 (2019). 10.1371/journal.pone.0219636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Miller A. C., Foti N. J., and Fox E., “Learning insulin-glucose dynamics in the wild,” in Machine Learning for Healthcare Conference (PMLR, 2020), pp. 172–197.
- 72.Cavanaugh K., Huizinga M. M., Wallston K. A., Gebretsadik T., Shintani A., Davis D., Gregory R. P., Fuchs L., Malone R., Cherrington A. et al., “Association of numeracy and diabetes control,” Ann. Intern. Med. 148, 737–746 (2008). 10.7326/0003-4819-148-10-200805200-00006 [DOI] [PubMed] [Google Scholar]
- 73.Gibson B., Marcus R. L., Staggers N., Jones J., Samore M., Weir C. et al., “Efficacy of a computerized simulation in promoting walking in individuals with diabetes,” J. Med. Internet Res. 14, e1965 (2012). 10.2196/jmir.1965 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Mamykina L., Levine M. E., Davidson P. G., Smaldone A. M., Elhadad N., and Albers D. J., “Data-driven health management: Reasoning about personally generated data in diabetes with information technologies,” J. Am. Med. Inf. Assoc. 23, 526–531 (2016). 10.1093/jamia/ocv187 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Mamykina L., Levine M. E., Davidson P. G., Smaldone A. M., Elhadad N., and Albers D. J., “From personal informatics to personal analytics: Investigating how clinicians and patients reason about personal data generated with self-monitoring in diabetes,” in Cognitive Informatics in Health and Biomedicine (Springer, 2017), pp. 301–313.
- 76.Albers D. J., Levine M. E., Stuart A., Mamykina L., Gluckman B., and Hripcsak G., “Mechanistic machine learning: How data assimilation leverages physiologic knowledge using Bayesian inference to forecast the future, infer the present, and phenotype,” J. Am. Med. Inf. Assoc. 25, 1392–1401 (2018). 10.1093/jamia/ocy106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Desai P. M., Levine M. E., Albers D. J., and Mamykina L., “Pictures worth a thousand words: Reflections on visualizing personal blood glucose forecasts for individuals with type 2 diabetes,” in Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems (ACM, 2018), p. 538.
- 78.Desai P. M., Mitchell E. G., Hwang M. L., Levine M. E., Albers D. J., and Mamykina L., “Personal health oracle: Explorations of personalized predictions in diabetes self-management,” in Proceedings of the 2019 CHI Conference on Human Factors in Computing Systems (ACM, 2019), p. 370.
- 79.Lum E., Jimenez G., Huang Z., Thai L., Semwal M., Boehm B. O., and Car J., “Decision support and alerts of apps for self-management of blood glucose for type 2 diabetes,” Jama 321, 1530–1532 (2019). 10.1001/jama.2019.1644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Glachs D., Namli T., Strohmeier F., Rodríguez Suárez G., Sluis M., Delgado-Lista J., Sont J. K., de Graaf A. A., Salzsieder E., and Vogt L., “A predictive model-based decision support system for diabetes patient empowerment,” in Public Health and Informatics (IOS Press, 2021), pp. 963–968. [DOI] [PubMed]
- 81.Mitchell E. G., Tabak E. G., Levine M. E., Mamykina L., and Albers D. J., “Enabling personalized decision support with patient-generated data and attributable components,” J. Biomed. Inf. 113, 103639 (2021). 10.1016/j.jbi.2020.103639 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Engl H. W., Hanke M., and Neubauer A., Regularization of Inverse Problems (Springer Science & Business Media, 1996), Vol. 375. [Google Scholar]
- 83.Kaipio J. and Somersalo E., Statistical and Computational Inverse Problems (Springer Science & Business Media, 2006), Vol. 160. [Google Scholar]
- 84.Wu S. and Furutani E., “Nonlinear model predictive glycemic control of critically ill patients using online identification of insulin sensitivity,” in 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (IEEE, 2016), pp. 2245–2248. [DOI] [PubMed]
- 85.Herpe T. V., Espinoza M., Haverbeke N., Moor B. D., and den Berghe G. V., “Glycemia prediction in critically ill patients using an adaptive modeling approach,” J. Diabetes Sci. Technol. 1, 348–356 (2007). 10.1177/193229680700100306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Hovorka R., Chassin L. J., Ellmerer M., Plank J., and Wilinska M. E., “A simulation model of glucose regulation in the critically ill,” Physiol. Meas. 29, 959 (2008). 10.1088/0967-3334/29/8/008 [DOI] [PubMed] [Google Scholar]
- 87.Oksendal B., Stochastic Differential Equations: An Introduction with Applications (Springer Science & Business Media, 2013). [Google Scholar]
- 88.Albers D. J., Levine M., Gluckman B., Ginsberg H., Hripcsak G., and Mamykina L., “Personalized glucose forecasting for type 2 diabetes using data assimilation,” PLoS Comput. Biol. 13, e1005232 (2017). 10.1371/journal.pcbi.1005232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Stuart A. M., “Inverse problems: A Bayesian perspective,” Acta Numer. 19, 451–559 (2010). 10.1017/S0962492910000061 [DOI] [Google Scholar]
- 90.Ha J. and Sherman A., “Type 2 diabetes: One disease, many pathways,” Am. J. Physiol. Endocrinol. Metab. 319, E410–E426 (2020). 10.1152/ajpendo.00512.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Albers D. and Hripcsak G., “A statistical dynamics approach to the study of human health data: Resolving population scale diurnal variation in laboratory data,” Phys. Lett. A 374, 1159–1164 (2010). 10.1016/j.physleta.2009.12.067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Hripcsak G., Albers D. J., and Perotte A., “Exploiting time in electronic health record correlations,” J. Am. Med. Inf. Assoc. 18, i109–i115 (2011). 10.1136/amiajnl-2011-000463 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Hripcsak G. and Albers D. J., “Next-generation phenotyping of electronic health records,” J. Am. Med. Inf. Assoc. 20, 117–121 (2012). 10.1136/amiajnl-2012-001145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Hripcsak G. and Albers D. J., “Correlating electronic health record concepts with healthcare process events,” J. Am. Med. Inf. Assoc. 20, e311–e318 (2013). 10.1136/amiajnl-2013-001922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Pivovarov R., Albers D. J., Sepulveda J. L., and Elhadad N., “Identifying and mitigating biases in EHR laboratory tests,” J. Biomed. Inf. 51, 24–34 (2014). 10.1016/j.jbi.2014.03.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Hripcsak G. and Albers D. J., “High-fidelity phenotyping: Richness and freedom from bias,” J. Am. Med. Inf. Assoc. 25, 289–294 (2017). 10.1093/jamia/ocx110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Albers D. J., Elhadad N., Claassen J., Perotte R., Goldstein A., and Hripcsak G., “Estimating summary statistics for electronic health record laboratory data for use in high-throughput phenotyping algorithms,” J. Biomed. Inf. 78, 87–101 (2018). 10.1016/j.jbi.2018.01.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Levine M. E., Albers D. J., and Hripcsak G., “Methodological variations in lagged regression for detecting physiologic drug effects in ehr data,” J. Biomed. Inf. 86, 149–159 (2018). 10.1016/j.jbi.2018.08.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Albers D. J., Hripcsak G., and Schmidt M., “Population physiology: Leveraging electronic health record data to understand human endocrine dynamics,” PLoS One 7, e48058 (2012). 10.1371/journal.pone.0048058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Albers D. J., Elhadad N., Tabak E., Perotte A., and Hripcsak G., “Dynamical phenotyping: Using temporal analysis of clinically collected physiologic data to stratify populations,” PLoS One 9, e96443 (2014). 10.1371/journal.pone.0096443 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Churchill G. A., Jr., “A paradigm for developing better measures of marketing constructs,” J. Mark. Res. 16, 64–73 (1979). 10.2307/3150876 [DOI] [Google Scholar]
- 102.Hardesty D. M. and Bearden W. O., “The use of expert judges in scale development: Implications for improving face validity of measures of unobservable constructs,” J. Bus. Res. 57, 98–107 (2004). 10.1016/S0148-2963(01)00295-8 [DOI] [Google Scholar]
- 103.Weiner I. B. and Craighead W. E., The Corsini Encyclopedia of Psychology (John Wiley & Sons, 2010), Vol. 4. [Google Scholar]
- 104.Sherman R. E., Anderson S. A., Dal Pan G. J., Gray G. W., Gross T., Hunter N. L., LaVange L., Marinac-Dabic D., Marks P. W., Robb M. A. et al., “Real-world evidence—What is it and what can it tell us,” N. Engl. J. Med. 375, 2293–2297 (2016). 10.1056/NEJMsb1609216 [DOI] [PubMed] [Google Scholar]
- 105.Hripcsak G. and Albers D. J., “Evaluating prediction of continuous clinical values: A glucose case study,” Methods Inf. Med. 61, e35–e44 (2022). 10.1055/s-0042-1743170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.MacKay D. J., Information Theory, Inference and Learning Algorithms (Cambridge University Press, 2003). [Google Scholar]
- 107.Owen A. B., Monte Carlo Theory, Methods and Examples (2013), see https://artowen.su.domains/mc/. [Google Scholar]
- 108.Van der Vaart A. W., Asymptotic Statistics (Cambridge University Press, 2000). [Google Scholar]
- 109.Liu J. S., Monte Carlo Strategies in Scientific Computing (Springer Science & Business Media, 2008). [Google Scholar]
- 110.Robert C. and Casella G., Monte Carlo Statistical Methods (Springer Science & Business Media, 2013). [Google Scholar]
- 111.Gelman A., Carlin J. B., Stern H. S., Dunson D. B., Vehtari A., and Rubin D. B., Bayesian Data Analysis (Chapman and Hall/CRC, 2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The Columbia University IRB approved the collection of these T2DM data with the number AAAM0057. The ICU data were collected from the Columbia University Clinical Data Warehouse, are identified data, and can be made available upon request and approval of a data use agreement. We are currently working to make these data publicly available.