Vertical and Leg Stiffness Modeling During Running: Effect of Speed and Incline

Abstract

A spring mass model is often used to describe human running, allowing to understand the concept of elastic energy storage and restitution. The stiffness of the spring is a key parameter and different methods have been developed to estimate both the vertical and the leg stiffness components. Nevertheless, the validity and the range of application of these models are still debated. The aim of the present study was to compare three methods (i. e., Temporal, Kinetic and Kinematic-Kinetic) of stiffness determination. Twenty-nine healthy participants equipped with reflective markers performed 5-min running bouts at four running speeds and eight inclines on an instrumented treadmill surrounded by a tri-dimensional motion camera system. The three methods provided valid results among the different speeds, but the reference method (i. e., Kinematic-Kinetic) provided higher vertical stiffness and lower leg stiffness than the two other methods (both p<0.001). On inclined terrain, the method using temporal parameters provided non valid outcomes and should not be used. Finally, this study highlights that both the assumption of symmetry between compression and decompression phases or the estimation of the vertical displacement and changes in leg length are the major sources of errors when comparing different speeds or different slopes.

Introduction

Considering legs as springs has been introduced by Cavagna et al. ¹ to explain the high efficiency of running. Indeed, if potential and kinetic energy are in anti-phase during walking, allowing for energy transfers, they are in phase during running ² . The observed running efficiency therefore implies an internal mechanism that absorb and restore mechanical energy. This mechanism has been used to describe a stretch shortening cycle, where animals can store and return elastic energy in muscles, tendons and ligaments while hopping, trotting or running ^{3 4 5 6} . Cavagna et al. ⁴ observed a lower deformation of the lower limb with the increase of the running speed and suggested a quicker and more rigid spring at higher speed.

A spring mass model was then proposed by Blickhan ⁷ considering the human body as a single point mass bouncing on a massless spring. The limits of the model were clearly addressed, as it supposed similar take-off and landing velocities and symmetrical acceleration and deceleration phases during stance. Based on this model, Mc Mahon and Cheng ⁸ and then Farley and Gonzalez ⁹ provided equations to determine both vertical stiffness (Kvert) and leg stiffness (Kleg). They used maximal vertical force value during stance (Fz _max ), vertical displacement of the center of mass (COM), running velocity (V) and foot contact time (T _contact ). They assumed that the angles of the spring respectively at foot initial contact and toe off were identical. Finally, Morin et al. ¹⁰ developed equations allowing to estimate the maximal force using T _contact and flight time T _flight . This method has been widely used, due to its simplicity since only spatio-temporal parameters are needed to calculate Kvert and Kleg. Globally, results based on the spring mass model seems to show constant leg stiffness as running speed increased ^{8 9 10 11} .

Arampatzis et al. ¹² developed another approach, using both kinetic and kinematic data to determine Kvert and Kleg (Eq.1–2).

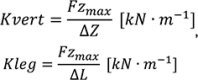
A force platform was used to determine the maximal force, while COM vertical displacement (ΔZ) and changes in leg length (ΔL) were calculated using synchronized cameras and a 15 segments body model ^{13 14} . They observed a clear effect of speed on Kleg, showing a discrepancy with the model-based method described above.

In a review by Brughelli and Cronin ¹⁵ , indirect evidence of increased Kleg with speed was highlighted. These authors analysed 14 studies evaluating running stiffness and compared running speeds below vs higher than 5 m·s ^-1 . The average Kleg was 11.2 vs 17.0 kN·m ^-1 in the low vs high speed, respectively. As several studies reported a constant leg stiffness with running speed increase ^{8 10 11} it is very interesting to gain more insight about these discrepancies. One may therefore hypothesize that the leg stiffness is dependent on the running speed, and that the calculation method per se modifies the outcome.

In addition to the effect of speed, another important aspect is the applicability of the spring-mass model for graded running. The model is indeed based on the assumption that the oscillations are symmetrical, which is not respected on a slope ¹⁶ . Nevertheless, using direct measurement of the maximal force and COM displacement should still provide coherent results, while the simplified equation developed by Morin et al. ¹⁰ should induce different outcomes. It would therefore be of interest to compare the different models for both Kvert and Kleg on different slopes. As Dewolf et al. ¹⁷ showed the progressive reduction of the rebound mechanism when slope increase, (both in uphill and downhill), one may hypothesize that both Kvert and Kleg would reach very important values on slopes.

Materials and Methods

Subjects

Twenty-nine healthy individuals (19 males, 10 females) volunteered in this study (age: 34±10 [mean±SD] years; height: 1.74±0.09 m; body mass: 68.3±12.2 kg). They were running between one and 5 times a week. Every participant was informed on the benefits and risks of this investigation prior to giving their written informed consent to participate in this study. The protocol was approved by the local ethical committee and conducted according to the declaration of Helsinki.

Design

All participants visited the laboratory on four occasions to perform each of the experimental tests. A level running incremental test was performed during the first session, with the first stage beginning at 8 km·h ^-1 during 4 min and the running speed then increased by 1 km·h ^-1 every minute. Then, during the next three sessions participants had to perform six to eight running bouts at different speeds (8, 10, 12 and 14 km·h ^-1 ) and different treadmill slopes (−20, −10, −5, 0, 5, 10, 15 and 20%). For each condition, participants had to run for 4 min to allow reaching a steady state ¹⁸ , following by two to five minutes of recovery between each trial. The high demanding conditions (20% at 12 and 14 km·h ^-1 and 15% at 14 km·h ^-1 ) were not performed, and the trials were also interrupted when the participant was not able to reach a steady state. The order of the speed and slope conditions was randomized for each participant and each session was separated by at least one week of recovery.

Methodology

An instrumented treadmill (T-170-FMT, Arsalis, Belgium) sampling at 1000 Hz was used to record 3D reaction force, and a 3D cameras system composed of eight infrared cameras (Vicon Motion System, Ltd., Oxford, UK) was used to record kinematic data at 200 Hz. Before each test session, participants were equipped with 39 retro-reflective markers (14 mm in diameter) following the integrated plug-in Gait Model. Kinetics and kinematics data were recorded during 30 s starting 45 s before the end of the trial.

A specific procedure (Matlab version R2019a, MathWorks Inc., Natick, MA, USA) was developed to process and analyze data ¹⁹ : To reduce the noise inherent to the treadmill’s vibrations, we first applied, on the vertical ground reaction force (GRF) signal, a 2nd-order stop-band Butterworth filter with edge frequencies set to 25 and 65 Hz. The filter configuration was chosen empirically to obtain a satisfactory reduction of the oscillations observed during flight phases (i. e., subject not in contact with the treadmill) while minimizing its widening effect during ground contact time.

The instants of initial contact (IC) and terminal contact (TC) were identified using a threshold of 7% of bodyweight on the filtered vertical ground reaction force signal, based on a previously published work ¹⁹ . The IC and TC of the left and right legs were combined to determine the T _contact (the time duration between IC and TC of the same leg) and the T _flight (the time duration between the TC of one leg and the IC of the other leg).

Depending on available instrument and possible application, three methods were used and compared to estimate Kvert and Kleg (Eq. 1–2) from Fz _max , ΔL and ΔZ:

Temporal method where only spatio-temporal parameters were provided using Eq. 3–5 ¹⁰ . The leg length (Lmod) was estimated as 0.53*height (in m) ²⁰ , m is the mass of the participant, g the gravity constant.

Kinetic method in which a force platform is available to determine the vertical force (Fz) and estimate the vertical speed (Vz) and vertical displacement of the center of mass (h) (Eq. 6–10) ²¹ .

Kinematic-Kinetic method, where kinematic data obtained from 3D motion capture system was used to estimate ΔZ and ΔL with morphological estimation models ^{13 14} , (Eq. 11–13). The variables X, Y and Z are the 3D coordinate of a given point in a global reference system, L represent the leg length. The point of force application on the treadmill (subscript _PFA ) was obtained directly from the force plate ^{22 23} and the subscript _Hip is given for the Hip 3D position calculated by the plug-in Gait Model.

Statistical analysis

Linear mixed models (LMM) were applied on the dependant variables Kvert, Kleg, ΔZ, ΔL and Fz _max obtained with the three methods, with a fixed effect on the method and on the slope as independent variables, and a random intercept effect on subjects. The Bonferroni pairwise comparison post-hoc test was then applied to identify differences between methods, slopes and speeds. All the statistical comparisons were obtained using Jamovi Software (Jamovi project 2020, Version 1.2, Sydney; Australia). The overall significance level was set at p<0.05. The Cohen’s coefficients f ² were also presented to assess effect size. They were calculated based on the marginal coefficient of determination R ² as proposed by Selya et al. ²⁴ . Values of 0.02 and over are considered small, 0.15 medium and 0.35 large ²⁵ . All data are expressed as mean±standard deviation (SD).

Results

Effect of speed

For the determination of Kvert, the LMM showed a significant difference between methods (p<0.001, f ² =0.16) ( Fig. 1a ). The post-hoc indicated significant lower values in Kvert with the Temporal and Kinetic methods than with the Kinematic-Kinetic method (both p<0.001), but not between Temporal and Kinetic (p=0.44). Each method showed a significant increase of Kvert with increase of speed (p<0.001, f ² =0.65).

Fig. 1.

a . Vertical stiffness given as a function of speed, calculated using a Temporal, Kinetic or Kinematic-Kinetic method. b . Leg stiffness given as a function of speed, calculated with either the Temporal, Kinetic or Kinematic-Kinetic method. *Significant difference between methods (p<0.05).

The LMM highlighted significant differences between methods to assess Kleg (p<0.001, f ² =0.21) ( Fig 1b ). The post-hoc showed lower values with Kinematic-Kinetic than with Kinetic as well as with Kinetic than Temporal (all p<0.001) ( Fig. 2 ). With the increase of speed, the Kleg significantly decreased, but with a small effect size (p<0.001, f ² =0.04).

Fig. 2.

a . Vertical displacement of the center of mass (ΔZ) given as a function of speed, calculated with either the Kinematic-Kinetic, Temporal or Kinetic method. b . Leg length change (ΔL) given as a function of speed, calculated with either a Kinematic-Kinetic, Temporal or Kinetic method. c . Maximal vertical force (Fzmax) given as a function of speed, calculated with either the Kinematic-Kinetic, Temporal or Kinetic method. *Significant difference between methods (p<0.05).

Looking at the intrinsic parameters allowing to determine Kleg and Kvert, ΔZ values were significantly different between methods (p<0.001, f ² =0.10) ( Fig. 2a ). The pairwise comparison indicated significant higher values of ΔZ with Kinetic compared to Kinematic-Kinetic (p=0.008), and for Temporal compared to both Kinetic and Kinematic-Kinetic (both p<0.001). The effect of speed was also significant (p<0.001, f ² =0.17), with a decrease of ΔZ with running speed increase. For ΔL, the LMM indicate a significant difference between methods (p<0.001, f ² =0.30) ( Fig. 2b ). The post-hoc comparison indicated significantly higher ΔL values with Kinematic-Kinetic compared to Temporal and Kinetic, and with Temporal than Kinetic (all p<0.001). The running speed also had significant impact on ΔL (p<0.001, f ² =0.44), with a positive correlation. Finally, the Fz _max calculation using either a force plate or a model based on temporal parameters didn’t show significant differences (p=0.065) ( Fig. 2c ). The Fz _max significantly increased with the speed (p<0.001, f ² =0.13)

Effect of slope

The determination of Kvert highlighted significant differences when using the three different methods (p<0.001, f ² =0.37) ( Fig. 3a ). Kvert with the Temporal method was significantly lower than with Kinematic-Kinetic or Kinetic (both p<0.001), and with Kinetic than with Kinematic-Kinetic (p=0.04). The slope also significantly impacted the calculation of the Kvert (p<0.001, f ² =0.18). Both the Kinematic-Kinetic and the Kinetic methods did not provide valid Kvert values on extreme slopes (i. e.±20%) as Kvert reached infinite values on such slopes.

Fig. 3.

a . Vertical stiffness given as a function of slope, calculated with either the Kinematic-Kinetic, Temporal or Kinetic method. b . Leg stiffness given as a function of slope, calculated with either the Kinematic-Kinetic, Temporal or Kinetic method. *Significant difference between methods (p<0.05).

The Kleg was also significantly affected by the calculation method (p<0.001, f ² =0.42) ( Fig. 3b ), Pairwise comparison indicated higher Kleg values with the Kinetic method than Kinematic-Kinetic and Temporal (both p<0.001) as well as with Temporal than Kinematic-Kinetic (p<0.001). The slope also had a significant impact on the Kleg calculation (p<0.001, f ² =0.17).

Looking at the intrinsic parameters allowing to determine Kleg and Kvert, ΔZ values were significantly different between methods (p<0.001, f ² =0.94) ( Fig. 4a ). The pairwise comparison indicated significant higher ΔZ values with the Temporal method compared to both Kinematic-Kinetic and Kinetic (p<0.001), and higher ΔZ values with Kinematic-Kinetic compared to Kinetic (p<0.001). The effect of slope was also significant (p<0.001, f ² =0.41).

Fig. 4.

a . Vertical displacement of the center of mass (ΔZ) given as a function of slope, calculated with either the Kinematic-Kinetic, Temporal or Kinetic method. b . Leg length change (ΔL) given as a function of slope, calculated using a Kinematic-Kinetic, Temporal or Kinetic method. c . Maximal vertical force (Fz _max ) given as a function of slope, calculated with either the Kinematic-Kinetic, Temporal or Kinetic method. *Significant difference between methods (p<0.05).

The LMM indicate a significant difference between methods (p<0.001, f ² =0.43) ( Fig. 4b ). The pairwise comparison indicated significantly higher ΔL values for Kinematic-Kinetic compared to both Temporal and Kinetic, as well as with Temporal than Kinetic (all p<0.001). The slope also had significant impact on ΔL (p<0.001, f ² =0.20). Finally, the Fz _max calculation using either a force plate or a model based on temporal parameters showed significant differences but with a very low effect size (p<0.001, f ² =0.01) ( Fig. 4c ). The Fz _max significantly decreased when the slope increased, with a low effect size (p<0.001, f ² =0.06).

Discussion

The present study is the first to clearly report the boundaries in which the model based on temporal parameters proposed by Morin et al. ¹⁰ can be applied. As expected, the model based on spatio-temporal parameters is not valid on slopes, even at low inclines (5% uphill and 10% downhill). Interestingly, Snyder and Farley ²⁶ found the same asymmetry in energy storage at slopes between a+3 and -3 degrees. In downhill running, the same amount of elastic energy was stored in the leg compared to level running, while significantly lower energy was stored during uphill running. The Kinetic and Kinematic-Kinetic models showed higher values in both Kvert and Kleg when slope increases (and decreases), whereas the Temporal method provides results that are constant and independent of the slope. The results obtained with the Kinetic and Kinematic-Kinetic models are consistent with the results of Dewolf et al. ¹⁷ , as the stiffness increased on steeper slopes. Indeed, as the energy stored in a spring is equal to half of the spring coefficient times the square of the displacement of the spring, the stored value will reach zero when the displacement come close to zero. Therefore, previous studies that used the Temporal method to determine Kvert and Kleg on incline terrain are questionable ^{27 28} .

The present study highlighted also a constant Kleg on a large speed range, and the validity of the Temporal model for level running. The three methods used in our study provided consistent outcomes, but the Kinematic-Kinetic method gave lower values then the Temporal and the Kinetic methods. This is in line with previous reports that compared different method and highlighted the good behavior of Temporal method ^{22 29} for different speeds. The Temporal and the Kinetic method provide similar values but lower Kvert values and higher Kleg values than with the Kinematic-Kinetic method. This difference is probably due to the calculation method of ΔZ and ΔL. These results are consistent with previously published work using the spring mass model ^{8 9 10 11} , but differs with the indirect evidence found by Brughelli and Cronin ¹⁵ and with the study of Arampatzis et al. ¹² , that used a method similar to our Kinematic-Kinetic method. The difference seems to come from the calculation of the ΔL, that is constant in Arampatzis et al. ¹² , but increases with speed in our work.

With the speed range used in this study, we can assume the symmetry of the deceleration and acceleration phases. Nevertheless, the Kinematic-Kinetic method should be adapted to estimate the compression and the decompression of the spring with two different stiffness, as proposed by Clark and Weyand ³⁰ . This method could probably provide more insights on the mechanisms involved when sprinting and explain the higher Kleg obtained at maximal speed ¹⁵ .

Overall, this study confirms that errors may arise from different sources across running speeds or slopes: the indirect estimation of ΔZ and ΔL and the symmetry of acceleration and deceleration phases – known to be wrong – have different weight on the inaccuracy when comparing different speeds or different slopes. While we argue that the assumption of the symmetry of land and take-off symmetry (known to be inexact) is an important source of inaccuracy, the derivation of the kinematics which drive the estimation of ΔZ and ΔL and consequently the differences in Kvert and Kleg is also an important limitation. Moreover, none of the models take into account the medial-lateral displacement estimated to be negligible ³¹ .

Stiffness calculation and analysis is used both in research and by practitioners to gather useful information of athletes’ physical state. It has been shown that both Kvert and Kleg are affected during marathon running ^{32 33} , providing insight about the accumulated fatigue. It is therefore important for coaches and researchers to understand the applicability and the limit of the calculation method, to make sur that their interpretation of the output is valid. As a consequence, the Temporal method ¹⁰ is perfectly adapted for level running, but should not been used in Trail or on slopes.

Conclusion

Using mathematical models is helpful to describe complex concepts, but caution is needed when applying these models. In this work, we analysed the range of application and the limits of different stiffness calculation methods. This study highlights that the assumption of symmetry between compression and decompression phases or the estimation of ΔZ and ΔL are the major sources of errors when comparing different speeds or different slopes.

Funding Statement

Funding Information Innosuisse – Schweizerische Agentur für Innovationsförderung — http://dx.doi.org/10.13039/501100013348; 32166.1