A Brief Primer on Conducting Regression-Based Causal Mediation Analysis

Abstract

Objective:

We provide an overview of regression-based causal mediation analysis in the field of traumatic stress and guidance on how to conduct mediation analysis using our R package regmedint.

Method:

We discuss the causal interpretations of the quantities that causal mediation analysis estimates, including total, direct and indirect effects, especially when interaction between exposure and mediator is permitted. We discuss the assumptions that must be fulfilled for mediation analyses to validly estimate these causal quantities, discuss suitable study designs for assessing mediation, and describe how causal mediation analysis differs from traditional methods for mediation. To illustrate how to conduct and interpret mediation analysis using our R package regmedint, we use data from a published longitudinal study to assess the extent to which children’s externalizing behavior mediates changes in parental negative feelings during the COVID-19 lockdown. We compare the results to those obtained using traditional methods, thus illustrating the importance of accounting for exposure-mediator interaction when an interaction may be present.

Results:

When the exposure and the mediator interact, traditional methods can provide estimates of direct and indirect effects that differ from those provided by more flexible causal mediation methods. When the exposure and the mediator do not interact, traditional methods and causal mediation method may estimate similar direct and indirect effects depending on the model specification.

Conclusions:

In contrast to traditional methods for mediation analysis, regression-based causal mediation methods seek to estimate specific interventional quantities, not mere associations, and the causal methods explicitly allow for exposure-mediator interactions. We recommend using these methods by default rather than using more restrictive traditional methods.

1. INTRODUCTION

Mediation analysis, an increasingly popular method in multiple scientific disciplines, seeks to clarify the causal mechanisms by which an exposure affects an outcome (MacKinnon, 2017). A mediator is a variable that lies on the causal pathway between an exposure and outcome in the sense that the exposure affects the mediator, and the mediator then affects the outcome. We say that an effect is “mediated” if at least some of the exposure’s effect on the outcome operates by way of the mediator (the “indirect effect”), while the rest of the exposure’s effect on the outcome operates by way of other mechanisms that do not include the mediator of interest (the “direct effect”). For example, in a study we will illustrate as a running example, Achterberg et al. (2021) assessed longitudinal trajectories in parental well-being before and during the COVID-19 lockdown. We used their dataset to assess the extent to which the effect of a parent’s reported negative feelings before the lockdown on their negative feelings during the lockdown (i.e., the total effect) would be mediated by their children’s externalizing behavior in the interim (the indirect effect).

We begin by discussing the quantities that mediation analysis seeks to estimate and their causal interpretations. We discuss important assumptions that must be fulfilled for mediation analyses to validly estimate these causal quantities and discuss suitable study designs in light of those assumptions. We then provide an overview of regression-based mediation analysis (Valeri & VanderWeele, 2013; VanderWeele, 2015) and illustrate how to conduct and interpret mediation analysis using our recently released R package, regmedint (Yoshida, Li, & Mathur, 2022). This package supplements existing software and tutorials for conducting regression-based mediation analysis in SAS, SPSS and STATA (Valente et al., 2020; Valeri & VanderWeele, 2013, 2015; VanderWeele, 2015).

2. A CAUSAL PERSPECTIVE ON TOTAL EFFECTS, INDIRECT EFFECTS, AND DIRECT EFFECTS

In causal mediation analysis, total effects, indirect effects, and direct effects are defined relative to a specific contrast of interest in the exposure A, namely between some reference level (termed a*) and another level (termed a). If the exposure is binary, then we would simply set a* = 0 and a = 1. The total effect, TE, represents the average change in the outcome if, for the entire population, the exposure were changed from the reference level to the new level a. Heuristically, direct effects correspond to changes in average outcomes that would occur if the exposure were changed while the mediator M were held fixed (Pearl, 2001; Robins & Greenland, 1992; VanderWeele & Vansteelandt, 2009). We will consider two types of direct effects. First, the controlled direct effect, CDE(m), represents the average change in the outcome if, for the entire population, the exposure were changed from the reference level a* to the new level a and, at the same time, the mediator were held constant at level m universally across individuals (Pearl, 2001; Robins & Greenland, 1992; VanderWeele & Vansteelandt, 2009). CDE(m) varies with the level of m, if there is interaction between exposure and mediator (details are explained in Section 4). Second, the natural direct effect, NDE, represents the average change in the outcome if, for the entire population, the exposure were changed from a* to a and, at the same time, for each individual the mediator were held constant to the level it would naturally take, for that individual, if the exposure were set to the reference level a* (Pearl, 2001; Robins & Greenland, 1992; VanderWeele & Vansteelandt, 2009).

In contrast to direct effects, indirect effects correspond to changes in average outcomes that would occur if the mediator were changed while the exposure is held fixed. More precisely, the natural indirect effect, NIE, represents the average change in the outcome if, for the entire population, the exposure were fixed to the new level a and, at the same time, for each individual, the mediator level were changed from what it naturally would have been if the exposure were set to the reference level a* to what it naturally would have been had the exposure been set to the new level a for that individual (Pearl, 2001; Robins & Greenland, 1992; VanderWeele & Vansteelandt, 2009). In the Supplement, we provide a more formal definition of these causal interpretations in terms of potential outcomes.

To illustrate these concepts, in the running example that we illustrate in Section 5 below, the exposure and the outcome are parents’ negative feelings scores in 2018 and 2020, respectively. The mediator is children’s externalizing behavior scores in 2019. The exposure, mediator and outcome variables are all continuous. Suppose the exposure levels we want to compare are the 1^st quartile, a lower level (the reference level, denoted as a*) and the 3^rd quartile, a higher level (the new level, denoted as a) of parents’ negative feelings in 2018. The CDE(m) is the direct effect of parents’ negative feelings in 2018 on those in 2020, when fixing the level of all children’s externalizing behavior in 2019 to some level m. NDE is the average change in parents’ negative feelings in 2020, if, for the entire population, parents’ negative feelings in 2018 were changed from the lower level to the higher level and, at the same time, for each individual parent, their children’s externalizing behavior were fixed to the level it would naturally take if the parents’ negative feelings in 2018 were set to its lower level. NIE is the average change in parents’ negative feelings in 2020 if, for the entire population, parents’ negative feelings in 2018 were fixed to the higher level and, at the same time, for each individual parent their children’s externalizing behavior were changed from what it would have been if the parent’s negative feelings in 2018 were set to the lower level, to what it would have if the parent’s negative feelings in 2018 were set to the higher level.

These three quantities (CDE(m), NDE, and NIE) provide complementary information. CDE(m) may help assess the effect of interventions that would essentially set the mediator to a specific value for all individuals in the population (e.g., in the running example mentioned above, setting the level of children’s externalizing behavior in 2019 to the sample mean). On the other hand, NDE and NIE allow the total effect to be decomposed into the sum of direct and indirect effects, providing useful intuition for the relative contribution of these pathways (VanderWeele, 2015).

3. WHEN DOES MEDIATION ANALYSIS HAVE A CAUSAL INTERPRETATION?

Assumptions

Because mediation analysis seeks to identify the causal mechanisms of effects, it relies on important assumptions regarding control for confounding variables (Valeri & VanderWeele, 2013; VanderWeele, 2015; VanderWeele, 2016). Just as the estimate of TE can be biased by variables that affect both the exposure and the outcome (i.e., confounding variables) in a simple analysis without considering mediation, estimates of direct and indirect effects in mediation analysis can likewise be biased if there are variables that affect both the exposure and outcome, as well as if there are variables that affect both the exposure and the mediator, or that affect both the mediator and the outcome. If such variables are not controlled in analysis, mediation analysis can provide severely biased estimates.

The simplest form of mediation analysis can be represented in the directed acyclic graph (DAG) shown in Figure 1. A represents the exposure, M the mediator, Y the outcome, C a set of pre-exposure covariates and L a set of post-exposure covariates that are measured and controlled in analysis.

Figure 1.

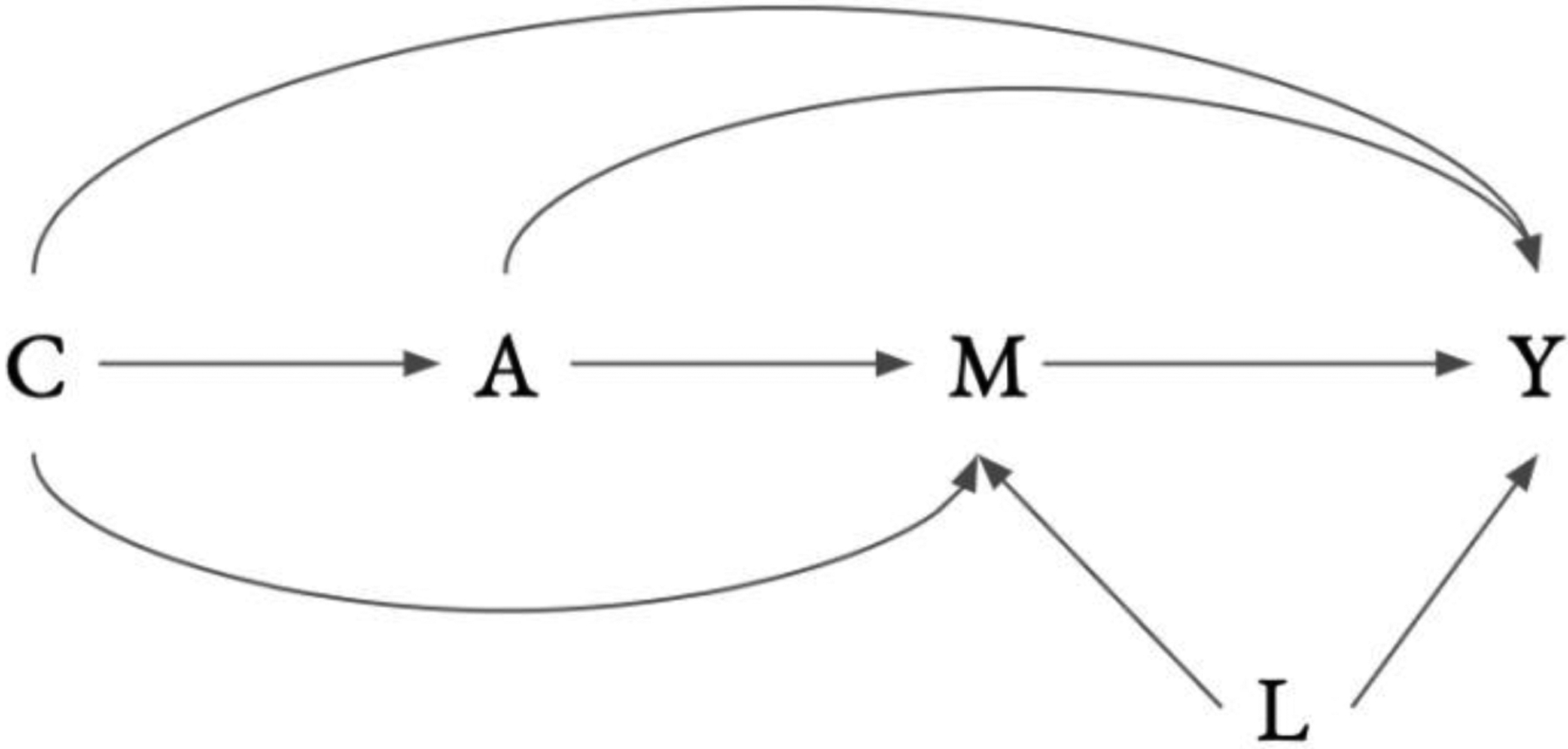
DAG

Throughout this article, we assume four fundamental assumptions that underlie causal inference in general: consistency, positivity, no measurement error, single unit treatment value assumption, and correct model specifications (Rothman, Greenland, & Lash, 2008; Hernán & Robins, 2020). These assumptions are not specific to mediation analysis. For the effect estimates from a mediation analysis to have a causal interpretation, we must also adequately control for confounding, and we assume that there is: (1) no unmeasured exposure-outcome confounding, (2) no unmeasured mediator-outcome confounding, (3) no unmeasured exposure-mediator confounding, and (4) no exposure-induced mediator-outcome confounding (i.e., no arrow from A to L in Figure 1). In the Supplement, we provide a more formal definition of these assumptions in terms of potential outcomes. It is critical to note that, although the first and the third assumptions will generally be satisfied in studies that randomize the exposure, the second assumption can still be violated because the mediator itself is usually not randomized (VanderWeele, 2015). The fourth assumption of no exposure-induced mediator-outcome confounding is somewhat challenging to interpret. In the running example on negative parental feelings, let’s consider a possible scenario where this assumption might be violated. An authoritarian parenting style could plausibly affect both children’s externalizing behavior and parents’ own negative feelings during the lockdown, and hence could act as a mediator-outcome confounder (Irvine et al., 1999). Since parents’ negative feelings before the lockdown might also affect parenting style, parenting style could in fact be an exposure-induced mediator-outcome confounder.

Again, in order for mediation analysis to provide the causal interpretations described above, confounders must be appropriately measured and controlled so that all these assumptions are met. If any of these four assumptions is violated due to uncontrolled confounding, mediation estimates can be biased. Specifically, to identify CDE(m), only the first two assumptions regarding confounding are needed; to identify NDE and NIE, all four assumptions regarding confounding are needed. In practice, because we can never be certain that all confounders have been controlled, it is prudent to conduct sensitivity analyses to characterize how robust the results may be to potential uncontrolled confounding (Ding & VanderWeele, 2016; Hafeman, 2011; Imai, Keele, & Yamamoto, 2010; Smith & VanderWeele, 2019; Tchetgen Tchetgen & Shpitser, 2012; VanderWeele, 2010; VanderWeele & Chiba, 2014).

Study Design Considerations

To allow appropriate control of confounders as described above, the confounders, exposure, mediator, and outcome must occur in that temporal order.¹ For this reason, with rare exceptions, mediation analysis should be conducted only if one has longitudinal data with at least three waves of data, where the exposure is measured in wave 1, the mediator is measured in wave 2 and the outcome is measured in wave 3. In some cases, the confounding variables clearly occur before the exposure even if they are measured at the same time as the exposure; this is often the case with demographic confounders such as age, sex, and race. However, if there are confounders that may occur before or after the exposure, such as psychological variables, these should be measured prior to the exposure, and one therefore needs four waves of data. As noted above, if there are confounders that may occur after the exposure, but before the mediator, this can introduce exposure-induced mediator-outcome confounding, thus violating Assumption 4 and potentially introducing bias (VanderWeele, 2015, 2016). This may be more likely to occur if the mediator is measured a very long time after the exposure.

It is almost never appropriate to conduct mediation analysis using cross-sectional data in which all variables are measured at the same time. With cross-sectional data, one usually cannot tell whether the purported exposure causes the mediator, or whether instead the purported “mediator” causes the “exposure”. Likewise, one cannot tell whether the purported mediator affects the outcome, or vice versa. For example, in Achterberg et al.’s (2021) own analysis, the mediator and outcome were measured at the same time (in May 2020). Thus, the mediator and outcome were effectively measured cross-sectionally, and one cannot rule out reverse causation between the mediator and outcome. Additionally, with cross-sectional data, it is also not possible to adequately control for confounding, because the confounders may temporally precede the exposure (VanderWeele, 2015). There are occasional exceptions in which the temporal ordering of the variables is clear even in cross-sectional data (VanderWeele, 2015). For example, if the exposure is a genetic variant that is fixed at birth, the mediator is smoking, and outcome is mortality, then it may be clear even in cross-sectional data that the exposure precedes the mediator, and the mediator precedes the outcome. However, again, cross-sectional data should not be used for mediation analyses except in these exceptional cases in which the temporal ordering is clear.

4. CONDUCTING MEDIATION ANALYSIS

Fitting the Mediator Model and Outcome Model

In regression-based causal mediation analysis (Valeri & VanderWeele, 2013, 2015), one fits two regression models: a mediator model and an outcome model². For the mediator model, the mediator is regressed on the exposure and the confounders. That is, the mediator is used as the dependent variable in this model, and the predictor variables are the exposure and the confounders. For the outcome model, the outcome for the mediation analysis is regressed on the exposure, the mediator, the confounders, and potentially also an interaction between the exposure and mediator. This interaction term captures the possibility that the strength or direction of mediation differs by levels of the exposure, which can often be the case in practice (VanderWeele, 2015). Please note that the “interaction between the exposure and mediator” means the “causal interaction” defined in Valeri & VanderWeele (2013), instead of “effect measure modification” (EMM) or “moderation” (a term used more often in social science literature). Detailed discussion on the distinction between EMM and interaction can be found in VanderWeele (2009).

We denote A, M, Y, and C as exposure, mediator, outcome, and a vector of all confounders (including baseline and post-exposure), respectively. If the mediator is continuous, one could fit the mediator model by ordinary least squares regression, such as:

$$\text{E}[M\mid A=a,C=c]={\beta }_0+{\beta }_{1}a+{\beta }_2^{T}c,$$

where β₂ is a column vector of coefficients for each confounder.

If instead the mediator is binary, one could fit the mediator model using logistic regression:

$$\text{logit}[\mathrm{Pr}(M=1\mid A=a,C=c)]={\beta }_0+{\beta }_{1}a+{\beta }_2^{T}c.$$

Similarly, if the outcome is continuous, one could fit the outcome model by ordinary least squares regression:

$$E[Y\mid A=a,M=m,C=c]={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_{3}am+{\theta }_4^{T}c,$$

where θ₄ is a column vector of coefficients for each confounder.

If instead the outcome is binary and rare (e.g., prevalence <15% in the population), one could fit the outcome model using logistic regression:

$$\text{logit}[\mathrm{Pr}(Y=1\mid A=a,M=m,C=c)]={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_{3}am+{\theta }_4^{T}c$$

If the outcome is binary and common, one could instead fit a log-linear model³. Using the estimated regression coefficients from the mediator model and outcome model, estimates of the total effect, direct effect, and indirect effect can then be obtained using the R package regmedint, which uses closed-form mathematical expressions developed by Valeri and VanderWeele (2013).

As noted above, if all four assumptions regarding control of confounding are met (see Section 3), along with the general assumptions for causal inference (i.e., consistency, positivity, no measurement error, and correct model specifications), then the resulting estimates from mediation analysis have causal interpretations. That is, the TE represents the casual effect of the exposure on the outcome, the NIE represents the effect of the exposure on the outcome that operates by way of the mediator, and the NDE represents the effect of the exposure on the outcome that does not operate by way of the mediator.

Estimating the Total Effect, Indirect Effect, and Direct Effect

After fitting the mediator and outcome models as described above, the indirect effects and direct effects can be calculated from the estimates of those models using simple closed-form expressions (Valeri & VanderWeele, 2013) that are implemented in the R package regmedint. For example, if both the mediator and the outcome are continuous:

$$CDE(m)=\left({\theta }_1+{\theta }_{3}m\right)\left(a-a^{\ast }\right)$$

$$NDE=\left({\theta }_1+{\theta }_3{\beta }_0+{\theta }_3{\beta }_1{a}^{\ast }+{\theta }_3{\beta }_2^{T}c\right)\left(a-a^{\ast }\right),$$

$$NIE=\left({\theta }_2{\beta }_1+{\theta }_3{\beta }_{1}a\right)\left(a-a^{\ast }\right).$$

Analogous expressions that apply when the mediator and/or outcome are binary are provided elsewhere (Valeri & VanderWeele, 2013, 2015; VanderWeele, 2015).

For a continuous outcome, the TE is simply the sum of the NDE and the NIE:

$$TE=NDE+NIE.$$

and for a rare binary outcome with a logistic regression outcome, a similar decomposition holds on the log-odds ratio scale:

$$\log \left({\text{OR}}^{TE}\right)=\log \left({\text{OR}}^{NDE}\right)+\log \left({\text{OR}}^{NIE}\right).$$

The Proportion Mediated

A convenient metric to summarize the strength of mediation, which can be reported along with the NIE, is the proportion of the exposure effect that is mediated. For a continuous outcome modeled by ordinary least squares regression model, the proportion mediated is:

$$PM=\frac{NIE}{NDE+NIE}=\frac{NIE}{TE}.$$

For a binary outcome modeled with logistic regression (VanderWeele & Vansteelandt, 2010):

$$\text{PM}=\frac{\exp \left[\log \left({\text{OR}}^{NDE}\right)\right]\cdot \left\{\exp \left[\log \left({\text{OR}}^{NIE}\right)\right]-1\right\}}{\exp \left[\log \left({\text{OR}}^{NDE}\right)\right]\cdot \exp \left[\log \left({\text{OR}}^{NIE}\right)\right]-1}=\frac{{\text{OR}}^{NDE}\cdot \left({\text{OR}}^{NIE}-1\right)}{{\text{OR}}^{TE}-1}.$$

Comparison of Causal Mediation Methods to Traditional Methods

Here, we briefly describe the differences between the causal mediation methods that are our focus (Valeri & VanderWeele, 2013, 2015) and two traditional approaches that predated them (Baron & Kenny, 1986; Judd & Kenny, 1981; MacKinnon, 2017). The first traditional method, the “difference method”, involves fitting two outcome models (Judd & Kenny, 1981). In the first outcome model, we regress the outcome on only the exposure and covariates. In the second outcome model, we additionally include the mediator in the model. For a continuous outcome, the two models would be:

$$E[Y\mid A=a,C=c]={\varphi }_0+{\varphi }_{1}a+{\varphi }_2^{T}c,$$

$$E[Y\mid A=a,M=m,C=c]={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_4^{T}c,$$

where both ϕ₂ and θ₄ are column vectors.

In the traditional difference method, the direct effect is defined as the coefficient of exposure in the second model (θ₁), and the indirect effect is taken to be the difference between exposure’s coefficient in the first model and its coefficient in the second model (ϕ₁ − θ₁) (Baron & Kenny, 1986; Judd & Kenny, 1981; MacKinnon, 2017).

The second traditional method is the “product method” (Baron & Kenny, 1986). Here, similarly to the causal mediation approach of Valeri & VanderWeele (2013, 2015), one again fits both a mediator model and an outcome model:

$$E[M\mid A=a,C=c]={\beta }_0+{\beta }_{1}a+{\beta }_2^{T}c,$$

$$E[Y\mid A=a,M=m,C=c]={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_4^{T}c.$$

Note that the outcome model here does not include an exposure-mediator interaction term as in the causal mediation approach of Valeri & VanderWeele (2013, 2015). In the product method, the direct effect is taken to be θ₁, and the indirect effect is taken to be θ₂β₁ (Baron & Kenny, 1986; MacKinnon, 2017).

Both traditional methods have two important limitations compared to the causal mediation approach of Valeri & VanderWeele (2013, 2015). Neither traditional method can accommodate exposure-mediator interaction, and these methods can provide biased results when such interactions are present.

Additionally, neither of the two traditional methods was designed to estimate rigorously defined causal quantities (i.e., via the counterfactual potential-outcome framework; Supplement). Instead, those methods simply defined direct and indirect effects in terms of regression coefficients, rather than in terms of specific causal quantities such as the CDE(m), NIE, and NDE. These traditional methods based on regression coefficients do not necessarily provide valid estimates of causal mediation effects, except in certain restricted cases. Namely, only when both mediator and outcome are modeled by linear regressions, the traditional methods will agree exactly with the causal methods if there is no exposure-mediator interaction (MacKinnon, 2012; MacKinnon et al., 2020; Rijnhart, Valente, MacKinnon, et al., 2021; Rijnhart, Valente, Smyth, et al., 2021; Valeri & VanderWeele, 2013).

5. EMPIRICAL EXAMPLE

We recently developed the R package regmedint (Yoshida, Li, & Mathur, 2022). It is the R counterpart to the SAS and SPSS macros by Valeri and VanderWeele (2013, 2015) and the PROC CAUSALMED procedure in SAS. In this section, we demonstrate how to conduct and interpret mediation analysis using the regmedint package by re-analyzing Achterberg et al.’s (2021) publicly available dataset, which we used to examine the extent to which effects of parents’ negative feelings before the COVID-19 lockdown on their negative feelings during the lockdown were mediated by their children’s externalizing behavior in the interim. Documentation and examples for the R package(https://cran.r-project.org/web/packages/regmedint/index.html) are publicly available athttps://kaz-yos.github.io/regmedint/articles/vig_01_introduction.html(Yoshida, Li, & Mathur, 2022). A detailed tutorial of conducting causal mediation analysis using regmedint and comparing with the traditional difference and product methods can be found in Section 2 in the Supplement.

The dataset comprises 106 households (106 primary parents and 151 children, in total) who completed five waves of data collection from 2016 to 2020 (Achterberg et al., 2021). The questionnaires assessed demographics, parental well-being (negative feelings, including anxiety, depression, hostility, interpersonal sensitivity), and children’s well-being (externalizing and internalizing behavior). For our reanalysis, the exposure is parents’ negative feelings measured via the 18-item Brief Symptoms Inventory (BSI) in 2018, before the lockdown (mean = 0.23, sd = 0.26, min = 0, max = 1.62). The outcome is parents’ negative feelings in 2020, during the lockdown (mean = 0.34, sd = 0.32, min = 0, max = 1.43). The mediator is children’s externalizing behavior measured via the 6-item Strengths and Difficulties Questionnaire (SDQ) in 2019 (mean = 0.41, sd = 0.32, min = 0, max = 1.50). Both parental negative feelings and children’s externalizing behavior are continuous scores. Covariates that were thought to be confounders include the primary parent’s age, highest education level, and positive and negative coping strategies. The primary parent’s age, and positive and negative coping strategies are continuous variables, and the primary parent’s highest education level is a categorical variable, with five levels. Although all confounders were measured in 2020 after the exposure, age and education are essentially static in time, and coping strategies are thought to be relatively stable over time as well (Navrady et al., 2018), so the 2020 measures of the confounders can reasonably be regarded as temporally preceding the exposure. After excluding households with missing measurements of the questionnaires, the final sample size is 99. The hypothesized relationships between these variables are depicted in Figure 2.

Figure 2.

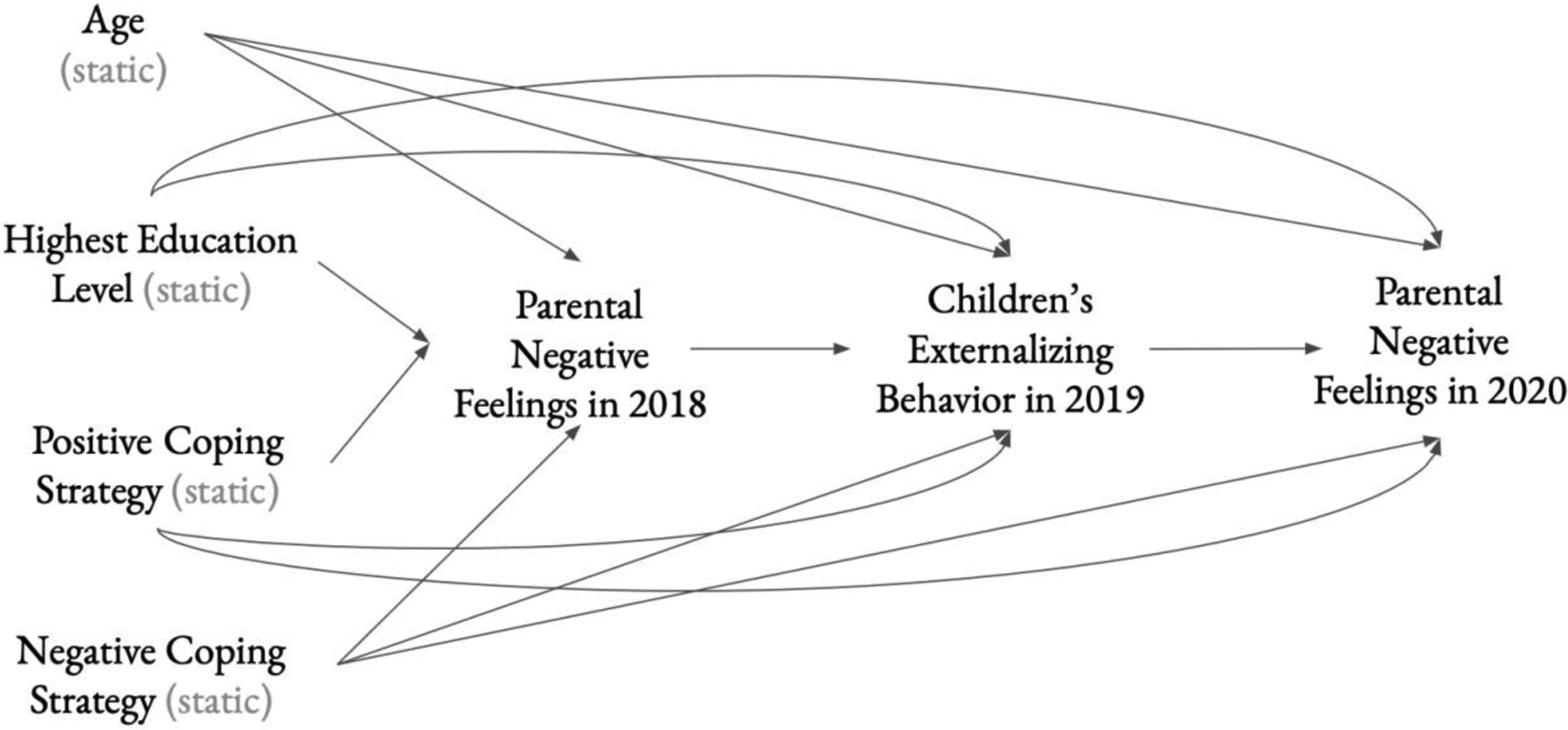
Hypothesized DAG for Achterberg et al.’s study on negative parental feelings

Table 1 shows the results, when assuming there is exposure-mediator interaction. The results would be interpreted as follows. The total effect of a one-unit increase in parents’ negative feelings score (i.e., one unit on the BSI scale) in 2018 on their negative feelings score in 2020 is estimated as 0.53 (95% CI: 0.28, 0.77) units on the BSI scale. Regarding mediation, the natural indirect effect via children’s externalizing behavior in 2019 is estimated as 0.06 (95% CI: −0.08, 0.21). The natural direct effect, representing effects of negative feelings before the lockdown that do not operate by way of children’s externalizing behavior in 2019, is estimated as 0.46 (95% CI: 0.24, 0.69). The estimate proportion mediated was 0.12 (95% CI: −0.13, 0.37); that is, we estimated that 12% (95% CI: −13%, 37%) of the effect of negative feelings in 2018 on negative feelings in 2020 during the lockdown is mediated by children’s externalizing behavior in 2019. The conditional direct effect of a one-unit increase in parents’ negative feelings score in 2018 on their negative feelings score in 2020 when holding children’s externalizing behavior score in 2019 to its mean level (which is 0.41) universally across the study population is 0.49 (95% CI: 0.27, 0.71). As noted above, given the levels of the covariates that we chose to condition on, these estimates are for the population of parents with a master’s or doctoral degree, at the age of 45, positive coping strategy score is 2.11 and negative coping strategy score is 0.93. Note that the 95% confidence intervals of NIE and PM include negative values. A PM outside the range of [0, 1] occurs if the NDE and NIE are in opposite directions, referred as “inconsistent PM” (VanderWeele, 2015), and is not interpretable. In our running example, a wide confidence interval around the PM may be due to small sample size and limited statistical precision.

Table 1.

Mediation analysis estimates when allowing for exposure-mediator interaction

Effect	Estimate	95% CI
CDE (m)	0.49	(0.27, 0.71)
NDE	0.46	(0.24, 0.69)
NIE	0.06	(−0.08, 0.21)
TE	0.53	(0.28, 0.77)
PM	0.12	(−0.13, 0.37)

Abbreviations. CDE: controlled direct effect. NDE: natural direct effect. NIE: natural indirect effect. TE: total effect. PM: proportion mediated.

CDE is measured at m = 0.41 (mean level of mediator). All effects are conditional on age = 45, positive coping strategy score = 2.11 and negative coping strategy score = 0.93, highest education level = 4.

To account for potential unmeasured confounding, one common approach is to conduct sensitivity analyses using E-value (VanderWeele & Ding, 2017; Mathur et al., 2018). E-value is a straightforward and intuitive measure that indicates the minimum strength of the association that an unmeasured confounder needs to have with both the exposure and the outcome, to fully explain away the estimated effect of the exposure on the outcome (VanderWeele & Ding, 2017). For sensitivity analyses in causal mediation analyses regarding NDE and NIE, similar E-values can be calculated to account for the unmeasured mediator-outcome confounding (VanderWeele & Ding, 2017; Mathur et al., 2018; Smith & VanderWeele, 2019). In this empirical example, to facilitate interpretation of the E-values, we dichotomized the exposure, mediator, and outcome at their medians; this is essentially equivalent to using approximate effect-size conversions that are generally used to obtain E-values for continuous outcomes (VanderWeele & Ding, 2017). We then fit a logistic mediator model and log-linear outcome model. The E-values for NDE and NIE estimates are 2.32 and 1.23, respectively. This indicates that to completely explain away the observed direct effect and indirect effect, respectively, unmeasured confounder(s) associated with both children’s externalizing behavior in 2019 and parents’ negative feelings score in 2020 with approximate risk ratios of 2.32-fold and 1.23-fold each, respectively, above and beyond the measured covariates, could suffice, but weaker confounding could not.

If we instead wished to assume there is no exposure-mediator interaction, the estimated natural direct and indirect effects are then 0.47 and 0.02 respectively, and the proportion mediated is reduced to 0.04 (i.e, 4.1%; Table 2).

Table 2.

Mediation analysis estimates when assuming there is no exposure-mediator interaction

Effect	Estimate	95% CI
CDE (m)	0.47	(0.25, 0.69)
NDE	0.47	(0.25, 0.69)
NIE	0.02	(−0.02, 0.06)
TE	0.49	(0.27, 0.71)
PM	0.04	(−0.05, 0.13)

Abbreviations. CDE: controlled direct effect. NDE: natural direct effect. NIE: natural indirect effect. TE: total effect. PM: proportion mediated.

CDE is measured at m = 0.41 (mean level of mediator). All effects are conditional on age = 45, positive coping strategy score = 2.11 and negative coping strategy score = 0.93, highest education level = 4.

We will now compare the results to those of the traditional difference and product methods. Note that we need to exclude the rows with missing values of exposure, mediator, outcome or covariates.

For the difference method, we fit a full outcome model (including the mediator as a covariate) and a reduced outcome model (not including the mediator as a covariate):

$$\text{ Reduced model: E}[Y\mid A=a,C=c]={\varphi }_0+{\varphi }_{1}a+{\varphi }_2^{T}c,$$

$$\text{ Full model: E}[Y\mid A=a,M=m,C=c]={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_4^{T}c\text{, }$$

where A is BSI in 2018, M is SDQ in 2019, C is the column vector of baseline age, highest education level, cognitive emotion regulation questionnaire (CERQ) positive and negative coping scores. As noted in the section “Comparison to traditional methods”, the indirect effect is taken to be the coefficient of the exposure in the full model, and indirect effect is taken to be the difference between the coefficients of the exposure in the two models. That is, the difference method calculates the direct effect as θ₁ = 0.47 and calculates the indirect effect as ϕ₁ − θ₁ = 0.02.

For the product method, we fit the following mediator and outcome models:

$$\text{ Mediator model: E}[M\mid A=a,C=c]={\beta }_0+{\beta }_{1}a+{\beta }_2^{T}c\text{, }$$

$$\text{ Outcome model: E}[Y\mid A=a,M=m,C=c]={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_4^{T}c\text{. }$$

The product method takes the direct effect to be the coefficient of exposure in the full model, and the indirect effect to be the product of the coefficient of exposure in the mediator model and the coefficient of mediator in the outcome model. Namely, the product method calculates the direct effect as θ₁ = 0.47 and calculates the indirect effect as ϕ₂β₁ = 0.02. The results from the product method and the difference method are the same, but are different from the results using causal mediation analysis if there is exposure-mediator interaction, where direct effect is 0.46 and indirect effect is 0.06 (Table 1).

When the exposure-mediator interaction term was omitted, the results from the traditional difference and product methods agree exactly with those of the causal mediation analysis. This is because, as noted in the section “Comparison to traditional methods”, the traditional methods will yield the same results as the causal mediation approach for a continuous outcome and a continuous mediator if there is no exposure-mediator interaction. However, the results differed somewhat when allowing for exposure-mediator interaction. Again, because traditional methods do not accommodate exposure-mediator interaction, using either the difference method or product method when there truly is an exposure-mediator interaction will generally result in biased estimates.

6. DISCUSSION

In this article, we have provided an overview of causal mediation analysis and demonstrated how to use the R package regmedint to analyze an empirical data example in the field of traumatic stress. In contrast to traditional methods for mediation analysis, regression-based causal mediation methods seek to estimate specific causal quantities, not mere associations, and the causal methods allow for exposure-mediator interaction. For mediation analysis to have a causal interpretation, assumptions of no unmeasured exposure-outcome, mediator-outcome, exposure-mediator confounding, and no exposure-induced mediator-outcome confounding need to be satisfied. These are fairly strong assumptions. Even if the exposure is randomized, researchers need to control for mediator-outcome confounding if they want to estimate direct and indirect effects. For the confounding assumptions to be plausible, studies must be designed with careful attention to obtaining longitudinal data with adequate control of confounders. To this end, the dataset must have a clear temporal ordering of confounders, exposure, mediator and outcome, and this is usually impossible in cross-sectional studies.

Because traditional methods do not accommodate exposure-mediator interaction, they can yield biased results if such an interaction is in fact present. In our re-analysis of Achterberg et al. (2021)’s dataset, we compared results obtained by assuming there was no exposure-mediator interaction to those that allowed for exposure-mediator interaction. The natural direct and indirect estimates differed slightly between these two approaches, and the proportion mediated was reduced by about 50% when including the interaction. However, the confidence intervals were wide, indicating considerable uncertainty, due to the small sample size. It has been previously reported that the proportion mediated is particularly unstable when sample sizes are modest (MacKinnon et al., 1995). In other data analyses, the discrepancy between estimates of the NDE and NIE using traditional and counterfactual methods can in fact be substantially larger than in our applied example. This is especially the case if confounding is not adequately controlled or there is a large exposure-mediator interaction. In such circumstances, the estimates of the NDE and NIE using traditional methods may even be in the wrong direction.

Although we have emphasized that causal mediation analysis needs at least three waves of data, previous literature has also shown that there could still be biases because of the potential inappropriate time lags between exposure and mediator, and between mediator and outcome (Gollob & Reichardt, 1987; Collins & Graham, 2012; Reichardt, 2011; Mitchell & Maxwell, 2013). This can occur if the time lags between measurements of these variables do not correspond well to the actual durations over which the variables affect one another. In our empirical data analysis, we used one-year time lag. If one year is not the true minimum for exposure to have an effect on mediator and for mediator to have an effect on outcome, this would be a limitation of our analysis.

The newest R package regmedint (version 1.0.0) has additional features that are beyond the scope of this article; these are detailed in the standard R documentation available on the Comprehensive R Archive Network. This is an extension of the original method by Valeri and VanderWeele (2013, 2015), and the package now allows one to add effect measure modification terms, accommodating the possibility that the effect of the exposure on the outcome differs for individuals with different levels of the covariates (Li, Mathur, & Yoshida, 2022; Li et al., 2022).

In addition to regression-based methods for causal mediation analysis (Valeri & VanderWeele, 2013, 2015), there are other modern methods for mediation analysis that seek to estimate causal quantities. The first a simulation-based Monte-Carlo approach, proposed by Imai et al. (Imai, Keele, & Tingley, 2010; Imai, Keele, & Yamamoto, 2010), and the corresponding R package is mediation (Tingley et al., 2014). It allows for more flexible modeling of mediator and outcome models than the regression-based closed-form method, but is more computationally expensive. The second method uses a unified marginal structural model (MSM) approach (Lange et al., 2012) and the corresponding R package is medflex (Steen et al., 2017). This method also allows for more flexible modeling and is less prone to model misspecification, but since it requires inverse probability of treatment weights, the estimates may be biased if there are extreme weights. When calculating standard errors, the regression-based method is more computationally efficient because it uses the closed-form delta method, while the unified MSM uses generalized estimating equations and bootstrap. Practitioners may want to choose which mediation method to use depending on the model forms they prefer to assume, their preferred scale of direct and indirect effect estimates, and the computational time associated with simulated-based approaches. In addition, Tchetgen Tchetgen & Shpitser (2012) proposed a generic semiparametric framework where they developed multiply robust locally efficient estimators and double robust sensitivity analyses for marginal natural direct and indirect effects.

For further decomposition of causal mechanisms, VanderWeele (2013, 2014) has proposed three-way and four-way decompositions of total effects that have components of both mediation and interaction effects. The decompositions are implemented in SAS and STATA (Discacciati et al., 2019; Valeri & VanderWeele, 2013). For multiple mediators, the joint effect of the set of mediators can be estimated using the causal mediation method (Valeri & VanderWeele, 2013, 2015) and easily obtained by using R package CMAverse (Shi et al., 2021). Recent work has established methods for decomposing certain pathway-specific effects (Tai et al., 2021).

Clinical Impact Statement:

In this article we provide an overview of modern, regression-based causal mediation analysis that overcomes some limitations of traditional methods. We also provide researchers in the field of traumatic stress with an introduction of implementing this causal mediation analysis method using our new R package regmedint.