Passive solar tracker using a bimetallic strip activator with an integrated night return mechanism

Abstract

Passive solar trackers face challenges in returning PV panels to the east position before sunrise. Specifically, bimetallic strip deflection-based trackers are unreliable due to ambient temperature changes at night, resulting in inconsistency across different locations and times. This study addresses this issue by designing a passive solar tracker with a bimetallic strip deflector independent of nighttime temperature differences. Field tests were conducted comparing a fixed system to the proposed tracker. Performance parameters included power output, power density, and energy collection. The proposed tracker achieved a daily average power output of 70–120 W, while the fixed system ranged from 10 to 120 W. The proposed system exhibited steady changes in power output, providing an additional 47 W per unit area compared to the fixed system. This optimization maximized power output within a given area, resulting in a cost savings of $71.75 per unit area. The proposed system also demonstrated 24.86% higher energy collection efficiency relative to the fixed system and 96.4% accuracy compared to an ideal tracking system. It is a cost-effective alternative to fixed-panel PV and easy to install and operate. Additionally, it can be used in conjunction with active tracking systems, offering comparable efficiency at a lower operational cost. The designed system presents a reliable solution by being independent of nighttime temperature fluctuations, making it more stable relative to other passive solar trackers.

1. Introduction

Many solar trackers were designed to capture morning and evening solar radiation, and thereby their efficiency was improved over the standstill system. Due to this advantage, tracking systems have become more prevalent on a global scale [1,2]. More specifically, passive-type solar trackers with bimetallic strip activators for PV panels are suitable for underdeveloped countries due to their limited access to technology, lower cost, and lower complexity than the active type. However, this kind of tracker is strongly dependent on the local weather conditions at the site where it is installed. This system is more advisable for areas near the equatorial region, such as Ethiopia [3].

Clifford et al. [4] designed a single-axis passive solar tracking system at the equator region with low-cost activation by using thermal deflection of aluminum/steel bimetallic strips, causing an imbalance in the panel weight and making panel movement possible in the direction of the sun. The movement was regulated by a viscous damper. The designed passive solar tracker was experimentally tested and evaluated, and the measured efficiency increased by 23.3%. The tracker used two bimetallic strips. One strip is exposed to the sun's radiation and gets heated, whereas the other strip is cooled by the shade. Because of this heat transfer, the bimetallic strip was bent, and the maximum deflections were located at the midpoint, where it is attached to the block mass. The imbalance moment results in generating tracker movements toward the sun. However, this passive solar tracking system has a problem with its night return mechanism. It uses the assumption of an extreme low temperature in the nights for the automatic night return mechanism, but in reality, the early morning response of the system was inadequate; hence, the solar panel's efficiency was affected by morning radiation losses. Maria M. Perez Sanchez et al. [5] proposed a dual-axis passive solar tracker for use in Yucatan. The system used a bimetallic strip with high thermal expansion properties as the base of operation for a passive solar tracker with two degrees of freedom: one to track the sun daily, operated automatically and actuated by the bimetallic strips; the second to manually adjust for seasonal changes to compensate for variation along with the decline of the sun throughout the year. However, the system has a problem associated with returning the panel because of the drawbacks of Clifford et al. [4]. Due to the return mechanism, it depends on the extreme nighttime temperature difference, which varies from season to season.

Fairbanks et al. [6] designed a single-axis passive solar array orientation device for terrestrial applications. In this system, a thermal heliotrope concept was used. A bimetallic helical coil is used as a sensing and driving element for the tracking mechanism. When the sun's radiation strikes the helical coil, it is sensed as heat and deflected. The deflection produced torque and angular displacement, and tracking was possible. To control the movement of the tracking system, shades are used to control the radiation incident on the helix, which in turn regulates the motion of the panel. Farooqui [7] substituted a manual solar tracking mechanism for a box-type solar cooker with a gravity-based tracking mechanism that has no motor or external power source. Water was used as an external power source. It works on the potential energy stored in a spring attached to a water container. Water is discharged at a constant, predetermined rate from the container, and then the spring is upstretched, allowing movement to follow the sun. The tracking mechanism did not require any external power source since the water is used as an external power source. The rate of water discharge was matched with the rate of change of the solar azimuth; it made the solar cooker follow the sun. This mechanism was innovative, simple, low-cost, easy to handle, and almost maintenance-free.

From the literature, passive solar trackers have a problem returning the panel to the east position before sunrises. In the case of the bimetallic strip activator type, researchers assumed the deflection of the bimetallic strips during the night was possible in the opposite direction from daylight time with the help of the night ambient temperature differences in order to return the panel to the east before dawn. However, in reality, the ambient temperature difference at night varies from place to place and depends on the seasonal weather of the place where the system will be installed. Due to these dependencies, the bimetallic strip activator-type passive trackers have limitations in precision for different areas with variable seasonal weather. This leads to the systems being less reliable and not applicable to different regions. But if the return mechanism to the east before morning is independent of changes in ambient temperature, the applicability of the system would be maximized. This would result in increasing the energy captured by the panel, saving time spent reorienting the panel after sunrises, and hence enhancing the efficiency of the system. Therefore, this paper will address the problem associated with returning the panel to the east position before dawn by designing a tracking system that will be independent of the nighttime ambient temperature changes to return the panel, and the rotation will be controlled by the potential energy difference between the weight and the spring force.

2. Materials and Methods

2.1. Description of the developed systems

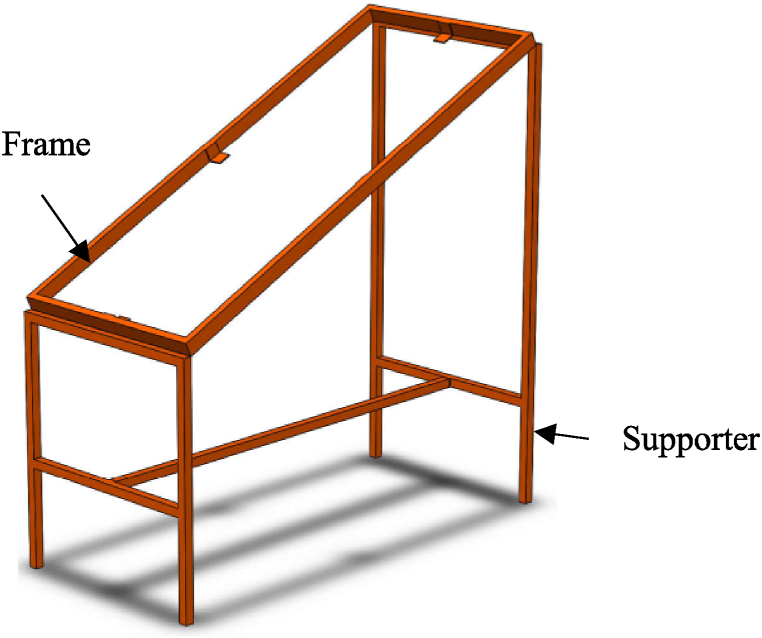
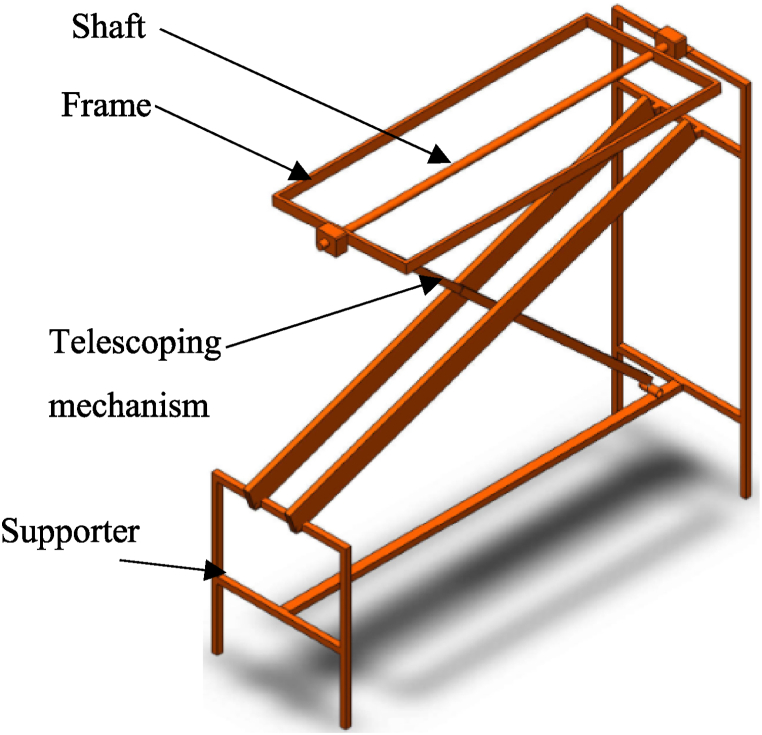
There are two systems in this work: stationery and tracking systems, shown in Fig. 1, Fig. 2, respectively. Fig. 3 shows the setup of the designed tracking system.

Fig. 1.

CAD assembly of the stationary system.

Fig. 2.

CAD assembly of the tracking system.

Fig. 3.

Present tracking system set-up.

A shaft of 20 mm nominal diameter made of low carbon steel is used in the tracking system to rotate the panel in an east-west direction. The telescoping mechanism is designed to adjust the seasonal shift in the sun's position in the sky. The material used for the frame and the support is also low-carbon steel, with a standard size of 2040 mm² and a thickness of 1.5 mm. A PV panel size of 1340 × 530 × 40 mm³ to generate solar power.

Bimetallic strip: Bimetallic strips were used as switches to control the flow of water. It deflects as a result of solar radiation. From Timoshenko, the radius of curvature of a bimetallic strip is given by Ref. [8]:

$$\rho =R=\frac{t.\left[3.{\left(1+m\right)}^2+\left(1+m.n\right).\left(m^2+\frac{1}{m.n}\right)\right]}{6.\left({\alpha }_2-{\alpha }_1\right)\left(T-T_o\right){\left(1+m\right)}^2}$$ (1)

Where, ρ = R = the radius of curvature, t = total thickness of the strip, m = is the ratio of thicknesses, $n=$ is the ratio of young's moduli, T = Temperature, T_o = initial bending temperature, α₁ = coefficients of linear thermal expansion1, α₂ = coefficients of linear thermal expansion 2

The deflection of the bimetallic strip is related to the radius of curvature:

$$d=\frac{L^2}{8R}$$ (2)

Where: L is the length of the bimetallic strip, which is 200 mm.

From equation (1): the temperature change can be given as:

$$\Delta T=\frac{8.d.t.\left[3.{\left(1+m\right)}^2+\left(1+m.n\right).\left(m^2+\frac{1}{m.n}\right)\right]}{6.L^2.\left({\alpha }_2-{\alpha }_1\right){\left(1+m\right)}^2}$$

$\Delta T$ = change in temperature, α1 = coefficients of linear thermal expansion 1 (Copper), α2 = coefficients of linear thermal expansion 2 (Aluminum).

The selected materials for the bimetallic strip are aluminum and copper, and their respective linear coefficients are ${\alpha }_2=24\times {10}^{-6}{K}^{-1}$ and ${\alpha }_1=16\times {10}^{-6}{K}^{-1}$. Length (L) of 200 mm, and thickness (t) of 0.5 mm with thickness ratio (m) of 1 is selected.

The young's modulus of copper (E₁) and aluminum (E₂) are 121.6 GPa and 68.6 GPa respectively. So, the ratio of the young's moduli (n) become 1.77. The minimum deflection required to activate the tracking system is assumed to be d = 1 mm.Then, the required temperature change from the atmospheric temperature can be determined by using equations (1), (2)), and the calculated temperature change is $\Delta T=8.5K$.

$T_o$ = 293 K, assumed ambient temperature, and then the minimum temperature (T) required for 1 mm deflection of the bimetallic strip is 301.5 K.

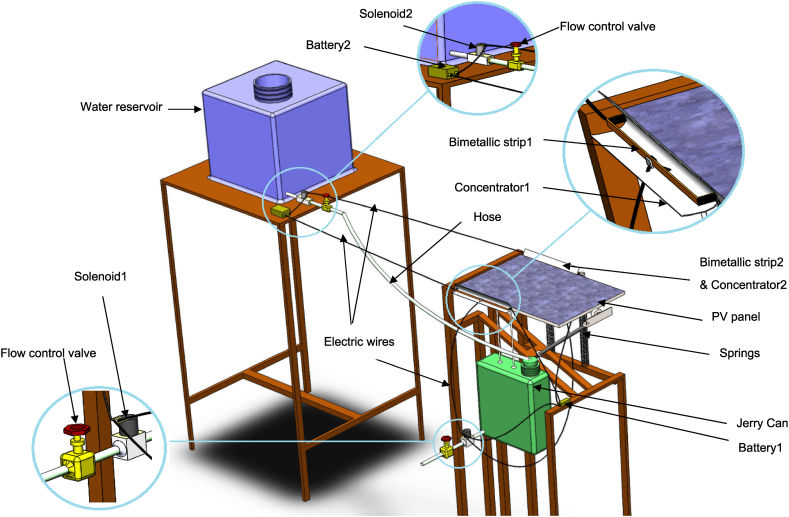
Aluminum and copper are the primary components of the bimetallic strip. To obtain 1 mm of deflection from a selected bimetallic strip, which requires an 8.5 K temperature change from the initial bending temperature of 293 K and to gain this temperature change in the early morning, the system uses a parabolic concentrator with a 20 cm depth and 20 cm length trough with a reflective material of aluminum installed to deflect the bimetallic strip.

Water flow system: the capacity of the suspended Jerry Can is 20 L and the flow rate of the water in the system is 2 L per hour. This flow rate is used to select the size of the solenoid valves. The capacity of the reservoir is 600 L and is refilled once a month. The flow rate of the water in the system is determined by the relative speed of the sun's position in the sky.

Brass springs were used to regulate the rotational speed of the panel due to its high sensitivity to small weight changes in the water. This deflection is directly related to the gravitational potential energy of the water in the suspended Jerry Can. The size of the spring is determined from equation (3) as [9]:

$$\tau =K\times \frac{8W_t\times D}{\pi d^3}=K\times \frac{8W_t\times C}{\pi d^2}$$ (3)

$\tau$ is the maximum shear stress, $W_t$ is the total applied load, C is the spring index = D/d, K is a Wahl's stress factor = $\frac{4C-1}{4C-4}+\frac{0.615}{C}$, D is the mean diameter of the spring, d is the diameter of the wire

And the length of the springs is 393 mm with parallel connections, as found from equation (4).

Then, d is found to be 5.00 mm, and D of the spring is 40 mm.

$$\frac{W}{\Delta s}=\frac{G.d^4}{8D^3.n_a}=\frac{G.d}{8C^2.n_a}=k=272.5N/m$$ (4)

Where $\Delta s$ is the deflection of the spring, G is Sheer Modulus of the spring material, n is number of active coils.

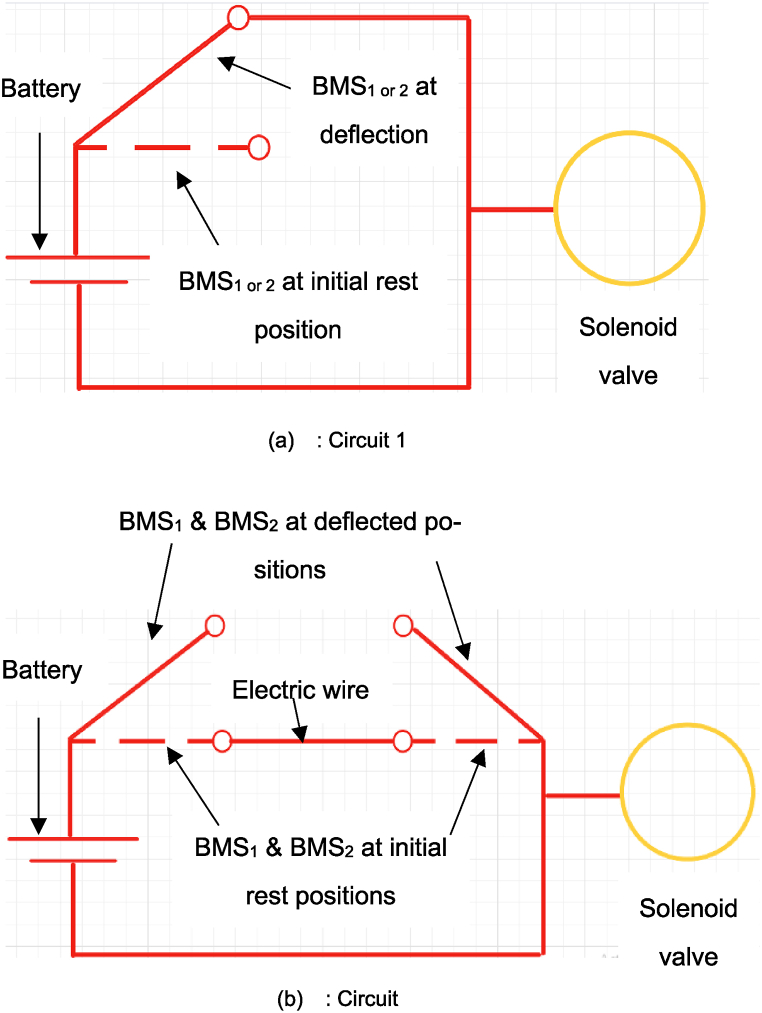
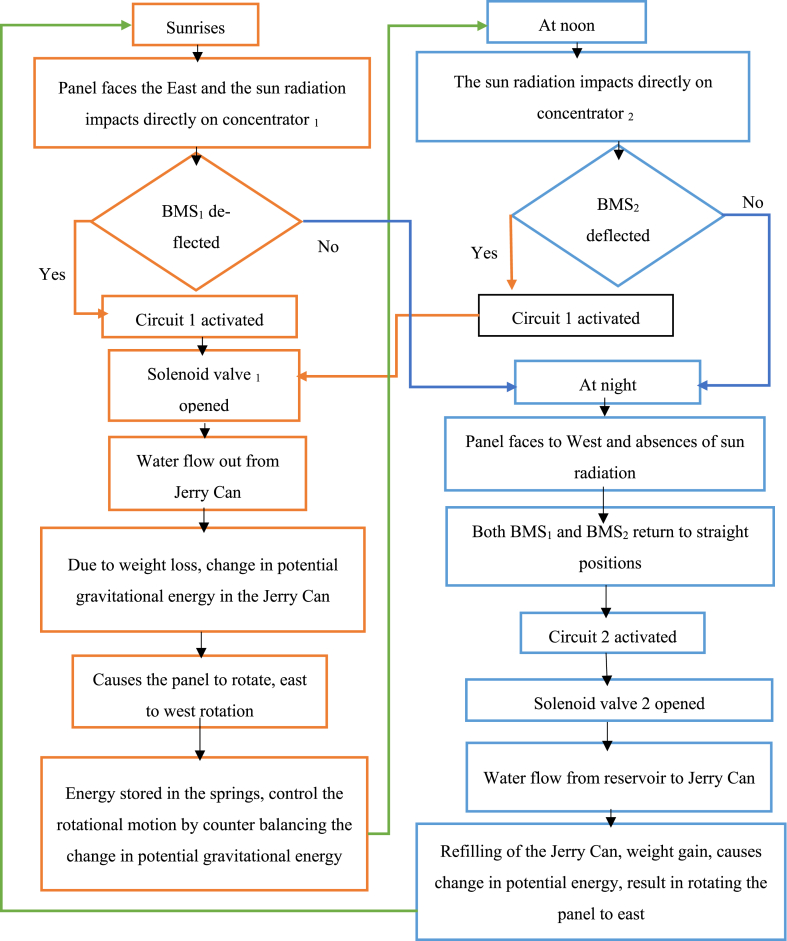
Circuits in the tracking system:Fig. 4 (a) is the control circuit for the daytime. When bimetallic strip 1 (BMS1) deflects and absorbs heat from solar energy, solenoid valve 1 will be opened (turned on), and the water will flow out of the Jerry Can. This water flow results in rotating the panel from the east to the west position due to the potential gravity energy loss in the suspended Jerry Can. And in the afternoon, the bimetallic strip 2 (BMS2) will deflect, solenoid valve 1 will be kept activated, and the water will flow continuously out of the Jerry Can. This water flow results in rotating the panel further to the west until dusk.

Fig. 4.

Circuits set up for the designed tracking system.

The circuit shown in Fig. 4 (b) controls the rotation of the night period. During the night, both BMS1 and BMS2 will return to their normal initial positions because there is no sunlight or solar energy and the valves 1 and 2 are in contact with an electric wire that activates circuit 2. The water is flowing out of the water reservoir into the Jerry Can, where the refilling of the suspended Jerry Can will be carried out and the panel will be returned to its original east position for the next morning. The flow chart that describes the working mechanism of the designed solar tracker is presented in Fig. 5.

Fig. 5.

Flow chart of the designed tracking system.

Table 1 shows the materials and equipment used in the present tracking system.

Table 1.

Materials and equipment used.

Material/equipment	Description	Model/brand	Material country origin
PV panel	150Wp Power tolerance 0–3% Voltage (Vmp) = 18.0 V Current (Imp) = 5.55 A Open circuit voltage (Voc) = 21.5 V Short circuit current (Isc) = 6.38 A Size of the panel: $H\times W\times D=1340\times 530\times 40{mm}^3$ Mass of the panel = 11 Kg	P150 Copex Solar	UAE
Bimetallic strips	Size = $200mm\times 25mm\times 0.5mm$ Mass = 70 g. Bimetal materials = Aluminum and copper	PH0383/Eisco	India
Solenoid valve	Size = $61mm\times 71mm\times 30mm$ Bimetallic material: Aluminum, Copper Exterior finish: Plastic, Metal Normally closed type		China
Battery	12 V 7.2 A H/20 H R	RT1272/RITAR	China
Solar charger control	Rated Voltage 12 V Rated Current 20 A	HF120D	China
Multimeter	Fluke-17 B + IN CATIII 1 9 V battery powered Digital	Fluke	USA
Thermocouple	EZDO YC-321 Portable K-type thermometer (2 channel, −200 °C to +1372 °C)	EZDO	Taiwan
Digital Angle Finder protractor	TBVHOMM-21 Size: $150mm\times 135mm\times 260mm$	TBVHOMM	China

2.2. Overview

This investigation was carried out at the Renewable Energy Center on the Bahir Dar Institute of Technology campus; the station is presented in Table 2 and shown in Fig. 6.

Table 2.

Station identification.

City, specific location	Bahir Dar, Bahir Dar Institute of Technology campus
Latitude	11.5742° N
Longitude	37.3614° E
Elevation from MSL (m)	1820

Fig. 6.

The designed tracker and fixed solar systems at BiT campus.

Fig. 7(a–e) shows the typical rotation of the panel during the daytime. From Fig. 7(f and g), it is easy to visualize that the panel is rotating from west to east or returning to its east position during the night, using bimetallic strips 1 and 2 to regain its original straight horizontal positions.

Fig. 7.

Present tracking system at various times during the day.

3. Results and Discussion

3.1. Power outputs

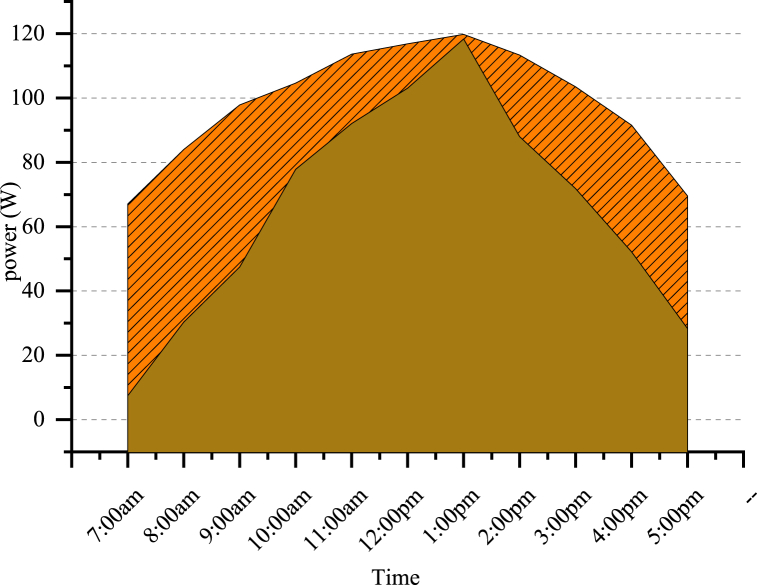
The power output from the experiment is represented graphically in Fig. 8. It shows that the tracking system has more smoothness and a subtler change over time compared to the fixed system, which has an irregular and scattered change of the power outputs for the same time period. This makes the power output of the PV panel unpredictable for the fixed system. In addition to that, it was found that the average power outputs of the tracking system were higher than those of the fixed system throughout the experiments. This power difference is pronounced in the morning and in the afternoon, but at noon, the power outputs are the same in both the fixed system and the present tracking system.

Fig. 8.

The average power outputs with time.

It is also shown that the average power outputs of the tracking system ranged in the interval between 70 W and 120 W, whereas for the fixed system, the variation range extended from 10 W to 120 W for the same operating time period. From these variations, it is concluded that the power outputs of the tracking system are more steadily changing within the 50 W range, but in the case of the fixed system, the variation range is around 110 W, and the changes are also found to be uneven.

3.1.1. Discussion related to economic comparison

The average price per watt for solar panels is $2.65 [12], and the extra power produced by the tracker panel is 47 W (as stated in the power density section). Therefore, the cost saved by using the tracker is the product of the price per watt with the extra power produced, and the calculated value is the cost of the tracking system is the other important factor in determining the economy of the system. The cost of the presented tracking system is listed in Table 3.

Table 3.

Components of the tracking system with costs.

Component	Quantity	Cost per piece (ETB)	Total cost (ETB)
Solenoid valve	2	300	600
Reservoir water tank	1	1500	1500
Suspended storage	1	50	50
Spring	2	50	100
Bearing	2	50	100
Shaft	1	50	50
Bimetallic strip	2	100	200
Wire Cable	–	100	100
hose	1	50	50
Gate valve	2	50	100
Grand total cost	–	–	2850 ETB or $52.8

$Theeconomyofthetracker=savedcostbythetracker-costofthetracker=\$71.75$.

Using this tracking system, it is possible to save $71.75 when compared to adding extra areas to the fixed panel with comparable power outputs.

The additional cost consumed by the water per year can be calculated as: 7200 L, or 7.2 m³ per year, of water will be consumed. The cost of water per m³ in Ethiopia is around $0.3 per m³ [13].

So, the additional cost due to the water consumption is $2.2 per year. The total cost, including one year's water consumption, will be around $55.

The cost of a conventional solar tracker is $0.92 per watt [14,15], and the maximum produced power is 120 W. The cost will be around $110.4, so from an economic point of view the designed system is less expensive by half compared to the conventional tracking system.

Efficiency comparison: Another parameter is efficiency. According to related literature an active dual-axis tracker has produced extra energy in the range of 35%–36.4% compared to fixed PV panel [16,17]. The designed system in this paper is 24.86% more efficient than the fixed panel (stated in the solar energy collected section), but the conventional tracker is 36.4% more efficient than the fixed panel; in other words, the conventional tracker produces an extra 9.26% energy compared to the designed passive type tracker; however, the cost of the designed system is half cheaper than the conventional solar tracker.

3.1.1.1. Power density

The power density of the panel surface is given as the ratio of the power output to the surface area of the panel. The surface area of the panel is given as 1.340 × 0.530 m². The result of the power density is given in Fig. 9. The average daily power density of the tracking panel is 139 W/m² and 92 W/m² on the fixed panel. Hence, within the same area, the power density of the tracking panel is greater than the fixed panel by 47 W/m². In other words, the tracking panel collects an additional 47 W within the 1 m² available area when compared with the fixed panel.

Fig. 9.

Power density over time.

This shows that it is possible to optimize the area or land usage simply by using a tracker. However, some scholars argue that instead of using a tacking mechanism, it is better to increase the area of the fixed panel by using additional panels in order to increase power output ][[1], [10]]. However, it is not economical and is very expensive. From the cost estimation analysis it is possible to save $71.75 when compared to adding extra area to the fixed panel with comparable power outputs.

3.2. Solar energy collected from the panels

The solar energy observed by the panels was calculated from equation (5) as [11].

$$Energy=\sum _{t=0}^n\underset{1}{\overset{2}{\int }}\left(power\right)dt$$ (5)

In Fig. 10, the area under the curve formed by the hatched lines represents the extra energy collected by the tracking panel. The mean daily energy collected by the fixed panel E_F and by the tracking panel E_T during the experiment was 716.7 W h and 1081.7 W h, respectively.

Fig. 10.

Area of power versus time graph.

The energy input to the solenoid valves is 96 W h; the effective energy saved by the tracking panel is the difference between the total energy of the tracking panel and the energy input of the solenoid valves. The excess energy efficiency obtained by the tracking panel relative to the fixed panel in terms of energy outputs (${\eta }_E$) is determined by equation (6) [12]:

$$\frac{E_T-E_F}{E_T}=0.2486=24.86\%$$ (6)

Hence, the tracking system is 24.86% more efficient than the fixed panel in terms of energy output.

From related literature [[4], [5], [6]], the efficiency increased by the passive solar tracker compared to a fixed PV panel was 23.3%, but in this modified tracking system, the efficiency increased to 24.86% due to the design of a tracking system that is independent of the nighttime ambient temperature changes to return the panel to the east position.

3.2.1. Sensitiveness of the tracking system

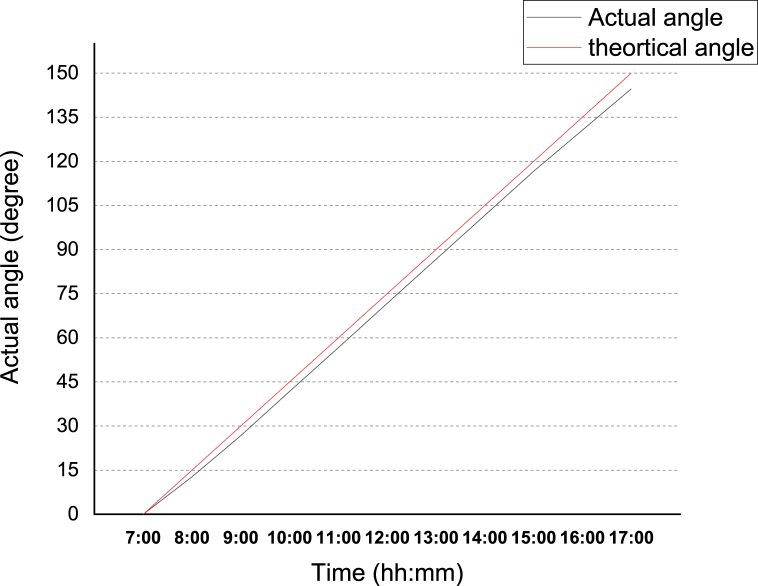
The tracker rotation during the day is designed to rotate a maximum angle of 150 degree from east to west direction, and the effective hours are from 7a.m. to 5p.m. Based on these parameters, the expected rotational speed of the panel is 150 degree per hour (or $7.27221\times {10}^{-5}\mathrm{r}\mathrm{a}\mathrm{d}/\sec$). This rotational speed is controlled by the potential energy difference between the spring force and the weight change due to the water flow rate from the Jerry Can. From the designed system, the accuracy of the system is compared with the expected hourly position of the panel and the actual position of the panel. The actual rotation on an hourly basis is recorded during the experimentation, and the graph is plotted in Fig. 11. Which compared the actual rotations of the panel with the expected rotational position.

Fig. 11.

Angle position over time.

From Fig. 11, the average angular position error expected from the present designed system is found to be 5.4°. Angles are measured with a digital angular finder tool. This angular variation indicates the degree of precision of the prototype with respect to the design system. The angular error is the result of the bimetallic strip material's sensitivity to small temperature differences. The effectiveness of the fabricated tracker rotation (effectiveness):

$$Effectiveness=\frac{\mathit{expected}rotation-angularerror}{\mathit{expected}rotation}=0.964$$

Therefore, the present fabricated tracking system has 96.40% accuracy compared to the expected rotation along with the sun's position (or an ideal tracking system).

3.2.2. Nighttime temperature changes

Related previous works assumed the return mechanism was possible during the night with the help of the deflection of the bimetallic strip in the opposite direction from daylight time or in the downward direction [4,5]. The minimum temperature change required to 1 mm of deflect the bimetallic strip in the upward or downward direction is determined at 8.5 K.

Fig. 12 shows the differences in nighttime temperature between sample days during the experiment conducted at Bahir Dar University. From the figure, it is calculated that there are 10 days with insufficient temperature changes to deflect the bimetallic strip in the downward direction in order to make the rotation of the panel possible at night. However, the fabricated new tracking system worked precisely throughout these sample days. As a conclusion, the problem of returning the panel to the east position for the morning period is precisely addressed in this research work and compared with the previous related works.

Fig. 12.

Temperature change in the night.

4. Limitations of the study

In the case of water shortages in the area of installation of the system, using a small pump instead of a large reservoir is advisable. Instead of a reservoir, there will be a small storage below the suspended storage to collect the water drops during the day, and during the night, this collected water will be returned to the suspended storage by the pump. There should be an automatic mechanism for the pump to only to return the water during the night.

To make the test results accuracy close to 100%, it is important to reconsider the materials of the bimetallic strip's sensitiveness to small temperature changes and the responsiveness of the spring's material to a small weight change. For future work, these two parameters can be investigated to enhance the system's accuracy.

Additionally, the investigation can be carried out in different locations and throughout different seasons to investigate how geographical and seasonal variation affect the efficiency of the designed system.

Author contribution statement

Mintesinot Alemayehu: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Wrote the paper.

Bimrew Tamrat Admasu: Contributed reagents, materials, analysis tools or data.

Data availability statement

Data will be made available on request.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Biographies

Bimrew Tamrat is an associate professor working at the Bahir Dar Institute of Technology, Faculty of Mechanical and Industrial Engineering, in the Thermal Engineering stream. He has got his PhD degree in Huazhong University of Science and Technology, China. His research interest is on thermal systems, renewable energy systems, fluid power systems and nanofluids as well).

Mintesinot Alemayehu is a lecturer working at the Bahir Dar Institute of Technology, Faculty of Mechanical and Industrial Engineering in the Thermal Engineering branch. His research interests are on thermo-fluid systems, and renewable energy systems particularly on solar energy.

Nomenclature

C

spring index = D/d

G

Shear Module of spring material

I

Solar irradiance, W/m²

K

Wahl's stress factor

L

length of the bimetallic strip, m

M

ratio of thicknesses

n_a

Number of active coils

N

ratio of young's moduli

P

Solar power, W

T

Temperature, K

R

Arc radius of bimetallic strip, m

W

Weight density, N/m³

D

Mean spring diameter, m

d

Spring wire diameter, m

T_o

initial bending temperature

Δs

Maximum deflection of the spring

Greek symbols

ρ

radius of curvature, m

α

coefficients of linear thermal expansion

$\tau$

Spring size

Subscripts

1

bimetallic strip 1

2

bimetallic strip 2