Machine learning algorithms for predicting the risk of fracture in patients with diabetes in China

Abstract

Background

Patients with diabetes are more likely to be predisposed to fractures compared to those without diabetes. In clinical practice, predicting fracture risk in diabetics is still difficult because of the limited availability and accessibility of existing fracture prediction tools in the diabetic population. The purpose of this study was to develop and validate models using machine learning (ML) algorithms to achieve high predictive power for fracture in patients with diabetes in China.

Methods

In this study, the clinical data of 775 hospitalized patients with diabetes was analyzed by using Decision Tree (DT), Gradient Boosting Decision Tree (GBDT), Logistic Regression (LR), Random Forest (RF), Support Vector Machine (SVM), eXtreme Gradient Boosting (XGBoost) and Probabilistic Classification Vector Machines (PCVM) algorithms to construct risk prediction models for fractures. Moreover, the risk factors for diabetes-related fracture were identified by the feature selection algorithms.

Results

The ML algorithms extracted 17 most relevant factors from raw clinical data to maximize the accuracy of the prediction results, including bone mineral density, age, sex, weight, high-density lipoprotein cholesterol, height, duration of diabetes, total cholesterol, osteocalcin, N-terminal propeptide of type I, diastolic blood pressure, and body mass index. The 7 ML models including LR, SVM, RF, DT, GBDT, XGBoost, and PCVM had f1 scores of 0.75, 0.83, 0.84, 0.85, 0.87, 0.88, and 0.97, respectively.

Conclusions

This study identified 17 most relevant risk factors for diabetes-related fracture using ML algorithms. And the PCVM model proved to perform best in predicting the fracture risk in the diabetic population. This work proposes a cheap, safe, and extensible ML algorithm for the precise assessment of risk factors for diabetes-related fracture.

1. Introduction

The diabetic population has grown rapidly over the past years. The report by the International Diabetes Federation (IDF) has indicated that the worldwide prevalence of diabetes in people aged 20–79 years would increase from 10.5% (536.6 million people) to 12.2% (783.2 million) in 2045 [1]. In terms of a chronic metabolic disease, complications of diabetes can affect multiple organs including the kidney, retina, nervous system, and bone [2]. The link between bone and diabetes has received increasing attention in recent years. Cheng et al. reported that the bone metabolic diseases of greatest concern to individuals with diabetes are osteoporosis and related fractures [3]. Diabetes-related abnormal bone nutritional status increases the probability of osteoporosis. With in-depth research on comorbid diabetes and osteoporosis, the concept of diabetic osteoporosis has been widely accepted. The characteristics of diabetic osteoporosis include bone loss, bone tissue changes, and fracture manifestations in the condition of diabetes [4]. Epidemiological surveys have shown that the incidence of osteoporosis is 48–72% in patients with type 1 diabetes, whereas those with type 2 diabetes have a prevalence of 25–60% [5]. In China, a meta-analysis showed that more than 1/3 of patients with type 2 diabetes suffer from osteoporosis. Furthermore, the duration of diabetes is associated with a progressive rise in the incidence of diabetic osteoporosis [6]. The pathogenesis of diabetic osteoporosis has yet to be elucidated in detail. Increasing evidence suggests that numerous factors such as the hyperglycemic state, oxidative stress response, and late accumulation of glycosylation products are involved in diabetic osteoporosis [7]. The fracture is the endpoint event of osteoporosis, and common sites of fracture include the vertebrae, hip, humerus, and distal forearm [8]. Numerous studies have confirmed that nonvertebral fractures are more likely to occur in people with diabetes than those without diabetes. In particular, patients with type 2 diabetes may have a 40%–70% greater risk of hip fracture and a 20% increased risk of any other type of fracture [9]. Fractures are extremely dangerous and are one of the leading factors of injury and even mortality in seniors. In the case of hip fractures, patients have a mortality rate of approximately 20–25% within one year, and more than 50% of survivors are left disabled [10]. Patients with disabilities have a significantly lower quality of life. The high cost of medical care for post-treatment of fractures is an immense financial strain for the countries and individuals [11,12]. Moreover, when fractures occur, the fracture healing time and the incidence of post-fracture complications are considerably higher in individuals with diabetes than those without diabetes, leading to longer hospital stays and poorer functional recovery, which in turn results in significantly higher disability rates, mortality rates, and increased medical costs for fracture patients with diabetes. Therefore, the early recognition of individuals with diabetes who are at high risk of fracture with appropriate risk assessment tools contributes to precise prevention and treatment of diabetes-related fractures.

The World Health Organization (WHO) recommends the use of dual-energy X-ray absorptiometry (DXA) to measure a patient's bone mineral density (BMD) as the gold standard for diagnosing osteoporosis, and it is the most common means to assess fracture risk. Nevertheless, some studies indicate that patients with diabetes-related fractures have normal or even increased BMD. Therefore, BMD alone cannot be used to adequately assess the risk of diabetes-related fractures. Several risk assessment tools are currently used to predict the fracture risk in clinical practice including the Fracture Risk Assessment Tool (FRAX), QFracture tool, and Garvan Fracture Risk Calculator (FRC). There are few appropriate tools to predict fracture risk in individuals with diabetes. These tools either have low predictive power in terms of diabetes or have not been directly validated in the Chinese population. Moreover, the complexity of these tools makes them difficult to be widely used in community-dwelling healthcare. Thus, it is necessary to develop a fracture risk prediction tool based on the clinical characteristics of Chinese patients with diabetes.

Artificial intelligence (AI) has become one of the technologies with the highest growth rates recently. Machine learning (ML) is at the heart of AI and has revitalized the field of intelligent medicine [[13], [14], [15], [16]]. The objective integration of data to predict results is made possible by ML, which utilizes statistical approaches to big datasets to identify correlations between patient features and outcomes. Given the inherent power of using ML algorithms to capture nonlinear relationships, a growing number of researchers are advocating the use of new predictive models based on ML to assess the risk of disease [[17], [18], [19]]. Due to the limited availability and accessibility of existing fracture prediction tools in the diabetic population, there is currently no ideal tool for predicting the fracture risk of patients with diabetes in China. After considering the methodological advantages of ML, we speculated that it would help identify individuals with diabetes who are more likely to be predisposed to fractures. Therefore, the objective of this study was to develop and verify AI models with high predictive power for fractures among Chinese individuals with diabetes by ML algorithms. At the same time, we also attempted to determine which class of ML algorithms had the highest prediction accuracy.

The prediction model proposed in the study is comprehensive and has high dimensional characteristics. Unlike several existing predictive tools for fractures, the proposed model integrates more clinical data about bone metabolism among individuals with diabetes and effectively predicts fractures by combining all the indicators, which can greatly improve the efficiency of traditional diagnostic techniques and are cheap, safe, and extensible. This study would help primary healthcare-providers identify individuals with diabetes who are more likely to suffer fractures. Early identification is helpful for early osteoporosis diagnosis and treatment.

2. Methods

2.1. Datasets

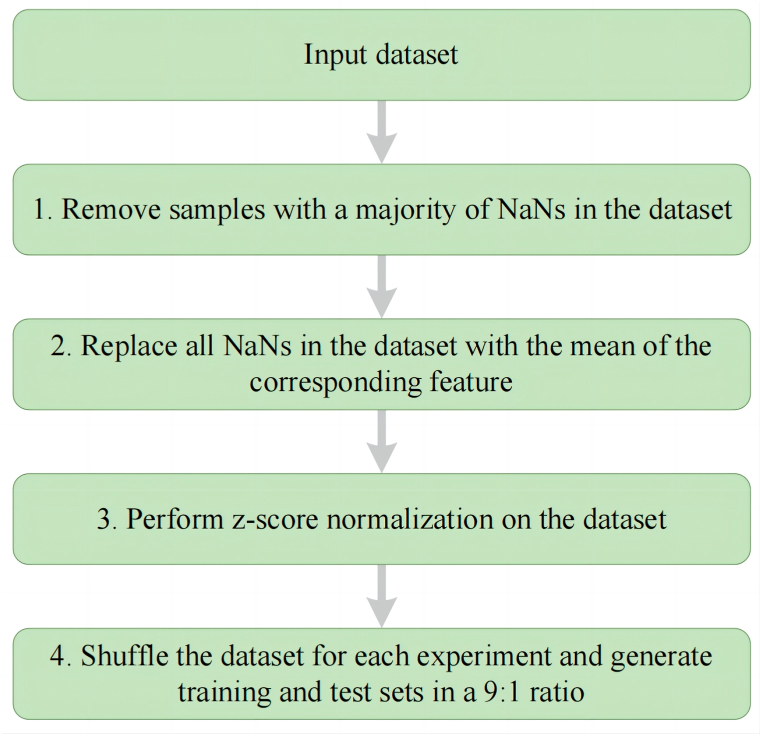
The clinical data of 775 patients with diabetes were obtained from the Department of Endocrinology at the First Affiliated Hospital of University of Science and Technology of China in this study. Diabetes was diagnosed by the 1999 World Health Organization criteria [20]. All participants received bone densitometry, as measured by DXA. Osteoporosis was diagnosed based on the 2017 criteria of the Chinese Society of Osteoporosis and Bone Mineral Research Guidelines [21]. Participants were excluded from this study based on the following criteria: (1) individuals with conditions including Cushing syndrome, hypothyroidism, parathyroid and hypogonadism, rheumatoid arthritis, chronic kidney disease, chronic liver disease, and malignancy, all of which have a significant impact on bone metabolism; and (2) patients who had fractures before being diagnosed with osteoporosis and those who had fractures before being diagnosed with diabetes. All patients were divided into three groups: the fracture group (n = 38), osteoporosis group (n = 146), and non-osteoporosis group (n = 591). We collected 37 baseline covariates for the participants as shown in Table 1. We also conducted a descriptive analysis of the collected demographic and clinical data, as shown in Table 2. The use of clinical data obtained ethical approval from the Ethics Committee of the First Affiliated Hospital of USTC (Approved No. 2020-KY-38). After considering that real-world clinical data may be missing, it was determined that appropriate data processing stages are necessary (Fig. 1). Data cleansing is the first stage while missing value completion is the second. The data are normalized in the third step to account for the imbalance between features. The fourth stage generates data for training.

Table 1.

Information on clinical dataset.

No	Features	Type	Description	No.	Features	Type	Description
1	Duration	Numeric	Duration of diabetes	20	HDL-C	Numeric	High-density lipoprotein cholesterol
2	Sex	Boolean		21	SBP	Numeric	Systolic blood pressure
3	Age	Numeric		22	DBP	Numeric	Diastolic blood pressure
4	Height	Numeric		23	ALP	Numeric	Alkaline phosphatase
5	Weight	Numeric		24	TG	Numeric	Triglyceride
6	BMI	Numeric	BMI (kg/m2) = weight (kg)/height2 (m)	25	TC	Numeric	Totalcholesterol
7	FPG	Numeric	Fasting plasma glucose	26	Alb	Numeric	Albumin
8	FINS	Numeric	Fasting Insulin	27	ALT	Numeric	Alanine aminotransferase
9	HbA1c	Numeric	Glycated hemoglobin A1c	28	AST	Numeric	Aspartate aminotransferase
10	C–P	Numeric	c-peptide	29	GGT	Numeric	γ-Glutamyltransferase
11	Cr	Numeric	Serum creatinine	30	25-OH-VD	Numeric	25-Hydroxyvitamin vitaminD
12	UALB/Ucr	Numeric	Urine albumin creatinine ratio	31	PTH	Numeric	Parathyroid hormone
13	UA	Numeric	Serum uric acid	32	BMD1	Numeric	Bone Mineral Density at the lumbar spines (L1-L4)
14	Ca	Numeric	Calcium	33	BMD2	Numeric	Bone Mineral Density at the distal radius
15	P	Numeric	Phosphorus	34	BMD3	Numeric	Bone Mineral Density at the femoral neck
16	OC	Numeric	Osteocalcin	35	BMD4	Numeric	Bone Mineral Density at the Ward's triangle
17	CTX	Numeric	C-terminal telopeptide of type I collagen	36	BMD5	Numeric	Bone Mineral Density at the greater trochanter
18	PINP	Numeric	N-terminal propeptide of type I procollagen	37	BMD6	Numeric	Bone Mineral Density at the total hip
19	LDL-C	Numeric	low-density lipoprotein cholesterol

Table 2.

Demographic characteristic and clinical data of the study population.

Variable	Osteoporosis group (n = 146)	Non-osteoporosis group (n = 591)	Fracture group (n = 38)
Age (years)	68 (62–77)	56 (49–65)	68 (60–76)
Gender
Male (n)	45 (30.8%)	345 (58.4%)	9 (23.7%)
Female (n)	101 (69.2%)	246 (41.6%)	29 (76.3%)
Weight (kg)	60.4 (53.0–66.0)	69.3 (61.0–76.0)	62.4 (55.0–68.3)
Height (cm)	158 (153–165)	166 (158–172)	158 (153–164)
Body mass index (kg/m2)	23.57 (21.00–25.60)	25.10 (22.89–26.96)	24.40 (21.99–27.33)
Duration of diabetes (years)	10.0 (5.0–18.5)	9.0 (3.0–14.0)	10.0 (5.0–16.3)
Systolic blood pressure (mmHg)	139 (127–148)	133 (123–145)	133 (122–147)
Diastolic blood pressure (mmHg)	80 (72–85)	82 (76–90)	78 (73–84)
Fasting plasma glucose (mmol/L)	8.7 (6.6–10.7)	8.3 (6.3–10.7)	7.85 (6.0–9.4)
Fasting Insulin (pmol/L)	104.32 (61.92–104.32)	84.62 (47.07–88.24)	97.93 (60.46–97.93)
Glycated hemoglobin A1c (%)	8.4 (7.1–9.7)	8.4 (7.2–10.3)	8.30 (7.1–9.1)
C-peptide (nmol/L)	0.39 (0.27–0.39)	0.41 (0.27–0.44)	0.51 (0.32–0.51)
Serum creatinine (umol/L)	64.0 (50.8–81.3)	63.0 (52.0–78.5)	66.0 (50.8–81.3)
Serum uric acid (umol/L)	282.5 (241.8–355.3)	315.1 (252.0–388.8)	275.5 (203.5–355.5)
Calcium (mmol/L)	2.23 (2.15–2.31)	2.22 (2.14–2.31)	2.26 (2.15–2.37)
Phosphorus (mmol/L)	1.20 (1.10–1.31)	1.19 (1.08–1.32)	1.20 (1.08–1.33)
Alkaline phosphatase (IU/L)	84.5 (68.8–103.3)	75.0 (61.0–90.0)	83.9 (55.8–95.6)
Triglyceride (mmol/L)	1.49 (1.04–1.81)	1.63 (1.1–2.33)	1.31 (0.90–1.86)
Totalcholesterol (mmol/L)	4.33 (3.84–5.10)	4.32 (3.66–4.99)	4.82 (3.81–5.48)
Low-density lipoprotein cholesterol (mmol/L)	2.38 (1.99–2.89)	2.41 (1.88–2.87)	2.56 (2.01–3.28)
High-density lipoprotein cholesterol (mmol/L)	1.03 (0.85–1.24)	0.92 (0.76–1.08)	1.08 (0.88–1.31)
Albumin (g/L)	39.5 (37.2–41.6)	40.5 (38.2–42.5)	38.7 (37.0–41.1)
Alanine aminotransferase (IU/L)	18.0 (13.0–26.0)	20.0 (15.0–31.0)	16.5 (12.8–30.0)
Aspartate aminotransferase (IU/L)	19.0 (16.0–24.0)	19.0 (16.0–25.0)	20.5 (15.0–26.6)
γ-glutamyltransferase (IU/L)	19.0 (14.8–30.0)	23.0 (15.0–39.6)	17.0 (13.0–24.8)
25-hydroxyvitamin vitaminD (ng/l)	13.44 (9.48–20.70)	15.5 (10.45–20.87)	14.20 (10.47–21.14)
Urine albumin creatinine ratio (mg/g)	26.95 (15.95–64.85)	20.41 (11.6–63.93)	40.63 (22.53–493.04)
Parathyroid hormone (ng/L)	47.0 (36.6–47.0)	40.7 (30.8–42.8)	43.4 (26.6–49.8)
Osteocalcin (ng/ml)	17.22 (13.41–25.00)	14.17 (11.06–18.95)	17.65 (10.62–24.28)
C-terminal telopeptide of type I collagen (Pg/ml)	469.6 (323.7–695.5)	406.3 (261.1–511.8)	295.4 (199.8–667.6)
N-terminal propeptide of type I procollagen (ng/ml)	50.67 (35.92–69.44)	42.47 (30.86–51.57)	49.15 (26.66–75.27)
Bone Mineral Density at the lumbar spines (L1-L4) (g/cm2)	0.852 (0.779–0.905)	1.117 (1.003–1.213)	0.982 (0.814–1.122)
Bone Mineral Density at the distal radius (g/cm2)	0.520 (0.461–0.574)	0.709 (0.650–0.769)	0.567 (0.472–0.643)
Bone Mineral Density at the femoral neck (g/cm2)	0.719 (0.666–0.800)	0.927 (0.838–1.004)	0.741 (0.649–0.826)
Bone Mineral Density at the Ward's triangle (g/cm2)	0.549 (0.494–0.640)	0.818 (0.696–0.911)	0.554 (0.489–0.653)
Bone Mineral Density at the greater trochanter (g/cm2)	0.629 (0.560–0.721)	0.816 (0.736–0.908)	0.652 (0.549–0.740)
Bone Mineral Density at the total hip (g/cm2)	0.795 (0.721–0.881)	1.010 (0.917–1.092)	0.810 (0.714–0.888)

Note:The data are presented as median (interquartile range) or number (%).

Fig. 1.

Flow chart for data processing. Abbreviations: NaN, Notanumber.

2.2. Machine learning

The task of predicting whether a patient with diabetes has fractures is a classification problem with 3 types of labels. To address this problem, we used 7 ML models to learn the function of the label result and the patient status. For a formal definition, the data consist of the test results of patients' various indicators, which is denoted as a numerical vector (${\mathrm{x}}_1,{\mathrm{x}}_2,\dots ,{\mathrm{x}}_{\mathrm{n}}$), and a label ranging from 1 to 3, indicating whether these patients with diabetes had a fracture, osteoporosis, or non-osteoporosis, respectively. The dataset consists of 775 records and they were divided into a training dataset and a testing dataset for 7 different ML models. Many different research domains have employed ML models from different paradigms [[22], [23], [24], [25], [26], [27]]. However, not all ML models are applicable or effective for a specific application scenario. Which ML model to use is determined by the characteristics and requirements of the task. A basic requirement is that the model's prediction outcomes used need to achieve high accuracy. On this basis, in order to make the prediction results for fracture have good interpretability and facilitate deployment and application, we mainly selected 7 kinds of ML classification algorithm models based on statistics. These models have a strong theoretical basis, and the prediction results have a strict basis. At the same time, these models are supported by a broad research community. The models are introduced as follows.

2.2.1. Decision tree (DT)

A decision tree is a flowchart-like tree structure, where each node represents a judgement condition and all the data that satisfy all conditions from the root node to this node are contained [28]. The decision tree algorithm selects the optimal attribute by selecting the attribute with the highest information entropy. The information entropy of the attribute is defined as:

$$\mathrm{E}\mathrm{n}\mathrm{t}\left(\mathrm{D}\right)=-\sum _{\mathrm{k}=1}^{\left|\mathrm{\gamma }\right|}{\mathrm{p}}_{\mathrm{k}}{\log }_2\left({\mathrm{p}}_{\mathrm{k}}\right)$$ (1)

where pk (k = 1, 2, …, $\left|\mathrm{\gamma }\right|$) represents the proportion of the kth sample in the data of the current node D.

Assuming that the selected attribute a has V different values. According to the rules of the decision tree, D will be divided into V different node data sets, and DV represents the vth node. The definition of the knowledge gain of attribute a is:

$$Gain\left(D,a\right)=Ent\left(D\right)-\sum _{\nu =1}^V\frac{\left|D^v\right|}{\left|D\right|}Ent\left(D^v\right)$$ (2)

The algorithm for selecting and dividing attributes is obtained by calculating the information gain obtained by dividing child nodes of each attribute and selecting the attribute with the largest information gain.

2.2.2. Gradient Boosting Decision Tree (GBDT)

The GBDT is an ensemble learning algorithm, which is based on the classic decision tree algorithm [29].

For a given data set $\mathcal{D}=\left\{\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right)\right\}\left(\left|\mathcal{D}\right|=\mathrm{n},{\mathrm{x}}_{\mathrm{i}}\in {\mathbb{R}}^{\mathrm{m}},{\mathrm{y}}_{\mathrm{i}}\in \mathbb{R}\right)$, suppose the learner we obtain at iteration t − 1 is ${\mathrm{f}}_{\mathrm{t}-1}\left(\mathrm{x}\right)$, and the loss function is $\mathrm{L}\left(\mathrm{y},{\mathrm{f}}_{\mathrm{t}-1}\left(\mathrm{x}\right)\right)$. In the next iteration, ${\mathrm{r}}_{\mathrm{t}\mathrm{i}}$ is defined as:

$${\mathrm{r}}_{\mathrm{t}\mathrm{i}}=-\left[\frac{\partial \mathrm{L}\left({\mathrm{y}}_{\mathrm{i}},{\mathrm{f}}_{\mathrm{t}-1}\left({\mathrm{x}}_{\mathrm{i}}\right)\right))}{\partial {\mathrm{f}}_{\mathrm{t}-1}\left({\mathrm{x}}_{\mathrm{i}}\right)}\right]$$ (3)

where L is a loss function that measures the difference between the prediction ${\mathrm{f}}_{\mathrm{t}-1}\left({\mathrm{x}}_{\mathrm{i}}\right)$ and the target ${\mathrm{y}}_{\mathrm{i}}$. By using $\left\{\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{r}}_{\mathrm{t}\mathrm{i}}\right)|\mathrm{i}=\mathrm{1,2},..,\mathrm{n})\right\}$ as the training data, a regression tree can be trained as the t-th regression tree. The leaf nodes of this regression tree are presented as ${\mathrm{R}}_{\mathrm{t}\mathrm{j}},\mathrm{j}=\mathrm{1,2},...,\mathrm{J}$, where $\mathrm{J}$ is the count of the leaf nodes.

The function learned from the first t iterations is presented as:

$${\mathrm{f}}_{\mathrm{t}}\left(\mathrm{x}\right)={\mathrm{f}}_{\mathrm{t}-1}\left(\mathrm{x}\right)+\sum _{\mathrm{j}=1}^{\mathrm{J}}{\mathrm{c}}_{\mathrm{t}\mathrm{j}}\mathrm{I}\left(\mathrm{x}\in {\mathrm{R}}_{\mathrm{t}\mathrm{j}}\right)$$ (4)

where ${\mathrm{c}}_{\mathrm{t}\mathrm{j}}$ is defined as:

$${\mathrm{c}}_{\mathrm{t}\mathrm{j}}=\mathrm{a}\mathrm{r}\underset{c}{\underbrace{\mathrm{g}\mathrm{m}}}\mathrm{i}\mathrm{n}\sum _{{\mathrm{x}}_{\mathrm{i}}\in {\mathrm{R}}_{\mathrm{t}\mathrm{j}}}\mathrm{L}\left({\mathrm{y}}_{\mathrm{i}},{\mathrm{f}}_{\mathrm{t}-1}\left({\mathrm{x}}_{\mathrm{i}}\right)+\mathrm{c}\right)$$ (5)

2.2.3. Logistic regression (LR)

The LR trains the model using the given n sets of data (training set), and classifies one or more given sets of data (test set) after training [30]. Each set of data is a p-dimensional vector. The model trained by logistic regression is a p-dimensional space. After classification, a certain category or some similar categories are in one of the dimensions. The sigmoid function in logistic regression is defined as follows:

$$h\left(x^i\right)=\frac{1}{1+e^{-\left(W^T{X}^i+b\right)}}$$ (6)

where xi is the i-th p-dimensional column vector ($x_1^i$, $x_2^i$, …, $x_p^i$)T of the test set, W and b are parameters to be determined, and W is also a p-dimensional column vector. After training, W and b can be determined according to the training set.

For sample i, its class is defined as $y_i\in \left(\mathrm{0,1}\right)$. h (xi) is the probability that y-i corresponds to 1 (that is, xi belongs to class 1), and 1-h (xi) is the probability that yi corresponds to 0 (that is, xi belongs to class 0). The maximum likelihood function is defined as:

$$L\left(w\right)=\frac{1}{n}\sum _{i=1}^n-y_i\ln \left(h\left(x_i\right)\right)$$ (7)

The loss function is made as small as possible through training, so that the obtained prediction function h (xi) will be as close to the real classification as possible.

2.2.4. Random forest (RF)

The RF is one of the types of ensemble learning algorithms [31,32].

For a given data set $\mathrm{D}=\left\{\left({\mathrm{x}}_1,{\mathrm{y}}_1\right),\left({\mathrm{x}}_2,{\mathrm{y}}_2\right),\dots \left({\mathrm{x}}_{\mathrm{m}},{\mathrm{y}}_{\mathrm{m}}\right)\right\}$, the random forest algorithm can be divided into the following steps: [31,33,34].

• 1.m number of random records are taken from the data set $\mathrm{D}$ as a sampling set, repeat T times, and the sampling set is presented as ${\mathrm{D}}_1,{\mathrm{D}}_2,...{\mathrm{D}}_{\mathrm{T}}$, where T is a hyperparameter.
• 2.The tth decision tree model ${\mathrm{G}}_{\mathrm{t}}\left(\mathrm{x}\right)$ is trained using the sampling set ${\mathrm{D}}_{\mathrm{t}}$. A portion of the sample features is selected from all of the sample features on the node while training the decision tree model's nodes.
• 3.The final output is considered based on majority voting or averaging for classification and regression respectively.

2.2.5. Support vector machine (SVM)

The SVM model can be trained by solving the following constrained optimal problem [35]:

$${\min }_{w,b}\frac{1}{2}{\Vert w\Vert }^2$$ (8)

$$s.t.y_i\left(w\cdot x_i+b\right)-1\ge 0,i=\mathrm{1,2},...,N$$ (9)

where ${\mathrm{x}}_{\mathrm{i}}$ is the feature vector of the ith sample of training data, ${\mathrm{y}}_{\mathrm{i}}$ is the label of xi valued as 0 or 1, w and b are the parameters to be learned, and ${\Vert \mathrm{w}\Vert }^2$ represents the L2 norm of $\mathrm{w}$.

Suppose that ${\mathrm{w}}^{*}$, ${\mathrm{b}}^{*}$ is the optimal solution of such problem, then the classification decision function is presented as:

$$f\left(x\right)=sign\left(w^{*}\cdot x+b^{*}\right)$$ (10)

In recent years, some studies have proposed that some parameters can be used to adjust the performance of the SVM method, and commonly used parameters include the error tolerance ε and penalty parameter C. The model complexity and empirical error are traded off according to the penalty parameter C. The degree to which errors are tolerated is controlled by the error tolerance ε., thus indirectly regulating the generalization ability. The performance and accuracy of SVM are largely affected by the above parameters. In this work, the values of these parameters are determined through multiple experiments.

2.2.6. eXtreme Gradient Boosting (XGBoost)

For a given data set $\mathcal{D}=\left\{\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right)\right\}\left(\left|\mathcal{D}\right|=\mathrm{n},{\mathrm{x}}_{\mathrm{i}}\in {\mathbb{R}}^{\mathrm{m}},{\mathrm{y}}_{\mathrm{i}}\in \mathbb{R}\right)$, XGBoost uses a set of addictive functions to predict the output [36].

$${\mathrm{F}}_{\mathrm{m}}\left(\mathrm{x}\right)={\mathrm{F}}_{\mathrm{m}-1}\left(\mathrm{x}\right)+{\mathrm{f}}_{\mathrm{m}}\left(\mathrm{x}\right)$$ (11)

where ${\mathrm{f}}_{\mathrm{m}}\left(\mathrm{x}\right)$ is the sub-model of the current step and ${\mathrm{F}}_{\mathrm{m}-1}\left(\mathrm{x}\right)$ is the first $\mathrm{m}-1$ sub-model that has been trained before.

The objective of the XGBoost model is defined as:

$$\mathrm{O}\mathrm{b}\mathrm{j}=\sum _{\mathrm{i}=1}^{\mathrm{N}}\mathrm{L}\left[{\mathrm{F}}_{\mathrm{m}}\left({\mathrm{x}}_{\mathrm{i}}\right),{\mathrm{y}}_{\mathrm{i}}\right]+\sum _{\mathrm{j}=1}^{\mathrm{m}}\mathrm{\Omega }\left({\mathrm{f}}_{\mathrm{j}}\right)$$ (12)

where $\mathrm{L}$ represents the difference between the target ${\mathrm{y}}_{\mathrm{i}}$ and the prediction ${\mathrm{F}}_{\mathrm{m}}\left({\mathrm{x}}_{\mathrm{i}}\right)$ as measured by the loss function. The complexity of the function ${\mathrm{f}}_{\mathrm{j}}$ is measured by the second term $\mathrm{\Omega }$. When XGBoost uses the decision tree as the base classifier, $\mathrm{\Omega }\left(\mathrm{f}\right)$ is defined as:

$$\mathbf{\Omega }\left(\mathrm{f}\right)=\mathrm{\gamma }\mathrm{T}+\frac{1}{2}\mathrm{\lambda }\parallel \mathrm{w}{\parallel }^2$$ (13)

where $\mathrm{T}$ is the number of leaf nodes of $\mathrm{f}$, $\mathrm{w}$ is the vector composed of the output of all leaf nodes, $\parallel \mathrm{w}{\parallel }^2$ is the L2 norm of $\mathrm{w}$, and $\mathrm{\gamma }$ and $\mathrm{\lambda }$ are hyperparameters.

A second-order approximation is used to quickly optimize the objective. After using second-order approximation and removing all the constant terms, the objective is defined as:

$$\mathrm{O}bj=\sum _{\mathrm{i}=1}^{\mathrm{N}}\left[{\mathrm{g}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{m}}\left({\mathrm{x}}_{\mathrm{i}}\right)+\frac{1}{2}{\mathrm{h}}_{\mathrm{i}}{\mathrm{f}}_{\mathrm{m}}^2\left({\mathrm{x}}_{\mathrm{i}}\right)\right]+\mathrm{\gamma }\mathrm{T}+\frac{1}{2}\mathrm{\lambda }\sum _{\mathrm{j}=1}^{\mathrm{T}}{\mathrm{w}}_{\mathrm{j}}^2=\sum _{\mathrm{j}=1}^{\mathrm{T}}\left[\left(\sum _{\mathrm{i}\in \mathrm{I}\left(\mathrm{j}\right)}{\mathrm{g}}_{\mathrm{i}}\right){\mathrm{w}}_{\mathrm{j}}+\frac{1}{2}\left(\sum _{\mathrm{i}\in \mathrm{I}\left(\mathrm{j}\right)}{\mathrm{h}}_{\mathrm{i}}+\mathrm{\lambda }\right){\mathrm{w}}_{\mathrm{j}}^2\right]+\mathrm{\gamma }\mathrm{T}=\sum _{\mathrm{j}=1}^{\mathrm{T}}\left[{\mathrm{G}}_{\mathrm{j}}{\mathrm{w}}_{\mathrm{j}}+\frac{1}{2}\left({\mathrm{H}}_{\mathrm{j}}+\mathrm{\lambda }\right){\mathrm{w}}_{\mathrm{j}}^2\right]+\mathrm{\gamma }\mathrm{T}$$ (14)

where ${\mathrm{g}}_{\mathrm{i}}=\frac{\partial \mathrm{L}}{\partial {\mathrm{F}}_{\mathrm{m}-1}\left({\mathrm{x}}_{\mathrm{i}}\right)}$, ${\mathrm{h}}_{\mathrm{i}}=\frac{{\partial }^2\mathrm{L}}{{\partial }^2{\mathrm{F}}_{\mathrm{m}-1}\left({\mathrm{x}}_{\mathrm{i}}\right)}$, $\mathrm{I}\left(\mathrm{j}\right)=\left\{{\mathrm{x}}_{\mathrm{i}}\mid \mathrm{q}\left({\mathrm{x}}_{\mathrm{i}}\right)=\mathrm{j}\right\}$, $\mathrm{q}\left({\mathrm{x}}_{\mathrm{i}}\right)$ is the index function that maps samples to leaf nodes, ${\mathrm{w}}_{\mathrm{j}}={\mathrm{f}}_{\mathrm{m}}\left({\mathrm{x}}_{\mathrm{i}}\right),\mathrm{i}\in \mathrm{I}\left(\mathrm{j}\right)$, ${\mathrm{G}}_{\mathrm{j}}={\sum }_{\mathrm{i}\in \mathrm{I}\left(\mathrm{j}\right)}{\mathrm{g}}_{\mathrm{i}}$, and ${\mathrm{H}}_{\mathrm{j}}={\sum }_{\mathrm{i}\in \mathrm{I}\left(\mathrm{j}\right)}{\mathrm{h}}_{\mathrm{i}}$.

The minimum point of the objective is ${\mathrm{w}}_{\mathrm{j}}^{*}=-\frac{{\mathrm{G}}_{\mathrm{j}}}{{\mathrm{H}}_{\mathrm{j}}+\mathrm{\lambda }}$, so the minimum value of the objective is:

$${\mathrm{O}\mathrm{b}\mathrm{j}}^{*}=\sum _{\mathrm{j}=1}^{\mathrm{T}}\left(-\frac{1}{2}\frac{{\mathrm{G}}_{\mathrm{j}}^2}{{\mathrm{H}}_{\mathrm{j}}+\mathrm{\lambda }}+\mathrm{\gamma }\right)$$ (15)

$${\mathrm{F}}_{\mathrm{m}}\left(\mathrm{x}\right)={\mathrm{F}}_{\mathrm{m}-1}\left(\mathrm{x}\right)+{\mathrm{f}}_{\mathrm{m}}\left(\mathrm{x}\right)$$ (16)

2.2.7. Probabilistic Classification Vector Machines (PCVM)

The PCVM is an excellent classification algorithm. In a two-class classification task, the data set of input-target training pairs is ${\left\{{\mathrm{x}}_{\mathrm{i}},{\mathrm{y}}_{\mathrm{i}}\right\}}_{\mathrm{i}=1}^{\mathrm{N}}$, where ${\mathrm{y}}_{\mathrm{i}}\in \left\{-1,+1\right\}$. The probit link function is used as follows to convert linear outputs to binary outputs [[37], [38], [39]].

$$\mathbf{\psi }\left(\mathrm{x}\right)=\underset{-\infty }{\overset{\mathrm{x}}{\int }}\mathrm{N}\left(\mathrm{t}|\mathrm{0,1}\right)\mathrm{d}\mathrm{t}$$ (17)

where $\mathrm{\psi }\left(\mathrm{x}\right)$ is the Gaussian cumulative distribution function. Then, the learning model becomes

$$\mathbf{l}\left(\mathrm{x};\mathrm{w},\mathrm{b}\right)=\mathrm{\psi }\left(\sum _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{w}}_{\mathrm{i}}{\mathrm{\Phi }}_{\mathrm{i},\mathrm{\theta }}\left(\mathrm{x}\right)+\mathrm{b}\right)=\mathrm{\psi }\left({\mathrm{\Phi }}_{\mathrm{\theta }}\left(\mathrm{x}\right)\mathrm{w}+\mathrm{b}\right)\text{.}$$ (18)

Each weight ${\mathrm{w}}_{\mathrm{i}}$ is given a truncated Gaussian prior, while the bias $\mathrm{b}$ is given a zero-mean Gaussian prior.

$$\mathbf{p}\left(\mathrm{w}|\mathrm{\alpha }\right)=\prod _{\mathrm{i}=1}^{\mathrm{N}}\mathrm{p}\left({\mathrm{w}}_{\mathrm{i}}|{\mathrm{\alpha }}_{\mathrm{i}}\right)=\prod _{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{N}}_{\mathrm{t}}\left({\mathrm{w}}_{\mathrm{i}}|0,{\mathrm{\alpha }}_{\mathrm{i}}^{-1}\right)$$ (19)

$$\mathbf{p}\left(\mathrm{b}|\mathrm{\beta }\right)=\mathrm{N}\left(\mathrm{b}|0,{\mathrm{\beta }}^{-1}\right)$$ (20)

where $\mathrm{b}$ is the inverse variance of the normal distribution, ${\mathrm{N}}_{\mathrm{t}}\left({\mathrm{w}}_{\mathrm{i}}|0,{\mathrm{\alpha }}_{\mathrm{i}}^{-1}\right)$ is a truncated Gaussian function, and ${\mathrm{\alpha }}_{\mathrm{i}}$ is the inverse variance. The truncated prior can be formalized as follows.

$$\mathbf{p}\left({\mathrm{w}}_{\mathrm{i}}|{\mathrm{\alpha }}_{\mathrm{i}}\right)=\{\begin{array}{l}2N\left({\mathrm{w}}_{\mathrm{i}}|0,{\mathrm{\alpha }}_{\mathrm{i}}^{-1}\right)，if{\mathrm{y}}_{\mathrm{i}}{\mathrm{w}}_{\mathrm{i}}\ge 0\\ 0，if{\mathrm{y}}_{\mathrm{i}}{\mathrm{w}}_{\mathrm{i}}<0\end{array}$$ (21)

To estimate the parameters and latent variables in the model, an EM algorithm is introduced for MAP estimation. The expectation (E) step and the maximization (M) step are performed alternately by the EM algorithm iteratively. In this method, a series of functions is used to estimate $\mathrm{w}$, $\mathrm{b}$, and $\mathrm{\theta }$.

Since the PCVM algorithm only fits two-class classification tasks, the experiment treats classes 2–3 as negative classes and 1 as a positive class and tests the performance of the algorithm.

2.3. Feature selection

Although the dataset used contains dozens of features that may affect fractures, not all of these features are useful [40,41]. Specifically, the features used to predict fracture can be classified into related features and irrelevant features. Among them, the relevant features are helpful for the fracture prediction task and can improve the effect of the learning algorithm, while the irrelevant features are not helpful to our algorithm and will not improve the effect of the algorithm [42,43].

The purpose of feature selection is to find and distinguish relevant features from irrelevant features through a well-designed method, thereby reducing the overfitting phenomenon of the model and reducing the detection cost in practical applications [40]. This paper uses the correlation coefficient based on the feature and the fracture label to obtain the ranking of the feature's relevant degree. The procedure can refer to the hypothesis testing form of linear regression. First, the hypothesis (null hypothesis) that there is no linear relationship between whether there is a fracture and the input features is constructed. Then, the corresponding p -value need to be calculated after formulating the null hypothesis. If the null assumption is correct, the p -value represents the likelihood that the sample would show an observation or more extreme outcomes. If the p-value is small enough, we can reject the null hypothesis and think that there is a linear relationship between the input feature and whether there is a fracture.

The specific calculation is divided into two steps. First, the correlation coefficient is calculated:

$$\mathrm{c}\mathrm{o}\mathrm{r}=\frac{\frac{1}{\mathrm{N}}{\sum }_{\mathrm{i}=1}^{\mathrm{N}}\left(\mathrm{x}-\bar{\mathrm{x}}\right)\left(\mathrm{y}-\bar{\mathrm{y}}\right)}{\mathrm{s}\mathrm{t}\mathrm{d}\left(\mathrm{x}\right)\mathrm{s}\mathrm{t}\mathrm{d}\left(\mathrm{y}\right)}$$ (22)

where $\bar{\mathrm{x}}$ is the mean of feature x, std(x) is the standard deviation of feature x and y is the label. The correlation coefficient is then converted to an F score (different from the F1 score that evaluates classification performance) according to the following formulation:

$$\mathrm{F}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{e}=\frac{{\mathrm{c}\mathrm{o}\mathrm{r}}^2}{1-{\mathrm{c}\mathrm{o}\mathrm{r}}^2}*\mathrm{d}$$ (23)

where d is the degree of freedom of the dataset. Finally, the corresponding p value can be obtained by querying the F score-p value correspondence table of the chi-square distribution.

2.4. Computational complexity and overfitting problem

In real-world scenarios, the time-consuming, formally computational complexity of ML methods is an important factor to consider. In this paragraph, we first specifically discuss the computational complexity of the methods mentioned above to ensure that these methods are not too time-consuming.

The time complexity of training decision trees is primarily determined by the number of samples (N), the number of features (M), and the maximum depth of the decision tree (D). During the construction process, it is imperative to traverse all features to identify the optimal splitting point. Assuming the adoption of a simple sorting algorithm for identifying the best split, the time complexity amounts to O(N * log N). As a result, at each node, a time complexity of O (M * N * log N) is necessary to ascertain the best splitting point. In this context, the time complexity for constructing a decision tree is O (M * N * D * log N).

When computing the time complexity of GBDT, the complexity of training individual decision trees as well as the quantity of trees being trained must be considered. As previously discussed in the context of decision trees, the time complexity for constructing a single decision tree is O (M * N * D * log N). In GBDT, we are required to train T such decision trees. Consequently, the overall time complexity of GBDT amounts to O (T * M * N * D * log N).

The training complexity of logistic regression primarily depends on the number of samples (N), the number of features (M), and the efficiency of the optimization algorithm. Logistic regression typically employs gradient descent or its variants for parameter optimization. During each iteration of gradient descent, it is necessary to compute the gradient for all samples, resulting in a time complexity of O (N * M) per iteration. Gradient descent usually requires multiple iterations to converge; assuming the number of iterations is I, the overall training time complexity is O (I * N * M).

When computing the training complexity of RF, the complexity of training individual decision trees as well as the number of trees being trained must be considered. Similar to GBDT, the computational complexity of RF is O (T * M * N * D * log N).

The training computational complexity of SVM mainly depends on the number of samples (N), the number of features (M), and the efficiency of the optimization algorithm. The SVM typically employs Quadratic Programming (QP) or Sequential Minimal Optimization (SMO) algorithms to solve for optimal parameters. In this context, we discuss the complexity of training using the SMO algorithm, as it is a more common and efficient method. The training computational complexity of the SMO algorithm is related to the number of iterations (I) and the number of support vectors (K) involved in the training. Each iteration involves the optimization of a pair of support vectors, resulting in a time complexity of O(K) per iteration. Assuming the number of iterations is I, the overall training time complexity is O(I * K).

The XGBoost also achieves classification by training multiple decision trees. The computational complexity of the XGBoost can be roughly represented as O (T * M * N * D * log N).

The training computational complexity of the PCVM mainly depends on the number of samples (N), the number of features (M), and the efficiency of the optimization algorithm. The training process of the PCVM involves solving a set of linear equations, typically using Iteratively Reweighted Least Squares (IRLS) or other optimization methods. Assuming the number of iterations is I, and each iteration involves the computation of N samples, the training time complexity can be expressed as O(I * N * M).

It can be seen that the computational complexity of the above methods mostly increases linearly with the number of samples, features, iterations or trees. Therefore, these methods are theoretically not too time-consuming.

Another problem that may be encountered is the overfitting of the model to the data. Overfitting is a common phenomenon in ML and statistical modeling. Overfitting can occur when a model is too complex or overfits the training data. This means that this model performs well on the training data, however, performs poorly on new, unseen data. In other words, the model builds too strong a dependence on the noise and specificity of the training data, without capturing the general laws behind the data well.

Luckily, each of these ML methods employs its own strategy to address the issue of overfitting. Decision trees mitigate overfitting by limiting the tree depth, setting a minimum number of samples required for node splitting, and pruning branches, thus reducing the complexity of the tree. The GBDT enhances the model performance through the combination of multiple weak learners, such as shallow decision trees. Then GBDT controls the model complexity and, consequently, alleviates overfitting by adjusting parameters such as the subsampling and learning rate.

The LR tackles overfitting by introducing L1 and L2 regularization parameters to control the model complexity. Larger regularization parameters lead to sparser model parameters or values closer to zero, effectively reducing the model complexity.

The RF reduces model variance by constructing multiple decision trees and aggregating their predictions through a voting mechanism. Each tree in a RF is built on a randomly sampled subset of training data and features, which helps to mitigate overfitting. The SVM introduces a regularization parameter (C) to balance the model complexity and classification margin. Smaller C values result in larger classification margins, thereby reducing the model complexity and alleviating overfitting.

The XGBoost controls the model complexity and counteracts overfitting through regularization terms (L1 and L2 regularization) and other parameters, such as learning rate and subsampling. Like the GBDT, the XGBoost also employs the combination of multiple weak learners to improve the model performance. The PCVM manages the model complexity and mitigate overfitting by adjusting regularization parameters and selecting appropriate kernel functions and their parameters.

In short, the above methods all have a certain ability to resist overfitting.

2.5. Statistical analyses

In the study, for continuous variables, the descriptive statistics are provided as the median (interquartile range), and for categorical variables, they are expressed as the absolute number (n) and relative frequency (%).The normally distributed measured data are expressed as the mean ± standard deviation, otherwise expressed as median and quartile range. Statistical analyses were carried out by SPSS Statistics for Windows (Version 25, IBM Corp., NY, USA).

3. Results

3.1. The results of fracture prediction in different models

The results for predicting fracture in diabetes are shown in Table 3. As a basic linear classification model, the LR model achieves a value of 0.75 in the classification task, but it is too simple to fit the data. As more complex models, The DT and SVM achieve a higher F1-score. Ensemble models such as the GBDT, RF and XGBoost combine the results of multiple classifiers and achieve better performance. However, the PCVM performs best among all algorithms, because it combines the benefits of the support vector machine and the relevant vector machine, it provides a sparse Bayesian solution to classification issues. From the perspective of time cost, The GBDT takes much more time than the other methods. In addition, while the SVM and XGBoost take more time, this is not a critical disadvantage. From the perspective of memory cost, the storage space required by all methods is not much different. In general, the PCVM has the finest performance.

Table 3.

The results of predicting fracture in diabetes.

Model	Precision	Recall	F1-score	Time cost(s)	Memory cost (MiB)
DT	0.85	0.85	0.85	0.7	2.0
GBDT	0.86	0.89	0.87	85.1	4.6
LR	0.82	0.71	0.75	1.5	5.0
RF	0.84	0.85	0.84	1.3	4.1
SVM	0.80	0.85	0.83	6.1	3.2
XGBoost	0.86	0.90	0.88	5.1	6.8
PCVM	0.97	0.97	0.97	8.2	9.6

Abbreviations: DT, Decision Tree; GBDT, Gradient Boosting Decision Tree; LR, Logistic Regression; RF, Random Forest; SVM, Support Vector Machine; XGBoost, eXtreme Gradient Boosting; PCVM, Probabilistic Classification Vector Machines.

3.2. The results of feature selection

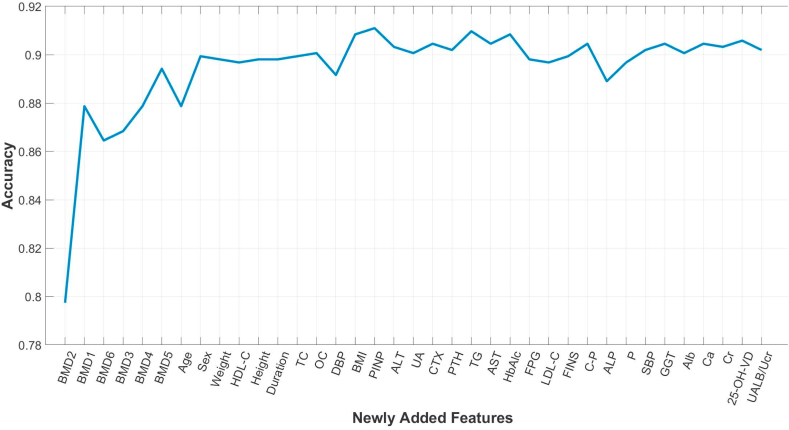
This section presents the features obtained by the feature selection method and the corresponding results. Specifically, according to the method in the feature selection section of the method, each specific feature was sorted by the obtained p-value [[44], [45], [46]]. Multiple experiments were then performed to verify the effect of the model when taking different sets of features as input. First, predictions were made using only the most relevant features (the BMD at the distal radius). Next, we selected the most relevant feature among the features that were not involved in the prediction, that is, the second most relevant feature among all the features, and added it to the features involved in the prediction (here, the BMD at the lumbar spines (L1–L4) was added). Similar operations were repeated, adding the most relevant features among the remaining features each time, until all features are included in the prediction. The XGBoost method was used when making predictions using the filtered features. The specific results are shown in Fig. 2. The abscissa represents the features added each time, and the ordinate represents the prediction accuracy. It can be seen that with the addition of features, the accuracy rate increases first and then stabilizes. This shows that features added earlier can improve the accuracy, while the performance of the algorithm is barely impacted by the later-added features. In particular, the prediction results of the most relevant 17 features as input reached the maximal accuracy including the BMD at the distal radius (BMD2), the BMD at the lumbar spines (L1–L4) (BMD1), the BMD at the total hip (BMD6), the BMD at the femoral neck (BMD3), the BMD at the Ward's triangle (BMD4), the BMD at the greater trochanter (BMD5), age, sex, weight, high-density lipoprotein cholesterol (HDL-C), height, duration of diabetes, total cholesterol (TC), osteocalcin (OC), diastolic blood pressure (DBP), body mass index (BMI), and N-terminal propeptide of type I (PINP).

Fig. 2.

The accuracy of prediction result based different selected set of features by XGBoost algorithm. Abbreviations: Duration, Duration of diabetes; BMI, Body Mass Index; FPG, Fasting plasma glucose; FINS, Fasting Insulin; HbA1c, Glycated hemoglobin A1c; C–P, c-peptide; Cr, Serum creatinine; UALB/Ucr, Urine albumin creatinine ratio; UA, Serum uric acid; Ca, Calcium; P, Phosphorus; OC, Osteocalcin; CTX, C-terminal telopeptide of type I collagen; PINP, N-terminal propeptide of type I procollagen; LDL-C, low-density lipoprotein cholesterol; HDL-C, High-density lipoprotein cholesterol; SBP, Systolic blood pressure; DBP, Diastolic blood pressure; ALP, Alkaline phosphatase; TG, Triglyceride; TC, Totalcholesterol; Alb, Albumin; ALT, Alanine aminotransferase; AST, Aspartate aminotransferase; GGT, γ-glutamyltransferase; 25-OH-VD, 25-hydroxyvitamin vitaminD; PTH, Parathyroid hormone; BMD1, Bone Mineral Density at the lumbar spines (L1-L4); BMD2, Bone Mineral Density at the distal radius; BMD3, Bone Mineral Density at the femoral neck; BMD4, Bone Mineral Density at the Ward's triangle; BMD5, Bone Mineral Density at the greater trochanter; BMD6, Bone Mineral Density at the total hip.

4. Discussion

Diabetes affects bone metabolism through multifaceted mechanisms such as a hyperglycemic state, oxidative stress, the accumulation of late glycosylation end products, chronic complications' effects on bone fragility, the application of glucose-lowering drugs, and an increased propensity to fall, all of which lead to an increased fracture risk. Fracture is the most harmful result of having both diabetes and osteoporosis, which places a significant financial strain on families and society while also significantly raising patient death and disability rates. Therefore, it is important to develop a tool or method to predict fracture in individuals with diabetes.

As the most widely used fracture prediction tool in the world, FRAX predicts the likelihood of hip fracture and major osteoporotic fracture in the following 10 years. Clinical guidelines in China, Europe, and the United States currently advise FRAX for the early identification and treatment of fractures. However, treatment thresholds vary between countries [47]. FRAX is also widely employed to predict the risk of fracture in diabetes, and a number of studies have suggested that FRAX may underestimate the risk of fracture in individuals with type 2 diabetes [48]. For example, a study by Giangregorio and colleagues has indicated that compared to the actual observed risk of major osteoporotic fractures and hip fractures, the FRAX score considerably underestimates the fracture risk in individuals with diabetes [49]. In addition to FRAX, the QFracture tool and Garvan FRC are used for the risk prediction of fractures. Nevertheless, these two assessment tools are only used in a few Western countries such as United Kingdom, Ireland, Australia, New Zealand, and Canada. The clinical data were obtained from Caucasians, and lack extensive population and regional validation [50].

Therefore, it is necessary to construct a convenient and accurate risk prediction model for the cost-effective screening and early detection of diabetes-related fractures in China. Today, AI techniques have shown powerful advantages in all aspects of medicine and health care and ML is the most widely used AI method. ML essentially means that the computer itself learns patterns in the data and makes predictions on future data based on the patterns obtained. Current studies have shown that ML methods can be used to predict osteoporosis, and ML algorithms for osteoporotic risk assessment have shown the advantages of high accuracy and simplicity [[51], [52], [53], [54], [55]]. However, most of these studies have focused on predicting osteoporosis in older adults and postmenopausal women, and few reports have emerged to demonstrate the risk factors for diabetes-related fractures in China using ML algorithms.

Seven ML algorithms were employed to predict the likelihood of fractures in individuals with diabetes in this study. Unlike traditional fracture prediction tools, these either contain fewer risk factors or are not yet validated in groups with diabetes. For example, diabetes is not listed as a risk factor in the Garvan FRC, which only covers five risk variables. Agarwal et al. showed that the Garvan FRC undervalues the likelihood of fracture in women with diabetes [56]. The QFracture tool's risk factors include diabetes, however the tool has not been tested explicitly in patients with diabetes. In this study, we applied ML algorithms directly to the Chinese diabetic population to predict fracture risk, and we included more risk factors than those in other tools. In a recent study, a hybrid deep learning model was preposed to predict risk of fracture in individuals with diabetic osteoporosis [57]. Compared with this study, we applied more types of ML algorithms and selected the most superior algorithms by comparing them.

Performance is greatly affected by feature selection, a crucial machine learning concept [44]. It is practical to identify individuals at high risk of fractures caused by diabetes and to pinpoint the clinical characteristics that are most closely associated with the higher risk for fractures through analysis and modeling in conjunction with the feature selection process. In this study, the 37 initial risk factors were reduced to 17 risk factors by ML algorithms. The proposed methods can be used as convenient tools that assist medical providers in makeing rapid and accurate predictions and assessments of diabetes-related fractures in the Chinese population.

In this study, 17 clinical factors that have been strongly linked to fractures in individuals with diabetes, and 6 of them were BMD indices. BMD is widely acknowledged as the key factor influencing bone strength. Our previous study suggested that glycemic status is a factor that affects BMD in patients with type 2 diabetes using a modified Bayesian networks algorithm [58]. Most studies indicate that patients with type 1 diabetes have reduced BMD compared to patients without diabetes, which is related to their enhanced bone resorption and decreased bone formation [59]. While the results of the association between type 2 diabetes and BMD are inconsistent in different findings. Although the BMD of these patients can be as expected, increased or decreased, the probability of fracture increased greater in patients with type 2 diabetes regardless of BMD [59,60]. Recent research by Wang et al. suggests that volumetric BMD measured with QCT may provide a more accurate assessment of osteoporosis and fracture risk than areal BMD measured with DXA in diabetes, providing a perspective that we can re-assess the link between BMD and type 2 diabetes [61].

In this study, PINP and OC were found to be closely related to patients with diabetes who are fractures. These two indicators are included in Bone turnover markers (BTMs). BTMs are recommended by several guidelines to assess bone metabolism and monitor the therapeutic effects of anti-osteoporosis drugs. However, there are clinical debates on whether BTMs can be routinely used for fracture risk assessment [62]. The prediction of diabetes-related fractures by BTMs is also highly controversial. Most studies have indicated significantly lower levels of BTMs in individuals with diabetes compared to those without diabetes, and the rate of bone formation is significantly decreased in diabetes [[63], [64], [65], [66]]. Nevertheless, previous study has reported no significant differences in bone formation markers between diabetes and non-diabetes [67]. The reports on bone resorption marker levels are also inconsistent. Some studies have shown similarly lower levels of bone resorption in the diabetic population than in the non-diabetic population, but others have shown that there is no difference, or even significantly higher levels in individuals with diabetes than non-diabetes [66]. Our finding using ML algorithms has added a new clue on the associations of PINP and OC with diabetes-related fracture.

In this study, age and sex were found to be risk factors for fracture in patients with diabetes, which meet the accepted notion that they are the most important determinants for fracture. Moreover, it is rational that height, weight and BMI were found to be related risk factors for fracture, since reduced mechanical load on the bones of thin patients is detrimental to bone formation, making them more susceptible to fracture [68]. A correlation between elevated DBP and fractures was also found in this study. No correlation between DBP and fracture has been reported yet, and the results from ML algorithms may provide a new direction for its exploration.

Our study indicated a long duration of diabetes was found to be a risk factor for fractures in individuals with diabetes. Numerous consequences, including renal toxicity, vasculopathy, and vitamin D insufficiency, can arise from long-term diabetes, which may interfere with calcium reabsorption by renal tubules and cause a significant loss of trace elements through urine, subsequently resulting in increased bone resorption and increased bone fragility [69]. Furthermore, TC and HDL levels were found to be positively correlated with the incidence of fracture, which may be explained by their effects on the differentiation and formation of osteoclasts [70].

The study has several advantages over traditional fracture prediction tools. First, these ML algorithms are easy to implement and have good community support. Second, unlike other prediction tools, the ML methods proposed in this study include clinical indicators associated with diabetes, which makes the risk prediction of diabetic-related fracture more reasonable. Finally, the study used the feature selection approach to identify factors that have a significant influence on risk of fracture in individuals with diabetes from dozens of possible risk factors, which helps primary health care providers predict fracture risk in diabetic populations more quickly and accurately. However, there are some limitations in this study. First, there is no certainty that the study's findings are representative because it relied on a cross-sectional survey, which only caught a population at one point in time. Second, this single-center study was based on the clinical medical record data from one hospital, which has not been verified by an external database, and the sample size collected is small, so multi-center research must be conducted to expand and confirm the model's effectiveness. Third, some medical history data were not included, such as presence of menopause, drinking history, smoking history, and fall history, which should be included in future studies to build a more accurate prediction model.

In conclusion, this work proposes a cheap, safe, and extensible AI strategy for the precise assessment of risk factors for diabetes-related fractures. Among the ML algorithms used in this study, PCVM was found to be the most effective in predicting the fracture risk in the diabetic population.

Ethics statement

The use of clinical data obtained ethical approval from the Ethics Committee of the First Affiliated Hospital of USTC (Approved No. 2020-KY-38).

Author contribution statement

Sijia Chu and Aijun Jiang: Performed the experiments; analyzed and interpreted the data; contributed reagents, materials, analysis tools or data; wrote the paper.

Lyuzhou Chen: Performed the experiments; analyzed and interpreted the data; wrote the paper.

Xi Zhang, Xiurong Shen, Wan Zhou, Shilu Zhang, Li Zhang and Yang Chen: Contributed reagents, materials, analysis tools or data.

Shandong Ye and Chao Chen: Conceived and designed the experiments.

Ya Miao: Performed the experiments; wrote the paper.

Wei Wang: Conceived and designed the experiments; analyzed and interpreted the data; contributed reagents, materials, analysis tools or data; wrote the paper.

Funding statement

This work was funded by National Natural Science Foundation of China (32271176, 81971264, 81100558 and 81800713) and Integrated Technology Application Research in Public Welfare of Anhui Province (grant number 1704f0804012).

Data availability statement

Data included in article/supp. material/referenced in article.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.