Raman spectral pattern recognition of breast cancer: A machine learning strategy based on feature fusion and adaptive hyperparameter optimization

Abstract

Raman spectroscopy, as a kind of molecular vibration spectroscopy, provides abundant information for measuring components and molecular structure in the early detection and diagnosis of breast cancer. Currently, portable Raman spectrometers have simplified and made equipment application more affordable, albeit at the cost of sacrificing the signal-to-noise ratio (SNR). Consequently, this necessitates a higher recognition rate from pattern recognition algorithms. Our study employs a feature fusion strategy to reduce the dimensionality of high-dimensional Raman spectra and enhance the discriminative information between normal tissues and tumors. In the conducted random experiment, the classifier achieved a performance of over 96% for all three average metrics: accuracy, sensitivity, and specificity. Additionally, we propose a multi-parameter serial encoding evolutionary algorithm (MSEA) and integrate it into the Adaptive Local Hyperplane K-nearest Neighbor classification algorithm (ALHK) for adaptive hyperparameter optimization. The implementation of serial encoding tackles the predicament of parallel optimization in multi-hyperparameter vector problems. To bolster the convergence of the optimization algorithm towards a global optimal solution, an exponential viability function is devised for nonlinear processing. Moreover, an improved elitist strategy is employed for individual selection, effectively eliminating the influence of probability factors on the robustness of the optimization algorithm. This study further optimizes the hyperparameter space through sensitivity analysis of hyperparameters and cross-validation experiments, leading to superior performance compared to the ALHK algorithm with manual hyperparameter configuration.

Graphical abstract

Highlights

• •MSEA-ALHK model is proposed for adaptive hyperparameter optimization.
• •Feature fusion enhances the difference of Raman spectra between different types of breast tissue from the perspective of mid-level data fusion.
• •Embedding the feature selection method into the feature fusion process helps to interpret the biochemical differences of breast tissue characteristic peaks.

1. Introduction

Breast cancer, being a prevalent malignant tumor, poses a serious threat to women's physical and mental health. According to statistics, the number of new cases of breast cancer in 2020 reached 2.26 million [1], and the global incidence of breast cancer increased at an annual rate of 3.1% [2]. Therefore, breast cancer holds a significant position in modern cancer diagnosis research. Traditional breast cancer diagnosis methods are generally carried out by imaging and physical examination and suspected breast cancer patients need puncture or excision biopsy [3]. However, 70%∼90% of patients had benign biopsy results, resulting in many patients bearing unnecessary physical, psychological, and economic pressure. In addition, pathological diagnosis took a long time, increasing the possibility of tumor metastasis. Raman spectroscopy can provide molecular composition and structure of biological tissue samples, which has the potential for the early detection of breast cancer. It is not easy to be interfered with by water, so it is suitable for human cancer diagnosis [4]. Currently, several diagnostic techniques, including Fourier transform Raman spectroscopy (FTRS), confocal Raman microspectroscopy (CRS), and surface-enhanced Raman spectroscopy (SERS), have been extensively studied to obtain high-quality spectral data. However, these methods are limited by the bulky size of the equipment, necessitating either a large Raman spectrometer or a large desktop microscope, which in turn results in high costs [[5], [6], [7]]. On the other hand, the utilization of a miniature Raman spectrometer equipped with an optical fiber probe enables real-time, low-cost, in vivo, and in-situ clinical diagnosis. This paper adopts a portable Raman spectrometer equipped with an optical fiber probe to facilitate rapid and cost-effective on-site breast cancer detection. The simplification of equipment will bring low SNR [8], so it is essential to realize higher precision pattern recognition algorithms in the application of high detection accuracy requirements such as breast tumor diagnosis.

Machine learning (ML) and deep learning algorithms are dedicated to solving complex pattern recognition tasks, making them a natural focus of attention within the field of analytical chemistry [9]. However, research on the application of these algorithms in the spectral analysis is still in its early stages, and several issues, including data fusion methods, model interpretability, and the optimal selection of hyperparameters, warrant further investigation.

1.1. Data fusion

Data fusion is the process of integrating multiple data sources to generate information that is more consistent, accurate, and valuable compared to any individual data source [10]. It is commonly classified into three levels: low-level, mid-level, and high-level, depending on the stage of processing where the fusion occurs [11]. The resulting fused data is expected to be more informative and comprehensive than the original input.

• (i)Low-level data fusion (LLDF) combines multiple raw data sources to produce new raw data.
• (ii)Mid-level data fusion (MLDF) (also referred to as “feature-level” fusion) is based on preliminary feature extraction, which retains relevant variables while eliminating variables that lack sufficient diversity and information from the dataset.
• (iii)High-level data fusion (HLDF) (also known as “decision-level” fusion) operates at the decision level. This entails fitting a supervised model to each data matrix as the first step [12].

Currently, in the field of spectroscopy, data fusion primarily occurs at the LLDF, leveraging complementary information sources across different types of spectra to enhance the model's output effectiveness. Examples include the fusion of FTIR spectroscopy and Raman spectroscopy [13], and the fusion of Raman spectroscopy and infrared spectroscopy [14], among others.

1.2. Characteristics and their interpretability

Raman spectral datasets are characterized by high dimensionality and typically exhibit a limited sample size. It is well known that standard classification models tend to yield poor performance on high-dimensional datasets [13] due to the curse of dimensionality. The combination of feature extraction and predictors has led to substantial performance improvements in biochemical fields, including gene sequence recognition [15]. This combination enables input space compression and reduces the complexity of processing classification models. Furthermore, research conducted by scholars has demonstrated that suitable feature selection methods can reliably identify the most discriminative dimensions, thereby enhancing the accuracy and stability of classification results [16]. Moreover, feature selection can provide a comprehensive explanation for the selection of a specific Raman shift based on the fingerprint information of corresponding biochemical substances in its specific dimension. For instance, the distinction between normal tissue and tumor tissue can be explained by the presence of characteristic peaks.

1.3. Adaptive hyperparameter optimization

Hyperparameters are predefined parameters that are distinct from the data-derived parameters obtained during training [17]. Generally, optimizing the hyperparameters of the pattern recognition algorithm is necessary to enhance its performance and effectiveness. When dealing with complex models, like deep learning networks or big data analysis in computational biology, it becomes essential to combine parallel and distributed computing models for accelerating deep neural networks [18]. Consequently, evaluating hyperparameters becomes more computationally expensive, and obtaining the gradient of the loss function to the hyperparameter is usually infeasible. Additionally, classical optimization methods often cannot rely on other properties of the objective function, such as convexity and smoothness [19]. In contrast, deep learning models heavily depend on the user's experience in hyperparameter optimization [20,21]. Conversely, machine learning models train and execute relatively quickly with only a few hyperparameters. This characteristic facilitates rapid adoption and application by medical researchers. Traditionally, hyperparameters have been manually set in a traditional manner, which is inefficient and fails to guarantee global optimization of the model [22]. The optimal hyperparameters are contingent upon the dataset. Consequently, it is imperative to discover an appropriate hyperparameter optimization method for pattern recognition. The Adaptive Local Hyperplane K-nearest Neighbor classification algorithm (ALHK) algorithm is a highly accurate pattern recognition algorithm that outperforms seven commonly used algorithms in pattern recognition, namely K-NN, LDA, SVM, NFL, HKNN, NNL, and CNN [23]. However, three hyperparameters of this algorithm are manually specified.

In light of the aforementioned issues, we propose a feature fusion method that utilizes feature extraction and selection. This method aims to reduce the dimensionality of spectral data while maintaining the biochemical interpretability of specific bands. Additionally, this paper presents an evolutionary algorithm (EA) based hyperparameter optimization method, namely the MSEA-ALHK model, for breast tumor pattern recognition. The MSEA algorithm is integrated into the ALHK algorithm to facilitate an automatic search for optimal hyperparameters and achieve optimal classification performance. The model primarily addresses three key problems. Firstly, the general pattern recognition algorithm fails to achieve global optimization through manual parameter configuration [24]. Secondly, the MSEA-optimized ALHK algorithm demonstrates higher recognition accuracy compared to the manual algorithm. Lastly, traditional evolutionary algorithms are susceptible to converging on local optimal solutions. Hence, this paper enhances the EA through three key aspects: multi-parameter serial coding, survival function, and individual selection, aiming to achieve global convergence.

Our work highlights the significance of Raman spectral analysis in the early diagnosis of breast cancer and addresses challenges related to pattern recognition accuracy. The study focuses on feature-level data fusion and explores different methods to improve classifier performance. Additionally, the proposed MSEA-ALHK model offers automatic and global optimization to address issues of time consumption and low accuracy in manual parameter adjustment. The findings of this study have broader implications for the recognition of spectral data in various contexts and can serve as a reference for cancer detection and biomedical diagnosis.

2. Materials and methods

2.1. Experimental instruments

The experiment utilized the QE65000 miniature Raman spectrometer (manufactured by Ocean Optics, USA), a 785 nm Raman laser, and the RIP-RPS-785 fiber probe(see Fig. 1). The QE65000 spectrometer boasts a quantum efficiency of 90%. Its two-dimensional pixel array consists of 1044 × 64 pixels, enabling the detection of optical signals within the wavelength range of 200–1000 nm. The scanning range of the spectrometer is from 0 to 2723 cm⁻¹, with a scanning interval of 12 cm⁻¹ [25].

Fig. 1.

Raman measurement system.

2.2. Samples

Breast tissue samples were collected from 16 patients at Peking University Third Hospital, including 4 healthy volunteers and 12 cancer patients. The average age of the participants was 56 years, with a range from 33 to 88 years old. The obtained samples were stored in liquid nitrogen and subsequently sent to the refrigeration department for HE staining diagnosis, which served as the reference standards for spectral analysis. The experimental procedures were approved by the Medical Ethics Committee of Peking University Third Hospital and the patients' consent was obtained.

Raman spectra of normal and tumor tissues were acquired using the QE65000 spectrometer with a 785 nm excitation wavelength. The samples, without any chemical treatment, were frozen in liquid nitrogen and then brought back to room temperature before being placed on a glass substrate for measurement. The sample thickness was approximately 2 cm. A laser power of 30 mW was employed for data acquisition. The probe had a penetration depth at the micron level. The spectrometer's integral time was set to 30 s, and the resulting spectra covered a wave number range of 700–1800 cm⁻¹. Three spectra were collected at each site, and the average spectrum of these three was considered representative of that site. The same measurement procedure was repeated on the following day under identical conditions. Over two days, a total of 125 Raman spectra were collected from 4 normal breast tissues and 12 tumor tissues. On the first day, 67 Raman spectra were obtained (16 normal and 51 neoplastic), while on the second day, 58 Raman spectra were obtained (18 normal and 40 neoplastic). Normal and tumor tissues were treated as dichotomies without considering further histological grading of tumor tissues.

2.3. Spectra preprocessing

Raman spectrum belongs to weak signals, and various interference signals (such as fluorescent background noise and stray light [26], etc.) will be mixed in the acquisition process, which will have adverse effects on data analysis and the establishment of the model [27]. In this paper, high-frequency noise, baseline drift, and fluorescence background interference were corrected by applying Savitzky-Golay (SG) smoothing, Standard Normal Variate (SNV), and adaptive iteratively reweighted penalized least squares (airPLS) algorithm in the spectra [28,29]. Subsequent analyses were performed within the 700-1800 cm⁻¹ band, which corresponds to the characteristic region of the breast Raman spectra

The preprocessing outcomes are depicted in Fig. 2.

Fig. 2.

Schematic diagram of breast tissue before and after spectral preprocessing (A): Typical original spectrum and preprocessed spectrum with Savitzky-Golay smoothing; (B): Preprocessed spectrum with SNV and preprocessed spectrum with airPLS.

The preprocessing was performed in the order of SG, SNV, and airPLS, and the output data of each algorithm was the input of the subsequent algorithm. Fig. 2 shows that SG smoothing can effectively filter out the high-frequency noise of the spectral signal. The SNV plays the role of removing constant baseline effects and scaling differences from spectra [30], while the intensity axis is also scaled down to near zero in this process. The airPLS performs nonlinear correction on the fluorescent background and corrects the intensity above “0”. After deducting the nonlinear low-frequency baseline background, the Raman spectrum peak difference becomes more obvious after comprehensive correction.

2.4. Optimization and partitioning of data sets

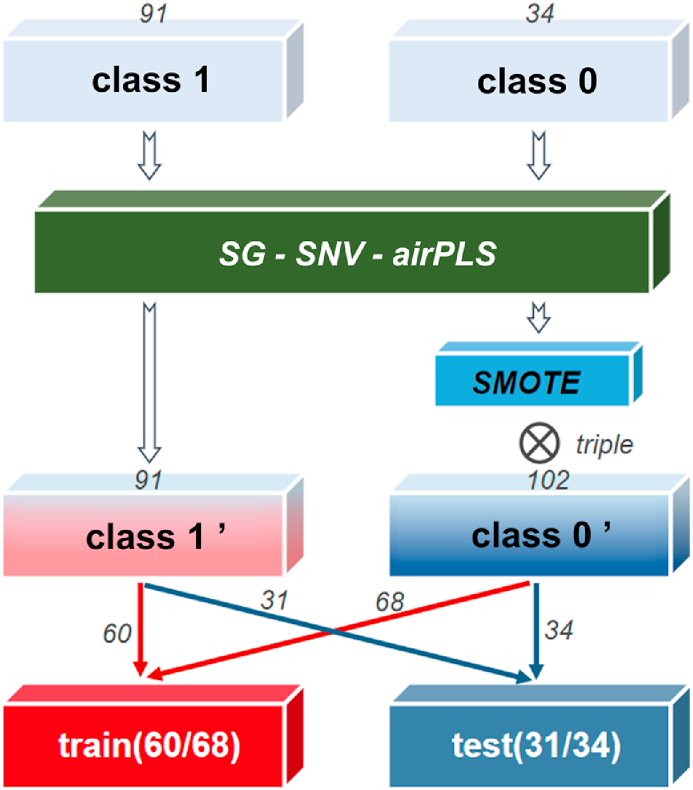
In the classification problem with labels, the difference of sample numbers in different categories affects the training of the model [31], which is reflected in the high accuracy of the test in the large category.

In this paper, considering the small amount of spectral data and the imbalance of the number of different types of data, the Synthetic Minority Oversampling Technique (SMOTE) algorithm was selected for the amplification of tumor tissue spectra (class 1). Based on the K-nearest neighbor information between samples, SMOTE generates new samples which can be represented by equation (1):

$${\mathsf{x}}_{new}=x_i+\lambda \left(x_{zi}-x_i\right)$$ (1)

where x_new is the generated new sample, x_i is the parent sample, x_zi is a single sample point in the K nearest neighbor of x_i, and λ is a random number between 0 and 1. Set the SMOTE percentage parameter according to the number of target samples in the training set and test set. Follow two principles:

• (Ⅰ). The size of train set and test set accounted for 2/3 and 1/3 of the total samples, respectively;

• (Ⅱ). The number of normal tissue spectra (class 0) and tumor tissue spectra (class 1) in each collection was basically the same.

The optimized data set flow constructed accordingly is shown in Fig. 3.

Fig. 3.

Optimization and partitioning of data sets.

In Section 2.2, 91 class 1 spectra and 34 class 0 spectra were collected by experimental instruments. After spectra preprocessing, SMOTE was designed to extend the number of class 0 spectra to 3 times, and we assign the number of the two kinds of spectra in the train set and test set by using the combination proportion principle above. The partition results in 128 data in the train set (60 neoplastic and 68 normal) and 65 data in the test set (31 neoplastic and 34 normal).

2.5. Feature fusion

Feature fusion, as an MLDF method, fuses data at the feature level. For Raman spectroscopy, we divided the process into two sub-processes: feature extraction and feature selection, and the obtained spectral feature information is fused to obtain better classification results.

2.5.1. Feature extraction

For high-dimensional data such as Raman spectra, an effective method of feature extraction is crucial in achieving dimension reduction through compression while preserving critical information. One classical technique for feature extraction is Principal Component Analysis (PCA) [32]. PCA utilizes a singular value decomposition process to decompose a limited number of independent variables into factors or principal components (PCs). These factors, referred to as Scores, contribute significantly to the original data. By employing a linear transformation that effectively captures the original data's characteristics, PCA selects a reduced number of important variables from a larger set, thereby achieving the objective of dimension reduction. The resulting PCs obtained from PCA are orthogonal to one another, providing a quantitative measure of each PC's contribution to the original data. Consequently, applying PCA to process Raman spectral data offers the advantage of eliminating background and noise interference while circumventing collinearity in spectral responses.

2.5.2. Feature selection

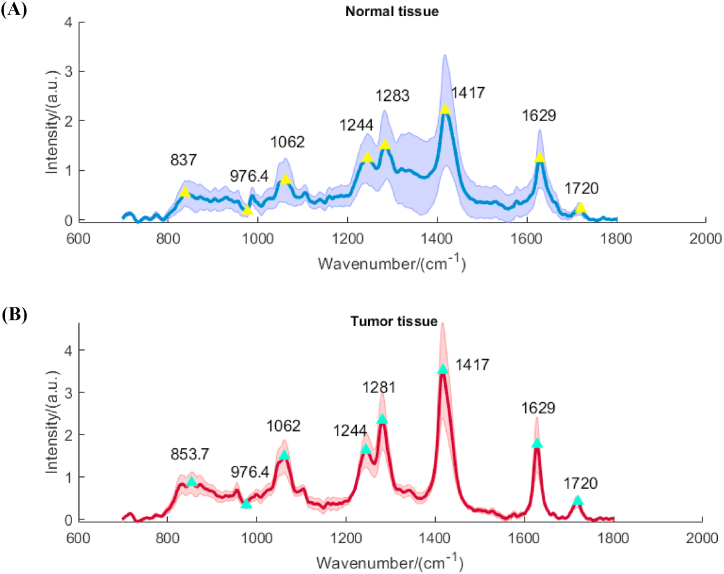
Feature selection involves the identification and selection of representative subsets from the original data while maintaining the integrity of the feature space. By preserving the spectral peak band information in the spectral analysis [33], feature selection enables dimension reduction while retaining meaningful biochemical interpretability in the realm of biological spectra. Fig. 4 illustrates the average Raman spectra of normal tissue (blue) and tumor tissue (red), with the shaded region indicating the extent of dispersion among similar data points. Through observation, eight significant points were selected as initial feature points, which were further refined using the ReliefF algorithm.

Fig. 4.

Average Raman spectra and feature points.(A):Normal tissue; (B):Tumor tissue.

The forms of feature selection include Filter Wrapper and Embedded. To reduce the coupling between algorithms and reduce the complexity of the algorithm, the ReliefF algorithm in the Filter method is used in this paper to calculate the weight of each feature, so as to intuitively select the features with large weight.

The execution process of the ReliefF algorithm is as follows:

• ①Sample i is randomly selected from N samples to search K nearest neighbor H of samples of the same class as I and K nearest neighbor M(C) of samples of different classes;

• ②Initialization weight W = 0;
• ③The weight of the r th feature, denoted as F_r, is updated using Formula (2).

$${\mathsf{W}}_r=W_r-\frac{f\left(F_r,S_i,H\right)}{n}+\sum _{C\ne C_R}\frac{f\left(F_r,S_i,M\left(C\right)\right)}{n}$$ (2)

in the formula, f(Fr, S_i, ζ) represents the geometric distance between sample I and ζ in the Fr dimension;

• ④Iteration repeats the previous step;
• ⑤Take the average of the weight W.

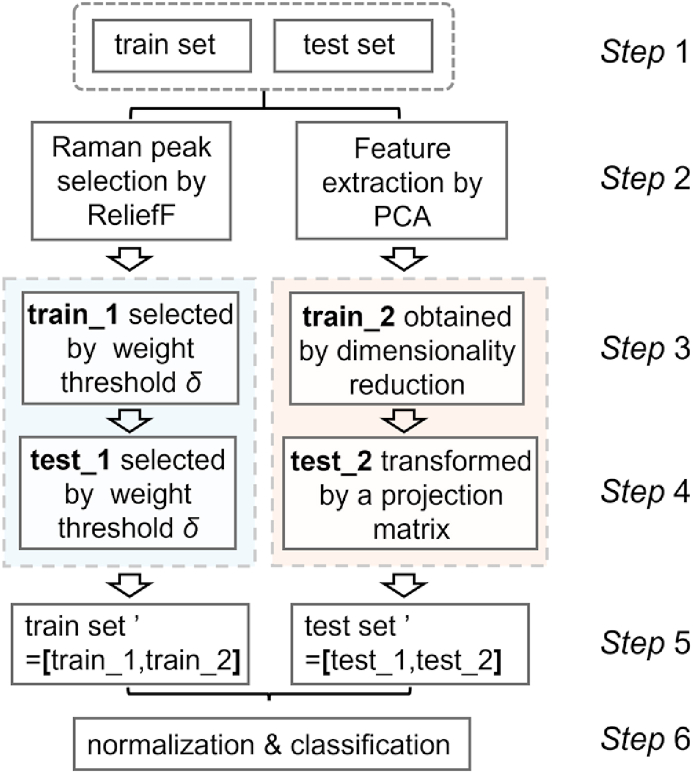
Upon acquiring the datasets outlined in Section 2.4, a parallel strategy was employed to divide the train set and test set into two branches. These branches underwent separate processing utilizing PCA and ReliefF methods. The left branch, depicted in Fig. 5, produced the train sets (train_1 and test_1) via ReliefF, following threshold screening of the feature matrix. Conversely, the right branch derived the training set (train_2) by subjecting the input train set to PCA processing. The resultant projection matrix from this process was applied to the input test set, generating test_2 and thus achieving feature space unification. Ultimately, the feature matrices obtained from both branches were combined, taking into account corresponding dimensions, to yield a novel feature fusion matrix (train set’ and test set').

Fig. 5.

Flow chart of feature fusion.

2.6. Classification and hyperparameter optimization approach

The datasets formed from features obtained from PCA and ReliefF are used to train a classification algorithm. In the following, we use Adaptive K-Local Hyperplane as the classifier and embed a multi-parameter serial encoding evolutionary algorithm into the classifier to realize hyperparameter adaptive optimization.

2.6.1. Adaptive Local Hyperplane K-nearest neighbor classification algorithm (ALHK)

ALHK is an improved method of the HKNN algorithm, which introduces feature weight to solve poor performance for large K-values [34].

From the principle of k-nearest neighbor selection, ALHK is another form of ALH algorithm: ALH selects the nearest neighbor of K prediction set samples from the whole training set samples while ALHK does it from various training set samples. Table 1 shows the algorithm flow of ALHK:

Table 1.

The algorithm flow of ALHK.

Inputs: Training set Ω1 = {(x,y)|x∈ℝn1×p,y∈ℝn1}; Test set Ω2 = {x|x∈ℝn2×p}; Hyperparameters Γ = {K, T, λ}
Step1: Calculate the feature weights of the training set samples;
Step2: Calculate the weighted Euclidean distance of test set samples and training set samples;
Step3: Search K-nearest neighbor training samples and construct hyperplane;
Step4: Calculate the minimum D (distance) from the test set sample to the hyperplane, and complete classification according to D.
Outputs: Classification result label: y’∈ℝn2

ALHK has three hyperparameters.

K: The number of nearest points, the value is 1–20 integer.

T: Used to control the influence of R_j on W_j, generally ranging from 1 to 20;

λ: Used to control the parameter whose value may be too large, generally ranging from 1 to 20.

The setting of these three parameters will affect the final accuracy of pattern recognition.

2.6.2. Multi-parameter serial encoding evolutionary algorithm (MSEA)

Evolutionary algorithm (EA) simulates the mechanism of biological evolution by using mechanisms, candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions. Evolution of the population then takes place after the repeated application of the above operators. EA has been widely used to solve complex problems, such as particle swarm optimization (PSO), and differential evolution algorithm (DE) [35].

Based on EA, MSEA proposed in this paper improves its global optimization ability from the following three aspects to realize synchronous optimization of multiple hyperparameters.

2.6.2.1. Multi-parameter serial encoding

In EA, the process of generating new individuals involves the use of crossover. Crossover facilitates the exchange and fusion of information between two parent nodes by randomly selecting breakpoints [36]. Since the hyperparameters targeted for optimization are typically real numbers, it is crucial to encode them in a manner that enables crossover within a spatial structure.

Binary code provides a convenient means of encoding and decoding, presenting a linear spatial arrangement. In this study, the parameter space is formed by the range of hyperparameter values as Θ, and each hyperparameter's initial value is represented by a binary random sequence α consisting of a specified number of bits ν. The sequence is subsequently converted into a decimal integer θ′, which enables the retrieval of the current pre-selected value of the hyperparameter θ using Interval Mapping, as illustrated in Formula (3).

$$\mathrm{\Theta }=\left\{\theta :{\theta }_1\le \theta \le {\theta }_2\right\},\theta ={\theta }_1+\left({\theta }_2-{\theta }_1\right)\cdot \theta \text{'}/\left(2^{\nu }-1\right)$$ (3)

After defining the basic encoding rules, the process of decoding the binary sequence α into its corresponding hyperparameters is facilitated by the function Decode (.) for the sake of convenience. Equations (4), (5) describe the individual decoded representations of the three parameters K, T, and λ, as well as their joint representation.

$$K=\text{Decode}\left({\alpha }_1|{\mathrm{\Theta }}_1\right),T=\text{Decode}\left({\alpha }_2\left|{\mathrm{\Theta }}_2),\lambda =\text{Decode}({\alpha }_3\right|{\mathrm{\Theta }}_3\right)$$ (4)

$$\mathrm{\Gamma }=\left(K,T,\lambda \right)=\text{Decode}\left({\alpha }_1,{\alpha }_2,{\alpha }_3|{\mathrm{\Theta }}_1,{\mathrm{\Theta }}_2,{\mathrm{\Theta }}_3\right)$$ (5)

For optimization problems with multiple hyperparameters, binary hyperparameters can be considered to form an individual in series, to realize parallel optimization in the crossover process. Two arbitrary samples from the initial individual data set can be denoted as A and B, as illustrated in Equation (6):

$$A=\left({\alpha }_1,{\alpha }_2,{\alpha }_3\right),B=\left({\beta }_1,{\beta }_2,{\beta }_3\right)$$ (6)

The iterative update of an individual can be performed by constructing the permutation operator T_Δ, which is computed as shown in Equation (7):

$$\begin{array}{l}\mathsf{A}=\left[\begin{array}{cc}{A}_1& A_2\end{array}\right]\\ B=\left[\begin{array}{cc}{B}_1& B_2\end{array}\right]\end{array},{\mathsf{T}}_{\Delta }\left(A,B\right)=\left(\left[\begin{array}{cc}{A}_1& B_2\\ B_1& A_2\end{array}\right]\right)$$ (7)

2.6.2.2. Anti-logarithm transformation

According to the hyperparameter Γ of each individual, its objective function value can be calculated and denoted as Viability. The model can be expressed as follows:

$$\begin{array}{l}\mathsf{\Gamma }\mathsf{=}\left(K,T,\lambda \right)\\ \max Viability=F\left(\mathrm{\Gamma }\right)\\ \mathrm{s}.\mathrm{t}.K\in {\mathrm{\Theta }}_1,T\in {\mathrm{\Theta }}_2,\lambda \in {\mathrm{\Theta }}_3\end{array}$$ (8)

in equation (8), a larger F(Γ) means a higher probability of being inherited to the optimal group in the next iteration [37], which presents a better individual.

In terms of the selection of the objective function in the optimization of the model hyperparameter optimization, if “precision” is used as the objective function, there will be the potential risk of optimization morbidity caused by the huge difference in the number of samples (That is, the high accuracy of a large number of models is pursued at the expense of another type of accuracy, but the results still appear to perform better. For example, assuming that only 1% of a binary prediction task is 1, then the model that predicts all values is 0 will reach an almost perfect accuracy). Therefore, in Section 2.4, SMOTE has made the class 1/0 number 91:102, thus resolving the imbalance.

When there are multiple local maxima and the differences between them are small, the optimal solution will be easily ignored in the process of selecting individuals. Therefore, it is necessary to adjust the form of Viability. The conventional EA takes F(Γ) as the optimal solution. In this paper, F(Γ) is subjected to a non-linear Anti-logarithm transformation in order to enhance the differentiation among values in proximity to 1, as demonstrated in equation (9).

$$x=\ln y^{1/\tau },y=\mathrm{G}\left[x\right]$$ (9)

where τ is the adjustable multiplier factor (τ = 7.0). Then, equation (10) describes the form of Viability:

$$Viability=\mathrm{G}\left[F\left(\mathrm{\Gamma }\right)\right]$$ (10)

To quantify the selection probability manifested by the viability function, we introduce the concept of relative viability, for which the calculation formula is presented as equation (11):

$$\text{Relative}\text{viability}=F\left({\mathrm{\Gamma }}_i)/\sum _{j=1}^{n}F({\mathrm{\Gamma }}_j\right)$$ (11)

By comparison in Table 2, the relative viability can be increased from 50.55% to 53.49% in this case, achieving the purpose of improving the probability of “choosing the best among the best".

Table 2.

Comparison of viability function before and after improvement.

Viability function	Viability		Relative viability
F(Γ)	0.90	0.92	49.45%	50.55%
G [F(Γ)]	544.57	626.41	46.51%	53.49%

2.6.2.3. Elitism

After the viability of all individuals is calculated, the traditional EA adopts the roulette algorithm for selection [38]. However, since roulette itself selects individuals based on probability, it cannot guarantee that the current optimal individual will be selected inevitably, so there is a risk of losing the optimal solution. To ensure the preservation of elite individuals in each generation of the population [39], the principle of elitism was adopted in this paper, we retain the duplicated part of elite individuals and eliminate the inferior individuals in equal numbers. After the elimination of inferior individuals, the remaining population carried out the crossover process for renewal. The process of population renewal among the elite can be depicted through Fig. 6.

Fig. 6.

Schematic diagram of elitist population renewal.

The MSEA-ALHK model is obtained by combining MSEA with ALHK to accomplish pattern recognition. As evident from Fig. 7, the ALHK hyperparameters are optimized and solved using MSEA through population iteration, with fitness serving as the transfer parameter.

Fig. 7.

Algorithm flow chart of MSEA-ALHK optimization model.

2.7. Statistics

The recognition of breast tumors was a binary classification problem. Therefore, the following three performance metrics were used for a comprehensive evaluation in this paper. The meaning of statistics used to construct indicators was shown in the confusion matrix(see Table 3). The influence of spectral feature fusion on classification accuracy and the impact of MESA-ALHK on the adaptability of hyperparameter optimization were evaluated based on these three indexes.

Table 3.

Confound matrix member list.

	Predicted: YES	Predicted: NO
Actual: YES	TP (True Positives)	FN (False Negatives)
Actual: NO	FP (False Positives)	TN (True Negatives)

2.7.1. Accuracy

Accuracy is a measure of the proportion of correctly classified samples within the entire dataset. It can be calculated by dividing the number of correctly classified instances in the test set by the total number of instances in the test set. The formula for accuracy, as depicted in equation (12), is given by:

$$Accuracy=\frac{TP+TN}{TP+FP+TN+FN}$$ (12)

2.7.2. Sensitivity

Sensitivity is used to evaluate the recognition performance of positive samples by the classifier, and the calculation formula is as follows:

Sensitivity is used to evaluate the classifier's recognition performance with respect to positive samples. The formula for sensitivity, presented in equation (13), is as follows:

$$TPR=\frac{TP}{TP+FN}$$ (13)

2.7.3. Specificity

Specificity serves as an indicator of the classifier's capability to correctly identify negative samples. The formula for specificity, as depicted in equation (14), is presented below:

$$TNR=\frac{TN}{FP+TN}$$ (14)

3. Results and discussion

3.1. Classification performance

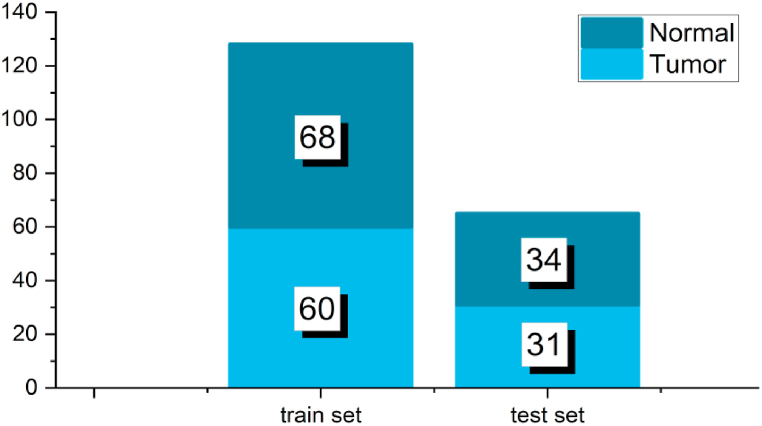
The assessment of classification performance encompasses two main aspects. The initial aspect involves comparing the classification metrics of various feature fusion methods. Specifically, after optimizing the hyperparameters, the highest achievable accuracy is determined for each fusion method for subsequent comparison. To ensure the reliability of the experimental findings, this study incorporates 10 sets of parallel experiments for each fusion method. The training and test sets are obtained through random sampling, and the distribution of data categories in the collection is depicted in Fig. 8. The second aspect involves establishing credible correspondences between biomarkers and the classification outcomes derived from feature fusion. This approach enhances the biochemical interpretability of the data in contrast to mathematical techniques such as projection transformation.

Fig. 8.

The composition ratio of the data set.

3.1.1. Spectral feature extraction and feature selection

During the feature fusion process, we established a threshold of 95% for the cumulative contribution of principal components using PCA. Subsequently, we extracted 20 principal components as the spectral features following dimension reduction. Simultaneously, ReliefF was employed to compute the weights of 8 features as depicted in Fig. 4. Subsequently, using a rigid threshold (δ = 0.020), we further screened 3 features (serial numbers 3, 5, and 6) that exhibited significant differences between spectral classes based on the obtained weights from Fig. 9.

Fig. 9.

ReliefF algorithm: calculate the weights of 8 features.

After conducting feature extraction and feature selection, it becomes crucial to assess the efficacy of feature fusion by comparing the impact of various data formats on pattern recognition accuracy. To facilitate this evaluation, we define the form set M as follows:

$$\mathsf{def}.M=\left\{X_O,X_E,X_S,X_F\right\}$$ (15)

Xo -- Original Raman spectra; XE -- Data after feature extraction; XS -- Data after feature selection; XF -- Data after feature fusion.

Utilizing the definition (15), every subset within M underwent 10 sets of classification experiments, with the corresponding matrix expression presented in equation (16).

To obtain the spectra for each set, the complete dataset was subjected to Monte Carlo sampling, following the procedure outlined in Fig. 8.

$$\left(\begin{array}{l}{\mathsf{X}}_O\\ X_E\\ X_S\\ X_F\end{array}\right)=\left(\begin{array}{cccc}{X}_{O1}& X_{O2}& ...& X_{O10}\\ X_{E1}& X_{E2}& ...& X_{E10}\\ X_{S1}& X_{S2}& ...& X_{S10}\\ X_{F1}& X_{F2}& ...& X_{F3}\end{array}\right)$$ (16)

To obtain the sequence number vector sampled from the dataset, we introduced the index capture function,Ind(.), as defined in definition (17), where p represents the number of samples in the dataset and q denotes the data dimension.

$$\mathsf{def}.ve{c}_{\left(p\right)}=Ind\left(X_{\left(p\times q\right)}\right)$$ (17)

To construct parallel experiments, the set M should fulfill the following conditions:

(i) Ind(X_Oi) = Ind(X_Ei) = Ind(X_Si)=Ind(X_Fi);

• (ii)For each dataset within M, the index obtained using the optimal hyperparameter after MSEA-ALHK processing serves as the output result for that particular group.

According to Fig. 10, all data sets exhibit classification results with specificity values above 87%, indicating a relatively strong recognition ability for normal tissue. Accuracy, which falls between specificity and sensitivity, does not exhibit noticeable model bias towards any particular sample type. This finding confirms the necessity of data amplification as outlined in Section 2.4. To further evaluate the impact of the four subsets within M on classification performance, we computed the average of the three metrics, as presented in Table 4.

Fig. 10.

Classification results of four subsets in M (A): Xo;(B): X_E;(C): X_S;(D): X_F.

Table 4.

Average Index of four groups of binary classification problems obtained by the MSEA-ALHK method and validated using random sub-sampling (10 repetitions).

Classification group	Method		Dimension of data	Average Index
	PCA	ReliefF		Accuracy (%)	Sensitivity (%)	Specificity (%)
XO	×	×	603	96.77	96.13	97.35
XE	✓	×	20	98.15	96.13	100.00
XS	×	✓	3	91.23	88.39	93.82
XF	✓	✓	23	98.31	96.45	100.00

Among the three average indices, X_F demonstrates the highest accuracy, followed by X_E. Notably, X_E possesses significantly smaller data dimensions compared to X_O, highlighting the effectiveness of feature extraction. This extraction process successfully eliminates redundant and noisy information from the original spectrum. On the other hand, X_S lags behind other groups in all three indicators, indicating that three-dimensional data alone fails to fully capture the distinguishing information between spectra. However, the fusion of X_S and X_E in the X_F product yields higher accuracy than either individual subset.

To evaluate the potential impact of using a different training and testing set ratio, we conducted an experiment where we employed an 80% vs. 20% split. We reran the model training and evaluation process using this new ratio.

Table 5 indicates that while there were slight differences in the performance metrics between the two ratios, the overall trends and conclusions remained consistent. The model trained with the 80% vs. 20% split yielded comparable results to the one trained with the 2/3 vs. 1/3 split (Refer to Table 4). This suggests that our findings are robust and not heavily dependent on the specific choice of training and testing set ratios. This outcome supports the notion that feature fusion enhances the complementary nature of information derived from feature extraction and feature selection, effectively improving the resolution capability of the classifier.

Table 5.

Impact evaluation of train set and test set ratio: An 80% vs. 20% Split.

Classification group	Method		Dimension of data	Average Index
	PCA	ReliefF		Accuracy (%)	Sensitivity (%)	Specificity (%)
XO	×	×	603	96.79	96.62	96.94
XE	✓	×	20	97.50	94.74	100.00
XS	×	✓	3	92.88	90.53	95.00
XF	✓	✓	23	98.25	96.84	99.52

3.1.2. Biochemical interpretation of selected features

The composition of the breast encompasses various biomolecules, including proteins, lipids, amides, amino acids, and nucleic acids. Consequently, these biomolecules contribute to the spectral region to differing extents. The distinctive information within Raman spectra primarily resides in peak values, which reflect significant differences in molecular structure. In Section 2.5, the concepts of feature extraction and feature selection are elucidated. Through PCA, the processed data and the original data are projected onto different feature spaces, leading to a loss of interpretability regarding the positional information of peaks in the spectrum. Feature selection, however, retains the original feature space and directly identifies the most valuable feature wavelengths (Raman shifts) for classification.

Table 6 presents the assignment of Raman peaks based on the features described in Fig. 4. It is important to note that certain Raman shifts may exhibit matching errors due to factors such as redshifts, blue shifts, and the observer's deviation during peak observation.

Table 6.

Raman spectral peak assignment [40].

Feature number	Weight ranking	Raman shift (cm−1)	Affiliation
1	6	853	Ring breathing mode of tyrosine and C–C stretch of proline ring
2	8	968	C–C stretching lipids
3	3	1064	Skeletal C–C stretch lipids
4	5	1244	Amide III: collagen (CH2 wag, C–N stretch)/pyrimidine bases (C, T)
5	2	1279	Amide III: a-helix
6	1	1417	CH2 deformation (lipid)
7	4	1632	C–O asymmetric stretching.Calcium oxalate dihydrate-Type I calcification
8	7	1743	C O stretch (lipid)

The disparity between normal tissue and tumor tissue arises from alterations in lipids, proteins, and specific chemical bond configurations [41,42]. Experimental findings reveal that Raman peaks carrying biomolecular characteristics can be integrated as features into the original data. This integration not only expands the data dimension but also enhances the differentiation among features, thereby rendering the peak extraction method more justifiable for biochemical interpretation.

Moreover, this framework offers a feature selection avenue for researchers in the field. It can be explored in conjunction with wavelength optimization strategies, such as utilizing particle swarm optimization algorithms, encoders, and other Raman peak optimization approaches. Such considerations bear significant relevance in enhancing pattern recognition accuracy following feature fusion.

3.2. Hyperparameter optimization

3.2.1. Sensitivity analysis

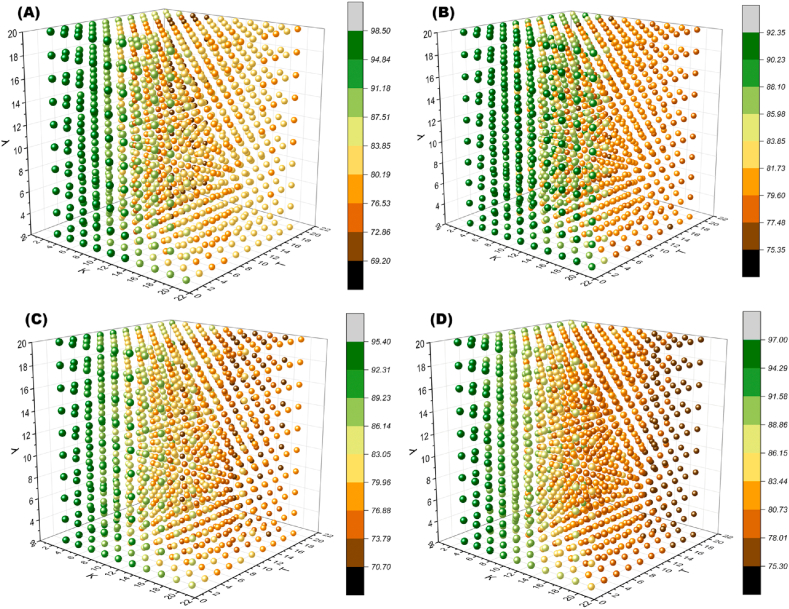
Incorporating an optimization algorithm into an ML model to maximize classification accuracy carries the risk of model overfitting, potentially leading to poor generalization performance when applied to other datasets. To further investigate this potential issue, a hyperparameter sensitivity analysis experiment was designed for the ALHK model. It is important to note that the concept of “sensitivity” discussed here differs from the evaluation metrics outlined in Section 2.7. Sensitivity analysis refers to studying how uncertainty in the output of a mathematical or numerical model can be attributed to different sources of uncertainty in its inputs [43]. Various hyperparameters have distinct effects on the classification performance of pattern recognition algorithms. Equation (7) demonstrates that the hyperparameter optimization model takes the input vector Γ and outputs Viability. As a result, the hyperparameter domain Θ₁ × Θ₂ × Θ₃ was constructed, and four sets were randomly selected from X_F in Section 3.1.1. The resulting four discretized hyperparameter cubes obtained through grid search are illustrated in Fig. 11.

Fig. 11.

The discretized hyperparametric cubes, where the degree of the gradient of color represents the size of Viability (%). (A)–(D) are obtained from randomly selecting four subsets from X_F using their respective hyperparameters. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Upon observing the discretized hyperparameter cubes, it becomes apparent that the distribution of Viability among different experimental groups (A)-(D) is similar (as shown in Fig. 11), with optimal parameters concentrated in the region where K and T's values are small. Group A serves as an example, where a cross-section of its discretized hyperparameter cube was taken to qualitatively analyze the impact of parameter variation on the model output using two-dimensional images.

Fig. 12(a) reveals that changes in K and T significantly influence Viability when λ is held constant. Higher Viability is observed in the hyperparameter space near the origin of the profile. Fig. 12(b) indicates that variations along the λ axis do not noticeably affect Viability, but there is a notable jump along the K axis. In Fig. 12(c), after fixing K, changes in λ and T do not lead to significant image variations. The preliminary judgment suggests that the impact of λ on the output accuracy of the ALHK model is relatively less pronounced compared to K and T.

Fig. 12.

Cross-section of the discretized hyperparametric cube. (a): Viability influenced by K and T with constant λ; (b): Viability influenced by K and λ with constant T; (c): Viability influenced by T and λ with constant K.

Based on these judgments, the Sobol method was employed to assess global sensitivity. Latin hypercube sampling (LHS) was conducted for hyperparameters K, T, and λ, with the classification accuracy serving as the objective function. First-order sensitivity indices (FOI) and Total Effect Index (TEI) were calculated and analyzed. Table 7 presents the value ranges and distributions of the hyperparameters.

Table 7.

The value range and distribution of hyperparameters.

Hyperparameters	Var Min	Var Max	Probability distribution
K	1	20	Uniform distribution
T	1	20	Uniform distribution
λ	1	20	Uniform distribution

The three hyperparameters were assigned a uniform distribution, and each parameter was sampled 100 times. As K is required to be a positive integer, it was pre-converted from a floating-point format before being applied to the ALHK model.

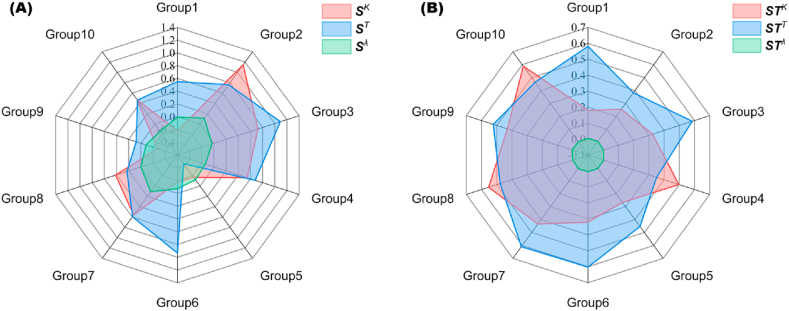
In Fig. 13, the coverage area of each hyperparameter legend's corresponding graph in the radar chart was utilized to assess the FOI and TEI. In panel (A) from Fig. 13, the average values for S^K, S^T, and S^λ were determined as [0.302, 0.495, −0.037], with S^λ exhibiting dominance in Group 5. Similarly, panel (B) from Fig. 13 displayed mean values of ST^K, ST^T, and ST^λ as [0.385, 0.503, 0.004], respectively. The parameters K and T displayed a more pronounced influence on the model, with their contribution values ranked in the following order: T > K > λ. This ordering aligns with the evaluation of both FOI and TEI, reinforcing their consistency. Importantly, the results obtained through Sobol's method corroborated the observations made in Fig. 12, thereby validating the efficacy of the sensitivity analysis.

Fig. 13.

FOI(A) and TEI(B) obtained by sensitivity analysis of ALHK.

3.2.2. Hyperparameter cross-validation experiments

The MSEA-ALHK model possesses the capability to adaptively acquire the optimal combination of hyperparameters for an individual dataset. However, the possibility of specific combinations leading to overfitting is a topic that necessitates further discussion. To examine and enhance the generalizability of the outcomes, hyperparameter cross-validation experiments were devised.

Firstly, by employing Monte Carlo sampling, 10 distinct groups of datasets were generated, each undergoing complete feature fusion. Subsequently, the MSEA-ALHK algorithm was utilized to obtain the optimal hyperparameter matrix Ψ.

$$\psi ={\left(\begin{array}{l}{\psi }_1\\ {\psi }_2\\ ...\\ {\psi }_{10}\end{array}\right)}_{10\times 3}=\left(\begin{array}{ccc}{K}_1& T_1& {\lambda }_1\\ K_2& T_2& {\lambda }_2\\ ...& ...& ...\\ K_{10}& T_{10}& {\lambda }_{10}\end{array}\right)=\left(\begin{array}{ccc}5& 1& 11.7\\ 7& 2.9& 9.5\\ 2& 3.3& 11.7\\ 1& 9.6& 17.9\\ 12& 3.7& 6.1\\ 4& 2.1& 13.9\\ 2& 1.4& 17.3\\ 7& 1.5& 5.8\\ 3& 7.4& 12.3\\ 2& 6.7& 9.8\end{array}\right)$$ (18)

Subsequently, employing equation (18), the hyperparameters within each row of Ψ were systematically investigated across the 10 dataset groups using the ALHK approach. The resulting output metrics formed the row vector of the hyperparameter cross-validation matrix, as depicted in Table 8. Notably, the diagonal elements of the matrix denoted the optimal solutions identified by the MSEA-ALHK procedure.

Table 8.

Hyperparameter cross-validation matrix.

Accuracy（%）										MIN	AVG
98.46	90.77	90.77	93.85	90.77	93.85	93.85	95.38	96.92	96.92	90.77	94.15
95.38	92.31	92.31	92.31	95.38	90.77	90.77	93.85	96.92	100.0	90.77	94.00
93.85	86.15	92.31	90.77	95.38	90.77	89.23	92.31	96.92	100.0	86.15	92.77
86.15	90.77	86.15	95.38	96.92	90.77	84.62	90.77	92.31	93.85	84.62	90.77
95.38	90.77	89.23	87.69	98.46	90.77	80.00	87.69	92.31	87.69	80.00	90.00
95.38	93.85	92.31	93.85	95.38	95.38	89.23	95.38	96.92	98.46	89.23	94.62
95.38	90.77	92.31	93.85	96.92	92.31	95.38	96.92	95.38	98.46	90.77	94.77
93.85	90.77	92.31	93.85	92.31	93.85	93.85	96.92	98.46	98.46	90.77	94.46
86.15	84.62	87.69	90.77	93.85	89.23	84.62	92.31	98.46	90.77	84.62	89.85
87.69	90.77	89.23	92.31	95.38	89.23	89.23	95.38	95.38	98.46	87.69	92.31

Sensitivity（%）										MIN	AVG
96.77	80.65	80.65	90.32	90.32	87.10	87.10	90.32	93.55	93.55	80.65	89.03
90.32	83.87	83.87	87.10	93.55	80.65	80.65	87.10	93.55	100.0	80.65	88.06
87.10	70.97	83.87	83.87	90.32	80.65	77.42	83.87	93.55	100.0	70.97	85.16
80.65	87.10	74.19	87.10	96.77	83.87	74.19	83.87	83.87	93.55	74.19	84.52
90.32	80.65	80.65	90.32	96.77	83.87	67.74	83.87	93.55	90.32	67.74	85.81
90.32	87.10	83.87	87.10	96.77	90.32	83.87	90.32	93.55	96.77	83.87	90.00
90.32	80.65	83.87	90.32	93.55	83.87	93.55	93.55	90.32	96.77	80.65	89.68
87.10	80.65	83.87	87.10	93.55	87.10	87.10	93.55	96.77	96.77	80.65	89.35
83.87	77.42	74.19	80.65	96.77	77.42	70.97	87.10	96.77	93.55	70.97	83.87
83.87	80.65	77.42	83.87	90.32	80.65	80.65	90.32	90.32	96.77	77.42	85.48

Specificity（%）										MIN	AVG
100.0	100.0	100.0	100.0	91.18	100.0	100.0	100.0	100.0	100.0	91.18	99.12
100.0	100.0	100.0	97.06	97.06	100.0	100.0	100.0	100.0	100.0	97.06	99.41
100.0	100.0	100.0	97.06	100.0	100.0	100.0	100.0	100.0	100.0	97.06	99.71
91.18	94.12	97.06	100.0	97.06	97.06	94.12	97.06	100.0	94.12	91.18	96.18
100.0	100.0	97.06	85.29	100.0	97.06	91.18	91.18	91.18	85.29	85.29	93.82
100.0	100.0	100.0	100.0	94.12	100.0	94.12	100.0	100.0	100.0	94.12	98.82
100.0	100.0	100.0	97.06	100.0	100.0	97.06	100.0	100.0	100.0	97.06	99.41
100.0	100.0	100.0	100.0	91.18	100.0	100.0	100.0	100.0	100.0	91.18	99.12
88.24	91.18	100.0	100.0	91.18	100.0	97.06	97.06	100.0	88.24	88.24	95.29
91.18	100.0	100.0	100.0	100.0	97.06	97.06	100.0	100.0	100.0	91.18	98.53

The impact of different Ψ configurations on each dataset was assessed using two evaluation measures: the minimum value (MIN) and the average value (AVG). Table 8 reveals that Ψ₅ corresponds to the smallest MIN value, with a sensitivity index reaching 67.74%. This observation suggests the potential presence of overfitting when utilizing this set of hyperparameters. Given the findings from the sensitivity analysis in Section 3.2.1, it is reasonable to assume that λ has minimal influence on the outcomes. To gain further insights into these results and optimize hyperparameter selection in such scenarios, Fig. 14 visualizes the K and T parameters.

Fig. 14.

Visualization of the K-T hyperparameters in Ψ (a):Distribution of Accuracy values across different K-T combinations.; (b):Distribution of Sensitivity values across different K-T combinations; (c):Distribution of Specificity values across different K-T combinations.

The results from Fig. 14(a–c) demonstrate that when K∈ [1,4] and T∈ [2,5], the three classification indexes surpass an average value of 85%. As mentioned earlier, the outlier position of Ψ₅ stems from its K value of 12, resulting in reduced classification accuracy. This confirms that the MSEA-ALHK model effectively identifies the optimal parameter intervals and enhances the performance of the three pattern recognition indicators through cross-validation.

4. Conclusion

Raman spectral has significant application in the early diagnosis of breast cancer due to its rapid and noninvasive advantages. To address the issue of improving the accuracy of pattern recognition for Raman spectra with high dimensionality and low signal-to-noise ratio (SNR), this paper utilizes feature extraction and feature selection to perform data fusion at the feature level. The feasibility of feature fusion in enhancing classifier performance has been evaluated by comparing the results of 10 parallel experiments using different data fusion methods. During the feature selection process, the molecular-level biochemical interpretation of the fusion strategy can be established by considering the attribution relationship of breast tissue Raman peaks. This instantiation idea contributes to the research and application of incorporating feature selection into the feature fusion process.

The application of machine learning in tumor recognition offers the potential to incorporate pathology and chemical characterization approaches into surgical procedures. To address issues such as prolonged time consumption and low accuracy resulting from manual parameter adjustment, we propose the MSEA-ALHK model to achieve automatic and global optimization. This approach attains a high level of recognition accuracy by employing sequential encoding of hyperparameters, a population selection method, and fitness function optimization. To assess the adaptability of the optimal hyperparameters from a single dataset to others, we conduct hyperparameter cross-validation experiments. Additionally, conducting a prior sensitivity analysis of the machine learning model hyperparameters helps narrow down the parameter space of interest. Based on these findings, we establish the specific range of the final hyperparameters, combined with cross-validation accuracy.

The concept of feature fusion and hyperparameter optimization presented in this study can be extrapolated to address pattern recognition challenges in spectral data (or high-dimensional data) in various contexts. This research can also serve as a reference for cancer detection and biomedical diagnosis in other domains.

Funding

This work was supported by the open project of Hebei Key Laboratory of Micro-Nano Precision Optical Sensing and Measurement Technology [grant No. NEUQ202103]. Thank Dr. Xuzhi, department of general surgery in Peking University Third Hospital for providing breast tissue samples.

Live subject statement

All experiments involving live human tissue were performed according to the relevant laws and guidelines and approved by the Peking University Biomedical Ethics Committee and the Institutional Review Board of the Peking University Third Hospital (IRB00001052-11034). All experiments involving a human patient were performed after obtaining informed consent.

Author contribution statement

Qingbo Li: Conceived and designed the experiments; Performed the experiments; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Zhixiang Zhang: Analyzed and interpreted the data; Wrote the paper.

Zhenhe Ma: Analyzed and interpreted the data.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.