Multistate Energy Decomposition Analysis of Molecular Excited States

Abstract

A multistate energy decomposition analysis (MS-EDA) method is described to dissect the energy components in molecular complexes in excited states. In MS-EDA, the total binding energy of an excimer or an exciplex is partitioned into a ground-state term, called local interaction energy, and excited-state contributions that include exciton excitation energy, superexchange stabilization, and orbital and configuration-state delocalization. An important feature of MS-EDA is that key intermediate states associated with different energy terms can be variationally optimized, providing quantitative insights into widely used physical concepts such as exciton delocalization and superexchange charge-transfer effects in excited states. By introducing structure-weighted adiabatic excitation energy as the minimum photoexcitation energy needed to produce an excited-state complex, the binding energy of an exciplex and excimer can be defined. On the basis of the nature of intermolecular forces through MS-EDA analysis, it was found that molecular complexes in the excited states can be classified into three main categories, including (1) encounter excited-state complex, (2) charge-transfer exciplex, and (3) intimate excimer or exciplex. The illustrative examples in this Perspective highlight the interplay of local excitation polarization, exciton resonance, and superexchange effects in molecular excited states. It is hoped that MS-EDA can be a useful tool for understanding photochemical and photobiological processes.

1. Introduction

Energy decomposition analysis (EDA) is widely used and plays an important role in the understanding of intermolecular interactions in molecular systems.¹⁻⁶ These studies provide insights into the interplay of Pauli exclusion, polarization and charge transfer effects that contribute to intermolecular forces. In turn, the information gained from these investigations can be useful to designing and optimizing empirical potential energy functions for condensed-phase and biomolecular simulations.^7,8 A large number of EDA models have been proposed, but they are almost exclusively limited to molecular complexes in the ground state.^4,6,9−49 On the other hand, a major current frontier of theoretical chemistry is to study chemical processes taking place in electronically excited states in areas such as photochemistry, photovoltaic devices,⁵⁰ photosynthesis and photoreception in biology,⁵¹⁻⁵⁴ catalysis, and even reactions in fuel cells and at the electrodes.⁵⁵ Electronic coupling among local states in these systems can be used to determine the rate of excited-state energy transfer. Unfortunately, little attention has been paid to energy decomposition analysis of intermolecular interactions in excited states,^5,56−58 although several studies of energy components of excited states have been reported.^59,60 Moreover, it is not always clear if the intuitive terms for the ground state can be adapted to molecular systems in the excited states. In this Perspective, we present a multistate energy decomposition analysis (MS-EDA) introduced in a recent preliminary report⁵ to define the energy terms relevant to intermolecular interactions in excited states. This is now possible following the development of multistate density functional theory (MSDFT) to treat the ground state, excited states and diabatic states on an equal footing with the inclusion of electron correlation.⁶¹⁻⁶⁴

Energy decomposition analysis was first introduced by Morokuma and Kitaura on the basis of Hartree–Fock theory in the 1970s,^9,65 who defined intuitive terms such as electrostatic, exchange repulsion, polarization and charge transfer energies, which are intimately related to concepts used in chemical research. The method was an instant success and has become extremely popular in computational chemistry.⁶⁶ Subsequently, a wide range of models have been proposed, attacking the energy components from different perspectives for different situations. Roughly speaking, these methods may be grouped into three categories: (1) physical approaches, either based on a formal perturbation theory or by intuitive construction and modification of the interaction terms; (2) variational methods, developed by constructing well-defined intermediate molecular wave functions that can be variationally optimized; and (3) perturbation theories using quantum chemical methods or classical electrostatics theory.

The original Kitaura–Morokuma EDA belongs to the first category through a gradual annihilation of the Fock and overlap matrix elements relevant to intermolecular interactions.⁶⁵ Other models that partition the energy terms through an electron density formulation such as the interacting quantum atom (IQA) method according to zero-flux density surfaces,⁶⁷ and the natural energy decomposition analysis (NEDA) by making use of natural bond orbitals.^13,68 EDA models that do not include variational energy minimization of the intermediate states can lead to an overestimation of the resonance energy and charge transfer effects.⁶⁹⁻⁷¹

EDA models belonging to the second category were developed with certain elements of variational optimization of key reference intermediate states for energy partition. In Mo’s block-localized wave function (BLW)⁷² approach and the absolutely localized molecular orbital analysis,^6,25 the strictly block-localized orbitals for every intermediate in the EDA are fully variationally optimized, providing a set of well-defined diabatic intermediate states for interpretation of the resonance energies of aromaticity, anomeric effects and forward-and-backward bonding interactions.^3,46,73 Other illustrative examples include the early constrained space orbital variations (CSOV) method by successively mixing occupied and virtual orbitals of different molecules,^11,74,75 and the reduced variational space self-consistent-field (RVS-SCF) model in which the orbitals of one fragment is optimized in the presence of the frozen orbitals of other fragments.¹² Another class of EDA theory features the extended transition state (ETS) scheme,^30,76,77 along with natural orbitals for chemical valence (NOCV) theory, in which not only noncovalent intermolecular interactions are decomposed, but also the energy of a chemical bond can be separated into unpaired electron contributions.^24,29 The ETS-NOCV method allows the analysis of bonding characteristics such as σ,π,δ bond types.⁷⁷

In category three,³⁵ perhaps the best known example is the popular symmetry-adapted perturbation theory (SAPT), which can be applied both to wave function theory and density functional theory.^36,78 The SAPT method relies on a series of monomer Fock, perturbation and interaction operators. The first order polarization and exchange corrections are assigned to electrostatic and exchange energies, and higher order terms result in induction and dispersion terms. However, separation of charge-transfer energy can be challenging in perturbation approaches.⁷⁹⁻⁸¹

Energy decomposition analysis for molecular complexes in the excited states is rare. Methods exist to extract local information and charge transfer contribution in excited states by analyzing density difference and transition density matrices.^{58−60,82−86} In principle, EDA methods for the ground state can be adapted to describe interactions in the excited states. One application was recently reported by Ge et al., who transferred the corresponding energy terms in the ground-state EDA to excited complexes.^57,87 In particular, the interaction energy for an exciplex is separated into frozen (froz), polarization (pol) and charge transfer (CT) terms, similar to that in the ground state: ΔE_int^* = ΔE_froz + ΔE_pol^* + ΔE_CT.⁵⁶ To obtain “frozen” excitations, the orbitals for each isolated monomer and its excitation amplitudes are combined to construct a supramolecular operator. Later, an excitation splitting term was incorporated to describe interactions between degenerate monomer states in a symmetric excimer.⁵⁶ While this excited-state decomposition scheme revealed interesting information in the lens of a ground-state microscope, the intermediate states cannot be variationally optimized because interfragment interactions were reconstructed from separate monomer terms. Yet, there is an interest in defining intermediate diabatic states which can be used to represent excitations localized on individual monomers to understand the reaction rates of excited-state energy transfer and excitation induced oxidation–reduction reactions.⁸⁸ Recently, we introduced a multistate approach,⁵ making use of multistate density functional theory (MSDFT),⁶¹ to define variationally optimizable intermediate states to interpret properties associated with excited-state processes,^89,90 including local excitation, exciton resonance, superexchange, and orbital-and-configuration delocalization. This Perspective further expands that work in several fronts. In addition to understanding intermolecular interactions in excited-state complexes, the energy terms and the associated diabatic states in this analysis can be used to investigate ultrafast photochemical reactions.^50,51,54

In the following, we first present the theory of multistate energy decomposition analysis (MS-EDA), and the fundamental principles and computational algorithms of MSDFT. Then, we illustrate the MS-EDA method with a set of applications to excited-state complexes which can be loosely classified as encounter exciplex, excitation-induced charge-transfer complex, and intimate excimer and exciplex. We validate the computational procedure by comparison with results from time-dependent density functional theory (TDDFT) that works well for most of these exciplexes and their monomers as well as with available experimental data. In some cases, the computational MS-EDA results shed light on experimental findings with new interpretations. It is hoped that the new MS-EDA method shall stimulate further analysis and interpretation of computational results on excited states from delocalized wave function theories and TDDFT.

2. Theory

We aim at developing a method for energy analysis of molecular complexes in an excited state. For the photochemical reaction producing the exciplex (XY)* between compounds X and Y

1

we define the binding energy of (XY)* in its Kth excited state as

2

where the superscript “0” denotes the energy and wave function of a molecule in the ground state, and E_(XY)*^K is the energy of the Kth excited state of the exciplex (XY)* associated with the wave function Ψ_(XY)*, and hν̅₀^K is the energy for chromophore excitation whose definition will be addressed next (not necessarily Y alone as indicated).

Before we discuss the energy components, we first take a closer look at the meaning of “binding energy” ΔE_b^K of an exciplex. It turns out that it is not as straightforward as that of a bimolecular complex in the ground state. From a viewpoint of the physical process, the external energy supplied (i.e., photoexcitation) to initiate the formation of an excited-state complex from two isolated molecules in their ground state is the vertical transition of one relevant monomer (or more) to the Franck–Condon region. Then, the excited species can quickly relax to its equilibrium geometry of a specific excited state (e.g., K), which in turn binds to another monomer and together relaxes to the equilibrium exciplex (Scheme 1). Alternatively, two molecules form a ground-state complex, the dimer absorbs a photon and gets excited into an exciplex, which then directly relaxes to its final geometry. The precise mechanism is not always known exactly, but the final state is well-defined (eq 1), and its energy can be related to the emission spectrum of the exciplex. However, the energy difference between the final exciplex and the vertical excitation energy is not ΔE_b since some of the vertical excitation energy may have dissipated (without discussing its possible mechanisms) into the environment in the relaxation process. Furthermore, it is not always clear if one, two or a fraction of each monomer are excited in the first place, e.g., in the case of a symmetric or nearly symmetric excimer where the excited state is delocalized over both monomers. Therefore, we need to define an effective external energy hν̅₀^K to produce the unbound monomers to form the corresponding exciplex in the Kth excited state.

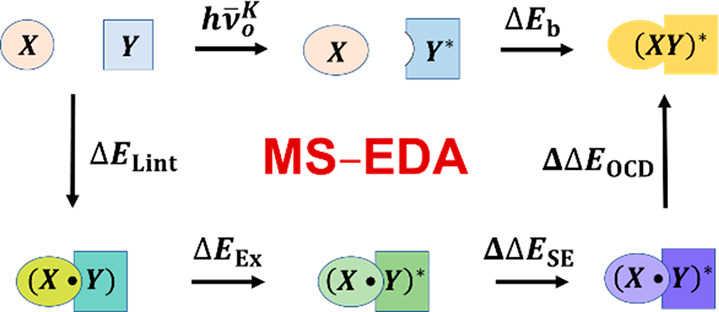
Scheme 1. Thermodynamic Cycle Relating the Energy Components in Multistate Energy Decomposition Analysis of Exciplex Binding Energy ΔE_b.

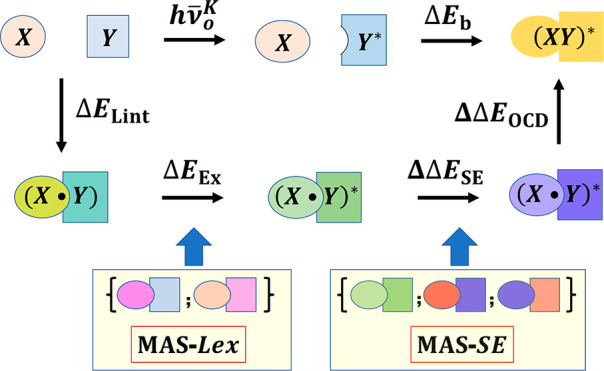
The top row corresponds to the physical process of exciplex formation (eq 2). The remaining illustration highlights the energy terms defined by eq 4. The shapes of objects represent molecular geometries, while different colors depict the polarized wave functions under different conditions. Blocks with boundaries denote fragment-localized wave functions, all of which can be variationally optimized. The lower panels in light-yellow shade specify the minimal active space (MAS) in nonorthogonal state interacion (NOSI) calculations, respectively, for the exciton state, derived from local excited states (Lex) shown in pink, and for the super-exchange (SE) contribution due to charge transfer diabatic states. Adapted with modifications from ref (5). Copyright 2023 American Chemical Society.

Here, we define hν̅₀^K in eq 1 as the minimum excitation energy associated with the formation of the exciplex in the Kth excited state, which is the weighted sum of the adiabatic excitation energies of the monomers at their geometries in the exciplex complex. It is related to the “vertical” emission energies of the monomers in the exciplex geometries and the geometrical distortion energy in going from the equilibrium structures of the ground-state monomers to the distorted geometries (X[S_K] and Y[S_K^EC]) in the excited complex.

3

where w_X^(K) and w_Y are the structure weights of monomer excited states in the exciton complex defined in section 2.2. Thus, hν̅₀^K is the effective external energy used to deform the monomer geometries and to excite them to the corresponding states at the fractions found in the exciton complex. Clearly, hν̅₀ is state-specific. Then, the energy change in going from the isolated, “fractionally” excited monomers to the final complex is the exciplex binding energy ΔE_b^K.

2.1. Multistate-Energy Decomposition Analysis (MS-EDA)

In MS-EDA, on the basis of the thermodynamic cycle in Scheme 1, we separate the binding energy of an exciplex in eq 2 into the following terms:

4

where ΔE_Lint[(X•Y)] denotes the interaction energy between monomers X and Y in the ground state, ΔE_Ex^K[(X•Y)*] is the excitation energy of the exciton (Ex) state and hν̅₀ is defined in eq 3, ΔΔE_SE^K[(X^±•Y^∓)*] specifies superexchange stabilization, and ΔΔE_OCD[(XY)*] represents the energy change due to orbital and configuration-state delocalization (OCD). The progressive energy terms in the MS-EDA procedure are schematically illustrated in Scheme 2 with a sequence of intermediate states leading to the final exciplex formation. Each state depicted in Scheme 1 has a well-defined wave function (or MSDFT configuration states) that can be variationally optimized.

Scheme 2. Energy Correlation Diagram, Energy Terms, and Associated States in Multistate Energy Decomposition Analysis.

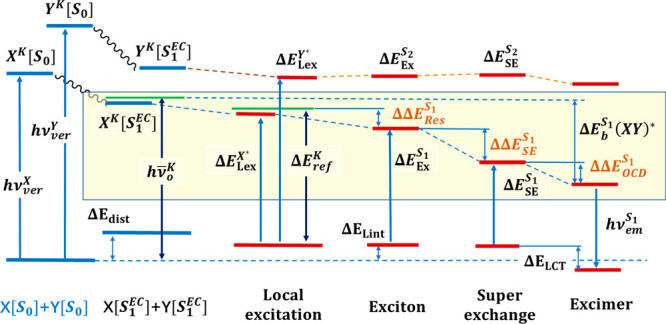
[S₀] and [S₁^EC] indicate geometries of X and Y in the respective equilibrium ground state and that in optimized exciplex complex (EC) in the first excited state. Blue lines are monomer compounds, and maroon lines denote dimer structures. Energies that can be observed spectroscopically are indicated by hν, except for local excitations given in relative energies. Resonance and delocalization energies are given in brown. Energy changes in light yellow shade are associated with the exciplex binding energy.

Although the binding energy of an excited-state complex is state-dependent, we will sometimes omit the superscript K for simplicity, but one needs to keep in mind that the intermediate states and energy terms in MS-EDA correspond to the same Kth state of the exciplex (not necessarily in the same order) and they must be matched in the analysis. Often, the lowest excited state of a given spin is of particular interest, although symmetry allowed and avoided curve crossings can take place and the order of states may differ at different stages of the MS-EDA scheme, in which case, analysis of more than one state is necessary.

The individual energy components in eq 4 can be further decomposed into more specific terms to gain insights into the intricacy of intermolecular interactions in an excited state. Some of these energy terms can be directly measured experimentally or extracted from experimental data. In this section, we define the interaction energy terms. In the next section, we analyze the additional components that constitute some of these terms in the exciplex.

Throughout this Perspective, we use Ψ and Φ to denote a physical adiabatic state or an intermediate diabatic state with further specification indicated by a subscript and the particular excited state specified by a superscript. Ψ and Φ are typically multistate wave functions, which are also used to represent the matrix density. The Greek letter Ξ is used to specify a single Slater determinant wave function for a given electronic configuration, typically monomer-block localized, to represent the corresponding electron density in block-localized excitation (BLE) and target state optimized density functional theory (TSO-DFT) calculations.^91,92 Occupied Kohn–Sham molecular spin orbitals, typically block localized, are denoted by χ_i, χ_j, ..., and unoccupied (virtual) orbitals are given as χ_a, χ_b, .... In the present MS-EDA method, we use the monomer block-localized Kohn–Sham (BLKS) determinant, Ξ_(X•Y)^KS, as a reference state, which is used to generate the initial guess for singly excited configurations Ξ_i, all of which are variationally optimized individually using BLE and TSO–DFT for block-localized excitation.^91,92 Together, these variationally optimized determinants states form a minimum active space denoted by a single subscript {Ξ_A; A = 1, ...}.

2.1.1. Ground-State Interaction Energy

The formation of a molecular aggregate in an excited state has energy contributions both from binding interactions in the ground state and from energy terms induced by photoexcitation (Scheme 1), keeping in mind that in many situations an exciplex is only stable in the excited state (thus, the ground-state effect could be repulsive). Since EDA has been thoroughly investigated for molecular interactions in the ground state, we separate ground-state and excited-state energies in the present multistate analysis. Consequently, the energy components leading to the monomer block-localized complex in the ground state are grouped into a single term called local interaction (Lint) energy in MS-EDA.

5

where (X•Y) denotes a bimolecular complex whose wave function is block-localized, indicated by the symbol “•”, the parentheses specify an antisymmetrized product wave function from the monomers, Ψ_(X•Y) = Â{Ω_XΩ_Y} with Ω_X and Ω_Y denoting products of BLKS orbitals, and Ξ_X^o and Ξ_Y are Kohn–Sham determinants for molecules X and Y in isolation in their equilibrium geometries (Figure 1). Here, the mutual polarization between the two monomers are naturally included in Ψ_(X•Y) as a result of variational optimization of the wave function; Ψ_(X•Y) can be a multistate wave function in which case it is replaced by a linear combination of configuration state functions in the active space. Note that an energy deformation term has been included in ΔE_Lint because the molecular geometry of the exciplex is used to determine E_(X•Y)[Ψ_(X•Y)] in eq 5.

Figure 1.

Reference state (dashed lines in red) for local excitations (lines black) and exciton-resonance stabilization energy (blue arrows). Local and exciton excitation energies relative to the block-localized complex are indicated by red arrows.

ΔE_Lint[(X•Y)] is called local-interaction energy because molecular orbitals are not globally delocalized over the full complex. In addition to the structural deformation energy, it includes an electrostatic term called Heitler–London energy, Ψ_(X•Y)^o = Â(Ω_X•Ω_Y⁰), and a polarization energy in the variationally optimized state Ψ_(X•Y) = Â{Ω_X•Ω_Y}.^3,27 Note that ΔE_Lint[(X•Y)] is not the binding energy of the bimolecular complex (XY) in the ground state because charge-transfer delocalization is not included. Additional details for ground-state analysis can be found in references.^1−3,6

2.1.2. Exciton Excitation Energy

In MS-EDA, we first define an exciton state, denoted by (X•Y)* (Scheme 1). Then, the energy difference between the exciton state and the ground state of the block-localized complex is called the exciton-excitation energy ΔE_Ex^K.

6

where E_(X•Y)*^K and E_(X•Y) are the energies of the Kth exciton state and the ground state, respectively, corresponding to the wave functions Ψ_(X•Y)* and Ψ_(X•Y) (eq 5). According to the Frenkel exciton model,⁹³ the wave function of the exciton state is expressed as follows.

7

where Ψ_(X*•Y)^K_X and Ψ_(X•Y*) are the spin-adapted, configuration state functions of the two locally excited monomers (MAS-Lex in Scheme 1), and a_1K and a_2K are the state coefficients. The superscripts K_X and K_Y specify, respectively, the states of the locally excited states of monomers X and Y that contribute to the exciton state K (again, the subscripts or even K are typically omitted without causing confusion). In general, both Ψ_(X*•Y)^K_X and Ψ_(X•Y*) are multiconfigurational wave functions, and more than one state from each monomer may be included.

Obviously, eq 7 can be extended to any number of monomers in an aggregate of n monomers or to condensed phases:

where Ψ_{(X1•···•XA*•···•Xn)}^K_A denotes the local excitation to the K_Ath state of monomer X_A* in the presence of the rest of the n – 1 monomers in the ground state. In solution, the local excitation energy of the chromophore includes a solvatochromic shift in comparison with the excitation energy of the isolated monomer. To limit the scope of this Perspective, we shall not further discuss condensed-phase properties including exciton delocalization in general situations.

2.1.3. Charge Transfer States and Superexchange Energy

The exciton state above from the interactions among strictly localized monomer states includes the mutual polarization induced by chromophore excitation, but charge transfer (CT) contributions are excluded by construction (i.e., monomer localization). In the second step of MS-EDA, we introduce CT resonance states by combining the forward and backward CT states:

8

We note that for a symmetrical excimer the amount of forward and backward CT is the same, leaving a net zero “CT”. Nevertheless, charge-transfer resonance in eq 8 can still stabilize the excimer complex significantly. On the other hand, in asymmetrical exciplexes, the significance of CT resonance strongly depends on the relative energies of the two directions of CT. Then, the CT state in the direction with the lower energy typically plays a dominant role, whereas the effect in the opposite direction of CT can be ignored. To encompass both scenarios, we borrow a term from electron transfer theory,^50,94 giving the name superexchange (SE) stabilization to the decrease in energy when superexchange states (eq 8) are admixed to the exciton states (eq 7).

9

where the wave function for the superexchange intermediate state in MS-EDA is given by

10

It should be emphasized that the notation |X⁺•Y^–⟩ (and |X^–•Y⁺⟩) defines a spin-adapted state obtained from MSDFT-NOSI for the spin-pairing interactions between the two spin-mixed determinants with single-electron transfer in α or β spin (MAS-SE in Scheme 1). The two resulting eigenstates correspond to a singlet state and a triplet component with M_s = 0 (see below).

2.1.4. Orbital and Configuration-State Delocalization

In the final step of MS-EDA, we relax the strictly localized BLKS orbitals to the fully delocalized molecular (or Kohn–Sham) orbitals over the entire exciplex system. In addition, the number of basis configurations used to define the intermediate states in the exciton and superexchange step is relatively small, which is useful for interpretation of excited-state energies. Thus, the difference between excited-state energies from TDDFT calculations for the delocalized exciplex and MSDFT-NOSI in analysis is also included. We denote the Kth adiabatic excited state of the exciplex as Ψ_(XY)*^K where the removal of the dot “•” emphasizes spatial delocalization of the orbitals and configuration space. The energy change in this step is called orbital and configuration-state delocalization (OCD) energy.

11

In principle, SE and OCD energies can be combined as the overall CT effects, similar to that in ground-state EDA, but it is useful to make the distinction and separation here in view of the difference in the number of basis configuration state functions to treat the intermediate states and the adiabatic states of the exciplex.

The ΔΔE_K^OCD term is defined in terms of excited-state energies (eq 11), but, in fact, it also includes ground-state effects, corresponding to the charge-transfer energy term in ground-state EDA, denoted by ΔE_LCT (Scheme 2). It can be extracted as the difference between the energy of the (XY) complex in the ground state and the local binding state (X•Y). Thus, the contribution to exciplex binding from the total ground-state effect is ΔE_Lb = ΔE_Lint + ΔE_LCT. Then, the OCD effect on the excited state is ΔΔE_OCD = ΔΔE_OCD^K – ΔE_Lb. In this paper, we do not further separate these two OCD terms, except in E_OCD In some specific cases, we comment on the numerical results of these terms.

On computation of the excited-state energy of an exciplex, multiconfiguration self-consistent-field (MCSCF) or configuration interaction-based approaches such as multireference configuration interaction (MR-CI) in wave function theory can be used to determine the energies and excited-state wave functions Ψ_(XY)*^K. Alternatively, MSDFT and linear-response TDDFT method can be used to obtain E_(XY)* and ρ_(XY)*^K in density functional theory. Given that MSDFT is a new variational DFT method and the development of approximate matrix correlation functionals hat not yet advanced to a level as that in KS-DFT, we employ TDDFT for estimating the excited state energies of the final exciplexes. Nevertheless, the accuracy of MSDFT in the MS-EDA analysis can be validated by comparison of the computed excitation energies for the monomer states with those obtained using TDDFT, employing a common approximate KS density functional and the same basis set. In this regard, the present MS-EDA method can also be viewed and used as an interpretative tool to dissect and understand the energies from TDDFT calculations.

2.2. Block-Localized Excited States

In the above MS-EDA, the exciton state is viewed as the resonance delocalization among monomer-localized excitations of individual chromophores.⁹³ Of interest is the relative contributions of locally excited states and the overall resonance energy in exciton formation (eq 7). In this regard, the term local excitation refers to the excited state of an individual monomer chromophore in the presence of other compounds in their ground state. This is achieved in TSO-DFT calculations by using the BLMO (in WFT) or BLKS orbitals (in MSDFT) that are strictly localized within each monomer by construction. These BLKS orbitals are clearly different from localized orbitals obtained through a particular symmetry orthogonal transformation.^95,96 Local excitation has a physical interpretation that can be directly related to experimental solvatochromic shifts induced by solvation (though this important physical property will not be addressed in this Perspective in view of space). In this section, we further decompose ΔE_Ex^K into specific components related to local excitation and resonance delocalization. This analysis also provides meaning to the structure weights used in the definition of hν̅_o in eqs 2 and 3.

2.2.1. Local Excitation and Polarization Effects

The excitation energy of a locally excited state of monomer X is given by ΔE_Lex^K_X(X*•Y):

12

where ν_Lex^K_X(X*•Y) is the excitation frequency of X if one considers Y as an environmental bath such as a solvent or simply another molecule in the present analysis (Scheme 2). The introduction of a frequency notation emphasizes the possibility that this quantity may be compared with the experimental absorption spectrum of a chromophore in solution or in a matrix of cluster molecules. Then, the solvatochromic shift of chromophore X in the presence of monomer Y (or in solution) relative to that in isolation (or in another reference solvent denoted by the subscript o), ν_o(X*), is given by

13

ν_o^K_X(X*) can have the same energy as that of the hν̅₀ term in eqs 1 and 2 for a single chromophore in special cases such as a symmetrical excimer.

Local excitation of monomer X changes its electrostatic field which polarizes the charge distribution of the other monomer Y in the ground state (or solvent). In turn, the reaction field of the ground state of Y further affects the energy of the excited monomer. The equilibrium state Ψ^K_X(X*•Y) is a result of their mutual polarization, and an understanding of its magnitude is of interest in MS-EDA. In fact, the local excitation energy of X* in the block-localized complex (X•Y) (eq 12) may be considered as photoexcitation of X in the hypothetic state ([X_o*]•Y) without interacting with Y in the complex i.e., the gas-phase adiabatic excitation energy hν₀^K_X(X*), followed by the mutual polarization of X* with its environment Y to the local excited state,

14

corresponding to the following two steps (see also Scheme 1):

Consequently, the polarization energy arising from local excitation ΔE_Lpol^K_X(X*•Y) is identical to the observable spectral shift:

15

For a symmetric dimeric excimer, the polarization energies for the two local excitations are identical. In this case, the block-localized excited states (X*•X) and (X•X*) are strongly correlated between two degenerate states, each corresponding to a diabatic state, which is also of interest in the study of excited-state energy transfer and exciton delocalization. The emission spectrum of the resonance state of the excimer may be used to determine the magnitude of the resonance energy relative to the variationally optimized diabatic states.⁹⁷ Note that the energies expressed in eq 14 can indeed be determined variationally by using the block-localized excitation (BLE) method,⁹² or the targeted state optimization (TSO) approach.⁹⁸

2.2.2. Exciton Resonance Energy

To determine the resonance energy of an exciton state, a variationally optimizable reference state in the absence of resonance (delocalized) excitation must be defined for comparison. For a perfectly symmetric excimer, it is straightforward simply to use the energy of one of the local excitation energies since both local excitations contribute equally. However, in the case of an asymmetric excimer or an exciplex of different monomers in which the two monomers contribute differently, a clear definition of the reference state is needed. Here, we introduce a structure-weighted reference state for estimating the resonance energy in an exciton state.

16

where the energies of the locally excited states Ψ^K_X(X*•Y) and Ψ^K_Y(X•Y*) are variationally minimized, and w_X^K and w_Y are the Chirgwin–Coulson configuration weights⁹⁹ of the Kth exciton state in eq 7.

The structure weights for locally excited states, Ψ_(X*•Y)^K_X and Ψ_(X•Y*), in the resonance exciton state (eq 7) can be determined according to the Chirgwin–Coulson partition:

17a

17b

where S₁₂ is the overlap integral between the two locally excited states, S₁₂ = S₂₁ = ∫dr{Ψ_(X*•Y)^K_X}*Ψ_(X•Y*).

Here, an exciton-state specific reference is defined because each locally excited state has different contributions in different exciton states. This is illustrated in Figure 1 in which two locally excited states in an exciplex interact to produce two exciton states, corresponding to the in-phase and out-phase combinations of Ψ_(X*•Y)^K_X and Ψ_(X•Y*). It would have been unfair if the energy of any individual state or the average energy of both states were used as the reference to determine exciton-resonance (ER) energy because the former does not consider the contribution from the other state, and the latter does not truly reflect the relative significance of individual states in the exciton state (eq 17a). The reference defined in eq 16 provides an adequate consideration of these factors. In the limit of an identical excimer, the weighted reference state is the same as the energy of one locally excited monomer.

With the same analogy, the structural weights determined at the exciton state are used to define a weighted adiabatic excitation energy for exciplex formation (eqs 2 and 3).

Having defined a reference energy, the exciton resonance energy (Figure 1) due to locally excited state-interaction is easily determined:

18

The use of eq 18 implies that the sum of the resonance energies for the resonance-stabilized and destabilized exciton states is not exactly the resonance splitting of the delocalized states (Figure 1). We further remark on the use of a weighted local-excitation energy as the reference state. First, the local excitations of all monomers contribute to the resonance-delocalized exciton state. Figure 1 highlights schematically the relative energies of the individual energy terms, including the weighted local-excitation energy (reference state), and the resonance stabilization energy for a given exciton state in the complex. In the case where monomers X and Y are asymmetric, the reference states for the in-phase and out-phase combinations of the locally excited states are different. In the former combination, the lower energy state (state K⁺ in Figure 1) is stabilized, whereas the higher energy exciton state (state L (K^–) in Figure 1) is destabilized. Since the stabilization and destabilization effects are relative contributions from all locally excited states, the state-specific, weighted local-excitation energy takes into account the relative significance to resonance energy and antiresonance energy. For an excimer complex, since both local-excitation energies are the same, a single reference state is naturally used for both resonance and antiresonance effects.

2.3. Multistate Density Functional Theory

Multistate density functional theory (MSDFT) is used to determine the intermediate states in multistate energy-decomposition analysis. Here, we summarize the fundamental theorems of MSDFT,^61,62 the definition of a Hamiltonian matrix density functional and the nonorthogonal state interaction (NOSI) method.^64,100,101 NOSI distinguishes from nonorthogonal configuration interaction (NOCI) in that the former includes dynamic correlation in each excited basis state in an active space, whereas the latter configuration space generally requires expensive corrections for dynamic correlation to yield quantitative results.⁶³

2.3.1. Fundamental Theorems

Although MSDFT has been used in a range of applications in the past,^64,100 it was in 2021 that Lu and Gao proved three fundamental theorems, establishing MSDFT as a rigorous density functional theory of quantum mechanics for any number of N states.⁶¹ For a system described by the Hamiltonian Ĥ = Ĥ° + v_ext(r), where Ĥ° consists of kinetic energies and electronic interaction energies, and v_ext(r) is the local external potential, the first theorem establishes the correspondence of the Hamiltonian and the N-dimensional multistate matrix density D(r). Theorem 2 is a variational principle, resulting in the energies and densities of all N eigenstates. Theorem 3 defines the representation of an N-dimensional multistate matrix density, enabling the design of different practical algorithms and procedures for computation.

• (1)
  Given the subspace 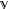spanned by the lowest N eigenstates of a molecular system described by Ĥ, the Hamiltonian Ĥ° is a universal matrix functional of the N-dimensional multistate density D(r), 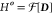, independent of the external potential v_ext(r). Then, the total Hamiltonian matrix density functional (HMDF) is

  

  Here, the multistate density D(r) is a matrix of electron densities {ρ_i(r) ≡ ρ_ii (r); i = 1, ..., N} and transition densities between any two basis states {ρ_ij(r); i ≠ j, i, j = 1, ..., N}. In other words, Theorem 1 establishes a one-to-one correspondence between D and .

  
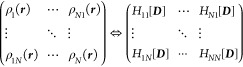
• (2)
  For any N-dimensional trial matrix density D'(r), the trace of 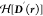, defined as the multistate energy E_MS[D'(r)] = Σ_iH_ii', is greater than or equal to the multistate energy E_MS[D] of the subspace :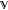

  

  The equal sign holds true if the trial density is a matrix density of the subspace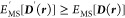 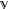, i.e., D’(r) = D(r). Then, diagonalization of the Hamiltonian matrix 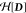yields exactly all N eigenstate energies (and densities), including the ground state and N – 1 excited states.
• (3)The N-dimensional multistate matrix density D(r) can be sufficiently represented by N² independent Slater determinant wave functions.

It is straightforward to see that the Hohenberg–Kohn theorem is a special case of Theorem 1 for the ground state, where N = 1. In this case, the HMDF reduces to a 1 × 1 matrix for one state, the ground state, becoming a scalar energy density functional of the ground state density ρ₀(r): E₀ = E[ρ₀(r)]. Then, according to Theorem 3, the density D(r) ≡ ρ₀(r) can be represented by a single Slater determinant, as in the Kohn–Sham formulation of HK-DFT.

A major departure, however, from the HKS-DFT is that state interaction is essential to representing the multistate density and determining the energies of excited states, rather than using a noninteracting KS reference system to represent the electron density of the ground state. Importantly, the implication of Theorem 3 is that for a given number of N states of interest, a finite number of N² determinant wave functions is sufficient to represent exactly the multistate density D(r). Consequently, it defines an upper bound of basis configurational states, i.e., a minimal active space (MAS), in MSDFT. Obviously, the number of determinants (N²) to exactly represent the multistate density D(r) is significantly smaller than that needed to represent the corresponding wave functions as in a full CI treatment or even in an approximate method employing a complete active space (CAS).

2.3.2. Correlation Matrix Functional

We next introduce the correlation matrix functional, leading to a method for optimizing the multistate matrix density via one-electron orbitals. Given the basis determinants {Ξ_A} of a MAS, representing exactly the multistate matrix density D(r) for the N states of interest {Ψ^K; K = 1, ..., N}, the Hamiltonian matrix density functional is written as

19

where the four terms on the right-hand side of the equation are, respectively, the matrix density functionals for the kinetic, Hartree-exchange, external potential, and correlation energies. The matrix elements for the first three terms in eq 19 are determined from the corresponding Slater determinants,

The correlation matrix functional 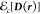is formally defined as follows according to Theorem 1,⁶¹

20

Note that for the ground state, i.e., N = 1, eq 20 is equivalent to the exchange-correlation functional in KS-DFT,

However, a difference from KS-DFT is that 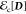defines the part of correlation energy not explicitly included in the minimal active space used to represent D(r).⁶³

2.3.3. Nonorthogonal State Interaction

The adiabatic ground and intermediate states in the present MS-EDA analysis are written as linear combinations of determinant basis states {Ξ_A} that form a minimal active space (MAS), consisting of the Kohn–Sham reference and singly excited configurations,

21

where Ξ_(X•Y)^KS is the reference BLKS determinant for the block-localized complex (eq 5), Ξ_i^a is a singly excited configuration, and {c} are configuration coefficients determined by NOSI by diagonalizing the Hamiltonian matrix functional . Although orbitals and {c} can be optimized simultaneously, in NOSI,⁶³ the determinant states Ξ_(X•Y) and in eq 21 are variationally optimized first using the block-localized excitation (BLE) method.^91,92,98 In particular, each constrained BLKS-determinant wave function is written

22

where χ_j^U (j=1, ⋯, N_U) is the jth block-localized spinorbital that is expanded over the basis functions located on atoms of monomer U (U = X, Y), N_U is the number of electrons, and χ_a indicates that the ith occupied spinorbital of monomer X in the BLKS reference Ξ_(X•Y)^KS is replaced by the ath virtual orbital. In MSDFT, we include all spin-complement configurations in the MAS, all of which are together labeled by a single index {Ξ_A}.

Subsequently, the matrix elements of the Hamiltonian matrix functional in the basis of {Ξ_A} are determined by

23

where the first term can be evaluated by a standard method for nonorthogonal matrix elements.^102−104 For the diagonal elements of the correlation matrix functional, the approximate density functional energy developed for KS-DFT is used,

24

keeping in mind that ρ_A(r) is obtained from a block-localized determinant Ξ_A with non-aufbau occupations for locally excited state.

The off-diagonal element 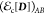called transition density functional (TDF)¹⁰⁰ is new, and does not exist in KS-DFT; currently, an explicit approximate TDF has not yet been developed. Thus, further approximations are needed. For spin coupling interactions between determinants that yield a pair of singlet and triplet (M_s = 0) states, the value of the TDF energy can be obtained consistently by enforcing the energy degeneracy among the components of a triplet state,^105−108 corresponding to a KS density functional used for the diagonal terms:

25

where E_xc^KS[ρ_AB(r)] is the “Kohn–Sham” correlation energy with the electron density ρ_AB^↑↑(r) of the spin-up triplet state Ξ_AB, and E_xc^KS[ρ_A(r)] is the KS correlation energy using ρ_A^↑↓(r) (equivalently with ρ_B) corresponding to the spin-mixed determinant state. The superscript sp in eq 25 indicates spin-pairing interactions. The subscript AB in ρ_AB^↑↑(r) is used to indicate that the determinant Ξ_AB refers to the triplet state with respect to the two spin complement determinants Ξ_A^↑↓ and Ξ_B. Applying the TDF term in eq 25 in NOSI yields a pair of singlet and triplet states (M_s = 0), thereby, the singlet–triplet energy gap without spin contamination. For all other situations, we use the overlap-weighted average correlation energy of the two interacting states to approximate their TDF:⁶⁴

26

We note that the use of a standard exchange-correlation functional or a hybrid density functional for the diagonal terms typically yields more accurate results than employing a correlation-only functional. In this case, the corresponding exchange term is reciprocally removed in the first term of eq 23. In other words, standard KS-DFT energies are used for the diagonal terms except that the determinant is block-localized nonaufbau occupation constrained.

3. Computational Details

Monomer and exciplex structures have been optimized using KS-DFT or TDDFT with the Minnesota M06-2X density functional¹⁰⁹ and the cc-pVTZ and cc-pVDZ basis sets.¹¹⁰ The Gaussian16 program is used in these calculations.¹¹¹ For the present multistate energy decomposition analysis, the MSDFT-NOSI method has been implemented into the Qbics program developed in our laboratories¹¹² and a separate program for BLW-ED analysis interfaced with the GAMESS-US program for electronic integrals.¹¹³ In NOSI calculations, we used a fine grid consisting of 96 radial shells and 302 angular points. In addition, EOM-CCSD, FIC-NEVPT2, and MRCI were performed with two basis sets for comparison in the Supporting Information. Throughout this Perspective, energies are given in electron volts (eV), widely used in spectroscopy of excited states.

4. Results and Discussion

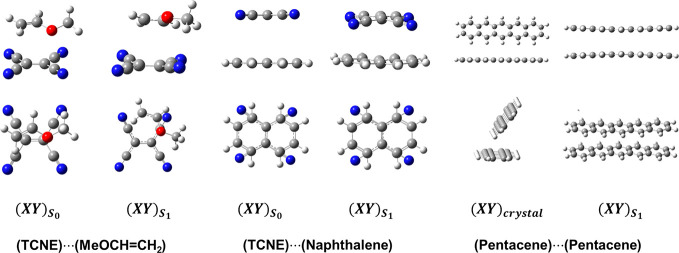
Based on the nature of stabilizing forces in exciplex formation, we roughly group the excited-state complexes into three categories: (1) encounter excited-state complex, (2) charge-transfer exciplex, and (3) intimate excimer or exciplex. Excited-state complexes in Category 1 originate dominantly from the same type of intermolecular forces as that in the ground state, in which one molecule is in an excited state and the geometry of the other molecule in the complex remains in the ground state with only a minor geometrical deformation induced by (nonphotochemical) intermolecular interactions. The excimer complex between two acetone molecules and the exciplex between acetone and methyl vinyl ether belong to this category, in which one acetone molecule is excited to its n → π* state that is loosely bound to the second molecule. In Category 2, interfragment charge-transfer excitation has a lower energy than or similar to that of valence excitations of either species in a bimolecular complex. The driving force for exciplex formation is electrostatic Coulomb interaction. Examples include complexes involving the strong electron acceptor tetracyanoethylene (TCNE). Category 3 complexes are produced as a result of the resonant excitation of all individual species in the complex. The pentacene excimer complex in the S₁ state is a vivid illustration.

We first discuss the performance of nonorthogonal state interaction (NOSI) method of MSDFT by comparison with results from TDDFT calculations employing the same approximate density functional (M06-2X). Then, we present findings from MS-EDA analysis of the three categories of excited-state complexes.

4.1. Excitation Energies and Validation of Method

The performance of the MSDFT-NOSI method along with a small MAS is validated on the computed excitation energies (Figure 2). Since intermediate reference states in the EDA procedure are electronic diabatic states, which are not direct observable experimentally, we focus on comparison of the excitation energies of the monomer compounds. Table 1 lists the total energies of the ground state and the vertical excitation energies of the first two singlet excited states from MSDFT-NOSI calculations for the monomer compounds considered in this work and related molecules. In addition, included in Table 1 are the emission energies using the optimized structures of acetone and pentacene in the first excited states. The NOSI results are compared with TDDFT values along with experimental data. For these simple organic chromophores, TDDFT is known to perform well in benchmark studies,¹¹⁴ providing a good reference for comparison with the NOSI method employing the same approximate density functional and basis set. Table 1 shows that the agreement between results from the two computational methods is excellent with a root-mean-square deviation (RMSD) of 0.11 eV for the S₁ states, 0.25 eV for the S₂ states, and 0.19 eV for all vertical excitation energies. A further indicator is the mean-signed-average (MSA) and mean-unsigned-error (MUE), which are −0.06 and 0.14 eV, exhibiting no systematic errors for the singlet excited states. We anticipate that this trend will be carried over to the energies of intermediate states in MS-EDA.

Figure 2.

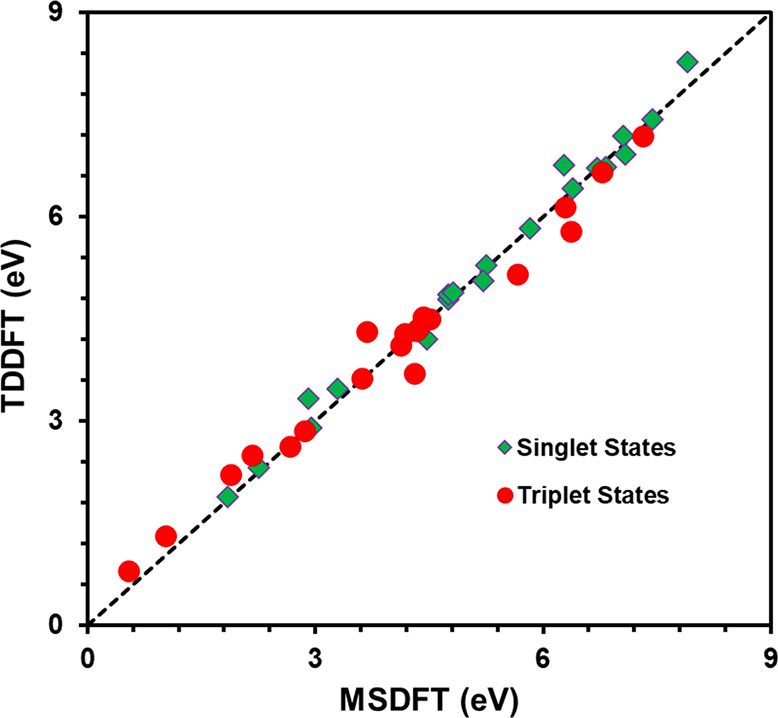
Comparison of vertical excitation energies obtained using multistate density functional theory (MSDFT) and time-dependent density functional theory (TDDFT). The Minnesota M06-2X functional is used.

Table 1. Computed Total Energies (au) for the Ground State and Excitation Energies (eV)^a.

	S0 (au)		S1			S1
moleculeb	MSDFT	ΔEKS	MSDFT	TDDFT	expc	MSDFT	TDDFT	expc
naphthalene	–385.76533	0.00000	4.75	4.78	4.7	4.81	4.89	3.97
pentacene	–846.54223	0.00000	2.25	2.32	2.3	3.29	3.47
PCA	–845.54485	–0.00007	5.25	5.29	5.08	5.83	5.83	6.41
TCNE	–447.41678	0.00000	4.75	4.85	4.75, 4.84	5.21	5.06	5.67
t-DME	–307.51100	–0.00015	6.71	6.71	6.2	7.08	6.91
c-DME	–307.50997	–0.00028	6.39	6.42	6.16	6.82	6.73
MVE	–193.03249	–0.00043	7.06	7.19	6.48	7.44	7.42	9.6
Me2C=O	–193.07551	–0.00055	4.47	4.20	4.38	7.90	8.27	6.35
Me2C=O (S1)	–193.04394	–0.00197	2.94	2.90	3.06	6.27	6.75
pentacene (S1)	–846.53459	0.00000	1.85	1.89		2.91	3.33

^aThe Minnesota M06-2X density functional is used both in NOSI and TDDFT calculations. Relative energy given in electron volts (eV) between results from MSDFT-NOSI and KS-DFT, ΔE_KS = E_NOSI – E_KSDFT. This is a reasonable indicator of possible double counting of electron correlation for single-reference molecules.

^bPCA: para-chloromethyl anisole, TCNE: tetracyanoethylene, MVE: methyl vinyl ether, DME: 1,2-dimethoxyethene.

^cReferences (115−120).

Another important finding is revealed in Table 1 by comparing the total ground-state energies from NOSI with those by KS-DFT calculations (Figure 2). The former method is a multistate, multiconfigurational DFT in which state interaction is key in determining both the ground state and excited state energies, whereas the latter employs a noninteracting system consisting of a single determinant wave function purely for representing the ground-state density. One lingering question in multiconfigurational DFT (MC-DFT) has been double counting of electron correlation since KS-DFT, in principle, includes all electron correlation, which is added to an MCSCF energy.^{100,121−123} MSDFT differs from other MC-DFT models in that the total electron density from a MCSCF wave function is not directly used in KS-DFT correlation energy evaluations. Rather, the MSDFT correlation functional is an implicit functional of the multistate density and the correlation functional developed for KS-DFT is used solely to approximate the correlation energy of a determinant state (diagonal terms) of the Hamiltonian matrix density functional . Consequently, we find that the difference in the ground-state energy between MSDFT and KS-DFT is negligibly small, even though the KS-DFT state is included as one member of the MAS in all NOSI calculations. Acetone exhibits a small amount of multistate stabilization of 0.55 meV (0.01 kcal/mol) in the ground-state geometry and ca. 2 meV (0.05 kcal/mol) using the S₁ state geometry, while multistate effects as compared to KS-DFT are generally less than 0.5 meV for other compounds. The data in Table 1 demonstrate that there is little double-counting of correlation in these systems when an approximate density functional developed for KS-DFT is directly used for the determinant states in MSDFT.

The computed triplet state energies are given in Table 2. For the lowest triplet T₁ state, KS-DFT is typically sufficient, whereas the T₂ states are obtained using TDDFT based on this reference. Table 2 shows that the accord between NOSI and TDDFT (KS-DFT) results is also reasonably good. In particular, the RMSD errors are 0.25 eV for T₁ states, 0.35 eV for T₂ states, and 0.31 eV overall. Further, the MSE and MUE are, respectively, 0.00 and 0.20 eV for all triplet states. However, the NOSI T₁ energies of pentacene (both in the S₀ and S₁ structures) and para-chloromethyl anisole (PCA) have somewhat greater deviations from KS-DFT values than other cases. We attribute the increased deviation to multiconfiguration characteristics in the T₁ triplet states for these two aromatic compounds, which is confirmed by the Chirgwin–Coulson structure weights, having values of 0.92 and 0.94 for the dominant configuration in the two (S₀ and S₁) pentacene structures, and a value of only 0.65 for the dominant configuration in PCA. Thus, the use of a single determinant in KS-DFT for the T₁ state may be questionable for these compounds and could indeed have large errors. In this regard, the results from MSDFT-NOSI may be more reliable. This is reflected in the computed T₁ energies, where NOSI yields a lower value than KS-DFT.

Table 2. Computed Total Triplet-State Energies (au) and Excitation Energies (eV) for the First Two Triplet States Relative to the Singlet Ground State^a.

	T1(X)		T1			T2
	MSDFT	ΔEKS	MSDFT	TDDFT	expb	MSDFT	TDDFT	exp
naphthalene	–385.63259	–0.00050	3.61	3.63	3.0	4.18	4.28	3.9
pentacene	–846.50452	–0.01088	1.03	1.32	0.86	2.17	2.50	>2.0
PCAb	–845.40970	–0.03489	3.68	4.32		4.42	4.53
TCNE	–447.31172	0.00000	2.86	2.86		5.66	5.16
t-DME	–307.35069	–0.00004	4.36	4.36		6.77	6.65
c-DME	–307.35079	–0.00026	4.33	4.33		6.29	6.14
MVE	–192.86691	0.00000	4.51	4.50	4.2	7.31	7.19	8.8
Me2C=O	–192.92376	0.00000	4.13	4.11	4.18	6.36	5.78	5.88
Me2C=O (S1)	–192.94603	–0.00001	2.66	2.63		4.30	3.70
pentacene (S1)	–846.51462	–0.00923	0.54	0.80		1.88	2.22

^aThe Minnesota M06-2X density functional is used.

^bReferences (124−128).

4.2. Encounter Excited State Complexes

The optimized structures (Figure 3) of the excimer complex of two acetone molecules and the exciplex between acetone and methyl vinyl ether in their first excited state using TDDFT/M06-2X/cc-pVTZ reveal that they are characterized as a single acetone excitation to its n → π* state with a bent geometry interacting with its binding partner in the ground state. This is clearly reflected by the geometrical distortion energies of 0.75 and 0.82 eV for the photochemically excited acetone in the two complexes (Table 3), respectively, corresponding to the change from the ground state in equilibrium to that found in the excited-state complexes. For the other partners in the complexes the energy changes are negligible (the small negative values are probably due to multistate effects). Table 3 lists the adiabatic and intermediate excited-state energies of the monomer and dimer species, all of which are given relative to that at the equilibrium ground state for direct comparison (Scheme 1). Therefore, the adiabatic excitation energies of acetone are about 3.8 eV in both complexes, significantly smaller than the vertical excitation energy of 4.47 eV (Table 1), but the vertical emission (hν_ad−ΔE_dist) energies of 3.05 and 2.97 eV of the excited acetone in the exciplex geometries in the two complexes are similar to that (2.94 eV) of the optimized S₁ structure of acetone (Table 1) from MSDFT-NOSI calculations. On the other hand, the “adiabatic” excitation energies of the second monomers in the two exciplexes are, respectively, 4.39 and 6.80 eV, close to the vertical excitation energies of the isolated monomers (4.47 and 7.06 eV). Thus, these two exciplexes are best described as dipolar van der Waals complexes.

Figure 3.

Optimized structures in the first singlet excited states of the acetone excimer and acetone···methyl vinyl ether exciplex.

Table 3. Excitation Energies of Adiabatic, Diabatic, and Intermediate States in the Lowest Singlet and Triplet Excited States Associated with the Acetone Dimeric and Acetone-Methyl Vinyl Ether (MVE) Exciplex Complexes^a.

(X)···(Y)		(Me2C=O)···(Me2C=O)		(Me2C=O)···(MVE)
energy terms		singlet	triplet	singlet	triplet
hνad	X*[EC]	3.80	3.53	3.79	3.53
	Y*[EC]	4.39	4.08	6.80	4.39
ΔEdist	X[EC]	0.75	0.75	0.82	0.82
	Y[EC]	–0.02	–0.02	–0.01	–0.01
ELex	(X*•Y)	3.58	3.31	3.64	3.38
	(X•Y*)	4.97	4.67	7.46	5.04
EEx	(X•Y)+*	3.58	3.31	3.64	3.38
	(X•Y)−*	4.97	4.67	7.34	5.04
ESE	(X•Y)+SE	3.52	3.26	3.64	3.38
	(X•Y)−SE	4.85	4.55	6.31 (CT),b 7.38	5.04
E(XY)	(XY)1*	3.53	3.22	3.63	3.39
	(XY)2*	4.66	4.46	5.76 (CT),b 7.27	4.51

^aAll energies are given in electron volts (eV), relative to the ground state energies of a monomer, X[S₀] and Y[S₀], or two separate molecules at their optimized structures, i.e., adiabatic ground-state energies are set equal to zero. Square brackets indicate optimized geometry used in energy calculations with S₀ for the ground state and EC as exciplex complex. All calculations for bimolecular complexes adopt the [EC] structure. The M06-2X density functional and the cc-pVTZ basis set are used in NOSI calculations. The energies terms may be compared with the illustration of Scheme 1.

^bCharge transfer (CT) state.

The triplet state energies are also shown in Table 3, exhibiting similar trends, but they are obtained using the same monomer and excimer geometries optimized for the singlet states. Thus, they are not further discussed nor listed for these complexes or any of the other systems below.

The local excitation energies of the excited acetone and its binding partner in both complexes exhibit different trends (Tables 1 and 2), with a large Stokes shift of 0.84 eV (3.80 eV excitation and 2.96 eV emission) in the acetone excimer and 0.79 eV (3.79 eV excitation and 3.00 eV emission) in the acetone-MVE exciplex for the excited acetone molecule, but with essentially no spectral change for the second monomer in the complex as it largely remains in the ground-state geometry. A relevant quantity is the exciton polarization energy, ΔE_Lpol^K, corresponding to the vertical excitation energy difference of the chromophore (acetone) in the same geometry with and without the presence of the second binding partner molecule, which is −0.09 eV (2.96 eV–3.05 eV) for the acetone excimer, and +0.03 eV (3.00 eV–2.97 eV) in the acetone-MVE exciplex. The polarization effects are small for the ground-state monomers, with energy changes of +0.06 and +0.01 eV in the two complexes, respectively. Note that the seemingly positive energy changes are compensated for by the binding energy of the isolated, distorted monomers to form the local complexes (−0.11 and −0.17 eV, respectively). The excited-state energies and relative energies in Table 4 are displayed in Figure 4 for the acetone-MVE exciplex, corresponding to the energy terms defined in Scheme 2, whereas results for the acetone excimer can be found in ref (5). Fluorescence quenching by alkyl vinyl ethers has been reported by Schore and Turro who attributed the observed quenching rates to the formation of acetone···ether exciplexes with charge transfer playing a role.¹²⁹ A correlation to the observed spectral shift of tetracyanoethylene···alkyl vinyl ethers discussed next was found.

Table 4. Relative Energies (eV) in Multistate Energy Decomposition Analysis of the Lowest Singlet and Triplet Excited States in the Acetone Excimer and Acetone-Methyl Vinyl Ether (MVE) Exciplex^a.

(X)···(Y)	(Me2C=O)···(Me2C=O)				(Me2C=O)···(MVE)
energy terms	S1	S2	T1	T2	S1	S2	T1	T2
hν̅oK	3.80	4.39	3.53	4.08	3.79	6.20	3.53	4.39
ΔErefK	2.96	4.35	2.69	4.05	3.00	6.70	2.74	4.40
ΔELint	0.62	0.62	0.62	0.62	0.64	0.64	0.64	0.64
ΔEExK	2.96	4.35	2.69	4.05	3.00	6.70	2.74	4.40
ΔΔEResK	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
ΔΔESEK	–0.06	–0.12	–0.05	–0.12	0.00	–1.03,b 0.04	0.00	0.00
ΔΔEOCDK	0.01	–0.19	–0.04	–0.09	–0.01	–0.55,b −0.11	0.01	–0.53
ΔΔELCTS0	–0.07	–0.07	–0.07	–0.07	–0.09	–0.09	–0.09	–0.09
ΔEb	–0.27	0.27	–0.41	0.38	–0.16	–0.44,b 1.07	–0.14	0.12

^aSee Scheme 1 and the footnote of Table 3.

^bCharge transfer state, energy given relative to the S₂ exciton state.

Figure 4.

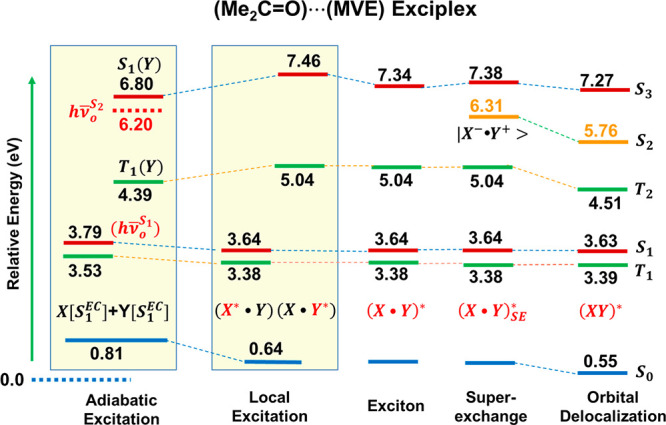
Ground and excited-state energies (eV) for the first singlet exciplex of acetone and methyl vinyl ether in multistate energy decomposition analysis. The energies of adiabatic ground state of isolated monomers in equilibrium geometries have been set equal to zero. The effective adiabatic excitation energies of the separate monomers in the exciplex geometries are given in red. Singlet (maroon) and triplet (green) states are labeled on the far right for exciplex complex. Energy levels are not drawn in scale.

The remainder of the energy terms for the two loosely associated excimer complexes are largely unremarkable except the second excited state of the acetone-MVE exciplex (recall that geometry is optimized for the S₁ state), where a charge transfer state emerges to be lower than the covalent excitation of MVE (state in brown in the superexchange intermediate in Figure 4). Thus, relative to the S₂ exciton state, corresponding to the first local excited state of MVE in the dimer complex, the superexchange stabilization is −1.03 eV, which is further lowered by −0.55 eV by orbital and configuration-state delocalization (OCD term). Therefore, the net binding energy of the S₂ exciplex state (S₁ state geometry) is −0.44 eV, relative to MVE reference valence excitation (hν̅_o^S₂). For the S₁ exciplexes of acetone dimer and acetone-MVE, the net binding energies (eq 4) are −0.27 and −0.33 eV, with a net ground-state contribution of 0.55 eV in both systems to overcome the large structural distortion energies.

4.3. Charge-Transfer Complexes

Tetracyanoethylene (TCNE) can form rather stable complexes (Figure 5) with methyl vinyl ether (MVE) and naphthalene (Naph) in the ground state with binding energies of −0.51 eV and −0.28 eV (−11.8 and −6.5 kcal/mol), respectively (Table 5). However, at the S₁ exciplex geometries, the binding energies in the ground state (ΔE_Lb) are repulsive (+0.41 eV) in the MVE structure and barely associative (−0.03 eV) for the naphthalene complex, indicating significant monomer structure distortion in the exciplex. In both exciplexes, the lowest excited state is of charge transfer character from the electron rich monomers to TCNE. In fact, the three lowest excited states in the TCNE-Naph exciplex are CT states, corresponding to the transfer of one electron from the HOMO, HOMO–1, and HOMO–2 orbitals of naphthalene to the LUMO of TCNE (Table 5 and Figure 6), in both the optimized complex structures of the ground state (S₀) and the first excited state (S₁). In the exciplex complex, the electron acceptor TCNE is noticeably distorted with a bent butterfly like geometry, having a geometrical distortion energy ΔE_dist of 0.17 eV in the MVE complex and 0.22 eV in the naphthalene state. Interestingly, covalent vertical excitation energies for both monomers in the two exciplex complexes are not significantly different in the S₀ and S₁ complex structures. Exciton delocalization only lowers the excited-state energies modestly by about 0.1 eV in the TCNE-MVE exciton state, and somewhat greater at 0.25–0.40 eV for the TCNE-Naph complex.

Figure 5.

Optimized bimolecular complex structures (side view on top, and top or tilt views in the bottom) for tetracyanoethylene (TCNE)···methyl vinyl ether, TCNE···naphthalene, and pentacene dimer in the optimized ground state (XY)_S0 (crystal structure for pentacene) and first singlet excited state (XY)_S1. M06-2X density functional and the cc-pVDZ basis set are used.

Table 5. Relative energies (eV) of Adiabatic, Diabatic, and Intermediate States in the Lowest Singlet Excited States of Tetracyanoethylene (TCNE)···Methyl Vinyl Ether and TCNE···Naphthalene Exciplex^a.

(X)···(Y)		(TCNE)···(MeOCH=CH2)		(TCNE)···(naphthalene)b
energy terms		[S0] geom	[S1] geom	[S0] geom	[S1] geom
hνabad	X*[EC]	4.68	4.41	4.58	4.44
	Y*[EC]	6.81	6.49	4.61, 4.69	4.65, 4.50
ΔEdist	X[EC]	0.00	0.17	0.02	0.22
	Y[EC]	–0.02	–0.03	–0.02	0.12
ELex	(X*•Y)	4.55	4.67	4.35	4.27
	(X•Y*)	6.60	7.04	4.40, 4.48	4.56, 4.42
EEx	(X•Y)+*	4.46	4.58	4.10	3.87
	(X•Y)-*	6.69	7.10	4.40, 4.69	4.56, 4.76
ESE	(X•Y)+SE	3.04 (CT), 4.42	1.90 (CT), 4.69	2.42 (CT)c	1.77 (CT)c
				3.16 (CT),c 4.12	2.81 (CT),c 3.98
				4.53 (CT)c	4.13 (CT)c
	(X•Y)-SE	6.65	7.10	4.41, 4.69	4.61, 4.81
E(XY)	(XY)1*	2.62 (CT), 4.29	1.19 (CT), 4.63	1.67 (CT)c	1.15 (CT)c
				2.46 (CT)c	2.29 (CT)c
				3.77 (CT)c	3.45 (CT)c
				4.32	4.12
	(XY)2*	NAd	NAd	4.40, 4.51	4.38, 4.53

^aAll energies are given relative to the adiabatic ground state energies of monomers. The M06-2X density functional and the cc-pVDZ basis set are used. The energy terms may be compared with the illustration of Scheme 1.

^bTwo close-lying states are given for naphthalene with L_b first followed by L_a.

^cCharge transfer (CT) states, respectively from HOMO, HOMO–1, and HOMO–2 of naphthalene to the LUMO of TCNE.

^dNot assigned.

Figure 6.

Ground (blue) and excited-state (maroon) energies (eV) for the singlet exciplex of tetracyanoethylene (TCNE) and naphthalene in multistate energy decomposition analysis. The S₀ complex geometry is used. The energies are given relative to that of adiabatic ground state of isolated monomers in equilibrium geometry. Three charge transfer states (in brown) appear at the superexchange stage of MS-EDA. The effective adiabatic excitation energies of the separate monomers in the exciplex geometries are 4.62, 4.61, and 4.65 eV for the first, second, and third exciton states, originating dominantly from the π → π* state of TCNE, and the L_b and L_a states of naphthalene. Energies corresponds to excitation and resonance terms defined in Scheme 2.

Not surprisingly, the greatest energy contribution in the MS-EDA analysis come from charge transfer (CT) effects in the direction from MVE or Naph to TCNE. For the TCNE-MVE complex, the charge-transfer superexchange stabilization is estimated to be 1.42 eV using the ground-state structure of the bimolecular complex, and 2.68 eV in the S₁ exciplex geometry. Similarly, for the TCNE-Naph exciplex, we found a CT stabilization of 1.68 eV in the S₀ complex geometry (Figure 6), and 2.10 eV in the S₁ exciplex structure. Orbital delocalization also significantly lowers the excitation energies of the exciplexes, contributing −0.42 and −0.71 eV in the two structures of TCNE-MVE exciplex, and −0.75 and −0.62 eV for the TCNE-Naph complexes. However, the charge delocalization effects from TDDFT calculations are likely overestimated due to delocalization errors on charge-transfer excitations.¹³⁰

For a CT exciplex, its binding energy is not directly related to covalent excitation of either monomer. Nevertheless, we can still consider the CT complex formation through an initial formation of the exciton complex, followed by an interfragment charge transfer as in the MS-EDA steps. Then, the definition of binding energy of eq 3 can still be used. Thus, for TCNE···MVE, the binding energies at geometries of the ground-state complex and the optimized S₁ exciplex are −2.15 and −3.28 eV, and for TCNE···Naph, they are −2.94 and −3.30 eV, respectively.

On the other hand, if one considers the starting reference state as the equilibrium geometry of the bimolecular complex in the ground state, the exciplex binding energy may be defined by the following photochemical process:

27

Equation 27 shows that for CT exciplex, the binding energy of the exciplex may be assigned to the energy change from the vertical charge-transfer absorption complex in the equilibrium ground-state geometry to the equilibrium exciplex geometry. From the data in Table 6, we immediately obtain a ΔE_b^CT of −1.13 eV in the TCNE···MVE exciplex and −0.36 eV in TCNE···Naph, as a result of structural relaxation induced by CT excitation. Then, the energy components will be the term-by-term difference in Table 5 obtained between the optimized geometries in the ground state (XY)[S₀] and the excited state of the exciplex (XY)[S₁]. The details of these energy differences are not further discussed here.

Table 6. Relative Energies (eV) in Multistate Energy Decomposition Analysis of the Lowest Singlet States in Tetracyanoethylene (TCNE)···Methyl Vinyl Ether and TCNE···Naphthalene Exciplex^a.

	(TCNE)···(MeOCH=CH2)				(TCNE)···(naphthalene)
	[S0] geom		[S1] geom		[S0] geom		[S1] geom
energy	S1	S2	S1	S2	S1	Lb/La	S1	La/Lb
hνoK	4.77	6.72	4.47	6.37	4.62	4.61/4.65	4.45	4.47/4.65
ΔELint	–0.23	–0.23	0.54	0.54	–0.22	–0.22	0.08	0.08
ΔErefK	4.86	6.75	4.18	6.46	4.62	4.62/4.65	4.24	4.27/4.48
ΔEExK	4.69	6.92	4.04	6.66	4.33	4.62/4.91	3.79	4.48/4.68
ΔΔEResK	–0.17	0.17	–0.18	0.20	–0.29	0.00/0.26	–0.45	0.21/0.20
ΔΔESEK	(−1.42)	–0.04	(−2.68)	0.11	(−1.68)	0.01	(−2.10)	0.05
					(−0.94)	0.00	(−1.06)	0.05
					(0.43)		(0.26)
					0.02		0.11
ΔΔEOCDK	(−0.42)	–0.13	(−0.71)	–0.06	(−0.75)	–0.02	(−0.62)	–0.28
					(−0.70)	–0.18	(−0.52)	–0.23
					(−0.76)		(−0.68)
					0.20		0.14
ΔELCTS0	–0.28	–0.28	–0.13	–0.13	–0.05	–0.05	–0.11	–0.11
ΔELbS0	–0.51		0.41		–0.27	–0.27	–0.03	–0.03
ΔEbK	(−2.15)		–3.28		(−2.94)b	–0.22	(−3.30)b	–0.14
covalent					–0.29	–0.14	–0.33	–0.07

^aCharge transfer (CT) states are shown in parentheses. See Scheme 1 for energy definition and the footnote of Table 3.

^bOnly binding energy for the lowest charge transfer state is shown.

Experimentally, a charge-transfer absorption spectrum for the TCNE···MVE complex has been reported with a maximum absorption wavelength of 401 nm (3.09 eV) in 90% cyclohexane and 10% CH₂Cl₂ solution.¹³¹ With the ground-state bimolecular complex structure, the computed values are 3.27 eV (3.04 – (−0.23)) at the superexchange stage using NOSI and 3.13 (2.62 – (−0.51)) eV, without considering solvent effects. The value for the exciplex geometry appears too low. In comparison with previous calculations using an optimized range-separated functional^132,133 and experimental data,¹³⁰ the excitation energies of the TCNE···Naph complex for the first two exciplex states (2.64 and 3.38 eV) using the S₀ structure from the present MS-EDA using NOSI at the superexchange stage are in good accord with experimental results (2.60 and 3.23 eV for S₁ and S₂)¹³⁰ and with specifically optimized range-separated TDDFT calculations (2.7 eV for S₁)¹³² and the CAM-QTP-02 functional (2.80 and 3.57 eV).¹³³

4.4. Intimate Excimers

For the third category of excited-state complexes, in which the electronic excitation is fully delocalized over the monomers in the exciplex, we illustrate the energy components of the anthracene dimer system in two geometry arrangements: the optimized S₁ excimer, and a fishbone configuration corresponding to that found in a crystal structure of anthracene Table 7. This system has been described in a preliminary report on the MS-EDA methodology, although a different reference state was used in binding energy calculations. Here, we list the binding energy relative to the reference energy for the unbound species defined in eq 3 and the locally excited reference state for exciton resonance energies in Table 8. We highlight the key contrasting features of the intimate excimer in comparison with conformation dependence of the anthracene dimer itself, and the other two categories of exciplexes. An energy correlation diagram for the excimer complex of pentacene dimer can be found in reference.⁵

Table 7. Computed Excitation Energies (eV) and Energy Components from Multistate Energy Decomposition Analysis (MS-EDA) for Pentacene Excimer and a Pentacene Dimer Fishbone Configuration^a.

	excimer		fishboneb
energy term	Lb	Lb	La	Lb
hν̅0K	2.10	3.14	2.21	3.24
ΔEdist	0.18	0.18	0.03	0.03
ELex[(X*•Y)K]	1.89	3.04	1.99/1.98	2.92/2.92
EEx[(X•Y)K–]	1.46	2.92	1.97	2.92
EEx[(X•Y)K+]	2.40	3.03	2.02	2.93
ESE[(X•Y)CTK–]	0.62	2.70	1.88	2.92
ESE[(X•Y)CTK+]	2.30 (CT), 2.47	3.38	1.97, 2.23 (CT)	2.93
E(XY)K–	0.94	2.49	1.71	3.07
E(XY)K+	2.11	2.87	1.92	3.10

^aAll excitation energies are given relative to that of the adiabatic ground state of isolated pentacene. The M06-2X density functional is used along with the cc-pVDZ basis set. Adapted from ref (5). Copyright 2023 American Chemical Society.

^bThe HOMO–1 → LUMO+1 configuration was not included.

Table 8. Relative Energies (eV) in Multistate Energy Decomposition Analysis of Singlet States of Pentacene Excimer and Pentacene Dimer in a Fishbone Configuration^a.

	excimer				fishbone
energy	La–	La+	Lb–	Lb+	La–	La+	Lb–	Lb+
hν̅oK	2.10	2.10	3.14	3.14	2.21	2.21	3.24	3.24
ΔErefK	1.89	1.89	3.04	3.04	2.32	2.31	3.25	3.25
ΔELint	0.07	0.07	0.07	0.07	–0.33	–0.33	–0.33	–0.33
ΔEExK	1.33	2.46	2.70	3.38	2.30	2.35	3.25	3.26
ΔΔEResK	–0.56	0.57	–0.34	+0.34	–0.02	0.04	0.00	0.01
ΔΔESEK	–0.84	(−0.10) 0.07	–0.22	0.35	–0.09	–0.05 (0.21)	0.00	0.00
ΔΔEOCDK	0.32	–0.19	–0.21	–0.51	–0.17	–0.05	0.05	0.07
ΔELCTS0	–0.13	–0.13	–0.13	–0.13	–0.14	–0.14	–0.14	–0.14
ΔELbS0	–0.05	–0.05	–0.05	–0.05	–0.47	–0.47	–0.47	–0.47
ΔEbK	–1.22	(0.14)	–0.80	0.15	–0.50	–0.29	–0.27	–0.24

^aCharge transfer (CT) states are shown in parentheses. Definition of energy terms can be found in Scheme 1. The M06-2X density functional is used along with the cc-pVDZ basis set.

As other polyaromatic acenes, anthracene has two close-lying excited singlet states termed as the L_a(S₁) and L_b(S₂) states. The dimeric excimer of anthracene molecules was optimized to a symmetric geometry using TDDFT with M06-2X/cc-pVDZ, whereas the two monomers in the fishbone configuration in the crystal structure are not fully equivalent. In the latter case the HOMO–1 to LUMO+1 excited configuration was not fully converged and thus not included in the calculation, which would affect the L_a energy slightly. In the excimer geometry it has a rather small contribution to the L_a state using the excimer structure with a structure weight of 0.06 (0.94 for the HOMO → LUMO configuration). The anthracene dimer as a category 3 excimer is distinguished from the other two classes of exciplexes by strong exciton resonance interaction in all excimer states between the two locally excited monomers, resulting in large energy splitting |ΔV_AB| in the L_a and in the L_b state. Table 8 shows that the L_a^± and L_b energy differences are 1.13 and 0.68 eV for the excimer, and that |ΔV_AB| is highly sensitive to the distance and relative orientation (overlap) between the monomers, reducing to values of 0.05 and 0.01 eV for the two pairs of states in the fishbone configuration. In the excimer complex, the charge-delocalization state lies between the L_a^- and L_a states, stabilizing the former by −0.84 eV, but increasing the energy of L_a⁺ by 0.07 eV in a three-state interaction scheme. On the other hand, at the fishbone configuration, the charge-delocalization state is higher in energy than the L_a states, thereby, lowering the energies of both L_a and L_a⁺ states by −0.09 and −0.05 eV. Surprisingly, superexchange stabilization is also highly dependent on the overlap between the two monomer states. Not surprisingly, the excimer complex has a strong binding energy of −1.16 eV, whereas for the fishbone configuration found in pentacene crystal it is only −0.50 eV, significant, but −0.47 eV comes from ground-state effect using the M06-2X density functional (Table 8).

4.5. Structure Weights

We finally comment on the computed structure weights of local states in the exciton and superexchange intermediates. In Table 9, we list the structure weights of three representative complexes, namely, the acetone⋯MVE and TCNE⋯naphthalene exciplex, and the anthracene excimer. In MS-EDA, the structure weights for the exciton states have been used to determine the corresponding weighted adiabatic excitation energy of the isolated molecules (hν̅_o^K), and the reference energy for the locally excited states (ΔE_ref) to determine exciton resonance energy. Further examination of the data in Table 9 reveals an interesting trend. For the intimate excimer complexes, strong state interactions are found among the symmetry allowed local states. Even though the exciton resonance stabilization is severely reduced in the tilted pentacene orientation of the fishbone structure, exciton delocalization is observed. However, the tilting effect clearly results in a preference for a directional charge transfer in the superexchange complex, with structural weights of 0.28, 0.02, and 0.70 for the L_a^- exciton state and the |P^–•P⁺⟩ and |P⁺•P^–⟩ charge transfer states, respectively. For comparison, this state (S₂) in the symmetric excimer complex has an equal forward and backward charge transfer contributions, resulting in a net zero charge transfer in the complex. The implication of this finding could be significant toward an understanding of the mechanism of directional multiexciton formation in singlet fission in pentacene monolayer materials.⁵⁰

Table 9. Structure Weights of Local Excited States and Individual Charge Transfer (CT) States in the Exciton and Superexchange Intermediates in Multistate Energy Decomposition Analysis (MS-EDA)^a.

	exciton (X•Y)*		superexchange (X•Y)SE
exciplex state	(X*•Y)	(X•Y*)	(X•Y)*	(X–•Y+)	(X+•Y–)
(Me2C=O)···MVE exciplex
(n → π*)X	1.00	0.00	1.00	0.00	0.00
CT			0.09	0.91	0.00
(π → π*)Y	0.20	0.80	0.98	0.02	0.00
TCNE···naphthalene exciplex
(CT)H			0.02	0.98	0.00
(CT)H−1			0.11	0.89	0.00
(π → π*)X	0.61	0.39	0.92	0.08	0.00
(CT)H−2			0.0	1.00	0.00
(Lb)Y	0.0	1.00	0.98	0.02	0.00
(La)Y	0.36	0.64	0.92	0.08	0.00
(pentacene)2 excimer
(La–)	0.43	0.57	0.64	0.18	0.18
(CT)			0.10	0.45	0.45
(La+)	0.58	0.42	0.90	0.05	0.05
(Lb–)	0.17	0.83	1.00	0.00	0.00
(Lb+)	0.92	0.08	1.00	0.00	0.00
(pentacene)2 fishbone configuration
(La–)	0.60	0.40	0.68	0.02	0.30
(La+)	0.40	0.60	1.00	0.00	0.00
(CT)			0.28	0.02	0.70
(Lb-)	0.57	0.43	1.00	0.00	0.00
(Lb+)	0.43	0.57	0.98	0.02	0.00

^aStates are listed in order of increasing energy of the exciplex, labeled by characteristic transitions of X (the first molecule in a (X•Y) complex) and Y (the second compound).

For class 2 and 3 exciplexes, although exciton state interactions can be strong in a particular state, they are generally not present for the remaining states. For example, in the acetone···MVE exciplex, the lowest singlet state is 100% of n → π* local excitation of acetone, whereas the second S₂ state, dominantly charge transfer from methyl vinyl ether to acetone, is mixed with the local n → π* state at 9% in structure weight. Furthermore, the local acetone n → π* state is strongly mixed with the MVE π → π* state, having structure weights of 20% and 80%, respectively. Yet, the contribution of the π → π* state of MVE to acetone n → π* excitation is negligible. This is also seen in the TCNE···naphthalene exciplex, in which the π → π* local state of TCNE is strongly coupled to the L_b state of the aromatic compound, but the L_a state is a pure local excitation. In all asymmetrical exciplexes, only one direction of charge transfer is dominant, rather than a charge-transfer resonance found in the symmetric pentacene excimer.

5. Concluding Summary

In this Perspective, we present a multistate energy decomposition analysis (MS-EDA) to dissect the energy components in molecular complexes in excited states. In particular, the total binding energy of an excimer or an exciplex is partitioned into a ground-state effect called local interaction energy ΔE_Lint, an exciton excitation energy ΔE_Ex^K resulting from the resonance state interaction of individual monomer excited states |Ψ_X•Ψ_Y^S₀⟩ and |Ψ_X•Ψ_Y^*⟩ , a superexchange stabilization energy ΔΔE_SE due to intermolecular charge transfer |Ψ_X⁺•Ψ_Y⟩ and |Ψ_X^-•Ψ_Y⟩, and an orbital and configuration-state delocalization energy ΔΔE_OCD^K as a result of a stepwise progression from monomer block-localized Kohn–Sham orbitals to the fully delocalized molecular orbitals. To determine the exciton resonance energy ΔΔE_Res, we have defined a local excitation energy via the structure-weighted reference state without excited-state interaction. Similarly, a structure-weighted adiabatic excitation energy, corresponding to the minimum (photoexcitation) energy needed to produce an exciplex (or excimer) complex, has been introduced to give a well-defined energy term for binding of the exciplex or excimer complex in the excited state.

An important feature of the present MS-EDA method is that key intermediate states associated with different energy terms can be variationally optimized, providing quantitative insights into widely used physical concepts such as exciton delocalization and charge transfer effects in excited states. Although local molecular excitation to a particular state K in the presence of other molecules in the ground state, ΔE_Lex^K|Ψ_X*•ΨY⟩ , is used as a reference state for the exciton resonance energy term, it also has a well-defined physical interpretation and the mutual polarization energy induced by such a local excitation can be related to experimental solvatochromic shifts of the excited chromophore in condensed phases or in molecular clusters. Furthermore, the electronic coupling matrix elements among locally excited states can also be used to determine the rates of excited-state energy transfer and photoexcitation-induced electron transfer. The availability of these diabatic states is made possible in the framework of multistate density functional theory (MSDFT), a rigorous variational DFT of excited states recently proved by Lu and Gao.⁶¹

Through MS-EDA analysis, it was shown that molecular complexes in the excited states can be broadly classified into three main categories: (1) encounter excited-state complex, (2) charge-transfer exciplex, and (3) intimate excimer or exciplex. Excited-state complexes in Category 1 are species produced dominantly using the same type of intermolecular forces as that in the ground state, with one molecule happening to be in an excited state. Category 2 exciplexes are formed through intermolecular charge-transfer excitation, which typically has a lower energy than the valence excitations of individual monomers. Clearly, the driving force of exciplex formation here is electrostatic interaction. Intimate excited-state complexes in Category 3 are often, but not limited to, excimers consisting of identical monomers. In this category, exciton delocalization is the main force to produce a fully delocalized excited state. In light of lack of a correlation matrix functional, charge transfer states in some cases such as that in the pentacene excimer are sometimes overestimated in the present analysis. Nevertheless, the illustrative examples presented in this Perspective highlight the interplay of local excitation polarization, exciton resonance and superexchange charge-transfer effects in molecular excited states. It is hoped that MS-EDA will become a useful tool for understanding photochemical and photobiological processes.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.3c00186.

• Computed first and second singlet excited states for monomer compounds using EOM-CCSD, FIC-NEVPT2, and MRCI with the cc-pVDZ and cc-pVTZ basis sets, and optimized structures used in this study (PDF)

Author Contributions

^∥ C.P.H. and X.Z. contributed equally. CRediT: Christian P. Hettich and Xiaoyong Zhang data curation, analysis, investigation; David Kemper data curation, investigation; Ruoqi Zhao analysis, programming, investigation; Shaoyuan Zhou data curation, investigation; Yangyi Lu analysis; Jiali Gao, theory, data curation, analysis; Jun Zhang programming; Meiyi Liu theory, data curation, investigation.

The authors declare no competing financial interest.