Behavioral aspects and the transmission of Monkeypox: A novel approach to determine the probability of transmission for sexually transmissible diseases

Abstract

Motivated by the 2022 worldwide Monkeypox (MPox) outbreak, a compartmental model is proposed to predict the evolution of the disease. Numerous models have been proposed for infectious diseases so far, although the number of variables makes it difficult to establish causation relations between individual factors and transmission rates. In order to evaluate the reaction of susceptible people to avoid infection during the outbreak, the rate of transmission is modeled through a unique phenomenological probabilistic approach, allowing the expression of the rate of generation of new cases in terms of two characteristics of the susceptible group: the frequency of sexual encounters and the probability of transmission given that there is a sexual encounter. Transmission rates are obtained and compared for the U.S. and several other countries. Results show reductions of up to 71% in the transmissibility parameter, which may be combined with variations in the frequency of sexual encounters (obtained through behavioral research) to determine the changes in the probability of transmission during an outbreak in a much more convenient way than current alternatives. This framework presents a valuable tool to health authorities in the understanding of future sexually transmissible disease outbreaks.

1. Introduction

The ongoing Monkeypox outbreak had its first case reported in the United Kingdom in May 2022, in a patient with recent travel history from Nigeria, where the disease is endemic (Monkeypox cases confirmed in England, 2022). The first case in the U.S was reported on May 17th, 2022, (Monkeypox technical reports, 2023). Transmission happens through close or intimate contact with infected objects or people (How it spreads, 2023). Close contact refers to objects infected with the virus, as well as contact with skin lesions, secretions or bodily fluids of an infected person (Kaler et al., 2022). Intimate contact pertains to sexual activity, as well as related acts and objects. The virus has an incubation time of 5–21 days (Mpox), (Signs and symptoms, 2023). The most common symptom is rash, which may or may not be accompanied by other mild symptoms, such as fever, chills, exhaustion and headache (Signs and symptoms, 2023).

At this time, data suggests that gay, bisexual, and men who have sex with men (MSM) make up the majority of the cases in the current outbreak (2022 outbreak cases and data, 2023), and men make up 98.7% of the cases (Philpott, 2022). This strongly suggests that sexual activity is the main means of transmission of monkeypox. CDC has issued recommendations to avoid transmission during intimate contact (Safer sex, 2023).

Given that sexual activity is the main driving factor behind the evolution of the disease, a simple question arises: how do susceptible people react to the outbreak of a STD? The development of a compartmental model allows the retrieval of general transmission rates from the data, though the mechanism through which new cases are generated is not yet clearly related to the behavior of susceptible people.

The use of compartmental models to understand disease transmission is not new, and multiple diseases can be modeled through this approach. Perhaps the most common model is the SIR, or susceptible-infected-recovered model (Blackwood & Childs, 2018), (The SIR Model for Spread). The simplicity of the SIR model makes it convenient to study the transmission rates for multiple diseases. The model has been extensively used in recent years to study the Covid-19 outbreak (The SIR Model for Spread of Disease).

Compartmental models have also been used to study Monkeypox transmission, even before the start of the 2022 outbreak. (Peter, Kumar, et al., 2022) considered parallel compartmental models for humans and rodents, finding reproduction numbers and stability conditions for disease-free and endemic equilibrium.

More nuanced mathematical models, such as the fractional order derivative model proposed by (Peter, Oguntolu, et al., 2022), provide alternatives to basic SIR-like models, although the parameters of disease dynamics considered are standard – transmission rates, stability conditions and reproduction numbers. After the start of the 2022 outbreak, (Michael et al., 2023) considered a modified SIR model to study the transmission dynamics of the disease transmission by incorporating surveillance and contact tracing as effective controls – again through the study of the standard parameters. (Greenhalgh & Rozins, 2021) identified one major shortcoming of the basic SIR model as the inability to account for the true infectious period distribution. Also, most models represent the parameters that move people between compartments as constant in time. By not considering time variations of these parameters, deeper details regarding disease transmission dynamics are neglected.

So far, to the best of our knowledge, no study has been able to link the behavior of the susceptible population in time to the transmission rate of Monkeypox or any other sexually transmissible disease. In order to uncover this underlying mechanism, we have investigated the generation of new cases through a phenomenological, behavior-based probabilistic approach to understand the transmission of Monkeypox beyond the usually studied transmission rate.

2. Model

Let us first consider a slight variation of the classic “SIR” (susceptible, infected, recovered) model for transmission of infectious diseases (The SIR Model for Spread), (The SIR Model for Spread of Disease) by the inclusion of two additional compartment: U (undetected infected), for individuals who have already been contaminated, but not yet detected (people in that compartment are particularly dangerous, since they are unaware of their condition and transmit the disease); and D, for individuals who perish as a result of the disease.

More complex variations including more compartments are possible, such as the “SQUIDER” model developed for Covid-19 (Khan et al., 2022), (Khan et al., 2020), which includes additional compartments for undetected patients who either recover or die, and a quarantine compartment to model the effect of the measures taken by the local health authorities.

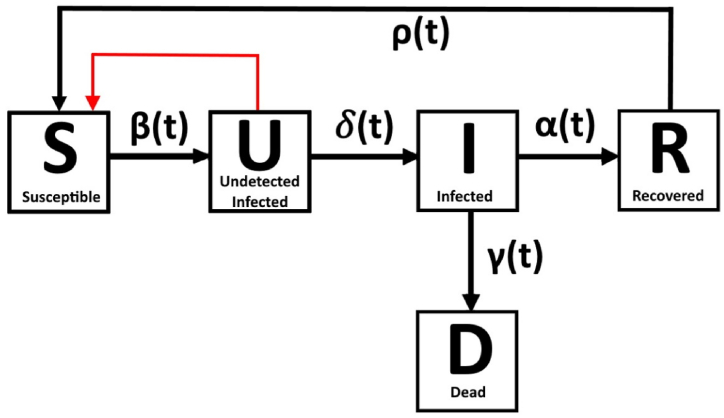
A scheme of our model, in the most general form possible, is shown in Fig. 1. Movement between the compartments is ruled by time-dependent parameters at each of the black arrows.

Fig. 1.

Schematic of the general model.

The number of people in each compartment is modeled as a function of time. We shall explore each of the compartments and explain how individuals move between them. Each of the compartments is explored in greater detail below.

• •S (susceptible) compartment: all male individuals who are gay, bisexual, or have sex with other men, henceforth referred to as “susceptible”. The only form of transmission considered is by close intimate contact. The function $\beta \left(t\right)$, also known as transmission rate, which moves people from S to U, is modeled as a function of time and will be explored in detail in the upcoming sections.
• •U (undetected infected) compartment: individuals who have been infected, but have not yet developed symptoms associated with monkeypox, especially rash; those individuals are responsible for transmitting the disease to susceptible patients.
• •I (detected infected) compartment: once individuals develop symptoms and test positive for monkeypox, they are moved from U to I and counted towards the total of cases. After detection happens, we consider patients to be no longer dangerous, as precautionary measures to avoid transmission are taken. Therefore, a patient in I cannot infect a susceptible patient, thus affecting the generation of new cases.
• •R (recovered) compartment: once individuals have tested positive, the virus stays active for a certain time in them. Even though we are not considering those to transmit the disease, they are not free from the disease itself; once there are no more symptoms, they are moved to the R compartment. In the case fatalities are a possibility, there is a compartment for dead patients (D), allowing movement from I would be moved to D instead of R.

This model makes use of several assumptions, listed in the following section. One important comment must be made about $\beta \left(t\right)$, the function which represents the generation of new infections. The black arrow pointing from S to U in Fig. 1 points in the direction of the movement of people, i.e., the generation of new infections. However, as we shall see, the mechanism of generation of new infections is dictated by people who are already infected (compartment U). Therefore, the generation of new infections is a closed feedback loop, as shown by the red arrow in Fig. 1.

2.1. Assumptions

The first major assumption concerns what we consider to be the susceptible group: all male individuals who are gay, bisexual, or have sex with other men. Despite the existence of cases outside of this group, the only mode of transmission contemplated by our model is intimate contact, which is the dominant mode as suggested by initial U.S. data (2022 outbreak cases and data, 2023), then confirmed by a multi-country study (Thornhill et al., 2022) claiming that 98% of infected individuals are gay or bisexual men. Since less than 2% of the infected patients are outside of this group, it is feasible to ignore the other forms of transmission, such as close contact transmission. The assumption of exclusive transmission by intimate contact is in line with previous literature for SIR-like models (Modeling Infectious Diseases in Humans, 2007), (Real et al., 2007).

Here, the distinction between close and intimate contact must be made; intimate contact is defined by “close, sustained physical contact, almost exclusively associated with sexual contact” (Safer sex, 2023). Close contact involves personal, often skin-to-skin contact, including contact with rash or scabs, saliva or respiratory secretions from an infected patient (How it spreads, 2023). We also consider the number of cases, S, small if compared to the overall susceptible population, N.

We consider that intimate contacts between two individuals are generated in a random manner. Generally, there is an average number of partners per individual. Research in the U.S. determined the average number of casual partners for MSM of different ethnicities as varying between 2.9 and 3.7 (Rosenberg et al., 2011). Numerous attempts were made to understand the effect of sexual networks in the transmission of STD dynamics, most notably for HIV (Gorbach & Holmes, 2003), (Rothenberg et al., 1998). However, accurately modeling sexual networks remains a challenge. Since the exact nature of partner networks is not understood for every susceptible individual, we are forced to assume that contacts are random.

Also, according to initial U.S. data (2022 outbreak cases and data, 2023), 100% of the reported patients developed rash, which became the key visual symptom for detection. Further study (Thornhill et al., 2022) found that 95% of patients develop a rash. Although patients who do not develop rash would be especially dangerous for the transmission of the disease, the lack of further information about detection forces us to consider that all infected patients will eventually develop symptoms, especially rash. In the absence of confirmed diagnostic tests it is very difficult to verify the disease and determine its cause based on clinical symptoms alone (Hraib et al., 2022).

With that in mind, for our model, detection of the disease (i.e., the passage from U to I) is a matter of when, not if, and happens as soon as symptoms are detected. This movement is governed by function $\delta \left(t\right)$ in Fig. 1. Each new case is reported as soon as a patient tests as positive.

There is typically some lag between acquiring infection and becoming infectious (Blackwood & Childs, 2018), but our model does not distinguish between infected and infectious individuals. We consider patients start transmitting the disease immediately after infection, also due to lack of research on this specific subject.

The incubation period for the virus, i.e., the number of days elapsed between infection and development of symptoms, takes a certain number of days for each patient. Initial research has shown that the virus has an incubation time of 5–21 days (Mpox), (Signs and symptoms, 2023). A multi country study (Thornhill et al., 2022) claimed that the incubation period has a median of 7 days, ranging from 3 to 20 days. However, more recent research (Miura et al., 2022) estimated the incubation period more accurately and fitted it to common probability distributions.

Once a patient develops symptoms, we consider detection of the disease to happen immediately. Function $\delta \left(t\right)$ will not be treated as a mathematical relationship between $S\left(t\right)$ and $U\left(t\right)$; rather, the incubation period for each patient will be computed individually.

After symptoms are no longer active, the patient is moved to the R compartment. The period during which symptoms stay active after detection is not of interest in this paper, since precautionary measures are supposedly taken to avoid transmission; It is important to mention, however, that once patients have recovered, they are not moved back to the susceptible compartment. The assumption that infection confers lifelong immunity is common in SIR models (Blackwood & Childs, 2018) and is especially true for common childhood diseases such as pox and measles.

This assumption is likely valid because not enough time has passed since the beginning of the outbreak and now for recovered people to lose immunity to the virus after being cured. Hence, there should be no movement of people from R to S. Also, there have been no new reported variants of monkeypox virus (during the Covid-19 outbreak, for example, the appearance of new variants directly affected the immunity of the recovered population). Since there is no possible movement from R to S, function $\rho \left(t\right)$ of Fig. 1 is equal to zero.

There is, then, no possible way that a patient who has recovered from the disease to affect the generation of new cases. As a result, it is not necessary to investigate the behavior of function $\alpha \left(t\right)$, since in this paper we are only interested in the mechanism of transmission of the disease.

We also assume that the total population does not change due to varying birth and death rates, as well as deaths related to the disease itself. That would need to be considered for a more deadly disease or over a longer period of time and is consistent with usual SIR models (Blackwood & Childs, 2018).

Currently, there is no publicly available information regarding the vaccinal coverage for MPox, even though immunization with Smallpox vaccines may have a protective effect against monkeypox virus and improve clinical manifestations (Rizk et al., 2022). One last, but important hypothesis is that the only way for a person to become immune is through infection and recovery from the disease. Recovery usually happens between two and four weeks of initial diagnosis (2022 outbreak cases and data, 2023).

Since the number of dead patients is quite small when compared to the overall number of cases (0.13% in the U.S. as of May 2023, (2022 outbreak cases and data, 2023)), death from monkeypox is an extremely rare occurrence. Therefore, compartment D and its corresponding function, $\gamma \left(t\right)$, are not of interest. Also, as will be discussed shortly, the mechanism of transmission of the disease is mostly related to the patients in the U compartment. In this research, we did not consider undetected recoveries or deaths. That assumption is in line with the removal of the D compartment in previous research (Peter, Kumar, et al., 2022).

Some SIR-based compartmental models also include quarantine compartments (Q), to properly model the removal of people from the susceptible compartment during the evolution of an outbreak. That was prevalent during the Covid-19 pandemic (The SIR Model for Spread), (The SIR Model for Spread of Disease), when the health authorities enforced lockdowns to reduce transmission rates.

Previous research for Monkeypox (Peter, Kumar, et al., 2022) claimed that quarantine measures are quite successful, though the lower severity of the disease has not encouraged health authorities to take that kind of measure. For that reason, our model will not feature a quarantine compartment.

After consideration of all assumptions, a simplified model is obtained, as shown in Fig. 2. The only relevant function remaining is the transmission rate $\beta \left(t\right)$, which will be explored in further detail in the next section. The SIR model was chosen for its simplicity and the easy integration of our phenomenological behavioral approach., although our approach can be applied to any model that deals with transmission rates.

Fig. 2.

Simplified model for the study of Mpox.

2.2. A phenomenological approach to the transmission of the disease through intimate contact

We shall investigate the phenomena associated with the generation of new infections, i.e., the process through which the disease is transmitted from one person to the other by intimate contact. Before the first case, the number of people in the susceptible compartment is equal to the total susceptible population, N $\text{.}$ Let us consider a specific time, $t_0$, at which the number of people in each of the S, U and I compartments are known. Some independent parameters, initially linked to the evolution of a STD are defined as follows:

$p\left(t\right)$: probability of sexual interaction between any two people on a single day. This may also be understood as the frequency at which susceptible people engage in sexual activities. $p$ is an average parameter for the entire group, not for one specific individual. All susceptible individuals are considered to have the same value of $p\left(t\right)$ for a specific time $t_0$. The reduction in the level of sexual activity of susceptible people will cause a drop in $p\left(t\right)$, which may be captured by behavioral research (Impact of mpox, 2022), (Crepaz & Marks, 2002). It is important to mention that, in our model, $p\left(t\right)$ contemplates only the interaction between two people. More complex alternatives, such as group interactions and multiple interactions within a same day, are assumed to be absorbed by the fact that $p\left(t\right)$ is an average parameter for the susceptible group.

$q\left(t\right)$: probability of transmission of the disease, given that there is intimate contact, one partner is infected and the other is not. Fluctuations in $q$ are not directly obtainable from our model, as well as other usual models; however, the use of precautionary measures against STDs, such as condoms, is likely to cause a reduction in $q$. The probability of transmission will be explored in greater detail at the end of the present section.

$n$: average number of partners per person in the susceptible group. Just as $p\left(t\right)$, changes in this parameter may be captured by behavioral research. All individuals are assumed to have the same value of $n$.

Qualitatively, all three parameters appear to be directly related to the transmission of the disease through intimate contact; for a STD, the main mode of transmission is sexual contact, which certainly depends on $p,q$ and $n\text{.}$ Increases in any of the parameters individually, as well as increases in a certain combination of the parameters, will likely cause the disease to spread more rapidly. Likewise, reduction either in each individual parameter or a certain combination of them will reduce the spread of the disease.

We shall find the specific combination of the parameters which accurately describes the transmission of STDs such as monkeypox. Let's define three events $E_1,E_2,E_3$ for one specific individual “A” infected but undetected, i.e., is in compartment U, at $t_0\text{;}$.

$E_1$: individual “A” is in the undetected infected group and engages in sexual activity at $t_0$. The probability of individual A being in the U compartment is the ratio between the number of people in U and the overall population at instant $t_0$, $S/N$; the probability of sexual contact is $p\left(t_0\right)$. Therefore, the probability of event $E_1$ is:

$$P\left(E_1\right)=\frac{U\left(t_0\right)\cdot p\left(t_0\right)}{N}$$

$E_2$: sexual partner of “A”, referred to as individual “B”, is susceptible (in compartment S) at the specific time $t_0$, with probability $P\left(E_2\right)$ to be determined. It can be split into three sub events:

Event $E_{2a}$, the choice of $n$ possible partners among the population, with probability

$$P\left(E_{2a}\right)=\frac{n}{N}$$

Event $E_{2b}$, the choice of one partner among the $n$ previously selected partners, with probability

$$P\left(E_{2b}\right)=\frac{1}{n}$$

Event $E_{2c}$, the presence of the selected partner in the susceptible group, with probability

$$P\left(E_{2c}\right)=\frac{S\left(t_0\right)}{N}$$

The probability of $E_2$ is the product of $P\left(E_{2a}\right),P\left(E_{2b}\right)$ and $P\left(E_{2c}\right)$:

$$P\left(E_2\right)=\frac{n}{N}\cdot \frac{1}{n}\cdot \frac{S\left(t_0\right)}{N}=\frac{S\left(t_0\right)}{N^2}$$

We immediately notice that the probability of event $E_2$ does not depend on the average number of partners, $n$. Apparently, this is a contradiction, since that is a very important parameter in sexual networks (Modeling Infectious Diseases in Humans, 2007), (Real et al., 2007), (Gorbach & Holmes, 2003), (Rothenberg et al., 1998). However, the previous assumption that contacts are random was made to bypass the difficulty of accurately taking that effect into account. In reality, not all individuals will have the same number of partners and, more importantly, that group does not necessarily remain fixed in time. Also, there is the possibility of encounters outside of the closer circle, which approaches a random event.

The simultaneous probability of events $E_{2a}$ and $E_{2b}$ accounts to $1/N$, which is exactly the probability of selecting one random partner out of a population of $N$ individuals. Indeed, there is no contradiction, but rather a confirmation that $P\left(E_2\right)$ was correctly obtained according to the relevant assumptions. Also, in event $E_2$, we are calculating the probability of a partner of individual A being infected, rather than the probability of a random individual being infected. This is consistent with previous research (Miller et al., 2011).

Another detail that illustrates the lack of dependence on $n$ is that the overall number of encounters observed in the population is dictated by $p\left(t\right)$; the expected number of sexual encounters per day is equal to $N\cdot p\left(t\right)$ in both cases. The average number of partners dictates the person with whom the encounter is more likely to happen. Generally, modeling STDs with SIR-like modes involves the assumption of unstructured sexually active populations (Real et al., 2007).

$E_3$: sexual encounter of “A” and “B’’ results in transmission of the disease. $P\left(E_3\right)=q\left(t_0\right)\text{;}$.

The simultaneous occurrence of events $E_1,E_2$ and $E_3$ generates a new monkeypox case, which means the transfer of individual “B” from S to U. The three events are statistically independent; therefore, the probability of their simultaneous occurrence is given by:

$$P\left(E_1\cap E_2{\cap E}_3\right)=P\left(E_1\right)\cdot P\left(E_2\right)\cdot P\left(E_3\right)=\frac{U\left(t_0\right)\cdot p\left(t_0\right)}{N}\cdot \frac{S\left(t_0\right)}{N^2}\cdot q\left(t_0\right)$$

The probability of a new infection is uniform across all the people in the susceptible compartment.

Here, a further simplification is possible: the number of cases of the disease is very small compared to the overall population. Therefore, $U\left(t\right)\ll N$ at any time considered. With that in mind, the disease removes very few people from the susceptible group, meaning that $S\left(t\right)\approx N\forall t$. This assumption is valid only if the cumulative number of cases is small compared to the total population, which certainly applies for the current monkeypox outbreak.

This simplification takes out the dependence of $S\left(t\right)$ in the rate of generation of new infections. Additionally, the overall population, N, is assumed to be constant. $S$ can also be normalized with respect to the overall population. The probability of new infections is found to be proportional to the product $U\left(t_0\right)\cdot p\left(t_0\right)\cdot q\left(t_0\right)$.

The addition of people to the U compartment is then governed by the ODE

$${\frac{dU}{dt}}_{@t=t_0}=U\left(t_0\right)\cdot p\left(t_0\right)\cdot q\left(t_0\right)$$

Which is consistent with the governing equations for U compartments (The SIR Model for Spread), (The SIR Model for Spread of Disease). Notice that, if in consecutive instants of time, there is a reduction in $U\left(t\right)$, the right side of the equation will be negative, an apparent contradiction since none of $U\left(t_0\right),p\left(t_0\right)$ or $q\left(t_0\right)$ can be negative at any given time. Considering the standard SIR model and its most common variations, the equation for the U compartment should be

$$\frac{dU\left(t\right)}{dt}=\beta \left(t\right)\cdot U\left(t\right)$$

Which matches what we got, as long as parameter $\beta$ is adequately chosen $\left(\beta \left(t\right)=p\left(t\right)\cdot q\left(t\right)\right)$. The parameter $\beta$ is known as transmission rate and is the product between the contact rate and the probability of transmission given contact. One important detail is that our analysis was performed for a specific instant $t_0$ when the model is valid. Section 2.5 explains the validity of our model in greater detail.

Negative variations in $U\left(t\right)$ are allowed, even if negative values for $\beta$ are not accepted. When performing calculations to retrieve the transmission rate from the data, special care must be taken to consider only the addition of people to the U compartment, which is exactly the number of generated infections, disregarding patients who exit the U compartment after being detected. The pertinent ODE for the compartment is, therefore,

$${\frac{d{U}^{+}}{dt}}_{@t=t_0}=U\left(t_0\right)\cdot p\left(t_0\right)\cdot q\left(t_0\right)$$

Where the plus sign at $\raisebox{1ex}{$d{U}^{+}$}\!\left/ \!\raisebox{-1ex}{$dt$}\right.$ included to stress that this calculation included only the addition of people to the U compartment.

The definition of the transmission rate in that format is consistent with that of general compartmental models (Blackwood & Childs, 2018), where $\beta$ is defined as the product between the total contact rate, $q\left(t\right)\text{,}$ and the probability of transmission given contact, $p\left(t\right)$.

In our case $\beta \left(t\right)$, depends only on two parameters, $p$ and $q$. That allows us to trace back the transmission of a STD to parameters related to the sexual behavior of people in the susceptible group.

In compartmental disease models, the transmission rate $\beta$ can usually be assigned a fixed value without paying much attention to the components that make up this quantity (Blackwood & Childs, 2018). Our model uses a time-dependent approach, which allows for better understanding of the transmission rate by the use of more nuanced assumptions. Essentially, a time-dependent approach allows the transmission rate to be broken up into individual behavioral parameters, each one also time-dependent.

In our model, we assume that every susceptible individual has the same contact rate. Previous research (Miller et al., 2011) has presented one alternative to deal with that particularity. Our phenomenological approach can be easily integrated into that framework, and any other types of compartmental models. In the upcoming sections, the significance of both parameters that comprise the transmission ratio will be explored.

2.3. The contact rate, $\mathit{p}\left(\mathit{t}\right)$

The contact rate, previously defined as the probability of sexual encounter between two people in one day, is the parameter directly driving the total number of contacts per day. It is affected exclusively by the choices of each susceptible individual, who freely chooses to engage in sexual activity. The occurrence of a STD outbreak may affect the sexual behaviors of susceptible individuals, thus reducing $p\left(t\right)$ and thus the number of generated cases. Usually, the local health authorities issue recommendations for increased care among susceptible individuals. In the U.S., a set of recommendations was issued by the CDC (Safer sex, 2023).

Reductions in $p\left(t\right)$ can be captured by simple behavioral research. One such study, performed after the start of the 2022 outbreak (Delaney, 2022), found that approximately one half reported reducing their number of sex partners, one-time sexual encounters, and use of dating apps because of the monkeypox outbreak. Although that study did not directly correlate the change in number of sexual encounters (proportional to $p$), the inclusion of additional quantitative questions can allow the determination of variations in $p$. The process is similar to election polls, and its statistical significance increases with the number of people interviewed. It is possible to achieve good accuracy by interviewing a small number of people compared to the overall size of the population.

As we shall see, determining variations in $p$ is much cheaper and less time-consuming than evaluating variations in $q$.

2.4. The probability of transmission given contact, $\mathit{q}\left(\mathit{t}\right)$

The other component affecting the transmission rate, $\beta$, is the probability of transmission given contact, $q\left(t\right)$. The parameter is also influenced by the choices made by individuals engaging in sexual contact, especially as it relates to the use of protection, such as condoms. Previous research on HIV (Crepaz & Marks, 2002) indicated that many seropositive individuals engaged in safer sex practices. Surprisingly, however, between 10% and 60% (depending on the specific profile of sexual activity) of seropositive individuals continued to engage in unprotected sexual behaviors that place others in risk of infection, as well as place themselves at risk of secondary infection. Since HIV is an uncurable and deadly disease, the initial perception is that seropositive individuals would be more careful.

Monkeypox is rarely fatal and curable; its consequences to overall health are only minor. Therefore, by expanding the previous study, we may assume that plenty of individuals continue to engage in unsafe sexual behaviors despite public information on the existence of the outbreak.

In addition to the behavioral aspect of $q\left(t\right)$, the effectiveness of the protective measures taken also affects the parameter. Previous research (Warner et al., 2004) has determined that the consistent use of condoms, for instance, was associated with reductions of 30% and 43% in the prevalence of gonorrhea and chlamydia, respectively.

There are two main ways through which $q\left(t\right)$ can be evaluated. Here, a simplified description of these methods will be presented. This theme is explored in depth in (Real et al., 2007). The first method, the secondary attack rate (SAR), focuses on the fate of a single infected index case (host) that comes into contact with a number of susceptible host individuals in the population. The secondary attack rate (Principles of Epidemiology, 2021) is simply defined as the ratio of the number of hosts exposed that develop disease relative to the total number of susceptible exposed hosts, i.e.,

$$SAR=\frac{totalsecondarycases}{totalsusceptibleexposed}$$

Application of that method is difficult, since it is necessary to place all cases on a timeline and determine who could have been infected by the index host, since secondary and tertiary infections are also possible. It is a plausible model, although the onset time has to be known with good accuracy.

The second method, particularly useful for sexually transmissible diseases, is the “chain binomial” method (A general chain), which involves successive application of the binomial probability distribution. The model assumes the probability of transmission given contact equal to $p$. The probability of a susceptible individual escaping $n$ contacts with infected individuals is given by ${\left(1-p\right)}^n\text{.}$ Therefore, the probability of that second individual becoming infected after exactly $n$ contacts is equal to ${1-\left(1-p\right)}^n$. The maximum likelihood estimate for $p$ is given by

$$\hat{p}=\frac{numberofindividualswhobecomeinfected}{totalnumberofcontactswithinfectives}$$

The only difference between the SAR method and the maximum likelihood estimator for $p$ is the denominator; the first method weighs transmission rates relative to contacts with susceptible individuals and the second method weighs transmission relative to contacts with infectious hosts. In the case each susceptible individual has contact with one and only one infectious host, both methods yield the same result. If we chose to perform that analysis on the current paper, either method would be suitable, since people are moved from S to U immediately after a contact resulting in infection.

Although both methods allow for the determination of $q\left(t\right)$, a number of practical obstacles exist. Studying transmission dynamics in human populations is a complex process, and estimating the probability of transmission often involves a combination of laboratory studies, observational data, clinical studies and mathematical modeling. These research studies often take very long and may not be suitable to provide timely information to educate the public and the health authorities about fast developing diseases.

Specifically, the long time necessary for that approach means that modelling the change in $q\left(t\right)$ will be available much later, when behavioral changes and measures taken by the health authorities have had time to take effect. Also, for ongoing outbreaks, these studies likely start only after the outbreak is ongoing; in that case, the results for $q$ will already be biased by the outbreak, making it difficult to establish a baseline value.

With that in mind, it is paramount to develop a faster, but still reliable, way to determine the evolution of $q\left(t\right)$ during the outbreak, preferably with minimal lag. That is indeed possible through the combination of any compartmental model (in our case, the SUIR model) and behavioral research of adequate statistical significance, which can be conducted quickly, generally within a few weeks at most. This unique approach will be explored in detail in Section 4.

2.5. Obtention of the transmission rate from data

The rate of generation of new cases may for a discrete domain is obtained by using the definition of derivative. Since we are only considering positive additions to the U compartment, the consecutive differences must be taken in the cumulative number of cases, $C\left(t\right)\text{.}$ If we perform them using $U\left(t\right)$, negative values for $\beta$ will be obtained for periods of time when the number of active cases is decaying.

The definition of derivative applied to the function $U\left(t\right)$ is as follows:

$${\frac{{dU}^{+}}{dt}}_{@t=t_0}={\mathit{lim}}_{\Delta t\to 0}\frac{C\left(t_0+\Delta t\right)-C\left(t_0\right)}{\Delta t}$$

For a discrete domain, the time step, $\Delta t$, is chosen as one day, the smallest possible given the way cases are reported. Then, the increment in infections is simply the difference between new infections in consecutive days. Again, it is important to notice that, since we are using the cumulative number of cases, $\frac{{dU}^{+}}{dt}$ only contemplates the addition of people in the $U$ compartment.

However, the overall rate of change of people of the U compartment, $\frac{dU}{dt}$, should also be determined to indicate the end of the first phase of the outbreak, i.e., the time after when new cases are generated slower than new cases are detected. Our analysis will be concentrated in the first phase of the outbreak, when exponential growth of the number of cases happens and the model can be applied. Using the same definition of derivative, we find

$${\frac{dU}{dt}}_{@t=t_0}=\frac{U\left(t_0+\Delta t\right)-U\left(t_0\right)}{\Delta t}$$

The evaluation of $\frac{dU}{dt}$ informs the period of time for which our analysis of $\frac{{dU}^{+}}{dt}$ is valid, and therefore when the transmission rate $\beta \left(t\right)$ is valid. The evaluation of $\beta \left(t\right)$ from $\frac{{dU}^{+}}{dt}$ at a specific time $t_0$ is given by:

$$\beta \left(t_0\right)=\frac{{\frac{{dU}^{+}}{dt}}_{@t=t_0}}{U\left(t_0\right)}$$

That analysis is value for any time $t_0$ at which the model is valid, allowing us to determine it as a time dependent parameter. More comments on the determination of the validity period are made in Section 3.

3. Methodology

In this section, the sequence of procedures necessary to our analysis is explained. All models were implemented in MATLAB.

The evolution of MPox was evaluated in the following countries/regions: USA, UK, Brazil, Portugal, Spain, France and Germany. Data for the outbreak in the USA was obtained from CDC (2022 outbreak cases and data, 2023); data for European countries other than the UK was obtained from the ECDC (Data on mpox, 2023). Data for the UK and Brazil was obtained from Our World in Data (Mathieu et al., 2022).

Data was obtained as number of reported MPox cases per day for each country. It is important to notice that the day a case is reported happened some days after the patient was infected. The onset period, in which the patient was in the “U” compartment, is of vital importance since the patient can transmit the disease and is not aware of the infection.

Therefore, determining the true date when each patient got infected is paramount to our analysis. Research in the Netherlands (Miura et al., 2022) has found that the incubation period may be considered as a lognormal distribution with average of 8.5 days for MPox, with 95% confidence. The percentiles for the disease onset for such distribution are show in Table 1.

Table 1.

Estimated percentiles for incubation period using a lognormal distribution (Miura et al., 2022).

Percentile	Estimated onset (days)
2.5th	3.6
5th	4.2
50th	8.5
95th	17.3
97,5th	19.9
99th	23.3

The parameters for this lognormal distribution allow us to randomly assign a specific incubation time for each patient, which can then be subtracted from the date of reporting to determine the true date of infection. The period of time between infection and reporting, which in our model is the time each patient stays in the “U” compartment, is referred to as the “active” time for such patient, when transmission is possible and likely.

In order to better understand this, Table 2 represents an extract from MPox data in Spain. Let's suppose the onset period for the first reported case, on May 13th, 2022, was 8 days, and the onset period for the second reported case, on May 16th, 2022 was 14 days. In that specific scenario, the first patient to get infected was the second case to be reported. Patient “1” was active between May 2–16, whereas patient “2” was active between May 5–13, despite testing positive before patient “1”.

Table 2.

Extract of data from Spain.

Patient number	Date reported	Onset time	Date infected
1	May 16th, 2022	14 days	May 2nd, 2022
2	May 13th, 2022	8 days	May 5th, 2022

This process is repeated to find the onset period for each reported patient in the data. Once that time has been determined, we know exactly the number of patients that are active in any given time, that is, $U\left(t\right)$ for any instant $t$. The number of cumulative cases, $C\left(t\right)$, is also determined. The results are smoothed out by a 7-day sliding average to compensate for inconsistent reporting of cases during different days of the week.

The sequence of events necessary to our analysis is as follows:

• •Load the data for a certain country. Perform a sliding average to account for inconsistent reporting of cases on different days of the week. For each positive case, determine the onset period by using the lognormal distribution.
• •Subtract this number from the date of reporting to determine the date of infection, i.e., when the patient entered the U compartment.
• •Determine the period of time during which each patient was active.
• •Combine data from all patients to determine the number of patients in the U compartment at any given time, $U\left(t\right)$, as well as the cumulative number of cases, $C\left(t\right)\text{,}$ for every $t$.
• •Calculate dU⁺/dt and dU/dt and divide by $U\left(t\right)$ to obtain the rate of generation of new cases, $\beta \left(t\right)$ and the overall $\beta \left(t\right)$, for every $t$.
• •Identify the first plateau date.
• •Perform an exponential regression of $\beta \left(t\right)$ during the period of time between the start of the outbreak and the first plateau.
• •Repeat the process for the other countries.

As mentioned previously, the SIR and consequently the modified SUIR models are valid only during the phase of exponential growth of the number of cases, therefore the importance of only considering the values of $\beta \left(t\right)$ for that period of time.

The SIR model is valid for the evolution of infectious diseases only when there is exponential growth, i.e., new cases are being generated faster than patients are getting cured. In this paper, we opted to evaluate the evolution of the disease during the first phase of the outbreak, i.e., from the start of the outbreak to the first plateau in the number of cases.

The first plateau date is detected by means of evaluation of $\beta \left(t\right)$. The cutoff date is determined as the day before three consecutive values of $\beta \left(t\right)$ are detected.

4. Results and discussion

The results for the rate of generation of new Mpox cases $\beta \left(t\right)$ are shown in Fig. 3 for multiple countries, highlighting the time dependence of the parameter. Additional information, such as the dates for the beginning and end of the first phase of the outbreak, are shown in Table 3. The values for $\beta$ for these specific dates are also shown, as well as the ration between both.

Fig. 3.

Rate of generation of new MPox cases for selected countries.

Table 3.

Additional information about the MPox outbreak.

Country	Start date	${\beta }_0$	End date	Duration	${\beta }_f$	${\beta }_f/{\beta }_0$
USA	May 10th, 2022	0.2157	August 11th, 2022	94 days	0.1106	0.512
UK	May 7th, 2022	0.2214	June 25th, 2022	50 days	0.1034	0.467
Brazil	June 10th, 2022	0.2103	August 14th, 2022	66 days	0.1105	0.525
Portugal	May 7th, 2022	0.3077	June 5th, 2022	30 days	0.1034	0.336
Spain	May 13th, 2022	0.2668	July 23rd, 2022	72 days	0.0905	0.339
France	May 19th, 2022	0.3105	July 16th, 2022	58 days	0.0931	0.299
Germany	May 20th, 2022	0.2868	July 23rd, 2022	65 days	0.0838	0.292

In order to facilitate the analysis, we will split the countries into two groups: the first group, formed by Portugal, Spain, France and Germany; and the second group, formed by the United States, Brazil, and the United Kingdom.

Group 1 is comprised of countries of similar location and other than Portugal, comparable geographical location and population size. Group 2 comprises much bigger countries, such as the United States and Brazil, both with 200+ million inhabitants, as well as the United Kingdom.

Portugal was the country which most quickly ended the first phase of the outbreak, just 30 days after the first case was reported. Spain, Germany and France had somewhat similar durations for the first phase, which ended within the week of July 16th −23rd. The four countries on group 1 had similar values of $\beta$ at the beginning of the outbreak, in the range $0.26-0.31$. And all four countries had reduced their generation of new cases to about 30% of the original values.

This confirms that the precautionary measures taken by the health authorities in those countries helped reduce the transmissivity rate by around 70% at the end of the first phase, which happened in close dates in all the group 1 countries except Portugal – which ended phase 1 much faster, perhaps for being the smallest and less populous country of the group.

In group 2, the U.S. and Brazil are very large countries with less homogeneous populations, which explains the bigger time necessary for preventive measures to take effect in the number of cases when compared to group 1 countries. Both the U.S. and Brazil ended the first phase at around mid-august. The duration of the first phase in Brazil, 66 days, is likely wrong due to late reporting of the first cases of Mpox there, since all other countries started reporting cases 20 or more days before. Therefore, the duration of the first phase in Brazil is likely similar to that of the U.S.

The initial transmissibility rates for the two countries are very similar, at around $0.21$, lower than all the group 1 countries. The U.S. and Brazil also had similar first phases when the reduction of transmissivity is concerned, with both countries reducing the transmissivity by around 48% during the first phase. This suggests reduced effect of the actions taken by the local health authorities when compared to group 1 countries, which reduced transmissivity by around 70%. Once again, the fact that the 2 countries are much bigger, populous than group 1 countries explains the reduced effect of precautionary measures.

Initially, we would expect the United Kingdom to have results closer to group 1 countries, due to the geographic location and population size. However, as far as the initial and final transmissibility rates, the results are closer to those experienced by the U.S. and Brazil. The reduction in the transmissibility rate during the first phase was around 53%.

When we consider the duration of the first phase, however, the UK was much closer to group 1 countries, being the second overall country to end the first phase, only after Portugal. These disparities indicate that the measures taken by the UK health authority took rapid effect. At the end of the first phase of the outbreak, the transmissibility rates for all countries was between around $0.09$ and $0.11$, with Germany presenting a slightly lower value of $0.0838$.

With all those numbers in mind, one question arises: how can we relate the transmissibility reduction for each country with the changes in the behavior of the susceptible group? Now, we can take advantage of the phenomenological approach to determine the answer.

The ratio between the transmissibility of the disease at the end and at the beginning of the outbreak is obtained as:

$$\frac{{\beta }_f}{{\beta }_0}=\frac{p\left(t_f\right)\cdot q\left(t_f\right)}{p\left(t_0\right)\cdot q\left(t_0\right)}$$

Let us briefly remember the meaning of each parameter:

• •$p\left(t\right)$ is the frequency of intimate sexual contact for the population;
• •$q\left(t\right)$ is the probability of transmission of Mpox given that sexual contact occurs.

Parameter $p$ is a behavioral aspect and can be directly changed through changes in the sexual behavior of the susceptible population. Parameter $q$ involves, in addition to behavioral aspects, the physical and chemical aspects of physical contact itself and can be changed less directly. For many STDs, the use of condoms is known to drastically reduce the risk of transmission $\left(q\right)$. The usage is recommended by CDC as a means to prevent the spread of Mpox during intimate contact (Safer sex, 2023), though the percentage of MSM who increased their condom usage was found to be just 8.1% (Delaney, 2022).

A complete discussion on $p$ and $q$ is available in sections 2, 2.4.5, respectively. Once again, we highlight the difficulties associated with the process of determining variations in $q$, especially when compared to $p$. In order to illustrate how our approach is a much easier and more direct way to evaluate the variations in $q$, the following analysis is presented.

As an example, let's take the results from the U.S., where a reduction in $\beta$ of 48.8% was reported between the start and end of the first phase of the outbreak. The ratio between the transmissibility rates is

$$\frac{{\beta }_f}{{\beta }_0}=\frac{p\left(t_f\right)\cdot q\left(t_f\right)}{p\left(t_0\right)\cdot q\left(t_0\right)}=0.512$$

Of course, the reduction of $\beta$ can be obtained through combinations of individual reductions in $p$ and $q$. As mentioned, simple behavioral research is able to determine variations in $p$ with good statistical significance. As soon as the reduction in $p$ is determined, the change in $q$ is known immediately. Possible results for this scenario are shown in Table 4.

Table 4.

Different possibilities of reduction of parameters in order to achieve the reduction in the transmissibility rates for the U.S. $q$ is supposed to be constant.

Reduction in $p$ (%)	Reduction in $q$ (%)
$10\%$	$43.11\%$
$20\%$	$36\%$
$30\%$	$26.85\%$
$40\%$	$14.66\%$

During the first months of the MPox outbreak, research was conducted to find out the strategies adopted by MSM to avoid the transmission of the virus (Delaney, 2022).; 49.8% of participants reported a reduction in the number of one-time sexual encounters, related to $p$. Although this data does not allow us to directly determine the variation in $p$, more detailed research will make it possible to calculate the overall reduction in the frequency of intimate contact $\left(p\right)$, allowing the determination of the probability of transmission $\left(q\right)$ through an alternative path to the usual methods (Section 2.5).

Overall, the phenomenological approach provides a great way to relate the evolution of not only MPox, but also other STDs, to behavioral changes in the susceptible group, as long as somewhat detailed research measuring the changes in frequency of sexual contact of the population is available.

5. Conclusion

In this paper, we studied the transmission of MPox, a sexually transmissible disease, through the combination of a SUIR compartmental model and a phenomenological approach to relate the evolution of the disease to parameters measuring intimate sexual contact. The evolution of Mpox was compared in several countries and the changes in transmissibility rates for each country were calculated between the beginning and end of the first phase of the outbreak. The breakdown of the transmissibility rates as a combination of behavioral parameters presents a valuable alternative to determine the evolution of the probability of transmission given contact, $q\left(t\right)$, during the outbreak of future sexually transmissible diseases, especially considering the burdensome processes employed by current alternatives to evaluate the parameter. The framework presented in the current paper presents an important tool to understand the effectiveness of precautionary measures taken by susceptible individuals to reduce the transmission of a sexually transmissible disease, presenting invaluable information to health authorities for the management of future outbreaks.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling Editor: Dr. Raluca Eftimie