Seafloor hydrothermal systems control long-term changes in seawater [Li⁺]: Evidence from fluid inclusions

Abstract

Secular variations in the major ion chemistry and isotopic composition of seawater on multimillion-year time scales are well documented, but the causes of these changes are debated. Fluid inclusions in marine halite indicate that the Li concentration in seawater [Li⁺]_SW declined sevenfold over the past 150 million years (Ma) from ~184 μmol/kg H₂O at 150 Ma ago to 27 μmol/kg H₂O today. Modeling of the lithium geochemical cycle shows that the decrease in [Li⁺]_SW was controlled chiefly by long-term decreases in ocean crust production rates and mid-ocean ridge and ridge flank hydrothermal fluxes without requiring changes in continental weathering fluxes. The decrease in [Li⁺]_SW parallels the 150 Ma increase in seawater Mg²⁺/Ca²⁺ and ⁸⁷Sr/⁸⁶Sr, and the change from calcite to aragonite seas, KCl to MgSO₄ evaporites, and greenhouse to icehouse climates, all of which point to the importance of plate tectonic activity in regulating the composition of Earth’s hydrosphere and atmosphere.

Declining hydrothermal fluxes drove a 7-fold decrease in seawater [Li⁺] over the last 150 Ma.

INTRODUCTION

The major ion (Mg²⁺, Ca²⁺, Na⁺, K⁺, SO₄²⁻, Cl⁻, HCO₃⁻) (1) and isotopic composition (i.e., δ⁷Li, ⁸⁷Sr/⁸⁶Sr) (2, 3) of seawater have varied in the Phanerozoic Eon. Systematic changes in the Mg²⁺, Ca²⁺, and SO₄²⁻ concentrations in Phanerozoic seawater regulate the alternating MgSO₄ and KCl mineralogies of marine potash evaporites (4). Variations in the Mg²⁺ and Ca²⁺ concentrations may have influenced the evolution of marine shell-building organisms, including dominant reef-builders and skeletal algae, because the Mg²⁺/Ca²⁺ ratio of seawater controls which carbonate, calcite, or aragonite precipitates during so-called calcite seas and aragonite seas (5). The Mg²⁺/Ca²⁺ ratio of seawater from the Jurassic to the present closely matches the marine ⁸⁷Sr/⁸⁶Sr curve, and both show a sharp rise in the Cenozoic similar to that exhibited by the marine lithium isotope (δ⁷Li) record from 60 to 0 million years (Ma) ago (Fig. 1) (3, 6, 7). Long-term changes in the major ion chemistry of seawater broadly correlate with variations in atmospheric CO₂ and icehouse-greenhouse climate, suggesting links to the carbon cycle (8).

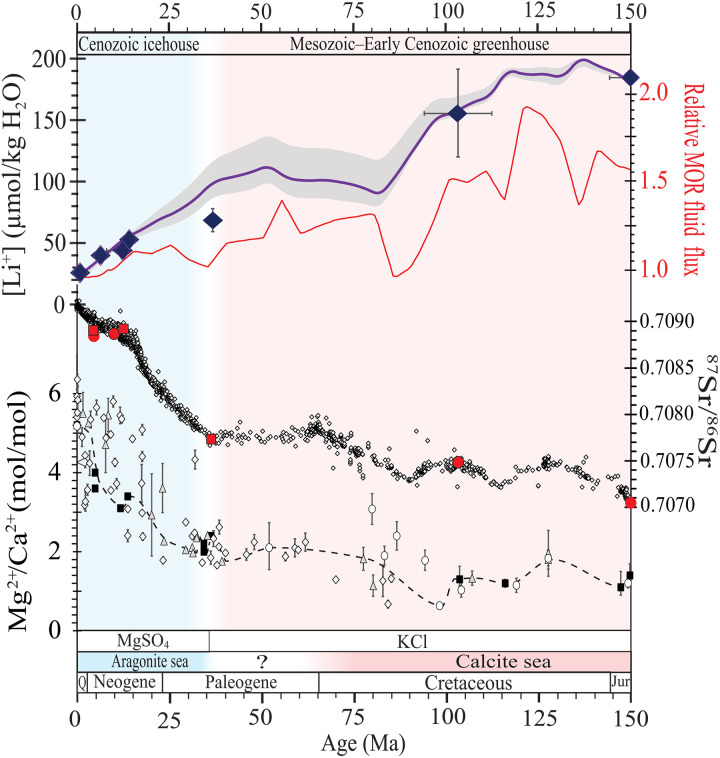
Fig. 1. Seawater [Li⁺] over the past 150 Ma compared to MOR fluid flux and other seawater records.

From top to bottom: seawater [Li⁺] from fluid inclusions in halite, global mean MOR fluid flux (38), ⁸⁷Sr/⁸⁶Sr from marine skeletal carbonates (2), Mg²⁺/Ca²⁺ from fluid inclusions in halite (black squares) (7), skeletal carbonates (ovals) (66), calcite veins (triangles) (67), and corals (diamonds) (68), MgSO₄ and KCl evaporites (4), calcite and aragonite seas (5), and greenhouse (peach) and icehouse (blue) climates (37). Indigo curve shows the modeling results for [Li⁺]_SW. Gray shading around the modeled [Li⁺]_SW curve shows the uncertainty from high-temperature axial (MOR) and low-temperature off-axis (AOC) hydrothermal fluid flux estimates. Error bars are the uncertainty of the data (minimum/maximum for [Li⁺]_SW and Mg²⁺/Ca²⁺). Red circles show ⁸⁷Sr/⁸⁶Sr values from fluid inclusions in marine halite (table S2) (30); red squares show ⁸⁷Sr/⁸⁶Sr values in sulfates interbedded with halite (31–33).

Long-term variations in seawater composition are now well documented, but there is disagreement over which input or output fluxes were responsible for those changes. Proposed controls of temporal changes in seawater chemistry include variations in the rates of (i) ocean crust production and mid-ocean ridge (MOR) hydrothermal discharge (4), (ii) river flux (RIV) and terrestrial weathering intensity (9), (iii) deposition of marine carbonates and dolomitization (10), (iv) low-temperature, off-axis alteration of oceanic crust (AOC) (11), and (v) formation of marine authigenic aluminosilicate clays (MAAC) (12). AOC and MAAC together can be considered reverse weathering (3).

Recent advances in laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) now allow quantitative measurement of minor and trace elements in fluid inclusions in halite, including lithium (Li⁺) (13). Li⁺, a trace element in seawater, is particularly useful for understanding the drivers of long-term changes in seawater chemistry. It is a conservative element not incorporated to any significant degree in minerals precipitated from evaporating seawater, such as calcite, aragonite, gypsum, or halite (fig. S1). Li⁺ is entirely derived from terrestrial silicate mineral weathering and seafloor-basalt interactions with hydrothermal fluids at MORs, and its concentration in seawater is not significantly influenced by biological processes or precipitation of carbonates (3). Li⁺ today is supplied to the oceans by MOR hydrothermal fluids (F_MOR = 13.7 ± 2.8 × 10⁹ mol/year, 58 ± 12% of global input flux) and rivers (F_RIV = 9.9 × 10⁹ mol/year, ~42%) (14, 15). [Li⁺] in MOR hydrothermal fluids are three orders of magnitude higher than rivers (457 ± 66 versus 0.265 μmol/kg of H₂O, here termed μmolal) and ~17 ± 3 times that of seawater (27 μmolal) (15–17). Small fluctuations in ocean crust production rates and hydrothermal fluxes could therefore change seawater Li⁺ ([Li⁺]_SW). Li⁺ is removed from seawater during low-temperature (off-axis) AOC (F_AOC = 2 to 21 × 10⁹ mol/year) (18, 19) and MAAC formation (F_MAAC = 11 to 20 × 10⁹ mol/year) (3, 20).

Recent records of δ⁷Li_SW in Cenozoic seawater from foraminifera (3) and brachiopods (21) show an increase of ∼8 to 9‰ over the past 60 Ma, which is thought to be due to (i) increased tectonic uplift that increased continental clay mineral formation (3), (ii) increased diagenetic reactions of marine clays (20), (iii) increased land surface reactivity and erosion (22), (iv) increased Li isotopic fractionation between seawater and oceanic crust (18), and (v) decreased continental soil formation (23). Modeling and interpretation of the Cenozoic δ⁷Li_SW record, however, are based on the assumption that the [Li⁺]_SW has been roughly constant (3, 18, 22, 23). Li and West (20) tested 12 model scenarios to explain the Cenozoic δ⁷Li_SW record and suggested that knowledge of [Li⁺] in ancient seawater would help distinguish the major controls responsible for changes in the global Li cycle. Here, we show from measurements of fluid inclusions in marine halite that [Li⁺]_SW in Jurassic and Cretaceous seawater was up to seven times greater than in modern seawater. Such variations are not included in any past modeling of the global geochemical cycle of Li reconstructed from Li isotopes. We present a 150 Ma record of [Li⁺]_SW and test the hypothesis that the decrease of [Li⁺]_SW since the Jurassic was produced by a decline of MOR and ridge flank hydrothermal fluxes.

RESULTS AND DISCUSSION

Li⁺/Mg²⁺ ratios in fluid inclusions

A total of 639 fluid inclusions along growth bands (fig. S2) in 65 halite samples (seven ages from 13 Mesozoic and Cenozoic marine evaporite basins; fig. S3) were analyzed using LA-ICP-MS to obtain Li⁺/Mg²⁺ ratios (Fig. 2, Table 1, table S1, and data S1; see Materials and Methods). Fluid inclusions from the same halites were used to document the major ion chemistry (7, 24–29) and Sr concentration (30) of Mesozoic and Cenozoic seawater. The ⁸⁷Sr/⁸⁶Sr ratios from these fluid inclusions (30) and associated sulfate minerals (31–33) lie on the marine curve, supporting the seawater origin of the brines from which halite precipitated (Fig. 1 and table S2; see Materials and Methods).

Fig. 2. Histograms and frequency distribution curves of Li⁺/Mg²⁺ ratios measured in (n) fluid inclusions from Cenozoic and Mesozoic halite.

(A) Normal distribution of the Li⁺/Mg²⁺ ratios for modern (0 Ma), Messinian (5.61 to 5.55 Ma), Serravallian-Tortonian (11.8 to 7.2 Ma), Langhian-Serravallian (13.81 to 13.1 Ma), Albian-Cenomanian (112.2 to 93.5 Ma), and Kimmeridgian-Tithonian (155.7 to 145.5 Ma) inclusion brines. (B) Bimodal distribution of Priabonian (~36 Ma) inclusions. Bin sizes were calculated using the Sturges’ Rule [log2(n) + 1, where n is the number of data points]. Small vertical dashed lines indicate the mode of Kernel density estimate. Outliers (red) outside of ±3σ (99.7% confidence interval) at the head and tail of the histograms (Serravallian-Tortonian, Langhian-Serravallian, Kimmeridgian-Tithonian, and Priabonian) were excluded from statistical analysis. Such outliers are due to poorly controlled laser ablation of fluid inclusions (13).

Table 1. [Li⁺] calculated for Mesozoic and Cenozoic seawater from measured [Li⁺]/[Mg²⁺] ratios and published [Mg²⁺].

[Li⁺] (μmol/kg H₂O) calculated for modern salinas (solar evaporation ponds) and evaporite basins/subbasins using [Li⁺]/[Mg²⁺] ratios (μmol/mmol) measured in (n) number fluid inclusions in (N) number of halite intervals and [Mg²⁺] (mmol/kg H₂O) in seawater from published fluid inclusion data (7). One SE was calculated from the average of (n) fluid inclusion analyses in halite of the same age. [Li⁺]/[Mg²⁺] ratios and [Li⁺] values for individual fluid inclusions are given in data S1.

Age	Age (Ma ago)	Basins/Subbasins/Salinas	Locality/Country	N	n	[Mg2+]calc	[Li+]/[Mg2+]measured		[Li+]calc
						(mmol/kg H2O)	(μmol/mmol)	1 SD	(μmol/kg H2O)	1 SD
Modern	0	Seawater	Atlantic and Pacific	2	47	55	0.49	0.0005	27	0
		Conti Vecchi	Mediterranean Salinas, Italy	1	18		0.52	0.05	29	3
		Sant’Antioco	Mediterranean Salinas, Italy	1	10		0.50	0.05	28	3
		Cabo de Gata	Mediterranean Salinas, Spain	1	6		0.58	0.05	32	3
		Great Inagua Island*	Caribbean Salinas, Bahamas	1	16		0.57	0.06	31	3
		Average					0.54	0.05	29	3
Messinian	~5.61–5.55 (5.6)	Caltanissetta	Sicily, Italy	1	10	51	0.85	0.05	43	3
Serravallian-Tortonian	~11.8–7.2 (11.6)	Gulf of Suez	Hurghada, Egypt	17	150	45	1.01	0.09	45	4
Langhian-Serravallian	~13.81–13.1 (13.6)	Carpathian Foredeep	Tarnow, Poland	6	64	43	1.24	0.13	53	6
		Carpathian Foredeep	Wieliczka, Poland	2	13		1.12	0.11	48	5
		Carpathian Foredeep	Bochnia, Poland	4	31		1.28	0.06	55	3
		Carpathian Foredeep	Hrynivka, Ukraine	2	15		1.38	0.12	59	5
		Carpathian Foredeep	Slanic-Prahova, Romania	4	30		1.23	0.06	53	3
		East Slovakian	Zbuzda, Slovakia	2	19		1.27	0.08	55	3
		Transcarpathian	Solotvyno, Ukraine	1	8		1.22	0.02	52	1
		Average					1.24	0.08	53	3
Priabonian	~36	Catalan	Catalonia, Spain	6	64	35	2.85	0.87	100	31
		Navarra	Navarra, Spain	2	25		1.93	0.14	67	5
		Average					1.93	0.24	68	8
Albian-Cenomanian	112.2–93.5 (103)	Sakon Nakhon	Vientiane, Laos	3	50	33	4.74	1.01	156	34
Kimmeridgian-Tithonian	~155.7–145.5 (150)	East Kuban	Northern Caucasus, Russia	2	25	38	4.98	0.62	189	24
		Foredobrogean	Izmail, Ukraine	8	77		4.81	0.67	183	26
		Average					4.85	0.66	184	25

*Data from von Borstel et al. (69).

Histograms and frequency distribution curves of Li⁺/Mg²⁺ ratios in halite inclusions for six of the seven ages reported show a normal distribution, with most data symmetrically distributed around the mean (Fig. 2A). The Li⁺/Mg²⁺ ratios of these inclusion brines fall within 7 and 21% RSD (relative standard deviation) equivalent to the LA-ICP-MS analytical uncertainty (<10% RSD) (13) and variability in the Li⁺/Mg²⁺ ratios of natural brines (<20% RSD). Modern brines from solar evaporation ponds at Atlit salt plant, Israel (34, 35) and Great Inagua Morton salt plant, Bahamas (36) show up to 20% variability in Li⁺/Mg²⁺ ratios of 0.5 ± 0.1, ranging between 0.4 and 0.6 μmol/mmol (fig. S1). Late Priabonian (~36 Ma old) fluid inclusions, however, show a bimodal distribution of Li⁺/Mg²⁺ ratios from the two main evaporite depocenters (300 km apart) in the Eocene South Pyrenean basin (26). Fluid inclusions from the Navarra subbasin have a mean Li⁺/Mg²⁺ ratio of 1.93 ± 0.24, whereas the mean Li⁺/Mg²⁺ ratio in fluid inclusions from the Catalan subbasin is 3.51 ± 0.24 (Fig. 2B). Fluid inclusions in halite from the Catalan subbasin contain variable Ca²⁺ and SO₄²⁺ concentrations, and associated anhydrite layers exhibit δ³⁴S values slightly higher than expected from Eocene seawater. Such data were interpreted by Cendón et al. (26) to reflect continental recharge and less seawater inflow to the Catalan subbasin, which was further from the open ocean than the Navarra subbasin. For these reasons, we only use Li⁺/Mg²⁺ ratios from the Navarra subbasin here.

Li⁺ concentrations in paleoseawater

Li⁺/Mg²⁺ ratios measured from fluid inclusions require known Mg²⁺ concentrations [Mg²⁺] to convert ratios into absolute [Li⁺]. The conversion is straightforward because Mg²⁺ and Li⁺ are conservative ions in seawater and inclusion brines measured in this study (fig. S1; see Materials and Methods). [Li⁺] of paleoseawater, therefore, is calculated using Li⁺/Mg²⁺ ratios and published paleoseawater [Mg²⁺] (Fig. 1, fig. S4, Table 1, table S1, and data S1) (7). Over the past 150 Ma, [Li⁺]_SW declined from 184 ± 25 to 27 μmolal. [Li⁺]_SW was high (156 to 184 μmolal) during the Kimmeridgian-Tithonian (155.7 to 145.5 Ma ago) and Albian-Cenomanian (112.2 to 93.5 Ma ago) stages and then decreased [~1.2 μmolal/Ma, r² = 0.99 (n = 558)] over the past ~150 Ma. [Li⁺]_SW decreased significantly (up to a factor of ~3 to 4) during the Cenozoic. [Li⁺]_SW during the Eocene (~36 Ma ago) was 68 ± 8 μmolal (n = 25), which decreased to 45 to 53 ± 3 μmolal (n = 330) during the Serravallian-Tortonian (~14 to 11 Ma ago), 43 ± 3 μmolal (n = 10) during the Messinian (~6 to 5 Ma ago), to 27 μmolal today.

Overall, the 150 Ma decrease in [Li⁺]_SW parallels (Fig. 1) (i) the increase in Mg²⁺/Ca²⁺ ratio from 1.3 ± 0.25 in the Jurassic to the modern value of 5.2, as seawater [Mg²⁺] increased and [Ca²⁺] decreased (7); (ii) the change from calcite seas in the Jurassic/Cretaceous to the aragonite seas of the late Cenozoic with the rise of Mg²⁺/Ca²⁺ (5); (iii) the change from KCl potash evaporites of the Mesozoic to the MgSO₄ type of the late Cenozoic as seawater [Mg²⁺] and [SO₄²⁻] rose and [Ca²⁺] decreased (4); (iv) the increase in ⁸⁷Sr/⁸⁶Sr from the Late Jurassic minimum of 0.7069 to the maximum today of 0.7092 (2); and (v) the change from the greenhouse climates of the Mesozoic–Early Cenozoic to the icehouse of the late Cenozoic accompanied by lower atmospheric CO₂ (37).

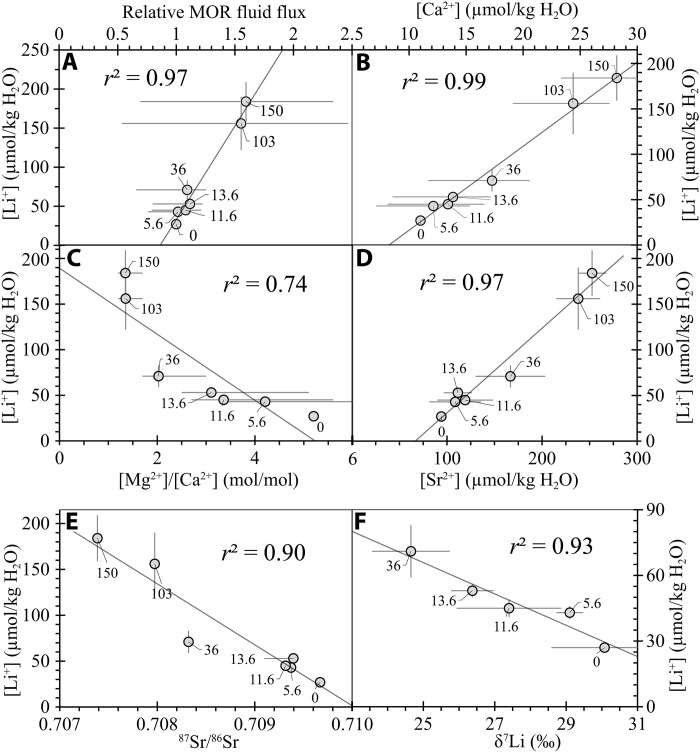
The 150 Ma record of [Li⁺]_SW is plotted against the mean MOR fluid flux (Fig. 3A) (38), recently estimated from oceanic crust reconstructions and data from modern hydrothermal systems. The strong positive correlation between [Li⁺]_SW and variations in MOR fluid flux (r² = 0.97) over the past 150 Ma suggests that long-term changes in [Li⁺] _SW were produced by variations in plate tectonic activity, primarily from fluctuations in ocean crust production and hydrothermal fluid flux. To test this hypothesis, we constructed a 150 Ma forward model of the global Li cycle to investigate the controls on [Li⁺]_SW.

Fig. 3. Covariation of [Li⁺] with MOR fluid flow and seawater constituents.

[Li⁺] in seawater from fluid inclusions versus relative MOR fluid flux (A) (38), seawater [Ca²⁺] (B) (7, 24, 25), Mg²⁺/Ca²⁺ (C) (7, 24, 25), [Sr²⁺] (D) (30), ⁸⁷Sr/⁸⁶Sr (E) (2), and δ⁷Li (F) (3). Ages in million years adjacent to symbols show average values of seawater [Li⁺], [Ca²⁺], Mg²⁺/Ca²⁺, [Sr²⁺], ⁸⁷Sr/⁸⁶Sr, and δ⁷Li with 1σ (2SE for [Sr²⁺]) and 2σ (δ⁷Li) error bars. Linear regressions show the relationship between [Li⁺]_SW and MOR fluid flow and other marine records.

[Li⁺]_SW model

The forward model equation (39) used for estimating [Li⁺] in paleoseawater can be represented by

$$\begin{array}{c}{[{\mathrm{Li}}_{\mathrm{SW}}]}_{\mathrm{t}+1}={[{\mathrm{Li}}_{\mathrm{SW}}]}_{\mathrm{t}}+\frac{\text{Δ}\mathrm{t}}{\mathrm{M}}\{(f_{\mathrm{RIV}}\times {[{\mathrm{Li}}_{\mathrm{RIV}}]}_{\mathrm{t}})+(f_{\mathrm{MOR}}\times {[{\mathrm{Li}}_{\mathrm{MOR}}]}_{\mathrm{t}})+\\ f_{\mathrm{AOC}}\times ([{\mathrm{Li}}_{\mathrm{AOC}}]-{[{\mathrm{Li}}_{\mathrm{SW}}]}_{\mathrm{t}})+f_{\mathrm{M}\mathrm{AAC}}\times ({[{\mathrm{Li}}_{\mathrm{M}\mathrm{AAC}}]}_{\mathrm{t}}-{[{\mathrm{Li}}_{\mathrm{SW}}]}_{\mathrm{t}})\}\end{array}$$ (1)

$${[{\mathrm{Li}}_{\mathrm{SW}}]}_{\mathrm{t}+1}={\mathrm{Li}}_{\mathrm{SW}(\mathrm{t})}+\frac{\text{Δ}\mathrm{t}}{\mathrm{M}}[{\mathrm{F}}_{\mathrm{RIV}(\mathrm{t})}+{\mathrm{F}}_{\mathrm{MOR}(\mathrm{t})}-{\mathrm{F}}_{\mathrm{AOC}(\mathrm{t})}-{\mathrm{F}}_{\mathrm{MAAC}(\mathrm{t})}]$$ (2)

where f_RIV, f_MOR, f_AOC, and f_MAAC are water fluxes (in kilograms per year) associated with RIV, the high-temperature axial portions of the MOR, off-axis low-temperature hydrothermal exchange with upper oceanic crust (AOC), and MAAC, respectively. [Li_SW]_t, [Li_RIV]_t, [Li_MOR]_t, [Li_AOC]_t, and [Li_MAAC]_t are the concentrations (in micromoles per kilogram) of Li⁺ in seawater, river water, MOR hydrothermal vent fluids, off-axis hydrothermal fluids, and marine aluminosilicate clay pore fluids, respectively, at time t. M is the total mass of seawater (~1.38 × 10²¹ kg) assumed constant in the past. Δt is the time step, 10 thousand years (ka), used in this model. F_RIV, F_MOR, F_AOC, and F_MAAC in Eq. 2 represent Li⁺ input and output fluxes (in moles per year) to the oceans associated with rivers, high-temperature MORs, off-axis ocean crust alteration, and marine clay diagenesis, respectively, used in calculating the seawater Li budget from Eq. 1. Li_SW is total Li⁺ in seawater; modern Li_SW(0) ≈ 3.5 × 10¹⁶ mol. Li⁺ inputs are MOR fluids (F_MOR) and river water (F_RIV), and the outputs are uptake during off-axis low-temperature weathering of oceanic crust (F_AOC) and diagenetic reactions between seawater and marine aluminosilicate clays (F_MAAC). Long-term variations of [Li_SW]_t reflect changes in the mass balance between the input and output fluxes given the residence time of Li⁺ (~1.5 Ma) (40) in the modern ocean.

[Li⁺]_SW model parameters and assumptions

The constraints and assumptions of the input and output fluxes used to model [Li⁺]_SW are shown in Fig. 4 and Table 2:

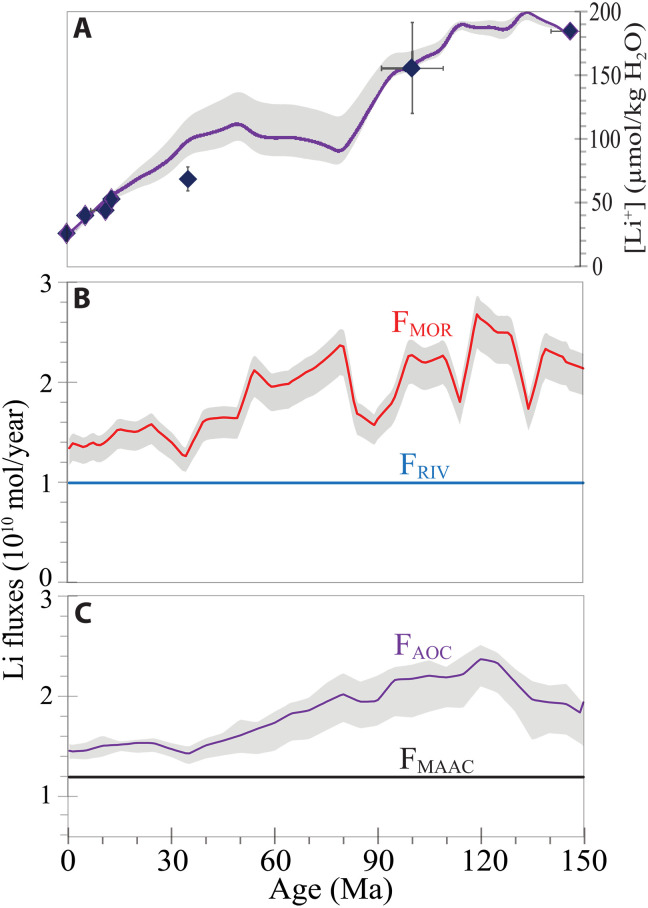
Fig. 4. [Li⁺] mass balance model parameters and [Li⁺] model output.

(A) [Li⁺] from fluid inclusions in halite and the [Li⁺]_SW model. Model input (B) and output (C) fluxes for [Li⁺] in seawater, using (i) variable high-temperature hydrothermal flux along MORs (F_MOR), with maximum at 120 Ma ago, (ii) variable low-temperature hydrothermal flux involving off-axis AOC (F_AOC), (iii) constant RIV equal to modern global riverine inflow (F_RIV), and (iv) constant uptake flux of Li by marine clays (F_MAAC). Gray shading shows the full range of uncertainty for AOC and ±15% uncertainty from the mean MOR Li fluxes (fig. S6).

Table 2. Parameters used to model [Li_SW].

Symbol	Description	Present-day values	150 Ma ago values	Units	References for present-day values
[LiSW]	Lithium concentration in seawater	27	184	μmol/kg H2O	(36)
[LiRW]	Lithium concentration in river water	0.265	0.265	μmol/liter	(15)
[LiMOR]	Lithium concentration in MOR hydrothermal vents fluids	457 ± 66	457 ± 66	μmol/kg H2O	fig. S5
[LiAOC]	Lithium concentration in off-axis hydrothermal fluids	9–16 (13.4 ± 3.7)	166 ± 46	μmol/kg seawater	(46)
[LiMAAC]	Lithium concentration in marine aluminosilicate clay diagenetic fluids	18–26		μmol/kg H2O	(3)
f RW	River water flux	3.75 × 1016	3.75 × 1016	liter/year	(39)
f MOR	Water flux through axial portions of the MORs	(3 ± 1.5) × 1013	(4.7 ± 0.5) × 1013	kg/year	(16)
f AOC	Water flux through off-axis oceanic crust	1.1–24 (1.1) × 1015	(1.5 ± 0.2) × 1015	kg/year	(44, 45)
f MAAC	Water flux through marine aluminosilicate clays
M	Mass of seawater	1.38 × 1021	1.38 × 1021	kg	Calculated using (39) and average density of seawater (1.025 kg/liter)
LiSW	Total Li in seawater	3.73 × 1016	2.54 × 1017	mol	Calculated using (36) and (39)
FRW	Riverine Li flux	9.94 × 109	9.94 × 109	mol/year	(15)
FMOR	High-temperature MOR hydrothermal Li flux	(13.7 ± 2.8) × 109	(21.6 ± 2.1) × 109	mol/year	Calculated using (16) and [LiMOR]
FAOC	Li flux related to low-temperature altered oceanic crust	11–41 (14.7 ± 0.8) × 109	(19.6 ± 2.5) × 109	mol/year	Calculated using (44) and (46)
FMAAC	Li flux related to MAACs	11.9 × 109	11.9 × 109	mol/year	Based on mass balance

1. MOR hydrothermal Li⁺ flux (F_MOR): Modern F_MOR was calculated from compilation of data on lithium concentrations in MOR hydrothermal vent fluids ([Li_MOR] = 457 ± 66 μmol/kg) along active spreading centers (fig. S5) and estimated global mean hydrothermal water flux [f_MOR = (3 ± 1.5) × 10¹³ kg/year] derived from geophysical and geochemical methods (16). We used a modern mean F_MOR of (13.7 ± 2.8) × 10⁹ mol/year, the same F_MOR used in previous δ⁷Li_SW models (3, 20, 22).

Reconstruction of past F_MOR requires knowledge of axial hydrothermal fluid flux, f_MOR, through time. Müller et al. (38) calculated f_MOR for the past 200 Ma from oceanic heat flow derived from reconstructions of the area of 0 to 1 Ma ocean crust (41) and data from modern hydrothermal systems (42), normalized to mean modern f_MOR of 3 × 10¹³ kg/year (fig. S6). In modern hydrothermal systems, about 30% of the total global hydrothermal water flux occurs in ocean crust younger than 1 Ma along active vents of MOR crests, and the remaining flux occurs in cooler, off-axis regions (38, 42). The uncertainties in estimating past f_MOR over the past 150 Ma increase by up to a factor of 4 (fig. S6) (38). These uncertainties are from (i) reconstructions of the age-area distribution of global ocean floor, including subducted oceanic crust (41), (ii) mapping of hydrothermal fluid flux as a function of crustal age (43), and (iii) partitioning of axial heat flux into high-temperature flow and diffuse flow (16). The impact of uncertainties in the estimation of f_MOR on the modeling of [Li_SW]_t was tested in the sensitivity analysis discussed below. F_MOR (11 × 10⁹ to 29 × 10⁹ mol/year) over the past 150 Ma was calculated here using variable f_MOR (38) and mean [Li_MOR] of 457 μmol/kg (Fig. 4B, fig. S6, and data S3).

Lower global mean hydrothermal fluid flux [f_MOR = (8 ± 2.1) × 10¹² kg/year] and F_MOR = (5.16 ± 1.43) × 10⁹ mol/year was estimated from a compilation of vent fluid compositions and altered sheeted dikes (14). This F_MOR is similar to the F_MOR (6.6 × 10⁹ mol/year) estimated from hydrothermal leaching of all Li in 1 km of ocean crust (3.4 km²) produced annually at the MOR (18). An alternative 150 Ma [Li_SW]_t model with lower modern f_MOR and F_MOR of 5.16 × 10⁹ mol/year is shown on fig. S7.

2. Off-axis Li⁺ uptake flux (F_AOC): The uptake of Li⁺ during off-axis low-temperature hydrothermal exchange {F_AOC = f_AOC × ([Li_AOC] – [Li_SW])} between seawater and upper ocean crust is estimated to be 11 × 10⁹ to 41 × 10⁹ mol/year based on the modern low-temperature off-axis hydrothermal fluid flux (f_AOC = 1.1 × 10¹⁵ to 24 × 10¹⁵ kg/year) (44, 45), and pore fluid/spring compositions ([Li_AOC] = 9 to 16 μmol/kg) from warm (25° to 63°C) seawater circulating within 3.5-Ma-old ocean crust of the Juan de Fuca Ridge at Baby Bare and 5.9-Ma-old crust from the Costa Rica Rift (58°C) (46). The contribution of cool versus warm off-axis hydrothermal fluids to ridge-flank Li sinks, however, is not well known. Experimental studies show that Li loss from seawater into secondary phases occurs below 150°C (47). Warm springs (25° to 63°C) from the Juan de Fuca Ridge show a positive linear correlation between Li and Mg (46), indicating removal of both species from seawater. More than 80% of seawater Mg is removed by secondary alteration phases at temperatures above 45°C, and <10% is lost at temperatures below 25°C (48). Here, we similarly assume that warm springs (>25°C) remove 80 to 90% of the Li in seawater, and 10% is lost at lower temperatures (<25°C) on ridge flanks.

Independent estimates of F_AOC, based on steady-state mass balance models (3, 20) and Li⁻ enrichment in altered off-axis ophiolites (18), dredged samples from the Atlantic seafloor (49), Ocean Drilling Program (ODP) sites 504, 896, and 1256 (19, 50), and Deep Sea Drilling Project (DSDP) data (51), together give a range of 2 × 10⁹ to 21 × 10⁹ mol/year. This wide range of F_AOC is due to the variable [Li] [5.2 to 75 parts per million (ppm)] measured from submarine basalts variably buried by marine sediments and subjected to different water/rock ratios, duration of reactions, and hydrothermal temperatures (18, 19, 51). For example, dredged basalts from the Atlantic seafloor exposed to seawater for ~46 Ma have higher [Li] (up to 75 ppm) than basalts in ocean drilling cores (ODP sites 504 and 896 and international ODP site 1256) (~9 ppm), which underwent low-temperature hydrothermal alteration for only ~5.9 Ma before they were buried by marine sediments (smaller water/rock ratio) (18, 51). Here, modern F_AOC (14.7 ± 0.8 × 10⁹ mol/year) is calculated using f_AOC of 1.1 × 10¹⁵ kg/year and mean warm spring composition ([Li_AOC] = 13.4 ± 3.7 μmol/kg), which is ~50% lower than seawater Li ([Li_SW] = 27 μmol/kg H₂O). This modern F_AOC is slightly higher than that used for a recent steady-state mass balance model (11 × 10⁹ to 12 × 10⁹ mol/year) (20, 22) but lower than mean F_AOC estimates from Li enrichment (23.1 to 27 ppm) in altered off-axis ocean crust from the Cretaceous Troodos ophiolite (14 × 10⁹ to 21 × 10⁹ mol/year) (18). The F_AOC estimates from the Troodos ophiolite are probably an upper limit for modern F_AOC because [Li⁺]_SW in late Cretaceous seawater, measured here from fluid inclusions in halite (156 ± 34 μmolal), contained far more Li⁺ than modern seawater (27 μmol/kg H₂O).

F_AOC (13.4 × 10⁹ to 25.4 × 10⁹ mol/year) over the past 150 Ma was calculated using the variable f_AOC (1.1 × 10¹⁵ to 1.9 × 10¹⁵ kg/year) (38), [Li_SW]_t, and [Li_AOC]_t (Fig. 4C and data S3). [Li_AOC]_t depends on [Li_SW]_t, f_AOC, and F_MOR (Eq. 1). f_AOC was determined from reconstructions of the area of 1 to 65 Ma old ocean crust and data from modern hydrothermal systems for ocean crust–seawater interactions between 30° and 60°C, normalized to mean modern f_AOC of 1.1 × 10¹⁵ kg/year (Fig. 4C and fig. S6) (38, 42). Hydrothermal flux in ocean crust older than 65 Ma old approaches zero because impermeable marine sediments disconnect the ocean from the underlying crust (43). The uncertainties involved in estimation of f_AOC are 20%, which are then propagated through the calculations for modeling of [Li_SW]_t (Eq. 1) (Figs. 1 and 4C and fig. S6).

Low-temperature spring fluids venting at 12.3° ± 0.01°C from a basaltic edifice on 23 Ma old seafloor at the Dorado outcrop on the Cocos Plate, eastern Pacific Ocean (52), are suggested to be more representative of Li removal from seawater into secondary phases than warmer pore and spring fluids from the Juan de Fuca Ridge at Baby Bare and the Costa Rica Rift (46). Dorado spring fluid composition ([Li_AOC] = 25.1 ± 0.1 μmol/kg) differs from seawater ([Li_SW] = 27 μmol/kg H₂O) by only ~4 to 7% (52). An alternative 150 Ma [Li_SW]_t model using larger fluid fluxes (f_AOC = 5.8 × 10¹⁵ to 9.9 × 10¹⁵ kg/year) and Dorado-like spring fluid composition [Li_AOC]_t is shown in fig. S7.

3. Riverine Li⁺ flux (F_RIV): Rivers, the conduit for global continental weathering, supply average annual dissolved Li⁺ (F_RIV = 9.94 × 10⁹ mol/year) to the ocean, calculated from modern river water flux (f_RIV = 3.75 × 10¹⁶ kg/year) and average [Li_RIV] = 0.265 μmol/kg (15). The modern flux of Li from rivers may not be completely representative because above average Li input from rapid chemical weathering during the last deglaciation has not yet declined to the Pleistocene average [Li_RIV] (53). Changes in RIV over the past 150 Ma are uncertain. Previous estimates, obtained from paleoclimate reconstructions, predicted decreased runoff from 150 to 0 Ma ago (54), whereas increased runoff and increased continental silicate weathering flux from 100 to 0 Ma ago were calculated from inverse modeling of the marine Sr, Os, C, and Li isotope records (20, 23, 55). Still, other models assumed constant riverine Li⁺ flux from the continents over the Cenozoic (3). There are no empirical data available to independently estimate changes in F_RIV over time, so here, F_RIV was assumed to be constant to test the sensitivity of the model to other parameters (F_MOR and F_AOC) (Fig. 4B and data S3).

4. Uptake of Li by MAAC (F_MAAC): Li enrichment in marine clay occurs when Li⁺ in seawater is incorporated in detrital and authigenic clays (56). The magnitude of removal of Li from seawater into aluminosilicate clays is poorly known in the modern ocean and even less well known in the past. Global rates of burial diagenesis of detrital clays and formation of authigenic minerals are unknown (18, 23, 51). A previous estimate of F_MAAC (20 × 10⁹ mol/year) (3) was based on the input of continental sediments to the ocean (13.5 × 10¹² kg/year), assuming that the average clay content of suspended sediment was 53% and that marine clays were enriched in Li⁺ by ~10 to 60 ppm (1 to 9 μmol/kg). Those assumptions gave an F_MAAC four times higher than that estimated from the mass-weighted average marine sedimentary flux of Li to subduction zones (F_MAAC = 5 × 10⁹ mol/year) (56). Uncertainties in the global flux of suspended sediment to the oceans, its clay/sand ratio, and the rate of formation of authigenic clays have complicated the calculation of global removal of Li⁺ into marine sediments. No empirical data are available to independently estimate present-day F_MAAC. Modern F_MAAC was estimated here to be 11.9 × 10⁹ mol/year, similar to that used recently for steady-state mass balance calculations (F_MAAC = 11 × 10⁹ mol/year) (20). F_MAAC in the past is further complicated because the change in terrestrial clay flux to the ocean and authigenic clay formation through time are unknown. Here, F_MAAC is assumed to be constant (11.9 × 10⁹ mol/year) over the past 150 Ma (Fig. 4C and data S3).

[Li⁺]_SW model implementation

The 150 Ma forward model for [Li⁺]_SW (Fig. 1) assumes the following: (i) variable Li fluxes from high-temperature hydrothermal fluids through the axial portions of the MOR systems (F_MOR) for crust 0 to 1 Ma old (38); (ii) variable removal rates of Li into off-axis (F_AOC) portions of the ridge flank crust, 1 to 65 Ma old (38); (iii) constant riverine Li flux (f_RIV) equal to modern global river discharge; and (iv) constant uptake flux of Li into marine clays (F_MAAC), which then allowed testing of model sensitivity to changes in F_MOR and F_AOC (Fig. 4). The forward model starts at steady state (total mass of Li input fluxes equals total output) at 150 Ma and then calculates [Li⁺]_SW at each 10 ka time step using the input and output fluxes of [Li⁺] from the sources and sinks until the present (0 Ma). The model agrees with measured [Li⁺]_SW from fluid inclusions (Fig. 1), which shows that the drop in [Li⁺]_SW over the past 150 Ma can be produced by decreasing high- and low-temperature seafloor hydrothermal fluxes without requiring changes in river input and MAAC uptake fluxes.

Given the uncertainties in estimating f_MOR (200 to 400%) and f_AOC (<20%) (fig. S6), the sensitivity of the model result is considered by propagating the f_MOR and f_AOC uncertainties through the calculations for [Li_SW]_t in Eq. 1. The uncertainty associated with f_AOC narrows the possible f_MOR range needed for the Li⁺ mass balance to within ±15% of the mean f_MOR (Eq. 1). These uncertainties (gray band around the mean f_MOR and f_AOC curves in Fig. 1 and fig. S6) replicate the [Li_SW]_t model result without requiring changes in the F_RIV and F_MAAC (Fig. 4). Modeling of [Li_SW]_t using f_MOR above or below the ±15% mean f_MOR range, however, requires changes in F_RIV and F_MAAC to reproduce the [Li]_SW record. A range of f_MOR, greater than ±15% of the mean f_MOR range (fig. S6), for example, produces an exceedingly large Li⁺ flux from MOR input, which requires an additional sink (F_MAAC) to remove the excess Li⁺. On the other hand, a lower range of f_MOR, less than ±15% of the mean f_MOR range, is compatible with interpretations that MOR activity has not varied significantly in the past (57). Such a lower range of f_MOR then requires higher F_RIV and F_MAAC to explain the [Li⁺]_SW record.

Covariation of [Li⁺]_SW with [Ca²⁺]_SW, [Mg²⁺]_SW, [Mg²⁺/Ca²⁺]_SW, and ⁸⁷Sr/⁸⁶Sr

The 150 Ma decrease of [Li⁺]_SW and the modeling results presented here have implications for interpreting secular changes in the major ion chemical composition of seawater. The positive correlation between [Li⁺]_SW and [Ca²⁺]_SW (r² = 0.99) (Fig. 3B) suggests that declining seafloor hydrothermal fluxes and concomitant lower rates of Ca²⁺ released to seawater via albitization and chloritization reactions (17, 58) produced the threefold decrease in [Ca²⁺]_SW over the past 150 Ma. The threefold decrease in [Ca²⁺] and the 1.6× increase in [Mg²⁺]_SW over the past 150 Ma are responsible for the negative correlation between [Li⁺]_SW and [Mg²⁺/Ca²⁺]_SW (Fig. 3C). The Mesozoic-Cenozoic increase in [Mg²⁺]_SW may be explained by decreased removal of Mg²⁺ from seawater at the MOR (4, 17, 58), a decrease in the rate of Mg²⁺ removal into marine clays attributable to Cenozoic cooling of ocean bottom waters by 10° to 15°C (8, 11) or even 20°C (59), and a decrease in the rate of dolomitization on the seafloor (60). The positive correlation between [Li⁺]_SW and [Sr²⁺]_SW (r² = 0.97) (Fig. 3D) suggests that declining seafloor hydrothermal fluxes over the past 150 Ma may be responsible for lower fluxes of Sr²⁺ and Li⁺ released to seawater because MOR hydrothermal brines are enriched in [Li⁺], [Sr²⁺], and [Ca²⁺] via reactions between MOR basalts and seawater. The increase in ⁸⁷Sr/⁸⁶Sr from the Late Jurassic (0.7069) to today (0.7092) and the negative correlation (r² = 0.90) between [Li⁺]_SW and ⁸⁷Sr/⁸⁶Sr (Fig. 3E) suggest that the progressive decline of MOR hydrothermal fluxes decreased input of low ⁸⁷Sr/⁸⁶Sr hydrothermal fluids (61). Last, the increase of δ⁷Li_SW by ∼5 to 6‰ over the past 36 Ma and the strong negative correlation (r² = 0.93) between [Li⁺]_SW and δ⁷Li_SW (Fig. 3F) suggest that decline of MOR hydrothermal fluxes decreased input of low δ⁷Li fluids (3). In addition, the Cenozoic increase in δ⁷Li_SW may also be explained by an increase in isotopic fractionation between seawater and oceanic Li sinks (ocean crust and marine clays) as ocean bottom water temperatures decreased (18). In summary, the previously unknown and unexpectedly large decrease in [Li]_sw over the past 150 Ma reported here has important implications for better understanding the global geochemical cycle of Li, and more broadly, how plate tectonic activity influences the long-term chemical composition of seawater, greenhouse-icehouse climate states, and the global carbon cycle.

MATERIALS AND METHODS

Sample selection

Fluid inclusions in halite were used to reconstruct the major ion chemistry of seawater in the Phanerozoic (1, 7, 29). Primary fluid inclusions along growth bands in bottom-grown crystals of marine halite (chevron and/or cornet structures) and cumulate crystals (hoppers, rafts, and sunken cubes formed at the air-brine interface and in the water column) record the chemistry of evaporating seawater (fig. S2) (62). A total of 639 fluid inclusions in 65 halite crystals from 3 Mesozoic [Kimmeridgian-Tithonian (155.7 to 145.5 Ma) and Albian-Cenomanian (112.2 to 93.5 Ma)] and 10 Cenozoic [Priabonian (~36 Ma), Langhian-Serravallian (13.81 to 13.1 Ma), Serravallian-Tortonian (11.8 to 7.2 Ma), Messinian (5.61 to 5.55 Ma), and modern (0 Ma)] marine evaporite formations (fig. S3), well documented for major ion chemistry (Mg²⁺, Ca²⁺, Na⁺, K⁺, SO₄²⁻, Clˉ) (7, 24–28), were reanalyzed to obtain Li⁺/Mg²⁺ ratios and Li⁺ concentrations (table S1 and data S1). Petrographic, geochemical, and paleontological criteria used to characterize the marine origin of the fluid inclusions in the halites studied include the following: (i) Brˉ concentrations in halite (24–29), (ii) δ³⁴S in sulfate minerals interbedded with halite (24–27, 31, 63), (iii) ⁸⁷Sr/⁸⁶Sr in sulfate minerals (31–33) and in fluid inclusions in halite (30), and (iv) marine fossils preserved in underlying carbonate/marl units (24, 25, 64). These records show that the parent waters of the inclusion brines reported here were marine in origin, especially because the ⁸⁷Sr/⁸⁶Sr ratio in halite fluid inclusions is the same as contemporaneous seawater (Fig. 1 and table S2).

Analytical methods

Fluid inclusions in halite were analyzed using an NWR193 (ESL, Bozeman, MT) ArF excimer laser ablation system coupled to an Agilent 7900 quadrupole mass spectrometer. Halite crystals were first cleaved with a razor blade into tabular fragments, approximately 8 mm by 5 mm by 1 mm in size, to expose fresh surfaces and to fit on glass slides within the laser ablation sample chamber. Each cleaved halite crystal was examined to document the primary nature of fluid inclusions along halite growth bands using a transmitted light Zeiss Axio Imager.A1 (Carl Zeiss AG, Oberkochen, Germany) at magnifications between 25× and 100× (fig. S2). Well-defined bands of single-phase fluid inclusions along primary growth zones were selected for LA-ICP-MS analysis. Recently developed analytical methods were used to obtain Li⁺/Mg²⁺ ratios of individual fluid inclusions in halite (13).

Typical analytical accuracy for Li⁺/Mg²⁺ ratios was within 7% of the expected value based on measurements of fluid inclusions with known chemical compositions, and precision was <10% RSD (13). Controlled and optimized laser ablation of fluid inclusions improved the analytical accuracy, precision, and lowered detection limits for Li⁺ and Mg²⁺to values below 50 and 100 μmolal, respectively. The accuracy of the method was verified using modern halite samples from the Dead Sea. Mg²⁺ and Li⁺ concentrations in modern Dead Sea brine measured using ICP–optical emission spectroscopy and the LA-ICP-MS analyses of fluid inclusions in Dead Sea halite formed from those brines show that fluid inclusion and brine chemistry agree within 7% error (13).

Calculation of [Li⁺]

Li⁺/Mg²⁺ ratios measured from fluid inclusions require known Mg²⁺ to convert ratios into absolute [Li⁺]. The conversion is straightforward because the Li⁺/Mg²⁺ ratio remains unchanged during evaporation of seawater through aragonite, gypsum, and halite precipitation until the first Mg-bearing salts form. For example, the Li⁺/Mg²⁺ ratio in modern seawater is 0.49 μmol/mmol (36), and this ratio remains constant until the Mg-bearing salt, polyhalite [K₂Ca₂Mg(SO₄)₄·2H₂O], precipitates at a degree of evaporation (DE) of 38.7. The formation of polyhalite applies to conditions where early formed minerals (gypsum or anhydrite) are allowed to back-react with the brine. In contrast, during “fractional crystallization,” which occurs in man-made solar evaporation systems, brines are removed from contact with precipitated minerals as evaporated seawater flows from pond to pond. In this case, the Li⁺/Mg²⁺ ratio remains conservative until epsomite (MgSO₄·7H₂O) and/or kainite (KMgSO₄Cl·3H₂O) precipitate at a DE of 60.5 and ~70, respectively. That is because gypsum, precipitated in ponds during the early stages of evaporation, never comes in direct contact with highly evolved seawater and so cannot react with brine to form polyhalite (fig. S1). Li⁺/Mg²⁺ ratios change slightly from 0.49 to 0.59 μmol/mmol between a DE of 0 and 100 due to a small amount of MgSO₄ salt precipitation between a DE of 70 and 100. This change is indistinguishable from the observed variability in Li⁺/Mg²⁺ ratios of 0.4 to 0.6 μmol/mmol during the early stages (DE <10) of solar evaporation ponds (fig. S1B).

Evaporative concentration of seawater to extreme levels beyond a DE of 100 causes the seawater Li⁺/Mg²⁺ ratio of 0.9 to increase to a maximum of 3.9 at DE of 870 as Mg²⁺ is removed from the brine to form kieserite, carnallite, and finally bischofite (35). In contrast, Li⁺ is conservative during the complete evaporation of seawater because there are no naturally occurring Li salts that incorporate significant amounts of Li (36). Experiments with solar evaporation of Black Sea water and Mediterranean seawater showed that Li⁺ increased conservatively up to a DE of 117 (65) and 870 (35), respectively. Halite analyzed in this study was not associated with Mg-bearing salts (30); thus, the Li⁺/Mg²⁺ ratio measured in fluid inclusions in halite is assumed to be the same as the ratio in unevaporated seawater.

The major ion chemistry of Phanerozoic seawater, including Mg²⁺, was previously estimated from chemical analyses of fluid inclusions in marine halite (7, 24, 25, 29). Here, we reanalyzed the same halites earlier used to evaluate the major ion chemistry of ancient seawater. Li⁺/Mg²⁺ ratios and published paleoseawater [Mg²⁺] allowed calculation of [Li⁺] in Mesozoic and Cenozoic seawater (Table 1, table S1, Figs. 1 and 2, and fig. S4) (7, 24, 25, 29). For example, the [Li⁺] of modern seawater (29 ± 3 μmolal) was calculated using the present-day [Mg²⁺] of 55 mmolal and the average Li⁺/Mg²⁺ ratio from 50 fluid inclusions in halite from three solar evaporation ponds on the coast of the Mediterranean Sea and the Caribbean Sea. For comparison, modern seawater has measured [Li⁺] of 27 ± 0.2 μmolal (Table 1 table S1, and data S1). The close agreement between modern seawater [Li⁺] and the [Li⁺] calculated from the Li⁺/Mg²⁺ ratio of fluid inclusions in halite from modern solar evaporation ponds shows the validity of calculated [Li⁺] in paleoseawater using Li⁺/Mg²⁺ ratios and published paleoseawater [Mg²⁺] (Figs. 1 and 2 and fig. S4).

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S7

Tables S1 and S2

Legends for data S1 to S3

References

Other Supplementary Material for this manuscript includes the following:

Data S1 to S3