Detecting dynamic domains and local fluctuations in complex molecular systems via timelapse neighbors shuffling

Significance

Many complex systems are controlled by local fluctuations triggering collective motions and rearrangements. Rapid direction changes in bird flocks or fish banks are a few examples but, even on the smallest scales, molecular systems make no exception. Local variations in microscopic molecular environments are at the origin of, for example, phase transitions, nucleation phenomena, and dynamic phases equilibria, but they are also typically difficult to detect. Here, we show a descriptor named Local Environments and Neighbors Shuffling (LENS), which allows tracking local fluctuations and unveiling the dynamic complexity of a variety of molecular systems. Analysis of LENS time series provides a insight into innately dynamic molecular ensembles and, will offer interesting perspectives on the behavior of complex systems in general.

Abstract

It is known that the behavior of many complex systems is controlled by local dynamic rearrangements or fluctuations occurring within them. Complex molecular systems, composed of many molecules interacting with each other in a Brownian storm, make no exception. Despite the rise of machine learning and of sophisticated structural descriptors, detecting local fluctuations and collective transitions in complex dynamic ensembles remains often difficult. Here, we show a machine learning framework based on a descriptor which we name Local Environments and Neighbors Shuffling (LENS), that allows identifying dynamic domains and detecting local fluctuations in a variety of systems in an abstract and efficient way. By tracking how much the microscopic surrounding of each molecular unit changes over time in terms of neighbor individuals, LENS allows characterizing the global (macroscopic) dynamics of molecular systems in phase transition, phases-coexistence, as well as intrinsically characterized by local fluctuations (e.g., defects). Statistical analysis of the LENS time series data extracted from molecular dynamics trajectories of, for example, liquid-like, solid-like, or dynamically diverse complex molecular systems allows tracking in an efficient way the presence of different dynamic domains and of local fluctuations emerging within them. The approach is found robust, versatile, and applicable independently of the features of the system and simply provided that a trajectory containing information on the relative motion of the interacting units is available. We envisage that “such a LENS” will constitute a precious basis for exploring the dynamic complexity of a variety of systems and, given its abstract definition, not necessarily of molecular ones.

Supramolecular assemblies and crystalline structures are characterized by a nontrivial internal dynamics that is often ambiguous and challenging to unveil (1–5). Self-assembled structures, composed of molecular units interacting with each other via reversible noncovalent interactions, offer a notable example of systems where a continuous reshuffling and exchange of the constitutive building blocks is at the origin of interesting bioinspired and stimuli-responsive properties (6–13). Also, other completely different systems, such as, for example, metallic structures, are known to possess a nontrivial internal dynamics. Already at ∼1/3 of the melting temperature (i.e., the so-called Hüttig temperature) metal surfaces are known to enter a dynamic equilibrium where atoms may leave their lattice positions and start moving on the atomic surface, inducing surface transformations and reconstructions (5, 14, 15). In nanosized metal systems (metal nanoclusters, nanoparticles, etc.), such atomic dynamics emerges even at lower (e.g., room) temperature (16). In all these cases, the dynamics and fluctuations in time of the building blocks are deeply connected to important properties of the materials, such as, for example, the mechanical properties of metals (17–19), their performance in heterogeneous catalysis (20–23), or, for example, the dynamics adaptivity and stimuli-responsiveness of supramolecular materials (13, 24–27). Gaining the ability to track the dynamics of the building blocks in complex self-organizing molecular systems is fundamental to studying and rationalizing most of their properties (6, 27–31). However, this is also typically challenging and demands efficient analysis approaches.

Molecular dynamics (MD) simulations are being increasingly used to obtain high-resolution insights into the behavior of a variety of systems (1, 32–40). One key advantage of MD trajectories is that these keep track of the motion of the individual molecular units and contains all phase-space information, hence the complete structure and dynamics of the complex system. Nonetheless, nontrivial aspects concern the extraction of relevant information from the large amount of data contained in the MD trajectories and their conversion to a human-readable form. Typical descriptors used to extract information from MD trajectories may be divided into system-specific or abstract (general) descriptors. Extensively used to investigate, for example, ice-water systems (41), or metal clusters (38, 42), ad hoc descriptors build on a priori knowledge of the system under consideration and are developed and optimized on it, but poorly transferable to different ones. Abstract descriptors, for example, smooth overlap of atomic positions (SOAP), radial distribution functions (g(r)), etc., are conversely less specific and more general (41, 43–49). Although less precise than the tailored ones, abstract descriptors offer an advantage in terms of transferability: They can be applied to different systems and do not require deep a priori knowledge of the system’s features (43, 48, 50). The high-dimensional data obtained using such descriptors are typically converted into lower-dimensional human-readable information via supervised and unsupervised machine learning (ML) approaches (e.g., clustering) and analyzed to characterize the internal dynamics of the studied systems (51–57). For example, unsupervised clustering of SOAP (43) data extracted from MD trajectories recently allowed studying the complex dynamics in self-assembling fibers, micelles, and lipid bilayers (47, 50, 58–60), in confined ionic environments (47, 59), as well as in metal nanoparticles and surfaces (5, 16).

Despite the advantages granted by such ML developments, the behavior of complex molecular systems is often determined by rare fluctuations and local dynamic rearrangements (6, 7, 27), poorly captured by average-based measurements. The dynamics of defects in materials science is a typical example of local events determining a variety of hierarchical materials’ properties (31, 61). However, detecting and tracking local fluctuations becomes increasingly difficult when dealing with complex molecular/atomic systems where a certain degree of structural order is coupled with a continuous exchange and reshuffling of molecules/atoms (25). Abstract descriptors that are transferable and at the same time effective in capturing local fluctuations in complex dynamic systems would be fundamental.

Here, we develop an abstract descriptor named “Local Environments and Neighbors Shuffling (LENS).” Combined with a ML-based analysis, LENS is capable of detecting different dynamic domains and tracking local fluctuations in complex molecular systems without deep prior knowledge of the chemical/physical features of the constituent building blocks but simply by tracing their reciprocal motion and instantaneous fluctuations in space and time. LENS builds on a relatively simple definition and can be transferred to a variety of complex systems with, liquid, solid, or diverse/hybrid dynamics (e.g., typical of phase transitions). The results obtained with LENS change the vision of complex molecular systems and, building on simple and general basic concepts, suggest broad applicability (e.g., not necessarily restricted to molecular ones).

Results

LENS: Local Environments & Neighbors Shuffling.

In this work, we analyze molecular dynamics (MD) trajectories of various molecular/atomic systems, from soft to crystalline ones, possessing liquid-like to solid-like dynamics. As examples of fluid-like systems, we use lipid bilayers and surfactant micelles (60), while for solid-like dynamics, we focus on metal surfaces (5) and nanoparticles (16). Furthermore, we also include systems with intrinsically nonuniform internal dynamics, such as, for example, a system where ice and liquid water coexist in dynamic equilibrium in correspondence with the solid–liquid transition, and soft self-assembled fibers whose behavior is dominated by local dynamic defects (see SI Appendix, Table S1 for system details) (6, 7, 50). Such a large diversity is functional to test the generality of our approach.

Despite their intrinsic differences, all these systems can be considered from an abstract point of view as composed of N dynamically interacting particles with their own individual trajectories. The analysis approach we present herein is based on the concept of molecular individuals (even in cases of systems of chemically identical particles). In particular, from the global trajectory of the system, we can identify the subtrajectory of the ith particle (with i ranging from 1 to N). From this, we can thus describe the local environment surrounding each ith particle in terms of its neighbor individuals (IDs) and monitor the changes of IDs at each interval between the sampled timestep Δt along the trajectory. Fig. 1A, Top-Left shows a representative scheme where, at a given time t, the neighbor ID units (gray circles) surrounding the ith particle (i = 1 – red circle) within a sphere of radius r_cut (namely, the neighborhood cutoff) are listed in a fingerprint string $C_{i=1}^t$. The local $C_{i=1}^{t+\mathrm{\Delta }t}$ environment at t + Δt may change from that one at time t ($C_{i=1}^t$) when neighbor switching (Fig. 1A, Top-Right), addition (Fig. 1A, Bottom-Left), or subtraction (Bottom-Right) occurs in Δt.

Fig. 1.

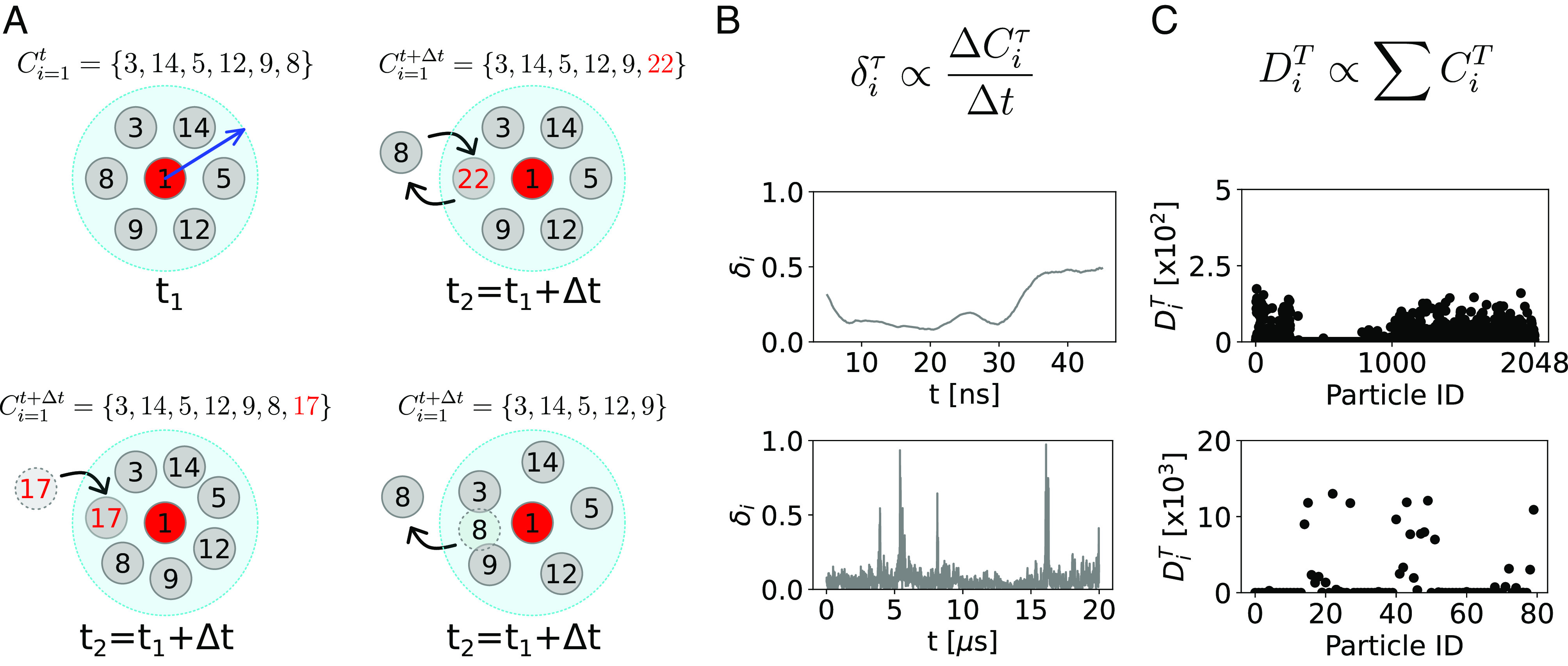
Tracking local neighbor environments in complex molecular systems with the LENS descriptor. (A) The local molecular environment of the particle i = 1 at time t is defined by an array C_i^t containing the identities (IDs) of all molecular units within a sphere of radius r_cut (blue arrow). Along the MD trajectory, C_i^t can be calculated for all constitutive particles at each sampled MD timestep t. The local molecular environment C_i^t of the unit i = 1 (red particle) at time t₁ (Top-Left). The local environment C_i^{t + Δt} at time t₂ = t₁ + Δt, when particle switching occurs in Δt (Top-Right). The local environment C_i^{t + Δt} at time t₂ = t₁ + Δt, when one particle enters (Bottom-Left) or leaves (Bottom-Right) the neighborhood sphere in Δt. (B) The LENS descriptor. The LENS signal for the generic particle iδ_i^τ is proportional to the number of changes in the neighborhood within a timestep τ (Top). Two examples of typical LENS signals, δ_i(t) (raw data smoothed as described in Materials and Methods), for a particle with fluid-like behavior (Center) and a particle with dynamics dominated by local fluctuations (Bottom). (C) Global statistical analysis. All contact events between the particle i and all the others in the system, visited along the entire trajectory T, are counted and listed in the D_i^T array. Two examples of contact counts, D_i^T, between a molecule i and all other IDs in the two distinct dynamics cases of C are shown.

Our analysis is based on monitoring the time-lapse sequence of the ID data along a given trajectory. We developed a descriptor named “LENS,” which allows us to track to what extent the ith local environment changes at every consecutive time interval (C_i^t, C_i^{t + Δt}, C_i^{t + 2Δt}, etc.) along its trajectory. LENS is built to detect essentially two types of changes in the local neighbor environments along a trajectory: i) changes in the number of neighbors (addition/leave of one or more neighbors) and/or ii) changes in the IDs of the neighbors (switching of one or more neighbor IDs). The instantaneous value of LENS (δ_i, in its variable form) is defined as

$$\begin{array}{c}\hfill {\delta }_i^{t+\mathrm{\Delta }t}=\frac{\#(C_i^t\bigcup C_i^{t+\mathrm{\Delta }t}-C_i^t\bigcap C_i^{t+\mathrm{\Delta }t})}{\#(C_i^t+C_i^{t+\mathrm{\Delta }t})},\end{array}$$ [1]

where the first (C_i^t⋃C_i^{t + Δt}) and the second terms (C_i^t⋂C_i^{t + Δt}) of the numerator are respectively the mathematical union and intersection of the neighbor IDs present within r_cut from particle i at time t and at time t + Δt. The denominator contains a normalization factor, which is the total length of the neighbor ID lists (strings) at the two consecutive timesteps. Thus, for every particle i, the δ_i(t) ranges from 0 to 1 for local neighbor environments which are respectively persistent to highly dynamic over time. For example, in the hypothetical case where no local neighbor changes occur in Δt, the union of C_i^t and C_i^{t + Δt} is identical to their intersection, and LENS gives δ_i^{t + Δt} = 0. In a case where, for example, all IDs permute in different IDs in Δt (complete shuffling while the number of neighbors remains constant), the numerator of the δ_i^t ((C_i^t + C_i^{t + Δt})−0) is equal to the denominator and LENS gives δ_i^{t + Δt} = 1. As shown in Fig. 1B, Top, the LENS signal (δ_i) for the generic particle i can be considered proportional to the local neighborhood changes within a time interval Δt. Fig. 1B reports two examples of LENS signals over time in the cases of a particle with fluid-like behavior (Center) and of another particle (Bottom) whose dynamics is dominated by local fluctuations.

The time-lapse analysis provided by LENS can be also corroborated/compared with a time-independent statistical analysis of the ID neighbor list data C_i. In particular, from the ID neighbor list data C_i calculated at every sampled time step (t, t + Δt, t + 2Δt, etc.), one can easily estimate how many times a particle i has been in direct contact with all the other N ID particles during a sampled trajectory T. All inter-IDs contacts visited along the trajectory T are then stored into an array D_i^T (Fig. 1C). In such global statistical analysis, the D_i^T data are useful to detect the presence of domains differing from each other in terms of dynamicity/persistence of the local neighbor individuals over time (i.e., in terms of how quickly/slowly the neighbor IDs change along the trajectory). In particular, analysis of the global D^T contact matrix (Fig. 2E) provides information on the propensity of a certain i unit to be, for example, persistently surrounded by the same neighbors (IDs) or by a population that is in continuous reshuffling during the simulation (see Materials and Methods for details).

Fig. 2.

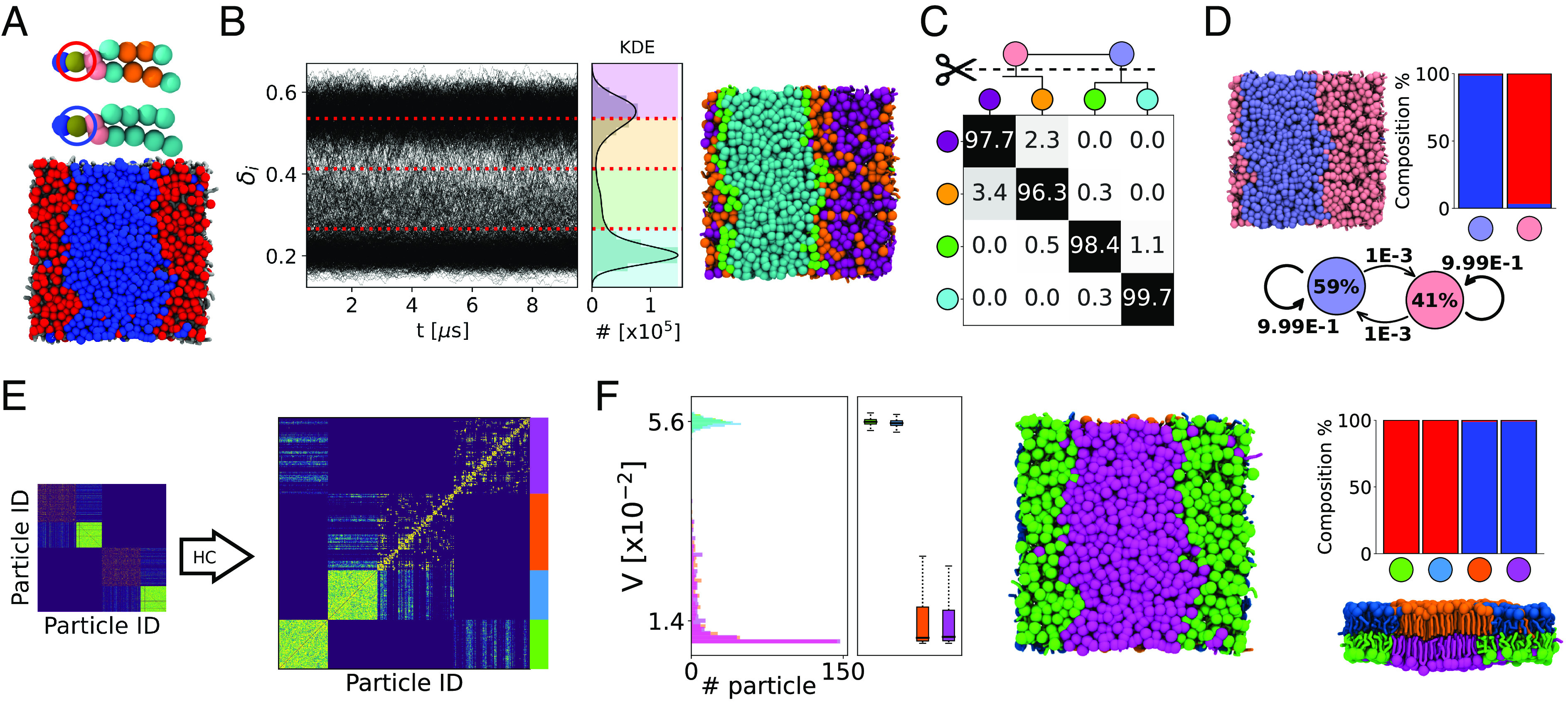
LENS analysis of fluid-like systems. (A) Bicomponent lipid bilayer made of 1,150 lipid molecules, namely DIPC:DPPC in 2:3 ratio (460:690 in total, 230:345 per leaflet) colored in red and blue, respectively. (B) Time series of LENS signals, δ_i(t), with the kernel density estimate (KDE) of LENS distribution classified into four clusters (Left). MD snapshot of lipids bilayer colored according to their clusters of belonging (Right). (C) Interclusters normalized transition probability matrix. The p_ii and p_ij matrix entries indicate the % probability that molecules with LENS signal typical of a cluster i remain in that dynamic environment or move to another one j (with different dynamics) in Δt. Hierarchical grouping of the dynamically closer clusters (dendrogram cutting) is reported on Top of the matrix, and it provides two macroclusters, merging cyan and green on one hand, and orange and purple on the other hand. (D) MD snapshot of the lipid bilayer colored according to macroclusters in (C): light blue identifying DPPC lipids and pink identifying DIPC lipids (Top-Left). Cluster composition histogram (Top-Right) and interconversion diagram (Bottom) with the transition exchange probabilities and the cluster population percentages (within the colored circle). (E) HC analysis of the D^T matrix identifying four main clusters (light blue, green, purple, and orange). (F) Variability, V, analysis of the clusters: distributions, median (first and third quartiles), maximum and minimum values (whiskers). The green and light blue clusters, arranging on separated bilayer leaflets, have higher V than the orange and magenta clusters (Left). MD snapshot front view of the lipid bilayer colored according to the HC of D^T matrix (Middle). Cluster composition histogram (Top-Right): The green and light blue clusters are made of DIPC lipids (in red in A), while the orange and magenta ones correspond to the DPPC lipids (in blue in A). MD snapshot lateral view of the lipid bilayer colored according to the HC of D^T matrix (Bottom-Right). Note that the subunits within each considered system are illustrated coherently to the color code of the belonging cluster.

To provide a more quantitative investigation, we define a variability ($V)$ parameter by estimating the Standard Deviation (SD) of the D_i^T counts. Namely, high SD of the D_i^T values means that, among all sampled timesteps, a generic unit i shows a high number of contact events with few neighbors and very low contact occurrence with the others (meaning that its closest neighbors tend to remain always the same along the trajectory). On the other hands, low SD of the D_i^T values implies a moderate but uniform number of neighboring events among all neighbor IDs (meaning that the closest neighbors of unit i change a lot along the trajectory). In this perspective, the variability $(V)$ parameter is then defined as the inverse of the SD of the D_i^T values: More dynamic neighborhood environments of i have high $V$ while more static neighborhood environments have low $V$ values.

As it will be discussed in the next sections, such global time-independent analysis does correlate with the LENS one for systems composed of statistically relevant dynamically diverse domains (populated by a relevant number of units that can be effectively detected via “dynamic-pattern recognition” approaches), while it does not for systems whose dynamics is dominated by sparse local fluctuations/transitions.

Into the Dynamics of Fluid-Like Systems.

We start testing LENS on a soft molecular system with nontrivial fluid-like dynamics (Fig. 2). In particular, we analyze a MD simulation trajectory of a coarse-grained (CG) bicomponent lipid bilayer composed of 1,150 DIPC:DPPC lipid molecules in a 2:3 ratio (see Fig. 2A, where DIPC and DPPC are colored in red and blue, respectively). It is well known that at T = 280 K, a 2:3 DIPC:DPPC lipid bilayer self-segregates into two distinct regions, populated by the two lipid species which do not mix in such conditions (62). For this lipid model, we ran 15 μs of CG-MD simulation using the Martini 2.2 force field (63) (see Materials and Methods and SI Appendix, Table S1 for details). The last 10 μs, representative of an equilibrated MD regime, are used for the analysis.

Being interested in the lipid shuffling dynamics, in our LENS analysis, we use the lipid heads as reference constituent particles, and we set a time interval of Δt = 10 ns with a neighborhood cutoff r_cut = 16 Å (SI Appendix, Fig. S2). On average, with such a setup, every reference lipid has ∼13 neighbors. Noteworthy, the robustness of the analysis while changing the r_cut or Δt is demonstrated in SI Appendix, Figs. S3 and S4. Fig. 2B shows on the Left the time-profiles of δ_i(t) for the 1,150 lipid heads forming the bilayer, while on the Right, the δ_i data distribution and the correlated KDE are reported. Here, two peaks are clearly detected. A simple supervised clustering analysis, carried out with the KMeans algorithm (64) on LENS signals, demonstrates that the δ_i distribution can be classified into four clusters (cyan, green, orange, and purple) denoted as dynamic clusters or domains. The time series data of the individual lipid IDs along the trajectory allows computing the exchange probability matrix represented in Fig. 2C and obtaining the associated dendrogram detailing the hierarchical interconnection/adjacency between such four detected clusters. In the exchange probability matrix, the p_nn and p_nm entries indicate the % probability for a lipid i belonging to a given dynamic cluster n—having a characteristic rate of change of its local neighbor environment—to remain in that dynamic domain or to undergo a transition into a different dynamic cluster m—with a different LENS fingerprint—in Δt (see Materials and Methods for additional details). The four obtained microclusters can be then hierarchically merged based on the dendrogram in Fig. 2C, by connecting those having a high probability of exchanging molecules. Such an approach provides two main macroclusters, colored in light blue and pink, whose populations and transition probabilities in Δt are reported in the interconversion diagram of Fig. 2D within circles and on the arrows, respectively.

The data show that the pink domain, obtained after merging orange and purple clusters, is dominated by those lipid units having a higher aptitude to mutate their neighborhood environment: in other words, by those having a more dynamic local neighbor environment (high δ_i). On the other hand, the lipids belonging to the light blue domain, resulting from blending the cyan and green microclusters, reveal a slower variation of their surrounding environment and hence weaker local mobility (low δ_i). Not surprisingly, while the pink dynamics domain overlaps with the DIPC molecules (red component), known to be in liquid phase (62), the light blue cluster matches up with the DPPC lipids (blue component) that are instead in gel phase (62) (see composition histogram in Fig. 2D, Top-Right). Furthermore, the estimated exchange probabilities between the pink and light blue macroclusters are very low (< 1%) in Δt = 10 ns, which is consistent with a sharp segregation between the gel and fluid phases.

In order to test the robustness of our descriptor LENS, we have also carried out a 2D Voronoi-based tessellation [a reference approach to detect, for example, liquid/gel phases in lipid bilayers (65)] on the MD trajectories of the DIPC-DPPC lipid bilayer at T = 280 K. The obtained results show how, in the case of phase segregation in the DIPC-DPPC bilayer, the Voronoi analysis while qualitatively matching with the results obtained with LENS, reports a less well defined and more blurred characterization of the liquid DIPC and gel DPPC segregated phases that are expected experimentally (62) (SI Appendix, Fig. S15).

We also tested the robustness of the LENS results against tuning the Δt (i.e., the time resolution) in the analysis (see SI Appendix, Fig. S4). Comparing the results of SI Appendix, Fig. S4 A and B, it is possible to note that the absolute values of LENS—which are related to the degree of reshuffling in the microscopic neighbor environments in the Δt—may differ while changing the sampling time step. This is expected, as changing the Δt in these analyses equals to changing the time resolution and the details that are consequently captured (i.e., events occurring faster than the used Δt cannot be captured). However, it is worth noting that i) the quantitative LENS numbers are of little interest, while their comparison, distributions, and the fashion of the LENS time series are the key interesting points. Furthermore, ii) while the microscopic details captured may change with the Δt (SI Appendix, Fig. S4, Left: for example, Δt = 5 ns vs. 50 ns), the analysis remains quite robust on a macroscopic level, and grouping the adjacent microclusters into dynamic macroclusters based on the hierarchical interconnection dendrogram provides the same (coarse-grained) results in both cases (SI Appendix, Fig. S4, Right). While, as in many other types of analyses, a preliminary phase of similar tests is useful to identify the best match between high-resolution and robustness/relevance in the obtained results, the LENS analyses reported herein demonstrated considerable robustness in the obtained global results.

Fig. 2 E and F illustrates the main outcomes of the global statistical analysis explained in the previous paragraph. The collected data, D_i^T, are organized into a count matrix where the single entry i, j defines the total number of neighboring events between lipids i and j (Fig. 2E). Although such statistical analysis is unrelated to the temporal sequence of the C_i^ts, the global D^T matrix allows distinguishing the propensity of a certain lipid to be, for example, persistently surrounded by the same neighbors or by a population in continuous exchange (reshuffling) during the simulation. After hierarchical clustering (HC) of the D^T matrix data (see Materials and Methods for details), four main dynamic domains are identified (Fig. 2E, Right): in green, light blue, orange, and purple. Lipid molecules characterized by a similar distribution of neighbor contacts in the D^T matrix are classified in the same dynamics domain. For a more quantitative investigation, we also define a variability (V) parameter by estimating the SD of the D_i^T: The broader is the distribution of the neighbor IDs, the higher is the variability (see Materials and Methods for details). The analysis shows that the green and light-blue domains are identically highly dynamic, while the orange and purple clusters, similar to each other from a dynamic standpoint, are ∼4 times more static (Fig. 2 F, Left). Note that, while having the same variability and local-shuffling dynamics, the two green/light-blue (and orange/purple) clusters are identified in this analysis as separate environments. In fact, since the bilayer model replicated on the xy through periodic boundary conditions, the DIPC and DPPC lipids belonging to the upper leaflet do not get in contact with those in the Bottom one (their D_i^T distributions do not overlap). The histograms in Fig. 2F, Right reveal that the green and blue clusters correspond to red DIPC lipids, while the orange and purple domains correspond to the blue DPPC molecules. This is consistent with the experimental evidence (62) showing that the DIPC lipids form a liquid phase segregating from gel-phase DPPC molecules at the simulation temperature. It is worth noting how the macroclusters obtained with the global statistical analysis (Fig. 2 E and F) correspond in this case to those obtained via LENS-based clustering. As anticipated, such correspondence occurs only in those systems composed of “statistically dominant” different dynamic domains, as in this case, where a liquid and a fluid phase coexist in the bilayer system. In the next sections, we will also discuss cases where LENS detects fluctuations that get lost and cannot be tracked via such global/average analyses since they are not statistically relevant.

To test the generality of our approach, we also tested the same analysis on a CG-MD simulation trajectory of a bicomponent micelle model (SI Appendix, Fig. S2) made of n-stearoyl L-histidine (H) and p-nitrophenyl ester of n-stearoyl L-phenylalanine self-assembling surfactant molecules (see Materials and Methods for details) (60). SI Appendix, Fig. S2 A–D show how both LENS and the corresponding time-independent Variability analyses identify two distinct dynamic domains: a “donut-like” region of H surfactants (red) and two separated, flatter circular sections of F-NP surfactants (in blue). Similarly to the bicomponent lipid bilayer case discussed above, the dynamics of such bicomponent micellar assembly appears to be thus characterized by different statistically relevant dynamic domains.

Into Phase Transitions & Dynamic Phases Coexistence.

We also tested the efficiency of LENS in characterizing phase transitions as well as the dynamic coexistence between different phases. To this end, we discuss two different example systems: i) a (soft) DPPC lipid bilayer system undergoing gel-to-liquid transition with increasing temperature and ii) a simulation box where crystalline ice and liquid water coexist in correspondence with the melting/solidification temperature.

For case (i), we analyze 1,001 consecutive snapshots taken along 1 μs of CG-MD simulations (Δt = 1 ns) of a lipid bilayer model composed of 1,152 self-assembled DPPC lipids parametrized with the Martini force field (63) at three distinct temperatures: 273 K, 293 K, and 323 K (see Materials and Methods for details) (58). It is known that DPPC lipid bilayers have a transition temperature gel-to-liquid of ∼315 K (66). However, detecting in a robust manner such gel-liquid phases is not straightforward and typically requires sophisticated analysis approaches that are not always trivial to handle (58, 67). After reducing the number of clusters detected by KMeans (SI Appendix, Fig. S6), LENS identifies two main phases dominating the DPPC bilayer at T = 293 K (Fig. 3A): The δ_i(t) data indicate that while the largest part of lipids shows a reduced local reshuffling of neighbors over time, a nonnegligible portion of them is more dynamic. As shown in Fig. 3A, Right, two phases coexist at T = 293 K: ∼8% of DPPC lipids are found in the red phase, which starts nucleating into the blue one (∼92%); see also SI Appendix, Movie S1. The transition probability between the two phases is also detected and reported on the black arrows. By using the same setup that detected the gel/liquid separation at 293 K, LENS-based clustering identifies two dominating phases in the DPPC bilayer at T = 273 K and T = 323 K, respectively: a cyan domain with lower δ_i vs. a red environment with higher δ_i, respectively (Fig. 3B). Global statistical analysis summarized in Fig. 3C by the Variability of D_i^T distributions reveals that the dynamic reshuffling of lipids is considerably reduced in the cyan domain compared to the red one (∼2 to 6 times). This indicates that the lipids assigned to the cyan cluster most probably correspond to the gel phase, while the lipids in the red environment behave as a liquid phase, as also evident in the red disordered lipid tails compared with the more extended/ordered cyan ones (see the snapshot in Fig. 3A). These data thus demonstrate how LENS can blindly distinguish between gel (cyan) and liquid (red) lipid phases and efficiently detect their nucleation and transitions across temperature variations. Furthermore, a 2D Voronoi analysis is found essentially inefficient compared to LENS in detecting the nucleation of small liquid domains and their coexistence within a dominant gel phase in a DPPC bilayer at T = 293 K (SI Appendix, Fig. S16). This shows how LENS, despite being a general descriptor, thus not optimized for any system in particular, may perform at least as well and even better for such soft dynamic systems than ad hoc tailored analyses which typically assume a considerable a priori knowledge of the analyzed systems and are also poorly transferable to different systems.

Fig. 3.

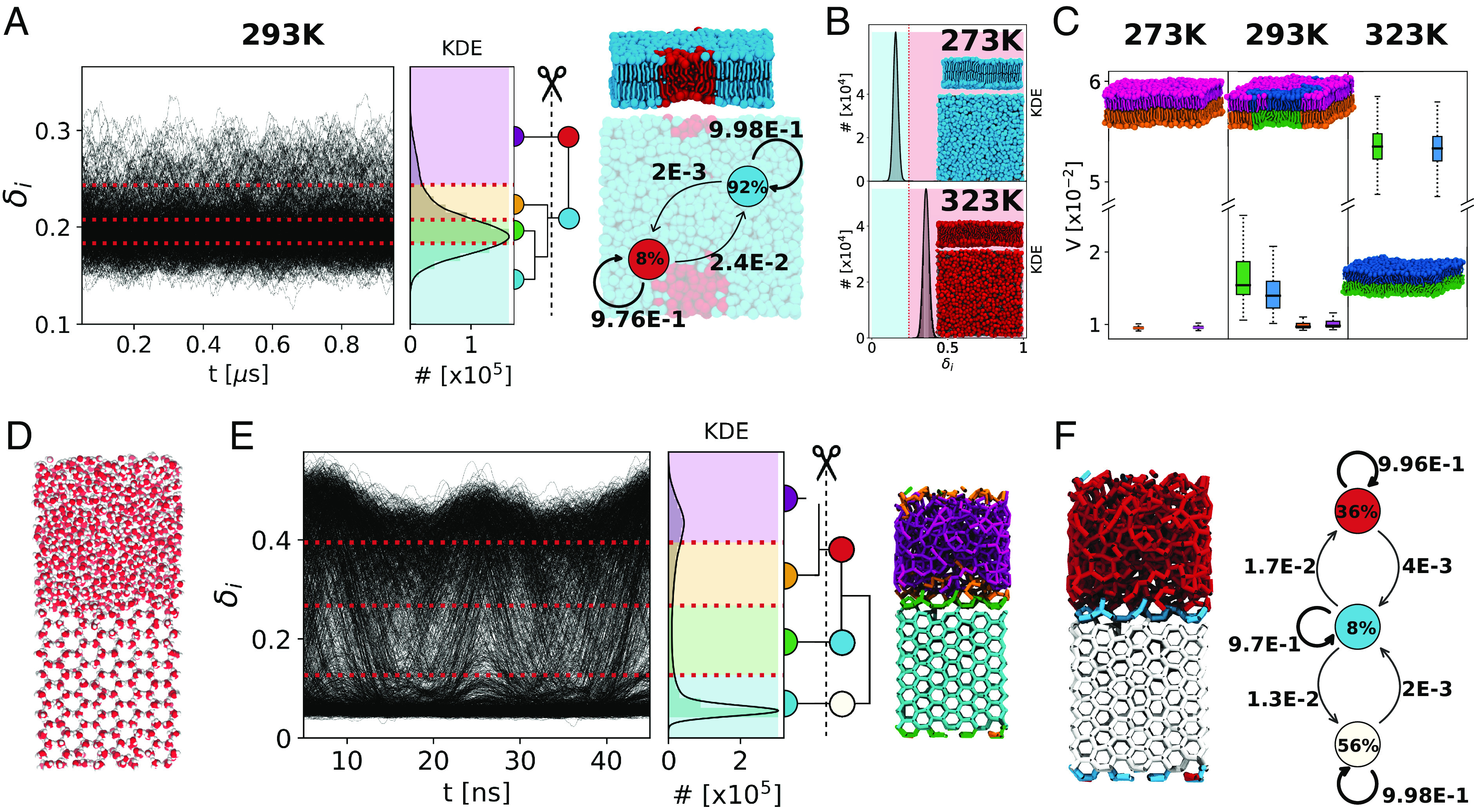
LENS analysis of multiphases coexistence. (A) LENS analysis for the DPPC lipid bilayer in coexistence conditions at T = 293 K: time series of LENS signals, δ_i(t), with the KDE of LENS distribution, and the interconnection dendrogram identifying two macroclusters in cyan and red (Left). MD snapshot of a DPPC lipid bilayer colored according to the two main LENS macroclusters (Top-Right) and related dynamic interconversion diagram (Bottom-Right). (B) LENS analysis, detecting phase transition at T = 273 K (gel) and T = 323 K (liquid) for a DPPC lipid bilayer. (C) Global statistical neighborhood analysis of the DPPC lipid bilayer across a phase transition: At T = 273 K, the bilayer is in gel state (low variability V); at T = 323 K, it is in the liquid state (high), while two domains (gel and fluid) are detected at T = 293 K. (D) Ice/water coexistence in an MD simulation [using the TIP4P/Ice water model at 268 K (68)]: oxygen atoms in red and hydrogen atoms in white. (E) LENS analysis of ice-water coexistence: time series of LENS signals (δ_i(t): Left) with the KDE of the LENS distribution, and the HC interconnection dendrogram–based clustering (Center). The four initially detected LENS microclusters, represented in different colors in the MD snapshot (Right), are merged via HC into three main dynamic environments/clusters. (F) Left: MD snapshot showing the three main LENS macroclusters, which identify the liquid phase (in red), the ice phase (in white), and the ice–liquid interface region (in cyan). Right: Dynamic interconversion diagram showing how water molecules undergo dynamic transitions from ice-to-liquid and vice versa, passing through the ice–liquid interface in such conditions. Note that the subunits within each considered system are illustrated coherently to the color code of the belonging cluster.

For case (ii), we analyze 500 consecutive frames taken every Δt = 0.1 ns along 50 ns of MD simulation at T = 268 K of a periodic box containing 2,048 water molecules in total, 1,024 of which are in the solid state and arranged in a typical hexagonal ice crystal configuration, while the other 1,024, segregated from the first ones, are in the liquid phase (Fig. 3D). Shown in Fig. 3E, the LENS signals for all water molecules (δ_i(t) data) clearly demonstrate the presence of two main phases coexisting: one corresponding to low δ_i values (more static behavior), while the second one characterized by higher δ_i values (more dynamic). HC on the dendrogram reduces the number of clusters (SI Appendix, Fig. S7A), identifying three main dynamic phases (Fig. 3E): the ice phase (in white), the liquid phase (in red), and the water–ice interface (in cyan). The interconversion diagram of Fig. 3F, Right reveals how the ice and liquid phases exchange molecules through such an interface cyan region. We underline how such a neat classification is typically nontrivial to be attained via sophisticated abstract structural descriptors such as, for example, SOAP (69–71), and typical pattern recognition algorithms. On the other hand, with LENS, the detection of different dynamic environments emerges in a straightforward manner and simply by tracking differences in the local reshuffling of the individual water molecules.

As additional tests, we have also carried out a systematic comparison between the information that can be inferred via our LENS-based analyses vs. state-of-the-art benchmark analyses for the ice/water system by using the dynamic propensity (DP) descriptor (SI Appendix, Fig. S19) (72). The characterization obtained via such DP analysis is found similar to those attained via the average KDE LENS distributions of Fig. 3E or via our V parameter. This demonstrates how LENS can work at least as well as state-of-the-art DP analysis for such systems. Nonetheless, it is worth noting that our LENS analysis also retains richer information than those evincible from such averaged analyses. Indeed, from dynamic propensity (DP), KDE LENS distributions, and V parameter analyses, one can extract only those dynamic domains which are statistically relevant along the sampled trajectory (e.g., ice in equilibrium with water, similar size gel–liquid segregated lipid domains, etc.), while hiding any information about the time–evolution of the contact data. This is a limit, for example, in the case of out-of-equilibrium trajectories—where the obtained distribution does not provide any information on the direction of the evolution of the system—or in the case of sparse/rare local events occurring in the trajectory of the units, which get lost in such averaged analyses due to their negligible statistical weight. While the ensemble average adopted for such analyses may prevent the detection of local (sparse, rare) events, these are instead explicitly captured by the raw LENS time series data (e.g., Fig. 3E, Left). The LENS analysis reported herein can be thus considered at least as powerful as, for example, a DP analysis, and, by definition, even more powerful as it retains complete information of all the microscopic events that can be captured along the trajectory (compatibly with the time-resolution Δt of the analysis).

Into Discrete Solid-Like Dynamics.

As completely different test cases, we also tested LENS on systems with solid-like dynamics. In particular, we focused on metal surfaces. While metallic crystals are typically considered hard matter, it is known that they may possess a nontrivial atomic dynamics even well below the melting temperature (5, 18, 19). In particular, we consider two Cu FCC surfaces Cu(210) and Cu(211), having a strikingly different dynamics.

We use a 150 ns-long atomistic MD trajectory of a Cu(210) composed of 2,304 Cu atoms at T = 700 K (Fig. 4A) conducted with a dynamically accurate deep-potential neural network force field trained on DFT calculations (5). We analyze with LENS 502 consecutive frames taken every Δt = 0.3 ns along the MD simulation (see Materials and Methods for details). The LENS signals indicate that the large part of the atoms of this surface is substantially static, while a considerable fraction of the atoms is more dynamic. The LENS-based clustering, applied coherently with the protocol described above, detects three main dynamic domains (Fig. 4B, Right), corresponding essentially to dynamic surface domains (in red), more static surface and subsurface domains (cyan), and the crystalline bulk of Cu(210) (gray), containing, respectively, ∼8%, ∼18%, and ∼74% of the Cu atoms in the model system (Fig. 4C: cluster populations in the colored circles). The dynamic interconversion plot in Fig. 4C reports the probabilities (in Δt = 0.3 ns) for atomic exchange between the three main LENS environments, revealing a continuous dynamic exchange of atoms between surface, subsurface, and bulk in the nanosecond-scale, consistent with what was recently demonstrated (5).

Fig. 4.

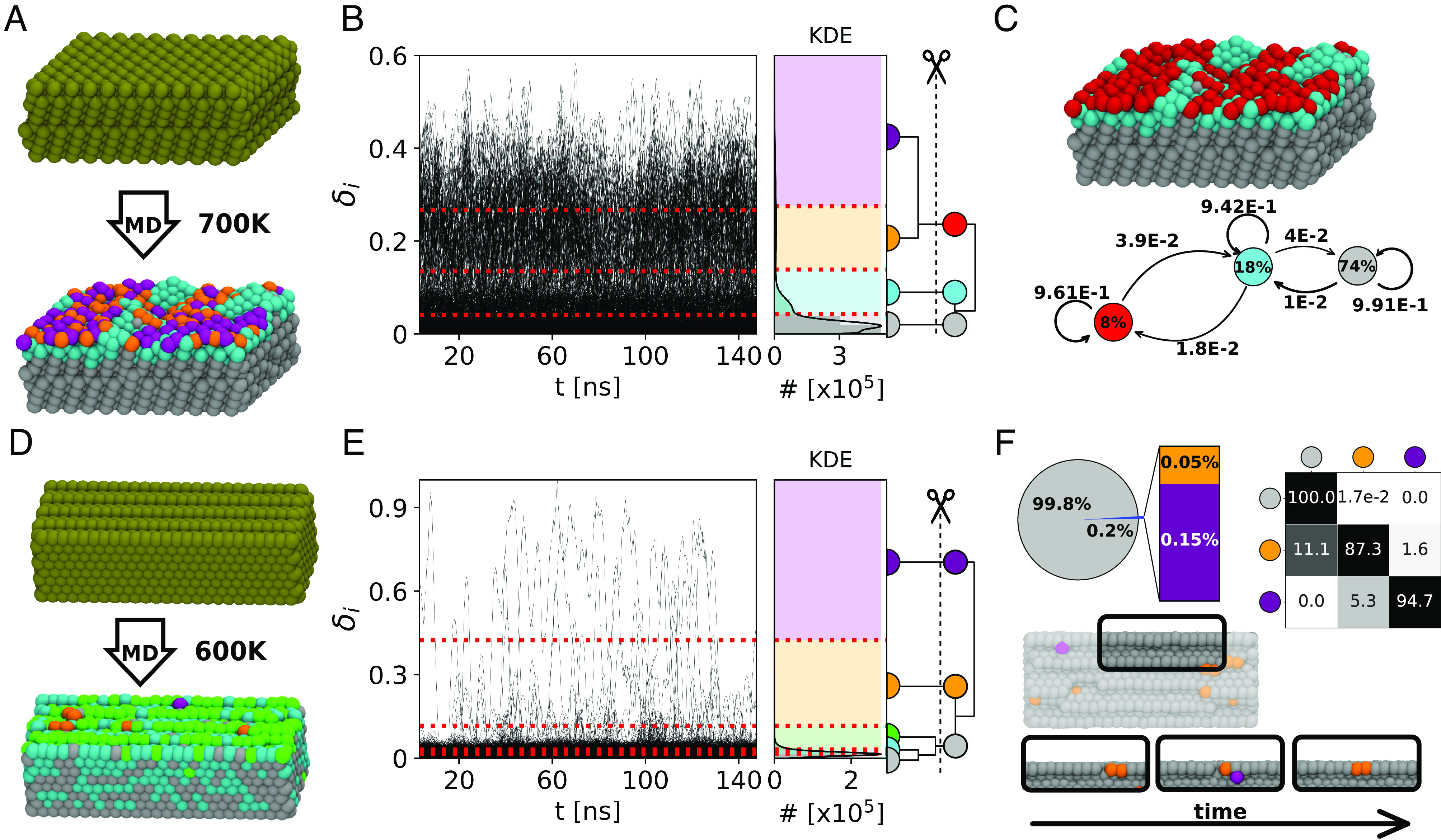
LENS analysis of dynamic metal (Cu) surfaces. (A) MD snapshots of an ideal Cu(210) surface (Top: 0 K) and of the same surface at T = 700 K (Bottom): atoms colored according to their LENS-detected dynamic environments of belonging. (B) Time series of LENS signals, δ_i(t), with the KDE of LENS distribution, and interconnection dendrogram. Four dynamic domains are first identified by KMeans and then merged into three clusters via HC. (C) MD snapshot of Cu(210) stable bulk in gray, surface in cyan, and dynamic surface spots in red (Top). Dynamic interconversion diagram reports the transition probabilities on the arrows and the cluster composition percentages within the colored circles (Bottom). (D) MD snapshots of Cu(211) ideal (Top) and equilibrated surface at T = 600 K (Bottom) colored according to LENS clusters. (E) Time series of LENS signals, δ_i(t), with the KDE of LENS distribution, and interconnection dendrogram. Five clusters are detected by the LENS-based analysis and merged into three macroclusters. (F) Pie chart of the clusters’ compositions and transition probability matrix of the clusters (Top). The merged clusters define the surface characterization: the bulk (silver domain) and dynamic atoms which move on the surface breaking/reconstructing rows (orange and purple). Representative MD snapshots showing the surface reconstructions over time are shown on the Bottom. Note that the subunits within each considered system are illustrated coherently to the color code of the belonging cluster.

As a second case, we analyze a Cu(211) surface composed of 2,400 atoms at 600 K (Fig. 4D). We analyze with LENS 502 consecutive frames taken every Δt = 0.3 ns along an MD simulation performed with the same deep-potential force field of the previous case (see Materials and Methods for details) (5).

Such a Cu(211) surface has completely different dynamics from the Cu(210) one. In this case, the time series δ_i(t) data provide clear evidence of strikingly nonuniform dynamics (Fig. 4E). In the Cu(210) simulation at 700 K, LENS shows a “fluid-like” atomic surface dynamics. Conversely, in the Cu(211) surface, the LENS-based clustering shows that most of this surface is solid/static (Fig. 4F: ∼99.8% of atoms in the gray cluster and have a low δ_i), while sparse atoms (Fig. 4F: ∼0.1 to 0.2% in the orange and violet clusters) diffuse and move fast on the surface (large δ_i LENS signal). Such sparse atoms dynamically emerge, diffuse, and reabsorb on the Cu(211) surface in a dynamic fashion: In total, we observe ∼200 gray-to-orange transitions over ∼500 sampled frames (transition frequency of one event every 750 ps of simulation). The transition matrix in Fig. 4F describes the kinetic hierarchy between the different static/dynamic LENS states, revealing in orange those atoms in the surface edges which are prone to move (Fig. 4F, Bottom: MD snapshot), while in violet are the atoms moving at high speed on the surface after leaving the orange edge defects (SI Appendix, Movie S2).

In this last case, LENS reveals a strikingly nonuniform dynamics governed by local rare fluctuations, which are typically poorly captured by average-based analyses such as, for example, pattern recognition approaches, or the global statistical analysis reported for the previous cases (SI Appendix, Fig. S12A) (5, 16). This underlines the efficiency of a local time-lapse LENS analysis to detect such rare fluctuations, which has been challenged further with other prototypical case studies as discussed below.

LENS Detection & Tracking of Local Fluctuations.

We tested LENS on other molecular systems whose dynamics is dominated by local fluctuations.

First, we focus on a 309-atoms icosahedral Gold nanoparticle (Fig. 5A: Au-NP). It is known that such metal NPs may possess nontrivial dynamics even at room temperature (16). We analyze 1,000 consecutive frames taken every Δt = 1 ns along 1 μs of MD simulation at 200 K of temperature (all atoms are thermalized to guarantee that the temperature is globally constant in the Au-NP; see Materials and Methods for details) (16). At T = 200 K, the atomic motion is reduced and the ideal icosahedral architecture of the Au-NP is consequently more stabilized than at, for example, room temperature (16). Nonetheless, after ∼180 ns of MD simulation, the LENS signal rapidly increases from ∼0.02 to ∼0.18 (Fig. 5B: δ_i(t)). HC of the dendrogram of Fig. 5B provides four main LENS dynamic domains (in gray, cyan, orange, and violet, going from the lowest to the highest δ_i values). Focusing on one Au-NP vertex (Fig. 5C, Bottom: in the Au-NP center), its surrounding area, initially static (in gray in the first MD snapshot on the Left), this vertex becomes suddenly more dynamic (second MD snapshot: in orange) and, as a dynamic wave, this area turns then violet (third snapshot). Between the second and third snapshots from the Left in Fig. 5C (Bottom), LENS detects a local event well known in icosahedral Au NPs: One vertex (having five neighbors in an ideal icosahedron) penetrates inside the NP surface generating a concave “rosette” (having six neighbors—in violet) (73). Such local transition/fluctuation breaks down the Au-NP symmetry, generating a dynamic region that then coexists with a more static area, in gray (SI Appendix, Movie S3). The data in Fig. 5 C, Top report the transition probabilities between the detected LENS dynamics domains. This case demonstrates how rare local fluctuations may generate larger collective rearrangements and the efficiency of LENS in detecting them.

Fig. 5.

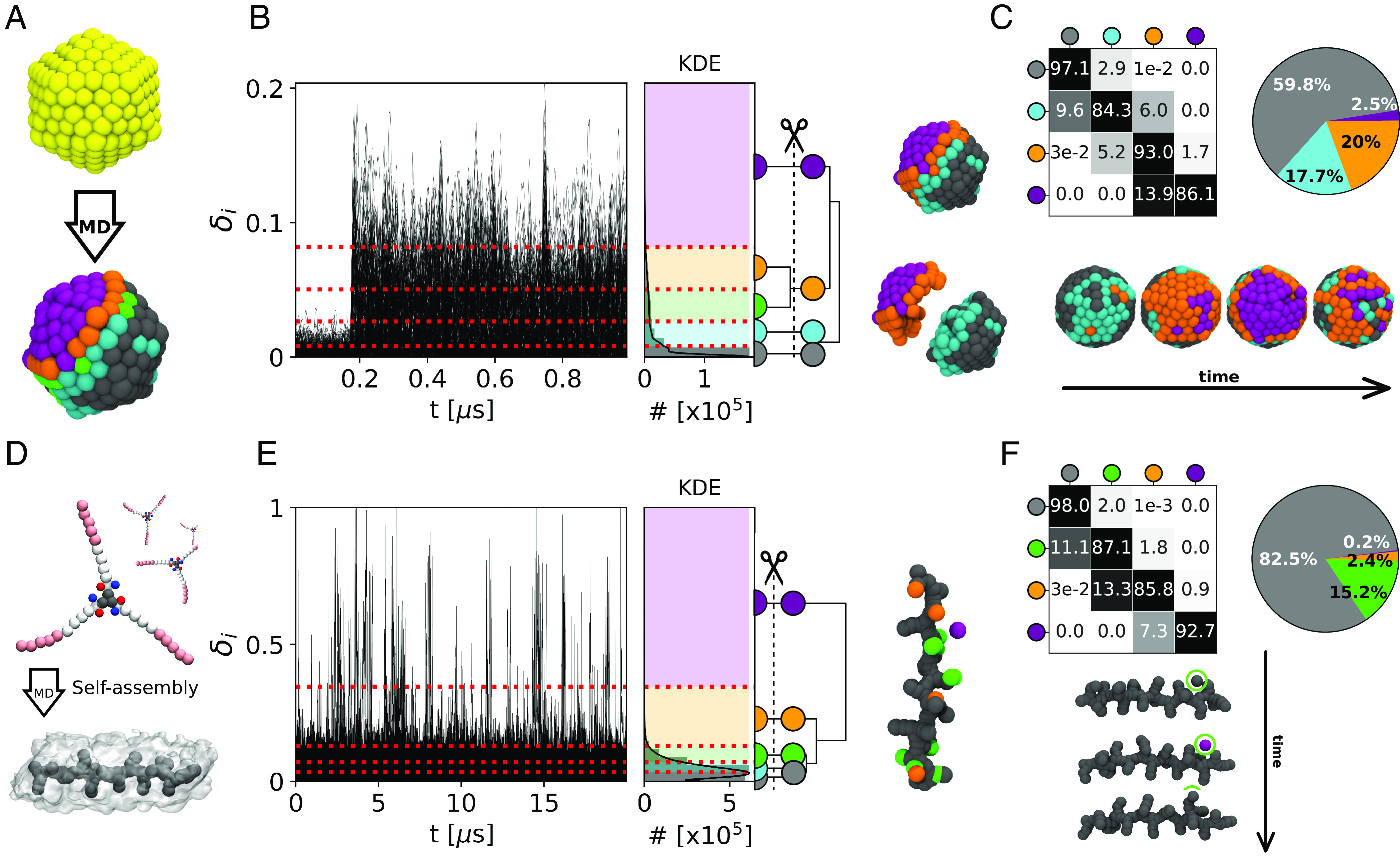
LENS analysis for discrete-like dynamics and local fluctuations. (A) Ideal icosahedral Au-NP (Top: at 0 K) and at 200 K (Bottom): atoms colored based on their LENS clusters of belonging. (B) LENS analysis: time series δ_i(t) signals (Left), with the KDE of LENS distribution and interconnection dendrogram (Center). Right: The four HC resulting LENS clusters show a clear characterization of the Au-NP: one ordered/static region (gray), one intermediate ordered/dynamic domain (cyan), and a mobile area (in orange and purple). (C) Transition probability matrix and cluster composition pie chart (Top). Bottom: example of local symmetry breakage in the icosahedral Au-NP. After ∼180 ns of MD simulation, between the second and third snapshots from the Left, one vertex (in orange: natively having 5 neighbor atoms) disappears and is replaced by a rosette (in violet: having 6 neighbor atoms). (D) BTA monomers (Top) and an equilibrated model of a BTA self-assembled fiber (Bottom). (E) LENS analysis: time series δ_i(t) data (Left), with related KDE of LENS distribution and interconnection dendrogram (Center). Right: Detected LENS clusters, corresponding to the bulk (in gray) and the defect domains in the BTA fiber (green and orange), and to the monomers diffusing from defect to defect on the fiber surface (in purple). (F) Transition probability matrix and cluster population pie chart (Top). Bottom: Example of monomer motion (in the green circle) between defects on the fiber surface, consistent with what the processes of monomer reshuffling demonstrated recently for these fibers (6, 7, 50). Note that the subunits within each considered system are illustrated coherently to the color code of the belonging cluster.

As additional tests, we have also carried out different control analyses using the Steinhardt (74) order parameters or SOAP (43) descriptors on the Cu(211) surface at T = 600 K and on the Au-NP at 200 K (SI Appendix, Figs. S17 and S18). These comparisons demonstrate how, while such sophisticated descriptors may preserve a structurally rich characterization of the systems (5, 16), the emergence of rare fluctuations or local transitions are typically overlooked in such structure-based pattern-recognition analyses (SI Appendix, Fig. S17). In particular, the few atoms running sensibly faster than all other ones on the Cu(211) surface at 600 K, are efficiently captured by LENS (see Fig. 4F and in SI Appendix, Movie S2 with clusters in orange and purple), but they get lost in such analyses due to their negligible statistical weight. In a similar way, the clear evidence provided in Fig. 5 that half Au-NP surface becomes highly dynamic following to the conversion of one vertex into a rosette, while the other half remains crystalline-like, is difficult to attain via averaging the dynamic transitions between the many atomic surface environments identified by structural-based analyses (16) (SI Appendix, Fig. S18). In this sense, LENS is found complementary to such structural analyses, providing details that cannot be easily captured by them and that are fundamental to understand the dynamic properties of such systems.

Local transitions/fluctuations are not exclusive of crystalline-like materials but may be present also in soft systems. We use LENS to analyze a water-soluble 1,3,5-benzenetricarboxamides (BTA) supramolecular polymer composed of monomers that self-assemble directionally via π − π stacking and hydrogen-bonding interactions (Fig. 5D) (75, 76). It has been demonstrated how these supramolecular fibers possess interesting dynamics due to defects that continuously form and annihilate in a dynamic way in the monomer stack (6, 7, 50). In this case, we analyze 20,001 consecutive frames taken every Δt = 1 ns along 20 μs of CG-MD simulation at room temperature (see Materials and Methods for details) (6, 7). Recently, unsupervised clustering of SOAP data extracted from the MD trajectories of such BTA-fibers allowed the unbiased detection of the fiber’s defects. However, unveiling a posteriori from such structural data the dynamics of these defects and of monomers’ diffusion between them is nontrivial (7, 50). Nonetheless, the time series δ_i(t) data in Fig. 5E clearly show how the dynamics of such fibers is strongly controlled by sharp local fluctuations that are well captured by LENS. HC of the LENS data distinguishes well the interior of the fiber as a more static environment (Fig. 5 E and F: gray cluster), the defects along the fiber as slightly more dynamic (green and orange), and also the monomers diffusing on the fiber surface (in violet) (6, 7). The transition matrix and pie chart of Fig. 5F show how the gray, green, and orange clusters include the majority of the BTA-monomers. On the other hand, sparse monomers (∼0.2%) belonging to the violet cluster undergo sharp transitions and instantaneous reshuffling of their local neighbors. These are the monomers that are diffusing defect to defect on the fiber surface, which provides a picture of the internal dynamics of such complex BTA fibers in optimal agreement with previous studies (6, 7, 32, 50).

Also in these cases (as in the Cu(211) surface of Fig. 4D–F), LENS is found to be efficient in detecting and tracking local fluctuations that play a dominant role in the dynamics of the entire system. It is worth noting how in all such cases a time-independent (pattern recognition-based) statistical analysis of neighbors’ variability is inefficient to outline such nonuniform dynamics, due to the low statistical weight of the local events occurring in these systems (SI Appendix, Fig. S12).

Discussion

Many molecular systems are controlled by local fluctuations that are often difficult to detect and typically lost in average-based analyses. Here, we present a general descriptor designed to track local fluctuations in complex dynamic systems, named LENS. Different from many descriptors, LENS is based on the concept of neighbor identities (IDs) instead of, for example, molecular/atomic species. At each sampled time frame along a trajectory, our analysis builds a string listing the neighbor IDs surrounding each particle i in the system. Within the time interval between consecutive time frames, LENS measures the variations in the neighbor IDs in terms of addition, subtraction, or reshuffling of neighbors (Fig. 1). Large time-lapse variations in the local neighborhood provide strong LENS signals, while weak LENS signals indicate reduced dynamics in the local environment surrounding a given particle i.

We tested LENS in a number of systems with strikingly different internal dynamics. Shown in Fig. 2, LENS reveals that a bicomponent lipid bilayer is characterized by surface patches, with different molecular reshuffling dynamics, which correspond to the segregation of the lipid species into two domains. In Fig. 3, we demonstrate how our time series LENS analysis detects efficiently phase transitions and coexistence of different phases: For example, in a DPPC lipid bilayer undergoing gel-to-liquid transition increasing the temperature from 273 K to 323 K or in a liquid water–ice system at freezing/melting temperature.

When a system is characterized by statistically dominant dynamic domains, the time-dependent LENS and global (time-independent) statistical analyses correlate (Figs. 2 and 3A–C). Conversely, system dynamics dominated by rare local fluctuations are poorly described by global statistical analyses (SI Appendix, Fig. S12). In the Cu(211) surface (Fig. 4D–F), for example, a global statistical analysis based on a pattern recognition approach identifies only one domain, as reported in SI Appendix, Fig. S12A, meaning that the sparse atoms diffusing fast on the metal surface are not statistically relevant and are statistically lost in such analyses. Rare local transitions are not captured by a global time-independent analysis even in the systems of Fig. 5. This is not necessarily an exclusive problem of time-independent analyses conducted with this specific descriptor: Also, other descriptors such as, for example, SOAP, coordination number, etc., are in fact efficient as far as they are used to detect statistically relevant dynamic/structural populations and patterns. Nonetheless, the results of Figs. 4D–F and 5 demonstrate how a local time-dependent LENS analysis is efficient in detecting and tracking such local fluctuations and, in this sense, appears as more general, complete, and robust than an average time-independent investigation. In addition, while average-based and global pattern recognition analyses work typically well when one knows what to search, this is less the case for LENS. The LENS analysis in fact only requires knowing the IDs of the interacting particles and having a sufficiently sampled trajectory. This is fundamental in most practical cases where the nature of a system is not known a priori. In principle, for ensuring a sufficient sampling of the events captured from the analyzed trajectories, it would be desirable to use a sampling Δt small enough to capture the interesting fluctuations/transitions and to have at disposal a sufficiently long trajectory to ensure that statistically relevant information on given events can be effectively attained. It would be ideal to analyze a very long trajectory using a very tight sampling (small Δt); however, in most practical cases, this is limited by, for example, the complexity of the system, the available computational power, and by the cost of the analysis (which could produce large dataset difficult to handle/analyze and full of irrelevant information and noise). Like in the majority of analyses, a preliminary test phase is thus required to optimize the resolution/cost of the LENS analysis. For example, in our cases, our preliminary tests demonstrated that a sampling time (Δt) in the range of 1 to 10 ns produced robust insightful results, for example, in the case of the CG simulations of lipids, while a smaller time step in the range of 0.1 to 1 ns was found best suited for, for example, the AA simulations and solid-state systems studied herein (water/ice, Cu surface, and Au-NP). The (temporal) resolution of the analysis (Δt) can be adjusted/optimized to focus on specific events of interest. The raw time series LENS data (as well as the transition matrices recomputed from them reported in the figures) provide information on the statistical confidence in the identification of the different dynamic domains populating the various systems and on the observation of the various transitions/fluctuations between them.

To test the robustness and efficiency of the LENS descriptor, we have carried out a systematic comparison between LENS and existing reference techniques, typically used as a benchmark for the various systems studied herein [Voronoi (65), Steinhardt (74), mean square displacement, and dynamic propensity (DP) (72) analyses]. These additional tests show how LENS works at least as well as such analyses, which are considered state-of-the-art for the various testes systems, and even better (SI Appendix, Figs. S15–S19). At the same time, a strong advantage of LENS is its generality. Differently from most of such benchmark analysis approaches, LENS is not tailored ad hoc on a specific system and does not require prior knowledge of the studied systems. LENS is thus in principle transferable and well suited to reveal the dynamic features of a variety of systems (as demonstrated by the diverse test systems used herein). Our tests also show how, while such benchmark techniques can capture structurally rich information, they may be inefficient, for example, in capturing local and rare dynamic events/fluctuations, key to unveil the system properties, and which are instead well described by LENS.

LENS has also some intrinsic limitations. Based on its definition, if in Δt the neighbors do not change (same IDs) but move remaining in the r_cut sphere (local structural rearrangement of the neighborhood), LENS provides no signal. This is opposed to descriptors such as, for example, SOAP that—being permutationally invariant—provide vice versa a signal in case of local rearrangements, but no signal in case of a switching of IDs (keeping the same structural displacement). This makes LENS best suited to measure local dynamicity rather than local structural variations, which is nonetheless key in many complex systems where dynamics plays a major role. At the same time, one key advantage of LENS is its abstract definition. This makes it well suited to analyze a variety of trajectories of systems for which the identities of the moving units are known and, in principle, not necessarily restricted to molecular ones.

Materials and Methods

MD Simulations.

All data concerning the molecular models and the MD trajectories analyzed herein are available at https://doi.org/10.5281/zenodo.8013279 (77).

The DIPC/DPPC lipid bilayer (Fig. 2) is simulated using the Martini2.2 force field (63). A binary mixture of dipalmitoyl-phosphat-idylcholine (DPPC) and dilinoleoyl-phosphatidyl-choline (DIPC), with 2:3 molar ratio, is used to model the coexistence of liquid-crystalline and gel phases into such self-assembled bilayer. To get the separation of the bilayer into domains of coexisting phases, the mixture is simulated at T = 280 K. The initial configuration of the binary lipid mixture in water is generated using insane (78) with the specified box dimensions (18 × 18 × 11 nm). The bilayer system is composed of 1,150 lipids, consisting of 2:3 DIPC:DPPC on each leaflet, and 17,987 (W) water molecules. To prevent water crystallization (T < 290 K in Martini) (63, ∼5% of regular water particles are substituted by the antifreezing water particles. For nonbonded interactions, a reaction-field electrostatics algorithm is used with a Coulomb cutoff of r_c = 1.1 nm and a dielectric constant of 15. The cutoff for Lennard-Jones interactions is set to r_LJ = 1.1 nm. The timestep used during the MD simulation is δt = 20 fs. The system is preliminarily minimized and equilibrated for t = 100 ns. A production run is then performed for t = 15 μs, and the data acquisition is performed every 1 ns. The solvent and membrane are coupled separately using a v-rescale thermostat with a relaxation time of t = 1.0 ps. During the equilibration, the pressure is maintained at p = 1 bar using the Berendsen barostat with the semiisotropic coupling scheme, a time constant of τ_p = 4 ps, and compressibility c = 3 * 10⁻⁴ bar⁻¹. During the production, the Parrinello–Rahman barostat is used, with a time constant of τ_p = 12 ps. An equilibrium part of the trajectory is analyzed (the last 10 μs) every Δt = 10 ns (1,001 sampled frames).

The bicomponent F-NP/H micelle (SI Appendix, Fig. S2) is simulated at T = 300 K in explicit water via Martini2.2 (63) scheme (see ref. 60 for further details). The system is a binary mixture of p-nitrophenyl ester of n-stearoyl L-phenylalanine (F-NP) and n-stearoyl L-histidine (H) with a 1:1 molar ratio (N_{F − NP} = 100 and N_H = 100). The initial configuration consists of N_{F − NP} = 100 and N_H = 100 randomly dispersed surfactants, which assemble into a single micelle within a 10-μs-long MD simulation sampled every 1 ns. The last 3 μs of the MD trajectory is considered representative of the equilibrium (60) and used for the analysis—3,001 analyzed frames taken every Δt = 1 ns along the MD.

All the DPPC lipid bilayer trajectories at T = 293 K, 273 K, and 323 K (Fig. 3A–C) are obtained from MD simulations of a bilayer model composed of N_DPPC = 1152 DPPC lipids, simulated and parameterized in explicit water via Martini2.2 (63), as reported in ref. 58. The equilibrated-phase MD trajectories used for the analyses are in all cases 1 μs. A total of 1,001 frames extracted every Δt = 1 ns along the MD trajectories are used for the analyses.

The atomistic ice/water interface model of Fig. 3D–F is simulated employing the direct coexistence technique. The TIP4P/Ice water model (79) is used to model both the solid phase of ice I_h and the phase of liquid water. The direct coexistence technique is based on the idea to put in contact more phases in the same box and at constant pressure. To get the coexistence, the temperature is set at T = 268 K, the energy is constant at 268 K, and the system melts at 269 K (68), kept constant using the v-rescale thermostat with a relaxation time of t = 0.2 ps. The initial configuration of the ice I_h is obtained using the Genice tool proposed by Matsumoto et al. (80) generating a hydrogen-disordered lattice with zero net polarization satisfying the Bernal–Fowler rules. To equilibrate the solid lattice, anisotropic NPT simulation is carried out using the c-rescale barostat, with a time constant of δt = 20 ps and compressibility of 9.1 * 10⁻⁶ bar⁻¹. The equilibration lasted 10 ns at ambient pressure (1 atm). The liquid phase is obtained from the same ice I_h solid phase, performing a NVT simulation at T = 400 K to quickly melt the ice slab. Thus, both the solid and liquid phases are obtained with the same number of molecules (1,024) and box dimensions. The liquid phase is then equilibrated at T = 268 K for t = 10 ns, using the c-rescale barostat in semiisotropic conditions and compressibility of c = 4.5 * 10⁻⁵ bar. The two phases are, then, put in contact and equilibrated for t = 10 ns using the c-rescale pressure coupling with the water compressibility (c = 4.5 * 10⁻⁵ bar) at ambient pressure. The production NPT ice/water coexistence MD simulation (Fig. 3D–F) is performed in semiisotropic conditions, with the pressure applied only in the direction perpendicular to the ice/water interface. This allows to reproduce the strictly correct ensemble for the liquid–solid equilibrium simulation by the direct coexistence technique. After the equilibration, a production run is performed for t = 50 ns, sampled and analyzed every 0.1 ns. All the trajectories analyzed for the systems simulated above are obtained using the GROMACS software (81).

The atomistic models of the Cu(210) and Cu(211) surfaces (Fig. 4) are composed of N₂₁₀ = 2,304 and N₂₁₁ = 2,400 atoms, respectively. The MD simulations are conducted at T = 700 K and at T = 600 K respectively for the two example surfaces. Deep-potential MD simulations of both Cu surfaces are conducted with LAMMPS software (82) using a neural network potential built using the DeepMD platform (83), as described in detail in ref. 5. The sampled trajectories are 150 ns long. A total of 502 frames are extracted every Δt = 0.3 ns along the MD trajectories and used for the LENS analyses.

The atomistic model for the icosahedral Au-NP is composed of N_{Au − NP} = 309 gold atoms (Fig. 5A–C). The Au-NP model is parametrized according to the Gupta potential (84) and is simulated for 1 μs of MD at T = 200 K using LAMMPS software (82) as described in detail in ref. 16. A total of 1,000 frames are extracted every Δt = 1 ns of the MD trajectory and then used for the analyses.

The coarse-grained BTA fiber model is built consistent with the MARTINI force field (63) and optimized as described in detail in refs. 6 and 37. In particular, the fiber model is composed of N_BTA = 80 BTA monomers. A trajectory of 20 μs, obtained with the GROMACS software (81), is then analyzed every Δt = 1 ns (20,001 sampled frames in total).

Preprocessing of the Trajectories.

All MD trajectories are first preprocessed in order to obtain plain xyz files keeping only the coordinates of the particles of interest, that is, considered during the neighborhood’s evaluation, as reported in SI Appendix, Table S1. For example, in the lipid bilayer analyses of Figs. 2 and 3A–C, we considered only the tan PO4 (MARTINI) beads as representative of the “center” position of each lipid molecule in the systems. For the analyses conducted herein, we used as the LENS centers respectively the centers of mass of the surfactant heads for the micelles of SI Appendix, Fig. S2, the oxygen atoms of each water molecule in the water/ice system (Fig. 3D–F), each individual atom in the metal surfaces and Au-NP (Figs. 4 and 5A–C) each atom, and the center of each monomer core in the BTA fiber (Fig. 5D–F). In all cases, the analysis is then conducted by building at each sampled timestep strings collecting the neighbor IDs of each unit i within a sphere of radius r_cut (which is set depending on the system and based on the shape and the minima of the radial distribution functions, g(r)_m—see SI Appendix, Table S1 and Fig. S1).

Time-Lapse LENS Analysis.

The instantaneous δ_i parameter for each unit i in each model system is calculated over time along the system’s trajectory from the C_i strings containing the IDs of the neighbor units calculated at times t and t + Δt as reported in Eq. 1. The analysis is then repeated for all units i at all time intervals Δt sampled along the analyzed trajectories, obtaining the δ_i(t) plots of Figs. 1B, 2B, 3 A and E, 4 B and E, and 5 B and E. The δ_i parameter is normalized such that it gives 0 when the local neighborhood does not change and 1 when it changes completely at each Δt. To reduce the noise in each δ_i(t) signal, we processed them by using a Savitzky–Golay (85) filter [as implemented in the SciPy python package (86)], obtaining smoothed ⟨δ_i(t)⟩ signals. In particular, each δ_i(t) signal is smoothed using a common polynomial order parameter of p = 2 on a time window of 100 frames for the bicomponent DIPC/DPPC lipid bilayer system, the F − NP/H micelle, DPPC lipid, and for the water/ice interface. A smaller time window of 20 frames is used for the crystalline Cu surfaces, for the gold Au − NP, and for the BTA systems, which allows to better capture the rapid emergence of rare fluctuations within them. Such setups are considered as the best compromise in the various cases after a preliminary phase in which we tested the reliability and robustness of results by systematically studying the effect of changing the smoothing windows on the results obtained for the various systems (SI Appendix, Figs. S5–S7). In order to simplify the notation, we refer to the ⟨δ_i(t)⟩ signal as δ_i.

After the noise reduction, the clustering of the δ_i data is performed by means of the KMeans algorithm (64) implemented in SciPy python package (86). The KMeans algorithm requires the definition of the number of clusters as an input. The initial number of microclusters is set (as a default choice) as twice the number of peaks/discontinuities in the δ_i data (distributions on the Right of Figs. 1B, 2B, 3 A and E, 4 B and E, and 5 B and E), while in case only one peak is detectable in the δ_i distribution, the initial number of microclusters is always set to five. This guarantees that KMeans always detects an excess of starting microclusters, allowing us to start from an excess of dynamic information. After such a preliminary step, a transition matrix is built collecting the probabilities for each single identity/subunit belonging to a certain specific cluster at time t to remain in that cluster (diagonal entries) or to undergo transition into another one in Δt (off-diagonal matrix entries). Then, the microclusters are merged hierarchically a posteriori into macroclusters based on a concept of direct closest adjacency (i.e., clusters having the smallest distance from each other are merged together). To this end, a single link algorithm based on the metrics correlation implemented in the HC interconnection dendrograms is used. Specifically, the HC algorithm first computes the distances, according to the selected metrics—correlation between any couple of rows (clusters) in the transition matrix; then, it couples/merges specific rows following the single- algorithm rational. This implies that clusters in the transition matrices having, for example, high diagonal % entries (higher than 50%) are kept as distinct, meaning that within the time resolution of the analysis, they are recognized as dynamically distinct environments with good statistical confidence, while clusters with low off-diagonal % entries (e.g., close to or lower than 50%) and high off-diagonal entries % (high probability to undergo transition into another cluster in Δt) are most likely merged together. Such a hierarchical clustering (HC) approach is used to relate all microclusters with each other and to provide the rationale for merging them into the macroclusters reported in our analyses based on their adjacency, thereby obtaining a coarse-grained characterization of the internal dynamics of the studied systems. This is the effect of cutting the HC dendrogram at different levels (SI Appendix, Figs. S6–S11).

We note that the results shown herein are obtained via such a simple iterative supervised clustering approach, which in the cases we discuss in this work was found simple, effective, and robust to against the tuning of clustering parameters (thus satisfactory from the robustness and reproducibility point of view). Nonetheless, we underline that other (e.g., unsupervised) clustering approaches could be used for the purpose, although they do not always provide consistent results with each other, and where the tuning of the setup parameters may be nontrivial.

Global Statistical Analysis.

Average information on the statistically dominant dynamic domains present in the systems can also be obtained from the global dataset of the C_i as described in the text. For each i unit, the numbers of the contacts with the other neighbor IDs along the trajectory (D_i^T, considering all T sampled frames) are collected from the global C_i dataset (see, e.g., Fig. 1C). The contacts data are then organized into a contact matrix where the individual entry i, j indicates the total number of neighboring events between the bead i and j in all sampled time intervals along the analyzed trajectory (Fig. 2E and SI Appendix, Fig. S2E).

The data related to each unit i (i.e., to each row of the contact matrix) are centered on the mean and normalized on the SD of the neighboring events. The variability (V) is then defined as the inverse of the SD of the D_i^T values: Low SD around a mean value implies that each unit i gets in direct contact with all other IDs along the trajectory; the variability (V) of its neighborhood is thus high. On the other hand, high SD identifies cases where the number of neighbors tends to remain the same along the trajectory and the number of visited neighbor IDs is thus low: This means that the neighborhood of unit i in such cases is rather static, and its variability (V) is low. What is important to note is that, rather than the quantitative V values (which may depend on, for example, the length of the trajectory, the dynamics of the system, etc.), the comparison between the (V) parameters of the individual units (i: from 1 to N) in the system, and the presence of molecular domains characterized by different V indexes (identifying the presence of different dynamic domains) are actually relevant. The matrix is then analyzed via hierarchical clustering (HC). In particular, the normalized contact data are gathered by means of the Ward method (87) with the Euclidean metric both implemented in SciPy python package (86), and the number of clusters is determined based on the dominant patterns from the sorted matrix (see, e.g., the matrices of Fig. 2E and SI Appendix, Fig. S2 E, Right).

Supplementary Material

Appendix 01 (PDF)

Movie S1.

LENS analysis of gel-liquid phase coexistence in a DPPC lipid bilayer at 293 K of temperature. Atoms are colored based on their main LENS environment of belonging: liquid-phase lipids in red, gel-phase lipids in cyan.

Movie S2.

LENS analysis of local dynamic transitions in a Cu(211) surface at 600 K of temperature. Atoms are colored based on their main LENS environment of belonging: static solid-phase atoms in gray, more dynamic surface edge atoms in orange, and fast-diffusing atoms in violet.

Movie S3.

LENS analysis of a local sharp transition in a icosahedral Au-NP at 200 K of temperature. Atoms are colored based on their main LENS environment of belonging: crystalline/ordered domains in gray, solid but more dynamic atomic environments in cyan, increasingly dynamic local environments in orange and violet respectively. The movie shows how the LENS analysis detects the local transformation event of one icosahedron vertex (having 5-neighbor atoms) into a concave “rosette” (with 6-neighbor atoms).

Data, Materials, and Software Availability

Details on the molecular models and on the MD simulations and additional simulation data are provided in Supporting Information. The LENS analysis code, together with complete molecular simulation data, complete data on all molecular models used for the simulations, and on the simulation parameters (input files, etc.) used in this work are available at https://doi.org/10.5281/zenodo.8013279 (77) and at https://github.com/GMPavanLab/LENS (88).