Early prediction of medical students' performance in high-stakes examinations using machine learning approaches

Abstract

Introduction

Since the advent of medical education systems, managing high-stakes exams has been a top priority and challenge for all policymakers. However, considering machine learning (ML) techniques as a replacement for medical licensing examinations, particularly during crises such as the COVID-19 outbreak, could be an effective solution. This study uses ML models to develop a framework for predicting medical students' performance on high-stakes exams, such as the Comprehensive Medical Basic Sciences Examination (CMBSE).

Material and methods

Prediction of students' status and score on high-stakes examinations faces several challenges, including an imbalanced number of failing and passing students, a large number of heterogeneous and complex features, and the need to identify at-risk and top-performing students. In this study, two major categories of ML approaches are compared: first, classic models (logistic regression (LR), support vector machine (SVM), and k-nearest neighbors (KNN)), and second, ensemble models (voting, bagging (BG), random forests (RF), adaptive boosting (ADA), extreme gradient boosting (XGB), and stacking).

Results

To evaluate the models' discrimination ability, they are assessed using a real dataset containing information on medical students over a five-year period (n = 1005). The findings indicate that ensemble ML models demonstrate optimal performance in predicting CMBSE status (RF and stacking). Similarly, among the classic regressors, LR exhibited the highest root-mean-square deviation (RMSD) (0.134) and coefficient of determination (R2) (0.62), whereas the RF model had the highest RMSD (0.077) and R2 (0.80) overall. Furthermore, Anatomical Sciences, Biochemistry, Parasitology, and Entomology grade point average (GPA) and grades demonstrated the strongest positive correlation with the outcomes.

Conclusion

Comparing classic and ensemble ML models revealed that ensemble models are superior to classic models. Therefore, the presented framework could be considered a suitable alternative for the CMBSE and other comparable medical licensing examinations.

Graphical abstract

Highlights

• •Providing a reliable ML-based alternative for medical licensing examinations.
• •Early prediction technique for medical licensing examinations.
• •A methodology for preprocessing the Comprehensive Education System (CES).
• •Evaluation of a real database that includes medical students' information over a 5-year period.
• •A comparative study using performance measurements (sensitivity, precision, accuracy, and area under the curves [AUCs]).

Abbreviations

EDM

Educational Data Mining

AI

Artificial Intelligence

ML:

Machine Learning

COMLEX-USA:

Comprehensive Osteopathic Medical Licensing Examination of the United States

CES

Comprehensive Education System

CMBSE

The Comprehensive Medical Basic Sciences Examination

LR

Logistic Regression

SVM

Support Vector Machine

KNN

K-Nearest Neighbors

Bagging

Bootstrap AGGregating

RF

Random Forests

ADA

Adaptive Boosting

XGB

Extreme Gradient Boosting; Stacking: Stacked generalization

Spe

Specificity

Acc

Accuracy

F1

F-measure

MCC

Matthew's Correlation Coefficient

AUC-ROC:

Area Under Curve of Receiver Operator Characteristic

AUC-PRC

Area Under Curve of Precision-Recall

BS

Brier Score

MSE

Mean Squared Error

RMSD

Root Mean Square Deviation

R2

Coefficient of determination

SHAP

SHapely Additive exPlanations

ROS

Random Over-Sampling

SMOTE

Synthetic Minority Oversampling Technique

RUS:

Random Under-Sampling

1. Introduction

With the current technological advancement, Big Data is acknowledged as the most effective data analysis technology. To this end, in recent decades, artificial intelligence (AI) and machine learning (ML) have been utilized in academic institutions to predict student performance [1,2]. In addition, data mining (DM) can provide experts with predictive information that lies outside of their expectations and reveal hidden patterns [3]. From a practical point of view, DM algorithms can predict future trends and enable universities to make proactive, knowledge-driven decisions. Compatibility of the modeling techniques, which typically focus on large, heterogeneous, and complex databases, is a significant aspect of DM [4]. Educational data mining (EDM) employs DM algorithms to analyze educational data [5], which can positively impact predicting students' exam performance, identifying at-risk students, increasing graduation rates, effectively assessing students' performance, and maximizing campus resources. Moreover, EDM could be an effective solution, particularly in crises such as the COVID-19 emergency, in which the administration of high-stakes exams was a top priority for all policymakers [6].

The two main approaches in EDM are classic and ensemble ML models. In classic ML models, such as logistic regression (LR) [7], k-nearest neighbors (KNN) [8], support vector machine (SVM) [9,10], artificial neural network (ANN) [11], decision tree (DT) [12], and Naïve Bayes [13]) primarily focus on developing a model with the most accurate predictions. Instead of developing a single model and attempting to create an accurate predictor, ensemble ML models combine multiple models and voting strategies to develop a model with superior predictive performance and higher reliability. Some of the most frequently used ensemble ML models are voting [14], bagging (BG) [15], random forest (RF) [16], adaptive boosting (ADA) [17], extreme gradient boosting (XGB) [18], and stacking [19].

Several studies have been conducted on EDM systems in the last few years. Most of these studies employed classic ML models, while a few utilized ensemble models. For instance, Castro et al. (2007) suggested approaches for EDM applications such as prediction, clustering, relationship mining, and discovery using models [4]. Shehata and Arnold (2015) reported deploying an engine to identify students at risk of failing based on social, demographical, and educational features [20]. Howard et al. (2018) developed a Bayesian additive regressive trees (BART)-based method for predicting final course grades [21]. Sekeroglu et al. (2019) proposed a system for predicting and classifying student performance using three ML algorithms (backpropagation [BP], support vector regression [SVR], and long-short term memory [LSTM]) with no data selection algorithm, while SVR achieving the highest accuracy [22].

Uskov et al. (2019) conducted a study that evaluated several classic ML algorithms (LR, SVM, KNN, and ANN, among others) as well as an ensemble model (RF) to predict the academic performance of students in mathematics courses. SVM and RF exhibited the highest accuracy among the examined models [23]. Embark (2020) investigated the effect of ML models (LR, Naïve Bayes, DT, and RF) on the prediction of college student's success in pre-college academic accomplishments and the identification of at-risk students based on their grade point average (GPA) [24]. Tomasevic et al. (2020) compared classic ML algorithms (ANN, KNN, LR, SVM, Naïve Bayes, and DT) to predict student performance in exams, where according to evaluation metrics, ANN achieved the highest performance [25]. Abu Saa et al. (2020) used the ANN, SVM, Nave Bayes, DT, GB, and RF algorithms to predict student academic performance from a new data set of a United Arab Emirates (UAE) university, with RF achieving the highest accuracy [26].

Tarik et al. (2021) presented several models to predict baccalaureate mean scores based on a large number of explanatory variables (the grades of the core subjects). They concluded that the RF algorithm's predictive ability was superior to all other methods examined [27]. Niyogisubizo et al. (2022) predicted university course-level student dropout using ensemble ML models, namely RF, GB, XGB, and stacking, and demonstrated the positive effects of ensemble methods. These models focused solely on the status prediction in each course and did not account for other features, such as demographic data [28].

Due to the importance of training well-educated medical students for society as a whole, proceeding with an assessment to determine competency for medical school graduation and maintaining performance standards for graduating physicians is one of the leading global educational issues [29]. Indeed, different countries have various approaches and strategies for conducting medical high-stakes examinations and assessments [30]. For instance, in many countries, medical students must pass a licensure exam covering basic medical sciences by the end of their second year of curriculum to be eligible to enroll in preclinical education and ultimately graduate with a Doctor of Medicine degree, e.g., the Comprehensive Osteopathic Medical Licensing Examination of the United States Level 1 (COMLEX-USA 1).

To this end, several governments have attempted to develop predictive models that employ students' academic accomplishments to estimate the probability of failing high-stakes exams based on their progressive assessment scores [2]. Applying ML models to predict the performance of medical students on high-stakes exams could undoubtedly lead to identifying students who may fail these exams. These models can increase the educational systems' and policymakers' understanding of the critical need for additional support through students' graduation, certification, or licensure. In addition, implementing these early warning systems can be advantageous for identifying students at risk, providing feedback, and reducing additional costs. However, developing a general model for comparable examinations can positively affect educational systems and provide an excellent basis for international comparison. Due to the difficulty of interpretation and the necessity of manually developing feature extraction strategies, the current models are frequently referred to as black-box models [31].

According to current research, only a few ML models have focused on high-stakes exams for medical students and primarily employed classic ML models. Zhong et al. (2021) developed predictive models based on LR to identify students at risk of scoring below 500 on COMLEX 1, achieving sensitivities ranging from 65.8 to 71% and specificities ranging from 83.2 to 88.2% in predicting scores [32]. Rayhan et al. (2022) recently proposed a novel system that employs an ML model to evaluate all students in the context of high-stakes exams. They combined an LR classifier with an ANN classifier to generate predictions that were as fair as possible for all learners [6]. Thus, ensemble ML models are rarely used to predict the performance of medical students on high-stakes exams.

This study aims to present a reliable framework for preparing data and developing and evaluating classic and ensemble ML models that can be adjusted to predict medical students' performance in a medical licensing examination, the Comprehensive Medical Basic Sciences Examination (CMBSE). The CMBSE is typically administered after the second year of medical school, and candidates were expected to have completed most required courses in basic medical sciences curricula. This exam consists of multiple-choice questions and is administered through a one-day session. The CMBSE's final score is a three-digit number within the range [0,200], and its final status can be passed or failed based on a threshold that varies from year to year.

The present study addresses the following three research questions:

Q1

To what extent can classic and ensemble ML models be a precise and reliable substitution for medical high-stakes examinations, such as the CMBSE, in unpredictable situations like the COVID-19 pandemic?

Q2

What are the most suitable classic and ensemble ML models for predicting medical students' performance in high-stakes examinations?

Q3

What are the most important features in outcome prediction among the medical students' attributes (e.g., demographic information and academic characteristics) extracted from the Comprehensive Education System (CES)?

This research article is organized as follows: Section 2 describes materials and the three-phased proposed method for predicting student outcomes in the CMBSE. Section 3 evaluates the results of the proposed ML models and compares the performance of classic and ensemble ML models. Section 4 addresses research questions, presents findings, compares them to prior research, and identifies limitations. Finally, Section 5 provides conclusions and recommendations for future work.

2. Material and Methods

2.1. Ethics and dissemination

This study was approved by the National Agency for Strategic Research in Medical Education (NASR) – Biomedical Research Ethics Committee - (IR.NASRME.REC 1400.029).

In this section, a framework comprising three main phases is proposed in the CMBSE for the early prediction of students' outcomes, status, and scores, including (1) Preprocessing and feature engineering (2), Models' development for prediction of status and scores, and (3) Evaluation of models and determination of the best models according to the outcomes. Fig. 1 depicts a summary of the proposed framework.

Fig. 1.

The framework of medical students' performance prediction in high-stakes Exams.

Several challenges emerged during the planning and development phases concerning the preliminary research. For instance, during the planning phase, four main challenges required resolution [1]: Heterogeneous and mixed type input and output data (binary, continuous, and categorical) [2], Extraction of different outcomes based on different aspects (score, status, number of test-takers attempts, and at-risk and top-ranked students) [3], Varying passing score thresholds across years, and [4] Imbalanced datasets. On the other hand, a comprehensive analysis and comparison of classic and ensemble classifications and regressions were vital for developing high-performance models. In addition, determining the optimal model parameters was essential without causing over- and under-fitting.

2.2. Study design and dataset description

In our framework, the prediction of medical students' CMBSE performance was based on students' features and their weighted average course grades (based on CMBSE topics) during the basic science curriculum of the Doctor of Medicine (M.D.) program. This research was conducted at several top-ranked medical schools in Iran, analyzing medical students' outcomes (statuses and scores) on 14 CMBSEs. We focused on students who took the CMBSEs between 2017 and 2022.

The extraction of intended educational data is one of the most crucial steps affecting the accuracy of the predictions. To this end, we collected all student data using the affiliated medical schools' Comprehensive Education Systems (CES) and performed manual data entry for the missing data. The CES is a centralized education system with several sub-systems, including the education system (consisting of academic archives, educational planning, exams, grades, and evaluations, etc.) and student information system (including demographic characteristics, exam statistics report, academic records, comprehensive exam results of basic sciences and pre-internship, and certification, etc.).

• i.Inclusion and Exclusion Criteria

The data of all medical students who participated in the CMBSEs between 2017 and 2022 were extracted from the CES based on the considered features. However, since the basic science curriculum phase of the M.D. program typically lasts 4 or 5 academic semesters, we faced the possibility of students transferring to other universities, which could result in unavailable and missed students' histories. In addition, these data were unavailable for students who withdrew from school or switched majors. As a result, student records with the aforementioned missing values were excluded from this study. In addition, a process was performed to eliminate noisy, irrelevant, and inconsistent data, where null and unrealistic values were also removed.

• ii.Input Data Description

The extracted data from CES included 1005 medical student records with 18 features and two outcomes, a continuous one (normalized exam score) and a binary one (pass or fail status), where the number of passed and failed students was 829 (82%) and 176 (18%), respectively. In the current data set, the mean CMBSE score for first-time test takers was approximately 114, while the standard deviation (SD) was approximately 23, which can vary slightly from year to year.

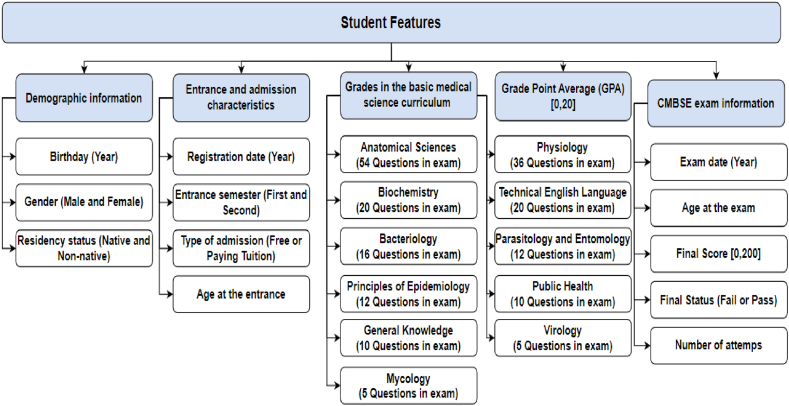
In this dataset, the five feature categories for each student were considered and used as input data for the models. Details of the features are illustrated in Fig. 2.

• •Demographic information: Date of birth (to calculate age), gender (male or female), and residency status (native or non-native) comprised the demographic data.
• •Entrance and admission features: Entrance and admission features included registration date (to determine age at the university entry), entrance semester, such as Autumn/First (September to February) and Spring/Second (February to July), and type of admission (free or paying tuition).
• •Grades in the basic medical science curriculum: Weighted average grades in the courses (based on the topics in the CMBSE) during the basic science curriculum of the M.D. program were considered, including Anatomical Sciences, Physiology, Biochemistry, Bacteriology, Virology, Public Health, Parasitology and Entomology, Mycology, Principles of Epidemiology, Technical English Language, and General Knowledge. The number of questions out of 200 total CMBSE questions for each course is depicted in Fig. 2.
• •Grade point average (GPA): GPA in the basic science curriculum of the M.D. program.
• •CMBSE exam information: CMBSE information, such as the student's age at the time of the exam and the number of exam attempts, were included.

Fig. 2.

Overview of the study's features.

To this end, for preprocessing and developing ML models, three types of features (binary, categorical, and continuous) were considered [1]: Continuous features (integer and real numbers), including scores in intended courses, age at entrance, age when taking the CMBSE, and GPA [2]; Categorical and binary variables, including gender, residency status, entrance semester, number of attempts (first, second, and so on), and type of admission.

• iii.Outcomes

In analyzing high-stakes exams, such as the CMBSE, “Pass or Fail Status” is regarded as the primary outcome, while “CMBSE Score” must also be determined. Notably, although several countries have considered changing the outcomes of medical licensure examinations from scores to only status (pass or fail), some recent studies have indicated that this strategy could result in uninteresting sequences and drawbacks [[33], [34], [35]]. Consequently, both outcomes (status and score) were considered in the current study.

2.3. Methodology

This study presents a three-phase method for predicting students' outcomes (status and score) in the CMBSE. During the first phase, the preprocessing and feature engineering were described. In the second, the development and settings of ML models (classic and ensemble) for predicting status and score were introduced. Finally, the evaluation of models and determination of the best ones based on the requested outcomes were presented. Fig. 3 depicts the three phases of the proposed method for predicting student outcomes in the CMBSE.

Fig. 3.

Three-Phases method for prediction of students' outcome in CMBSE.

2.3.1. First phase: data preprocessing and feature engineering

Four main preprocessing steps were required to prepare input data for the development of models. First, input characteristics and outputs (CMBSE status and score) were statistically analyzed, and their correlations were discussed. In the second step, data scaling and normalization techniques were applied to address heterogeneous and mixed-type input data (binary, continuous, and categorical) and varying passing score thresholds during different years. Thirdly, the effects of features on predictions were estimated, and the most significant ones were identified. Finally, data sampling strategies were implemented to mitigate the effects of imbalanced datasets. The following sections describe each step in detail.

• i.Statistical Analyses

A descriptive analysis was conducted on the features and outcomes. The statistically significant differences between the values of categorical and continuous features in two groups (pass and fail students) were compared using the Chi-square test and the t-test, respectively. In addition, correlations between each pair of features and outcomes were determined to eliminate possible redundancies.

• ii.Data Scaling and Normalization

Data scaling methods were proposed to eliminate the impact of the diverse range of continuous feature values and categorical feature labels on the performance of ML models. It is essential to note that the final score falls within the range [0,200] and that the Ministry of Health and Medical Education calculates the passing score threshold annually using standard scores (Z-scores). As a result, students' CMBSE normalized scores in the range [0,1] were utilized in this study, with the first and last deciles, i.e. [0,0.1) and (0.9,1], representing students at risk and those with the highest scores, respectively. In addition, a standard scaler (MaxMin) was applied to other continuous features, including course grades (values in the range [0,20]) and GPA (values in the range [0,20]), and their values were normalized to the range [0,1]. The weighted course averages were then calculated according to the number of questions per topic in the CMBSE. Moreover, one-hot encoding was applied to categorical ones, such as the admission type of a student, and these data were normalized to zero and one.

• iii.Feature Importance

When deploying ML models, a suitable feature selection method is typically used to identify the essential features. This study used SHapely Additive exPlanations (SHAP) [36,37] to determine the significance of training dataset features. This method, which is based on cooperative game theory, is used to improve the interpretability and transparency of ML models. This method measures features' local and global effects and demonstrates the superior quality of ML models. Accordingly, the SHAP values were utilized to select the most relevant features for developing final models.

• iv.Resampling Imbalanced Data

Similar to the majority of databases related to high-stakes exams, the imbalanced distribution of classes, the majority (Pass) and minority (Fail) classes, were one of the most challenging issues in the current database, which can lead to overfitting and under-performance of ML models [27]. Over-sampling and under-sampling sampling methods have been proposed to address this issue in educational data mining [38]. Over-sampling algorithms, such as Random Over-Sampling (ROS), Synthetic Minority Oversampling TEchnique (SMOTE), and borderline SMOTE, increase the number of samples in the minority class, whereas under-sampling algorithms, such as Random Under-Sampling (RUS) and Tomek links, decrease the number of samples in the majority class [[39], [40], [41], [42]]. The SMOTE Tomek algorithm combines oversampling and undersampling techniques. It is a hybrid method that combines under-sampling (Tomek) and over-sampling (SMOTE) techniques [38]. In addition, it utilizes SMOTE for data augmentation on the minority class and Tomek Links, a method based on nearest neighbors, to eliminate some samples from the majority class. This method improves the performance of ML models and eliminates noisy or ambiguous decision boundaries.

Using a basic LR model, the current study evaluates sampling strategies (ROS, SMOTE, RUS, Tomek, and SMOTE Tomek). SMOTE Tomek has demonstrated the best performance among other methods. As a result, SMOTE Tomek was selected and implemented on our training date to address the imbalanced data issue.

2.3.2. Second phase: ML models development

This section briefly introduces the candidate. Later, we present our strategy for training models using cross-validation and the tuning procedure for determining the optimal model parameters and settings.

• i.Step 1: Candidate ML models

Predictive ML models have the potential to predict student performance on high-stakes exams. Despite the remarkable achievements of classic ML models [32], such as LR [43], KNN [8], and SVM [9,10], their performance can be impacted by complex data, including unbalanced, high-dimensional, and noisy data [44]. Therefore, it is recommended to utilize cutting-edge solutions such as ensemble ML models.

Unlike classic models, in meta-models such as ensemble ML models, robust classifiers or regressors are obtained by developing multiple weak models and aggregating their results via voting or adaptively boosting schemes. These models attempt to generate accurate predictions by balancing the bias-variance trade-off and developing generalized models. Ensemble methods are typically categorized into four categories: (i) voting, (ii) bootstrap aggregating, (iii) boosting, and (iv) stacking methods. Some of the most popular ensemble methods are voting [14], bagging (BG) [15], RF [16], ADA, XGB [18], and stacking [19]. Table 1 provides additional information on a selection of classic and ensemble ML models.

Table 1.

Classic and ensemble ML candidate models for predicting student outcomes.

Category	ML Model	Description
Classic	Logistic Regression (LR)	LR is a statistical method describing data and the relationship between one dependent and independent variable. This is one of the most widely used methods for classification and regression [43].
	K-Nearest Neighbor (KNN)	KNN is a supervised learning algorithm that is mainly used in classification problems. The algorithm assigns labels based on the K-closest patterns in the training dataset. Subsequently, new data are labeled according to their minimum distance from the classes.
	Support Vector Machines (SVM)	SVMs are a set of supervised learning algorithms used for classification problems. SVMs are non-parametric algorithms and rely on kernel functions whose computational complexity does not depend on the dimensions of the input space. The SVM classifier is based on determining a hyperplane that lies in a transformed input space and divides the classes [45,46].
	Support Vector Regression (SVR)	SVR is a supervised learning algorithm used for regression problems. Decision boundaries are determined to predict the continuous output. SVR is trained using a symmetric loss function, penalizing high and low false estimates equally [47].
Ensemble	Voting	Voting predicts the output class based on the maximum number of votes received from ML models [14].
	Bootstrap Aggregation (Bagging)	Bagging is based on the decision tree classifiers. This technique uses bootstrap sampling with replacement to generate the subset of training data. Later, these subsets are utilized to develop weak and homogeneous models independently. Weak models are trained in parallel, and predictions from voting week models yield a more accurate model [15,48].
	Random Forest (RF)	RF is a robust bagging method based on developing multiple decision tree models. This method focuses on two aspects of the sampling, reducing the number of training data and the number of variables. Multiple decision trees are trained on randomly selected training subsets to alleviate the over-fitting problem. The final aggregate is obtained using a majority voting procedure on the models' results. Therefore, the models have less correlation, and the final model is more reliable [16].
	Boosting	Boosting is an ensemble method that builds a strong model based on the iterative training of weak models. Unlike bagging, boosting models are not generated independently by training weak models but are built sequentially on samples from the training dataset. The accuracy of the decision model is improved by learning from previous mistakes [49,50].
	Adaptive Boosting (ADA)	ADA is a tree-based boosting method that focuses on samples that are difficult to classify. This method assigns lower weights to misclassified samples, which are adjusted sequentially during retraining. The final classification is obtained by combining all weak models, while the more accurate ones receive more weight and have more impact on the final results.
	Extreme Gradient Boosting (XGB)	XGB is a tree-based boosting method where random sample subsets are selected to generate new models, and successive ones reduce the previous models' errors. A regularization for penalizing complex models, tree pruning, and parallel learning are utilized to alleviate overfitting and reduce time complexity [18,51].
	Stacked generalization (Stacking)	Stacking is an ensemble ML model that generally consists of heterogeneous models. This model obtains the final prediction by combining several robust models and aggregating their results. At the first level, stacking models are composed of several base models, while at the second level, a meta-model is developed, which considers the outputs of the base models as input. Therefore, the variety of models at the first level could lead to higher performance of the final models [19].

In this study, the most representative classic ML models, which achieved the highest performance in previous studies, were considered candidate models for predicting students' performance in the CMBSE, along with ensemble ML models from the categories above. In addition, the problem of predicting students' exam performance involves two distinct types of output (discrete status and continuous scores). Consequently, two methods (classification and regression) were implemented. The process used to predict each output type is described in the following section.

• 1.Using classifiers for status prediction: In order to predict the status of students enrolled in the CMBSE, models must be able to discriminate between binary classes in the presence of mixed input features. This study used two types of classifiers: In the first layer, classic classifiers such as LR, KNN, and SVM were created. In addition, ensemble ML methods such as voting, bagging, RF, ADA, XGB, and stacking were utilized in the second layer.
• 2.Using regressors for score prediction: Continuous outcomes must be considered to predict students' CMBSE scores. Thus, suitable methods for continuous outcomes were considered, and classic regressors, such as LR and SVR, and ensemble regressors, such as bagging, RF, ADA, XGB, and stacking, were developed.
• ii.Step 2: K-Fold Cross-Validation for Training ML Models

This study employed K-fold cross-validation [52] for training models and avoiding the problem of overfitting. Cross-validation involves separating the dataset into training and test datasets. The training dataset was then subdivided into K-folds, and models were trained and validated in these K rounds. K-fold cross-validation was performed and evaluated based on performance metrics on the training dataset. Finally, the models with the highest average performance were selected as the final predictors.

• iii.Step 3: Tuning of Models' Parameters and Settings

Identifying the optimal parameters for each model is one of the most challenging aspects of ML model development. GridSearchCV [53], a hyper-parameter tuning technique, was utilized to address this issue. In hyper-parameter tuning, an exhaustive search was conducted over the parameter space, and as a result, models were optimized using performance metrics based on the best parameters. In Table A1 of Appendix A, the parameter value adjustments for model training are described in detail.

2.3.3. Third phase: models' performance evaluation

The evaluation metrics for classifiers and regressors were determined based on the current state-of-art references. In this study, a true positive (TP) indicates the number of students correctly predicted to pass, while a false negative (FN) shows the number of students wrongly predicted to fail the CMBSE. Meanwhile, true negative (TN) indicates the number of participants correctly predicted to fail, and false positive (FP) represents the number of participants wrongly predicted to pass the CMBSE.

The effectiveness of classifiers was evaluated using the following metrics: Precision (PPV = TP/(TP + FP)), Sensitivity (Recall = TP/(TP + FN)), Specificity (Spe = TN/(TN + FP)), Accuracy (Acc= (TP + TN)/(TP + FP + FN + TN)), F-measure (F1 = 2*(Precision*Recall)/(Precision + Recall)), Matthew's Correlation Coefficient (MCC=(TP*TN – FP*FN)/√(TP + FP)(TP + FN)(TN + FP)(TN + FN)). Moreover, the Area Under Curve of Receiver Operator Characteristic (AUC-ROC), the Area Under the Curve of Precision-Recall (AUC-PRC), the Calibration Plot, and the Brier Score (BS = Mean Squared Error) was computed [[54], [55], [56], [57], [58], [59], [60]]. Several metrics were utilized for the evaluation of regressors, such as Mean Squared Error (MSE), Root Mean Square Deviation (RMSD), and coefficient of determination (R2) [61].

3. Experiments and Results

In the present research, all models were developed, evaluated, and visualized using Python 3.9.1 (Anaconda) and Scikit-learn, Pandas, and NumPy frameworks and executed on a computer with Microsoft Windows 10 Enterprise with an Intel core i7 x64 processor, 2.5 GHZ CPU, and 16 GB RAM. Our framework is freely available at: https://github.com/SMARTDXCLOUD/Ensemble-ML-for-CMBSE.

The following subsections will discuss the results of the statistical analysis of input features and the importance of features in predictive models. In addition, the performance of models in predicting status and score is evaluated. This study employed five experiments to compare classic and ensemble ML models for predicting CMBSE's status and score.

3.1. Statistical analysis results

The results of a descriptive statistical analysis of categorical and continuous features are shown in Table 2. In this study, data on 1005 medical students enrolled in CMBSE were collected, and after removing redundant features, only 18 were considered. The mean ± SD was calculated for continuous features, while the number and percentage were described for categorical (binary) ones. In addition, the Chi-square test was applied to categorical features to determine whether there was a statistically significant difference between the two study groups (passing and failing students), and the independent samples t-test was used to analyze continuous features. The results indicated statistically significant differences between most features of the two groups, with a 95% confidence interval and a P-value less than 0.05. However, there were a few exceptions, such as the gender, residency status, entrance semesters, and entrance ages of the students, which were not significantly different between the two groups. Figures A.2 and A.3 in Appendix A provide more information on the distribution of status in groups and normalized scores in the CMBSE, respectively.

Table 2.

Baseline characteristics of the study population.*

Features		Total 1005 (100)	Fail 176 (18)	Pass 829 (82)	P-Value	Test-Statistics
		N (%)	N (%)	N (%)
		Mean ± SD	Mean ± SD	Mean ± SD
Gender	Male	526 (52.3)	85 (48.3)	441 (53.2)	0.237a	1.398
	Female	479 (47.7)	91 (51.7)	388 (46.8)
Residency Status	Native	525 (52.2)	84 (47.7)	441 (53.2)	0.187a	1.741
	Non-Native	480 (47.8)	92 (52.3)	388 (46.8)
Entrance Semester	Autumn	449 (44.7)	80 (45.5)	369 (44.5)	0.819a	0.052
	Spring	556 (55.3)	96 (54.5)	460 (55.5)
Type of Admission	Free Tuition	767 (76.3)	117 (66.5)	650 (78.4)	0.001a	11.433
	Paying Tuition	238 (23.7)	59 (33.5)	179 (21.6)
Age at Entrance		18.86 ± 1.80	19.03 ± 1.54	18.83 ± 1.85	0.188b	1.319
Age at CMBSE		21.25 ± 1.88	21.60 ± 1.76	21.17 ± 1.90	0.006b	2.763
Anatomical Sciences		16.42 ± 2.52	13.93 ± 2.42	16.95 ± 2.21	<0.001b	−16.149
Physiology		16.02 ± 2.37	14.17 ± 2.48	16.41 ± 2.16	<0.001b	−11.112
Biochemistry		16.16 ± 2.44	13.74 ± 2.16	16.68 ± 2.17	<0.001b	−16.327
Bacteriology		15.05 ± 2.46	13.07 ± 2.17	15.47 ± 2.30	<0.001b	−12.641
Parasitology and Entomology		15.98 ± 2.21	14 ± 2.15	16.4 ± 1.98	<0.001b	−14.338
Principles of Epidemiology		15.97 ± 2.21	15.25 ± 2.12	16.12 ± 2.20	<0.001b	−4.787
Public Health		16.96 ± 2.32	15.34 ± 2.35	17.31 ± 2.17	<0.001b	−10.794
Mycology		16.36 ± 2.52	14.68 ± 3.05	16.71 ± 2.24	<0.001b	−8.395
Virology		16.94 ± 2.52	14.82 ± 2.65	17.39 ± 2.24	<0.001b	−12.007
Technical English Language		15.29 ± 2.36	13.40 ± 1.98	15.69 ± 2.24	<0.001b	−12.543
General Knowledge		17.81 ± 1.92	17.06 ± 2.19	17.96 ± 1.81	<0.001b	−5.121
Grade Point Average (GPA)		16.29 ± 1.66	14.46 ± 1.41	16.68 ± 1.44	<0.001b	−18.726

*The statistically significant differences between the pass/fail groups due to the intended features are bolded, where ‘a' indicates the results of Chi-Square and ‘b' Independent Samples Tests.

*Values of Spearman Correlation Coefficient (R) are indicated in cells.

In addition, the Spearman correlation test was used to evaluate the potential correlations between the continuous features and outcomes (normalized CMBSE scores). A heatmap plot was generated to illustrate these correlations (Fig. 4). The Spearman correlation is a non-parametric test that makes the same assumptions as the Pearson correlation without any reliance on the normality of the data distribution [62,63]. Warm colors on the heatmap indicate high correlation coefficients, while cool colors indicate low correlation coefficients.

Fig. 4.

The pairwise correlation between features and scores in CMBSE.

Fig. 4 shows the pairwise correlation between features and scores in the CMBSE. According to the correlation coefficients (denoted as R), there were significant correlations (R > 0.80) between the GPA and two courses (P-value <0.001): Biochemistry (R = 0.83) and Anatomical Sciences (R = 0.81). In addition, there were positive correlations between course grades and CMBSE outcomes. The GPA strongly correlates positively with normalized CMBSE scores (R = 0.75, P-value <0.001). Meanwhile, negative correlations can be observed between age at entrance and age when taking CMBSE and the normalized CMBSE scores, indicating that an increase in a candidate's age may result in lower CMBSE scores. Overall, students' grades in Anatomical Science (52 out of 200 CMBSE questions), Biochemistry (20 out of 200), and Physiology (36 out of 200) were positively correlated with their CMBSE scores. Similarly, weak correlations were observed between the Principles of Epidemiology (12 out of 200) and General Knowledge (10 out of 200). Table A4 in Appendix A provides additional information regarding the heatmap's absolute R- and P-values.

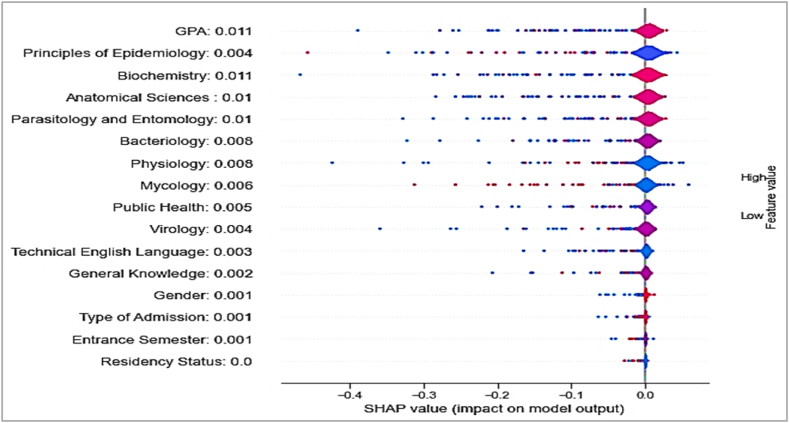
SHAP [64], a method for feature selection, was utilized to assess the positive and negative influences of the features on the decision-making process and outcome prediction. Fig. 5 depicts a summary plot of the estimated SHAP values for each sample. In this plot, features are ordered based on their SHAP values, and the impact of each feature on the models' predictions is shown in red and blue, respectively, to indicate high and low impacts. Furthermore, the mean SHAP value for each feature is shown before its name, with higher values indicating greater importance. In Fig. 5, the SHAP values suggest that final CMBSE scores were positively associated with high GPAs and course grades in Biochemistry, Anatomical Sciences, Parasitology, and Entomology (their mean SHAP values were between 0.01 and 0.011). In addition, similar to the statistical analysis findings, there were weak correlations between the CMBSE outcomes of students and their grades in courses such as General Knowledge.

Fig. 5.

Evaluation of features' importance by SHAP summary plot.

3.2. Quality assessment

The predictive ML models of students' CMBSE performance were developed using a training dataset comprising 67% of the primary dataset's records. They were also evaluated on the test dataset, which included 33% of the records. In addition, GridSearchCV was employed to tune and determine the model parameters during the 10-fold cross-validation. In the current data set, the majority class (pass) accounted for 82% (n = 829) of the total, while the minority class (fail) accounted for 18% (n = 176). SMOTE Tomek was also implemented to create a more balanced training dataset. The percentage of students who failed in the training dataset increased from 18% to 50% (552/1104) due to the improvement, while the percentage of students who passed decreased from 82% to 50% (552/1104). The following subsections evaluate the predictive accuracy of models (classifiers and regressors) for two outcomes (status and score).

3.2.1. Quality assessment of classifiers in predicting student status in the CMBSE

The student status in the CMBSE was predicted using nine ML models [1]: Classic models, which consisted of LR, KNN, and SVM classifiers, and [2] Ensemble models, which included voting, BG, ADA, XGB, RF, and stacking. In the subsequent experiments, the developed models will be compared comprehensively from three perspectives [1]: Models' predictive performance [2], Evaluation of models' ability to discriminate using the area under the curves (AUCs), and [3] Goodness-of-fit in models using a calibration plot.

3.2.1.1. Experiment 1: evaluating the classifiers' predictive performance

The performance of models for predicting CMBSE status was compared using the metrics described in Section 2.2, Phase 3. Table 3 indicates that the suggested ML models exhibited high values for the majority of measures. LR and SVM demonstrated superior results among the classic models in most metrics. In a large number of ensemble metrics, RF and stacking appeared to be superior to the others. RF accomplished the modeling phase with the highest values of AUC-ROC (0.813), AUC-PRC (0.93), precision (0.871), and MCC (0.515). In addition, stacking achieved the highest levels of sensitivity (0.828), accuracy (0.829), and F-measure (0.837).

Table 3.

Predictive performance of classifiers for predicting status in CMBSE.

Models Categories	Models Name	AUC-ROC	AUC-PRC	PPV	Sen	Acc	F1	MCC	BS
Classic	LR	0.786	0.919	0.857	0.804	0.803	0.821	0.481	0.133
	KNN	0.747	0.906	0.837	0.762	0.762	0.785	0.404	0.179
	SVM	0.739	0.902	0.836	0.804	0.804	0.816	0.422	0.125
Ensemble	Voting	0.747	0.906	0.837	0.762	0.765	0.785	0.404	0.179
	Bagging	0.739	0.902	0.836	0.804	0.803	0.816	0.422	0.121
	ADA	0.711	0.892	0.825	0.804	0.804	0.813	0.388	0.193
	XGB	0.756	0.908	0.847	0.822	0.823	0.832	0.461	0.137
	RF	0.813	0.93	0.871	0.814	0.803	0.823	0.515	0.143
	Stacking	0.760	0.909	0.850	0.828	0.829	0.837	0.472	0.136

*The best values in each column are bolded.

**Precision (PPV), Sensitivity (Recall), Accuracy (Acc), F-measure (F1), Matthew's Correlation Coefficient (MCC), Area Under Curve of Receiver Operator Characteristic (AUC-ROC), Area Under Curve of Precision-Recall (AUC-PRC), Calibration Plot, Brier Score (BS).

3.2.1.2. Experiment 2: evaluating the discrimination ability of models using AUCs

The receiver operating characteristic curves (AUC-ROC) and precision-recall curves (AUC-PRC) were used to assess the discrimination ability of models. AUC-ROC reveals the trade-off between specificity and sensitivity, whereas AUC-PRC reveals precision values for recall (sensitivity) values. Notably, AUC-PRC and AUC-ROC are generally among the most informative metrics for imbalanced datasets and binary outcomes [65]. Due to the unequal status of students in the CMBSE, AUC's results were used to determine the model with the highest level of discrimination.

Fig. 6A and 6.B illustrates AUC plots for nine models. In both plots, RF achieved the highest overall value (AUC-ROC = 0.813 and AUC-PRC = 0.93), whereas other models demonstrated acceptable abilities in predicting the CMBSE status of students. In addition, the accuracy of the methods was compared in Fig. 6C, where the LR (Acc = 0.803) and RF (Acc = 0.83) models demonstrated the greatest average accuracy in repeated experiments. Moreover, according to the confusion matrices, RF had the highest TP and the best FP among models, while LR and RF had the best FN and TN. Figure A5 of Appendix A provides additional information about the confusion matrices of models.

Fig. 6.

A) AUC-ROC, B) AUC-PRC, C) Average accuracy of models in prediction of the status.

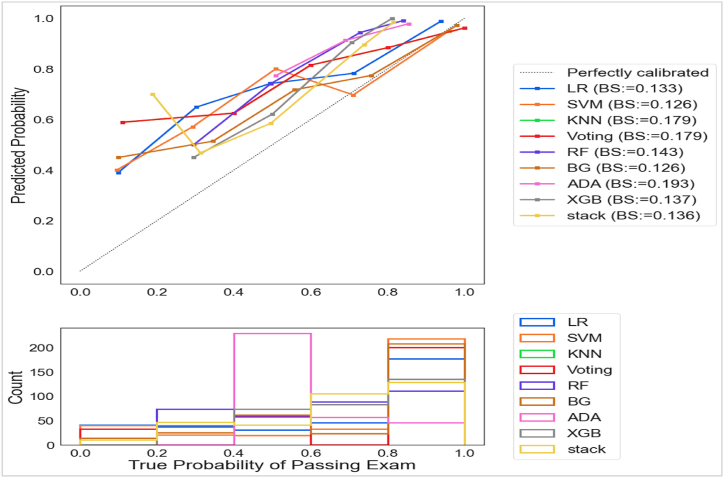
3.2.1.3. Experiment 3: evaluating the goodness-of-fitting in models using a calibration plot

The calibration plot indicated the consistency between predictions and observations in various percentiles of the predicted values, and comparing the calibration of all models through a scatter plot signifies the concordance between predictions and observations. According to Fig. 7, models experienced challenges in calibrating the minority class while calibrating the majority class successfully. Moreover, SVM (BS = 0.125) and BG (BS = 0.121) achieved the best Brier Score Loss values (BS, a metric composed of calibration and refinement terms). Moreover, RF and Stacking calibrated the majority class with success and the minority class and Brier Score loss values with moderate success.

Fig. 7.

Calibration plots of models for predicting status in CMBSE.

3.2.2. Quality assessment of regressors in predicting student scores in the CMBSE

The students' CMBSE scores were predicted using classic (LR and SVM) and ensemble models (ADA, RF, XGB, and stacking). The performance of models in determining the scores of students was comprehensively compared from two perspectives [1]: The predictive performance of the models and [2] A comparison of the distributions of observations and predictions. Table A.6 in Appendix A further explains the parameter value adjustments for model training.

3.2.2.1. Experiment 1: evaluating the regressors' predictive performance

In this section, we focused on models for predicting CMBSE scores and compared them based on their measured performance. The suggested regressors exhibited superior performance in most measures, as shown in Table 4. RF performed the best measurement on the test data, with MAS, RMSD, and R2 values of 0.063, 0.094, and 0.80, respectively.

Table 4.

Overall performance of models for predicting the scores in CMBSE*.

Models Categories	Models Names	MAE	RMSD	R2
Classic	LR	0.092	0.134	0.618
	SVR	0.095	0.120	0.675
Ensemble	ADA	0.092	0.134	0.613
	RF	0.053	0.077	0.80
	XGB	0.063	0.094	0.775
	Stacking	0.078	0.113	0.717

*The best value in each column represents in bold.

**Mean Absolute Error (MAE), Root Mean Square Deviation (RMSD), and coefficient of determination (R2).

3.2.2.2. Experiment 2: comparison of the distribution of models' observation and prediction

Fig. 8 compares the distributions of scores in observations and model predictions. According to the outcome distribution of the models, LR and RF predicted scores significantly closer to the actual values. In addition, these models performed better in identifying at-risk and top-ranked students. To provide more information about the distributions of the results, they were compared in the histogram plots in Figure A7 of Appendix A, where RF showed the highest similarity between observations and predictions.

Fig. 8.

Distribution of observation and prediction in scores' prediction models in CMBSE.

4. Discussion

A significant issue for educational systems is assessing the proficiency of medical students and graduates through qualification methods such as licensure examinations. Although these challenging assessments play an essential role in students' futures, numerous educational systems struggle to control costs and manage the lengthy process. To this end, research has been conducted on EDM systems for predicting student performance, with a few studies focusing specifically on medical high-stakes exams [6,32]. Prior research typically employed classic classifiers (e.g., LR) for early prediction of at-risk students or complex models such as RF, stacking, GB, and XGB for determining status in course examinations – but not high-stakes ones. In addition, the majority of strategies focused on deciding whether participants fail or pass rather than their scores; however, recent research suggests that this tactic is insufficient and may produce uninteresting results [[33], [34], [35]].

To address these issues, we focused on predicting the status and score for the CMBSE – one of the most common medical exams in the world – using classic and ensemble ML models supplied by student demographic data, admission, and entrance information, grades from the basic medical sciences curriculum, and GPA. In addition, a three-phase framework was developed to be applicable and extended to other comparable tests.

Due to the unique characteristics of high-stakes exams, predicting their outcomes presents four challenges: heterogeneous and mixed input and output data, diverse outcomes from different aspects, varying passing score thresholds, and imbalanced datasets. We attempted to overcome these challenges by applying a preprocessing phase that considered the correlations between features and the importance of features based on their SHAP values. Our results were consistent with previous research indicating that demographic factors played a minor role [20]. However, admission type (free or paying tuition) substantially affected CMBSE outcomes. In addition, the models highlighted GPA as the most influential factor in the results. Additional analysis revealed that higher grades in Anatomical Science, Biochemistry, and overall GPA were associated with better test performance. Conversely, lower scores in Principles of Epidemiology appeared to be linked to subpar outcomes.

Previous research [23,26,27] focused on developing classic models indicate that the LR model performed better than other classic models. When identifying at-risk students in COMLEX 1, LR achieved sensitivities ranging from 65.8 to 71% and specificities ranging from 88.2 to 83.2% [32]. However, the proposed method used classic and ensemble classification methods to predict the status. In line with previous research findings [23,26,27], LR outperformed the classic models examined in this study across most metrics, while the proposed preprocessing phase improved LR's performance by 9–11% compared to previously utilized methods [32]. Notably, among all models, ensemble models (such as RF and stacking) produced the best-reported results. For example, RF outperformed LR in AUC-ROC, AUC-PRC, and F1 metrics, increasing by 0.07, 0.03, and 0.11, respectively. Furthermore, the proposed ensemble models achieved a prediction accuracy of 0.83% for student status. Even with high model calibration in identifying passed students, particularly bagging models with the highest BS metrics (0.125), models struggle in identifying students who failed the high-stakes exam with borderline scores.

In addition to predicting the status of the students on the high-stakes exams, we predicted their normalized scores. Due to the continuous output value, both classic and ensemble regression models were employed. LR and RF forest achieved the highest performance among classic and ensemble models. RF achieved a high R2 value (0.80%) compared to the LR model and reduced MAE and RMSD by 0.014 and 0.021, respectively. Similar trends were observed in the distribution of predicted scores, with LR and RF having the highest similarity to actual data and being more effective at predicting at-risk and top-performing students based on the distribution of observations and predictions.

4.1. Limitations and future work

Although our framework achieved high values in various measurement matrices, our study had limitations. The presented models covered the basic medical sciences in the M.D. curricula, which are common in most countries, such as CMBSE-IR and COMLEX-USA; however, for the generalization of these models to other contexts, some courses, such as General Knowledge, may be omitted from modeling due to the varying curriculums across settings and countries. In addition, the weight of courses must be adjusted based on the number of questions per course due to CMBSE topics. A further limitation of the current study was that we did not have access to the student information from the university entrance exam, which would have improved the performance of the models if included as an input parameter. Moreover, to fully exploit the potential of these models, it is recommended to test them on larger populations for improved evaluations and to demonstrate their applicability.

5. Conclusions

In conclusion, governments and educational systems can save resources and time by developing ML models to predict students' performance on licensure exams, where these models can provide a suitable alternative for high-stakes exams in unforeseen circumstances (such as the COVID-19 pandemic). Furthermore, these models may be effective from an outcome-based perspective in medical education by facilitating proactive and knowledge-based decision-making, fostering academic success by tracking student progress, and preventing failures by early identification of at-risk students.

Funding

This project was funded by the National Agency for Strategic Research in Medical Education, Tehran, Iran. Grant No. 994079. We thank the National Agency for Strategic Research in Medical Education (NASR) for funding the project (Grant Number 994079), which provided the context for the writing of this article (Webpage of the grant number: http://rms.nasrme.ac.ir).

Production notes

Author contribution statement

Haniye Mastour, Toktam Dehghani: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Ehsan Moradi: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.

Saeid Eslami: Conceived and designed the experiments; Wrote the paper.

Data availability statement

To accelerate the utilization of the current models for similar high-stakes examinations, our framework is available at: https://github.com/SMARTDXCLOUD/Ensemble-ML-for-High- stakes-exams/releases/tag/V.1.2022.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Haniye Mastour reports was provided by National Agency for Strategic Research in Medical Education (NASR) Grant Number 994079 awarded.

Appendix A. Supplementary data

The following is the Supplementary data to this article: