Quantum interferometry and pathway selectivity in the nonlinear response of photosynthetic excitons

Significance

Substantial developments in the generation and control of quantum light sources have sparked considerable interest in applying them to spectroscopy. Quantum light introduces additional degrees of freedom that can be used to unravel novel molecular information. Entangled photons possess unusual time–frequency correlations unmatched by classical light sources, enabling better resolution of molecular processes at much lower intensities, thus avoiding damage in fragile samples. We show how they may be used to study quasiparticle interactions in matter. An interferometric technique is proposed, which leads to a higher degree of control over the induced processes in the sample. It further allows a more precise measurement of quasiparticle scattering with high time–frequency resolution and the elimination of unwanted background contributions.

Abstract

We propose a time–frequency resolved spectroscopic technique which employs nonlinear interferometers to study exciton–exciton scattering in molecular aggregates. A higher degree of control over the contributing Liouville pathways is obtained as compared to classical light. We show how the nonlinear response can be isolated from the orders-of-magnitude stronger linear background by either phase matching or polarization filtering. Both arise due to averaging the signal over a large number of noninteracting, randomly oriented molecules. We apply our technique to the Frenkel exciton model which excludes charge separation for the photosystem II reaction center. We show how the sum of the entangled photon frequencies can be used to select two-exciton resonances, while their delay times reveal the single-exciton levels involved in the optical process.

Two-photon absorption (TPA) has been a common target of entangled light spectroscopy. In the low-intensity regime, a second-order nonlinear crystal produces pairs of spectrally and temporally entangled (signal and idler) photons. The sum of their frequencies is determined by the pump field frequency, and their arrival time difference is controlled by the phase-matching conditions inside the crystal (the entanglement time). It has been shown theoretically that since the signal and idler photons appear in pairs with unusual time–frequency correlations, they can be used to enhance the TPA process in molecules at low light intensities (1–3) and minimize radiation damage in fragile samples. Additionally, in contrast to classical spectroscopy, the time–frequency relations can be used to achieve joint spectral and temporal resolutions which are not bound by the Fourier uncertainty (4–6).

Several experimental studies have reported the observation of entanglement-enhanced TPA in molecular systems (7, 8). Generally, the rate of TPA events can be inferred only indirectly since both photons are absorbed. However, the measured cross-sections are typically several orders of magnitude higher than theoretical estimates (9, 10), and some experimental findings report much lower values (11–13). Recent studies suggest that single-photon scattering (13) or hot-band absorption (14) could be responsible for this discrepancy.

Quantum optics mainly focuses on generating new states of quantum light through the use of interferometers and nonlinear crystals. Here, the light–matter interaction results in the interaction between photons of different frequencies. Entangled light provides an exciting platform for novel spectroscopic and imaging applications beyond TPA (15).

Quantum spectroscopy combines quantum optics technology with spectroscopic techniques to obtain new information about light–matter interaction and improve the sensitivity of classical spectroscopic techniques (16). For example, the Hong–Ou–Mandel two-photon interferometer has been used to measure ultrafast dephasing times in the presence of strong losses (17–20). Pathway indistinguishability can be used to, for example, measure the linear response of a material in the infrared frequency regime by detection of photons in the more convenient visible range (21, 22). It emerges in nonlinear interferometers where beam splitters are replaced with nonlinear crystals, leading to coherences between photons generated at different crystals (23–27).

Classical spectroscopy signals are mostly controlled via their phase-matching conditions, which are used to select certain Liouville space pathways (28). Phase matching allows the control over the signs of the wave vectors of the fields, and different combinations can describe effects like two-exciton scattering, transport, or their combinations. Quantum light interferometry can provide additional control over the left/right degrees of freedom in Liouville space (i.e., whether the interaction takes place on the bra or the ket), complimenting classical techniques which are entirely based on phase matching (29, 30).

In this theoretical study, we propose a protocol for studying two-exciton scattering effects which combines entangled photon pairs with a nonlinear interferometer by using two coherently pumped parametric down-conversion (PDC) crystals. The interferometer combines two-exciton scattering pathways constructively while transport effects are interfering destructively with each other, such that all interactions only appear either on the left (ket) or the right (bra) side of the density matrix in Liouville space. Control over path delays in the interferometer arms provides a time-dependent read-out of two-exciton scattering processes with temporal resolution determined by the entanglement time of signal and idler. We provide an example of the signal for a Frenkel exciton model of the photosystem II reaction center of purple bacteria. We show that the pump frequency generating the entangled photons can be used to select two-exciton resonances, and the signal/idler time delays reveal information about which single-exciton states are coupled to a given two-exciton state.

The nonlinear two-exciton scattering effects appear on top of a large background containing interference terms of the unperturbed entangled photons and the linear response of the sample. We show how either phase matching or polarization filtering can be used to isolate the nonlinear term, so that in contrast to entangled TPA measurements, no ambiguity remains about the origin of the signal. Our signal further shares the same advantages of entangled TPA, i.e., linear scaling with intensity and increased frequency-time resolution. It may thus address the feasibility of resolving nonlinear effects with single entangled photon pairs (9, 10).

1. Pathway-Selectivity through Interferometry

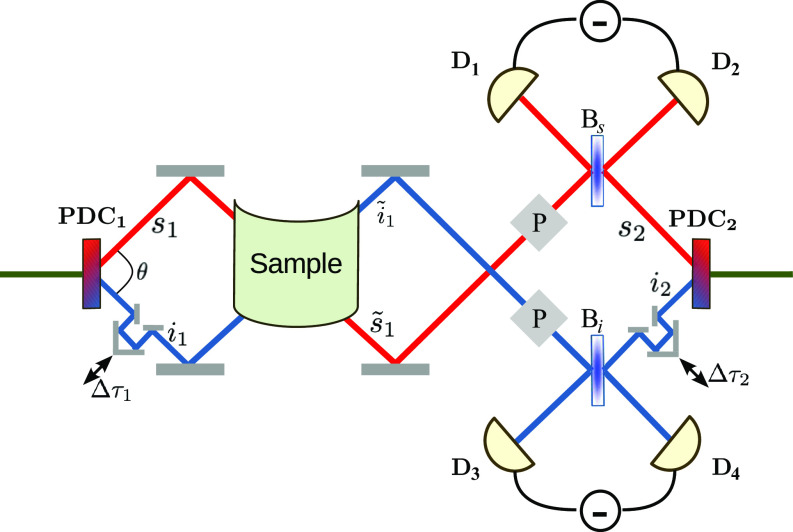
We consider the set-up shown in Fig. 1. Two second-order nonlinear crystals are pumped by a common coherent pump field. The pump intensity is sufficiently weak, so that only a single entangled photon pair is generated, either in crystal 1 or 2. The signal (idler) photons of the two crystals are then interfered at the beamsplitters B_s(i), respectively, and detected at the two output ports. The signal photon is thus measured either at detector D₁ or D₂, while the idler photon is measured either at D₃ or D₄. Prior to their interference at the beamsplitter, the signal and idler photons generated at the first crystal can interact with a sample consisting of a large number of noninteracting molecules. The measured signal is finally given by a combination of detections at the signal and idler photon detectors, ⟨𝒮⟩=⟨(D₁ − D₂)(D₄ − D₃)⟩. It is the coincidence of two heterodyne measurements where the signal (idler) from the first crystal after interaction with the sample is heterodyned with the signal (idler) of the second crystal. A similar interferometer has been considered in refs. 31–33 without a sample to study the coherences between the signal and idler photons of both crystals. On their own, the signal (idler) photons show no coherence between the two crystals since the idler (signal) photons can be measured to distinguish them. However, a two-photon (fourth-order) coherence is present when coincidences between the signal and idler are measured. This coherence is used here to study the nonlinear response of the sample.

Fig. 1.

The proposed interferometric setup. Two nonlinear crystals PDC₁ and PDC₂ are weakly pumped by the same pump field such that only a single entangled photon pair is generated, whose origin can be either PDC₁ or PDC₂. The photons emitted at PDC₁ can interact with a sample before they are mixed at the beam splitters B_{s, i} with the photons emitted from PDC₂ and send into the four detectors D_i (i = 1, 2, 3, 4). The signal is given by a combination of four coincidence detections between the Upper and Lower detectors, ⟨𝒮⟩=⟨(D₁ − D₂)(D₄ − D₃)⟩. Delay lines Δτ₁ and Δτ₂ between the s₁, i₁ and s₂, i₂ paths, respectively, lead to a time-dependent read-out of the two-exciton scattering process. The rotatable polarizers P are used for tunable polarization filtering. A similar interferometer has been studied in refs. 31–33.

We study the fourth-order nonlinear response of Frenkel excitons in the reaction center of the photosystem II photosynthetic complex, described by the Hamiltonian

$$\begin{array}{c}\hfill H=H_F+H_M+H_{\mathit{int}},\end{array}$$ [1]

where H_F is the free field Hamiltonian, H_M is the matter Hamiltonian, and H_int is the field–matter interaction Hamiltonian. The matter Hamiltonian is given by

$$\begin{array}{c}\hfill H_M={\displaystyle \sum _{n,m=1}^{N_c}}{h}_{\mathit{mn}}{B}_m^{†}{B}_n+g{\displaystyle \sum _{n=1}^{N_c}}{B}_n^{†}{B}_n^{†}{B}_n{B}_n,\end{array}$$ [2]

where N_c is the number of chromophores in the molecular aggregate, the Boson operators B_n with [B_n, B_m^†]=δ_mn describe the deexcitation of the chromophore at site n, h_mn contains the single-excitation energies of each chromophore and their mutual couplings, and g is the anharmonicity.

For the field Hamiltonian H_F, we introduce a simple model (Materials and Methods) that describes the propagation of signal and idler photons in space along their respective pathways through the interferometer. Note that this is an effective Hamiltonian which can be derived from first principles using an effective action approach (for more details see SI Appendix). Each pathway segment has its own set of annihilation and creation operators. Beam splitters are used to mix the pathways between single photons, and the sample introduces a local interaction between the signal and idler photons, whose evolutions are otherwise independent. In the interaction picture, the signal described in the caption of Fig. 1 is given by

$$\begin{array}{cc}\hfill 〈\mathcal{S}〉& =\int {\int }_{-\infty }^{\infty }d{t}_{s}d{t}_i〈{\tilde{a}}_{s_2}^{†}(t_s-{\tau }_{s_2}-{\tau }_D){\tilde{a}}_{i_2}^{†}(t_i-{\tau }_{i_2}-{\tau }_D)\hfill \\ \hfill & \times {\tilde{a}}_{{\tilde{s}}_1}(t_s-{\tau }_{{\tilde{s}}_1}-{\tau }_D){\tilde{a}}_{{\tilde{i}}_1}(t_i-{\tau }_{{\tilde{i}}_1}-{\tau }_D)+\mathrm{h}.\mathrm{c}.〉,\hfill \end{array}$$ [3]

where ${\tilde{a}}_k(t)$ is the annihilation operator acting at the beginning of the pathway k (Fig. 1), and τ_k is the optical path length of pathway k (note that τ_D refers to the path length between the beam splitter and the detectors and is assumed to be the same for all four detectors).

The dipole interaction Hamiltonian between the signal and idler photons and the sample is given by

$$\begin{array}{c}\hfill {\tilde{H}}_{\mathit{int}}(t)=\mathbf{V}(t)·{\tilde{\mathbf{E}}}^{†}(t)+\mathrm{h}.\mathrm{c}.,\end{array}$$ [4]

where V(t)=∑_nμ_nB_n(t) is the dipole operator in the interaction picture and μ_n is the dipole moment of the nth chromophore. The positive-frequency part of the electric field operator is given by $\tilde{\mathbf{E}}(t)=\sum _k\sqrt{\frac{ħ{\omega }_{c,k}}{4\pi {\epsilon }_{0}cA}}{\mathit{ϵ}}_k{\tilde{a}}_k(t)+\sum _j\sqrt{\frac{ħ{\omega }_{c,j}}{4\pi {\epsilon }_{0}cA}}{\mathit{ϵ}}_j{\tilde{a}}_j(t-{\tau }_j)$ with $k\in \left\{{\tilde{s}}_1,{\tilde{i}}_1\right\}$, j ∈ {s₁,i₁}, ε₀ as the vacuum permittivity, c as the speed of light in vacuum, and ϵ_{k, j} the respective polarization vector. We assume plane waves with a transversal area A and wave packets with well-defined central frequencies ω_{c, k} and ω_{c, j}.

Using this interaction Hamiltonian, the formal expression for the signal 𝒮 is given by

$$\begin{array}{c}\hfill ⟨\mathcal{S}⟩=\mathrm{tr}\left\{\mathcal{S}\mathcal{T}exp\left(-\frac{i}{ħ}{\int }_{-\infty }^{\infty }dt{\tilde{H}}_{int,-}(t)\right){\rho }_M\otimes {\rho }_F\right\}.\end{array}$$ [5]

We have introduced the interaction Hamiltonian superoperator in Liouville space whose action on an ordinary operator X is defined as H_{int, −}X = [H_int, X]. Using the left/right superoperators, we can rewrite $H_{int,-}(t)={\mathbf{V}}_L(t)·{\tilde{\mathbf{E}}}_L^{†}(t)-{\mathbf{V}}_R(t)·{\tilde{\mathbf{E}}}_R^{†}(t)+\mathrm{h}.\mathrm{c}.$, where A_LX = AX and A_RX = XA for arbitrary Hilbert space operators A, X. 𝒯 denotes superoperator time ordering, and ρ_M = |g⟩⟨g| is the initial matter density operator, assumed to be in the ground state.

The initial field density operator is given by ρ_F = |Ψ⟩⟨Ψ|, where

$$\begin{array}{cc}\hfill |\mathrm{\Psi }⟩& =\int {\int }_0^{\infty }d{\omega }_{s}d{\omega }_i{\psi }^{(1)}({\omega }_s,{\omega }_i)a_{s_1}^{†}({\omega }_s)a_{i_1}^{†}({\omega }_i)|0⟩\hfill \\ \hfill & +{\psi }^{(2)}({\omega }_s,{\omega }_i)a_{s_2}^{†}({\omega }_s)a_{i_2}^{†}({\omega }_i)|0⟩.\hfill \end{array}$$ [6]

Here, ψ^{(1, 2)}(ω_s, ω_i) plays the role of a two-photon wave function of the signal and idler generated at PDC_1/2, respectively. These are not true wave functions of light but rather correlation functions of the signal and idler modes conditioned on the placement of the mirrors used to collect and send them to the sample. This correlation function can be derived by using an effective action (SI Appendix) to describe the generation of the signal and idler photons inside the crystal and their subsequent propagation with single-photon Green’s functions from their point of origin to the mirrors used to redirect the two beams into the sample. The two-photon wave function depends on the fixed angles of the propagation directions of signal and idler beams (at their central frequency) with respect to the classical pump when leaving the crystal, which are controlled by the mirror positions (see angle θ in Fig. 1). Additional changes to the wave function appear due to the propagation length of the signal and idler which is included explicitly in our effective Hamiltonian.

We focus on signals obtained by expanding the exponential in Eq. 5 to fourth order. Eq. 3 contains two annihilation operators associated with the output from the sample and two creation operators associated with the output from PDC₂ and vice versa. This implies that only coherence terms of the field density operator are measured, where the ket side describes photons originating from PDC₁ and the bra side describes those originating from PDC₂ or vice versa. Since the operators associated with the output from PDC₂ do not interact with the sample and do not appear in the interaction Hamiltonian in Eq. 4, only pathways where all interactions happen either on the Left or the Right side of the density matrix can contribute to this signal. The signal further contains a four-point correlation function, which is why two photons must be generated either on the ket or bra, accompanied by two deexcitations in the molecule. This also means that the molecule, which is assumed to be initially in the ground state, needs to be excited twice. The relevant ladder diagrams selected by the interferometric setup are shown in Fig. 2A. Here, all interactions are on the Left side (ket), and contributions with all interactions on the right are their hermitian conjugates. The Left diagram in Fig. 2A contains two excitations (together with the absorption from signal and idler of PDC₁), followed by two deexcitations (together with the emission of two photons measured in coincidence by the two detectors). The other diagram describes a sequential excitation and deexcitation process. We have assumed that the signal appears before the idler, which can be controlled by the external delays.

Fig. 2.

(A) Ladder diagrams of the contributing processes in the sum-over-state picture, where all interactions are on the Left (complex conjugated processes with all interactions on the right are not shown). Right/Left-pointing arrows denote photon annihilation/creation, and red/blue color denote signal/idler photons. |g⟩ is the ground state, |e, e′⟩ denote the single-exciton eigenenergies, and |f⟩ denote the two-exciton eigenenergies obtained from a diagonalization of the matter Hamiltonian in Eq. 2. The time-orderings of incoming and outgoing signal and idler are controlled by the time delays of their respective paths (Eq. 14). The two diagrams are the ones selected by the interferometric setup. Note that if the linear background is suppressed by either phase matching or polarization filtering, the factorized linear contribution needs to be subtracted from these ladder diagrams. In this case, the second ladder diagram cancels with its factorized contribution. (B) Incoming and outgoing wave vectors of signal and idler at their respective central frequencies. The black arrows show polarization filtering where the incoming polarizations are chosen in the plane of the incoming wave vectors, and the outgoing polarizations lay in a perpendicular plane, suppressing the linear background. Alternatively, the freedom in the phase matching can be used to suppress the linear background. The outgoing wave vectors can be rotated around the sum of the incoming wave vectors (green arrow) while conserving the angle between them.

Calculating the expectation value over the field degrees of freedom in Eq. 5 gives

$$\begin{array}{cc}\hfill ⟨\mathcal{S}⟩& =C{\displaystyle \sum _{\mathit{ijkl}}}{\int }_{-\infty }^{\infty }\mathrm{d}{t}_1\mathrm{d}{t}_2\mathrm{d}{\overline{t}}_1\mathrm{d}{\overline{t}}_2{\psi }^{(1)}(t_1-{\tau }_{s_1},t_2-{\tau }_{i_1})\hfill \\ \hfill & \times {\mathcal{B}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2){\psi }^{(2)\ast }({\overline{t}}_1+{\tau }_{{\tilde{s}}_1}-{\tau }_{s_2},{\overline{t}}_2+{\tau }_{{\tilde{i}}_1}-{\tau }_{i_2})\hfill \\ \hfill & \times \left({\mathit{\mu }}_i·{\mathit{ϵ}}_{{\tilde{s}}_1}\right)\left({\mathit{\mu }}_j·{\mathit{ϵ}}_{{\tilde{i}}_1}\right)\left({\mathit{\mu }}_k·{\mathit{ϵ}}_{s_1}\right)\left({\mathit{\mu }}_l·{\mathit{ϵ}}_{i_1}\right)+\mathrm{h}.\mathrm{c}.,\hfill \end{array}$$ [7]

where the indices i, j, k, l run over the chromophores in the aggregate, $C=\sqrt{{\omega }_{c,s_1}{\omega }_{c,i_1}{\omega }_{c,{\tilde{s}}_1}{\omega }_{c,\tilde{i}1}}/{(4\pi ħ{\epsilon }_{0}cA)}^2$, and ${\mathcal{B}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)=〈B_{i,L}({\overline{t}}_1)B_{j,L}({\overline{t}}_2)B_{k,L}^{†}(t_1)B_{l,L}^{†}(t_2)〉$. In this equation and in the following, all multipoint expectation values are time ordered. ${\mathcal{B}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)$ thus describes contributions due to both ladder diagrams in Fig. 2A.

Note that due to the interferometric setup, contributions of other ladder diagrams with interactions both on the left and the right vanish identically in the integrand of Eq. 7. An expression of Eq. 7 derived from an effective action approach is given in SI Appendix.

As discussed earlier, the interferometry setup forces all exciton operators to act either on the left or on the right side of the density operator. In general, n field–matter interactions can generate 4ⁿ Liouville space pathways since each interaction can either annihilate or create a photon on the left or the right side of the density operator. In classical spectroscopy, Liouville pathway selectivity is obtained by phase matching, where pathways are selected depending on whether the interaction with each field involves either a or a^†. Here, different selections based on whether interactions happen on the left or right side of the density operator are possible. The quantum nature of light therefore introduces new control knobs for light–matter interactions and allows for a better isolation of matter pathways.

Note that in Eq. 7, the wave function ψ⁽²⁾ describing the entangled photons of PDC₂ appear to be stimulating the emission of the signal and idler photons of the sample. In reality, the entangled photons of PDC₂ never pass through the sample but are combined with the emitted signal and idler at the beam splitters and thus heterodyne them. Both viewpoints can be shown to be identical (34).

2. Rotational Averaging and Background Suppression

Eq. 7 describes the response of a single aggregate. However, in general, the sample consists of a large number N_s of randomly oriented molecular aggregates. The initial density matrix must therefore be replaced by N_s replicas, ${\tilde{\rho }}_M={|g⟩⟨g|}^{\otimes N_s}$, and the scalar products between the polarizations and the dipole moments should be averaged over all possible orientations. Additionally, the large number of molecules (in a region much larger than the optical wavelength) leads to phase-matching conditions that must be satisfied in order to obtain a measurable macroscopic signal.

The expectation value over the matter degrees of freedom will contain N_s² terms where the four-point correlation function ${\tilde{\mathcal{B}}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)$ factorizes into two two-point correlation functions (a product of linear responses) acting on different molecules and N_s irreducible four-point correlation functions (nonlinear response), where all operators act on the same molecule. Due to the different scaling with N_s, the nonlinear response of interest is given by a small correction on top of a huge background given by the products of linear responses as well as the signal from photons that did not interact with the sample (i.e., went straight from PDC₁ to the detectors). However, the different factorizations must be paired with their corresponding rotational averages over the dipole moments and will also possess unique phase-matching conditions. This allows to suppress the background contributions by either collecting the emitted signal and idler beams from the sample at certain orientations or by performing a polarization-dependent measurement. Fig. 2B sketches the phase-matching conditions and the polarization filtering.

The expectation value in Eq. 7 over the matter degrees of freedom combined with the rotational averaging gives

$$\begin{array}{cc}& {\mathcal{B}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2){〈\left({\mathit{\mu }}_i·{\mathit{ϵ}}_{{\tilde{s}}_1}\right)\left({\mathit{\mu }}_j·{\mathit{ϵ}}_{{\tilde{i}}_1}\right)\left({\mathit{\mu }}_k·{\mathit{ϵ}}_{s_1}\right)\left({\mathit{\mu }}_l·{\mathit{ϵ}}_{i_1}\right)〉}_{\mathrm{\Omega }}\hfill \\ \hfill & =(N_s^2{\mathcal{B}}_{i,k}^{(2)}({\overline{t}}_1,t_1){\mathcal{B}}_{j,l}^{(2)}({\overline{t}}_2,t_2){〈\left({\mathit{\mu }}_i·{\mathit{ϵ}}_{{\tilde{s}}_1}\right)\left({\mathit{\mu }}_k·{\mathit{ϵ}}_{s_1}\right)〉}_{\mathrm{\Omega }}\hfill \\ \hfill & \times {〈\left({\mathit{\mu }}_j·{\mathit{ϵ}}_{{\tilde{i}}_1}\right)\left({\mathit{\mu }}_l·{\mathit{ϵ}}_{i_1}\right)〉}_{\mathrm{\Omega }}+(k,s_1,t_1)\leftrightarrow (l,i_1,t_2))\hfill \\ \hfill & +N_s{\tilde{\mathcal{B}}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)\hfill \\ \hfill & \times {〈\left({\mathit{\mu }}_i·{\mathit{ϵ}}_{{\tilde{s}}_1}\right)\left({\mathit{\mu }}_j·{\mathit{ϵ}}_{{\tilde{i}}_1}\right)\left({\mathit{\mu }}_k·{\mathit{ϵ}}_{s_1}\right)\left({\mathit{\mu }}_l·{\mathit{ϵ}}_{i_1}\right)〉}_{\mathrm{\Omega }}.\hfill \end{array}$$ [8]

Here, ${\mathcal{B}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)$ denotes the four-point correlation function evaluated by the trace over the space of N_s molecules in the ground state, ${\tilde{\rho }}_M={|g⟩⟨g|}^{\otimes N_s}$, ⟨•⟩_Ω denotes rotational averaging, and ${\mathcal{B}}_{i,j}^{(2)}(t,t\prime )={〈B_{i,L}(t)B_{j,L}^{†}(t\prime )〉}_M$ with ⟨•⟩_M denoting the time-ordered trace over the single-molecule space ρ_M = |g⟩⟨g|. Note that (k, s₁, t₁)↔(l, i₁, t₂) denotes the same term as the previous under permutation of the three variables. We have further introduced the nonlinear response

$$\begin{array}{cc}\hfill {\tilde{\mathcal{B}}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)& ={〈B_{i,L}({\overline{t}}_1)B_{j,L}({\overline{t}}_2)B_{k,L}^{†}(t_1)B_{l,L}^{†}(t_2)〉}_M\hfill \\ \hfill & -{\mathcal{B}}_{i,k}^{(2)}({\overline{t}}_1,t_1){\mathcal{B}}_{j,l}^{(2)}({\overline{t}}_2,t_2)\hfill \\ \hfill & -{\mathcal{B}}_{i,l}^{(2)}({\overline{t}}_1,t_2){\mathcal{B}}_{j,k}^{(2)}({\overline{t}}_2,t_1).\hfill \end{array}$$ [9]

Note that the first two terms in Eq. 8 contain two independent rotational averages over two dipole moments, each, while the last term contains a single rotational average over a product of four dipole moments. Rotational averaging over two dipole moments results in ${〈\left({\mathit{\mu }}_i·{\mathit{ϵ}}_{{\tilde{s}}_1}\right)\left({\mathit{\mu }}_k·{\mathit{ϵ}}_{s_1}\right)〉}_{\mathrm{\Omega }}=\left({\mathit{\mu }}_i·{\mathit{\mu }}_k\right)\left({\mathit{ϵ}}_{{\tilde{s}}_1}·{\mathit{ϵ}}_{s_1}\right)$ (35). Therefore, choosing ${\mathit{ϵ}}_{{\tilde{s}}_1/{\tilde{i}}_1}$ to be perpendicular to ϵ_s1/i1 suppresses the background terms entirely [note that terms that mix signal and idler paths of the form $\left({\mathit{ϵ}}_{{\tilde{s}}_1}·{\mathit{ϵ}}_{i_1}\right)$ do not appear because of phase matching].

The rotational averaging of four dipole moments can be performed by applying basic considerations of representation theory on the group of three-dimensional rotations SO(3). It can be expressed in terms of three independent isotropic tensors resulting in three possible pairings of scalar products of the four vectors for both the polarization vectors and dipole moments,

$$\begin{array}{cc}& {〈\left({\mathit{\mu }}_i·{\mathit{ϵ}}_{{\tilde{s}}_1}\right)\left({\mathit{\mu }}_j·{\mathit{ϵ}}_{{\tilde{i}}_1}\right)\left({\mathit{\mu }}_k·{\mathit{ϵ}}_{s_1}\right)\left({\mathit{\mu }}_l·{\mathit{ϵ}}_{i_1}\right)〉}_{\mathrm{\Omega }}\hfill \\ \hfill & ={\mathcal{M}}_{\mathit{ijkl}}^{(1)}\left({\mathit{ϵ}}_{{\tilde{s}}_1}·{\mathit{ϵ}}_{{\tilde{i}}_1}\right)\left({\mathit{ϵ}}_{s_1}·{\mathit{ϵ}}_{i_1}\right)+{\mathcal{M}}_{\mathit{ijkl}}^{(2)}\left({\mathit{ϵ}}_{{\tilde{s}}_1}·{\mathit{ϵ}}_{s_1}\right)\hfill \\ \hfill & \times \left({\mathit{ϵ}}_{{\tilde{i}}_1}·{\mathit{ϵ}}_{i_1}\right)+{\mathcal{M}}_{\mathit{ijkl}}^{(3)}\left({\mathit{ϵ}}_{{\tilde{s}}_1}·{\mathit{ϵ}}_{i_1}\right)\left({\mathit{ϵ}}_{{\tilde{i}}_1}·{\mathit{ϵ}}_{s_1}\right),\hfill \end{array}$$ [10]

where ${\mathcal{M}}_{\mathit{ijkl}}^{(p)}=c_1^{(p)}({\mathit{\mu }}_i·{\mathit{\mu }}_j)({\mathit{\mu }}_k·{\mathit{\mu }}_l)+c_2^{(p)}({\mathit{\mu }}_i·{\mathit{\mu }}_k)({\mathit{\mu }}_j·{\mathit{\mu }}_l)+c_3^{(p)}({\mathit{\mu }}_i·{\mathit{\mu }}_l)({\mathit{\mu }}_k·{\mathit{\mu }}_j)$ is a linear combination of the three possible combinations of the dipole moments (35). Selecting ${\mathit{ϵ}}_{{\tilde{s}}_1/{\tilde{i}}_1}$ to be perpendicular to ϵ_s1/i1 therefore eliminates one of the combinations but still leaves the two other possibilities. If the two incoming polarizations are chosen to be in the same plane and the two outgoing ones in an orthogonal plane, only the first term in Eq. 10 survives.

In addition to this polarization filtering, phase matching may also be used to suppress the linear background. Here, we do not treat the phase matching explicitly but assume that a certain phase-matching direction has been selected by choosing the angles at which the signal is collected and sent to the detector. The linear response forces the incoming and outgoing beam directions to be equal. Therefore, both beams generated by the sample propagate in the same direction as the incoming signal and idler beams, i.e., ${\mathbf{k}}_{s_1}={\mathbf{k}}_{{\tilde{s}}_1}$ and ${\mathbf{k}}_{i_1}={\mathbf{k}}_{{\tilde{i}}_1}$, where k_i is the wave vector of the photon associated with pathway i at its respective central frequency. For the nonlinear response, the sum of outgoing wave vectors needs to be equal to the sum of the incoming wave vectors, ${\mathbf{k}}_{s_1}+{\mathbf{k}}_{i_1}={\mathbf{k}}_{{\tilde{s}}_1}+{\mathbf{k}}_{{\tilde{i}}_1}$, which allows for additional freedom in the combinations of outgoing directions than in the linear response. If we fix the central frequencies of the outgoing photons to be equal to their incoming counterparts, an obvious solution is the one equal to the linear response terms where signal and idler leave the sample in the same direction as they came in. Additional solutions are obtained by rotating the signal and idler around the direction k_s1 + k_i1. This means that the plane spanned by the outgoing propagation directions can be chosen perpendicular to the incoming propagation direction plane. It is therefore always possible to collect a signal for the nonlinear response in a background-free direction. The origin of the measured signal due to a fourth-order interaction can be further verified by studying its scaling with respect to the pump intensity used to generate the entangled photon pair. In this case, the signal should scale linearly with the pump intensity, in analogy to TPA with entangled photons.

3. The Two-Exciton Scattering Matrix

Having discussed how the nonlinear response may be separated from the linear background, we now turn to the calculation of the four-point correlation function ${\tilde{\mathcal{B}}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)$ in Eq. 9. The nonlinear response will be calculated using an exciton/quasiparticle picture (36, 37). In this approach, the chromophores are treated as interacting anharmonic oscillators, and the response is expressed in terms of single-exciton/quasiparticle Green’s functions and the scattering matrix describing their interaction. Here, the interference between noninteracting and interacting double-exciton transitions is built in from the start. The sum-over-state approach in contrast requires the diagonalization of H_M, and the resulting terms in the nonlinear response contain both noninteracting and interacting double-exciton contributions which cancel each other identically, i.e., a large number of terms are unnecessarily calculated.

For the Frenkel exciton model in Eq. 2 that conserves the number of excitations, with the exciton–exciton interaction diagonal in the chromophore basis set, the nonlinear response assumes the form

$$\begin{array}{cc}& {\tilde{\mathcal{B}}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)\hfill \\ \hfill & =-2{\displaystyle \sum _{\mathit{pq}}}{\displaystyle \sum _{\alpha ,\beta =L,R}}{(-1)}^{p(\alpha )+p(\beta )}\int {\int }_{-\infty }^{\infty }d{\tau }_{+}d{\tau }_{-}\hfill \\ \hfill & \times G_{iq,L\beta }({\overline{t}}_1-{\tau }_{+})G_{jq,L\beta }({\overline{t}}_2-{\tau }_{+}){\tilde{\mathrm{\Gamma }}}_{qp,\beta \alpha }({\tau }_{+}-{\tau }_{-})\hfill \\ \hfill & \times G_{pk,\alpha L}({\tau }_{-}-t_1)G_{pl,\alpha L}({\tau }_{-}-t_2),\hfill \end{array}$$ [11]

with the left/right parity defined as p(L)=0, p(R)=1, and $G_{jk,\alpha \beta }(t)=⟨B_{j,\alpha }(t)B_{k,\beta }^{†}(0)⟩$ (37). In our model, a chromophore is described by an anharmonic oscillator with a fourth-order anharmonicity g (Eq. 2) that conserves the number of excitations. Two-level chromophores are recovered in the g → ∞ limit. Since the number of excitations is conserved and the aggregate is initially in the ground state, the exact expression for the scattering matrix $\overline{\mathrm{\Gamma }}$ is given by a sum of ladder diagrams. The interaction term in Liouville space is given by $g\sum _n(B_{n,L}^{†}{B}_{n,L}^{†}{B}_{n,L}{B}_{n,L}-B_{n,R}^{†}{B}_{n,R}^{†}{B}_{n,R}{B}_{n,R})$. Since in a model with a conserved number of excitations, $⟨B_{j,L}(t)B_{k,R}^{†}(t\prime )⟩=0$, we can show by induction, starting with the right-most bare vertex in a ladder diagram, that only the left components of bare vertices contribute. Eq. 11 can be therefore recast in the form

$$\begin{array}{cc}& {\tilde{\mathcal{B}}}_{ij,kl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)=\hfill \\ \hfill & =-2{\displaystyle \sum _{\mathit{pq}}}\int {\int }_{-\infty }^{\infty }d{\tau }_{+}d{\tau }_{-}{G}_{\mathit{iq}}({\overline{t}}_1-{\tau }_{+})G_{\mathit{jq}}({\overline{t}}_2-{\tau }_{+})\hfill \\ \hfill & \times {\tilde{\mathrm{\Gamma }}}_{\mathit{qp}}({\tau }_{+}-{\tau }_{-})G_{\mathit{pk}}({\tau }_{-}-t_1)G_{\mathit{pl}}({\tau }_{-}-t_2),\hfill \end{array}$$ [12]

with $G_{\mathit{jk}}(t)=⟨B_{j,L}(t)B_{k,L}^{†}(0)⟩$. Summation of the ladder diagram results in the exciton scattering matrix ${\tilde{\mathrm{\Gamma }}}_{\mathit{mn}}(t)=\int \frac{d\omega }{2\pi }{e}^{-i\omega t}{\overline{\mathrm{\Gamma }}}_{\mathit{mn}}(\omega )$ with ${\overline{\mathrm{\Gamma }}}_{\mathit{mn}}(\omega )=g{({(I-g\overline{F}(\omega ))}^{-1})}_{\mathit{mn}}$ and ${\overline{F}}_{\mathit{mn}}(\omega )={\int }_0^{\infty }dt{e}^{i\omega t}{G}_{\mathit{mn}}(t)G_{\mathit{mn}}(t)=\int \frac{d\epsilon }{2\pi }{G}_{\mathit{mn}}(\epsilon )G_{\mathit{mn}}(\omega -\epsilon )$. The two-level chromophore case is obtained in the limit g → ∞, resulting in

$$\begin{array}{c}\hfill {\overline{\mathrm{\Gamma }}}_{\mathit{mn}}(\omega )=-{({\overline{F}}^{-1}(\omega ))}_{\mathit{mn}}.\end{array}$$ [13]

For simplicity, the effect of the environment is modeled by introducing a finite lifetime to the exciton states of the aggregate (inversely proportional to the number of excitations in the state). Note that Eq. 12 inherently includes the subtraction of single-exciton contributions given by the second and third terms in Eq. 9. This can be verified by the fact that the scattering matrix ${\overline{\mathrm{\Gamma }}}_{\mathit{mn}}(\omega )$ vanishes for g = 0 in Eq. 2. Only the linear background is present in this case since the sample does not possess any nonlinearity. In the sum over state approach, the ladder diagrams in Fig. 2A do not vanish for g = 0. The single-exciton contribution needs to be subtracted manually. For the Hamiltonian H_M in Eq. 2, doing so erases the second ladder diagram and gives a correction to the first. This subtraction must be carried out because of the four-point correlation function that is being measured here, which allows for a factorization of the signal discussed in Eq. 8. This is not the case for intensity measurements used in classical spectroscopy.

4. Application to the Reaction Center of Photosystem II

We now apply our results to the reaction center of photosystem II (PSII). Photosystem II is a large protein dimer complex responsible for photosynthetic light harvesting in many biological species, i.e., plants, bacteria, and other living organisms (38–40). Its reaction center core receives excitation energy from the sunlight-absorbing light-harvesting complex attached to it. This energy leads to charge separation (41) among the associated chlorophylls, and this separated charge is used for the oxidation of H₂O. The reaction center generates O₂ as a result of a complex—but well-understood—sequence of biochemical reactions. Considerable effort has been made in understanding the various biochemical reactions happening in this complex due to the high efficiency of various processes occurring on femtosecond time scales.

Various exciton models have been developed for understanding the spectroscopic experimental data of the PS II reaction center. We consider a simplified model of the reaction center, which includes six close-by chromophores. A further simplification is made by excluding charge transfer excited states. This makes it possible to describe the reaction center complex by the Hamiltonian in Eq. 2 in the g → ∞ limit which then has six single-exciton and fifteen two-exciton states.

We use the single-exciton Hamiltonian and the direction of transition dipole moments, extracted by modeling the experimental spectroscopic data in ref. 42. The rotationally averaged interferometric signal is computed by assuming that the two outgoing polarizations lay in a plane perpendicular to the plane of incoming polarizations. This selects the first term on the right-hand side of Eq. 10 and results in

$$\begin{array}{cc}& \mathcal{S}(\text{Δ}{\tau }_1,\text{Δ}{\tau }_2)\\ & ={\displaystyle \sum _{ijkl}}\int d{t}_{1}d{t}_{2}d{\overline{t}}_{1}d{\overline{t}}_2{\mathcal{M}}_{ijkl}^{(1)}{\tilde{\mathcal{B}}}_{ijkl}({\overline{t}}_1,{\overline{t}}_2;t_1,t_2)\\ & \times {\psi }^{(2)\ast }\left({\overline{t}}_1+\frac{\text{Δ}{\tau }_2}{2},{\overline{t}}_2-\frac{\text{Δ}{\tau }_2}{2}\right)\\ & \times {\psi }^{(1)}\left(t_1+\frac{\text{Δ}{\tau }_1}{2},t_2-\frac{\text{Δ}{\tau }_1}{2}\right).\end{array}$$ [14]

Here, we have introduced the controllable time delays Δτ_{1, 2} between the signal and idler originating from PDC_{1, 2}, respectively (Fig. 1). These are used to control the first and last interaction time intervals in the left ladder diagram in Fig. 2A. Using Eq. 12, the signal in the frequency domain is given by

$$\begin{array}{cc}\hfill \mathcal{S}& (\mathrm{\Delta }{\tau }_1,\mathrm{\Delta }{\tau }_2)={\displaystyle \sum _{\mathit{ijkl}}}{\mathcal{M}}_{\mathit{ijkl}}^{(1)}{\int }_{-\infty }^{+\infty }\frac{d{\omega }_3}{2\pi }\frac{d{\omega }_3}{2\pi }\frac{d{\omega }_2}{2\pi }\frac{d{\omega }_1}{2\pi }\hfill \\ \hfill & \sum _{\mathit{pq}}{G}_{\mathit{iq}}({\omega }_1+{\omega }_2-{\omega }_3)G_{\mathit{jq}}({\omega }_3){\overline{\mathrm{\Gamma }}}_{\mathit{qp}}({\omega }_1+{\omega }_2)\hfill \\ \hfill & \times G_{\mathit{pk}}({\omega }_2)G_{\mathit{pl}}({\omega }_1){\psi }^{(2)\ast }({\omega }_3,{\omega }_1+{\omega }_2-{\omega }_3){\psi }^{(1)}({\omega }_1,{\omega }_2)\hfill \\ \hfill & \times exp\left(i\frac{{\omega }_1-{\omega }_2}{2}\mathrm{\Delta }{\tau }_1-i\frac{2{\omega }_3-{\omega }_1-{\omega }_2}{2}\mathrm{\Delta }{\tau }_2\right).\hfill \end{array}$$ [15]

We assume the monochromatic pump used to generate the entangled photons and the two nonlinear crystals to be identical. The two-photon correlation function is then given by ${\psi }^{(1,2)}({\omega }_1,{\omega }_2)\propto \delta ({\omega }_1+{\omega }_2-{\mathrm{\Omega }}_p)\mathrm{sinc}(\frac{{\omega }_1-{\omega }_2}{2}{T}_e)$, where Ω_p is the monochromatic pump frequency and T_e is the entanglement time of the signal and idler photons. This approximation is justified as long as the spectral width of the pump field ΔΩ_p is much shorter than the dephasing times γ_fg of the two-exciton states, ΔΩ_p ≪ γ_fg. In this case, the first and last interaction-time interval is fixed by the delay Δτ_{1, 2}, respectively (Fig. 2A). The uncertainties in these time intervals are given by the entanglement time T_e. The intermediate interaction-time interval which is spent in the |f⟩⟨g| coherence is integrated over a time interval given by the temporal width of the pump field.

The spectral information content of the system correlation function is displayed by Fourier transformation with respect to the two time delays and for a fixed pump frequency,

$$\begin{array}{cc}& \mathcal{S}({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2)\hfill \\ \hfill & ={\int }_0^{\infty }d\mathrm{\Delta }{\tau }_{1}d\mathrm{\Delta }{\tau }_{2}exp\left(i{\mathrm{\Omega }}_1\mathrm{\Delta }{\tau }_1+i{\mathrm{\Omega }}_2\mathrm{\Delta }{\tau }_2\right)S(\mathrm{\Delta }{\tau }_1,\mathrm{\Delta }{\tau }_2).\hfill \end{array}$$ [16]

The spectra are plotted versus Ω₁ + Ω_p/2 and Ω₂ + Ω_p/2. From Eq. 12, it is clear that Ω_p selects a particular two-exciton resonance of the scattering matrix. The Ω_1/2 axes provide information about the single excitation coherence evolution during the two time delays between the first two and last two interactions represented in the Liouville space pathway shown in Fig. 2A.

The first two columns in Fig. 3 show the absolute value of the signal |𝒮(Ω₁, Ω_p, Ω₂)| for two pump frequencies Ω_p and two entanglement times T_e. The horizontal and vertical axes of the 2D spectra mark the single-exciton energies, corresponding to the Liouville space pathways |g⟩⟨g|→|e⟩⟨g|→|f⟩⟨g|→|e′⟩⟨g|→|g⟩⟨g| illustrated by the left ladder diagram in Fig. 2A. The energy levels of the photosystem II reaction center are shown in Fig. 4B. Eq. 15 shows that the pump frequency Ω_p can be used to select specific f-states. The horizontal axis then gives the energy difference E_e − E_g, and the vertical axis gives E_e′ − E_g. Evidently, the 2D spectra have both diagonal and off-diagonal peaks depending on the possible excitation pathways through the single-exciton manifold leading to the two-exciton state selected by the pump frequency Ω_p. The diagonal contributions arise from the Liouville space pathways with e′=e. They provide information about which single-exciton states are coupled to the selected two-exciton state. The off-diagonal peaks arise from pathways with e′≠e and provide information about the coherence between different excitation pathways. The reasons for the absence or presence of the diagonal and off-diagonal peaks are subtle. They either arise due to interference effects induced by entanglement of the two-exciton eigenstates (43) or can be suppressed by rotational averaging because of the orientation of the transition dipole moments. Further, the spectral range of the spectra decreases with increasing entanglement time. This is because, for the continuous pump limit considered here, the individual spectral ranges of signal and idler are centered around $\frac{{\mathrm{\Omega }}_p}{2}$ with a bandwidth of approximately $\frac{2\pi }{T_e}$. Hence, as T_e is increased, only certain excitation pathways contribute to the signal, and other resonances are suppressed.

Fig. 3.

Absolute value of the (normalized) signal |𝒮(Ω₁, Ω_p, Ω₂)| (Eq. 16) for two pump frequencies (Top and Bottom rows). The first two columns show the signal for entangled photons for two different entanglement times T_e = 10 f_s (Left column) and T_e = 100 f_s (Center column). The Right column depicts the respective absolute value of the signal obtained by classical double-quantum-coherence spectroscopy. The classical spectra show additional resonances due to the ladder diagram in Fig. 5 present in the classical spectroscopy. These resonances may be different single-exciton resonances. For visual clarity, a grid is drawn to indicate the single-exciton energies.

Fig. 4.

(A) The photosystem II reaction center complex consists of six chlorophylls and is described by the Frenkel exciton model. (B) Energy levels of the photosystem II reaction center with 6 single-exciton eigenstates and 15 two-exciton eigenstates.

Finally, we note that in double-quantum-coherence spectroscopy (DQC), both using classical light and quantum light, phase matching selects two ladder diagrams which contribute to the 2D spectra (44, 45). These are shown in Fig. 5. The first diagram is the same as in Fig. 2A. The last column in Fig. 3 shows the spectra obtained from classical DQC spectroscopy after a Fourier transform of the intermediate time interval has been performed and the respective two-exciton resonance has been selected. Note that, here, data have to be collected over three time intervals using ultrashort pulses, while the spectra with entangled photons only require scanning over two time intervals. The second diagram in Fig. 5 can either add or suppress the peaks of the first diagram which is isolated by the interferometer in Fig. 1. Additional resonances at ω_fe = (E_f − E_e)/ℏ appear along the Ω₂ axis that do not lie on the single-exciton energy grid and leads to an asymmetric spectrum with respect to switching Ω₁ and Ω₂. The additional resonances and cancellation effects lead to more congested spectra that are harder to interpret. Hence, comparing and contrasting the 2D spectra obtained by phase matching in DQC spectroscopy and those using the coincidence measurement proposed in the current work can help understand the detailed structure of two exciton states in molecular aggregates.

Fig. 5.

Additional ladder diagram which appears in the double quantum coherence signal of classical spectroscopy. These diagrams can be selected using phase matching and pulse shaping with the use of coherent pulses.

Entangled photons with an entanglement time of T_e <  20 fs can be generated in a periodically poled lithium tantalate crystal (13). Another possibility is given by β − BaB₂O₂ (BBO) crystals with type-II phase matching. Numerical simulations show that an entanglement time of T_e = 10 fs (T_e = 100 fs) could be achieved for a crystal length of L ≈ 50 μm (L ≈ 500 μm), respectively (46). This estimate holds for a slightly lower pump frequency of Ω_p = 3.05 eV, but similar crystal lengths for the pump frequencies used in this work are expected.

5. Conclusions

We have demonstrated how an entangled photon pair combined with a nonlinear interferometer can be used to monitor quasiparticle scattering processes in chromophore aggregates in real time. All interactions with the matter density operator take place either on the left (ket) or the right (bra) side, and the signal may thus be understood as a two-photon analogue of a heterodyne measurement, where the two-photon wave function of one crystal heterodynes the two-photon wave function of the other crystal after it is scattered off the sample. This pathway selectivity of the left/right superoperators is achieved by the nonlinear interferometer and cannot be mimicked by classical phase-matching schemes.

The proposed signal involves a four-point correlation function of the electric fields. The fourth-order correction in terms of the dipole operators possesses both a nonlinear contribution and a factorized linear contribution, given by the product of two independent linear processes for both signal and idler. We have shown how for macroscopic samples consisting of large numbers of molecules, which is typically the case for samples used in spectroscopy, the linear background can be suppressed by using either phase matching or polarization filtering. Isolating the nonlinear response means that in contrast to TPA with entangled photons, there is no ambiguity about the origin of the measured signal. The cross-section of our signal should be similar to the TPA cross-section with entangled photons and could thus be used to settle the current debate about the discrepancy in reported cross-sections of fourth-order processes with entangled photons.

The antifrequency correlation between signal and idler may be used to overcome the time/frequency Fourier limit. It is possible to obtain good spectral resolution of the two-exciton scattering matrix according to the spectral width of the pump field, while maintaining good temporal resolution in the single-exciton Green’s function according to the entanglement time set by the nonlinear crystal. The pump field frequency can select a single two-exciton state while the delay lines can be used to scan the single-exciton manifold. These control knobs give information about the two-exciton pathways as well as the coupling between excitons. We have used this signal to study the response of the photosystem II reaction center without charge transfer. Note that the same signal may also be obtained with only one crystal combined with a Franson interferometer (47), by placing the sample into the long pathways of both signal and idler.

Interferometry enables greater control over the Liouville space pathways. Reducing the number of contributing pathways leads to cleaner, less congested signals, which are easier to interpret. Here, we have shown how to isolate quasiparticle scattering processes and resolve them in real time. Other interferometric techniques could enable the isolation of transport processes with joint time–frequency resolution. The current theoretical study is based on an effective field Hamiltonian which describes the propagation along the interferometric arms, together with an effective wave function for the entangled photons. A more general description of the evolution of the field operators is given in terms of single-photon Green’s functions and an effective action describing the generation of the entangled photons. Such a theoretical framework would allow us to discuss spatial aspects of the interaction including effects due to focusing and a precise estimation of the nonlinear interaction cross-section.

6. Materials and Methods

Below, we introduce a simple quantum model that helps the interpretation of the interferometric signals. We consider the case when the signal and idler photons are distinguishable. To that end, we introduce four directed graphs (signal and idler each have two graphs depending on which crystal they originate from), representing the pathways of the signal and idler photons. The vertices describe sources (outgoing arrows), sinks (incoming arrows), and beam splitters (two incoming, two outgoing arrows), and the edges describe free evolution of the respective photon wave packets. With each edge α, we associate an open interval I_α = (x_{α, L}′,x_{α, R}′), with [x_{α, L}, x_{α, R}]⊂(x_{α, L}′,x_{α, R}′), with |x_{α, L} − x_{α, L}′|, |x_{α, R}′−x_{α, R}|≪|x_{α, R} − x_{α, L}| and |x_{α, R} − x_{α, L}| being the length of the optical path between the components, represented by the vertices α_L and α_R. With each edge, we associate a family of photon creation/annihilation operators $a_{\alpha }^{†}(x)$ and a_α(x), where x ∈ I_α, with the commutation relations $[a_{\alpha }(x),a_{\beta }^{†}(x\prime )]={\delta }_{\alpha \beta }\delta (x-x\prime )$. The one-particle Hamiltonian of the effective quasi-one-dimensional photon system is given by

$$\begin{array}{cc}\hfill H_0& =-i{\displaystyle \sum _{\alpha }}{\int }_{I_{\alpha }}dx{a}_{\alpha }^{†}(x)\frac{d}{\mathit{dx}}{a}_{\alpha }(x)+{\displaystyle \sum _{a\in {\tilde{\mathrm{\Gamma }}}_1}}{H}_a^{(0)},\hfill \end{array}$$ [17]

$$\begin{array}{cc}\hfill H_a^{(0)}& ={\displaystyle \sum _{\alpha }^{{\alpha }_R=a}}{\displaystyle \sum _{\beta }^{{\alpha }_L=a}}{S}_{a,\beta \alpha }{a}_{\beta }^{†}(x_{\beta ,L})a_{\alpha }(x_{\alpha ,R})+\mathrm{h}.\mathrm{c}.,\hfill \end{array}$$ [18]

where ${\tilde{\mathrm{\Gamma }}}_1$ is the subset of the graph vertices that represent the splitters, with S_a being the scattering matrix of a splitter, represented by the vertex a.

The total Hamiltonian of the matter-field system has the form

$$\begin{array}{c}\hfill H(t)=H_0+H_M+H_{\mathit{int}},\end{array}$$ [19]

with H_M and H_int being the system under study and the system–field interaction Hamiltonians, respectively. It is important to observe that both H_M and H_int involve the photon operator values at the sources and sinks so that one can associate the annihilation and creation operators a_b and $a_b^{†}$, associated with sources $a\in {\mathrm{\Gamma }}_1^L$ and sinks $a\in {\mathrm{\Gamma }}_1^R$.

Since our graph does not have directed loops, and due to the simple nature of the Hamiltonian H₀, one can easily derive an explicit expression for the interaction-picture sink operators $\tilde{a}(t)$ in terms of the source counterparts; that is, for a sink $j\in {\mathrm{\Gamma }}_1^R$, we have

$$\begin{array}{c}\hfill {\tilde{a}}_j(t)={\displaystyle \sum _{k\in {\mathrm{\Gamma }}_1^L}}{\displaystyle \sum _{\gamma \in h(k,j)}}S(\gamma ){\tilde{a}}_k(t-l(\gamma )),\end{array}$$ [20]

where h(k, j) is the set of all (directed) paths that start at source k and end at sink j, and l(γ) is the total optical length of path γ, while S(γ) is the product of the proper elements of the scattering matrices over the intermediate (splitter) vertices on path γ. Using this result, the annihilation operators $\mathbf{b}={\left({\tilde{a}}_{D_1,R}(t),{\tilde{a}}_{D_2,R}(t)\right)}^T$ at the detectors D_{(1, 2)} are given by

$$\begin{array}{c}\hfill \mathbf{b}=\mathbf{c}+U\mathbf{d},\end{array}$$ [21]

with $\mathbf{c}={\left({\tilde{a}}_{D_1,L}(t-{\tau }_D),{\tilde{a}}_{D_2,L}(t-{\tau }_D)\right)}^T$, $U=\frac{1}{\sqrt{2}}\left(\genfrac{}{}{0pt}{}{1i}{i1}\right)$, and $\mathbf{d}={\left({\tilde{a}}_{s_2,L}(t-{\tau }_{s_2}-{\tau }_D),{\tilde{a}}_{{\tilde{s}}_1,L}(t-{\tau }_{{\tilde{s}}_1}-{\tau }_D)\right)}^T$. The annihilation operators for the other two operators are obtained analogously by changing D₁ → D₃ and D₂ → D₄ in the definition of b and c, and s → i in the definition of d. We assumed a balanced 50 : 50 beam splitter, and τ_i describes the optical path length of the respective path. Here, the L/R indices are not to be confused with the Liouville superoperator indices but indicate whether the operator describes annihilation at the source/sink of the path, respectively. Note that we assume that the path lengths between the two beam splitters and the four detectors τ_D are all equal.

This model can now be used to calculate the signal

$$\begin{array}{cc}\hfill \mathcal{S}& =\int {\int }_{-\infty }^{\infty }d{t}_{s}d{t}_i⟨({\tilde{a}}_{D_1,R}^{†}(t_s){\tilde{a}}_{D_1,R}(t_s)-{\tilde{a}}_{D_2,R}^{†}(t_s){\tilde{a}}_{D_2,R}(t_s))\hfill \\ \hfill & \times ({\tilde{a}}_{D_4,R}^{†}(t_i){\tilde{a}}_{D_4,R}(t_i)-{\tilde{a}}_{D_3,R}^{†}(t_i){\tilde{a}}_{D_3,R}(t_i))⟩,\hfill \end{array}$$ [22]

which leads to Eq. 3. Here, we have ignored the first term in Eq. 21 since photons are only generated at the crystal or the sample. Terms containing the product of annihilation operators where one is associated with the output form the sample (indices ${\tilde{s}}_1,{\tilde{i}}_1$) while the other is associated with PDC₂ (indeces s₂, i₂) can also be neglected since either photons are generated together in the paths s₁, i₁ (and converted by the sample to paths ${\tilde{s}}_1,{\tilde{i}}_1$) or the paths s₂, i₂. Mixed populations between these paths never occur.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

There are no data underlying this work.